Journal of Electromagnetic Analysis and Applications
Vol. 1 No. 4 (2009) , Article ID: 1112 , 9 pages DOI:10.4236/jemaa.2009.14031
Power Network Asymmetrical Faults Analysis Using Instantaneous Symmetrical Components
![]()
Department of Energy, Politecnico di Milano, Via La Masa, Milano, Italy.
Email: sonia.leva@polimi.it
Received October 9th, 2009; revised November 3rd, 2009; accepted November 10th, 2009.
Keywords: Power System Fault Analysis, Asymmetrical Faults, Symmetrical Components, Lyon Transformation
ABSTRACT
Although the application of Symmetrical Components to time-dependent variables was introduced by Lyon in 1954, for many years its application was essentially restricted to electric machines. Recently, thanks to its advantages, the Lyon transformation is also applied to power network calculation. In this paper, time-dependent symmetrical components are used to study the dynamic analysis of asymmetrical faults in a power system. The Lyon approach allows the calculation of the maximum values of overvoltages and overcurrents under transient conditions and to study network under non-sinusoidal conditions. Finally, some examples with longitudinal asymmetrical faults are illustrated.
1. Introduction
The general Fortescue Symmetrical Components Transformation (SCT) [1,2] is formalized in phasor terms. It can only be used to study steady-state conditions that follow the fault transient condition. The maximum values of overvoltages and overcurrents can only be calculated in an approximate way by means of corrective factors [3].
Recently, the space-vector transformation – used in machine vector control – has been applied to power system analysis, too [4,5]. Currently, network theory and complex transformation suggest that the study of asymmetrical faults can be carried out by means of instantaneous sequence components [6–9].
As a matter of fact, by using the same topological approach of the SCT, it is possible to directly analyze the faulty network by differential equations that represent the faults not only in steady-state conditions but also under transient conditions.
As shown by W. Lyon [10,11], the formal aspects of the procedure can be summarized by the following points:
1) the phasors that represent phaseand sequencevariables, are substituted by time-dependent functions, so that the concept of Fortescue sequences can be generalized to the concept of instantaneous sequences;
2) the Fortescue matrix 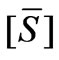 remains the same, and hence the method confirms the SCT topological and modal-analysis approach [11,12];
remains the same, and hence the method confirms the SCT topological and modal-analysis approach [11,12];
3) the phasor operator jw is replaced by the derivative operator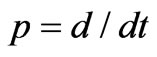 . Under this assumption, differential analysis is required and depends on the Cauchy initial conditions; and 4) the sequence impedances are converted form
. Under this assumption, differential analysis is required and depends on the Cauchy initial conditions; and 4) the sequence impedances are converted form 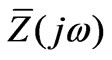 to generalized form z(p), maintaining the same circuital and topological meaning.
to generalized form z(p), maintaining the same circuital and topological meaning.
This time-domain analysis is characterized by three fundamental features. The first is an applicative one, which regards the ability to calculate - without the use of corrective coefficients – the maximum values of overvoltages and overcurrents during the transient conditions. This is very important for circuit-breaker sizing and the evaluation of the electro-dynamic force between busbars and in transformer windings. The second characteristic concerns the possibility of studying not only sinusoidal, but also non sinusoidal sources. The last characteristic regards the formal and methodological aspects introduced by using the Lyon approach. By means of the Lyon approach, the procedures of dynamic analysis of the network can be unified. In addition, by substituting the SCT with the Lyon approach, fault analysis can be carried out by using the state equations that can be integrated by classic procedures based on system analysis and the graph approach. The state-equation solutions, can be expressed in literal form by means of analytical formulations if the network is linear and time-invariant.
The relations between real and complex transformations, steady-state phasors and well-known sequence networks are given and illustrated through the use of an example with an asymmetrical fault in [6]. The use of dynamic phasors together with space-vectors – incorporating the frequency information – in power system analysis is presented in [7] and [8]. To complete these studies in the following, a systematic analysis of the asymmetrical faults is developed and deeper investigated both from the theoretical and applicative points of view, giving some important observations that are very useful to achieve the numerical analysis and to better understand the results obtained by using industrial software packages.
The Lyon approach to study transient and steady-state conditions of transversal and longitudinal faults is developed in terms of the following scheme: in Section 2, the Lyon Transformation is recalled and its link with SCT is investigated. In Section 3, the application of the Lyon method to the study of asymmetric transversal and longitudinal faults is formalized and some remarks concerning the connection conditions and the use of state-equation approach are put in evidence; furthermore the equivalent model of each fault is calculated. Finally, in Section 4, some numerical examples emphasize the validity of the proposed approach by comparing the obtained results with those derived by the SCT method.
2. The Lyon Transformation
Considering an arbitrary time function three-phase set {wa(t), wb(t), wc(t)}, the Lyon transformation gives the following decomposition (where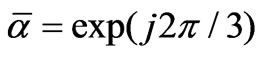 ):
):
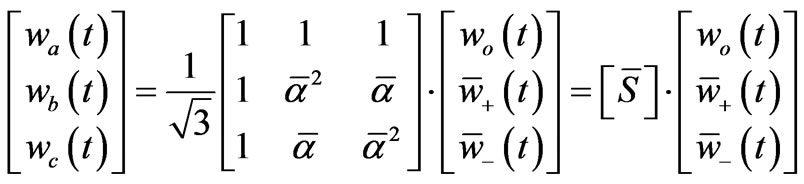 (1)
(1)
from which it is possible to observe that the matrix 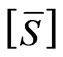 is formally the same for both SCT and Lyon transformation. On the other hand, the functions subjected to the Lyon Transformation assume a generic time trend.
is formally the same for both SCT and Lyon transformation. On the other hand, the functions subjected to the Lyon Transformation assume a generic time trend.
Taking into account that
then:
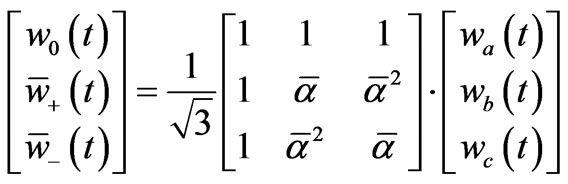 (2)
(2)
Therefore, it is possible to define, starting from a generic three-phase set in time domain, the instantaneous symmetric components named, respectively.
zero-, positive-, and negative-sequences. The zerosequence component  is always real. The negative-sequence component
is always real. The negative-sequence component 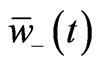 is the complex conjugate of the positive sequence component
is the complex conjugate of the positive sequence component .
.
Analyzing Equations (1) and (2) we can see that the Lyon method suggests, time by time and referring to a generic waveform in time domain, the same topological procedures just used with SCT. Moreover, the Lyon transformation, applied to a generic sinusoidal three-phase set, gives the same results provided by the SCT.
Furthermore, the positive Lyon vector satisfies the following identity:
 (3)
(3)
and hence it is linked to both Clarke 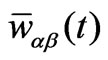 and Park
and Park 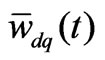 vectors, except for a trivial proportionality factor.
vectors, except for a trivial proportionality factor.
The Lyon transformation, in the context of the modal analysis procedure of the actual three-phase theory, unifies all transformations normally used for dynamic analysis of power networks. In particular – as  – the real and complex pair of time functions
– the real and complex pair of time functions 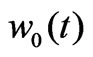 and
and 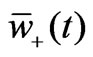 is totally representative of the generic three-phase set of real time functions {wa(t), wb(t), wc(t)}.
is totally representative of the generic three-phase set of real time functions {wa(t), wb(t), wc(t)}.
The instantaneous power, in terms of the Lyon component, is [13]:
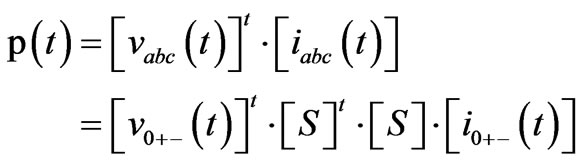 (4)
(4)
3. Lyon Approach to the Study of Asymmetrical Faults
Lyon decomposition in instantaneous sequence components allows the use of the SCT topological procedures for studying asymmetrical faults that can occur in a power network, by using the Substitution Theorem and the Superposition Principle as in SCT [12-14].
Some fundamental remarks about the application to the fault analysis of the Lyon method rather than the SCT are discussed in the following sections.
3.1 Fault Equivalent Networks
In aggreement with Fortescue SCT, the instantaneous sequence networks connection corresponding to the analysed fault configuration starting from the phase circult fault conditions calculation is necessary.
The Lyon transformed fault conditions show how to handle both realand complextime functions, while this is not possible using Fortescue analysis. Consequently, it is important to verify that the connection conditions obtained starting from the real conditions are coherent with respect to the definition of an instantaneous sequence components given by (2).
As an example, in the case of a single-phase-to-ground fault, the following relationa are obtained:
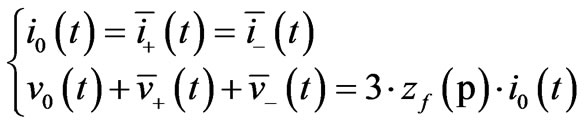 (5)
(5)
where zf (p) is the fault impedance. The first line of (5) shows that the two current Lyon vectors, which are conjugates, have to be real in order to obtain the zero-sequence current. Moreover, from the second line of (5):
 (6)
(6)
Equation (6) confirms that v0(t) is a real time function, too. Similar observations can be applied to the other fault conditions.
The equivalent sequence networks for each fault type are reported in Table 1. Examination of Table 1 reveals that the instantaneous sequence networks connections for the different fault types are equal to that obtained by using Fortescue SCT. This is in agreement with the fact that the Lyon and Fortescue transformations use the same transformation matrix . In the time-differential domain it is possible to use the same phasor expression only by substituting the
. In the time-differential domain it is possible to use the same phasor expression only by substituting the 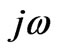 factor with the p operator. The complex impedance
factor with the p operator. The complex impedance 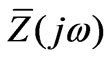 becomes the real impedance
becomes the real impedance  [15]. Nevertheless, the Lyon transformation is of greater generality than the Fortescue transformaation: Lyon acts on the time domain, not only in the phasor domain. The SCT can be considered as a particular case of the more general instantaneous sequence components approach.
[15]. Nevertheless, the Lyon transformation is of greater generality than the Fortescue transformaation: Lyon acts on the time domain, not only in the phasor domain. The SCT can be considered as a particular case of the more general instantaneous sequence components approach.
The results shown in Table 1 and the listed remarks complete the study presented in [6] and [8] analyzing in a systematic way all the asymmetrical faults and presenting the equivalent models of the faults.
Furthermore, Table 1 data together with the aforementioned remarks are very important not only from the theoretical point of view, but, as a matter of fact, these results can be very useful also to the power system analyst to verify the results obtained by using industrial software packages.
3.2 The State-Matrix Approach
The Lyon dynamic analysis of asymmetrical faults can be performed by using the state-matrix approach. It is divided into three distinct stages. In the first step the power system is represented by the appropriate equivalent sequence networks. The corresponding Lyon state variables (voltages across the capacitors and current flowing in the inductors) are deduced and collected in the Lyon state-vector [x].
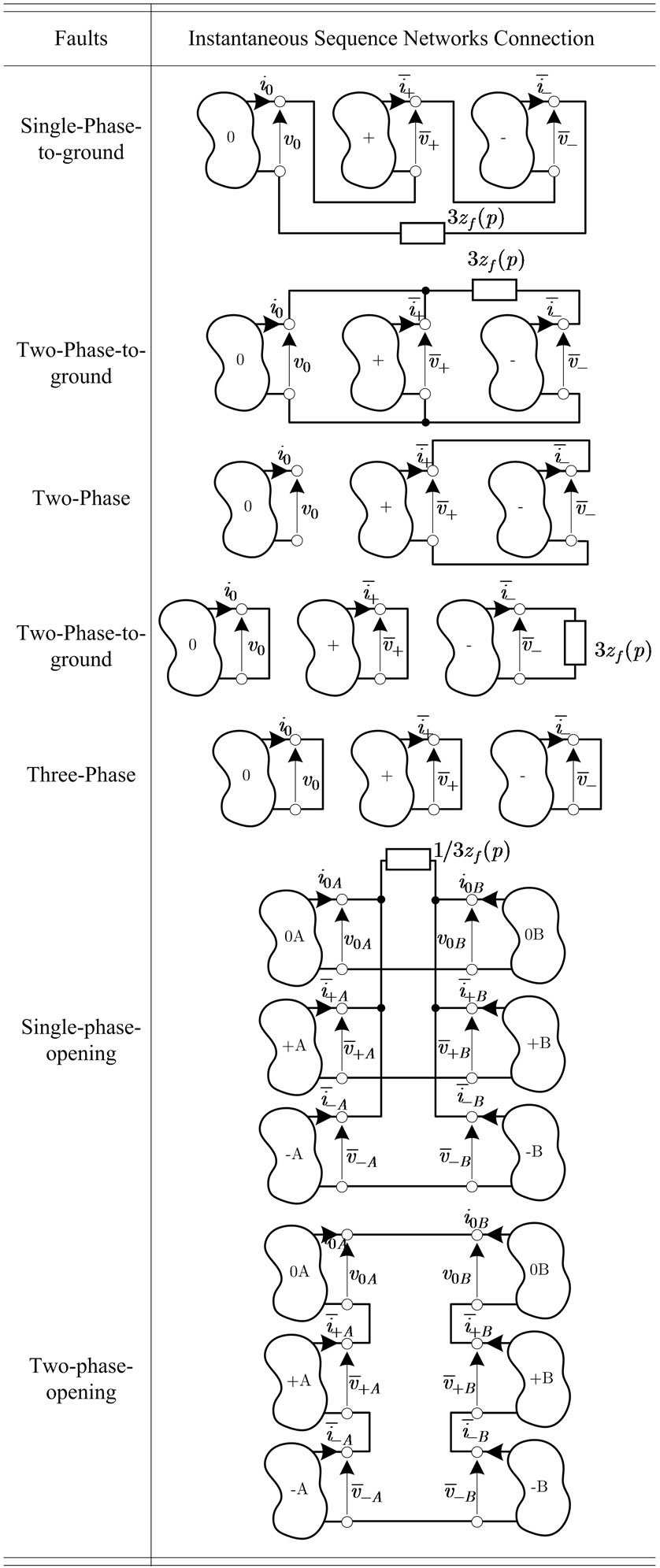
Table 1. Instantaneous sequence networks connection
In the second step, by means of the system and topological procedures of network theory [14], the mathematical model of the dynamics of the fault is deduced. Assuming the constitutive relations linear and timeinvariant, it is a priori formalized as:
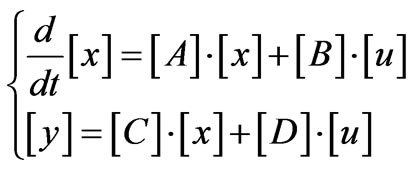 (7)
(7)
where the input [u(t)] and the network variables [y(t)] Lyon vectors are present. The [y(t)] vector can be regarded as the output of the system.
The solution of (7) is well-known and can be obtained in closed form. In fact, knowing the initial values of state variables (at time t=t0), it is possible to assume the following expression [14-16]:
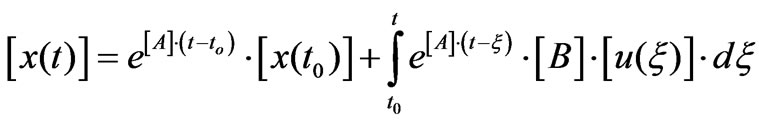 (8)
(8)
where the first term represents the solution with zero inputs and the second term represents the zero state solution. This last term is calculated considering the general sources [u(t)] expressed in the time domain. In the particular case of sinusoidal inputs, it corresponds to the results also obtained in the phasor domain with SCT when the transient is finished.
The dynamics of the fault depends on the state fault matrix [A], and its elements depend on the sequence parameters related to the type of fault that occurs in the considered power network, and on the initial conditions [x(t0)] analyzed in the following paragraph. The eigenvalues of the fault matrix [A] depend on the type of fault and characterize the dynamic of the power system during the fault.
Finally, in the third stage of the study, the network variables [y(t)] are calculated from the second line of (7). The network variables are usually Lyon voltages [v(t)] and currents [i(t)] expressed in the time domain. Equation (1) allows the derivation of the fault dynamics expressed in phase quantities.
Regarding the role of initial conditions, the zero-state network represents the simpler case for a dynamic analysis. In fact, in this case, the inductances and the capacitances are in zero-state conditions.
If the fault occurs in a non-zero state network, the state variables assume a non-zero initial state [x(t0)]=[x0]; in this case, the voltage vC(t) across a capacitor C and the current iL(t) flowing in an inductor L result to be:
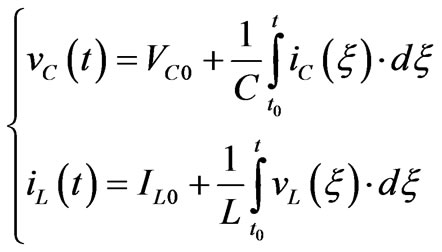 (9)
(9)
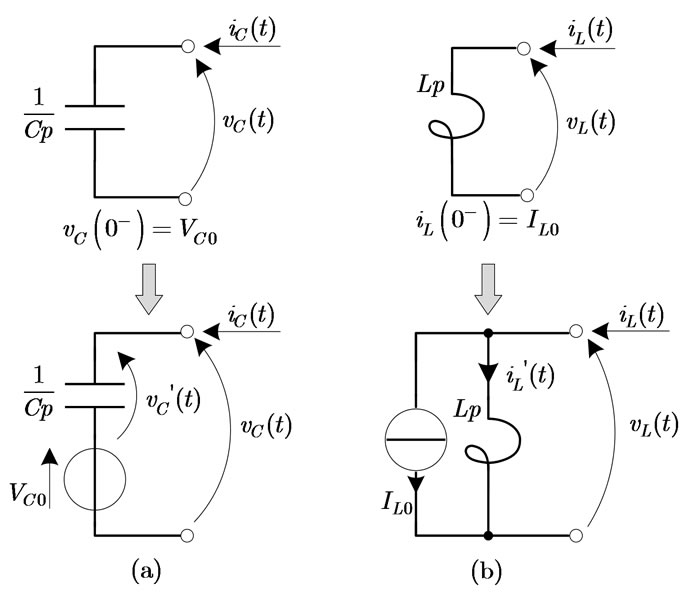
Figure 1. Method that can be used to include the initial condition of the state variables in the proposed approach; case of the capacitance (a) and of the inductance (b). It is represented in the general case, and it is valid for all the instantaneous sequence (+, − and 0)
The reactive elements can be considered in the dynamic analysis with an initial zero state condition simply by linking them with a generator that represents the initial conditions (see Figure 1).
In this way, the capacitor must be connected in series with a voltage generator (equal to VC0) and the inductor must be connected in parallel with a current generator (equal to IL0). The new state variables are represented by the voltage  across the capacitor C and the current
across the capacitor C and the current 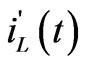 flowing in the inductor L, respectively.
flowing in the inductor L, respectively.
Equation (8) becomes:
 (10)
(10)
where [A’], [B’] and [u’(t)] are calculated considering the new network.
This method is particularly important and useful in the analysis of power networks where some inductances (capacitors) are connected in series (in parallel) with different initial conditions.
4. Applicative Case
The Lyon approach to studying power system faults presented in this paper is now applied to investigate the current fault in two different power systems. The first power system is represented by a classic three-phase line considered by other Author [15]. This example can be considered to validate the Lyon method. The second example regards the fault analysis in a real network used in Italy.
4.1 Transient Fault Analysis of a Basic Power System
The network shown in Figure 2 is composed of a generator A, a transformer T2 to elevate the voltage, a threephase line L, and a transformer T1. The system has no load when the fault occurs. No information about the grounding connection of the neutral conductor of the generator and transformers is reported in [15], consequently only the three-phase and two-phase faults are analyzed because they are independent to the grounding connection.
The corresponding positiveand negativeinstantaneous sequence networks are reported in Figure 3; the quantities indicated are deducted from the data reported in Figure 2 [5]. The analysis of the previously indicated fault types does not require the zero-sequence instantaneous network.
The Lyon quantities ,
, 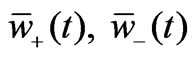 are be expressed as follows:
are be expressed as follows:
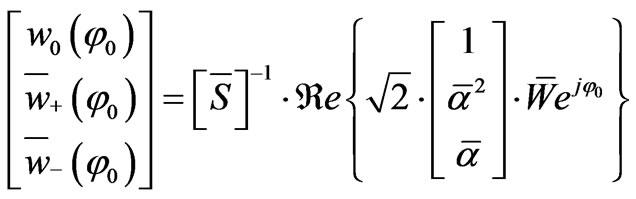 (11)
(11)
where 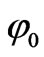 represents the a phase angle (respect to the real axis) in which the fault occurs.
represents the a phase angle (respect to the real axis) in which the fault occurs.
The corresponding state equations are:
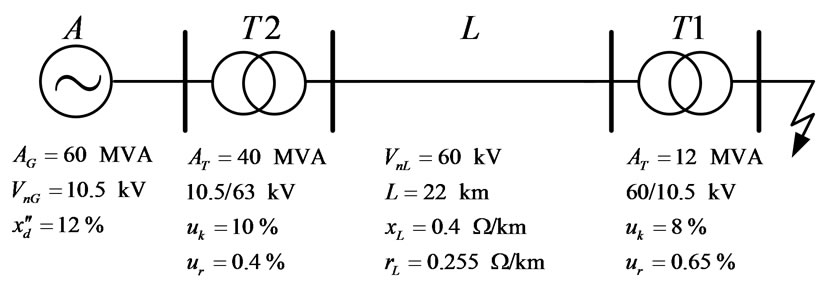
Figure 2. Power system under analysis
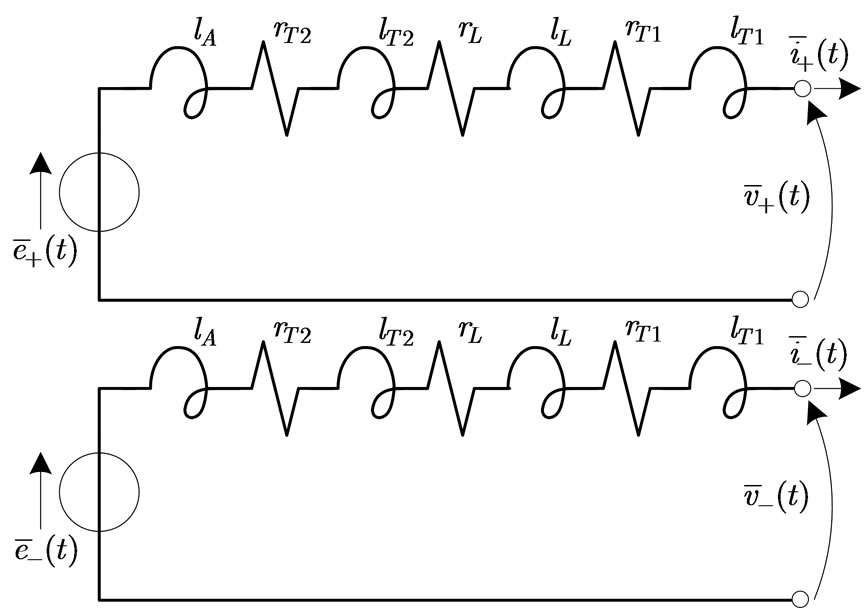
Figure 3. Positiveand negativeinstantaneous sequence net
works for the analysis of three-phase and two-phase faults
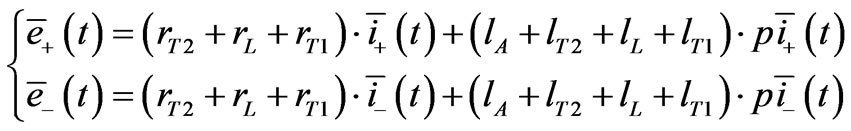 (12)
(12)
where r and l are the pu resistances and impedances respectively.
The line phase currents calculated during the fault are shown in Figure 4. Figure 4 shows the transient movement considering φ0=0 and φ0=π/4 respectively, where φ0 represents the phase angle a in the fault instant.
The steady state (sinusoidal condition) values match those calculated by using STC. The maximum value in the steady state condition of the phase fault currents is equal to 0.5208 pu. Under transient conditions the phase currents calculated by using Lyon or STC are instead different. The maximum value reached by the currents during the entire transient depends on φ0. In fact, during the first period of the transient with φ0 = 0, two phase currents reach the value of 0.8 pu, while with φ0 = π/4 the phase b reaches 0.83 pu.
In Figure 5, the vector  is depicted in the complex plane. By using a complex vector and its polar representation the vector magnitude can easily be depicted [5]. The initial magnitudes correspond to the initial condition equal to zero. During the first fault transient instant the current reaches its instantaneous maximum value. At the end of the transient, under steady-state and symmetric condition, the current
is depicted in the complex plane. By using a complex vector and its polar representation the vector magnitude can easily be depicted [5]. The initial magnitudes correspond to the initial condition equal to zero. During the first fault transient instant the current reaches its instantaneous maximum value. At the end of the transient, under steady-state and symmetric condition, the current  describe a perfect circle.
describe a perfect circle.
 (13)
(13)
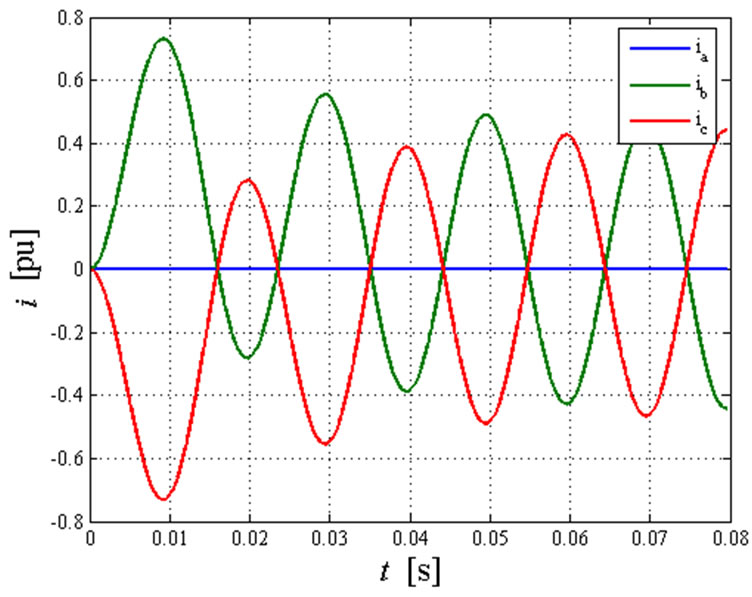
Figure 6 shows the line phase currents during the entire transient fault calculated with 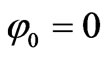 and
and 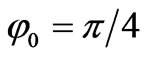 respectively. The maximum value of the currents at the end of the transient (sinusoidal steady-state condition) is 0.451 pu equal to that calculated by using SCT.
respectively. The maximum value of the currents at the end of the transient (sinusoidal steady-state condition) is 0.451 pu equal to that calculated by using SCT.
Whit φ0 = 0, the b and c phase fault currents reach, during the first period, a maximum value equal to 0.7317 pu. With φ0 = π/4, the maximum value is 0.64 pu.
In this case the real part of the current vector 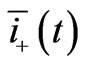 is approximately zero. In accordance with (2), the vector only moves along the imaginary axis of the complex plane starting from 0.
is approximately zero. In accordance with (2), the vector only moves along the imaginary axis of the complex plane starting from 0.
4.2 Transient Fault Analysis of an Existing Power System
The Lyon approach to study power system faults presented in this paper is now applied to perform transversal fault analysis in an Italian exiting power network (Figure 7). The network under analysis is constituted by a high voltage external grid EG, a transformer T, a line L, and a medium voltage load LD. The faults occur on the medium voltage busbars.
 (a)
(a)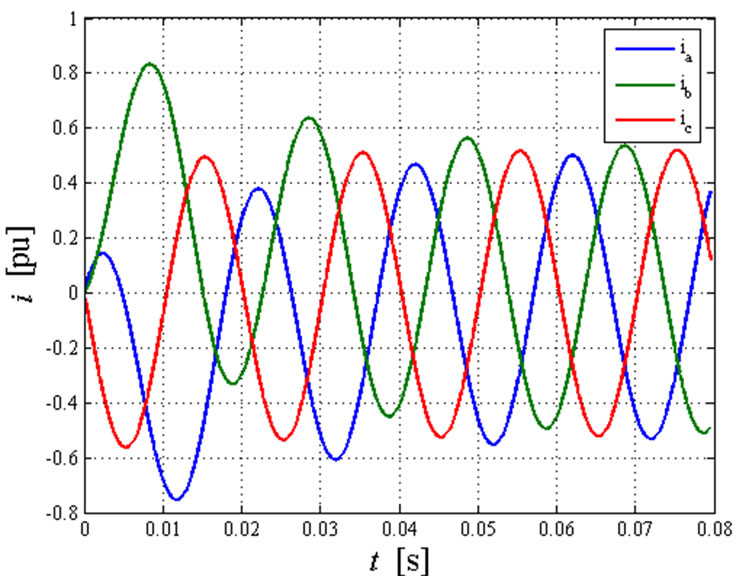 (b)
(b)
Figure 4. Three-phase fault: phase currents transient with (a) φ0=0 and (b) φ0=π/4
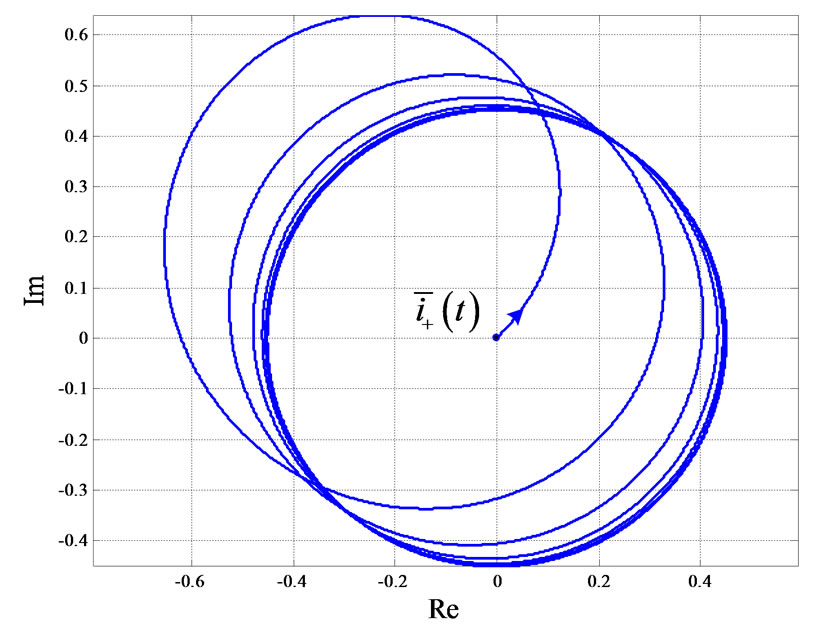
Figure 5. Three-phase fault: Lyon time vector 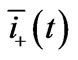 with
with 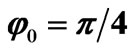
 (a)
(a) (b)
(b)
Figure 6. Two phase fault: phase currents transient with (a) φ0 = 0 and (b) φ0 = π/4
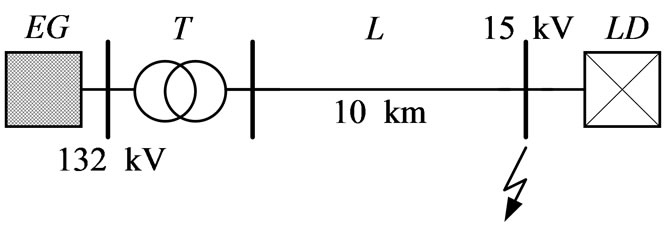
Figure 7. One line diagram
To set up the network circuit, the line L is represented by a “Γ” cell, while the transverse parameters of the transformer T are neglected. Furthermore, the transformer is shell core type, which means that the zero-sequence flux component flows in the low reluctance core. Consquently, the zero-sequence impedance is very high. The load is represented by a simple set of impedances. The neutral condition of the external high voltage grid EG isgrounded, while the medium voltage side is not grounded. The network data are reported in Table 2.
Sequence networks and initial conditions. The instantaneous sequence networks are shown in Figure 8where the quantities indicated are the pu parameters
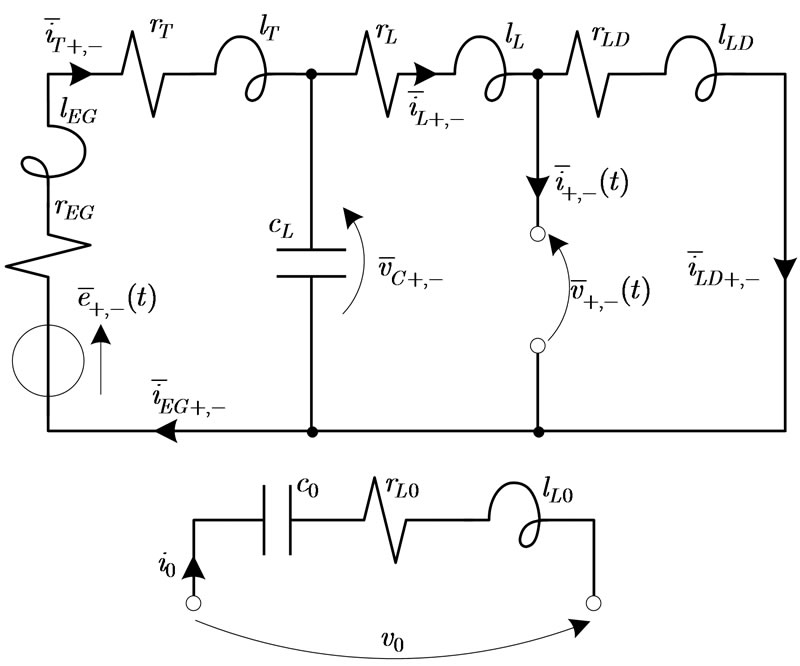
Figure 8. Positive-, negative-, and zero-sequence instantaneneous sequence networks for the transversal fault analysis of the network depicted in Figure 7
calculated starting from the data reported in Table 2. Based on the hypothesis about the type of load and the neutral point connection, the instantaneous zero-sequence network is composed only by the line zero-sequence parameters.
The computation of the initial condition is performed considering the network under the sinusoidal condition before the fault occurs. The state quantities result:
 (14)
(14)
Single-phase-to-ground fault. The sequence networks are connected in series. The fault does not change the line current values very much: no more than a very small transient in the first instants of the fault transient is present. The fault current (see Figure 9) instead presents in the first instant high frequency oscillations superimposed to the fundamental network frequency (50 Hz). These oscillations with high amplitude decay very rapidly. Nevertheless, the fault current is very low because the network is not grounded: the unique path to the ground is represented by the line capacitors.
Table 3 shows the maximum value of the line currents and voltages calculate by using Fortescue SCT and Lyon ISCT, which are – at the end of the transient - sinusoidal and equal.
Two-phase fault. In this case, the positiveand negative-instantaneous sequence networks are connected in parallel, the zero-instantaneous sequence network is open
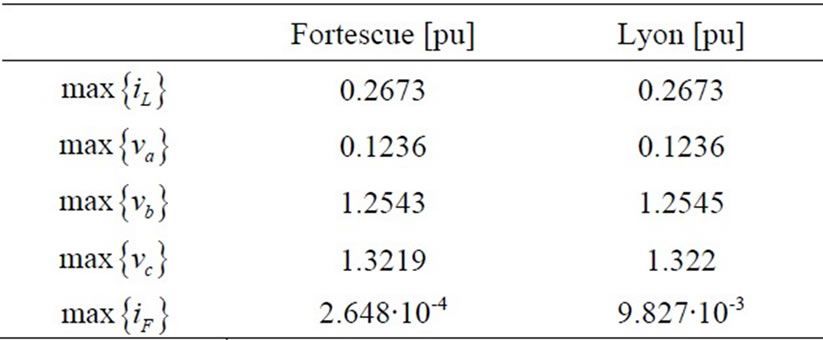
Table 3. Comparison between maximum value evaluated by SCT and ISCT
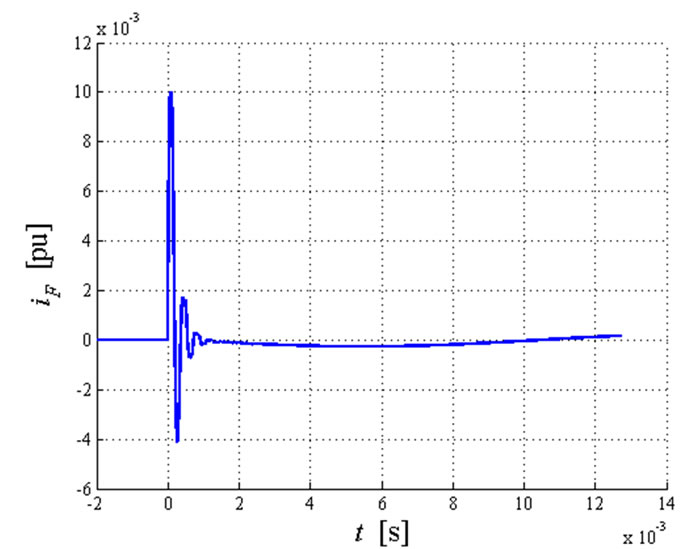
Figure 9. Fault current in the first instant of the fault
as shown in Figure 10. Figure 11 shows the line current movement during the fault transient calculated considering φ0 = 0. A high peak in the considered quantities can be observed. In particular, the phases b and c show a peak in the first instants equal to 1.5141 pu and 1.3826
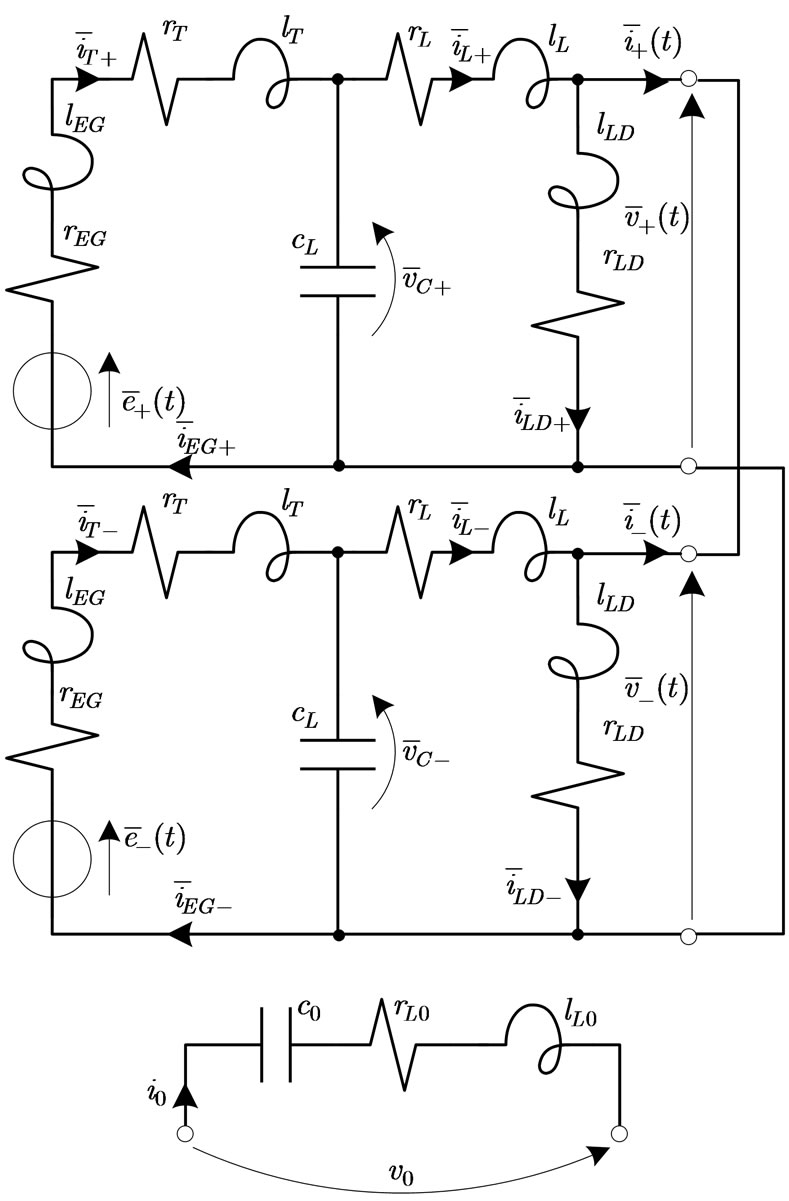
Figure 10. Instantaneous sequence networks connection for the analysis of two-phase fault

Figure 11. Two phase fault: line phase currents transient calculated with φ0=0

Figure 12. Two phase fault: Lyon time vector  with φ0 = 18°
with φ0 = 18°
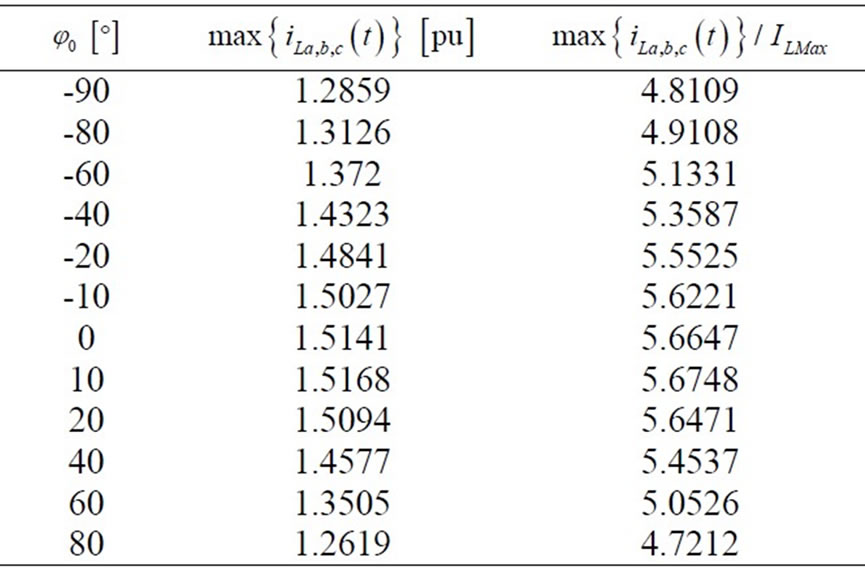
Table 4. Current maximum values as a function of φ0
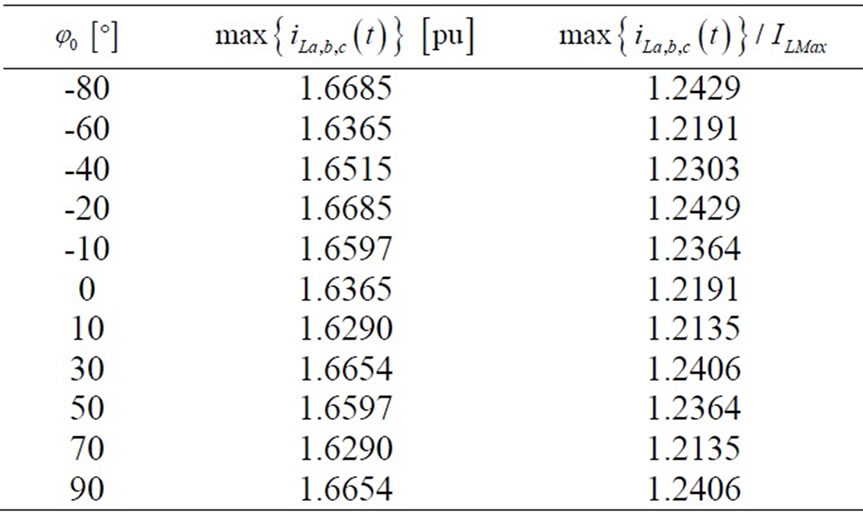
Table 5. Current maximum value as a function of φ0
pu respectively: these peak values cannot be calculated by using Fortescue analysis.
In this kind of fault, the line currents assume large values in the first instant of the fault. The maximum value depends on the phase angle φ0. In Table IV the maximum values reached by the line phase currents ( ) and the ratio between this value and the maximum value under the pre-fault sinusoidal condition (
) and the ratio between this value and the maximum value under the pre-fault sinusoidal condition (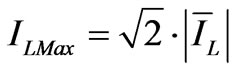 ) calculated for different phase angles
) calculated for different phase angles  are reported. The maximum value is reached for φ0=18°: the ratio (
are reported. The maximum value is reached for φ0=18°: the ratio (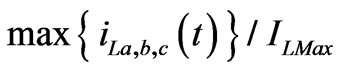 ) is close to 5.70.
) is close to 5.70.
Figure 12 shows the Lyon vector 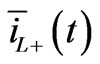 in the complex plane. During the first fault transient instant the current reaches its instantaneous maximum value. At the end of the transient, in steady-state but in asymmetric condition, the current
in the complex plane. During the first fault transient instant the current reaches its instantaneous maximum value. At the end of the transient, in steady-state but in asymmetric condition, the current 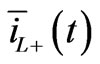 describes an ellipse.
describes an ellipse.
The two-phase-to-ground fault analysis leads to very similar results. It depends on an ungrounded network that has a very high neutral to ground impedance.
Three-phase fault. In this case the instantaneous sequence networks are short-circuited at the point where the fault occurs. As for the two-phase fault case, Table V shows the maximum values reached by the line phase currents (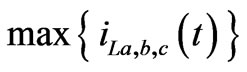 ) and the ratio between this value and the maximum value under the pre-fault sinusoidal condition (
) and the ratio between this value and the maximum value under the pre-fault sinusoidal condition (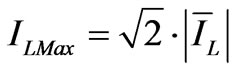 ) calculated for different phase angles
) calculated for different phase angles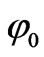 . In this case, the peak value achieved in the first instants is 1.24 times the maximum value of the current in the final steady-state condition.
. In this case, the peak value achieved in the first instants is 1.24 times the maximum value of the current in the final steady-state condition.
5. Conclusions
The use, in the time-domain analysis, of Lyon transformation of asymmetric transversal faults is shown. The proposed approach allows the derivation of the Lyon state model of the faulted network and of the transient and steady state voltages and currents of interest.
Thanks to the Lyon approach, the peak values reached in the first instants of the fault by the network voltages and currents can be calculated. Furthermore, the complex vectors allow the use of the state equations approach to perform the network dynamic analysis and provide simple relations to steady-state phasors and their rms values. The Lyon approach can also be used for derivation of equivalent circuits that characterize the different faults and – thanks to the state-matrix approach – its eigenvalues. These information can be very useful to the power system analysts before starting their analysis by software package simulations.
The SCT, traditionally employed for fault analysis, can be considered as a particular case of the more general instantaneous sequence components approach proposed by Lyon.
Finally, the examples here presented confirm that the use of time-dependent symmetrical component in network calculations has several advantages with respect to the SCT and simulation software: the Lyon transformation allows transient calculations; the simple relation with their steady-state phasors facilitates the interpretation of the results by the well-known steady-state phasor theory and by using complex plane diagrams.
Finally, it is important to underline that network component data are usually available in these coordinates.
REFERENCES
- C. L. Fortescue, “Method of symmetrical coordinates applied to the solution of polyphase networks,” AIEE Trans., pt. II, Vol. 37, pp. 1027–1140, 1918.
- C. F. Wagner and R. D. Evans, “Symmetrical components,” Mc-Graw-Hill Book Company, Inc., New York, 1933.
- H. Edelman, “ThEorie Et Calcul Des REseaux De Transport D’Energie Electrique, Dunod, ” Paris, 1966.
- L. O. Chua, C. A. Desoer, and E. S. Ku, “Linear and non linear circuits,” McGraw-Hill Inc, New York, 1994.
- S. Leva and A. P. Morando, “Analysis of physically symmetrical lossy three-phase transmission lines in term of space vectors,” IEEE Transactions on Power Delivery, Vol. 21, No. 2, pp. 873–882, 2006.
- G. C. Paap, “Symmetrical components in the time domain and their applications to power networks calculations,” IEEE Transactions on Power Systems, Vol. 15, No. 2, 522–528, 2000.
- A. M. Stanković and T. Aydin, “Analysis of asymmetrical faults in power systems using dynamic phasors,” IEEE Trans. on Power Systems, Vol. 15, No. 3, pp. 1062–1068, 2000.
- S. Huang, R. Song, and X. Zhou, “Analysis of balanced and unbalanced faults in power systems using dynamic phasors,” IEEE Proceedings of International Conference on Power Systems Technology, Vol. 3, pp. 1550–1557. 2002.
- J. M. Aller, A. Bueno, M. I. Giménez, V. M. Guzmán, T. Pagà, and J. A. Restrepo, “Space vectors applications in power systems,” IEEE proceedings of Third International Conference on Devices, Circuits and Systems, Caracas, pp. 78/1–78/6, 2000.
- W. Lyon, “Transient analysis of alternating-current machinery,” J. Wiley & Sons, New York, 1954.
- G. J. Retter, “Matrix and space-phasor theory of electrical machines,” Akadémiai Kiadó, Budapest, 1987.
- A. Gandelli, S. Leva, and A. P. Morando, “Topological considerations on the symmetrical components transformation,” IEEE Transactions on Circuits and Systems, Vol. 47, No. 8, pp. 1202–1211, 2000.
- A. Ferrero, S. Leva, A. P. Morando, and A systematic, “Mathematically and physically sound approach to the energy balance in three-wire, three-phase systems,” L’Energia Elettrica, Vol. 81, No. 5–6, pp. 51–56, 2004.
- W. Lyon, “Application of the method of symmetrical components,” Mc Graw-Hill Book Company, New York, 1937.
- S. Leva, A. P. Morando, and D. Zaninelli, “Evaluation of line voltage drop in presence of unbalance, harmonics and interharmonics: Theory and applications,” IEEE Transactions on Power Delivery, Vol. 20, No. 1, pp. 390–396, 2005.
- A. J. Stubberud and I. J. Williams, J. J. DiStefano, Schaum's, “Outline of feedback and control systems,” Schaum's, McGraw-Hill, New York (USA), 2nd Edition. 1990.
- R. Roeper, “Short-circuit currents in three-phase systems,” Berlin and München, Siemens Aktiengesellschaft - John Wiley and Sons, 1985.


