Natural Science
Vol.06 No.10(2014), Article ID:46946,8 pages
10.4236/ns.2014.610069
Impact of Convective Parameterization Schemes on the Quality of Rainfall Forecast over Tanzania Using WRF-Model
Alfred L. Kondowe
Department of Weather Forecast and Numerical Weather Prediction, Faculty of Meteorology, Russian State Hydrometeorological University (RSHU), St. Petersburg, Russia
Email: alfredkondowe@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 March 2014; revised 30 April 2014; accepted 7 May 2014
ABSTRACT
To describe the evolution of atmospheric processes and rainfall forecast in Tanzania, the Ad- vanced Weather Research and Forecasting (WRF-ARW) model was used. The principal objectives of this study were 1) the understanding of mesoscale WRF model and adapting the model for Tan- zania; 2) to conduct numerical experiments using WRF model with different convective paramete- rization schemes (CP’s) and investigate the impact of each scheme on the quality of rainfall fore- cast; and 3) the investigation of the capability of WRF model to successfully simulate rainfall amount during strong downpour. The impact on the quality of rainfall forecast of six CP’s was in- vestigated. Two rainy seasons, short season “Vuli” from October to December (OND) and long sea- son “Masika” from March to May (MAM) were targeted. The results of numerical experiments showed that for rainfall prediction in Dar es Salaam and (the entire coast of the Indian Ocean), GD scheme performed better during OND and BMJ scheme during MAM. Results also showed that NC scheme should not be used, which is in agreement to the fact that in tropics rainfall is from con- vective activities. WRF model to some extent performs better in the cases of extreme rainfall.
Keywords:
Tanzania, WRF-ARW, Convective Parameterization Scheme (CP’s)

1. Introduction
The economy of the United Republic of Tanzania like many other African countries depends much on agricul- tural sector, which is highly vulnerable to amounts and rainfall distribution. The performance of the rainy season has significant impact on the volume of crops production and corresponding level of income and poverty. The income from the agricultural sector is more than half of Gross Domestic Production (GDP). More than 80 per- cent of the population of the government of the United Republic of Tanzania lives in rural areas and their live- lihood depend on agriculture which in turn depends on the start, duration and longevity of the rainy season [1] .
To describe the evolution of atmospheric processes and rainfall forecasting in Tanzania, the Weather Re- search and Forecasting model of Advanced Weather Research core (WRF-ARW) version 3.1 has been used.
To achieve this goal, the following principal tasks were involved:
1) The understanding of mesoscale numerical WRF model and adapting the model for Tanzania,
2) To conduct numerical experiments using WRF model with different CP’s and investigate the impact of each scheme on the quality of rainfall forecast and,
3) The investigation of the ability of mesoscale numerical WRF model to successfully simulate rainfall amount during strong downpour.
Rainfall in East Africa (Tanzania, Uganda, Kenya) experience a greater spatial and temporal variability due to the difficult terrain, the presence of large water bodies such as Victoria, Nyasa, Tanganyika, the influence of the Indian Ocean, and synoptic-scale circulation features (such as the Inter-Tropical Convergence Zone (ITCZ), monsoon circulation) and mesoscale circulations [2] .
These features cause climatic differences in rainfall regime which varies from wet areas to dry areas where severe meteorological drought and low rainfall are a constant threat to life [3] .
Therefore, the task of using mesoscale WRF model in Tanzania for the purpose of improving the quality of rainfall forecast is very important.
WRF model is a numerical weather prediction (NWP) and atmospheric simulation system designed for both research and operational applications. WRF is supported as a common tool for the university/research and oper- ational communities to promote closer ties between them and to address the needs of both. The development of WRF has been a multiagency effort to build a next-generation mesoscale forecast model and data assimilation system to advance the understanding and prediction of mesoscale weather and accelerate the transfer of research advances into operations.
WRF-ARW is a fully compressible non-hydrostatic model which use time splitting scheme in order to in- crease model efficiency. The equations used in the model allow acoustic waves due to their compressibility na- ture and therefore require short time step for the model stability to be achieved. Slow waves which are of me- teorological important are integrated using a third-order Runge-Kutta (RK3) time integration scheme, while the high-frequency acoustic modes are integrated over smaller time steps to maintain numerical stability.
For spatial discretization WRF-ARW model uses Arakawa C grid staggering due to the fact that it conserve mass and energy for long run simulations.
Advantage of using WRF model is that it provides a large set of options from which to choose suitable para- meterization scheme for the description of physics of non adiabatic processes.
2. Study Area
The Government of the United Republic of Tanzania is the largest country in East Africa. It is located south east of the equator, lying from 29˚E to 42˚E and from 1˚S to 12˚S. To the north the country is borders with Kenya and Uganda, with Mozambique, Malawi and Zambia to the south, Democratic Republic of Congo, Burundi and Rwanda to the west and with Indian Ocean to the east.
The United Republic of Tanzania has a total area of 945,090 km2. Out of which, land (including the islands of Mafia, Pemba and Zanzibar) occupies 886,040 km2 of which 36% of land area covered by forests, 40% perma- nent pasture, 24% arable land and permanent crops, and water bodies counting for 59,050 km2.
The climate of the United Republic of Tanzania mainly is sub-equatorial (equatorial monsoon climate), while in the northern part of the country the climate is equatorial. The climate in Tanzania has strong seasonal and an- nual cycles with precipitation being highly variable in its temporal and spatial distribution. Two rainfall seasons are experienced over the country. The long rains “Masika”, of March-May (MAM) and short rains “Vuli” of October-December (OND).
3. Data and Methodology
To describe the evolution of atmospheric processes and rainfall forecasting in Tanzania, the Weather Research and Forecasting model of Advanced Weather Research core (WRF-ARW) Version 3.1.1 has been used.
In order to conducts numerical experiments, a model domain of 92 points from west to the east and 75 points from south to the north, a horizontal resolution of 30 km and 27 vertical levels was established. At this horizon- tal grid spacing, the main features of the bottom topography in the domain are well resolved. Center point of the model domain is located at 5.46˚S and 39.0˚E (in Figure 1). In this study, for correct description of atmospheric processes in equatorial zone Mercator map projection was used in the Cartesian system coordinate.
Initial and boundary conditions which used in this study were downloaded from NCEP [4] . Initial conditions must specify the three-dimensional distribution of three velocity components, temperature, pressure and humid- ity, and the boundary conditions for temperature, humidity and velocity components, as well as the heat, mois- ture and momentum fluxes at the lower boundary of the model domain.
The systems of equations the WRF model uses directly describe large-scale atmospheric processes, they do not temporally and spatially forecast convection over their large scale domain, and so cumulus parameterization schemes are used in the model to estimate the release of latent heat and development of convection within each grid box of the larger scale of the model.
The WRF model offers multiple physics options that can be combined in many ways. In this study, we ex- amined the impacts of six convective parameterization schemes (Table 1) on the quality of rainfall forecast in Tanzania.
4. Results and Discussions
For WRF model adaptation for modeling atmospheric processes in Tanzania, numerical experiments were con- ducted. Since this work is based on rainfall forecast then model verification was carried out against observed rainfall data. Simulations were conducted for 24 hours from 06Z daily for the following periods:
Table 1. Convective parameterization schemes used in this research.
Figure 1. WRF modeling domain for Tanzania used in this research.
From 4th to 14th May 2006;
From 2nd to 11th April 2008;
From 24th to 29th April 2010;
From 10th to 19th November 2011.
In these selected days over Tanzania especially in Dar es Salaam and the entire coastal of Indian Ocean, such as Mtwara, Lindi, Morogoro and Tanga, including the islands of Zanzibar and Pemba, observed a record high rainfall amount. This led to flooding and enormous material damage and life losses.
WRF model verification was done against the observed rainfall at Dar es Salaam meteorological station. By knowing the coordinate of the station, model forecasts were interpolated to the station coordinate with the help of a code written in FORTRAN. Results of six different schemes of convective and non convective rainfall were calibrated against the observed values at Dar es Salaam meteorological station.
In this work, the quality of rainfall forecasts was analyzed in two ways, quantitatively and qualitatively. The following statistical moments were computed;
Forecast error is calculated from Equation (1)
 (1)
(1)
Root Mean Square Error (RMSE)
 (2)
(2)
Mean Bias (MB)
 (3)
(3)
where, in all the formula above:
Quantitative analysis tells us about the model performance, when the difference between the observed and re- forecasted rainfall is less than zero then the model is said to under predicting and over predicting when the dif- ference is greater than observed value.
RMSE is the good overall measure of the model performance because of the weighing of re-forecasted to its observed rainfall by its square which tends to inflate RMSE, especially when we have extreme values. For per- fect model, RMSE must approach zero.
Mean Bias is also used to examine the performance of the model. It represents the degree of correspondence between the mean re-forecasted and mean observed rainfall. The lower MB value the better the model is and less than zero MB indicates that the model is under predicting.
In this research work, the above criterion has been used for the selection of the best model configuration.
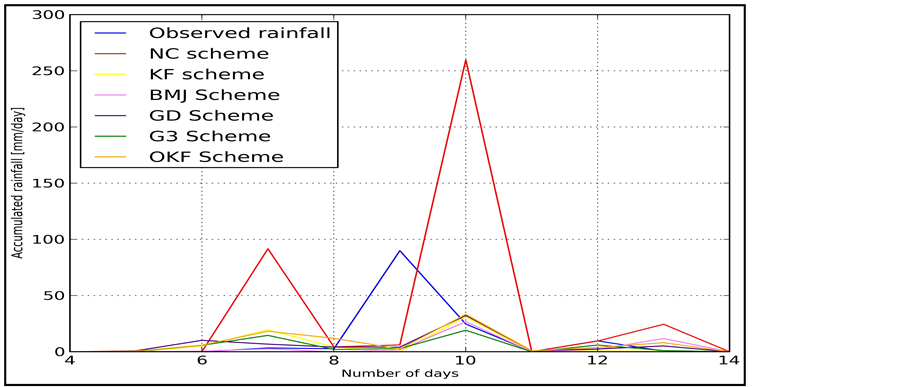
The first cycle of numerical experiments refers to the 4th to 14th May 2006. In this cycle, the mean and stan- dard deviation of the observed rainfall was 12.0 and 25.7 mm/day.
The average error of re-forecasted rainfall varies from −24.1 to 4.2 mm/day and the average re-forecasted rainfall range from 4.1 to 36.0 mm/day (Table 2).
Assessment of the results in this cycle of numerical experiment (Table 2 and in Figure 2) showed that old KF scheme performs better than any other scheme while qualitative analysis indicated that KF scheme is the best.
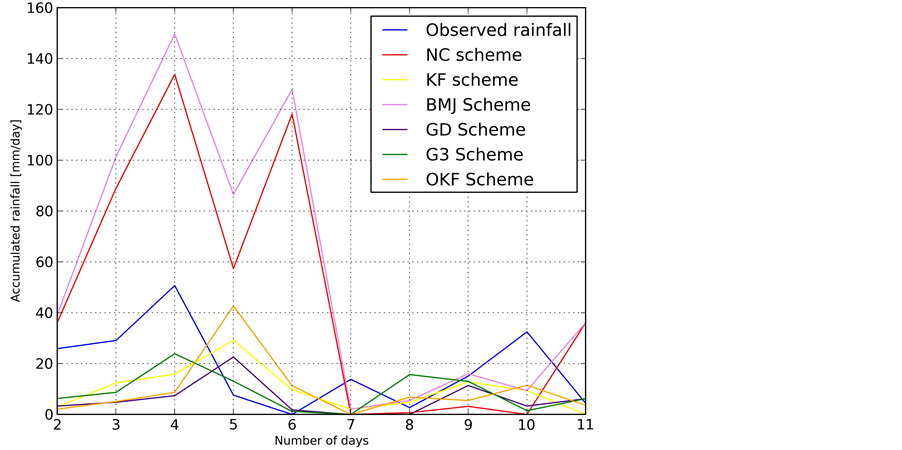
The second cycle of numerical experiments refers to 2008. Analysis of the results (Table 3 and in Figure 3) shows that in the period from 2nd to 11th April 2008, average rainfall error varies from −29.3 to 12.1 mm/day, and mean re-forecasted rainfall varies from 6.1 to 47.5 mm/day.
Table 2. Qualitative and quantitative results for each CP’s from 4th to 14th May 2006.
Table 3. Qualitative and quantitative results for each CP’s from 2nd to 11th April 2008.
Figure 2. Impact of each CP’s on the rainfall forecast for the period from 4th to 14th May 2006.
Average and standard deviation of the observed rainfall was respectively 18.2 and 16.1 mm/day.
Results showed that KF and OKF schemes have the average error of 8.3 and 8.5 mm/day, and deviation relative to average values of 17.0 and 21.8 mm/day, with the average re-forecasted rainfall value of 9.9 and 9.7 mm/day, and RMSE of 8.5 and 12.2 mm/day, respectively.
BMJ scheme has the average error and standard deviation relative to the mean of 3.3 mm/day and 7.12 mm/day.
Ensemble GD scheme and ensemble Grell 3 have mean and standard deviation forecast errors of 12.1 mm/day and 9.2 mm/day and 17.7 mm /day and 15.0 mm/day respectively. Analysis of the results from the second cycle
Figure 3. Impact of each CP’s on the rainfall forecast for the period from 2nd to 11th April 2008.
of numerical experiment showed, that NC scheme perform poorer than any other scheme, has mean error of −29.3 mm/day and the standard deviation of 12.7 mm/day, the mean −47.5 mm/day and standard re-forecasted rainfall value −50.8 mm/day.
Qualitative analysis in this cycle showed that the best schemes are BMJ and G3d, having RMSE of 0.70 and MB of 3.93 respectively. Ensemble GD and KF schemes are not suitable for having negative MB.
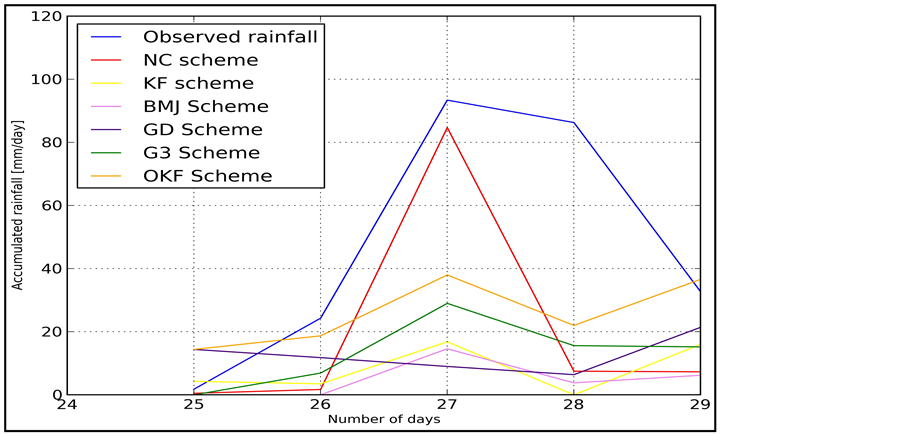
In the third cycle of numerical experiments, from 25th to 29th April 2010, mean and standard deviation of the observed rainfall was 47.7 and 40.2 mm/day.
From the model results the mean rainfall error, mean re-forecasted rainfall, RMSE and MB for each convec- tive parameterization scheme were computed (Table 4).
Analyses of the results (Table 4 and in Figure 4) in this cycle of numerical experiments showed that the av- erage forecast error varies from 27.4 to 44.4 mm/day with the mean re-forecast rainfall varies from 3.3 to 20.3 mm/day.
In this cycle of numerical experiments, the mean and the error in standard deviation of re-forecasted rainfall when the model was set with NC scheme was 27.4 and 4.3 mm/day respectively, the mean and standard devia- tion of re-forecasted rainfall was 20.3 and 36.1 mm/day.
When KF and OKF schemes were used, average rainfall error and error in standard deviation were 39.9, and 39.4 mm/day and 44.4 and 38.4 mm/day respectively. When the model was configured with ensemble schemes GD and G3, mean rainfall error and error in standard deviation were 35.1 and 44.1 mm/day and 38.0 and 43.8 mm/day respectively. Average and standard deviation of re-forecasted rainfall was 12.6 and 5.8 mm/day and 9.7 and 50.3 mm/day respectively.
Results in this cycle showed that BMJ scheme has average rainfall error of 42.8 mm/day with the average re- forecasted rainfall value of 4.9 mm/day.
Qualitative analysis revealed that ensemble GD scheme shows the better forecast skill by RMSE values while in terms of MB ensemble G3 perform better. In this cycle of numerical experiment BMJ and OKF schemes should not be used.
Thus, quantitative analysis of the quality of rainfall forecast in this cycle of numerical experiment, period from 25th to 29th April 2010 showed paradoxical result because NC scheme shows the best rainfall forecast skill than any other scheme while OKF scheme perform poorer.
This abnormality can be explained as follows. During this cycle of numerical experiment on April 27th ap- pears to have a record high rainfall amount, this extreme amount was not cached up by WRF model when it was configured with convective parameterization schemes. This extreme rainfall seems to be associated with large amount of moisture reserves in the atmosphere, which in the absence forcing mechanism of convection parame-
Figure 4. Impact of each CP’s on the rainfall forecast from 25th to 29th April 2010.
Table 4. Qualitative and quantitative results for each CP’s from 25th to 29th April 2010.
terization scheme was fully realized through the parameterization of large-scale condensation. A qualitative analysis was affected by that maximum value from a single case, and therefore it is necessary to be excluded from consideration, taking into account that extreme high rainfall cannot be predicted using NC scheme especial in the tropics where rainfall in most cases is due to convective activities.
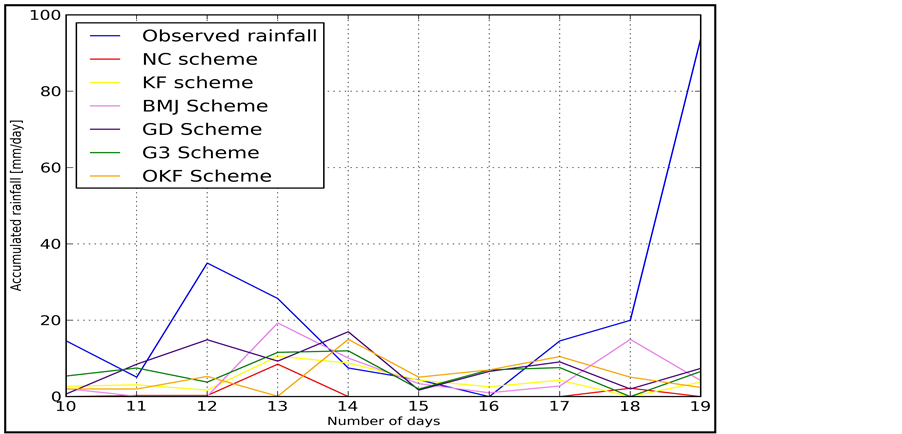
Numerical experiments in the fourth cycle, from 10th to 19th November 2011 showed that the average and standard deviation of the observed rainfall value was 22.1 and 27.4 mm/day, respectively.
Analysis of the results (Table 5 and in Figure 5) shows that average forecast error was ranging from 14.4 to 21.0 mm/day while the average value of the re-forecasted rainfall ranges 1.1 to 7.7 mm/day.
Quantitative analysis in this cycle of numerical experiments showed that ensemble schemes GD and G3d have the lowest mean rainfall error of 14.4 and 15.7 mm/day. The mean re-forecasted value was 7.7 and 6.4 mm/day with RMSE and MB of 1.3 and 1.9 mm/day respectively.
When the model was configured with BMJ scheme the average forecast error was 16.3 mm/day and standard deviation was 27.9 mm/day. Average re-forecasted rainfall was 5.8 mm/day when RMSE and MB was 1.41 and 1.63 mm/day.
Using KF and OKF the following statistical characteristics were obtained: average error was 17.9 and 16.6 mm/day with average forecast of 4.2 and 5.5 mm/day, and the RMSE forecasts is 3.2 and 4.5 mm/day, respectively.
Figure 5. Impact of each CP’s on the rainfall forecast from 25th to 29th April 2010.
Table 5. Qualitative and quantitative results for each CP’s from 10th to 19th 2011.
5. Conclusions
For the mesoscale WRF model adaption for modeling of atmospheric process in Tanzania, numerical experi- ments were conducted. Rainfall forecast was carried out for 24 hours starting from 06Z daily for the following periods: from 4th to 14th May 2006, 2nd to 11th April 2008, 25th to 29th April 2010 and 10th to 19th November 2011.
In these selected days in Tanzania especially in Dar es Salaam and all the cities that are located along the coast of Indian Ocean, such as Mtwara, Lindi, Morogoro and Tanga, including the islands of Zanzibar and Pemba, observed a record high rainfall amount. This led to flooding and enormous material damage and human losses.
For the purpose of model verification, the re-forecasted convective and non convective rainfall amounts were calibrated against the observed rainfall from Dar es Salaam meteorological station.
The impact on the quality of rainfall forecast of six CP’s namely: Non Convective (NC), modified Kain-Fritch (KF), Betts-Miller-Janjic (BMJ), Ensemble Grell-Devenyi (GD), Ensemble Grell 3 (G3) and Old Kain-Fritch (OKF) were investigated.
In this research work, model results were assessed in two ways: quantitavely (forecast error) and qualitavely (root mean square error and mean bias).
The main findings of this work are:
1) for rainfall prediction in Dar es Salaam and (the entire coast of the Indian Ocean), GD scheme performed better than any other CP’s during OND rainfall season while BMJ scheme perform better during MAM rainfall season.
2) For rainfall forecasting over Tanzania, the model should not be configured with NC scheme and this is in agreement with the fact that in tropics rainfall is from convective activities.
3) WRF model to some extent performs better in the cases of extreme rainfall.
Mechanism of rainfall formation in Tanzania during OND seasonal rainfall is much related to high evapora- tion rate from the water bodies around the country while during MAM seasonal rainfall is much associated with winds convergence and instability in the regions of ITCZ.
The principal difference between adjustment scheme BMJ and ensemble GD scheme is that in GD scheme convection is favorable when there is strong vertical winds and initiated by the ability of the model to respond to the differences between the model and the statistical convective available potential energy over tropic water bo- dies while BMJ scheme tends to do better when there is little convective available potential energy.
From these results, it can be recommended that for operational purposes at Tanzania Meteorological Agency, WRF model better be configured with BMJ scheme during MAM and ensemble GD scheme during OND sea- son.
The author will keep on investigating the impact on the quality of rainfall forecast over Tanzania of the phys- ical block of mesoscale WRF model. The main objective is to find the best model configuration of convective, microphysics and radiation schemes for rainfall forecast in Tanzania.
Acknowledgements
I would like to thank my supervisor Olga G. Aniskina for her exemplary guidance, monitoring and constant en- couragement throughout my research period.
References
- Mhita, M.S. (1990) The Analysis of Rainfall Data for Agriculture in Tanzania. Tanzania Meteorological Research Publication (TMRP), Research Report No. 2/90, Directorate of meteorology Tanzania.
- Ogallo, L.J. (1982) The Statistical Prediction of East African Rainfalls Using Quasi-Biennial Oscillation Phases Information. Kenya Journal of Science and Technology, A3, 43-54.
- Ntale, H.E. (2003) Prediction of East Africa Seasonal Rainfall Using Simplex Canonical Correlation Analysis. Journal of Climate, 16, 2105-2112. http://dx.doi.org/10.1175/1520-0442(2003)016<2105:POEASR>2.0.CO;2
- National Centers for Atmospheric Research’s (NCAR) (2014) CSIL Research Data Archive. http://rda.ucar.edu/datasets/ds083.2/?hash=access/
- Kain, J.S. (2004) The Kain-Fritsch Convective Parameterization: An Update. Journal of Climate and Applied Meteor- ology, 43, 170-181. http://dx.doi.org/10.1175/1520-0450(2004)043<0170:TKCPAU>2.0.CO;2
- Kain, J.S. and Fritsch, J.M.A. (1990) One Dimensional Entraining/Detraining Plume Model and Its Application in Convective Parameterization. Journal of the Atmospheric Sciences, 47, 2784-2802. http://dx.doi.org/10.1175/1520-0469(1990)047<2784:AODEPM>2.0.CO;2
- Fritsch, J.M. and Chappell, C.F. (1980) Numerical Prediction of Convectively Driven Mesoscale Pressure Systems. Part I: Convective Parameterization. Journal of the Atmospheric Sciences, 37, 1722-1733. http://dx.doi.org/10.1175/1520-0469(1980)037<1722:NPOCDM>2.0.CO;2
- Betts, A.K. and Miller, M.J. (1993) The Betts-Miller Scheme. In: Emmanuel, K.A. and Raymonds, D.J., Eds., Representation of Cumulus Convection in Numerical, American Meteorological Society, Boston, 246.
- Grell, G.A. and Devenyi, D.A. (2002) Generalized Approach to Parameterizing Convection Combining Ensemble and Data Assimilation Techniques. Geophysical Research Letters, 29, 38-1-38-4.
- Grell, G.A. (1993) Prognostic Evaluation of Assumptions Used by Cumulus Parameterizations. Monthly Weather Re- view, 121, 764-787. http://dx.doi.org/10.1175/1520-0493(1993)121<0764:PEOAUB>2.0.CO;2