Natural Science
Vol.6 No.3(2014), Article ID:43232,6 pages DOI:10.4236/ns.2014.63015
Depreciation factor equation to evaluate the economic losses from ground failure due to subsidence related to groundwater withdrawal
1Instituto de Investigaciones en Ciencias de La Tierra, Universidad Michoacana de San Nicolás de Hidalgo, Morelia, México; vitorio_manuel@yahoo.it
2Universidad Nacional Autónoma de México, Morelia, México
Copyright © 2014 Víctor Manuel Hernández-Madrigal et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Víctor Manuel Hernández-Madrigal et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received 29 October 2013; revised 29 November 2013; accepted 7 December 2013
Keywords: Aseismic Ground Failure; Groundwater Withdrawal Related Subsidence; Equation; Depreciation; Economic Losses
ABSTRACT
Subsidence due to groundwater withdrawal is a complex hydrogeological process affecting numerous cities settled on top of fluviolacustrine deposits. The discrete spatial variation in the thickness of these deposits, in combination with subsidence due to groundwater withdrawal, generates differential settlements and aseismic ground failure (AGF) characterized by a welldefined scarp. In cities, such AGF causes severe damages to urban infrastructure and considerable economic impact. With the goal of arriving to a general criterion for evaluating the economic losses derived from AGF, in the present work we propose the following equation: ELi = PVi*DFi. Where PVi is the value of a property “i”, and DFi is a depreciation factor caused by structural damages of a property “i” due to AGF. The DFi is calculated empirically through:  . This last equation is based on the spatial relations of coexistence and proximity of property polygons and the AGF axis. The coexistence is valued as the quotient of the affectation area divided by the total area of the involved property; and the proximity to the AGF axis is expressed as the inverse of the perpendicular distance from the centroid of the property polygon to the AGF axis. The sum of these terms is divided by two to determine the percentage that affects the property value (PVi). These equations are relevant because it is the first indicator designed for the discrete assessment of the economic impacts due to AGF, and can be applied to real estate infrastructure from either urban or rural areas.
. This last equation is based on the spatial relations of coexistence and proximity of property polygons and the AGF axis. The coexistence is valued as the quotient of the affectation area divided by the total area of the involved property; and the proximity to the AGF axis is expressed as the inverse of the perpendicular distance from the centroid of the property polygon to the AGF axis. The sum of these terms is divided by two to determine the percentage that affects the property value (PVi). These equations are relevant because it is the first indicator designed for the discrete assessment of the economic impacts due to AGF, and can be applied to real estate infrastructure from either urban or rural areas.
1. INTRODUCTION
Aseismic ground failure (AGF) is produced by human-induced groundwater level declines, and is mostly associated with land subsidence caused by compaction of underlying unconsolidated sediment [1]. Lacustrine and fluviolacustrine unconsolidated terrains favor the development of AGF. Two types of AGF are recognized: earth fissures, and surface faults. The first are tensile failures whose opposite sides move perpendicularly to the fault plane, and the second are aseismic shear faults in which blocks move in parallel with the fault plane [1] as a consequence of differential settlement. In Mexico, surface faults are known as creep-fault subsidence processes [2] originated by the differential compaction of lacustrine and fluviolacustrine sediments with heterogeneous thickness, which can be due to abrupt contrasts in the relieve of their basement, or to burial by sediments of preexisting regional normal faults (Figure 1).
AGF is the product of a complex and dynamic hydrogeological-anthropic process [3], because of which their

Figure 1. Ground failure by groundwater withdrawal subsidence. Observe that the compaction of lacustrine sediments deposited upon earlier normal faults generates differential sinking and new aseismic faults on the surface of the sediment covering the scarp of the previous geological structures.
number and their geometry expand in proportion with over-exploitation of groundwater. AGF damages urban infrastructure causing considerable economic losses through two processes: 1) scarps formed by faulting that by small, continual displacements due to their formation mechanisms are enough to damage rigid engineering structures located immediately upon them and nearby buildings susceptible to small inclinations (Figure 1); and 2) deep seated-walled gullies of sizeable dimensions that may potentially harm livestock and humans [1].
Such occurrences have been documented worldwide, that the reports concentrate in southeastern US (Arizona, California, Idaho, Nevada, Texas and Utah) [1,4,5]; China, in the provinces on the lower Yellow River basin (Shaanxi, Shanxi, northern Henan, Hebei, Shandong, Jiangu and Anhui) [6-8], and in Shanghai [9]; Thailand in Bangkok [10]; Italy in Venice [11]; and central México in the cities of Aguascalientes, Celaya [12,13], Irapuato, Mexico City [14], Morelia [2,3,15]; Querétaro [16] and Salamanca [17,18].
The results of general and approximate estimates of economic losses due to damage and depreciation of property are reported to be of millions of dollars [19,20]. However, there are no previous works attempting to quantify the economic losses at the scale of individual properties. Because of this, we are proposing an empirical equation for calculating the economic losses in terms of depreciation of property value. In order to demonstrate the effectiveness of these equations and the methodology applied, we also present in this paper the results obtained from a hypothetical case of study.
2. MATERIALS AND METODOLOGY
The equation we are proposing was designed based on field observations and identifications of spatial relations of properties relative to the trajectories of AGF axes (earth fissures and surface faults). The required inputs are: a land registry map with property value database, a ground failure map, and a map of influence band that is done in the field based on the spatial distribution of fractures and other AGF deformations. The variables of the equation are evaluated in a geographic information system (GIS) through the algorithm represented in Figure 2. The analysis of the hypothetical case herein presented was made in ArcGis 10 [21].
The Economic Loss of a property caused by structural damages due to AGF is calculated in the present work with the equation:
 (1)
(1)
where: ELi is the Economic Loss of a property “i” (USD). PVi is the property value (USD), and DFi is a depreciation factor (percent). The DFi is obtained from an empirical equation based on the spatial relations of coexistence and proximity between property polygons, and the axes of faulting scarps and deep seated-wall gullies. It is assumed that the depreciation of property is directly proportional to the ratio of affected property area, and inversely proportional to the proximity to the AGF linear trajectory, as follows:
 (2)
(2)
where:
DFi = depreciation factor (percent);
AAi = affected area of property (m2);
Ai = total area of property (m2);
di = perpendicular distance from the centroid of the property to the AGF axes (m) (di ≥ 1).
On the one hand, the coexistence is assessed as the quotient obtained by dividing the affected area (AAi) by the total area of property (Ai). On the other hand, the

Figure 2. Graphic representation of the algorithm for quantification in a geographic information system of the economic impact of ground failure.
proximity is calculated as the inverse distance between the centroid of the property polygon and the axis of the trajectory of the AGF ( ). The sum of both terms is divided by two to determine the percentage that affects the property value. Additionally, the economic impact (EI) in USD produced by the AGF in a particular site may be calculated by:
). The sum of both terms is divided by two to determine the percentage that affects the property value. Additionally, the economic impact (EI) in USD produced by the AGF in a particular site may be calculated by:
 (3)
(3)
The algorithm for the calculations (Figure 2) initiates by the identification of properties coexisting with the influence band, with which the layer “affected property” is created. Next, the affected area in each property is obtained by clipping the influence band relative to the affected area of the corresponding property (Figure 3). Multiplying the quotient that results from dividing the affected area by the total area of each property provides the coexistence term (AAi) to be used in Equation (2). Also, the inverse of the perpendicular distance (d−1) from the centroid of each property to the axis of the AGF (Figure 3), discretized the proximity relation for each affected property, which corresponds to the second term in Equation (2).
These two products (AAi and d−1) are appended to the database of the affected property layer. The application and result of Equation (2) is written in a new attribute column (DFi) that corresponds to the depreciation factor for each property. The reclassification of properties with the values from the DFi attribute renders the map of depreciation factor of properties.
Multiplying DFi times the property value (PVi) (Equation (1)) generates the map of economic loss (ELi). Finally, the sum of the partial economic losses (Equation (3)) corresponds to the total economic impact (EI) of AGF.

Figure 3. Map of properties affected by ground failure. The affected area (AAi, hatched area) is the area of the property overlapping the influence band polygon; Ai is the total area of the property. The attribute of spatial proximity is evaluated for each property from the perpendicular distance (yellow lines) from its centroid (open circles) to the trajectory axis of the aseismic ground failure (red line).
3. RESULTS
The proposed algorithm was applied to a hypothetical case of properties near an AGF, all having equal values of USD$ 50000.00. Figure 4 shows the cartographic inputs of property (polygons), ground failure (line) and influence band (polygon) as layers on a GIS. In Figure 5 the affected properties are highlighted, and their corresponding centroids are shown, together with a table containing the distances of each affected property centroid to the linear trajectory of the AGF (di). The area of each affected property within the influence band is shown in Figure 6, from which the proportion of affected property area was calculated as shown in the corresponding database (AAi).
The results of the application of Equation (2) are shown in Figure 7 together with the corresponding database. It is observed that the spatial distribution of the depreciation factor (DFi) for each affected property agrees with the assumptions made, given that properties having higher weighed proximity (1/di)—being closer to the AGF line—and weighed coexistence (AAi/Ai)—with larger affectation areas—display higher DFi values (red polygons).
Given that in our hypothetical case all properties have an equal value (USD$ 50,000), the spatial distribution of the economic losses (ELi) calculated by Equation (1) is the same as that of the depreciation factor (DFi). In a real scenario the value of properties is seldom equal so that
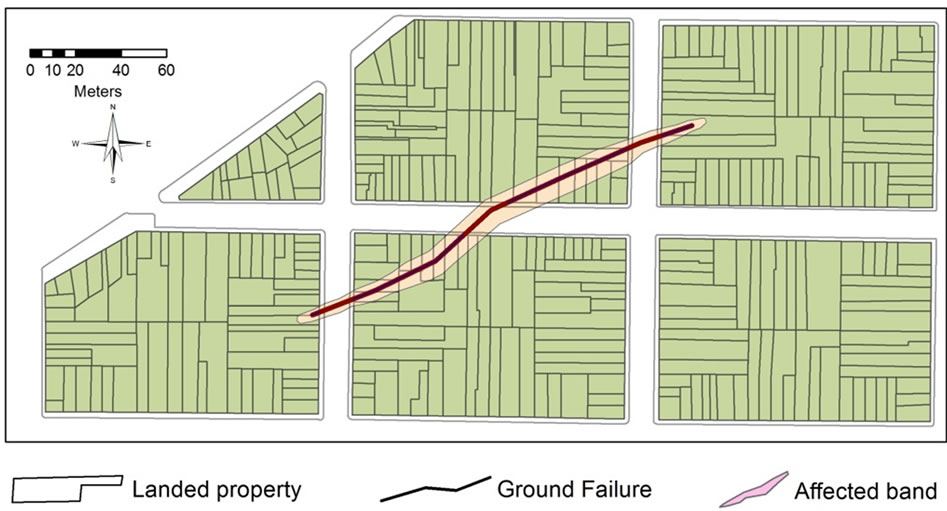
Figure 4. Cartographic inputs: property (polygon), aseismic ground failure (line) and influence band (polygon).
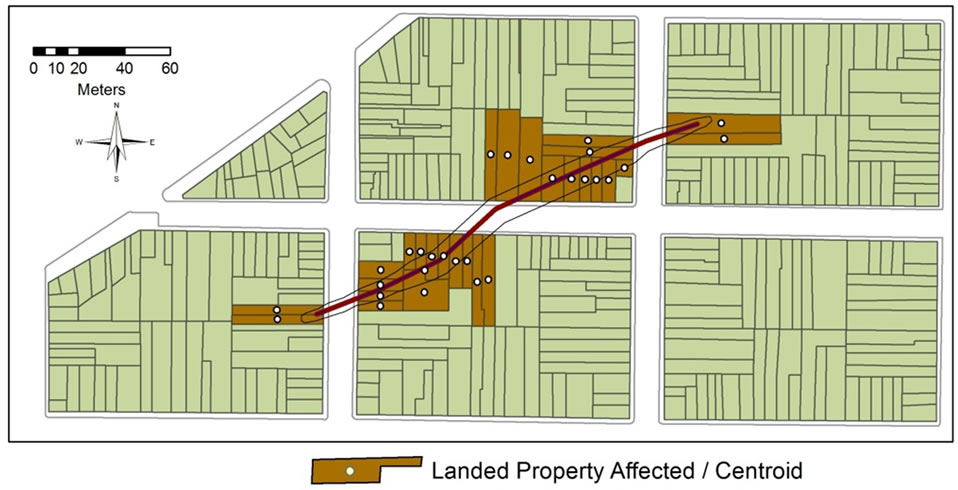
Figure 5. Centroids of affected properties.
the spatial distribution of economic losses will vary relative to the depreciation factor. The economic impact calculated by Equation (3) using the database shown in Table 1 were of USD$ 393,219.
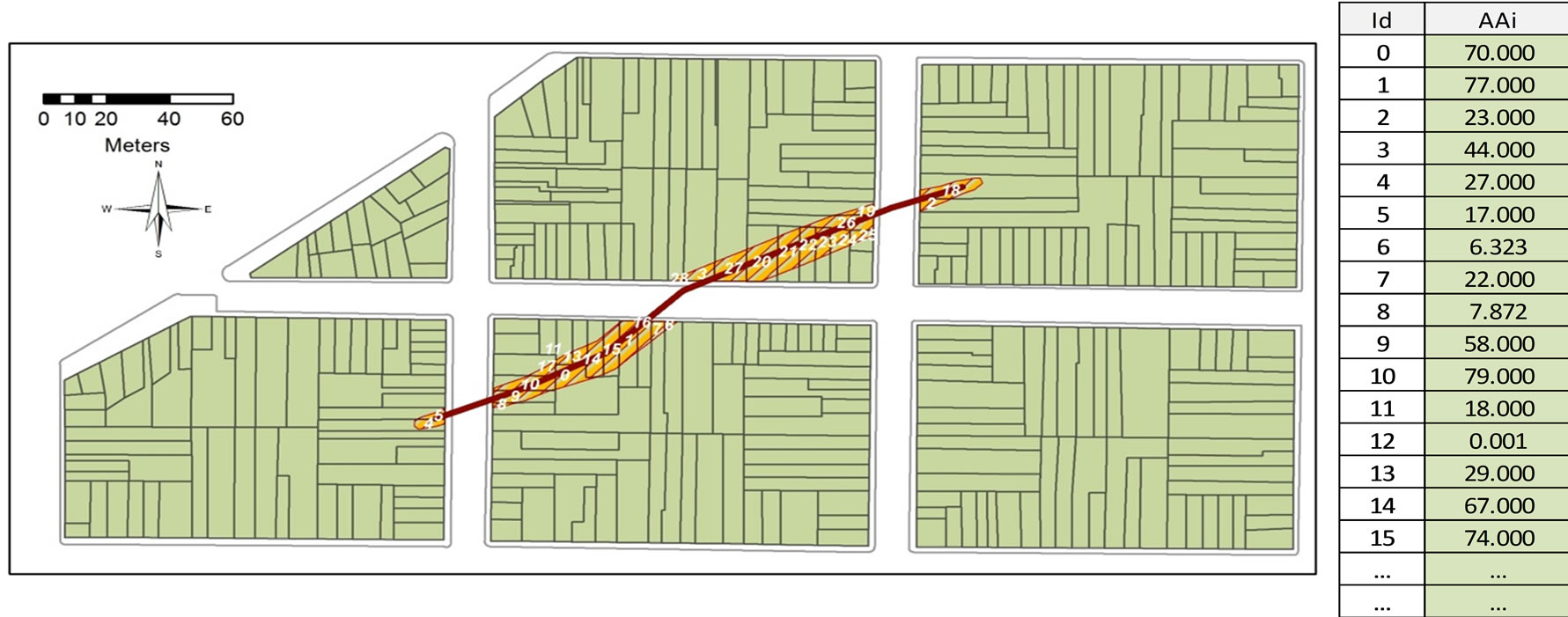
Figure 6. Area of each property affected by the influence band (AAi). To the right, the corresponding database is shown.
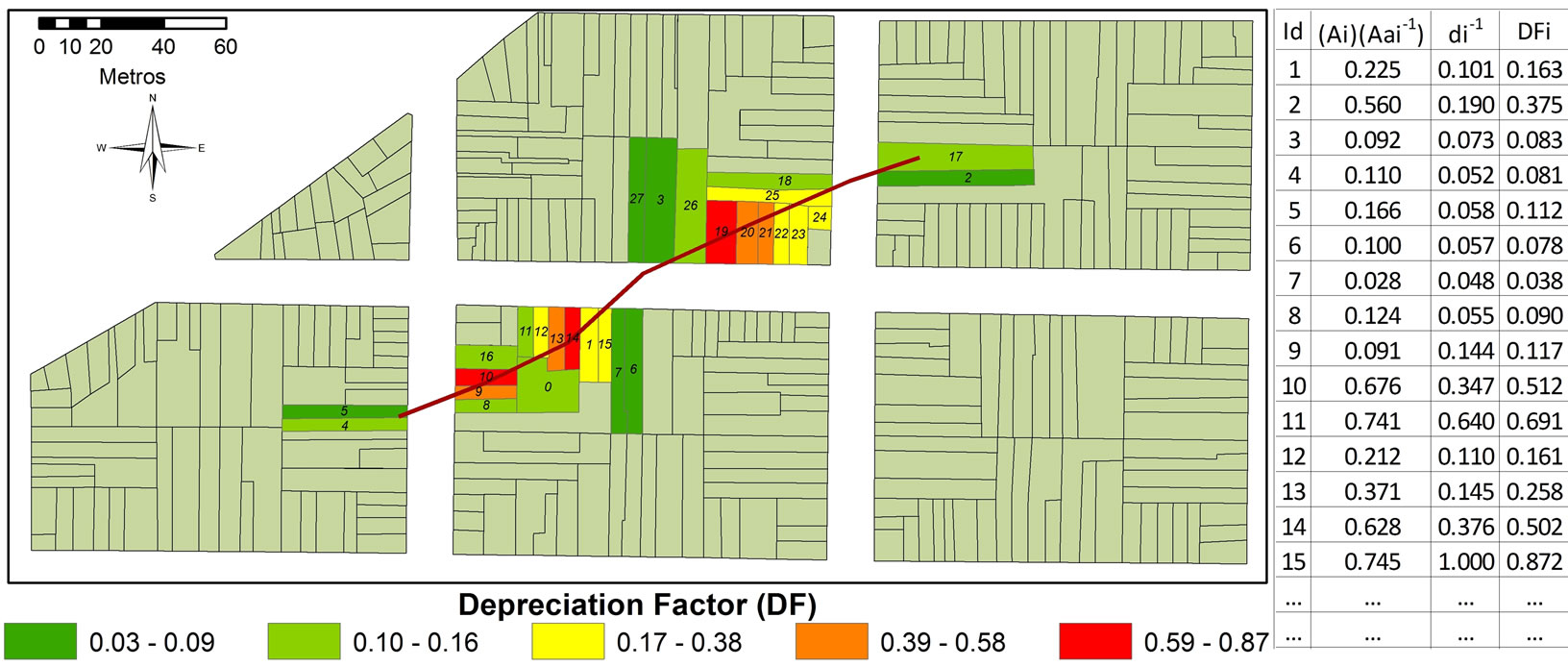
Figure 7. Depreciation factor (DFi) map and final database after joins and calculation of the first (0.75 AAi/Ai) and second (0.25/di) terms of Equation (1).
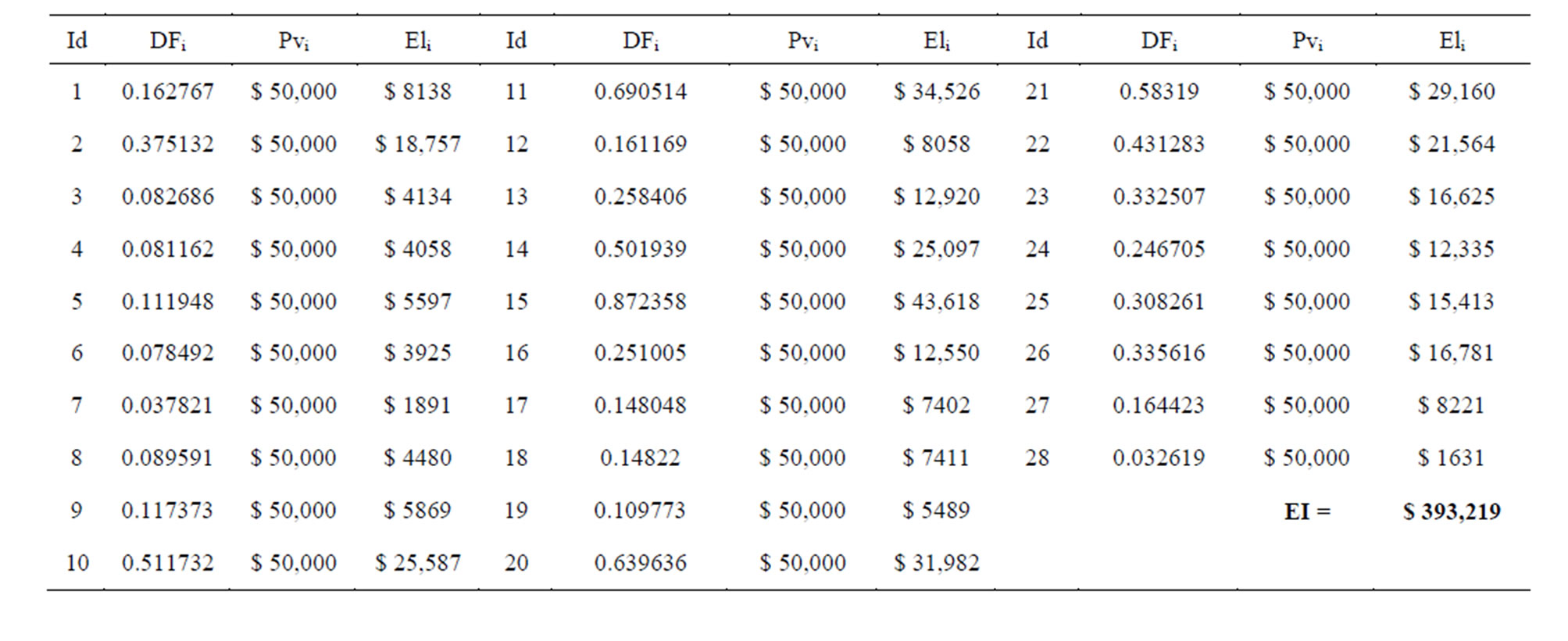
Table 1. Economic losses database. Assuming a constant property value of USD$ 50,000 and applying Equation (3), the total economic impact were of USD$ 393,219.
4. DISCUSSION
The equation for calculating demerit factor presented here has the following advantages: it allows the assessment spatial, temporal and discrete economic loss caused by AGF; can be taken as a criterion standard in the practice of the valuation of real property affected; is an important tool for the calculation of vulnerability and risk for AGF, and can be adapted to the calculation of economic losses caused by other phenomena such as slope instability and flooding. However, this equation is based only on spatial relationships and excludes other important variables such as: type of construction, civil structure deformation and geotechnical properties of the land affected. This situation makes it susceptible of modification and improvement of specialists with different approaches.
The results shown in this paper, obtained from a fictional case, show the effectiveness of the proposal to discretize and quantify the economic loss caused by the AGF in each of the properties affected. It is therefore a key element in quantifying the economic damage caused by natural disasters, and will social support claims for the design of public policies of mitigation and prevention.
5. CONCLUSION
The evaluation of economic losses (Equation (1)) from AGF is made feasible through the calculation of a factor of depreciation value of damaged properties. The degree of the depreciation (Equation (2)) is discretely and specifically assessed for each considered property. Overall, this means that the total economic losses or economic impact will be objectively estimated (Equation (3)) as a function of geometric characteristics, level of exposure (coexistence and proximity), and the value of affected properties. The three equations that we herein propose are deemed as a standard criterion and a basic tool that could be adopted by the different governmental levels (Federal, State and Municipal) for valuing of urban and rural property made for commercial and tax calculation purposes, economic disaster, and as an analytic factor for urban planning and development.
ACKNOWLEDGEMENTS
The authors acknowledge support from CONACYT for the Basic Science Project 134575 and Scientific Research Coordination of the Universidad Michoacana de San Nicolás de Hidalgo, Project 1.37- 2013.
REFERENCES
- Holzer, T.L. (1984) Ground failure induced by groundwater withdrawal from unconsolidated sediment. In: Holzer, T.H., Ed., Man-Induced Land Subsidence, VI, Geological Society of America. Reviews in Engineering Geology, Colorado, 67-105. http://dx.doi.org/10.1130/REG6-p67
- Garduño-Monroy, V.H., Arryegue-Rocha, E., IsradeAlcántara, I. and Rodríguez-Torres, G.M. (2001) Efectos de las fallas asociadas a sobreexplotación de acuíferos y la presencia de fallas potencialmente sísmicas en Morelia, Michoacán, México. Revista Mexicana de Ciencias Geológicas, 18, 37-54.
- Hernández-Madrigal, V.M., Garduño-Monroy, V.H. and Ávila-Olivera, J.A. (2011) Atlas de peligros geológicos de la ciudad de Morelia, Mich: Estandarización del documento, actualización cartográfica de la fallas geológicas de la zona urbana, y evaluación de tasas de hundimiento. Secretaría de desarrollo Social (SEDESOL), H. Ayuntamiento de Morelia, Morelia.
- Sandoval, J.P. and Bartlett, S.R. (1991) Land subsidence and earth fissuring on the Central Arizona Project, Arizona. Proceedings of the Fourth International Symposium on Land Subsidence, Houston, May 1991, 249-260.
- Galloway, D., Jones, D.R. and Ingebritsen, S.E. (1999) Land subsidence in the United States. US Geological Survey Circular 1182.
- Geng, D.-Y. and Li, Z.-S. (2000) Ground fissure hazards in USA and China. Acta Seismologicasinica, 13, 466-476. http://dx.doi.org/10.1007/s11589-000-0029-4
- Wang, G.Y., You, G.G., Shi, B., Wu, S.L. and Wu, J.Q. (2010) Large differential land subsidence and earth fissures in Jiangyin, China. Environmental Earth Sciences, 61, 1085-1093. http://dx.doi.org/10.1007/s12665-009-0430-9
- Wang, G.Y., You, G., Shi, B., Qiu, Z.L., Li, H.Y. and Tuck, M. (2010) Earth fissures in Jiangsu Province, China and geological investigation of Hetang earth fissure. Environmental Earth Sciences, 60, 35-43. http://dx.doi.org/10.1007/s12665-009-0167-5
- Zhang, A.G. and Wei, Z.X. (2005) Land subsidence in China. Shanghai Science and Technology Press, Shanghai, 240.
- Phien-wej, N., Giao, P.H. and Nutalaya, P. (2006) Land subsidence in Bangkok, Thailand. Engineering Geology, 82, 187-210. http://dx.doi.org/10.1016/j.enggeo.2005.10.004
- Gambolati, G. and Frezze, R.A. (1973) Mathematical simulation of the subsidence of Venice: Theory. Water Resources Research, 9, 721-733. http://dx.doi.org/10.1029/WR009i003p00721
- Díaz-Salmerón, J.E. (2010) Geometría y monitoreo con GPS de los procesos de subsidencia-cree-falla (PSCF), en la ciudad de Celaya, Guanajuato, México. Master Thesis, Universidad Michoacana de San Nicolás de Hidalgo, Michoacán.
- Giordano, N. (2010) Estudio con georadar (GPR) de la geometría de los procesos de subsidencia-creep-falla (PSCF), en la ciudad de Celaya, Guanajuato, México. Master Thesis, Universidad Michoacana de San Nicolás de Hidalgo, Michoacán.
- Adrian, O.G., Rudolph, D.L. and Cherry, J.A. (1999) The analysis of long term land subsidence near Mexico City: Field investigations and predictive modeling. Water Resources Research, 35, 3327-3341. http://dx.doi.org/10.1029/1999WR900148
- Garduño-Monroy, V.H., Rodríguez-Torres, G.M., IsradeAlcántara, I., Arreygue-Rocha, E., Canuti, P. and Chiesa, S. (1999) Efectos del clima (El Niño) en los fenómenos de fluencia de las fallas geológicas de la ciudad de Morelia. GEOS, Unión Geofísica Mexicana, 9, 84-93.
- Pacheco, J., Arzate, J., Rojas, E., Arroyo, M., Yutsis, V. and Ochoa, G. (2006) Delimitation of ground failure zones due to land subsidence using gravity data and finite element modeling in the Querétaro valley, México. Engineering Geology, 84, 143-160. http://dx.doi.org/10.1016/j.enggeo.2005.12.003
- Trujillo-Candelaria, J.A. (1985) Subsidencia de terreno en la ciudad de Celaya, Gto. In: Reunión sobre Asentamientos Regionales, México, DF, Sociedad Mexicana de Suelo, Asociación Geohidrología Mexicana, Veracruz, 1- 2.
- Martínez-Reyes, J. and Nieto-Samaniego, A.F. (1990) Efectos geológicos de la tectónica reciente en la parte central de México. Universidad Nacional Autónoma de México, Instituto de Geología, Revista, 9, 33-50.
- Alexander, D. (1993) Natural disasters. UCL Press, London.
- Rodríguez-Castillo, R. and Rodríguez-Velázquez, I. (2006) Consecuencias sociales de un desastre inducido, subsidencia. Boletín de la Sociedad Geológica Mexicana, 2, 265-269.
- ESRI (2011) ArcGIS Desktop: Release 10. Environmental Systems Research Institute, Redlands.

