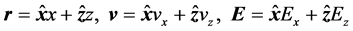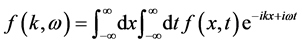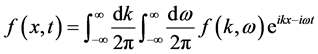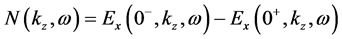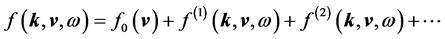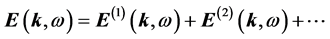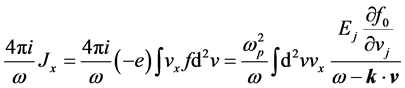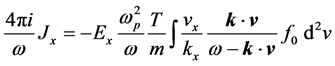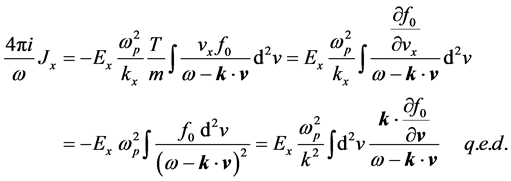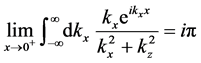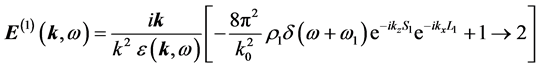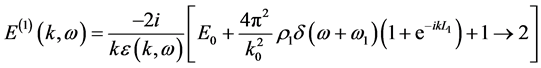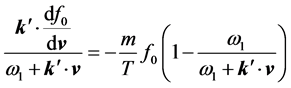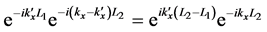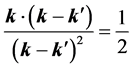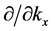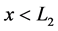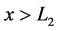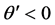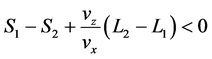Journal of Modern Physics
Vol.07 No.12(2016), Article ID:69578,13 pages
10.4236/jmp.2016.712127
Surface Wave Echo in a Semi-Bounded Plasma
Hee J. Lee, Myoung-Jae Lee
Department of Physics, Hanyang University, Seoul, Korea

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2016; accepted 5 August 2016; published 8 August 2016
ABSTRACT
Plasma echo theory is revisited to apply it to a semi-bounded plasma. Spatial echoes associated with plasma surface wave propagating in a semi-bounded plasma are investigated by calculating the second order electric field produced by external charges and satisfying the boundary conditions at the interface. The boundary conditions are two-fold: the specular reflection condition and the electric boundary condition. The echo spots are determined in terms of the perpendicular coordinate to the interface and the parallel coordinate along which the wave propagates. This improves the earlier works in which only the perpendicular coordinate is determined. In contrast with the echo in an infinite medium, echoes in a bounded plasma can occur at various spots. The diversity of echo occurrence spots is due to the discontinuity of the electric field at the interface that satisfies the specular reflection boundary condition. Physically, the diversity appears to be owing to the reflections of the waves from the interface.
Keywords:
Plasma Echo, Semi-Bounded Plasma, Boundary Condition

1. Introduction
Plasma echoes in an infinite plasma have long been known theoretically [1] [2] as well as experimentally [3] . Spatial echoes were theoretically investigated in a static situation where the non-propagating electric field is directed perpendicular to the interface of a semi-bounded plasma [4] [5] . If the perpendicular direction is designated as the x direction, the electric field E as well as the distribution function f is spatially one- dimensional: 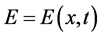 and
and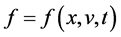 , where
, where  (
(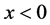 ) is the plasma (vacuum) region. In this case, the corresponding Vlasov equation takes the form of a first order differential equation, and can be solved by satisfying the specular reflection boundary condition at the interface
) is the plasma (vacuum) region. In this case, the corresponding Vlasov equation takes the form of a first order differential equation, and can be solved by satisfying the specular reflection boundary condition at the interface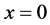 :
: 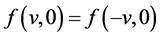 [6] . This differential equation approach with the specular reflection boundary condition for a semi-bounded plasma has been shown to be entirely equivalent with the Fourier transform (with respect to x) under the recipe that the
[6] . This differential equation approach with the specular reflection boundary condition for a semi-bounded plasma has been shown to be entirely equivalent with the Fourier transform (with respect to x) under the recipe that the 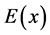 is extended into the region
is extended into the region 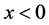 in an odd function manner,
in an odd function manner, 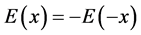 [5] . This odd function extension of
[5] . This odd function extension of 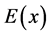 gives rise to a surface term in the Fourier transform of the Poisson equation, which plays a significant role in the determination of the echo spots. It appears that this surface term, which the earlier authors entirely neglected, gives rise to diversity of echo spots [5] . Physically, the surface term manifests the reflection of the electric field at the boundary.
gives rise to a surface term in the Fourier transform of the Poisson equation, which plays a significant role in the determination of the echo spots. It appears that this surface term, which the earlier authors entirely neglected, gives rise to diversity of echo spots [5] . Physically, the surface term manifests the reflection of the electric field at the boundary.
The echo phenomena is the result of a quadratic interaction of the two primary waves launched by two external charges at different locations (spatial echoes) or different times (temporal echoes). In response to the external charges, the plasma distribution function 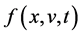 is modulated with the exponential phase
is modulated with the exponential phase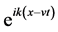 , which is derived from the singularity at
, which is derived from the singularity at 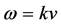 of the linear response function. This term is called the free streaming term since
of the linear response function. This term is called the free streaming term since 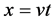 is the characteristic line of the Vlasov equation for a free particle. This rapidly modulating exponential phase makes the
is the characteristic line of the Vlasov equation for a free particle. This rapidly modulating exponential phase makes the 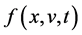 more and more oscillatory as t or x increases, and con- sequently,
more and more oscillatory as t or x increases, and con- sequently, 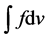
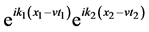
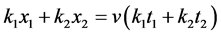
In this work, we investigate spatial echoes in a semi-bounded plasma, taking a full account of the boundary terms which originate from the oddly continuation of the electric field. This work is an extension of the earlier paper by Lee and Lee [5] ; the distribution function and the electric field are now spatially two-dimensional, allowing for the z-dependance. Therefore, the echoes are associated with the surface wave which is propagating in the z-direction. The second order electric field endowed with the additional z-dependance can be Fourier- inverted by contour integration with unstraightforward analytic exercise, and delineating the echo condition requires extra complexity. The important boundary term is the discontinuity of the perpendicular electric field at the interface that is necessary to have the specular reflection boundary condition satisfied [5] . The diversity of echo occurrence spots has been experimentally reported [7] and can be explained by this boundary term. The identification of the echo spot associated with surface wave appears to be useful in experimental point of view [7] .
2. Formulation of the Problem
We consider a plasma consisting of electrons and stationary ions, the latter forming the uniform background. The plasma is assumed to occupy the half-space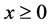
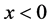
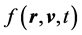
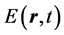
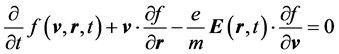
with
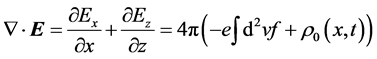
where f is a two-dimensional distribution function, and 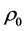
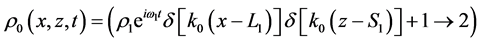
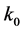
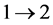
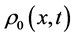
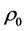
The kinetic equation is supplemented by the kinematic boundary condition which we assume to be the specular reflection condition
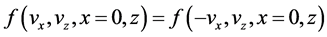
This specular reflection boundary condition is automatically satisfied by extending the electric field com- ponent 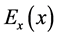
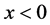
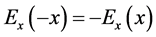
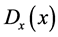
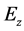
Let us Fourier transform Equations (1)-(3) with respect to t and z to write
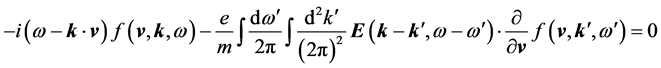
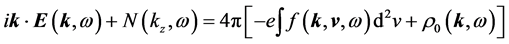
where
is derived from the discontinuity of 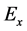
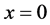
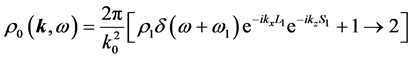
Equations (5) and (6) constitute a set of nonlinear simultaneous equations. We solve the set of equations by successive approximations in terms of perturbation series:
Breaking down Equations (5) and (6) order by order, we have
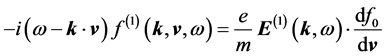
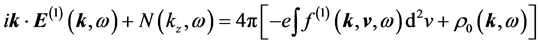
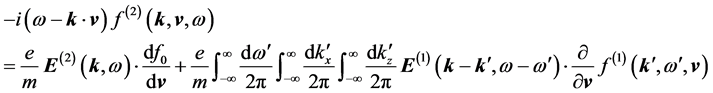
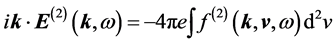
The quantity 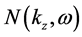
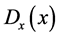
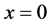
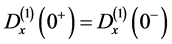
where 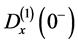
3. Linear Solution
Equations (8) and (9), and 
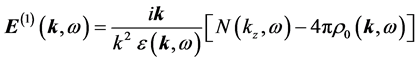
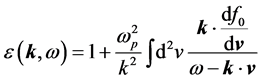
is the dielectric function (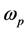
boundary condition (12). By definition, 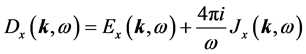
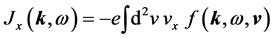
where we used Equation (8). The above quantity equals to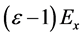
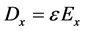
can be most easily proved by assuming 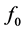
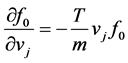
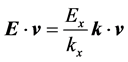
for the last term
Put
Using the above result, we obtain
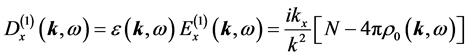
To invert Equation (15), we write
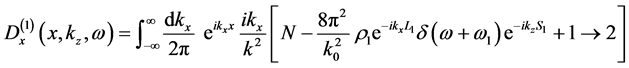
In the above integral, we take the limit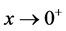
Note that we set up the contour encircling the upper half plane since
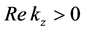
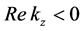
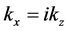
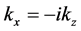
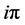
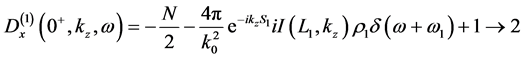
where 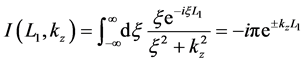
where + (−) sign corresponds to 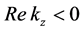
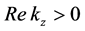
contour winding the lower half plane. Taking the limit 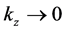
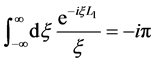
independently of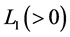
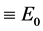
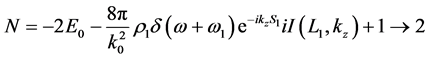
Using the above equation in Equation (13) gives
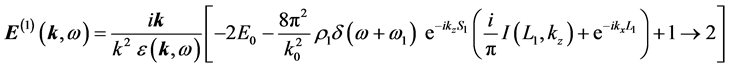
For an infinite plasma without boundary, we have 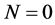
Note that in Equation (20), the 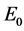
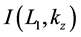
In the static situation where the electric field is nonpropagating, we put 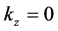
4. Second Order Solution and Echo Occurrence
Next, we deal with the second order equations, Equations (10) and (11). Using Equation (10) in Equation (11) yields, owing to the electrostatic nature of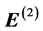
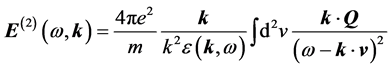
where 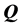
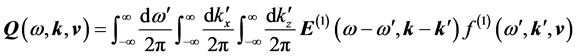
Substituting the first order solutions [Equations (8) and (20)], into the above equations, we can write 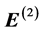
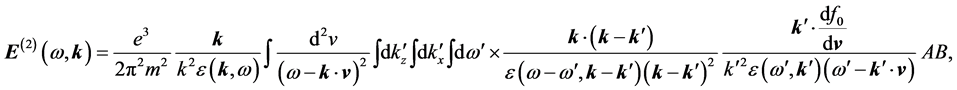
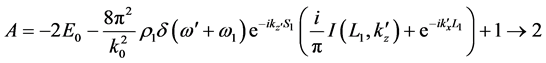
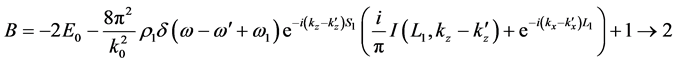
where I stands for the exponential function as given by Equation (18). Since we don’t know yet which sign should be chosen, we keep on using the symbol I. Equation (23) is to be used for investigation of echo occurrence. The various cross terms in the product (AB) are the candidates of echo resonances to see if the condition for vanishing phase can be met.
We choose to investigate a cross term which is 1-term in A multiplied by 2-term in B. With this term, the t-inversion of Equation (23) can be easily carried out by simply putting 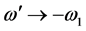

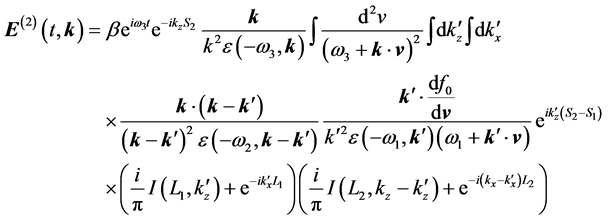
where
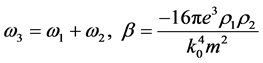
In the above equation, we can assume that the poles associated with the dielectric functions contribute negligibly in the 
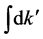
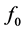
where 1 can be assumed to contribute nothing to the inversion integral in the following, due to phase mixing. Thus, Equation (26) can be further simplified as
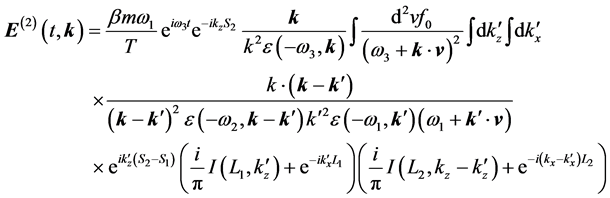
Let us write explicitly the inversion integral of Equation (28) with respect to k:
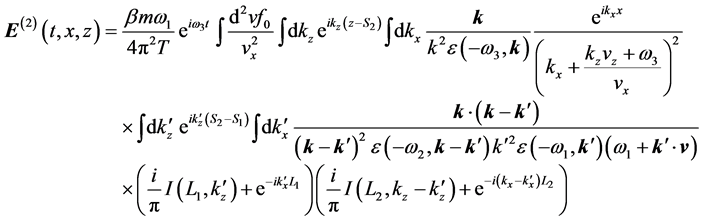
This equation will be examined in view of the possibility of the vanishing phase.
(1) First, we shall consider the interference of two exponential terms in Equation (29):
The important singularities are: the double pole at 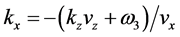
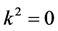
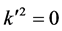
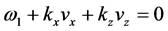
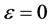
and all the e’s can be taken out of the integral. The residue at the double pole is obtained by taking
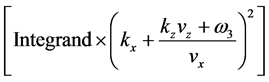
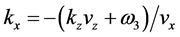
only the exponential functions because they yield asymptotically dominant result. [Or integrate by parts with respect to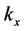
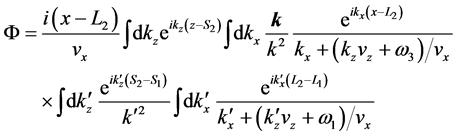
Then 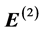
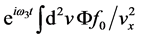
Integral 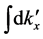
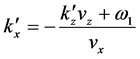
For definiteness we assume
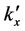
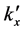
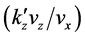
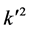
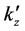
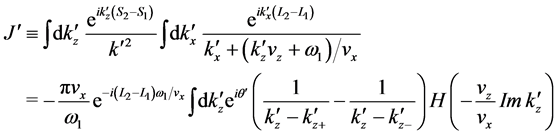
where
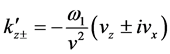
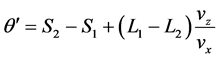
and 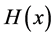
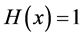

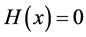
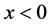
The contour in 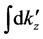
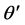
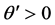
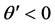
upper (lower) 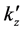
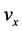
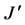
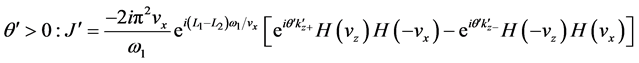
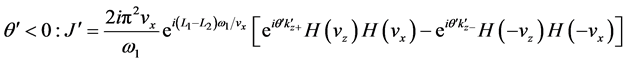
Next, taking on the first part of the integral in Equation (30)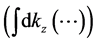
1)
In this case, the 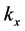
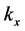
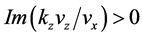
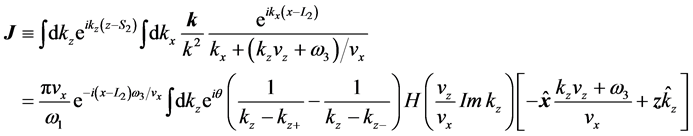
where
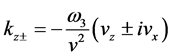
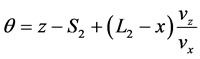
Analogously to the foregoing calculation in
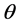
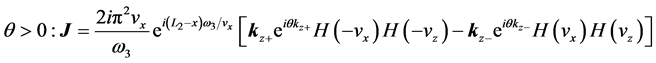
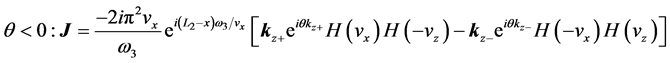
2)
Repeating a similar analysis, we obtain
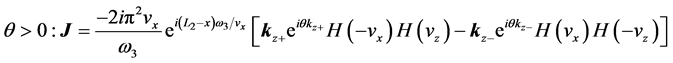
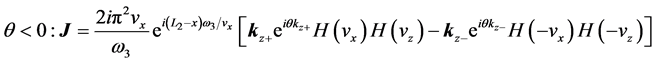
where
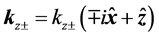
Now, we have to multiply 
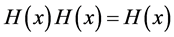
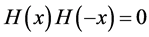
a)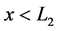
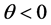
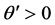
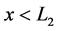
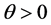
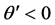
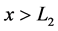
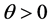
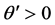
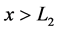
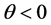
Let us first consider case a). Using Equations (35) and (41), we obtain
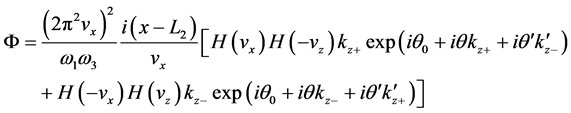
where
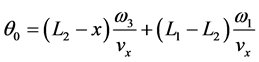
Using Equations (34), (39), and (46), we can obtain the exponential phases:
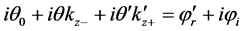
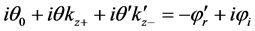
with
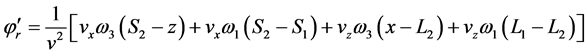
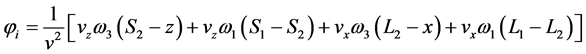
Thus Equation (45) can be written in the form
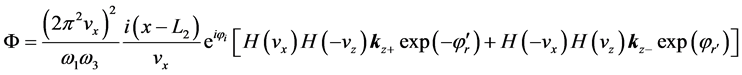
Therefore the velocity integrals in Equation (29) survive the phase mixing when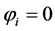
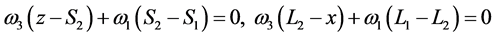
or 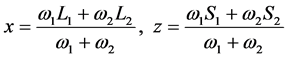
where an echo is given rise to. The electric field 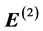
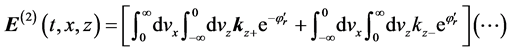
where 
Next, let us calculate case (b). Using Equations (36) and (40) gives
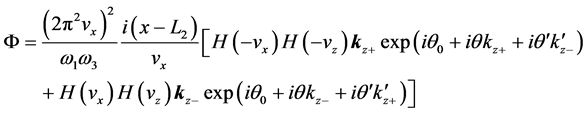
This equation is identical with Equation (45) if 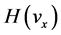
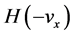
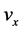
The cases (a) and (b) predict the same echo spot because they yield the same imaginary phase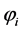
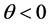
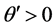
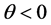
which is the condition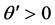
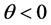
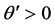
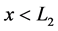
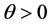
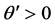
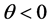
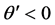
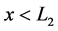
(2) Next, we consider the product of two boundary terms, 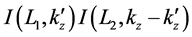
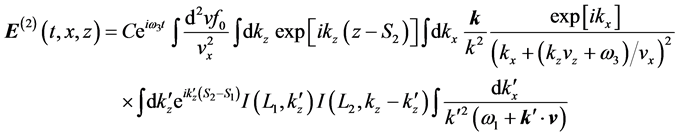
where C is a nonessential constant factor. For definiteness, we assume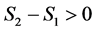
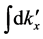
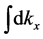
integral can be done easily by picking up the relevant poles, and we can write
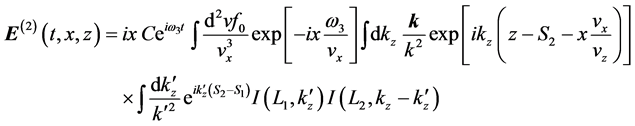
where
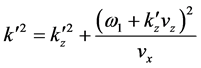
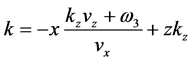
The contour of 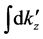
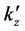
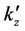
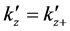
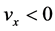
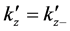
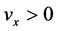
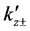
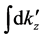
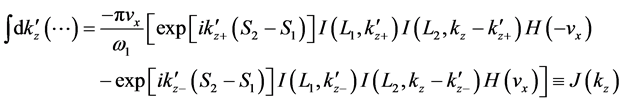
where
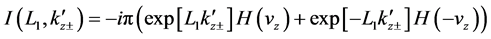
To carry out 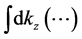
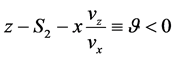
Now we are ready to evaluate 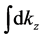
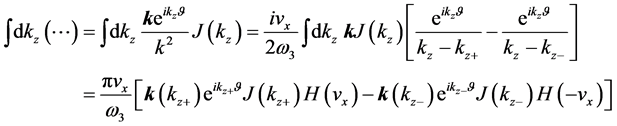
Using Equation (60) in Equation (62) yields
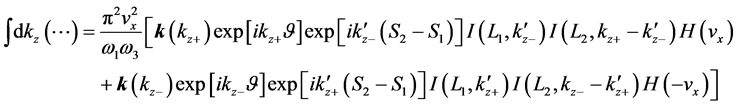
where we have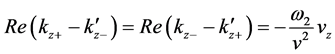
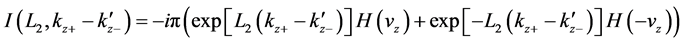
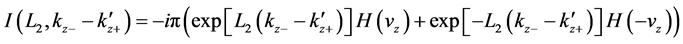
The above two equations and Equation (61) yield
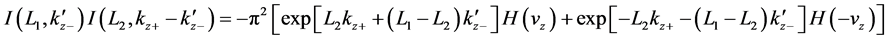
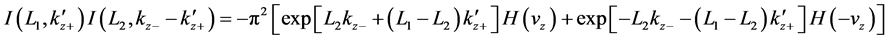
Now we are ready to carry out the velocity integral in Equation (59) by substituting Equation (63) into it. Because of the step functions 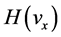
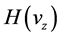
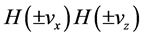
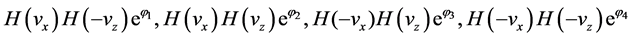
Straightly we can identify:
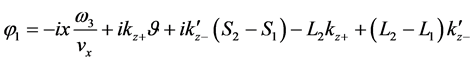
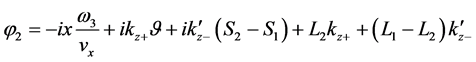
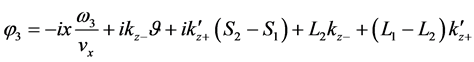
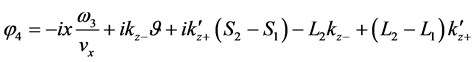
From above, the imaginary phases are obtained as
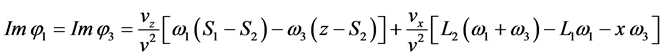
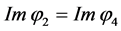
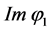
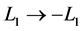
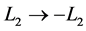
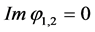
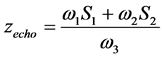
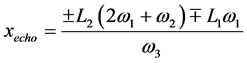
In Equation (75), 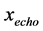
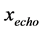
the condition 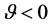
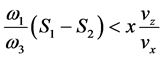
liberty in choosing the sign of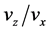
5. Discussion
In Section 3, the plasma electric field was determined in terms of the vacuum electric field. Judicious application of the boundary conditions at the interface enables one to determine the plasma electric field entirely in terms of the external charges without introducing the vacuum electric field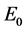
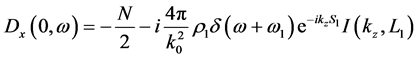
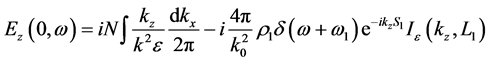
where 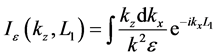
Next, we turn to the vacuum solution.
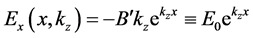
where 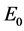
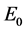
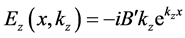
Continuity of 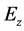
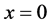
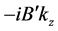
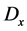
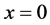
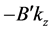
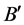
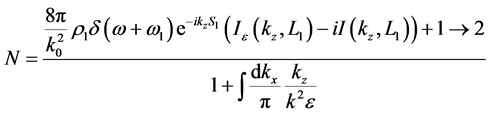
Substituting the above equation into Equation (13) yields
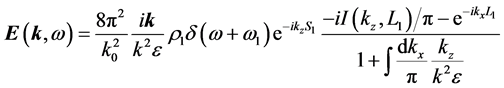
Equation (82) should be compared with Equation (20). Eliminating the vacuum field introduces the
denominator 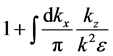
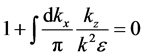
is the electrostatic dispersion relation of the surface wave in a semi-bounded plasma [10] .
In the investigation of echo occurrence, 
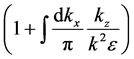
Equations (53) and (74) and (75) are the main results of this work in locating the echo spots associated with the surface wave in a semi-bounded plasma launched by the oscillating external charges at 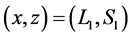
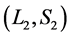
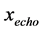
In reality, bounded plasmas are usual rather than exceptional. Important literatures to get acquainted with this field are References [8] and [9] , among others. Surface wave dispersion relation in a plasma slab is derived in Ref. [10] . An exact nonlinear solution of a surface wave excited by external charges is obtained in Ref. [11] .
Acknowledgements
Hee J. Lee thanks Professor L. Stenflo for correspondence. The work of MJL is supported by the National R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (Grant No. 2015M1A7A1A01002786). This support is greatly appreciated.
Cite this paper
Hee J. Lee,Myoung-Jae Lee, (2016) Surface Wave Echo in a Semi-Bounded Plasma. Journal of Modern Physics,07,1400-1412. doi: 10.4236/jmp.2016.712127
References
- 1. Gould, R.W., O’Neil, T.M. and Malmberg, J.H. (1967) Physical Review Letters, 19, 219-222.
http://dx.doi.org/10.1103/physrevlett.19.219 - 2. Krall, N.A. and Trivelpiece, A.W. (1974) Principles of Plasma Physics. McGraw-Hill, New York, p. 547.
http://dx.doi.org/10.1109/tps.1974.4316834 - 3. Malmberg, J.H., Wharton, C.B., Gould, R.W. and O’Neil, T.M. (1968) Physical Review Letters, 20, 95-98.
http://dx.doi.org/10.1103/physrevlett.20.95 - 4. Sitenko, A.G., Pavlenko, V.N. and Zasenko, V.I. (1975) Physics Letters A, 53, 259-260.
http://dx.doi.org/10.1016/0375-9601(75)90431-4 - 5. Lee, H.J. and Lee, M.-J. (2015) The Open Plasma Physics Journal, 8, 1-7.
http://dx.doi.org/10.2174/1876534301508010001 - 6. Landau, L. (1946) Journal of Physics, 10, 25-34.
- 7. Shivarova, A. and Zhelyazkov, I. (1982) Surface Waves in Gas-Discharge Plasmas. In: Boardman, A.D., Ed., Electromagnetic Surface Modes, Wiley, New York, p. 516.
- 8. Vukovic, S. (1986) Surface Waves in Plasmas and Solids. World Scientific, Hong Kong.
- 9. Gradov, O.M. and Stenflo, L. (1983) Physics Reports, 94, 111-137.
http://dx.doi.org/10.1016/0370-1573(83)90004-2 - 10. Lee, H.J. and Lim, Y.K. (2007) Journal of the Korean Physical Society, 50, 1056-1061.
http://dx.doi.org/10.3938/jkps.50.1056 - 11. Stenflo, L. and Yu, M.Y. (2002) Physics of Plasmas, 9, 5129-5130.
http://dx.doi.org/10.1063/1.1521715