Journal of Modern Physics
Vol.5 No.6(2014), Article ID:44624,16 pages DOI:10.4236/jmp.2014.56042
Dark Energy Calculations Using the Paraquantum Gamma Factor (γPψ) on the Relativistic Energy Equation
João Inácio Da Silva Filho1,2
1Group of Applied Paraconsistent Logic, Santa Cecília University-UNISANTA, Santos, Brazil
2Institute for Advanced Studies of the University of São Paulo-IEAUSP, São Paulo, Brazil
Email: inacio@unisanta.br
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 15 February 2014; revised 8 March 2014; accepted 26 March 2014
ABSTRACT
A Paraconsistent Logic (PL) is a non-classical logic which revokes the principle of non-Contradiction and admits the treatment of contradictory information in its theoretical structure. Paraquantum Logic (PQL) is based on a type of PL denominated Paraconsistent Annotated Logic with annotation of two values (PAL2v). The PAL2v have a representative Lattice of four vertices (Lattice FOUR) where are made interpretations with construction of Paraquantum Logical Model and equations capable computation values extract of Observable Variable measurements. The studies of the PQL are based on propagation of Paraquantum logical states ψ in a Paraquantum Universe represented by PQL-Lattice of four vertices. These studies of PQL are based in two Paraquantum factors: the Paraquantum Gamma Factor (γPψ) that has his action in the measurements of Observable Variables in the Physical world and the Paraquantum Factor of quantization hψ, which has his action in the Paraquantum Universe. In this paper we analyze the application of Paraquantum Gamma Factor γPψ and its intrinsic characteristics that add important information into the equation of Einstein’s relativistic Energy (E = MC2). In this article were made several calculations to demonstrate the effects of applying the Paraquantum Gamma Factor (γPψ) in relativistic energy equation. It is found that the factors of using the Paraquantum Logical Model make an adjustment in the equation of Einstein’s relativistic Energy and identify related values with recent results found for the Dark Energy and dark matter. In the Paraquantum/Relativistic Energy equation the γPψ appears as an important factor of transition between the relativistic universe and the Newtonian Universe. The results suggest that its use would be very important in the interpretation of the behavior of other astronomical factors as the cosmological constant and gravitation.
Keywords:Paraconsistent Logic, Paraquantum Logic, Dark Energy, Dark Matter, Relativity Theory

1. Introduction
Models capable of simulating with precision our reality need to work with uncertainties, ambiguities and inconsistencies when it is extracting information in measurements of real world. For calculations based on Classic Logic (binary logic), the uncertain values cause great difficulties for the creation of efficient models to simulate phenomena of real physical systems. Nowadays many researches are being developed to find models based on non-Classic Logics [1] . In this work we use the fundamentals of a non-classical Logic called Paraconsistent Logic (PL) [2] . Paraconsistent logic, in its extended form named Paraquantum Logic (PQL), was used in Physics with good results, where the calculations are based on a factor related to measurements of Observable Variables in the physical world. This factor, called Paraquantum Gamma Factor  was originated in the interpretations of the special relativity theory. In this paper we will explore the characteristics of the Paraquantum Gamma Factor to provide a mathematical modelling that can help to clarify the values relating to dark energy and dark matter found in recent cosmological measurements. Below we present the main concepts of Paraconsistent Logic.
was originated in the interpretations of the special relativity theory. In this paper we will explore the characteristics of the Paraquantum Gamma Factor to provide a mathematical modelling that can help to clarify the values relating to dark energy and dark matter found in recent cosmological measurements. Below we present the main concepts of Paraconsistent Logic.
1.1. Paraconsistent Annotated Logic
Paraconsistent Logic is a non-classical logic which revokes the principle of non-Contradiction and admits the treatment of contradictory information in its theoretical structure [1] -[4] . The Paraconsistent Annotated Logic with annotation of two values (PAL2v) [5] is a class of Paraconsistent Logics particularly represented through a Lattice FOUR (Hasse Diagram) [2] . As seen in [5] [6] , with PAL2v we can get equations that allow quantization calculations of values extracted from measurements on Observable Variables. For calculations the measurement values are expressed as evidence Degrees μ and λ, where:  and
and  and
and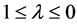 . By geometric transformations the representative values of uncertainties can be considered in two axes of the PAL2v-Lattice [5] : First is through the certainty Degree on the horizontal axis:
. By geometric transformations the representative values of uncertainties can be considered in two axes of the PAL2v-Lattice [5] : First is through the certainty Degree on the horizontal axis:
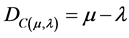 (1)
(1)
Second is through the Contradiction Degree on the vertical axis:
 (2)
(2)
These two values will compose a Paraconsistent Logical State (eτ), located within of the PAL2v-Lattice.
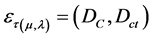 (3)
(3)
where: eτ is the Paraconsistent Logical State.
DC is the Certainty Degree obtained from the evidence Degrees μ and λ.
Dct is the Contradiction Degree obtained from the evidence Degrees μ and λ.
Some features found in the analyses of the PAL2v allow us to consider it as a quantum logic called Paraquantum Logic (PQL) [6] [7] . That way, a Paraquantum function y(Py) is defined as the Paraquantum logical State y:
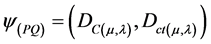 (4)
(4)
For each measurement performed in the physical world of μ and λ, we obtain a unique duple 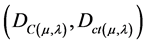
which represents a unique Paraquantum logical state ψ which is a point of the PQL-Lattice [6] -[8] . On the vertical axis of contradictory degrees, the two extreme real Paraquantum logical states are:
a) The contradictory extreme Paraquantum logical state which represents Inconsistency T:

b) The contradictory extreme Paraquantum logical state which represents Indeterminate ^:

On the horizontal axis of certainty degrees, the two extreme real Paraquantum logical states are:
c) The real extreme Paraquantum logical state which represents Veracity t:
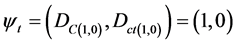
d) The real extreme Paraquantum logical state which represents Falsity F:
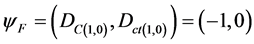
The Vector of State P(ψ) will always be the vector addition of its two component vectors:
 Vector with same direction as the axis of the certainty degrees (horizontal) whose module is the complement of the intensity of the certainty degree:
Vector with same direction as the axis of the certainty degrees (horizontal) whose module is the complement of the intensity of the certainty degree: 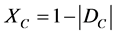
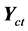 Vector with same direction as the axis of the contradiction degrees (vertical) whose module is the contradiction degree:
Vector with same direction as the axis of the contradiction degrees (vertical) whose module is the contradiction degree: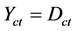 . Figure 1 represents a Paraquantum Logical State with all these features.
. Figure 1 represents a Paraquantum Logical State with all these features.
1.2. The Paraquantum Factor of Quantization hψ
As it was seen in [6] [7] the continuous variation of measurements in the Observable Variables in the physical world results in Paraquantum Logical State (y) propagation in the PQL-Lattice (Paraquantum Universe). When the superposed Paraquantum logical state (ysup) propagates on the lattice of the PQL a value of quantization for
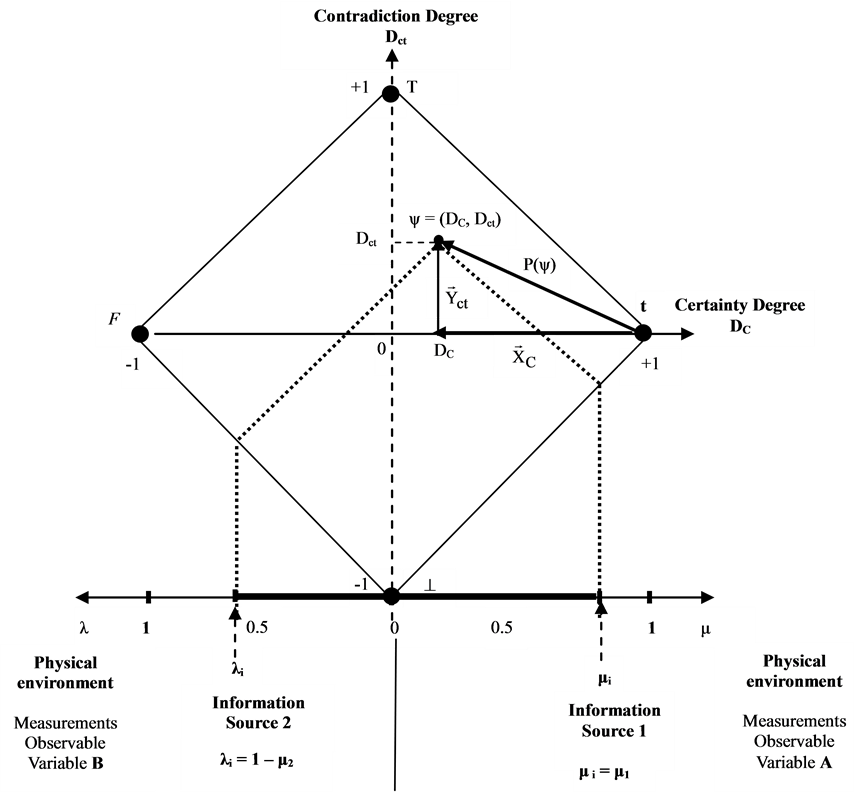
Figure 1. Paraquantum Logical State (ψ) into the Paraquantum Lattice on the point (DC(μ,λ), Dct(μ,λ).
each equilibrium point is established [6] . This point is the value of the contradiction degree of the Paraquantum logical State of quantization yhy, such that:
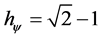 (5)
(5)
where: hy is the Paraquantum Factor of quantization.
The factor hy quantifies the levels of energy through the equilibrium points where the Paraquantum Logical State of quantization yhy is located [7] . In order to completely express it, we have to take into account the factor related to the Paraquantum Leaps which will be added to or subtracted from the Paraquantum Factor of quantization [6] such that:
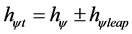 (6)
(6)
where, we can make the calculations:
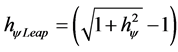 (7)
(7)
So, the Paraquantum Factor of quantization in its complete or total format, which acts on the quantities, is:
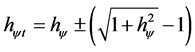 (8)
(8)
1.3. Newton Gamma Factor
In the International System of units (SI), to express the value of force (F) in a unit of Newton (N) an adjustment on the value of mass is necessary [9] . Doing such comparisons and analogies between the International unit Systems (SI) and the British System we obtain for the proportionality factor k in the equation which expresses Newton’s second law (see [9] [10] ).
 in the British System.
in the British System.
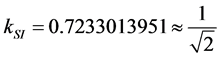 in the International System of units (SI).
in the International System of units (SI).
Given the importance of the Factor , which will be largely used in the equations of the PQL, its value is called Newton Gamma Factor whose symbol is
, which will be largely used in the equations of the PQL, its value is called Newton Gamma Factor whose symbol is  [11] [12] . Therefore, in order to apply classical logics in the Paraquantum Logical model, the Newton Gamma Factor is
[11] [12] . Therefore, in order to apply classical logics in the Paraquantum Logical model, the Newton Gamma Factor is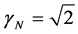 .
.
1.4. Paraquantum Gamma Factor γPψ
The Lorentz Factor 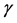 can be identified in the infinite Power Series of the binomial expansion [13] [14] related to the series obtained from consecutively applying the Newton Gamma Factor
can be identified in the infinite Power Series of the binomial expansion [13] [14] related to the series obtained from consecutively applying the Newton Gamma Factor  (see [11] ). In the Paraquantum analysis [8] we define a correlation value called Paraquantum Gamma Factor
(see [11] ). In the Paraquantum analysis [8] we define a correlation value called Paraquantum Gamma Factor  such that:
such that:
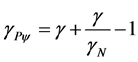 (9)
(9)
where: 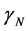 is the Newton Gamma Factor:
is the Newton Gamma Factor: 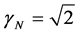
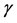 is the Lorentz factor which is:
is the Lorentz factor which is: 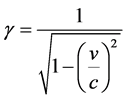
Using the Paraquantum Gamma Factor 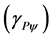 allows the computations, which correlate values of Observable Variables on the Physical World to the values related to quantization through the Paraquantum Factor of quantization (hψ) in the PQL-Lattice (Paraquantum Universe) [6] . The quantitative analysis on the PQL-Lattice defines a quantitative value (QValue) of any physical quantity, which can be represented on the PQL-Lattice horizontal axis of the certainty Degrees and on the vertical axis of the contradiction degrees. Since the maximum value is normalized on the PQL Fundamental Lattice [6] [8] [11] [12] , considering the Paraquantum factor of quantization only, we can write:
allows the computations, which correlate values of Observable Variables on the Physical World to the values related to quantization through the Paraquantum Factor of quantization (hψ) in the PQL-Lattice (Paraquantum Universe) [6] . The quantitative analysis on the PQL-Lattice defines a quantitative value (QValue) of any physical quantity, which can be represented on the PQL-Lattice horizontal axis of the certainty Degrees and on the vertical axis of the contradiction degrees. Since the maximum value is normalized on the PQL Fundamental Lattice [6] [8] [11] [12] , considering the Paraquantum factor of quantization only, we can write:
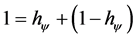 (10)
(10)
In the PQL Fundamental Lattice the unitary value of the quantization is equivalent to a paraquantum quantization represented in the Paraquantum Logical state (ψhψ) added to the value of its complement. We have:
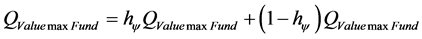 (11)
(11)
where:  is the value of the total amount represented on the unitary axis of the PQL Fundamental Lattice.
is the value of the total amount represented on the unitary axis of the PQL Fundamental Lattice.
Equation (11) shows that the maximum amount of any quantity in the physical environment is composed by two quantized fractions where: one is determined on the Paraquantum Logical state of Quantization ψhψ by the Paraquantum Factor of quantization hψ and the other is determined by its complement (1 − hψ). When the Paraquantum Gamma Factor 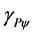 is applied on the paraquantum quantities, besides correlating the paraquantum values to the physical environment, it also works as a factor of expansion or contraction of the PQL-Lattice [11] [12] . Figure 2 represents the PQL-Lattice with a Paraquantum logical State in equilibrium point by these two Factors.
is applied on the paraquantum quantities, besides correlating the paraquantum values to the physical environment, it also works as a factor of expansion or contraction of the PQL-Lattice [11] [12] . Figure 2 represents the PQL-Lattice with a Paraquantum logical State in equilibrium point by these two Factors.
2. The Paraquantum Analysis in Newtonian Universe
As it was seen in [11] [12] , on the Paraquantum analysis of the Physical Systems in the Newtonian universe the
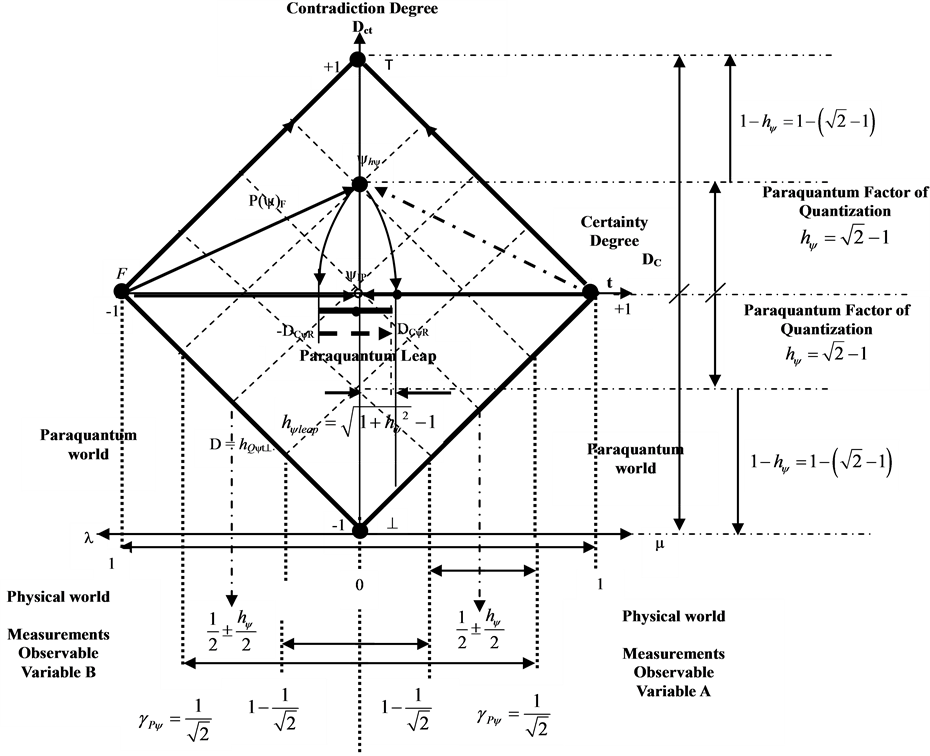
Figure 2. The Paraquantum Factor of quantization hy related to the evidence Degrees with value  in the equilibrium point.
in the equilibrium point.
space as Variable Observable, and the time as Variable Observable, are considered separately. In this way, the action of the Paraquantum Gamma Factor 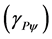 is only in the Variable Observable of the time [11] -[13] . In this case, information Source 1 presents the variation of the space is:
is only in the Variable Observable of the time [11] -[13] . In this case, information Source 1 presents the variation of the space is: 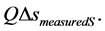
And information Source 2 presents the variation of the time is: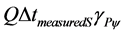 .
.
This manner, in the Newtonian universe the favorable Evidence Degree of Observable Variable velocity is extracted of two source of information.
For the unitary value of the Discourse Universe (or Interest Interval), in the Newtonian universe the Paraquantum Gamma Factor acting in the time correlates in the equilibrium point the three greatness physics [8] [13] , such that:
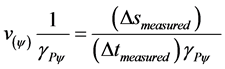 (12)
(12)
where: 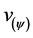 = paraquantum velocity.
= paraquantum velocity.
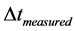 = measured variation of time.
= measured variation of time.
 = measured variation of space.
= measured variation of space.
 = Paraquantum Gamma Factor by (9), were in Newtonian universe, is:
= Paraquantum Gamma Factor by (9), were in Newtonian universe, is: 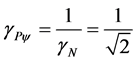
The Paraquantum velocity is the representation of the velocity of the body which is considered as a physical state of motion in the PQL because it is represented by a Paraquantum Logical State (ψ). For a type of static analysis, therefore without propagation of the Paraquantum logical State (ψ) [6] [8] [13] , the quantized Paraquantum velocity in the equilibrium point is:
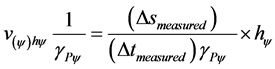 (13)
(13)
where:  = Paraquantum quantized velocity.
= Paraquantum quantized velocity.
According to the foundations of the PQL, the quantized paraquantum velocity in the equilibrium point is represented in the vertical y-axis of the contradiction Degrees of PQL-Lattice. When the analysis is made for a dynamical process Equation (13) of quantization velocity considers the Paraquantum Leap and becomes [8] [13] :
 (14)
(14)
From Equation (8):  then:
then:
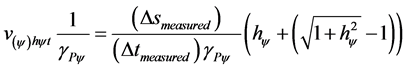 (15)
(15)
We can rewrite (14) as follows: 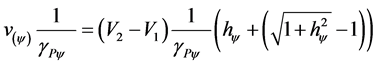
According to the physical laws [9] [10] [14] -[16] , and using the previous equation, we can obtain the paraquantum acceleration in the Newtonian universe [8] [13] :
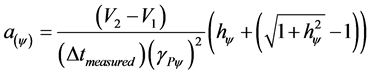 (16)
(16)
where: 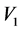 = value of velocity measured at the start.
= value of velocity measured at the start.
 = measured time variation.
= measured time variation.
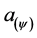 = quantized value of the state of acceleration of the system.
= quantized value of the state of acceleration of the system.
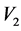 = value of velocity measured at the end.
= value of velocity measured at the end.
 = Paraquantum Gamma Factor (Equation (14)).
= Paraquantum Gamma Factor (Equation (14)).
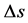 = measured of traveled space.
= measured of traveled space.
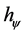 = Paraquantum Factor of quantization.
= Paraquantum Factor of quantization.
Considering the equation that expressed Newton’s second law [9] [10] [14] -[16] , we can isolate the Force (F)
of the Paraquantum analysis, such that: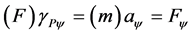 . Being Force obtained by:
. Being Force obtained by: 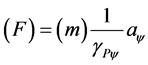
With this equation, the expression of the Paraquantum acceleration (16), we have:
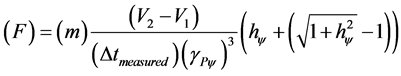 (17)
(17)
This last Equation (17) can be rewritten in such a way the one of the Observable Variables may be represented with quantized values by the action of the Paraquantum Gamma Factor, such that:
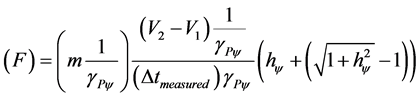 (18)
(18)
In the equilibrium point from Equation (16) we can isolate V2 obtaining: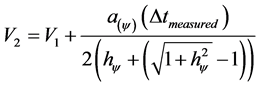 .
.
The average velocity in the Paraquantum Logical Model has a value computed according to the laws of physics [11] : . However, in the Newtonian universe, inverse value of the Newton Factor is considered, so the equation of average velocity can be expressed in a paraquantum form as follows:
. However, in the Newtonian universe, inverse value of the Newton Factor is considered, so the equation of average velocity can be expressed in a paraquantum form as follows:
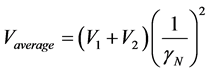 (19)
(19)
The equation of traveled space can be written in a paraquantum fashion as follows:
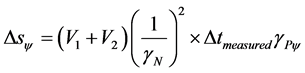 (20)
(20)
Replacing this value of V2 of traveled space ∆s, we results in:
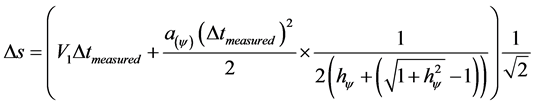 (21)
(21)
Going back to the value of the Paraquantum Gamma Factor, the equation of space which due to the use of paraquantum largenesses expresses a paraquantum value producing it by:
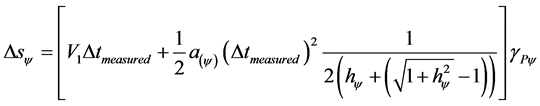 (22)
(22)
where:  = variation of space traveled obtained from paraquantum values.
= variation of space traveled obtained from paraquantum values.
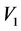 = measured value of initial velocity.
= measured value of initial velocity.
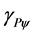 = Paraquantum Gamma Factor.
= Paraquantum Gamma Factor.
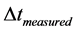 = measured variation of time.
= measured variation of time.
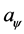 = value of acceleration of the body in study related to the paraquantum world.
= value of acceleration of the body in study related to the paraquantum world.
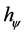 = Paraquantum Factor of quantization.
= Paraquantum Factor of quantization.
Isolating 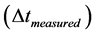 in Equation (16), we have:
in Equation (16), we have: 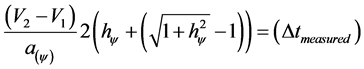
Which replaced in (22) produces: 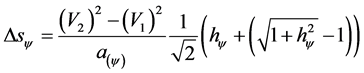
Going back to the value corresponding to the Paraquantum Gamma Factor in the Newtonian universe, we have:
 (23)
(23)
When the Observable Variables that produce the Evidence Degrees are values of space traveled with square velocity, we can obtain the equation that determines the Paraquantum acceleration:
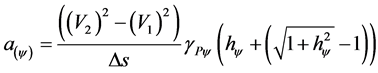 (24)
(24)
Using Equation (24) of acceleration and equation which expresses Newton’s second law mathematically [10] [11] , Force can be computed by multiplying mass by the Paraquantum acceleration, such that:
 (25)
(25)
From the laws of classical physics [11] we obtain Work multiplying the value of Force by the displacement, then:
 (26)
(26)
Paraquantum Kinect Energy
A full Paraquantum Work (Wψ) is identified with the total kinetic Energy at the equilibrium point where the Paraquantum Logical State is located: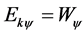 . Therefore, the total kinetic Energy is expressed by:
. Therefore, the total kinetic Energy is expressed by:
 (27)
(27)
And the equation of the Paraquantum kinetic energy, represented at the equilibrium point of the PQL-Lattice, is expressed by:
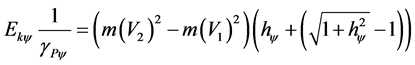 (28)
(28)
where: 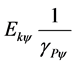 = is the kinetic energy quantized with respect to the physical world.
= is the kinetic energy quantized with respect to the physical world.
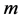 = Mass of the body being considered.
= Mass of the body being considered.
The Work performed in the physical universe is identified with the quantity of paraquantum kinetic energy quantized with respect to the physical environment. Being the kinetic Energy the system’s energy variation [9] [10] [14] -[16] , then, from the previous equation we can obtain the paraquantum final energy such that:
 (29)
(29)
where: 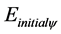 = Quantized initial kinetic energy.
= Quantized initial kinetic energy.
 = value of the velocity measured at the start.
= value of the velocity measured at the start.
And the paraquantum final energy such that:
 (30)
(30)
where: 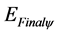 = Quantized final kinetic energy.
= Quantized final kinetic energy.
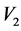 = value of the velocity measured at the end.
= value of the velocity measured at the end.
The total amount of energy involved in the Paraquantum Logical Model [13] in a static state is that one computed at the value of the measured final velocity such that:
 (31)
(31)
when related to the physical environment, the Paraquantum total energy in the static state is expressed by:
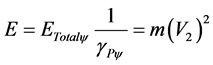 (32)
(32)
where:
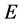 = Total energy of the system involved by the Paraquantum Logical Model in the static state.
= Total energy of the system involved by the Paraquantum Logical Model in the static state.
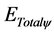 = Total quantized Energy of the system involved by the Paraquantum Logical Model.
= Total quantized Energy of the system involved by the Paraquantum Logical Model.
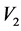 = Final value of measured velocity.
= Final value of measured velocity.
As the analysis is done in the Newtonian Universe the velocity in these equations is not related to the speed of light in a vacuum c, but obtained by dividing the space and time, where only time suffers the action of Paraquantum Gamma Factor [8] [13] . As, for these equations the velocity that is related to the speed of light in vacuum is equal to zero, then the Lorentz factor is unitary . This causes the value of the Paraquantum Gamma Factor [13] , which acts in these equations extracted in the Newtonian universe, is always the inverse of the factor of Newton:
. This causes the value of the Paraquantum Gamma Factor [13] , which acts in these equations extracted in the Newtonian universe, is always the inverse of the factor of Newton: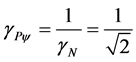 . Figure 3 shows the representation of time (t), space (s) and of the mass
. Figure 3 shows the representation of time (t), space (s) and of the mass
(m) that is multiplying the velocity squared (V2).
3. The Paraquantum Analysis in Relativistic Universe
Is verified that for Newtonian universe the mass is constant and the total Paraquantum energy Et(ψ) is represented only in the y-axis of the PQL-Lattice. Comparing the amounts of total energy with the quantized pure final kinetic energy at the equilibrium point, therefore, comparing the Equation (11) with Equation (31), we have:
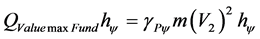
Being the quantized pure final kinetic energy obtained at the equilibrium point represented by:
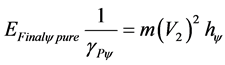 (33)
(33)
Since the Paraquantum Logical Model is normalized, there is a complemented quantized pure kinetic energy, therefore:
 (34)
(34)
So, the total amount of total kinetic Energy, without adding the effect of the Paraquantum Leaps to it, appears as the unit on the axis of the contradiction degrees of the PQL-Lattice, so that the normalized value is computed by:
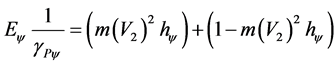 (35)
(35)

Figure 3. Representation of time (t), space (s) and of the mass (m) that is multiplying the velocity squared (V2)―with the Paraquantum kinetic energy E(ψ) represented in they-axis of the PQL-Lattice.
Equation (35) is for generalized values, however, for the relativity theory the pure complemented final kinetic energy can be written taking the unitary value in which it is bounded by the speed of the light c in the vacuum [14] [16] . That is, for the speed V listed as a fraction of the speed of light in vacuum: .
.
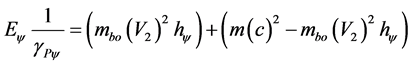 (36)
(36)
where:  Relativistic mass, that is, the mass produced by Relativistic effects.
Relativistic mass, that is, the mass produced by Relativistic effects.
 body mass, that is, the mass of the body studied.
body mass, that is, the mass of the body studied.
The first part of energy Equation (36) is the Kinect Energy of the universe Newtonian [14] :
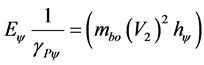 (37)
(37)
which related to the physical environment it is expressed by:
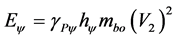 (38)
(38)
The second part of Equation (36) is the energy complemented, is the part corresponding relativistic analysis, therefore:
 (39)
(39)
From Equation (39) we can write the Paraquantum Relativistic Energy equation such that:
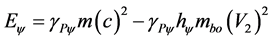 (40)
(40)
where:  = complemented final quantized kinetic Energy or Paraquantum relativistic Energy.
= complemented final quantized kinetic Energy or Paraquantum relativistic Energy.
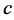 = Constant value of the velocity of light in the vacuum, imposed as maximum value.
= Constant value of the velocity of light in the vacuum, imposed as maximum value.
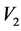 = measured value of the particle’s velocity related c.
= measured value of the particle’s velocity related c.
 = Relativistic mass, that is, the mass produced by Relativistic effects.
= Relativistic mass, that is, the mass produced by Relativistic effects.
 = Mass of the particle.
= Mass of the particle.
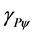 = Paraquantum Gamma Factor by Equation (9).
= Paraquantum Gamma Factor by Equation (9).
For this condition the PQL-Lattice is bounded by the velocity c of light in the vacuum [14] [16] , such that now it is possible to obtain the paraquantum pure total energy based on the maximum bound which is the speedof light in the vacuum. Equation (39) represents the value of the kinetic energy from the equilibrium point depending on the speed of the body related to the speed of light in vacuum. For the final value of the amount of energy in a given speed, the equation will be:
 (41)
(41)
If we consider in the Equation (41) the condition: 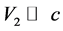 or small values of mass, then we can make an equation of approximated values:
or small values of mass, then we can make an equation of approximated values:
 (42)
(42)
where: 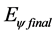 = Paraquantum pure total kinetic Energy of the system.
= Paraquantum pure total kinetic Energy of the system.
 = Constant value of the light speed in the vacuum, imposed as maximum value.
= Constant value of the light speed in the vacuum, imposed as maximum value.
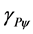 = Paraquantum Gamma Factor.
= Paraquantum Gamma Factor.
3.1. Paraquantum/Relativistic Energy Equation
A full Paraquantum Relativistic Energy equation is obtained if we consider the irradiant Energy caused by the Paraquantum leap [6] [8] [11] [12] [17] . In this way Equation (36) will be written as:
 (43)
(43)
As from Equation (8),  , then we have the total energy equation:
, then we have the total energy equation:
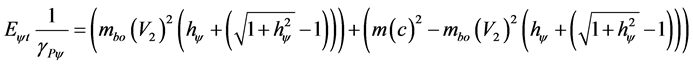 (44)
(44)
The first part of the Energy Equation (44) is the Kinect Energy of the Newtonian universe:
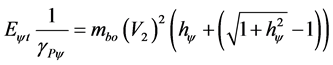 (45)
(45)
which related to the physical environment it is expressed by:
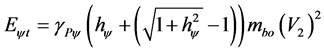 (46)
(46)
As in the Newtonian universe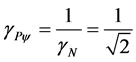 , then:
, then:
 (47)
(47)
The second part of Equation (44) is the energy complemented of the part corresponding at relativistic analysis, therefore:
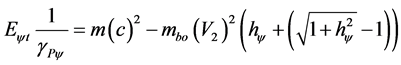 (48)
(48)
From Equations (47) and (48) we can write the Paraquantum Relativistic Energy equation, such that:
 (49)
(49)
The Equation (49) represents the value of the kinetic energy from the Paraquantum equilibrium point hψ [6] depending on the mass and speed of the body related to the speed of light in vacuum.
In the Paraquantum equilibrium point between the Newtonian and Relativistic Universe is possible to match the value of rest energy with the Newtonian kinetic energy value. So, making the equality of relativistic part with Newtonian part of Equation (49), we have: 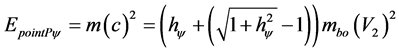
For Paraquantum equilibrium point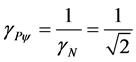 , then the Equation (49) can be write:
, then the Equation (49) can be write:
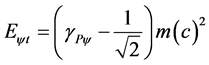 (50)
(50)
And from Equation (44) we have the final equation of the energy:
 (51)
(51)
Equation (51) is the Paraquantum/Relativistic Energy Equation.
3.2. Expanded Paraquantum/Relativistic Energy Equation
As 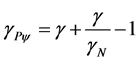 the final Paraquantum/relativistic Energy Equation (51) can be writing:
the final Paraquantum/relativistic Energy Equation (51) can be writing:
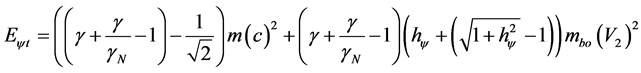 (52)
(52)
And  is the Newton Factor with value
is the Newton Factor with value  then:
then:
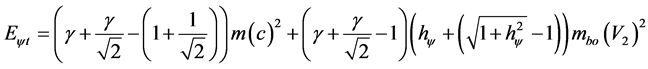 (53)
(53)
The rigid body or referenced object with null speed (V2 = 0) the Lorentz Factor is equal to 1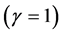 . This results in:
. This results in: 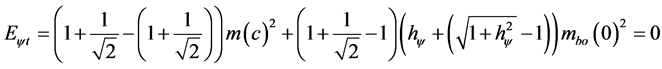
If we consider in Equation (45), the condition: 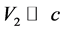 or small values of mass, then
or small values of mass, then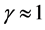 , and:
, and:
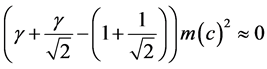
and Kinect energy is calculated by Equation (47):
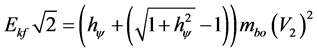
where: the Paraquantum Factor of Quantization 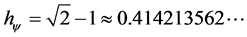
And: the Paraquantum Leap value 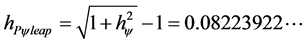

But since the rigid body or referenced object are moving there is a Lorentz factor value, therefore the equation (51) can always be used in its overall shape. This means that the final energy equation can be used in the relativistic Universe, as well as in the Newtonian universe.
3.3. Results and Discussion about Paraquantum/Relativistic Energy Equation
As seen in [9] [11] [14] -[16] when the Lorentz factor tends to 1 the relativistic math expressions tend to classic expressions. Thus, the Lorentz factor can be listed as:
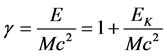 (54)
(54)
From Equation (54) the relativistic Energy (E) by the special relativity theory [14] [16] can be written as:
 (55)
(55)
Or:
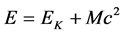 (56)
(56)
Using Equation (54) the relativistic kinetic energy can be written as:
 (57)
(57)
If ,
, 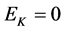 , then, from Equation (56) we have:
, then, from Equation (56) we have:
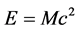 (58)
(58)
For the conventional kinetic energy calculation [14] [16] is used Equation (57) and with the use of the Paraquantum Logical Model is applied to Equation (50). In relation to the results of Equation (57) it is an established fact that the values obtained by Equation (50) always is added 
In percentage means that the Energy value obtained by Equation (50) has 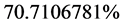 more than the value obtained by applying Equation (57). This percentage value is equivalent to the dark energy [18] [19] obtained in the latest astronomical observations. This happens because the use of conventional relativistic equation (Equation (50) does not take into account Relativistic effects related to the matter. Using Equation (51) it is an established fact that this effect can only be despised when speed is very low in relation to speed of light, or when the mass of the body is very small. Therefore, compared to conventional energy equation (Equation (57)), Equation (51) adds the value of the relativistic effects and also the value related to speed and with mass of body in the Newtonian universe.
more than the value obtained by applying Equation (57). This percentage value is equivalent to the dark energy [18] [19] obtained in the latest astronomical observations. This happens because the use of conventional relativistic equation (Equation (50) does not take into account Relativistic effects related to the matter. Using Equation (51) it is an established fact that this effect can only be despised when speed is very low in relation to speed of light, or when the mass of the body is very small. Therefore, compared to conventional energy equation (Equation (57)), Equation (51) adds the value of the relativistic effects and also the value related to speed and with mass of body in the Newtonian universe.
This value added to more amounts to  or
or 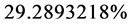 of remaining energy, or dark matter [18] [19] . This added value of
of remaining energy, or dark matter [18] [19] . This added value of 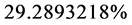 can still be distributed for Relativistic effects, which vary by the action of the Lorentz factor, constant mass-related effects and effects caused by Paraquantum Leap, that it is related to acceleration [6] -[8] (Paraquantum Irradiant Energy). This energy distribution is studied by expansion of second part of Equation (51), as is seen below.
can still be distributed for Relativistic effects, which vary by the action of the Lorentz factor, constant mass-related effects and effects caused by Paraquantum Leap, that it is related to acceleration [6] -[8] (Paraquantum Irradiant Energy). This energy distribution is studied by expansion of second part of Equation (51), as is seen below.
From Equation (51): 
We can make the distribution of the Paraquantum Gamma Factor for the second part, such that:

Therefore, as seen in Equation (51) this second part is about the rest energy, now with the relativistic effects:
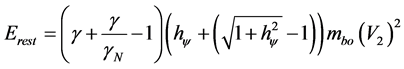
Making the distributive to only the Lorentz Factor-related values, we get:
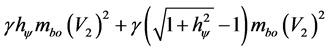
Continuing, we have: 
With the values for the constants: 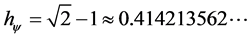 and
and 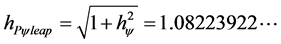
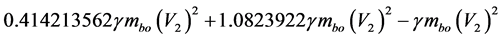
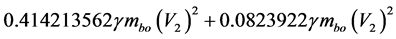
So this is the relativistic value of part related to Lorentz factor:
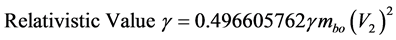
Similarly we can calculate the value for the Lorentz factor divided by root of 2,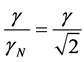 :
:
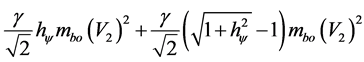
Continuing, we have: 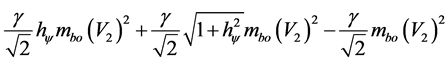
Considering the constant values: 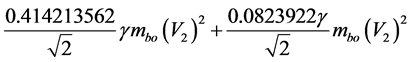
So this is the relativistic value of part related to Lorentz factor divided by root of 2:

Similarly we can calculate the value related at constant −1: 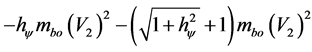
Continuing, we have: 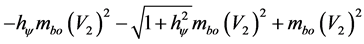

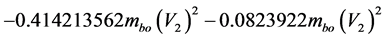
So this is the non-relativistic value of part related to constant −1:
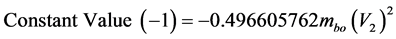
Added the relativistic effects, we have: 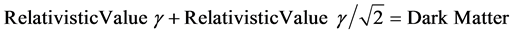
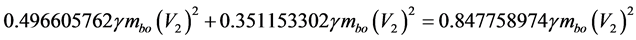
The percentage in the rest Energy: 
That is 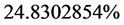 of Relativistic Dark Matter.
of Relativistic Dark Matter.
Then 
That is 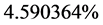 of Ordinary Matter.
of Ordinary Matter.
The total of relativistic effects is: 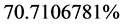 plus
plus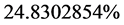 .
.
That is 
And the effect of constant −1 is the Kinect Energy value calculates by Newtonian Universe.
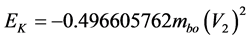
These values found by Paraquantum Logical Model are compatible with the values found by The Wilkinson Microwave Anisotropy Probe (WMAP) [18] [19] . The WMAP [18] [19] is also known as the Microwave Anisotropy Probe (MAP), and Explorer 80. It is a spacecraft which measures differences in the temperature of the Big Bang’s remnant radiant heat – the Cosmic Microwave Background Radiation—across the full sky. Figure 4 shows the relationship between the values found by WMAP and the values calculated by the equations of the Paraquantum Logical Model.
In the values obtained by WMPA the universe comprises only 4.6% atoms. A much greater fraction, 24% of the universe, is a different kind of matter that has gravity but does not emit any light, called “dark matter”. The

Figure 4. Relationship of the values of dark energy and dark matter found by calculation of the paraquantum logical model and those observed by WMAP.
biggest fraction of the current composition of the universe, 71%, is a source of anti-gravity (sometimes called “dark energy”) that is driving an acceleration of the expansion of the universe [18] [19] .
4. Conclusion
In this paper we presented a method calculation based on Paraconsistent Logic that uses structured interpretations in an equilibrium point related to Paraquantum Factor of quantization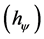 . This factor is located in the Paraquantum universe represented by a lattice of four vertices. Relating the equilibrium point with values measured in Observable Variables in physical world we can work with another factor called Paraquantum Gamma factor
. This factor is located in the Paraquantum universe represented by a lattice of four vertices. Relating the equilibrium point with values measured in Observable Variables in physical world we can work with another factor called Paraquantum Gamma factor . The equations related to the
. The equations related to the  and
and 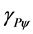 factors allowed that we could obtain an equation of Paraquantum/Relativistic Energy with adjustments that allowed calculating values similar to those of Dark Energy and Dark Matter observed recently. It turns out that the equation for the relativistic Energy presented in this work is unifying, because it can be used in calculations in the Newtonian universe and also in the Relativistic universe. Results demonstrate that the application of Paraquantum Logic demonstrates a great efficiency to answer questions related to Dark Energy and Dark Matter. The expansion of the Paraquantum/Relativistic Energy Equation presented in this work shows that there are intrinsic parts in future works that may lead to elucidation of other constants and physical quantities, such as gravitation and cosmological constant.
factors allowed that we could obtain an equation of Paraquantum/Relativistic Energy with adjustments that allowed calculating values similar to those of Dark Energy and Dark Matter observed recently. It turns out that the equation for the relativistic Energy presented in this work is unifying, because it can be used in calculations in the Newtonian universe and also in the Relativistic universe. Results demonstrate that the application of Paraquantum Logic demonstrates a great efficiency to answer questions related to Dark Energy and Dark Matter. The expansion of the Paraquantum/Relativistic Energy Equation presented in this work shows that there are intrinsic parts in future works that may lead to elucidation of other constants and physical quantities, such as gravitation and cosmological constant.
References
- Krause, D. and Bueno, O. (2007) Scientific Theories, Models, and the Semantic Approach. Principia, 11, 187-201.
- Da Costa, N.C.A. and Marconi, D. (1989) An Overview of Paraconsistent Logic in the 80’s. The Journal of Non-Classical Logic, 6, 5-31.
- Da Costa, N.C.A. (1974) On the Theory of Inconsistent Formal Systems. Notre Dame Journal of Formal Logic, 15, 497-510. http://dx.doi.org/10.1305/ndjfl/1093891487
- Jas’kowski, S. (1969) Propositional Calculus for Contradictory Deductive Systems. Studia Logica, 24, 143-157. http://dx.doi.org/10.1007/BF02134311
- Da Silva Filho, J.I., Lambert-Torres, G. and Abe, J.M. (2010) Uncertainty Treatment Using Paraconsistent Logic―Introducing Paraconsistent Artificial Neural Networks. IOS Press, Amsterdam, 328.
- Da Silva Filho, J.I. (2011) Paraconsistent Annotated Logic in analysis of Physical Systems: Introducing the Paraquantum Factor of quantization hψ. Journal of Modern Physics, 2, 1397-1409. http://dx.doi.org/10.4236/jmp.2011.211172
- Da Silva Filho, J.I. (2012) An Introductory Study of the Hydrogen Atom with Paraquantum Logic. Journal of Modern Physics, 3, 312-333. http://dx.doi.org/10.4236/jmp.2012.34044
- Da Silva Filho, J.I. (2011) Analysis of Physical Systems with Paraconsistent Annotated Logic: Introducing the Paraquantum Gamma Factor γψ. Journal of Modern Physics, 2, 1455-1469. http://dx.doi.org/10.4236/jmp.2011.212180
- Mckelvey, J.P. and Grotch, H. (1978) Physics for Science and Engineering. Harper and Row Publisher, Inc., New York, London.
- Tipler, P.A. (1976) Physics. Worth Publishers Inc., New York.
- Da Silva Filho, J.I. (2012) Relativity Theory and Paraquantum Logic—Part I: The Time and Space in the Paraquantum Logical Model. Journal of Modern Physics, 3, 957-971. http://dx.doi.org/10.4236/jmp.2012.39126
- Da Silva Filho, J.I. (2012) Relativity Theory and Paraquantum Logic—Part II: Fundamentals of a Unified Calculation. Journal of Modern Physics, 3, 972-988.
- Da Silva Filho, J.I. (2013) Introducing the Paraquantum Equations and Applications. Journal of Modern Physics, 4, 712-733. http://dx.doi.org/10.4236/jmp.2013.46098
- Tipler, P.A. and Llewellyn, R.A. (2007) Modern Physics. 5th Edition, W. H. Freeman and Company, New York.
- Tipler, P.A. and Tosca, G.M. (2007) Physics for Scientists. 6th Edition, W. H. Freeman and Company, New York.
- Einstein, A. (1955) Relativity the Special and the General Theory. Methuen & Co. Ltd., London.
- Da Silva Filho, J.I. (2012) Analysis of the Spectral Line Emissions of the Hydrogen Atom with Paraquantum. Journal of Modern Physics, 3, 233-254. http://dx.doi.org/10.4236/jmp.2012.33033
- Spergel, D.N., et al. (2006) WMAP Collaboration. Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology.
- Ade, P.A.R., Aghanim, N., Armitage-Caplan, C., et al. (2013) (Planck Collaboration) Planck 2013 Results. I. Overview of Products and Scientific Results—Table 9. Astronomy and Astrophysics (Submitted).

