Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8047 , 5 pages DOI:10.4236/jmp.2011.210136
Separation Method in the Problem of a Beam-Plasma Interaction in a Cylindrical Warm Plasma Waveguide
1Mathematical Department, Faculty of Science, King Abduel Aziz University, Jeddah, Saudi Arabia
2Plasma Physics and Nuclear Fusion Department, Nuclear Research Center, Atomic Energy Authority, Cairo, Egypt
E-mail: *drkhalede@yahoo.com
Received February 5, 2011; revised March 26, 2011; accpeted April 8, 2011
Keywords: Separation Method, Beam-Plasma Interaction, Warm Plasma Waveguide
ABSTRACT
The stabilization effect of a strong HF electric field on beam-plasma instability in a cylindrical warm plasma waveguide is discussed. A mathematical technique “separation method” applied to the two-fluid plasma model to separate the equations, which describe the system, into two parts, temporal and space parts. Plasma electrons are considered to have a thermal velocity. It is shown that a HF electric field has no essential influence on dispersion characteristics of unstable surface waves excited in a warm plasma waveguide by a low-density electron beam. The region of instability only slightly narrowing and the growth rate decreases by a small parameter and this result has been reduced compared to cold plasma. Also, it is found that the plasma electrons have not affected the solution of the space part of the problem.
1. Introduction
A great number of publications [1-4], and refs. Cited therein, are devoted to theoretical study of beam-plasma instability.
The investigation of beam-plasma instabilities evokes interest only from the point of view of understanding of this particular type of instability but also as a method of modeling the instabilities caused by resonant interactions in more complex cases, in particular in that of modeling the transition from the laminar to the turbulent state, the turbulence resulting from instabilities, and the control of instabilities.
It is well known that (e.g. [1,5]) propagation of charged particle beams through plasma leads to development of great variety of instabilities. Sometimes such an instabilities could be used as a basis for the construction of an effective generators of electromagnetic radiation, for heating of magnetically confined plasmas, and for particle acceleration. But often beam instabilities are undesirable. This is true particularly for the experiments on magnetic fusion research where instabilities may cause an appreciable enhancement in the transport of particles and heat across the confining magnetic field. Therefore stabilization of instabilities excited by a beam of charged particles in plasmas is an important part of the more general problem of controlling instabilities in magnetic traps.
The stabilization effect of a uniform HF electric field on a two-stream (Buneman) instability in uniform unbounded plasma has been for the first time investigated in [6]. The dispersion equation for characteristic frequencies of electrostatic oscillations excited by relative motion of electrons and ions in a HF electric field has been obtained and analyzed. The presence of a pump wave strongly modifies the dispersion equation of Buneman instability. As a consequence the growth rate of instability reduces in comparison with the growth rate at vanishing external field amplitude.
The extremely interesting properties of plasma located in a strong high frequency (HF) electric field have stimulated a broad range of theoretical investigations in this promising field of physics.
A broad class of instabilities was predicted to accompany the processes taking place in plasma placed in a HF field. On the other hand, for a number of cases the stabilizing effect of a HF field on unstable plasma states was pointed out. A detailed review of the theory of the plasma HF field interaction was given in ref. [7].
Parametric interaction of external HF electric field with an electrostatic surface wave in an isotropic nonuniform plasma has been investigated in ref. [8] using special method based on the separation of variables.
Different from previous works on beam-plasma instability [9-11], we study the effect of both the effects of both plasma inhomogeneity and the thermal electron motion on the quenching of the beam-plasma instability. Investigation of beam-plasma interaction presents a great interest for development of effective methods via plasma stability, amplification and generation of electromagnetic waves, acceleration of charged particles in plasma, high frequency heating of plasma, and so on [12-14].
It has been shown that [15] dispersion equation describing parametric excitation of surface waves at the boundary of isotropic plasma-vacuum to within the eigen frequency renormalization coincide with the equations that determine the parametric excitation of volumetric waves in uniform unbounded plasma. Proceeding from this conclusion the method for investigation of parametric interaction of external HF electrical field with electrostatic oscillations in isotropic bounded nonuniform plasma has been proposed [8]. The method makes it possible to separate the problem into two parts. The “dynamical” part describes the parametric build up of oscillations and corresponding equations within the renormalization of eigen frequencies coincide with equations for the parametrically unstable waves in an infinite uniform plasma. Natural frequencies of oscillations and spatial distribution of the amplitude of the self-consistent electrical field are determined from the solution of a boundary-value problem (“space” part) taking into account specific spatial distribution of the plasma density. The proposed approach (“separation method”) is significantly simpler than the method ordinarily employed in the theory of parametric resonance in nonuniform plasma [10,15,16]. Therefore it is of special interest to apply the separation method to solution of different problems involving parametric excitation of electrostatic waves in bounded nonuniform plasma.
In the present work we investigate the suppression of HF electric field on beam-plasma interaction in the cylindrical warm plasma waveguide.
2. The Influence of HF Electric Field on the Instability of a Low-Density Electron Beam Passing through Plasma Waveguide
We assume that a uniform cold electron beam propagating along radially nonuniform cylindrical plasma waveguide. The radius of the beam R is supposed to coincides with the radius of the plasma cylinder.
Let us now assume that an electron beam of low density 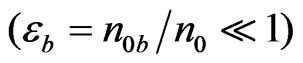 is passing through a quasineutral plasma with the velocity
is passing through a quasineutral plasma with the velocity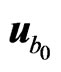 . We shall also suppose that both plasma components are at rest
. We shall also suppose that both plasma components are at rest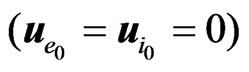 . We take the vector of the external HF field
. We take the vector of the external HF field  to be oriented along the axis of the plasma cylinder. Equilibrium density of plasma
to be oriented along the axis of the plasma cylinder. Equilibrium density of plasma 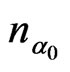 varies along the radius.
varies along the radius.
The “separation method” has been described [6,17] in application to the problem of parametric excitation of surface waves in a cold isotropic plasma. Here we shall follow this paper. Representing the perturbations of velocity, density and electrical potential in the form 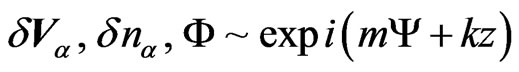 the linearized set of hydrodynamical equations together with Poisson equation can be reduced to the form
the linearized set of hydrodynamical equations together with Poisson equation can be reduced to the form
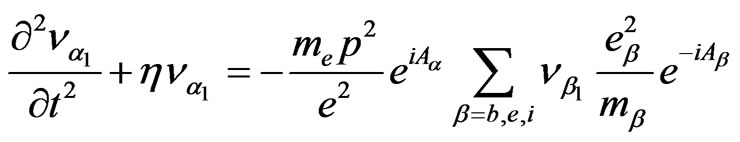 (1)
(1)
where, 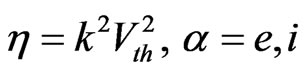 or
or 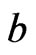 and
and ![]() is a separation constant, and
is a separation constant, and 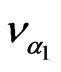 is the temporal part of the density perturbations
is the temporal part of the density perturbations 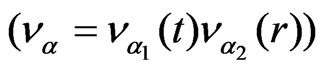
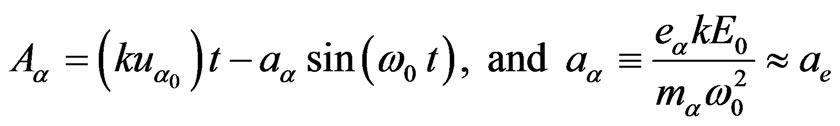 (2)
(2)
Assuming that the ions are at rest 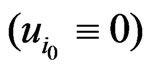 and that the frequency of the HF field is much larger than the eigen frequencies of the excited surface waves
and that the frequency of the HF field is much larger than the eigen frequencies of the excited surface waves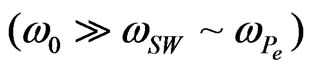 , we may use the method of averaging.
, we may use the method of averaging.
Introducing the explicit form of 
and a new variable 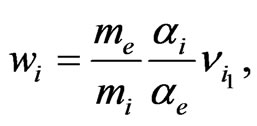 we find the final form of the equations, which describes the dynamical (temporal) part of our problem
we find the final form of the equations, which describes the dynamical (temporal) part of our problem
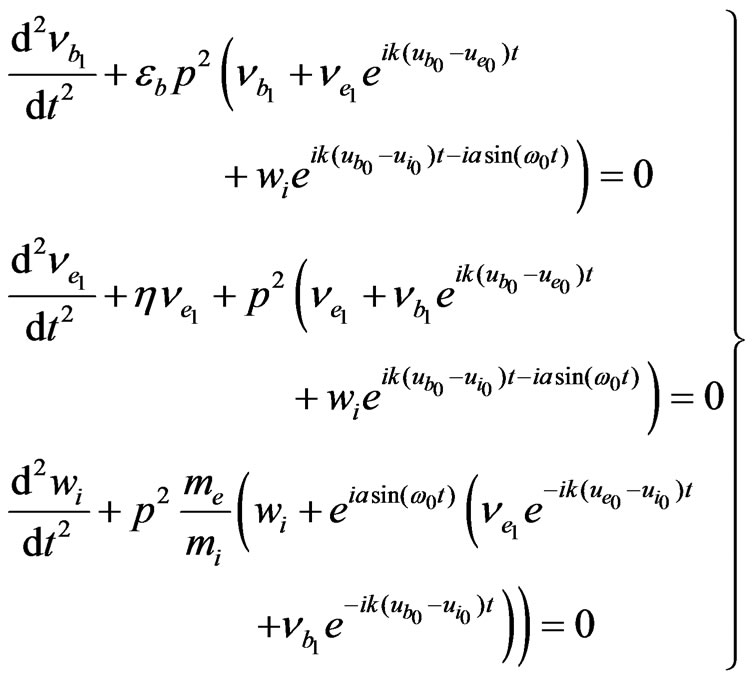 (3)
(3)
where,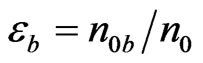 .
.
Here we shall confine our analysis for the influence of the HF electric field on the dispersion characteristics of unstable surface waves excited in a plasma waveguides by an electron beam.
Using the Jacobi-Anger formula [18-20],
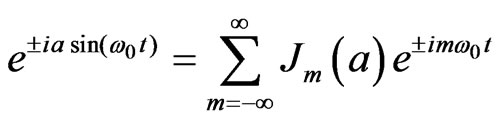
where, 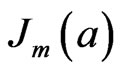 are the Bessel functions, we obtain from Equations (3):
are the Bessel functions, we obtain from Equations (3):
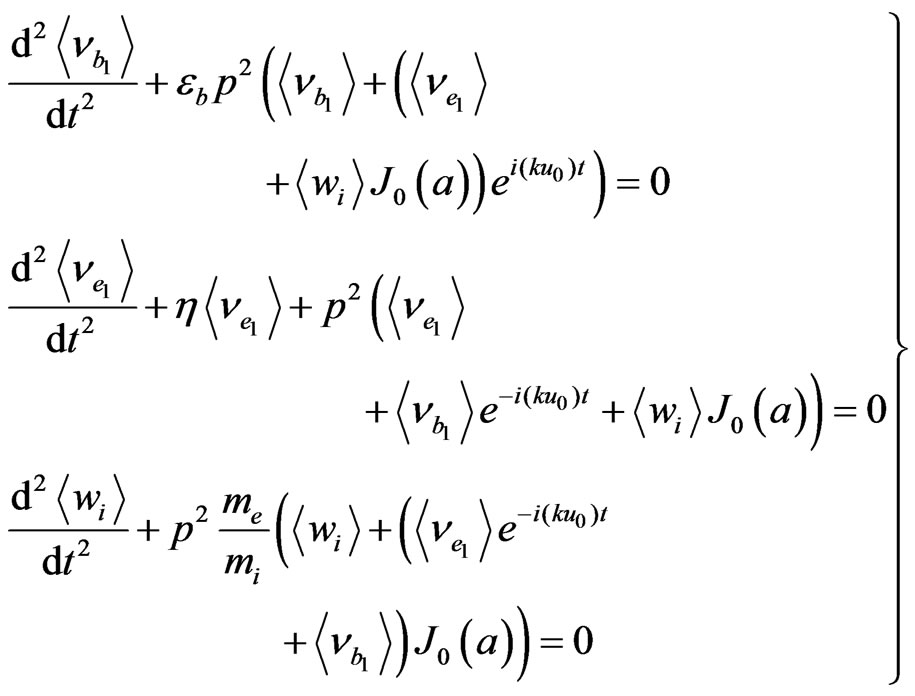 (4)
(4)
where,
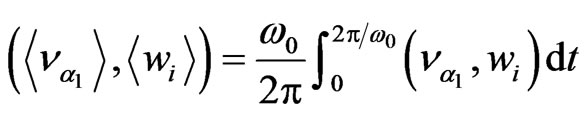
The system of Equations (4) coincides (if 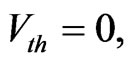
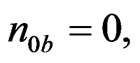
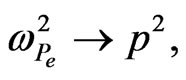
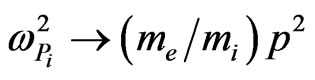 ) with the system describing the HF stabilization of the two-stream instability in a uniform (or nonuniform) unbounded (or bounded) plasma [8] or [17].
) with the system describing the HF stabilization of the two-stream instability in a uniform (or nonuniform) unbounded (or bounded) plasma [8] or [17].
If there is no externally injected beam ( ) then the system of Equations (4) coincides with the system describing the HF stabilization of the Buneman instability in a nonuniform bounded relativistic cold (warm) plasma [20-24].
) then the system of Equations (4) coincides with the system describing the HF stabilization of the Buneman instability in a nonuniform bounded relativistic cold (warm) plasma [20-24].
3. Solution of the “Temporal” (Time-Dependent) Equations
According to Equations (4), plasma oscillations are then described by the dispersion equation
 (5)
(5)
where
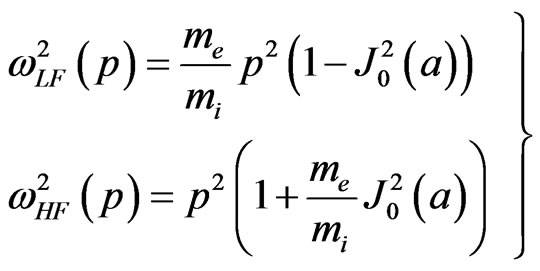 (6)
(6)
In the case of vanishing electric field amplitude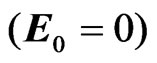 , then Equation (5) agrees with the dispersion Equation which describes the unstable oscillations that excited in a uniform unbounded (bounded) plasma by a low - density electron beam [8,17]. Same as in [8,17] we shall analyze Equation (5) in two cases:
, then Equation (5) agrees with the dispersion Equation which describes the unstable oscillations that excited in a uniform unbounded (bounded) plasma by a low - density electron beam [8,17]. Same as in [8,17] we shall analyze Equation (5) in two cases:
3.1. Non-Resonant Case (
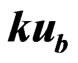 )
)
We have from (5)
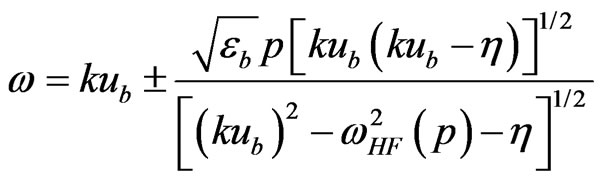 (7)
(7)
Under the conditions
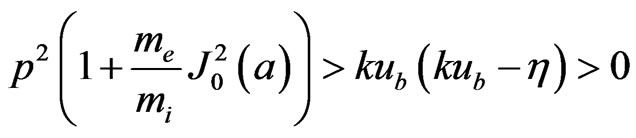 (8)
(8)
the roots of Equation (7) are complex and one of them corresponds to an instability with the growth rate
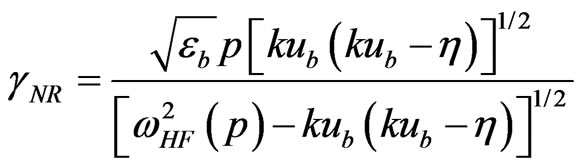 (9)
(9)
At 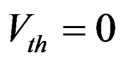 the result agrees with the result for cold plasma [17].
the result agrees with the result for cold plasma [17].
3.2. Resonant Case (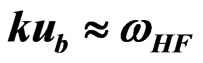 )
)
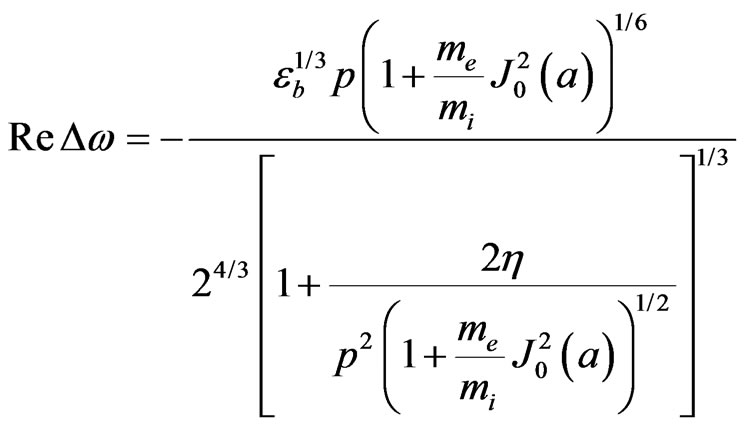 (10)
(10)
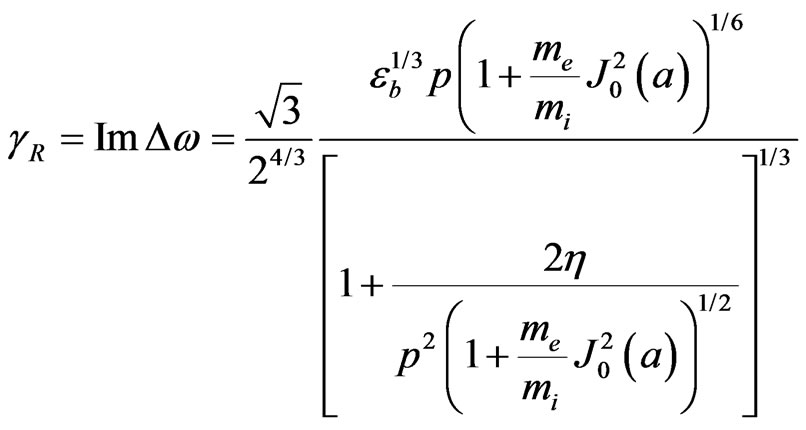 (11)
(11)
where ![]() is determined by the equation of the space part of the problem.
is determined by the equation of the space part of the problem.
It follows from expressions (8)-(11) that the HF electric field has no essential influence on the dispersion characteristics of unstable surface waves excited in a plasma waveguides by a low-density electron beam. The region of instability only slightly narrows and the growth rate decrease by a small parameter.
The results obtained are in a full agreement with the conclusion that an external HF field may have a stabilizing effect on the electron beam-plasma interaction in uniform (or nonuniform) plasma [8,17]. The warm plasma reduced the growth rate.
We conclude that the growth rate of the electron beamplasma interaction decreases more in a warm plasma than in a cold plasma [17].
4. Solution of the Space (Spatial) Part of the Problem
The main feature of the expression (6), (7) and (9) consists in an existence of a separation constant![]() , which enables us to consider the plasma boundaries.
, which enables us to consider the plasma boundaries.
To find an explicit expression for the constant ![]() it is necessary to solve the following differential equation (for details see [8]).
it is necessary to solve the following differential equation (for details see [8]).
 (12)
(12)
where,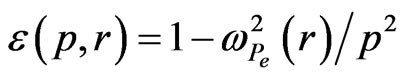 . If the radial profile of the plasma density and boundary conditions are specified, the solution of Equation (12) gives us desired value of the separation constant
. If the radial profile of the plasma density and boundary conditions are specified, the solution of Equation (12) gives us desired value of the separation constant![]() . The feature of the Equation (12) is that neither the amplitude of HF electric field nor electron beam parameters enters into it. Therefore Equation (12) coincides with equation describing propagation of natural (free of external influence) electrostatic surface waves in a nonuniform plasma cylinder (see e.g., [25] and ref. therein). Supposing that plasma density is uniform and the interface between plasma and vacuum is sharp.
. The feature of the Equation (12) is that neither the amplitude of HF electric field nor electron beam parameters enters into it. Therefore Equation (12) coincides with equation describing propagation of natural (free of external influence) electrostatic surface waves in a nonuniform plasma cylinder (see e.g., [25] and ref. therein). Supposing that plasma density is uniform and the interface between plasma and vacuum is sharp.
In such case the relations determine the solution of Equation (12)
 (13)
(13)
where 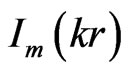 and
and 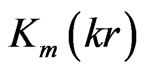 are the modified Bessel functions and
are the modified Bessel functions and 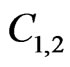 are the constants. Using the continuity condition of
are the constants. Using the continuity condition of 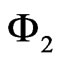 and
and 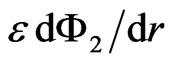 at the boundary, the following equation is found (see e.g. [25] and refs. therein)
at the boundary, the following equation is found (see e.g. [25] and refs. therein)
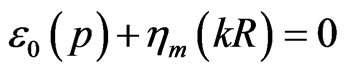 (14)
(14)
with
 (15)
(15)
where the stroke means differentiation with respect to the argument. Equation (14) gives us the relation between the separation constant![]() , electron plasma frequency
, electron plasma frequency 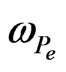 and the axial wave number
and the axial wave number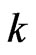 :
:
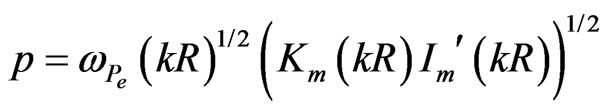 (16)
(16)
In the limiting case of small radius of plasma waveguide (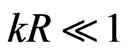 ), from (16) we find
), from (16) we find
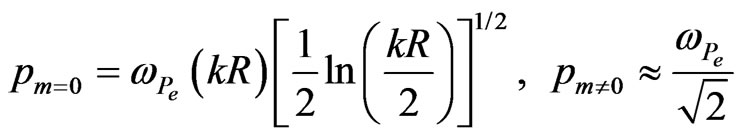
For 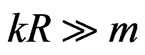 (“thick” waveguide) always
(“thick” waveguide) always 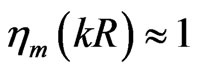 and we have
and we have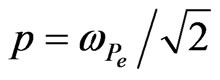 .
.
This equation is the same equation in cold plasma waveguide [8,17] i.e.; the warm plasma waveguide has no effect on the space part of the problem.
5. Conclusions
The paper deals with parametric excitation of the potential surface waves in bounded nonuniform warm plasma by monochromatic HF electrical field. It is shown that the problem can be reduced to the solution of the “temporal” (parametric) and “stationary” (spatial) parts. The “temporal” part determining frequencies and growth rates of unstable oscillations coincides with accuracy to redefinition of natural frequencies with equations describing parametric resonance in homogeneous plasma. Natural frequencies of oscillations and spatial distribution of the amplitude of the self-consistent electrical field are determined from the solution of a boundary-value problem (“space” part) taking into account specific spatial distribution of the plasma density. The method described is used to solve the effect of HF field on the excitation of surface waves by an electron beam under the development of instability of low-density beam passing through a cylindrical warm plasma waveguide.
The method was used for the solution of the stabilization effect of a strong HF electric field on beam-plasma interaction in a cylindrical warm plasma waveguide. We solved the “temporal” (time-dependent) equations and obtained the corresponding dispersion Equation (5) in a cylindrical geometry, which was analyzed for two cases: nonresonant instability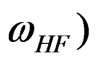
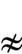
![]() , and resonance one
, and resonance one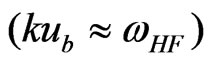 . In both cases the frequency growth rates of the oscillations are obtained (relation (9) and (11)). The separation constant
. In both cases the frequency growth rates of the oscillations are obtained (relation (9) and (11)). The separation constant ![]() is obtained from relation (16), the results are compared with the case when the external electric field is absent (
is obtained from relation (16), the results are compared with the case when the external electric field is absent (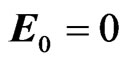 ) and a cold plasma (
) and a cold plasma (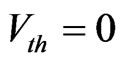 ).
).
In conclusion it is shown that a HF electric field has no essential influence on dispersion characteristics of unstable surface waves excited in a warm plasma waveguide by a low-density electron beam. The region of instability only slightly narrowing and the growth rate decreases by a small parameter and this result has been reduced compared to cold plasma. Also, it is found that the plasma electrons have not affected the solution of the space part of the problem.
REFERENCES
- M. V. Nezlin, “Dynamics of Beams in Plas Mas,” Springer Verlag, Heideleberg, 1991.
- L. S. Bogdankevich and A. A. Rukhadze, “Stability of Relativistic Electron Beams in a Plasma and the Problem of Critical Currents,” Soviet Physics—Uspekhi, Vol. 14, No. 2, 1971, pp. 163-179. doi:10.1070/PU1971v014n02ABEH004456
- A. F. Alexanddrov, M. V. Kuzelev and A. N. Khalilov, “Beam Instability Regimes in a Plasma,” Soviet Physics— JETP, Vol. 66, No. 5, 1987, pp. 978-988.
- W. H. Amein and Y. A. Sayed, “Long Wavelength Oscillation in Electron Beam-Plasma Interaction,” Physica Scripta, Vol. 50, No. 2, 1994, pp. 147-149. doi:10.1088/0031-8949/50/2/010
- A. B. Mikhailovskii, “Theory of Plasma Instabilities,” Consultants Bureau, New York, 1974.
- Yu. M. Aliev and V. P. Silin, “Plasma Oscillations in a High-Frequency Electric Field,” Soviet Physics—JETP, Vol. 21, No. 3, 1965, pp. 601-607.
- V. P. Silin, “A Survey of Phenomena in Ionized Gases,” IAEA, Vienna, 1968.
- V. V. Demchenko and A. Ya. Omelchenko, “On the Problem of Parametric Resonance in a Cold Inhomogeneous Isotropic Plasma,” Radiophysics and Quantum Electronics, Vol. 19, No. 3, 1976, pp. 332-334. doi:10.1007/BF01034594
- H. Bohmer, E. A. Jacson and M. Rather, “Quenching of the Beam-Plasma Instability by Mode Mixing at a Density Discontinuety,” Physics Fluids, Vol. 16, No. 7, 1973, pp. 1064-1071. doi:10.1063/1.1694468
- W. H. Amein, V. V. Dolgopolov, A. M. Hussen and K. E. Zayed, “Beam Instability in the Case of Sharp Changes in Plasmadensity,” Physica, Vol. 79C, No. 6, 1975, pp. 628- 631.
- W. H. Amein, V. V. Dolgopolov, A. M. Hussen and K. E. Zayed, “Beam Instability in Inhomogeneous Bounded Plasma,” Plasma Physics, Vol. 17, No. 6, 1975, pp. 497- 500.
- P. Kaw, W. Kruer, C. Liu and K. Nishikawa, “Advances in Plasma Physics,” Wiley, New York, 1976.
- M. V. Kuzelev and A. A. Rukhadze,” Electrodynamics of Dense Electron Beam in Plasma,” Nauka, Mosco, 1990.
- M. V. Kuzelev and A. A. Rukhadze, “English Completed Edition, Plasma Free Electron Lasers,” Edition Frontier, Paris, 1995.
- Yu. M. Aliev and E. Ferlengi, “Parametric Excitation of Surface Oscillations of a Plasma by an External High Frequency Field,” Soviet Physics—JETP, Vol. 30, No. 5, 1970, pp. 877-879.
- O. M. Gradov and L. Stenflo, “On the Parametric Transparency of a Magnetized Plasma Slab,” Physics Letters A, Vol. 83, No. 6, 1981, pp. 257-258. doi:10.1016/0375-9601(81)90977-4
- V. V. Demchenko, Kh. H. El-Shorbagy, Sh. M. Khalil and N. G. Zaki, “The Effect of HF Electrical Field on Beam-Plasma Interaction in a Plasma Waveguide,” 15th National Radio Science Conference, Cairo, 24-26 February 1998, IEEE Catalog Number 98EX109.
- P. Richards, “Manual of Mathematical Physics,” Pergmon Press, New York, 2009.
- A. H. Nayfeh, “Perturbation Methods,” John Wiley, New York, 2006.
- V. A. Yakubovich and V. M. Strazhinskii, “Linear Differential Equations with Periodic Coefficients,” Wiley, New York, 2009.
- Kh. H. El-Shorbagy, “HF Electric Field Effect on Buneman’s Instability in a Relativistic Plasma Waveguide,” Physica Scripta, Vol. 62, No. 2-3, 2000, pp. 186-188.
- V. V. Demchenko, Kh. H. El-Shorbagy, Sh. M. Khalil and N. G. Zaki, “Stabilization of Buneman Instability by Intense Hfelectric Field in a Plasma Wave Guide,” XXXIII International Conference on Phenomena in Ionized Gases, Toulouse, France, 17-22 July 1997.
- Kh. H. El-Shorbagy, “Stabilization Effect of a Strong HF Electrical Field on Beam-Plasma Interaction in a Relativistic Plasma Waveguide,” Physics Letters A, Vol. 287, No. 1-2, 2001, pp. 120-124. doi:10.1016/S0375-9601(01)00204-3
- Kh. H. El-Shorbagy, “Relativistic Warm Plasma Waveguide under the Effects of Plasma Electrons and HF Electrical Field on Buneman Instability,” Physics Letters A, Vol. 372, No. 9, 2008, pp. 1494-1497. doi:10.1016/j.physleta.2007.10.042
- V. V. Demchenko and K. E. Zayed, “Propagation of Potential Surface Waves in Non-Homogeneous Plasmas at the Plasma Resonance in the Transition Layer,” Physica, Vol. 59, No. 3, 1972, pp. 385-400. doi:10.1016/0031-8914(72)90195-4

