Journal of Modern Physics
Vol. 2 No. 2 (2011) , Article ID: 4366 , 4 pages DOI:10.4236/jmp.2011.22010
Energy Content of Gravitation as a Way to Quantify Both Entropy and Information Generation in the Early Universe
Department of Physics, Chongqing University, Chongqing, China
E-mail: beckwith@iibep.org,abeckwith@uh.edu
Received January 10, 2011; revised February 21, 2011; accepted February 23, 2011
Keywords: Graviton, Hubble Parameter, Entropy Generation
ABSTRACT
Based upon Alcubierre’s formalism about energy flux of gravitational waves, as well as Saunder’s treatment of temperature dependence of the Hubble parameter in the early universe, we initiate a particle count treatment of gravitons, and subsequent entropy generation which gives, via the standard model treatment of the FRW metric a way to explain/justify a value of entropy of the order of 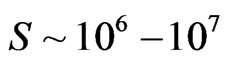 at the very onset of inflation.
at the very onset of inflation.
1. Introduction
The supposition advanced in this article is that relic energy flux initially is central to making predictions as to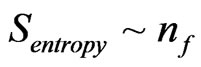 , where
, where  is a “particle count” per phase space ‘volume’ in the beginning of inflation. The author is aware of how many researchers have linked relic GW as to initial phase transitions as to the electro weak phase transition, in cosmology. The supposition is that
is a “particle count” per phase space ‘volume’ in the beginning of inflation. The author is aware of how many researchers have linked relic GW as to initial phase transitions as to the electro weak phase transition, in cosmology. The supposition is that 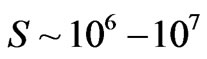 is demonstrable as an initial entropy/information count in the onset of inflation if the Weyl scalar is initially time independent.
is demonstrable as an initial entropy/information count in the onset of inflation if the Weyl scalar is initially time independent.
1.1. What Can be Said about Gravitational Wave Density Value Detection?
We begin with a use of particle count 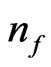 for a way to present initial GW relic inflation density using the definition given by Maggiore [1] as a way to state that a particle count algorithm is de rigor experimentally. And that the first place to start would be in obtaining a way to quantify
for a way to present initial GW relic inflation density using the definition given by Maggiore [1] as a way to state that a particle count algorithm is de rigor experimentally. And that the first place to start would be in obtaining a way to quantify 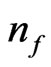 generation in relic conditions, as a way of showing a linkage between relic GW generation, entropy, and energy flux values for the onset of inflation. We begin with
generation in relic conditions, as a way of showing a linkage between relic GW generation, entropy, and energy flux values for the onset of inflation. We begin with
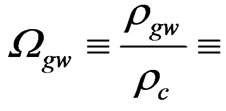
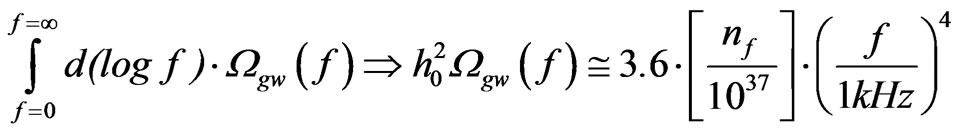 (1)
(1)
where 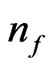 is the frequency-based numerical count of gravitons per unit phase space. While Maggiore’s explanation [1], and his treatment of gravitational wave density is very good, the problem we have is that any relic conditions for GW involve stochastic back ground, and also that many theorists have fixated upon either turbulence/and or other forms of plasma induced generation of shock waves, as stated by Duerrer [2] and others looking at the electro weak transition as a GW generator. The energy flux formalism of Alcubierre [3] is a natural way to obtain a criteria which we think explains how ultra low values of entropy, as given by Smoot [4], and others in the Ercole Chalonge Paris colloquia 2007, would arise in initial inflationary cosmology.
is the frequency-based numerical count of gravitons per unit phase space. While Maggiore’s explanation [1], and his treatment of gravitational wave density is very good, the problem we have is that any relic conditions for GW involve stochastic back ground, and also that many theorists have fixated upon either turbulence/and or other forms of plasma induced generation of shock waves, as stated by Duerrer [2] and others looking at the electro weak transition as a GW generator. The energy flux formalism of Alcubierre [3] is a natural way to obtain a criteria which we think explains how ultra low values of entropy, as given by Smoot [4], and others in the Ercole Chalonge Paris colloquia 2007, would arise in initial inflationary cosmology.
In doing so, we will expand upon a counting algorithm for entropy as given by both the author and Y. J. Ng [5], which will, when combined with an expression of energy carried per graviton complete our analysis of the relative importance of particle counting, GW energy, energy per graviton and the linkage of all these factors to initially low entropy.
The author suggests that 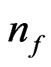 may also depend upon the interaction of gravitons with neutrinos in plasma during early-universe nucleation, as modeled by M. Marklund et al [6]. But the main datum to consider would be in analyzing an expression given by Alcubierre’s [3] formalism about energy flux, assuming that there is a solid angle for energy distribution
may also depend upon the interaction of gravitons with neutrinos in plasma during early-universe nucleation, as modeled by M. Marklund et al [6]. But the main datum to consider would be in analyzing an expression given by Alcubierre’s [3] formalism about energy flux, assuming that there is a solid angle for energy distribution  for the energy flux to travel through.
for the energy flux to travel through.
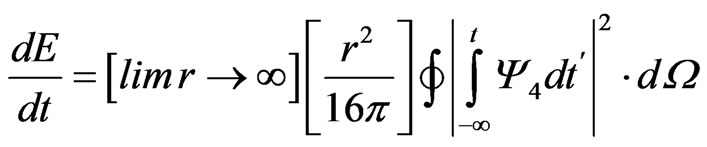 (2)
(2)
The expression 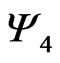 is a Weyl scalar which we will write in the form of. (See Equation (3)).
is a Weyl scalar which we will write in the form of. (See Equation (3)).
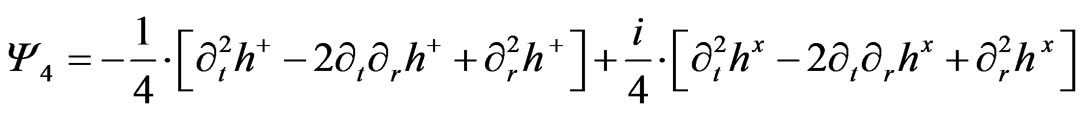 (3)
(3)
Our assumptions are simple, that if the energy flux expression is to be evaluated properly, before the electro weak phase transition, that time dependence of both 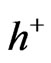 and
and 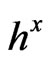 is miniscule and that initially
is miniscule and that initially , so as to initiate a re write of Equation (4) below as
, so as to initiate a re write of Equation (4) below as
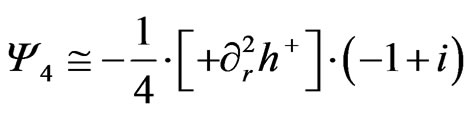 (4)
(4)
The upshot, is that the initial energy flux about the inflationary regime would lead to looking at
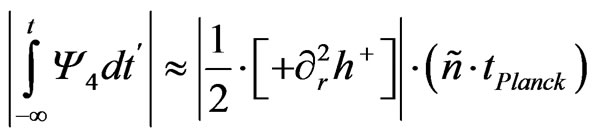 (5)
(5)
This will lead to an initial energy flux at the onset of inflation which will be presented as
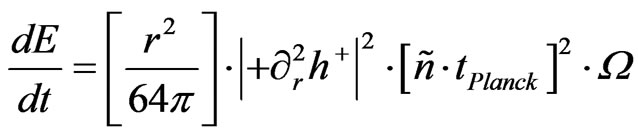 (6)
(6)
If we are talking about an initial energy flux, we then can approximate the above as
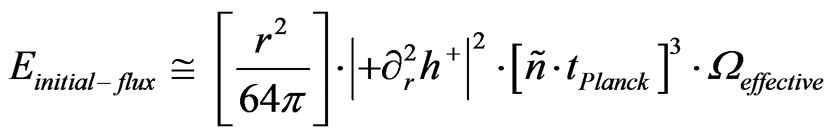 (7)
(7)
Inputs into both the expression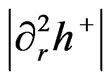 , as well as
, as well as 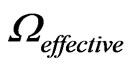 will comprise the rest of this document, plus our conclusions. The derived value of
will comprise the rest of this document, plus our conclusions. The derived value of  as well as
as well as 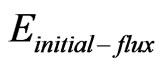 will be tied into a way to present energy per graviton, as a way of obtaining
will be tied into a way to present energy per graviton, as a way of obtaining 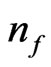 The
The 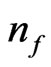 value so obtained, will be used to make a relationship , using Y. J. Ng’s entropy [5] counting algorithm of roughly
value so obtained, will be used to make a relationship , using Y. J. Ng’s entropy [5] counting algorithm of roughly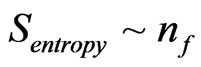 . We assert that in order to obtain
. We assert that in order to obtain 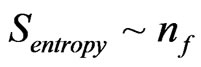 from initial graviton production, as a way to quantify
from initial graviton production, as a way to quantify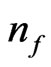 , that a small mass of the graviton can be assumed.
, that a small mass of the graviton can be assumed.
2. Does the Graviton Have Small Mass Initially? Seeming Violation of the Correspondence Principle and a Macro Effect from Small Graviton Mass
We begin our inquiry by initially looking at a modification of what was presented by R. Maartens [7,8]
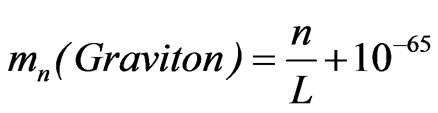 grams(8)
grams(8)
Note that Rubakov [9] writes KK graviton representation as, after using the following normalization
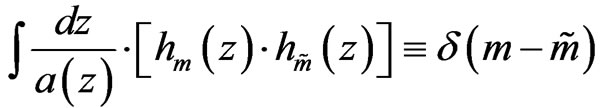 where
where 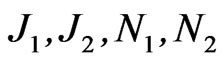 are different forms of Bessel functions, to obtain the KK graviton/DM candidate representation along RS dS brane world. (Equation (9)).
are different forms of Bessel functions, to obtain the KK graviton/DM candidate representation along RS dS brane world. (Equation (9)).
This Equation (9) is for KK gravitons having a TeV magnitude mass 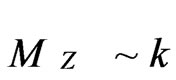 (i.e. for mass values at .5 TeV to above a TeV in value) on a negative tension RS brane. What would be useful would be managing to relate this KK graviton, which is moving with a speed proportional to
(i.e. for mass values at .5 TeV to above a TeV in value) on a negative tension RS brane. What would be useful would be managing to relate this KK graviton, which is moving with a speed proportional to 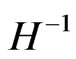 with regards to the negative tension brane with
with regards to the negative tension brane with 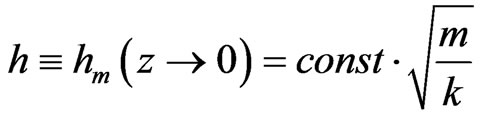 as an initial starting value for the KK graviton mass, before the KK graviton, as a ‘massive’ graviton moves with velocity
as an initial starting value for the KK graviton mass, before the KK graviton, as a ‘massive’ graviton moves with velocity 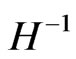 along the RS dS brane. If so, and if
along the RS dS brane. If so, and if
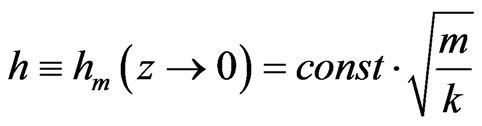 represents an initial state, then one may relate the mass of the KK graviton, moving at high speed, with the initial rest mass of the graviton, which in four space in a rest mass configuration would have a mass lower in value, i.e. of
represents an initial state, then one may relate the mass of the KK graviton, moving at high speed, with the initial rest mass of the graviton, which in four space in a rest mass configuration would have a mass lower in value, i.e. of 
 , as opposed to
, as opposed to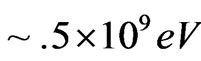
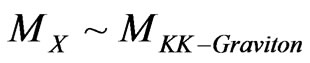 . Whatever the range of the graviton mass, it may be a way to make sense of what was presented by Dubovsky et al. [10] who argue for graviton mass using CMBR measurements, of
. Whatever the range of the graviton mass, it may be a way to make sense of what was presented by Dubovsky et al. [10] who argue for graviton mass using CMBR measurements, of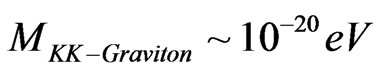 Dubosky et al. [10] results can be conflated with Alves et al. [9] arguing that non zero graviton mass may lead to an acceleration of our present universe, in a manner usually conflated with
Dubosky et al. [10] results can be conflated with Alves et al. [9] arguing that non zero graviton mass may lead to an acceleration of our present universe, in a manner usually conflated with
 (9)
(9)
DE, i.e. their graviton mass would be about
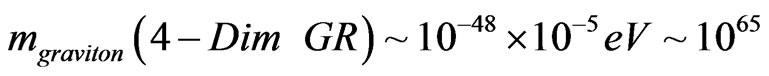 grams. Also Equation (10) will be the starting point used for a KK tower version of Equation (11) below. So from Maarten’s [8] 2005 paper,
grams. Also Equation (10) will be the starting point used for a KK tower version of Equation (11) below. So from Maarten’s [8] 2005 paper,
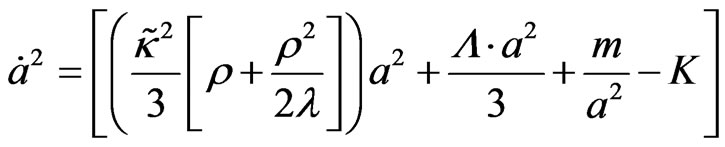 (10)
(10)
Maartens [8] also gives a 2nd Friedman equation, as
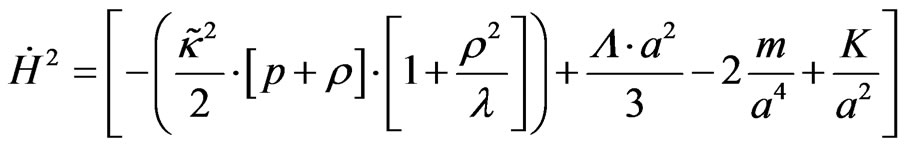 (11)
(11)
Also, if we are in the regime for which 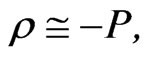 for red shift values z between zero to 1.0-1.5 with exact equality,
for red shift values z between zero to 1.0-1.5 with exact equality, 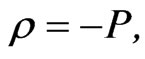 for z between zero to .5. The net effect will be to obtain, due to Equation (10), and Equation
for z between zero to .5. The net effect will be to obtain, due to Equation (10), and Equation
(11), and use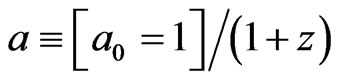 . As given by Beckwith [7]
. As given by Beckwith [7]
 (12)
(12)
Equation (10) assumes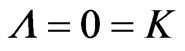 , and the net effect is to obtain, a substitute for DE, by presenting how gravitons with a small mass done with
, and the net effect is to obtain, a substitute for DE, by presenting how gravitons with a small mass done with , even if curvature K = 0. The ‘density’ function,
, even if curvature K = 0. The ‘density’ function,  , assumed is similar to what was done by Alves [11], et al..
, assumed is similar to what was done by Alves [11], et al..
2.1. Consequences of Small Graviton Mass for Reacceleration of the Universe
Using Equation (12) leads to the prediction given in Figure 1 below:
Now that this is presented, we should consider what the effects of a small graviton mass would be for initialentropy/information counting at the onset of inflation.
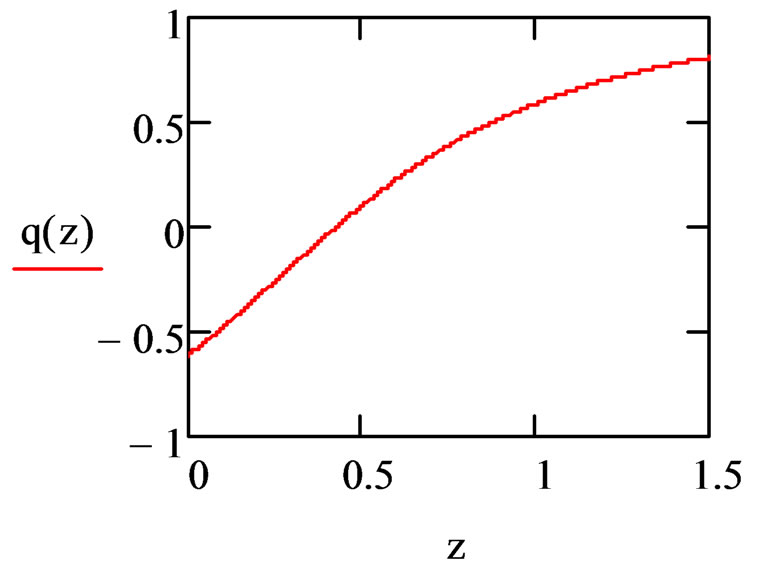
Figure 1. Reacceleration of the universe based on Beckwith [7] (note that q < 0 if z < .423).
3. Examination of Weyl Scalar in the Onset of Inflation, to Obtain Entropy Counting Initially?
Note, from Valev [12]
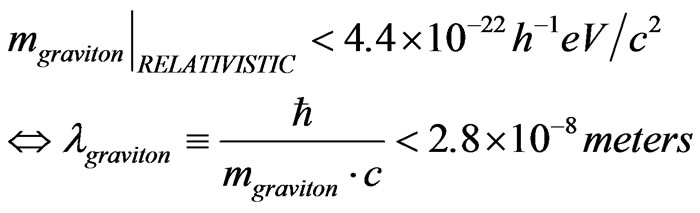 (13)
(13) This could be an argument with non zero graviton mass what to expect as a way to formulate our 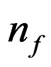 which would permit, if given a frequency range more precise ways to obtain
which would permit, if given a frequency range more precise ways to obtain 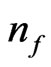 , so as to find a better way to use Equation (1) more effectively. To start this, look at setting, with
, so as to find a better way to use Equation (1) more effectively. To start this, look at setting, with 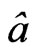 a radiation constant, and using a value given by Sander’s [13] with an observationally based Friedman Equation based value of
a radiation constant, and using a value given by Sander’s [13] with an observationally based Friedman Equation based value of
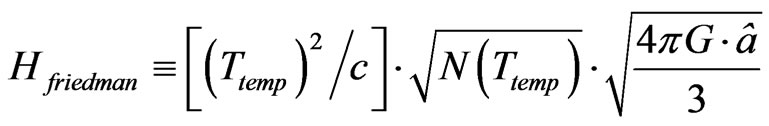 (14)
(14)
So, then that , if one uses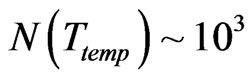 , as opposed to an upper limit specified by Kolb, et al of , at or after electro weak ,
, as opposed to an upper limit specified by Kolb, et al of , at or after electro weak , 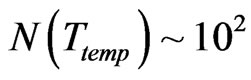 , that then
, that then
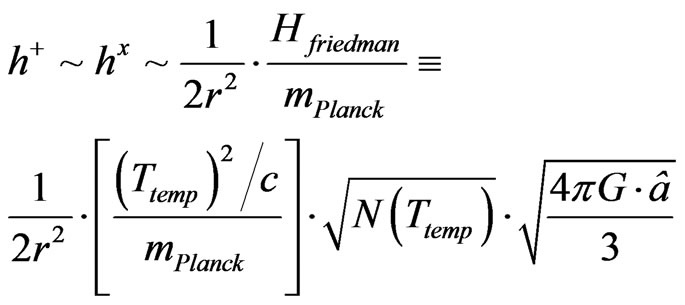 (15)
(15)
For the sake of inflationary applications, we will assume that 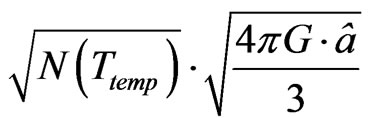 has no spatial dependence worth speaking of, which leads to, if
has no spatial dependence worth speaking of, which leads to, if 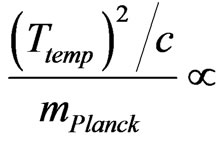 constant of order unity. Also
constant of order unity. Also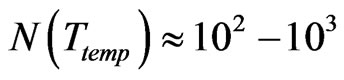 . Then one has
. Then one has
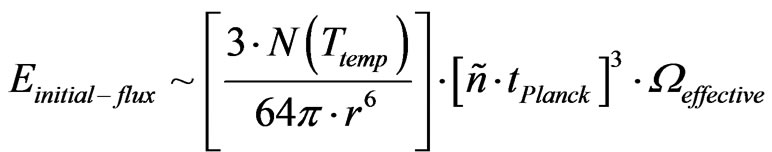 (16)
(16)
For the sake of argument, Beckwith used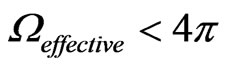 , and experimented with values of
, and experimented with values of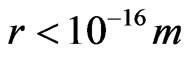 , and also, of
, and also, of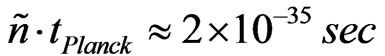 ,
,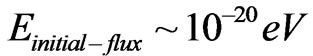 . If one uses the
. If one uses the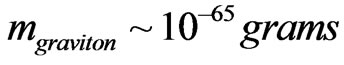 , then Beckwith obtained
, then Beckwith obtained . This is assuming a very high initial frequency for the relic particles. We will in the next section comment upon.
. This is assuming a very high initial frequency for the relic particles. We will in the next section comment upon.
4. Conclusions. Examining Information Exchange between Different Universes?
Beckwith [7] has concluded that the only way to give an advantage to higher dimensions as far as cosmology would be to look at if a fifth dimension may present a way of actual information exchange to give the following parameter input from a prior to a present universe, i.e. the fine structure constant, as given by [7]
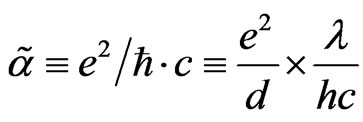 (17)
(17)
The wave length as may be chosen to do such an information exchange would be part of a graviton as being part of an information counting algorithm as can be put below, namely:
Argue that when taking the log, that the 1/N term drops out. As used by Ng [5]
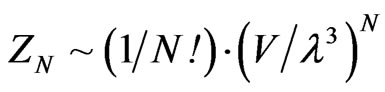 (18)
(18)
This, according to Ng, [5] leads to entropy of the limiting value of, if 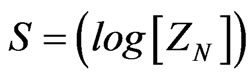 will be modified by having the following done, namely after his use of quantum infinite statistics, as commented upon by Beck - with [7]
will be modified by having the following done, namely after his use of quantum infinite statistics, as commented upon by Beck - with [7]
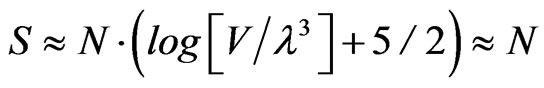 (19)
(19)
Eventually, the author hopes to put on a sound foundation what ‘tHooft [14] is doing with respect to t’Hooft [14] deterministic quantum mechanics and equivalence classes embedding quantum particle structures. Furthermore, making a count of gravitons with 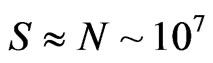 gravitons [7], with Seth Lloyd’s [15]
gravitons [7], with Seth Lloyd’s [15]
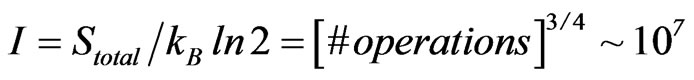 (20)
(20)
as implying at least one operation per unit graviton, with gravitons being one unit of information, per produced graviton [7]. Note, Smoot [4] gave initial values of the operations as
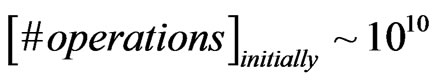 (21)
(21)
The argument so presented, gives a first order approximation as to how to obtain Equation (21)
REFERENCES
- M. Maggiore, “Gravitational Waves, Volume 1: Theory and Experiment,” Oxford University Press, Oxford, 2008.
- R. Durrer and M. Rinaldi, Physical Review, D79: 063507, 2009, http://arxiv.org/abs/0901.0650. doi:10.1103/PhysRevD.79.063507
- M. Alcubierre, “Introduction to Numerical Relativity,” Oxford University Press, 2008. doi:10.1093/acprof:oso/9780199205677.001.0001
- G. Smoot, http://chalonge.obspm.fr/Paris07_Smoot.pdf
- Y. Ng, Entropy, Vol. 10, No. 4, 2008, pp. 441-461. doi:10.3390/e10040441
- M. Marklund, G. Brodin and P. Shukla, Physica Scripta Vol. T82, 1999, pp. 130-132.
- A. Beckwith, http://vixra.org/abs/0912.0012, v 6 (newest version).
- R. Maartens, “Brane-World Gravity,” http://www.livingrev iews.org/lrr-2004-7, 2004; R. Maartens, “Brane World Cosmology,” Lecture Notes in Physics, Vol. 653, Springer Verlag, Berlin, 2005, pp. 213-247.
- V. Rubakov, “Classical Theory of Gauge Fields,” Princeton University Press, Princeton, 2002.
- S. Dubovsky, R. Flauger, A. Starobinsky and I. Tkachev,
- report UTTG-06-09, TCC-23- 09. http://arxiv.org/abs/0907. 1658
- E. Alves, O. Miranda and J. de Araujo, arXiv: 0907.5190 (July 2009).
- D. Valev, Aerospace Research in Bulgaria, Vol. 22, 2008, pp. 68-82. http://arxiv.org/abs/hep-ph/0507255; http:// arxiv.org/abs/1004.2449.
- R. Sanders, “Observational Cosmology,” pp. 105-137, in “The Physics of the Early Universe,” Lecture Notes in Physics, pp. 653, E. Papantonopoulou, Ed., Springer Verlag, Berlin, 2005.
- G. 't Hooft, http://arxiv.org/PS_cache/quant-ph/pdf/0212/ 0212095v1.pdf, 2002; G. 't Hooft., In: Th. M. Nieuwenhuizen et al., Eds., Beyond the Quantum, World Press Scientific, http://arxiv.org/PS_cache/quant-ph/pdf/0604/ 0604008v2.pdf, 2006.
- S. Lloyd, Physical Review Letters, Vol. 88, 237901, 2002.

