Applied Mathematics
Vol.5 No.7(2014), Article ID:44806,8 pages DOI:10.4236/am.2014.57099
A New Look for Starlike Logharmonic Mappings
Zayid Abdulhadi
Department of Mathematics, American University of Sharjah, Sharjah, UAE
Email: zahadi@aus.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 25 November 2013; revised 25 December 2013; accepted 2 January 2014
ABSTRACT
A function f(z) defined on the unit disc U is said to be logharmonic if it is the solution of the nonlinear elliptic partial differential equation 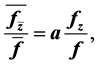 where
where  such that
such that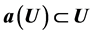 . These mappings admit a global representation of the form
. These mappings admit a global representation of the form 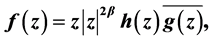 where
where 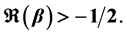 In this paper,we shall consider the logharmonic mappings
In this paper,we shall consider the logharmonic mappings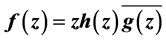 , where
, where 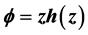 is starlike. Distortion theorem and radius of starlikess are obtained. Moreover, we use star functions to determine the integral means for these mappings. An upper bound for the arclength is included.
is starlike. Distortion theorem and radius of starlikess are obtained. Moreover, we use star functions to determine the integral means for these mappings. An upper bound for the arclength is included.
Keywords:Logharmonic, Univalent, Starlike, Integral Means, Arclength

1. Introduction
Let B denote the set of all analytic functions 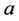 defined on the unit disk
defined on the unit disk 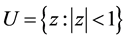 having the property that
having the property that 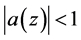 for all
for all 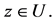 A logharmonic mapping defined on the unit disk
A logharmonic mapping defined on the unit disk 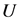 is a solution of the nonlinear elliptic partial differential equation
is a solution of the nonlinear elliptic partial differential equation
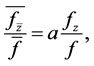 (1.1)
(1.1)
where the second dilatation function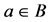 . Because
. Because 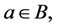 the Jacobian
the Jacobian
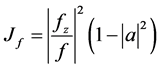
is positive and hence, non-constant logharmonic mappings are sense-preserving and open on U. If f is a nonconstant logharmonic mapping of 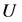 and vanishes at
and vanishes at 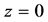 but has no other zeros in U, then f admits the following representation
but has no other zeros in U, then f admits the following representation
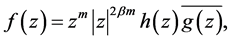 (1.2)
(1.2)
where m is a nonnegative integer, 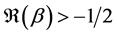 and,
and,  and
and 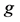 are analytic functions in
are analytic functions in 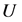 with
with 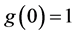 and
and 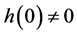 ([1] ). The exponent
([1] ). The exponent 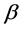 in (1.2) depends only on
in (1.2) depends only on 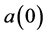 and can be expressed by
and can be expressed by
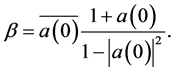
Note that  if and only if
if and only if  and that a univalent logharmonic mapping on
and that a univalent logharmonic mapping on 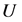 vanish at the origin if and only if
vanish at the origin if and only if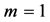 . Thus, a univalent logharmonic mappings on
. Thus, a univalent logharmonic mappings on 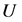 which vanishes at the origin will be of the form
which vanishes at the origin will be of the form
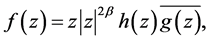
where 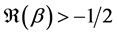 and
and 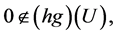 and have been studied extensively in the recent years, see [1] -[7] . In this case, it follows that
and have been studied extensively in the recent years, see [1] -[7] . In this case, it follows that 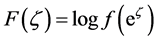 are univalent harmonic mappings of the half-plane
are univalent harmonic mappings of the half-plane
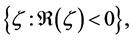 a detail study of univalent harmonic mappings to be found in [8] -[14] . Such mappings are closely related to the theory of minimal surfaces, see [15] [16] .
a detail study of univalent harmonic mappings to be found in [8] -[14] . Such mappings are closely related to the theory of minimal surfaces, see [15] [16] .
Let 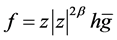 be a univalent logharmonic mapping. We say that
be a univalent logharmonic mapping. We say that 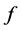 is starlike logharmonic mapping if
is starlike logharmonic mapping if
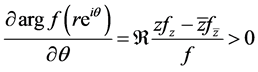
for all . Denote by
. Denote by  the set of all starlike logharmonic mappings, and by
the set of all starlike logharmonic mappings, and by  the set of all starlike analytic mappings. It was shown in [4] that
the set of all starlike analytic mappings. It was shown in [4] that
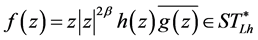 if and only if
if and only if 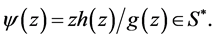
It is rather a natural question to ask whether there exists a linkage between the starlikeness of  and
and 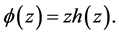
In Section 2, we determine the radius of starlikeness for the logharmonic mapping 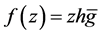 where
where 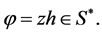 A distortion theorem and an upper bound for the arclength of these mappings will be included.
A distortion theorem and an upper bound for the arclength of these mappings will be included.
In Section 3, we discuss the integral means for logharmonic mappings associated to starlike analytic mappings.
2. Basic Properties of Mappings from 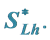
We start this section by establishing a linkage between the starlikeness of 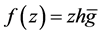 and
and 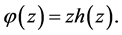
Theorem 1 a) Let 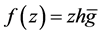 be a logharmonic mapping where
be a logharmonic mapping where 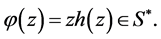 Then f maps the disk
Then f maps the disk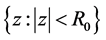 , where
, where 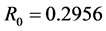 onto a starlike domain.
onto a starlike domain.
b) If . Then
. Then 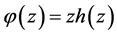 maps the disk
maps the disk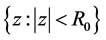 , where
, where  onto a starlike domain.
onto a starlike domain.
Proof. a) Let 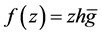 be a logharmonic mapping with respect to
be a logharmonic mapping with respect to 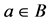 and
and 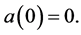 Suppose that
Suppose that 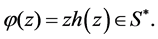 Then
Then 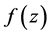 can be written in the form
can be written in the form
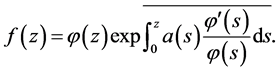 (2.1)
(2.1)
A simple calculations leads to
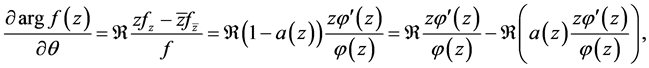
where 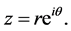 Since
Since 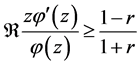 and
and 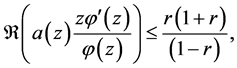
we obtain
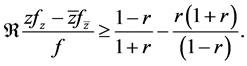
This gives
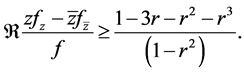
Thus 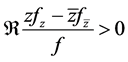 if
if 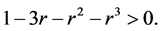 Therefore, the radius of starlikeness
Therefore, the radius of starlikeness 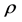 is the smallest positive root (less than 1) of
is the smallest positive root (less than 1) of 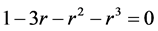 which is
which is 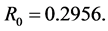 We conclude that f is univalent in
We conclude that f is univalent in  and maps the disk
and maps the disk 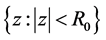 onto a starlike domain.
onto a starlike domain.
b) Let 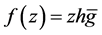 be a starlike logharmonic mapping defined on the unit disk
be a starlike logharmonic mapping defined on the unit disk 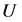 with respect to
with respect to 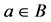
with 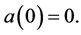 Then by [4]
Then by [4] 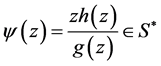
and also,
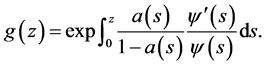
Hence,
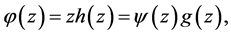
and then simple calculations give that
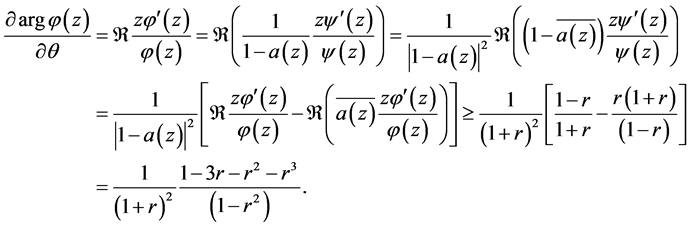
Thus 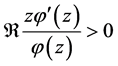 if
if 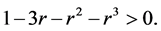 Therefore, the radius of starlikeness
Therefore, the radius of starlikeness 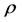 is the smallest positive root (less than 1) of
is the smallest positive root (less than 1) of 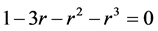 which is
which is 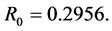 We conclude that
We conclude that 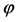 is univalent in
is univalent in 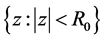 and maps the disk
and maps the disk 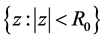 onto a starlike domain.
onto a starlike domain.
Our next result is a distortion theorem for the set of all logharmonic mappings 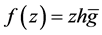 where
where 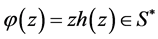
Theorem 2 Let 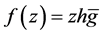 be a logharmonic mapping defined on the unit disk U where
be a logharmonic mapping defined on the unit disk U where
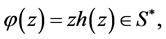 then for
then for 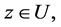
i) 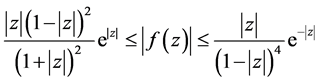
ii) 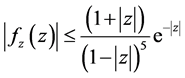
iii) 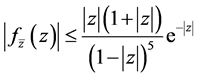
Equality holds for the right hand side if and only if 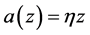 and
and  which leads to
which leads to
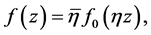 where
where

Proof. i) Let 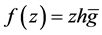 be a logharmonic mapping with respect to
be a logharmonic mapping with respect to 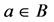 with
with 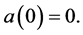 Suppose that
Suppose that 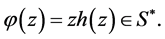 Then
Then  can be written in the form
can be written in the form
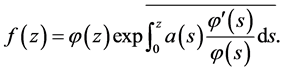 (2.2)
(2.2)
For 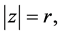 we have
we have
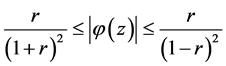 (2.3)
(2.3)
and
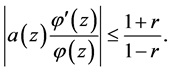 (2.4)
(2.4)
Combining (2.2), (2.3) and (2.4), we get
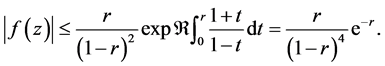
Equality holds for the right hand side if and only if 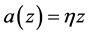 and
and 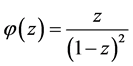 which leads to
which leads to
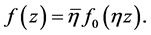
For the left hand side inequality, we have
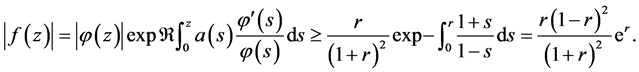
ii) and iii) Differentiation  in (2.2) with respect to
in (2.2) with respect to 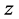 and
and  respectively leads to
respectively leads to
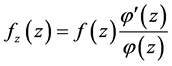 (2.5)
(2.5)
and
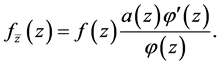 (2.6)
(2.6)
The result follows from substituting from Theorem 2(i), (2.3) and (2.4) into (2.5) and (2.6).
In the next theorem we establish an upper bound for the arclength of the set of all logharmonic mappings 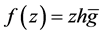 where
where 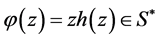
Theorem 3 Let 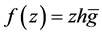 be a logharmonic mapping defined on the unit disk U where
be a logharmonic mapping defined on the unit disk U where
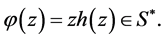 Suppose that for
Suppose that for 
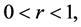
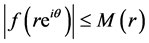 then
then
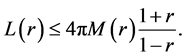
Proof. Let  denote the closed curve which is the image of the circle
denote the closed curve which is the image of the circle  under the mapping
under the mapping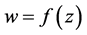 . Then
. Then
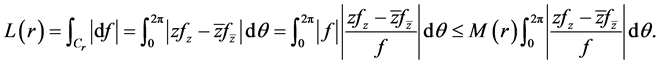
Now using (2.5) and (2.6) we have
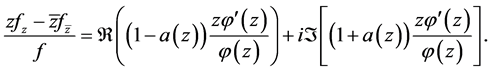
 Therefore,
Therefore,
 (2.7)
(2.7)
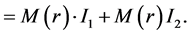 (2.8)
(2.8)
Since 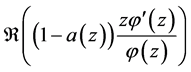 is harmonic, and by the mean value theorem for harmonic functions,
is harmonic, and by the mean value theorem for harmonic functions, 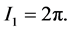 Also,
Also, 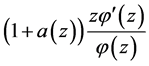 is subordinate to
is subordinate to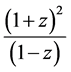 therefore, we have
therefore, we have
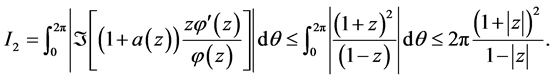
Substituting the bounds for  and
and  in (2.8), we get
in (2.8), we get
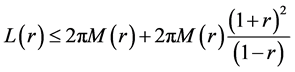
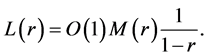
3. Integral Means
Theorem 4 of this section is an applications of the Baerstein star functions to the class of logharmonic mappings 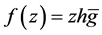 defined on the unit disk
defined on the unit disk 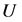 where
where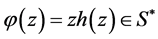 . Star function was first introduced and properties were derived by Baerstein [17] [18] , [Chapter 7]. The first application was the remarkable result, if
. Star function was first introduced and properties were derived by Baerstein [17] [18] , [Chapter 7]. The first application was the remarkable result, if 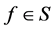 then
then
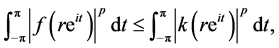 (3.1)
(3.1)
where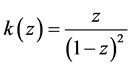 ,
, 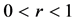 and
and 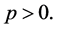
If 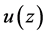 is a real
is a real 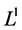 function in an annulus
function in an annulus 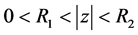 then the definition of the star function of
then the definition of the star function of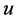 ,
, 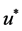 is
is
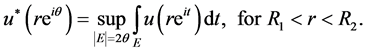
One important property is that when 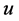 is symmetric (even) re-arrangement then
is symmetric (even) re-arrangement then
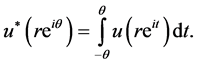 (3.2)
(3.2)
Other properties [18] , [Chapter 7] are that the star-function is sub-additive and star respects subordination. Respect means that the star of the subordinate function is less than or equal to the star of the function. In addition, it was also shown that star-function is additive when functions are symmetric re-arrangements. Here is a lemma, quoted in [18] , [Chapter 7] which we will use later.
Lemma 1 For 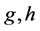 real and
real and 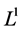 on
on 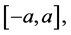 the following are equivalent a) For every convex non-decreasing function
the following are equivalent a) For every convex non-decreasing function 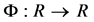

b) For every 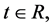
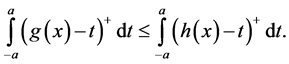
c) For every 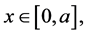
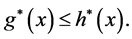
Our main result of this section is the following theorem.
Theorem 4 If 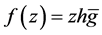 be a logharmonic mapping defined on the unit disk U where
be a logharmonic mapping defined on the unit disk U where 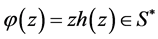 then for each fixed
then for each fixed 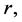
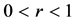 and as a function of
and as a function of 
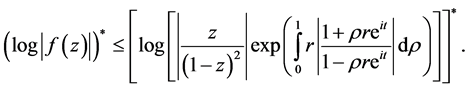
Equality occurs if and only if 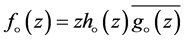 is one of the functions of the form
is one of the functions of the form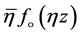 ,
, 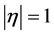 , where
, where
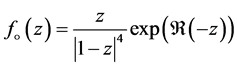
Proof. Let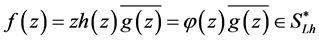 , then by (2.2), we have
, then by (2.2), we have
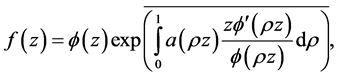
where 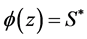 and
and 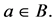
Then
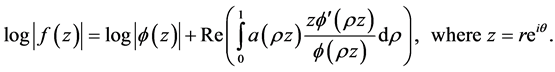 (3.3)
(3.3)
Write 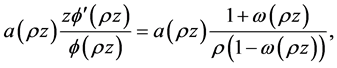 where
where 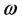 is analytic,
is analytic, 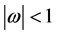 and
and 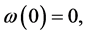 (see [9] ).
(see [9] ).
As the star-function is sub-additive,
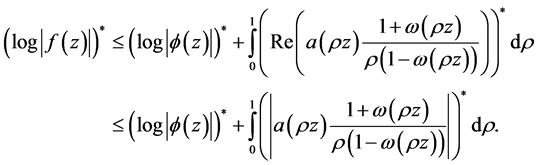 (3.4)
(3.4)
But since
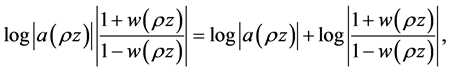
each is subharmonic.  is subordinate to
is subordinate to 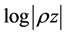 and
and 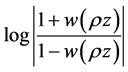 is subordinate to
is subordinate to
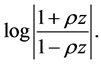 Hence
Hence
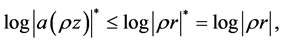
and
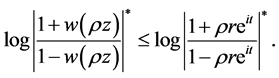
Then,
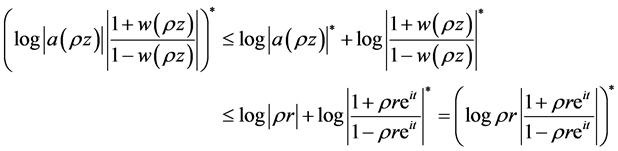
Thus,
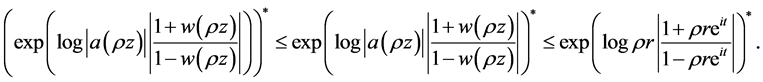
It follows that
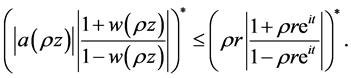 (3.5)
(3.5)
Consequently, by combining (3.4), (3.5) and using the fact that star-functions respect subordination, it follows that
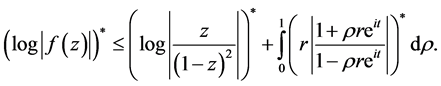
Hence, as star-functions are additive when functions are symmetric re-arrangements,
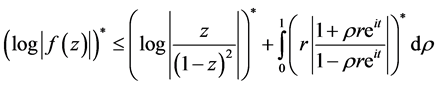 (3.6)
(3.6)
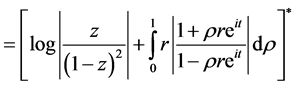
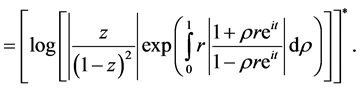
Now by using Theorem 4 we have Corollary 1 If 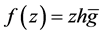 be a logharmonic mapping defined on the unit disk U where
be a logharmonic mapping defined on the unit disk U where 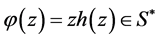 then
then 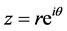
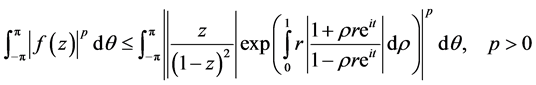
and
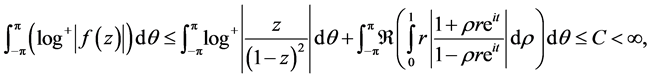
the later implies that 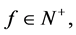 hence
hence 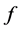 has radial limits.
has radial limits.
Proof. Let 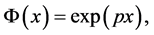 this is non-decreasing convex function .The first integral mean can be obtained using part (a) of Lemma 1 and Theorem 4. Moreover, the choice
this is non-decreasing convex function .The first integral mean can be obtained using part (a) of Lemma 1 and Theorem 4. Moreover, the choice 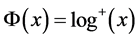 yields the second integral mean.
yields the second integral mean.
References
- Abdulhadi, Z. (1996) Close-to-Starlike Logharmonic Mappings. The International Journal of Mathematics and Mathematical Sciences, 19, 563-574.
- Abdulhadi, Z. (2002) Typically Real Logharmonic Mappings. The International Journal of Mathematics and Mathematical Sciences, 31, 1-9.
- Abdulhadi, Z. and Bshouty, D. (1988) Univalent Functions in
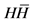 . Transactions of the AMS—American Mathematical Society, 305, 841-849.
. Transactions of the AMS—American Mathematical Society, 305, 841-849. - Abdulhadi, Z. and Hengartner, W. (1987) Spirallike Logharmonic Mappings. Complex Variables, Theory and Application, 9, 121-130.
- Abdulhadi, Z., Hengartner, W. and Szynal, J. (1993) Univalent Logharmonic Ring Mappings. Proceedings of the American Mathematical Society, 119, 735-745.
- Abdulhadi, Z. and Hengartner, W. (1996) One Pointed Univalent Logharmonic Mappings. Journal of Mathematical Analysis and Applications, 203, 333-351.
- Abdulhadi, Z. and Hengartner, W. (2001) Polynomials in
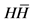 . Complex Variables, Theory and Application, 46, 89- 107.
. Complex Variables, Theory and Application, 46, 89- 107. - Abu-Muhanna, Y. and Lyzzaik, A. (1990) The Boundary Behaviour of Harmonic Univalent Maps. Pacific Journal of Mathematics, 141, 1-20. http://dx.doi.org/10.2140/pjm.1990.141.1
- Clunie, J. and Sheil-Smal, T. (1984) Harmonic Univalent Functions. Annales Academiæ Scientiarum Fennicæ Mathematica, 9, 3-25.
- Duren, P. and Schober, G. (1987) A Variational Method for Harmonic Mappings on Convex Regions. Complex Variables, Theory and Application, 9, 153-168. http://dx.doi.org/10.1080/17476938708814259
- Duren, P. and Schober, G. (1989) Linear Extremal Problems for Harmonic Mappings of the Disk. Proceedings of the American Mathematical Society, 106, 967-973. http://dx.doi.org/10.1090/S0002-9939-1989-0953740-5
- Hengartner, W. and Schober, G. (1986) On the Boundary Behavior of Orientation-Preserving Harmonic Mappings. Complex Variables, Theory and Application, 5, 197-208. http://dx.doi.org/10.1080/17476938608814140
- Hengartner, W. and Schober, G. (1986) Harmonic Mappings with Given Dilatation. Journal London Mathematical Society, 33, 473-483. http://dx.doi.org/10.1112/jlms/s2-33.3.473
- Jun, S.H. (1993) Univalent Harmonic Mappings on
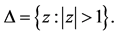 Proceedings of the American Mathematical Society, 119, 109-114. http://dx.doi.org/10.1090/S0002-9939-1993-1148026-3
Proceedings of the American Mathematical Society, 119, 109-114. http://dx.doi.org/10.1090/S0002-9939-1993-1148026-3 - Nitsche, J.C.C. (1989) Lectures on Minimal Surfaces. Vol. 1, Translated from the German by Jerry M. Feinberg, Cambridge University Press, Cambridge.
- Osserman, R. (1986) A Survey of Minimal Surfaces. 2nd Edition, Dover, New York.
- Baernstein, A. (1974) Integral Means, Univalent Functions and Circular Symmetrization. Acta Mathematica, 133, 139- 169. http://dx.doi.org/10.1007/BF02392144
- Duren, P. (1983) Univalent Functions. Springer-Verlag, Berlin.

