Applied Mathematics
Vol.06 No.01(2015), Article ID:52955,12 pages
10.4236/am.2015.61002
Higher-Order Minimizers and Generalized
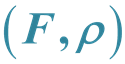 -Convexity in Nonsmooth Vector Optimization over Cones
-Convexity in Nonsmooth Vector Optimization over Cones
S. K. Suneja1, Sunila Sharma1, Malti Kapoor2*
1Department of Mathematics, Miranda House, University of Delhi, Delhi, India
2Department of Mathematics, Motilal Nehru College, University of Delhi, Delhi, India
Email: *maltikapoor1@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 1 November 2014; revised 29 November 2014; accepted 16 December 2014

ABSTRACT
In this paper, we introduce the concept of a (weak) minimizer of order k for a nonsmooth vector optimization problem over cones. Generalized classes of higher-order cone-nonsmooth (F, ρ)- convex functions are introduced and sufficient optimality results are proved involving these classes. Also, a unified dual is associated with the considered primal problem, and weak and strong duality results are established.
Keywords:
Nonsmooth Vector Optimization over Cones, (Weak) Minimizers of Order k, Nonsmooth (F, ρ)-Convex Function of Order k

1. Introduction
It is well known that the notion of convexity plays a key role in optimization theory [1] [2] . In the literature, various generalizations of convexity have been considered. One such generalization is that of a
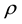 -convex function introduced by Vial [3] . Hanson and Mond [4] defined the notion of an F-convex function. As an extended unification of the two concepts, Preda [5] introduced the concept of a
-convex function introduced by Vial [3] . Hanson and Mond [4] defined the notion of an F-convex function. As an extended unification of the two concepts, Preda [5] introduced the concept of a
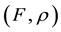 -convex function. Antczak gave the notion of a locally Lipschitz
-convex function. Antczak gave the notion of a locally Lipschitz
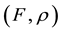 -convex scalar function of order k [6] and a differentiable
-convex scalar function of order k [6] and a differentiable
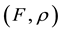 - convex vector function of order 2 [7] .
- convex vector function of order 2 [7] .
L. Cromme [8] defined the concept of a strict local minimizer of order k for a scalar optimization problem. This concept plays a fundamental role in convergence analysis of iterative numerical methods [8] and in stability results [9] . The definition of a strict local minimizer of order 2 is generalized to the vectorial case by Antczak [7] .
Recently, Bhatia and Sahay [10] introduced the concept of a higher-order strict minimizer with respect to a nonlinear function for a differentiable multiobjective optimization problem. They proved various sufficient optimality and mixed duality results involving generalized higher-order strongly invex functions.
The main purpose of this paper is to extend the concept of a higher-order minimizer to a nonsmooth vector optimization problem over cones. The paper is organized as follows. We begin in Section 2 by recalling some known concepts in the literature. We then define the notion of a (weak) minimizer of order k for a nonsmooth vector optimization problem over cones. Thereafter, we introduce various new generalized classes of cone- nonsmooth
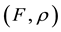 -convex functions of higher-order. In Section 3, we study several optimality conditions for higher-order minimizers via the introduced classes of functions. In Section 4, we associate a unified dual to the considered problem and establish weak and strong duality results.
-convex functions of higher-order. In Section 3, we study several optimality conditions for higher-order minimizers via the introduced classes of functions. In Section 4, we associate a unified dual to the considered problem and establish weak and strong duality results.
2. Preliminaries and Definitions
Let
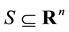 be a nonempty open subset of
be a nonempty open subset of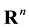 . Let
. Let
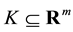 be a closed convex cone with nonempty interior and let
be a closed convex cone with nonempty interior and let
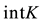 denote the interior of K. The dual cone K* of K is defined as
denote the interior of K. The dual cone K* of K is defined as
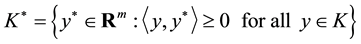 .
.
The strict positive dual cone
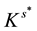 of K is given by
of K is given by
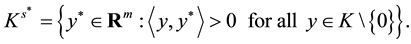
A function
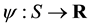 is said to be locally Lipschitz at a point
is said to be locally Lipschitz at a point
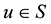 if for some
if for some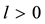 ,
,


A function

Definition 2.1. [11] Let






The Clarke’s generalized gradient of



Let








The generalized gradient of f at u is the set

where



Every element




A functional


(i)


(ii)


(i) and (ii) together imply
We consider the following nonsmooth vector optimization problem
(NVOP) K-minimize

subject to
where







Let

The following solution concepts are well known in the literature of vector optimization theory.
Definition 2.2. A point
(i) a weak minimizer (weakly efficient solution) of (NVOP) if for every

(ii) a minimizer (efficient solution) of (NVOP) if for every

With the idea of analyzing the convergence and stability of iterative numerical methods, L. Cromme [8] introduced the notion of a “strict local minimizer of order k”. As a recent advancement on this platform, Bhatia and Sahay [10] defined the concept of a higher-order strict minimizer with respect to a nonlinear function for a differentiable multiobjective optimization problem. We now generalize this concept and give the definition of a higher-order (weak) minimizer with respect to a function

Definition 2.3. A point

(i) a weak minimizer of order





(ii) a minimizer of order





Remark 2.1. (1) If f is a scalar valued function,


(2) If


(3) If

Remark 2.2. (1) Clearly a minimizer of order k for (NVOP) with respect to


(2) A direct implication of the fact that


(3) Note that if





In the sequel, for a vector function




We now define various classes of nonsmooth

Definition 2.4. A locally Lipschitz function









If the above relation holds for every



Remark 2.3. (1) If f is a scalar valued function and


(2) If f is a differentiable function,






(3) If







(4) If





Definition 2.5. A locally Lipschitz function









Equivalently,

If f is K-nonsmooth





Clearly, if f is K-nonsmooth




Example 2.1. Consider the following nonsmooth function




Here


Define


Let




Then, at

for every


Hence, f is K-nonsmooth


However, for



so that f is not K-nonsmooth

Definition 2.6. A locally Lipschitz function









Equivalently,

If the above relation holds for every


We now give an example to show that a K -nonsmooth




Example 2.2. Consider the following nonsmooth function




Here


Let



Then, at

for every


Therefore, f is K-nonsmooth



However, for




Thus, f is not K-nonsmooth


Definition 2.7. A locally Lipschitz function









If the above relation holds at every


Definition 2.8. A locally Lipschitz function









If f is K-nonsmooth





Remark 2.4. When f is a differentiable function,




3. Optimality
In this section, we obtain various nonsmooth Fritz John type and Karush-Kuhn-Tucker (KKT) type necessary and sufficient optimality conditions for a feasible solution to be a (weak) minimizer of order k for (NVOP).
On the lines of Craven [15] we define Slater-type cone constraint qualification as follows:
Definition 3.1. The problem (NVOP) is said to satisfy Slater-type cone constraint qualification at




Remark 3.1. The following inclusion relation is worth noticing.
For



Thus,

Since a weak minimizer of order

Theorem 3.1. If a vector







The necessary nonsmooth KKT type optimality conditions for (NVOP) can be given in the following form.
Theorem 3.2. If a vector








Proof. Assume that




If possible, suppose


So there exists


Now, since Slater-type cone constraint qualification holds at








Now, we give sufficient optimality conditions for a feasible solution to be a higher-order (weak) minimizer for (NVOP).
Theorem 3.3. Let







Further, assume that f is K-nonsmooth












Proof. Assume on the contrary that





As


As (6) holds, there exist



Since f is K-nonsmooth





Adding (8) and (10), we get

As

Also, since g is Q-nonsmooth






However,



Adding (11) and (12), we get

which implies that

Using sublinearity of F under the assumption



which on using (9) and (1), gives

This is impossible as






Theorem 3.4. Suppose there exists a feasible solution

















Proof: Let if possible,




Since



As (6) holds, there exist


Since f is K-nonsmooth




As

Now,




If

Since g is Q-nonsmooth





so that

If
Now, proceeding as in Theorem 3.3, we get a contradiction. Hence,


Theorem 3.5. Assume that all the conditions of Theorem 3.3 (Theorem 3.4) hold with


Proof: Let if possible,





Proceeding on similar lines as in proof of Theorem 3.3 (Theorem3.4) and using (17) we have

As

This leads to a contradiction as in Theorem 3.3 (Theorem 3.4). Hence,


4. Unified Duality
On the lines of Cambini and Carosi [16] , we associate with our primal problem (NVOP), the following unified dual problem (NVUD).
(NVUD) K-maximize

subject to


where




Note that Wolfe dual and Mond-Weir dual can be obtained from (NVUD) on taking


Definition 4.1. Given the problem (NVOP) and given a vector


Theorem 4.1. (Weak Duality) Let x be feasible for (NVOP) and









then,

Proof: Assume on the contrary that

Since




Since f is K-nonsmooth




Adding (21) and (23), we obtain

As

Also, since g is Q-nonsmooth





Adding (24) and (25), we get

or,

Using sublinearity of F under the assumption that



As




This contradicts the feasibility of
Theorem 4.2. (Weak Duality) Let x be feasible for (NVOP) and



(i) If




(ii) If






Then, we have

Proof: Case (i): Let


Since x is feasible for (NVOP) and



Adding (26) and (27), we get

That is,

As





Since,


or

so that

Now, since


Therefore, there exists



which is a contradiction, as

Case (ii): Let

Let if possible,

Since f is K-nonsmooth




As

Since x is feasible for (NVOP) and


If

As g is Q-nonsmooth




Since

If
Since



Adding (29) and (31), we get

or

Using sublinearity of F with the fact that



This contradicts the assumption that
Theorem 4.3. (Strong Duality) Let








Proof: As





Since


Thus,






or,

Since,


which contradicts Theorem 4.1 (Theorem 4.2). Hence


5. Conclusion
In this paper, we introduced the concept of a higher-order (weak) minimizer for a nonsmooth vector optimization problem over cones. Furthermore, to study the new solution concept, we defined new generalized classes of cone-nonsmooth (F, ρ)-convex functions and established several sufficient optimality and duality results using these classes. The results obtained in this paper will be helpful in studying the stability and convergence analysis of iterative procedures for various optimization problems.
References
- Bector, C.R., Chandra, S. and Bector, M.K. (1988) Sufficient Optimality Conditions and Duality for a Quasiconvex Programming Problem. Journal of Optimization Theory and Applications, 59, 209-221.
- Mangasarian, O.L. (1969) Nonlinear Programming. McGraw-Hill, New York.
- Vial, J.P. (1983) Strong and Weak Convexity of Sets and Functions. Mathematics of Operations Research, 8, 231-259. http://dx.doi.org/10.1287/moor.8.2.231
- Hanson, M.A. and Mond, B. (1982) Further Generalization of Convexity in Mathematical Programming. Journal of Information and Optimization Sciences, 3, 25-32. http://dx.doi.org/10.1080/02522667.1982.10698716
- Preda, V. (1992) On Efficiency and Duality for Multiobjective Programs. Journal of Mathematical Analysis and Applications, 166, 365-377. http://dx.doi.org/10.1016/0022-247X(92)90303-U
- Antczak, T. and Kisiel, K. (2006) Strict Minimizers of Order m in Nonsmooth Optimization Problems. Commentationes Mathematicae Universitatis Carolinae, 47, 213-232.
- Antczak, T. (2011) Characterization of Vector Strict Global Minimizers of Order 2 in Differentiable Vector Optimization Problems under a New Approximation Method. Journal of Computational and Applied Mathematics, 235, 4991- 5000. http://dx.doi.org/10.1016/j.cam.2011.04.029
- Cromme, L. (1978) Strong Uniqueness: A Far Criterion for the Convergence Analysis of Iterative Procedures. Numerische Mathematik, 29, 179-193. http://dx.doi.org/10.1007/BF01390337
- Studniarski, M. (1989) Sufficient Conditions for the Stability of Local Minimum Points in Nonsmooth Optimization. Optimization, 20, 27-35. http://dx.doi.org/10.1080/02331938908843409
- Bhatia, G. and Sahay, R.R. (2013) Strict Global Minimizers and Higher-Order Generalized Strong Invexity in Multiobjective Optimization. Journal of Inequalities and Applications, 2013, 31. http://dx.doi.org/10.1186/1029-242X-2013-31
- Clarke, F.H. (1983) Optimization and Nonsmooth Analysis. Wiley, New York.
- Studniarski, M. (1997) Characterizations of Strict Local Minima for Some Nonlinear Programming Problems. Nonlinear Analysis, Theory, Methods & Applications, 30, 5363-5367. http://dx.doi.org/10.1016/S0362-546X(97)00352-0
- Ward, D.W. (1994) Characterizations of Strict Local Minima and Necessary Conditions for Weak Sharp Minima. Journal of Optimization Theory and Applications, 80, 551-571. http://dx.doi.org/10.1007/BF02207780
- Nahak, C. and Mohapatra, R.N. (2012) Nonsmooth
-Invexity in Multiobjective Programming Problems. Optimization Letters, 6, 253-260.
http://dx.doi.org/10.1007/s11590-010-0239-1 - Craven, B.D. (1989) Nonsmooth Multiobjective Programming. Numerical Functional Analysis and Optimization, 10, 49-64. http://dx.doi.org/10.1080/01630568908816290
- Cambini, R. and Carosi, L. (2010) Mixed Type Duality for Multiobjective Optimization Problems with Set Constraints. In: Jimėnez, M.A., Garzȯn, G.R. and Lizana, A.R., Eds., Optimality Conditions in Vector Optimization, Bentham Science Publishers, Sharjah, 119-142.
NOTES

*Corresponding author.



 -Invexity in Multiobjective Programming Problems. Optimization Letters, 6, 253-260.
-Invexity in Multiobjective Programming Problems. Optimization Letters, 6, 253-260.