ABSTRACT

Patent pools are established by the patent holders in order to promote R & D and technological standards, etc. This paper investigates the patent holders’ incentive to form a patent pool, the patent pool’s licensing behavior, and the anticompetitive effect of a patent pool. Our model is characterized by the following two features. First, we consider the different two types of patent: basic and optional. Second, we consider a patent pool that offers two types of a package license: single and multiple. Our results yield some implications for a patent pool that is characterized by the complementarity between basic and optional patents.

1. Introduction

This paper investigates the anticompetitive effect of a patent pool that offers a package license. Our analysis is characterized by the following two features. First, we consider different two types of patents: basic and optional. The basic technology can be used by itself, it becomes more valuable when used in combination with the optional technology. The optional technology cannot be used by itself. Second, we consider not only a patent pool that offers a single package license, but also a patent pool that offers multiple package licenses. The single package license includes both basic and optional patents in the patent pool. In the multiple package case there are two package licenses: one includes only basic patents, whereas the other includes both basic and optional patents.

A patent pool refers to organizations where patent holders concentrate their own patents for commercializing new innovations or for setting standards, and offer a package license that is inclusive of many patents in the pool¹. A patent pool plays an important role in solving the “tragedy of the anticommons”, which is discussed in Heller and Eisenberg (1998) [1]. The well-known “tragedy of the commons” is the situation wherein a resource can be overused when it is not protected by property rights. “Tragedy of the anticommons”, as Heller and Eisenberg indicated, refers to a situation wherein “excessive” property rights render the resource underused when there are multiple property rights holders. In the case of patents, excessive property rights can have the perverse effect of stifling or discouraging innovation. A patent pool is expected to be a useful means to solve this “tragedy of the anticommons” that arises, particularly in advanced technology fields. A patent pool enables firms to reduce the cost of seeking technologies and to negotiate by simplifying the license contract. Furthermore, a patent pool can avoid patent litigations and can help establish standardization committees such as MPEG-LA, DVD 6C Licensing Agency, and 3G².

Unfortunately, the competition authorities in many countries have a deep-rooted suspicion of patent pools, which involve cooperative activity between patent holders. There is the possibility that a patent pool can exercise monopoly power as a major cartel³. Thus, many discussions have been held between economists, legal scholars, and antitrust enforcement leagues as to whether patent pools benefit both intellectual property owners and consumers. Our concern is to determine whether patent pools are competitive or anticompetitive.

The US competition authority focuses primarily on the technical relationships between the patents included in the pool⁴. Its viewpoint is that a pool of technical substitute patents is more suspicious than a pool of technical complementary patents. In addition to this view of the US antitrust enforcement agency, Shapiro (2001) [2], Lerner and Tirole (2004) [4], and Azetsu and Yamada (2011) [5] focused on the technical relationships between the patents included in a pool, and investigated whether patent pools have an anticompetitive effect. They concluded that a patent pool is pro-competitive when the patents are of the technical complementary type, whereas a patent pool always operates as a cartel when the patents are technical substitutes. These results are consistent with the current US and European policies (see Lerner and Tirole 2008 [6]).

Most of the literature on patent pools has sought to determine the social implications of the pool under the situation where all firms join the pool (Lerner and Tirole 2004 [4]). Recently, some works have focused on the firm’s incentive problem in relation to participation in the pool (Aoki and Nagaoka 2004 [7]; Brenner 2009 [8]; Langinier 2009 [9]; Lerner and Tirole 2008 [6])⁵. Our paper considers both the patent pool that offers only a single package license and the patent pool that offers the multiple package licenses. There are no theoretical discussions of the patent pool in the literature that offered a choice of single package and multiple package licenses⁶. The multiple package licenses are packaged within the subsets of all the patents in the pool. In practice, it is observed that about 12% of the pools surveyed by Lerner et al. (2003) [15] offer multiple package licenses (that is, about 88% of the pools offer the single package license)⁷. One enormous advantage of multiple package licenses is that they give users various choices of patents, because a single package license inclusive of all the patents in the pool could be tie-in sale. The recent guidelines of the European Commission encourage patent pools to offer the multiple package licenses as a useful way to provide users with a broader choice⁸.

In this paper, we investigate the patent holders’ incentive to form a pool, the patent pool’s licensing behavior, and the anticompetitive effect of a pool. In particular, we focus on the patent pool that offers multiple package licenses. When does a patent pool offer the multiple package licenses and when does it not do so? When does the patent pool have an anticompetitive effect? Should the competition authorities, such as the European Commission, encourage patent pools to offer the multiple package licenses? We find that the technical complementarity between the patented technologies in a pool plays a critical role in answering the above questions.

The paper is organized as follows. Section 2 defines patented technologies and the users’ gross surplus for using patent in our models. Section 3 characterizes the licensing fees in the case where the patent pool licenses monopolistically. Section 4 characterizes the licensing fees in the case where patent holders license individually. Section 5 analyzes the anticompetitive effect of a patent pool, using the outcomes of Sections 3 and 4, and then investigates patent holder’s incentives to form a patent pool. Finally, Section 6 discusses the results derived from the analysis conducted in the paper.

2. Basic Set-Up

We suppose that there are two patents, A and B, which are owned by patent holder A and B, respectively. Patent A relates to basic technology, whereas patent B involves optional technology, which is valuable only when used in combination with the basic technology. Although the basic technology can be used by itself, it becomes more valuable when used in combination with the optional technology. The optional technology cannot be used by itself. Each patent is owned by a patent holder, A and B. Following Shapiro (2001) [2] and Lerner and Tirole (2004) [4], we distinguish between patent holders and users. Patent holders do not have the ability to comercialize the patented technology on their own. The patent holder obtains the licensing fee from patent users, and the users obtain a surplus using the patents⁹.

Users make their products by using patents and obtain a surplus, which is represented by 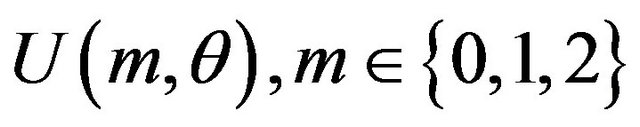denotes the number of patents employed by the user to make a product, and represents the heterogeneity between users. Note that the users buy license A first because it is basic. Therefore, implies that the user uses only patent A and implies that the user uses both patents A and B. For simplicity, we assume that users’ size 1 is and they are distributed uniformly on the interval. Our model specifies the user’s gross surplus function as the following quadratic form

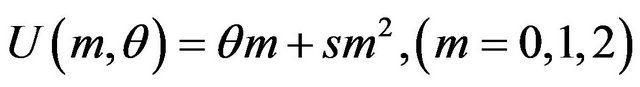. (1)

where ¹⁰. The levels of gross surplus for each number of patents are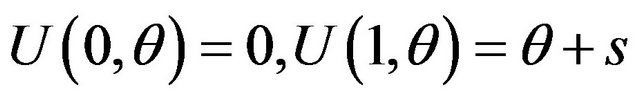, and. We find that a user with a high obtains a high level of gross surplus for any number of patents used. The heterogeneity of the gross surplus between users is also assumed by Lerner and Tirole (2004) [4]. They explained heterogeneity in terms of a) the fixed cost for the user to adopt the patent, b) the user’s opportunity costs of choosing the patent, and c) the benefits that the user derives from the patent.

The initial differences in the gross surplus are and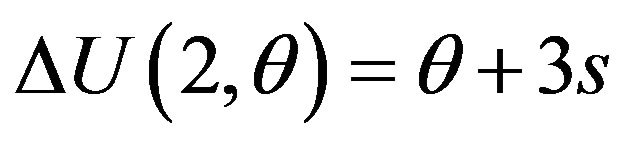. The difference, 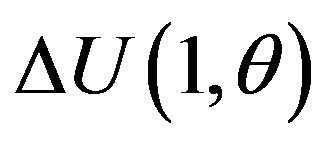, implies the user’s willingness to pay for patent A when the user does not access any patent, and 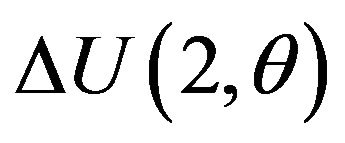is the user’s willingness to pay for patent B when the user already has access to patent A¹¹. Note that the willingness to pay for an additional patent depends on, and the user with a high obtains a high additional surplus¹². Lerner and Tirole (2004) [4] assumed that the willingness to pay for an additional patent is the same between users. Under this assumption, a patent pool solely offers single package licenses because all users demand the same number of patents. In practice, however, 12% of the patent pools in the Lerner et al. (2003) [15] sample offered multiple package licenses. To explain the observed offering of multiple package licenses by 12% of the patent pools, we must allow for differences in the willingness to pay for an additional patent between users. In reality, because of the variations in the ability or knowledge of each user, it is no wonder that there are differences in their benefits from using an additional patent.

The second difference in the gross surplus is. The value of 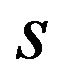represents the complementarity between basic and optional patents. When an optional patent significantly enhances the usefulness of a basic patent, the value of s cannot be negative (complementarity is strong)¹³. Then, the gross surplus function is convex for the number of patents. The user’s additional gross surplus for an optional patent is larger than that for a basic patent: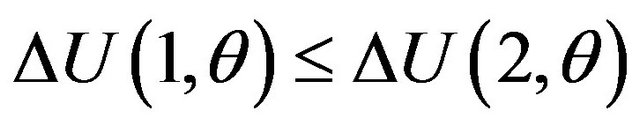. An example is the combination of a PC and MS Office, containing MS Word and Excel, etc. The PC is the basic patent and MS Office is the optional patent. If we use MS Office installed on a PC, we would have a significantly larger additional gross surplus.

When an optional patent does not significantly enhance the usefulness of the basic patent, then the value of could be negative (the complementarity is weak). Then, the gross surplus function is strictly concave for the number of patents. In this case

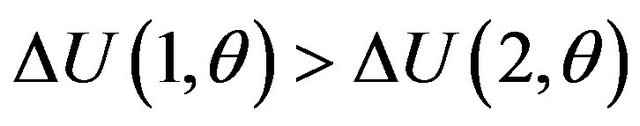
is satisfied. We can consider a PC and typing software as an example. Typing software is an application software program for teaching touch typing. However, installing typing software, which is optional, would not result in a significantly large additional gross surplus.

3. Patent Pool Pricing

3.1. Users’ Decisions and the Demand for Package Licenses

In this section, we characterize the equilibrium for the case where patents A and B are monopolistically licensed only by the patent pool formed by patent holders A and B¹⁴. The patent pool could offer users two package licenses, A and AB. In package A, the pool licenses patent A for users for a licensing fee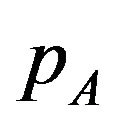. In package AB, the pool licenses patents A and B for users for the licensing fee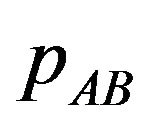; the package AB is a bundled good. If a user wants only the basic patent, he or she can buy package A, whereas if a user wants both the basic and the optional patent, he or she can buy the package AB. In addition, we assume that a pool must pay very low costs for offering a package license. The pool does not offer the package that no users buy.

Given the licensing fees, and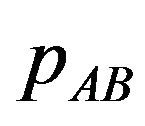, the users choose the number of patents to maximize their net surplus. When packages A and AB are offered by the patent pool, the type user chooses which package to buy in the following manner:

• The user does not buy any packages (the user chooses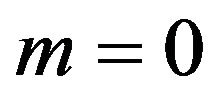) if.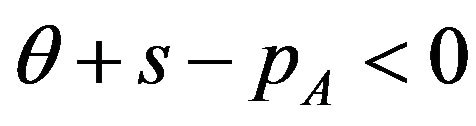

• The user buys package A (the user chooses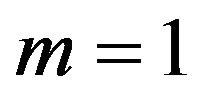) if θ + s − p_A ≥ 0 and θ + 3s < p_B, where.

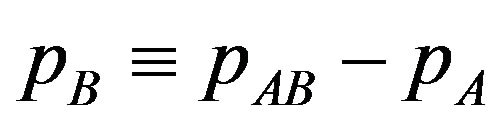• The user buys package AB (the user chooses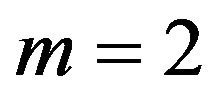) if.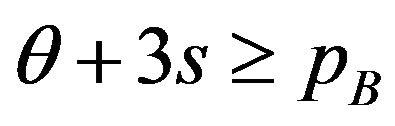

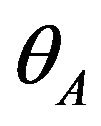As the surpluses differ across different users, the number of patents chosen by each user also differs across users. Now, we define. The type user is indifferent between buying package A and not buying any package. The type user is indifferent between buying package A and package AB. Each user behaves as follows:

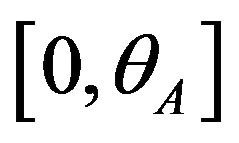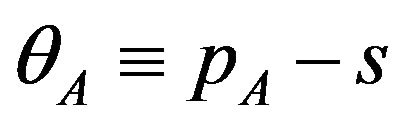• The users on interval where do not buy any packages.

• The users on interval where buy package A.

• The users on interval 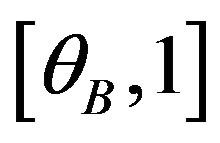buy package AB.

Lemma 1. When given licensing fees satisfy the inequality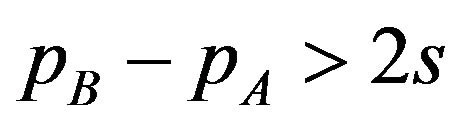, there are users who buy package A.

Proof. When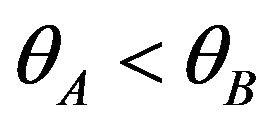, there are users who buy package A. From the definition of and, we can find that.□

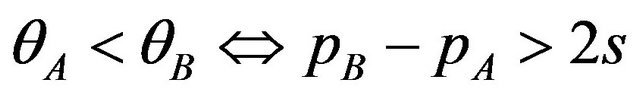When licensing fees satisfy the inequality p_B − p_A > 2s, there are both users who buy package A and users who buy package AB. Then, the demand for the package A is

. (2)

The demand for the package AB is

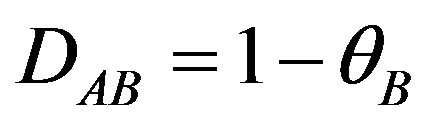. (3)

When licensing fees do not satisfy the inequality p_B − p_A > 2s, then no user buys package A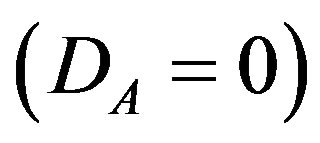. The type user decides whether to buy the package AB in the following manner:

• The user does not buy any packages (the user chooses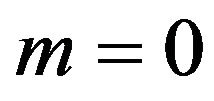) if.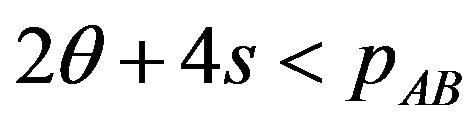

• The user buys package AB (the user chooses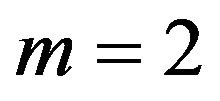) if.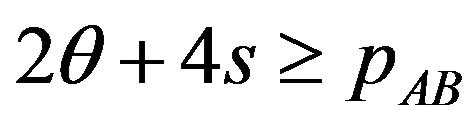

Then, defining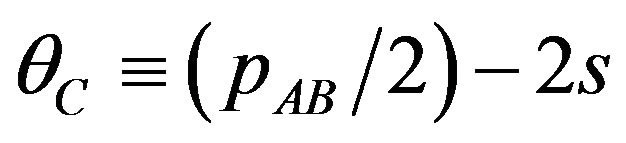, the demand for the package AB is

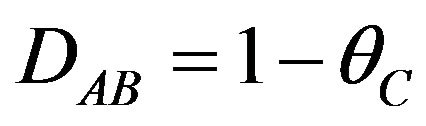. (4)

3.2. Patent Pool Equilibrium

For simplicity, we ignore the costs paid by the pool members (the patent holders) for developing their own patents. Under the demand function of each package license, the patent pool’s profit is

.

Note that 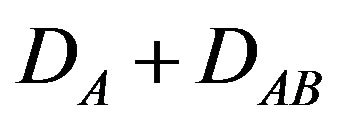is the demand for patent A. The patent pool decides and 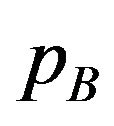to maximize the profit. From lemma 1 and the definition of demand (2) - (4), the profit is rewritten as the follows

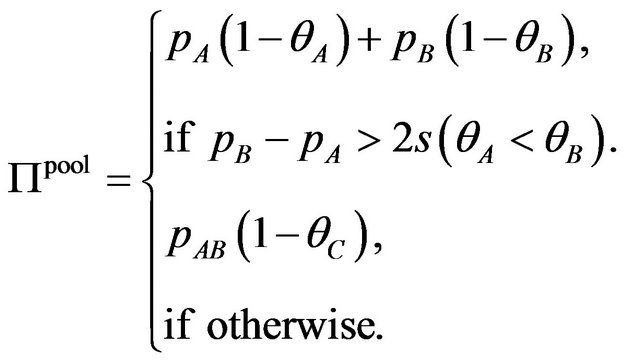
The equilibrium licensing fees are given by the solution of above profit maximization problem. Now we consider the case where patent pool offers both package A and AB. The optimal licensing fees are the solution of the following profit maximization problem

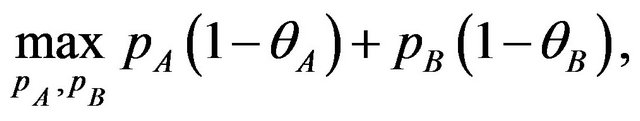
where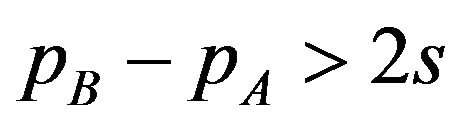. The interior solution should satisfy the following equations

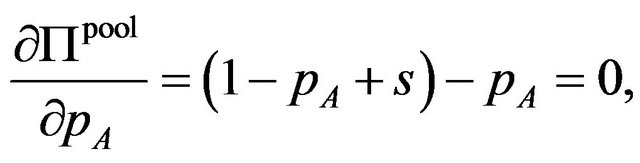(5)

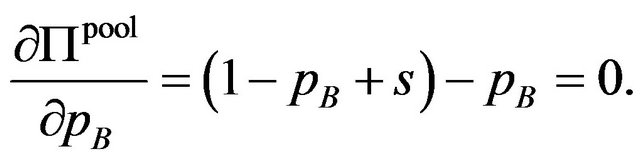(6)

Since the second order condition is warranted, the licensing fees which satisfy (5) and (6) are

.

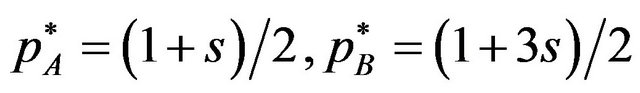Checking these licensing fees satisfy the inequality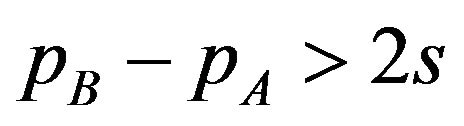, we find that the optimal solution is

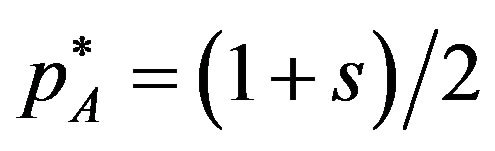
and              

(that is if 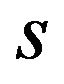is negative value.

If 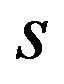is not negative value, then the patent pool does not offer the package A. The patent pool’s problem is

.

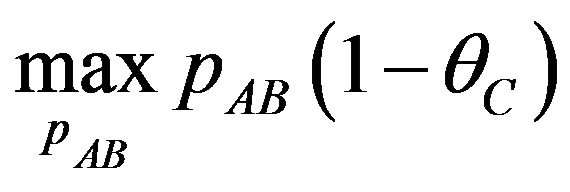The optimal licensing fee satisfies

. (7)

Since the second order condition is warranted, the licensing fees which satisfy (7) is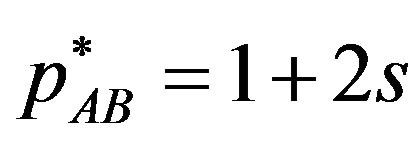. Then we get the following proposition.

Proposition 1. Patent pool pricing

1) Multiple package licenses: When is negative value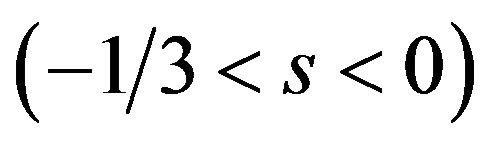, the patent pool offers two package licenses A and AB, the licensing fees are

.

2) Single package license: When 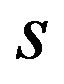is not negative value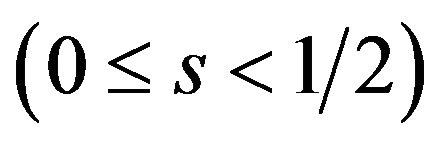, the patent pool offers only single package AB, and the licensing fee is.

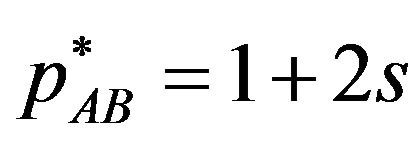Proof. If the optimal licensing fees 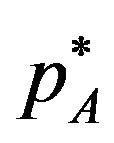and 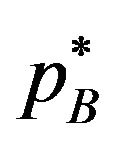satisfy the inequality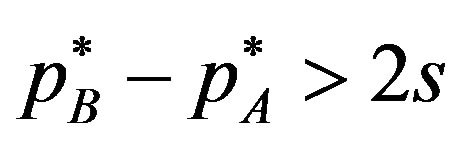, the licensing fees are determined by (5) and (6). Then and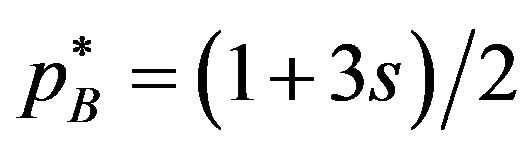. Substituting the licensing fees into the inequality, we can find the licensing fees satisfy the inequality when s is negative value. When s is not negative value, the optimal licensing fee satisfies (7), so that.□

Proposition 1 shows that patent pool pricing is characterized by the value of ¹⁵. When the complementarity between A and B is weak, both the package license A, inclusive of only basic, and the package license AB, inclusive of basic and optional, are offered by the patent pool. Each package licensing fee is 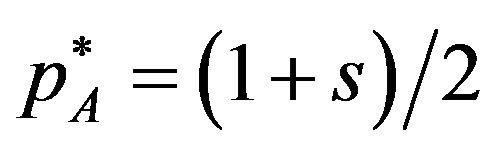and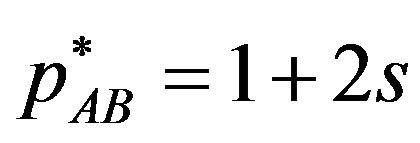. In this case, there are both users who buy the package license A and who buy the package license AB. The patent pool is willing to offer the multiple package licenses by offering not only the package license AB but also the package license A in order to maximize his/her own profit. On the other hand, when the complementarity is strong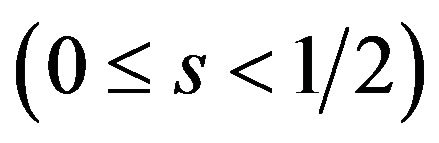, only the package license AB, inclusive of basic and optional, is offered by the patent pool. The package licensing fees is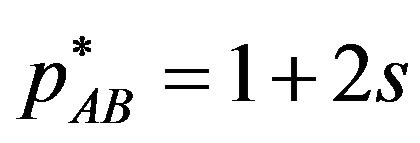. In this case, there are users who buy only the package license AB, if they buy the license. Since the complementarity is strong, there are not the users who use only patent A. This case corresponds to the patent pool pricing in Shapiro (2001) [2] and the demand margins bind in Lerner and Tirole (2004) [4].

The patent pool offers only the package AB which is similar to the tie-in sale and is not willing to offer multiple package licenses in order to maximize his/her own profit. In order to avoid the tie-in sale, EU committee encourages patent pools to offer multiple package licenses. But our result is that none of users buy package licenses when s is negative. Therefore, the recommendation of the competition authority makes no senses in the case 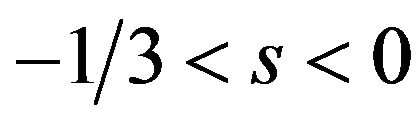under our model.

4. Individual Pricing

4.1. Demand for Each Patent

In this section, we consider the case where a patent pool is not established. Patent holder A and B individually licenses the users to his/her own patent. If a user wants to use patent A (patent B), the user must access to patent holder A (patent holder B). If a user wants to use both patent, then the user must access with both the patent holders.

Given the licensing fee, the users decide whether or not to choose each patent to maximize their net surplus. In the same manner of Section 3, we describe the users behavior as the follows. When given licensing fees satisfy the inequality• The users on interval where do not buy any packages.

• The users on interval 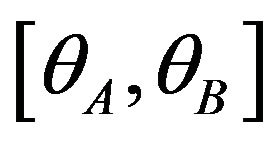where 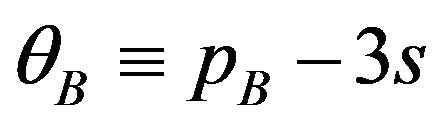buy package A.

• The users on interval 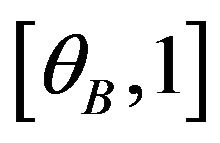buy both license A and B.

When given licensing fees satisfy the inequality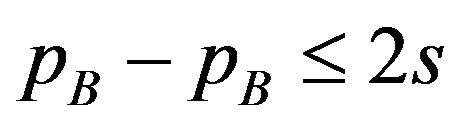• The users on interval where

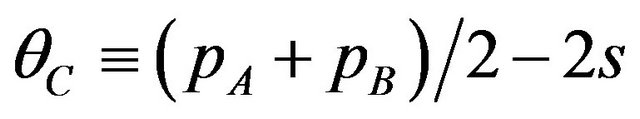
do not buy any packages.

• The users on interval 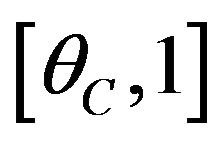buy both license A and B.

Given the licensing fee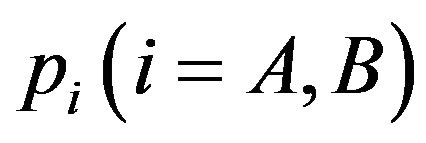, the users decide whether or not to choose each patent to maximize their net surplus. The demands for patent A and B are

, (8)

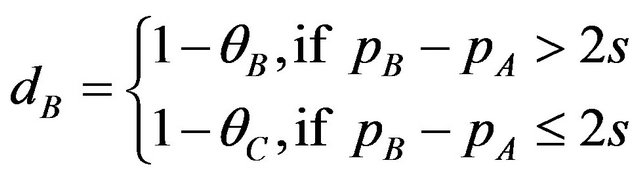. (9)

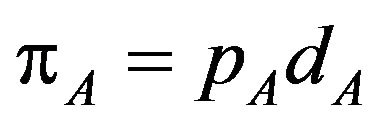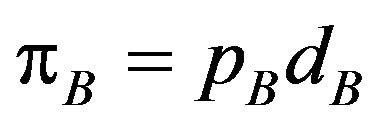Under each demand of patent, the profits of patent holder A and B are and, respectively.

4.2. Individual Pricing Equilibrium

The patent holders decide their licensing fees to maximizing their own profit, as a given other licensing fee. Individual pricing equilibrium is characterized by the follows:

Proposition 2. Individual pricing

1) When 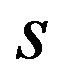is negative value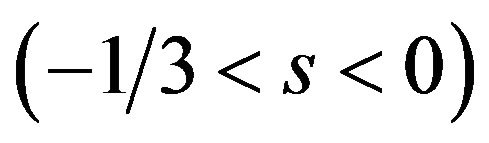, Nash equilibrium licensing fees are

.

2) When 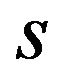is not negative value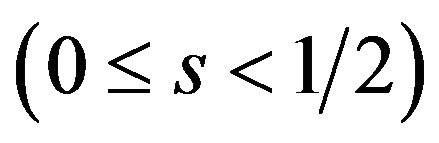, Nash equilibrium licensing fees are

.

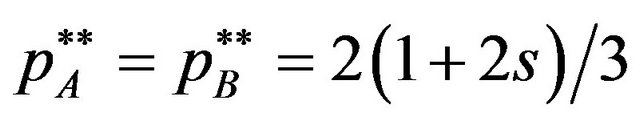Proof. If the equilibrium licensing fees 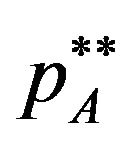and 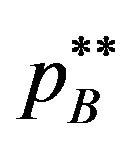satisfy the inequality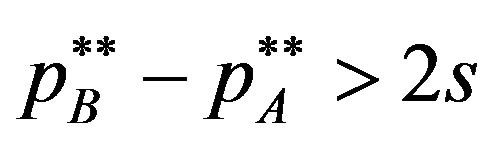, the patent holder A and B are faced on the demands of their patents 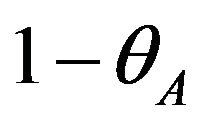and, respectively. Then the licensing fee of patent A is, which maximizes the profit of patent holder A, for any licensing fee of patent B, as far as is satisfied. The licensing fee of patent B is, which maximizes the profit of patent holder B, for any licensing fee of patent A, as far as 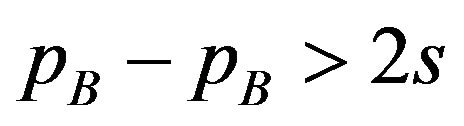is satisfied. Substituting the licensing fees into the inequality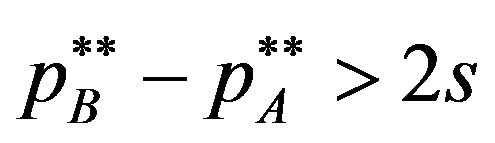, we can find       and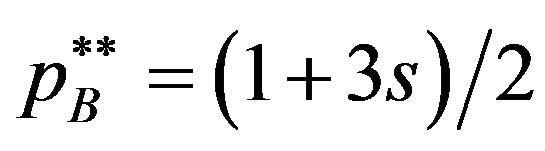

is equilibrium licensing fees when.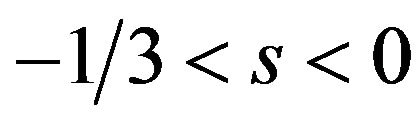

Next, if the equilibrium licensing fees 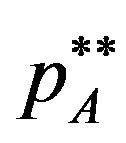and satisfy the inequality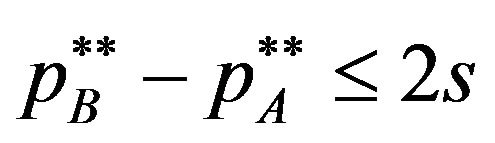, the patent holder A and B are faced on the same demands. The licensing fees of patent A and B must maximize each profit of patent holders for each licensing fee. Then optimal response of patent holder A is

and the optimal response of patent holder B is

.

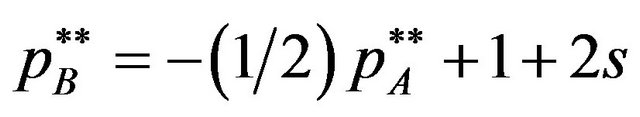Therefore Nash equilibrium licensing fee is

.

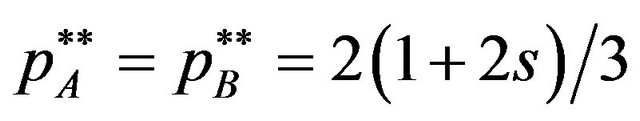Substituting the licensing fees into the inequality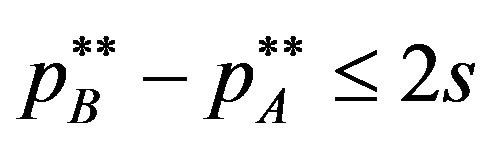, we can find

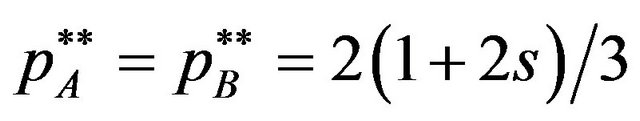
is equilibrium licensing fees when.□

Similar to Proposition 1, Proposition 2 shows that individual pricing is characterized by the value of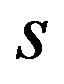. When the complementarity is weak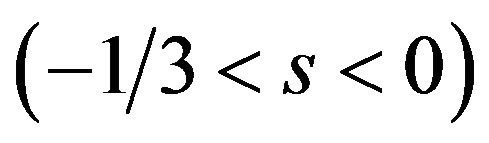, patent holder A of the basic offers the equilibrium licensing fee 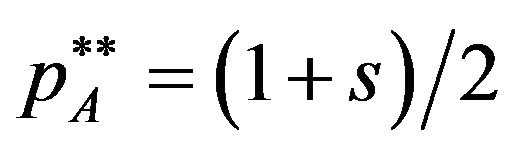and patent holder B of the optional offers the equilibrium licensing fee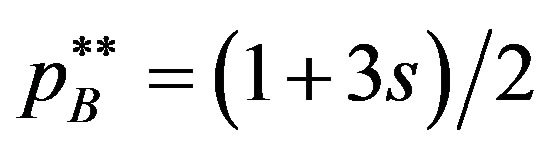. In the case, there are the users who buy only basic and who buy both basic and optional. Since the complementarity is weak, the demand for patent A is independent of the demand for patent B. Then each patent holder sets his/her licensing fee, without the strategic interaction between patent holders. The licensing fee of basic patent is set higher than that of optional, because price elasticity of demand for patent holder A is lower than that of demand for patent holder B. As the result, when is negative value, these licensing fee is asymmetric.

When the complementarity is strong, each patent holder A and B offers the equilibrium licensing fee. In the case, the users decide whether they buy two licenses from patent holder A and patent holder B, since the complementarity is strong. Since the users who buy any license buy both patent A and B, the demand for the patents depends on the sum of licensing fees. Therefore each patent holder must set his/her licensing fee under the strategic interacttion between patent holders. The concern of the users who buy both patent A and B is only the sum of licensing fees. Then patent holder A does not have technical advantage as the patent holder of basic patent, and these licensing fee is symmetric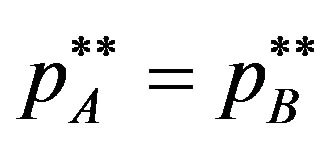. This case corresponds to the Cournot-Shapiro argument in Shapiro (2001) [2] and Demand margin bind in Lerner and Tirole (2004) [4].

5. Welfare Analysis

In Sections 3 and 4, we characterize the licensing fees in the equilibrium under a patent pool and in the absence of a patent pool. Firstly, we investigate the effects of a patent pool on the licensing fees. Comparing the licensing fees of patent pool pricing with those of individual pricing, we get the following lemma.

Lemma 2. A patent pool does not affect the licensing fees when 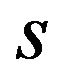is negative value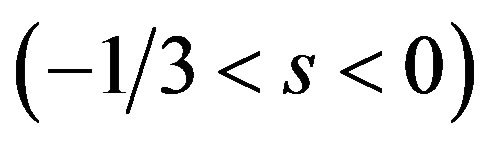, but decreases the licensing fees when is not negative value.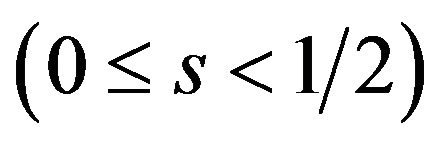

Proof. We consider the case where the value of is negative. From Proposition 1-(1) and Proposition 2-(1), we know that the licensing fees in patent pool pricing are same as in the individual pricing (and). Then we can find that a patent pool does not affect the licensing fees when 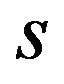is negative value.

We consider the case where 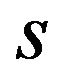is not negative. From Proposition 1-(2) and 2-(2), the licensing fee is 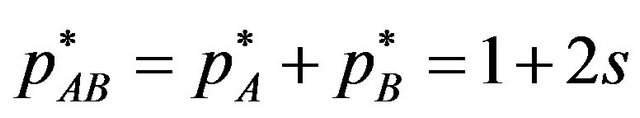in the patent pool pricing, and 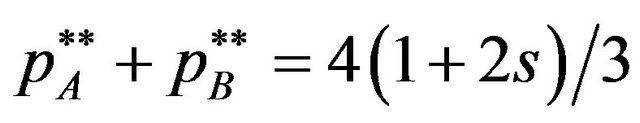in the individual pricing. Then we can find that a patent pool decreases the licensing fees when 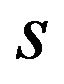is not negative value.□

When complementarity is weak, a patent pool does not affect the licensing fees. From Proposition 2, we find that each patent holder does not set his/her licensing fee without any strategic interacttion between the patent holders in the individual pricing. Since the complementarity is weak and the patent cannot be replaced by the other patent (not substitute) in this paper, the demand for each patent is determined only by each licensing fee but not the other licensing fee¹⁶. Then the patent holders can set their licensing fees monopoly as a patent pool pricing.

When complementarity is strong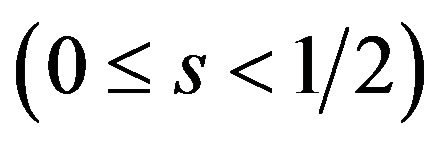, a patent pool decreases the licensing fees. When 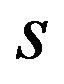is not negative, the concern of the users who buy patents is the sum of licensing fees, since the user buys both patents. The patent holder must set his/her licensing fee under the strategic interaction between the patent holders. In order to raise their own profit, they will raise their own licensing fee without corporative pricing (failure of corporation). Then the licensing fee 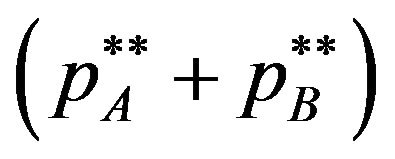in the individual case is higher than that in the patent pool pricing 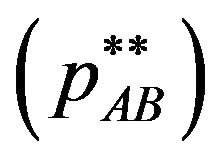where the patent holders set the licensing fee cooperatively. That is, the patent pool which includes complementary patents is pro-competitive. This result corresponds to Shapiro (2001) [2] and the demand margins bind in Lerner and Tirole (2004) [4].

Now we investigate whether or not a patent pool enhances social welfare, and whether or not the patent holders have the incentive to form a patent pool. We define the social welfare as the sum of users’ net surplus and patent holders’ profit. Since users’ payment for the patent is equal to the profit of patent holder A and B, the social welfare is equal to the gross surplus of users. If there are the users who buy only patent A, then the social welfare (that is the sum of users’ net surplus) is

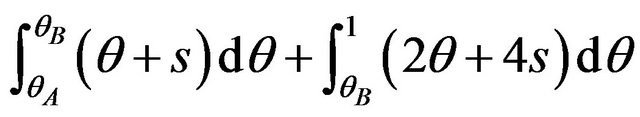, (10)

where 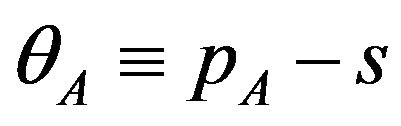and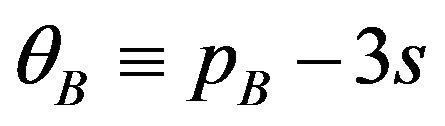. Therefore the social welfare depends on the licensing fee of patent A and B (or licensing fees of patent packages), and ¹⁷.

If there are not the users who buy only patent A, then the social welfare is

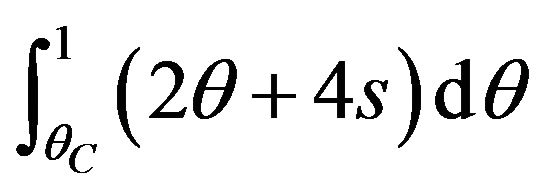, (11)

where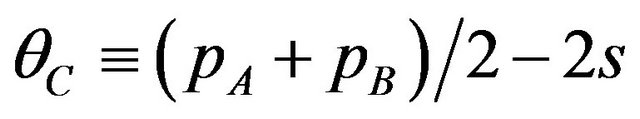. The social welfare depends on the sum of licensing fees (or licensing fee of the package AB),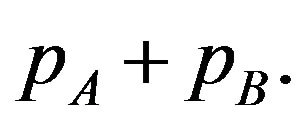

Proposition 3. A patent pool does not affect the welfare when s is negative value, but enhances welfare when 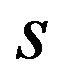is not negative value.

Proof. We know the social welfare depends only on licensing fees. When is negative, a patent pool does not affect the licensing fees from lemma 2. Then we find that a patent pool does not affect the social welfare too. When 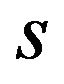is not negative, a patent pool decreases the licensing fee from lemma 2. Then a patent pool increases the social welfare.□

Next, we investigate whether the patent holder A and B have the incentive to form a patent pool. As the standard assumption of the corporate merger theory, we assume that the patent holders A and B form a patent pool if the patent pool’s profit is larger than the sum of the profit of the patent holders A and B 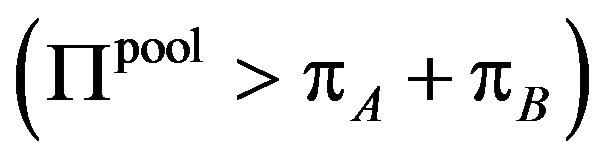¹⁸, with the profit of patent pool, 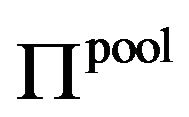, we can get the following Proposition.

Proposition 4. When 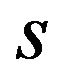is negative value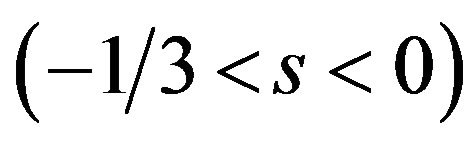, is satisfied. Then the patent holder A and B does not have the incentive to form a patent pool. When 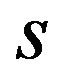is not negative value, 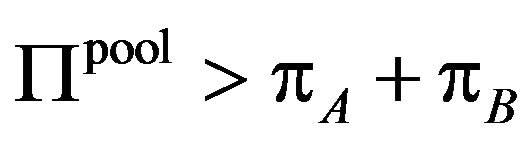is satisfied. Then the patent holder A and B have the incentive to form a patent pool.

Proof. Firstly we consider the case where 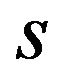is negative value. We already know the licensing fees in patent pool pricing are same as in the individual pricing (and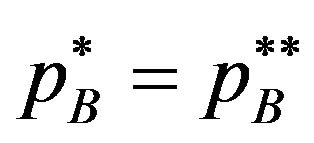). The profit of the patent pool is same as the sum of profit of patent holders A and B.

.

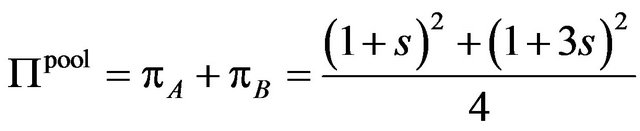Then the patent holder A and B does not have the incentive to form a patent pool.

Next we consider the case where s is not negative value. From the Proposition 1-(2), we get the patent pool profit is

.

On the other hand, the profits of patent holders A and B are

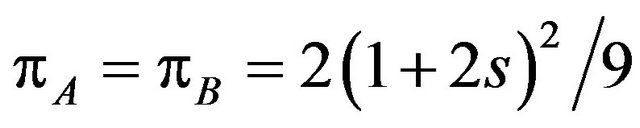from the Proposition 2-(2). Then we can find that 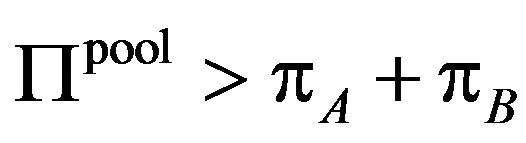is satisfied. When 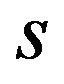is not negative, the patent holders A and B have the incentive to form a patent pool.□

Propositions 3 and 4 show that the effect of a patent pool on the welfare and the patent holders’ incentive to form a pool are characterized by the value of. When the complementarity is weak, a patent pool does not affect the welfare and patent holders do not have the incentive to form a patent pool. From Proposition 2, we find that each patent holder sets his/her licensing fee without influencing each other in ex-post, when 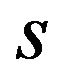is negative. The patent pool pricing is equal to the individual pricing: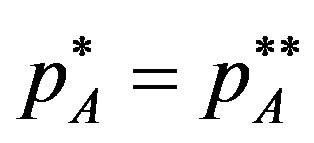,. Then the patent pool does not affect the welfare. Further, the patent holders do not have the incentive to form patent pool, since the corporative pricing does not change their own profit.

On the other hand, a patent pool enhances the welfare and patent holders have the incentive to form a patent pool when the complementarity is strong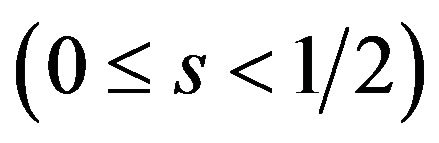. From Proposition 2, we find that each patent holder sets his/her higher licensing fee in order to get his/her more profits. As the result, the licensing fee of the patent pool is lower than the sum of licensing fees of individual patent holders:. Then the patent pool enhances the welfare. Further the patent holders have the incentive to form a pool, since the corporative pricing by forming a pool can reduces the licensing fees to the levels which maximize both profit of patent holders.

6. Conclusions

This paper investigates the anti-competitive effect of the patent pool which offers the package license. The most important work of the paper is to consider the complementarity between basic and optional patents. We find that the complementarity characterizes the licensing behavior of the patent pool, the social welfare, and the patent holders’ incentive to form the patent pool. Our main results are as follows.

1) If the complementarity between basic and optional is weak, the patent holders do not have the incentive to form the patent pool; otherwise, there is other patent holders’ incentive beyond our model. If the patent pool is formed for any reasons, both the package license inclusive of only basic , and the package license inclusive of basic and optional are offered by the patent pool (multiple package licenses). Then the form of the patent pool does not change the licensing fee which user pay to patent holders. As a result, the patent pool does not affect the welfare.

2) If the complementarity between basic and optional is strong, the patent holders have the incentive to form the patent pool. Only the package license inclusive of basic and optional is offered by the patent pool (single package license). Then the form of the patent pool reduces the licensing fee which users pay to patent holders. As the result, the patent pool enhances the welfare.

These results lead to four suggestions. First, we suggest that actually-observed many patent pools could include only strong complementary patents. It is observed that about 88% of the patent pools, surveyed by Lerner et al. (2003) [15], offers the single package license. From our model, it is when the complementarity is strong that the single package license is offered by the patent pool. Therefore, we can guess that actually-observed many patent pools include only strong complementary patents.

Second, we suggest the reason why actually-observed many patent pools include only strong complementary patents. Our model explains that the patent holders have strong incentive to form a patent pool, if the complementarity is strong, conversely the patent holders do not have the incentive to form a patent pool, if the complementarity is weak. Furthermore, the antitrust guidelines require the patent pools only to include “essential patents” which implies strong complementary among the patents.

Third, it is less important on our model that the competition authorities, such as the European Commission etc, encourage patent pools to offer the multiple package licenses. The licensing behavior of patent pools is determined by the profit maximization of the patent pools. If multiple package licenses increase the profit of a patent pool, the patent pool is willing to offer the multiple package licenses. Otherwise, the patent pool does not offer the multiple package licenses as long as the competition authorities enforce the patent pool to offer the multiple package licenses. Even if the competition authorities enforce the patent pool which offers the single package license to offer the multiple package licenses, any users dose not buy the package license which include only basic as long as the licensing fee of the single package license change.

Finally, we suggest the criterion for pro-competitive patent pools. The antitrust guidelines indicate that the patent pools should not include patents except “essential patents” which implies strong complementary among patents. On our model, the complementarity characterizes the anticompetitive effect of a patent pool on the social welfare. We find that the patent pool is pro-competitive when the complementarity is strong. This corresponds to the case where the patent pool includes complementary patents in Shapiro (2001) [2] and the demand margins bind in Lerner and Tirole (2004) [4]. Further, the theoretical criterion is consistent to the antitrust guidelines which require the patent pools to include only “essential patents”.

On the other hand, the patent pool is neither procompetitive nor anti-competitive when the complementtarity is weak. Lerner and Tirole (2004) [4] concludes that a patent pool is anticompetitive when the patent pool includes only substitutes which can replace other patents, that is to say similar patents. Our paper finds that a patent pool does not affect the social welfare if the patent pool includes only patents which are weak complementtary between the patents. Therefore weak complementary patents need not be included in patent pools, since there is not social benefit. Furthermore other factors outside our model might give negative effect to the social welfare. We conclude that the antitrust guidelines which require the patent pools only to include “essential patents” are appropriate for competition policy.

In this paper, we find that patent holders do not have the incentive to form the patent pool which offers the multiple package licenses voluntarily. But some patent pools which offer multiple package licenses are observed actually. This is the problem which remains to be solved in our paper. This problem could be related to the discussion about the type space with the heterogeneity of the user’s gross surplus. Our paper assumes that the type space with the heterogeneity of the user’s gross surplus is one dimension in order to simplify the analysis. But the type space of multi-dimension used in a series of researches beginning on Adams and Yellen (1976) [19] might be more realistic. When we extend to the setting where the type space is multidimension, we cannot analyze analytically but numerically. The analysis under the type space of multi-dimension is further research.

7. Acknowledgements

We would like to thank Reiko Aoki, Sadao Nagaoka, Taiji Hagiwara, Toshihiro Matsumura, Takao Okawa, Kotaro Suzumura, Takashi Yanagawa. The financial support offered by KAKENHI (19830108) is also gratefully acknowledged.

REFERENCES

NOTES

¹Examples of comprehensive surveys on patent pools are Shapiro (2001) [2] and Gilbert (2004) [3].

²The standardization committees are the organizations that set international technological standards. Technological standards aim at the wide adoption of technologies in the marketplace. However, this wide adoption of technologies may bring about patent conflict between patent holders or firms. Standardization committees establish patent pools in order to avoid these conflicts. MPEG-LA, DVD 6C Licensing Agency, and 3G are examples of such standardization committees.

³See “Antitrust Guidelines for the Licensing of Intellectual Property”, April, 1995 [10] for the competition authority’s suspicion of patent pools as cartel. Historically, patent pools have been abused since the early 1900s; Gilbert (2004) [3]. Priest (1977) [11] indicated that it is possible that a patent pool is a means to disguise a cartel, formed by using a cross-license between the members in the pool.

⁴The US Department of Justice focused on the technical relationship between the pools in three business review letters regarding an MPEG patent pool and two DVD patent pools. See Shapiro (2001) [2] for details.

⁵Patent pools are often utilized the way to promote technical standardization. Indirect network effect, where increases in usage of one product increases in the value of a complementary product, which can in turn increase the value of the product, is important to promote technical standardization. Patent pools is used as the way to develop the compatibility between basic goods and optional goods to exert indirect network effect; Katz and Shapiro (1985) [12], Church and Gandal (1992, 1993) [13,14].

⁶The package licenses offered by patent pools can be regarded as bundling goods which is tie-in sale of monopoly firm in the Industrial organization literatures. In the literatures, “single package license” corresponds to “pure bundling” and “multiple package licenses” corresponds to ”mixed bundling”.

⁷For example, MPEG-LA, which is the patent pool administrator in regard to MPEG compression technological standards, offers multiple package licenses.

⁸See “Guidelines on the Application of Article 81 of the EC Treaty to Technology Transfer Agreements,” (2004/C101/02) [16].

⁹Similarly to the literatures on patent pools, this paper investigates the anticompetitive effect of a patent pool by focusing on patent pricing decision without the cost of seeking technologies and to negotiate by simplifying the license contract and the risk of patent litigations.

¹⁰We assume the parametric restrictions for the value of s in order to focus on interesting solution. If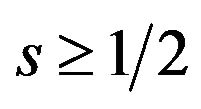, all users buy both basic and optional patents. If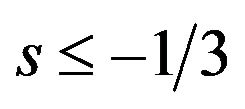, no one buys the patent.

¹¹When s is negative, the initial differences in the gross surplus of the users whose θ is near zero are negative. But, this does not affects the results of our analysis, since they do not buy any patents.

¹²This specification satisfies the discrete form of what we refer to as the Spence-Mirrlees single-crossing condition in the Contract Theory literature; see, for example, Salanie (2002) [17] and Bolton and Dewatripont (2005) [18]. The condition is known for separating different types of agents by offering larger allocations to higher types and making them pay for the privilege.

¹³This definition is different from the price-theoretic definition of complementarity. For example, Lerner and Tirole (2004) [4] and Azetsu and Yamada (2011) [5] etc. define technical complementarity between the technologies using the second difference in the gross surplus. The definition of complementarity in our paper is similar to these literatures.

¹⁴Patent pool pricing in our model is closely related with bundling pricing; Adams and Yellen (1976) [19] and McAfee et al. (1989) [20]. Especially, the bundling literature of the basic and the optional is Adachi et al. (2011) [21]. The bundling literatures assume that the reservation utility for each good is different from users so that the type space of the users is multi-dimensions. Our model assumes that type space of users is one-dimension. In that sense, patent pool pricing in our model is closely related with Spence (1976) [22] and Maskin and Riley (1984) [23] which analyze non-linear pricing of monopoly; especially quantity discounts.

¹⁵Our paper assumes that the technological relationship of patents (the second difference in the gross surplus) is the same among users. Actually, the technological relationship of patents may be different among users. Considering the general functional form, 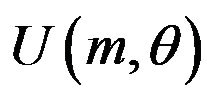, the sufficient conditions which a patent pool offers multiple package licenses are that one of these two 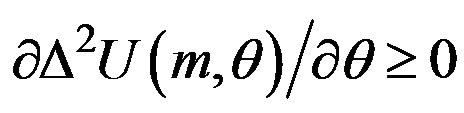and 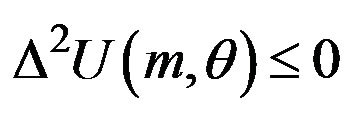is inequality at least. Under the setting of our paper, , 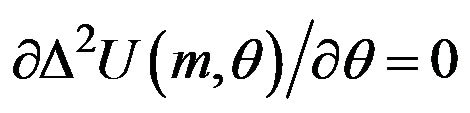is satisfied. Then the sufficient condition is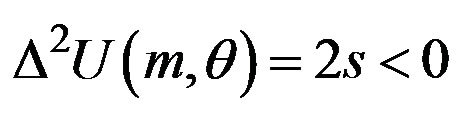. Therefore, our analysis in the paper is applicable to only the case where the technological relationship of patents is not so different among users.

¹⁶Lerner and Tirole (2004) [4] and Azetsu and Yamada (2011) [5] assume that the patents are symmetry. Under this setting, the technological relationship is substitute when complementarity is weak (s is negative). Then the price competition among the patent holders is occurred in the individual case. As the results, a patent pool increases the licensing fees since the patent pool avoid the price competition. In this paper, complementarity is weak implies that the patents are technical independent of each other but not substitute. The patent cannot be replaced by the other patent. Then price competition as Lerner and Tirole (2004) [4] and Azetsu and Yamada (2011) [5] is not occurred in our model.

¹⁷Our model does not define R & D cost of patent holders. As the result, the social welfare is same as the sum of all users’ gross surplus, and the social welfare does not include the social cost for R & D. Once information goods such as technical information are developed, the additional cost for licensing information goods is zero (R & D cost is lump cost). The social welfare is all users’ gross surplus minus R & D lump cost. But this does not influence our results.

¹⁸We do not focus on the process of patent pool formation and the stability of pools, as Brenner (2009) [8] and some other studies have undertaken. In our paper, the patent holders have the incentive to form a patent pool if the profit of the pool is larger than the sum of the patent holders’ profits, since the equilibrium in the pool case is equal to the corporative solution of the patent holders (the pool maximizes their joined profits).