World Journal of Mechanics
Vol. 1 No. 4 (2011) , Article ID: 7126 , 9 pages DOI:10.4236/wjm.2011.14023
Mathematical Modelling of Mass Transfer and Free Convection Current Effects on Unsteady Viscous Flow with Ramped Wall Temperature
1Fundamental and Applied Sciences Department, Universiti Teknologi PETRONAS, Perak Darul Ridzuan, Malaysia
2Department of Engineering and Mathematics, Sheaf Building, Sheffield Hallam University, Sheffield, UK
3Department of Mathematics, Narajole Raj College, West Bengal, India
E-mail: marneni@petronas.com.my, O.Beg@shu.ac.uk, g_swapan2002@yahoo.com
Received May 10, 2011; revised June 11, 2011; accepted July 2, 2011
Keywords: Natural convection, Vertical plate, Ramped wall temperature, Heat and Mass transfer
ABSTRACT
An exact analysis of the flow of an incompressible viscous fluid past an infinite vertical plate is conducted taking into account the presence of foreign mass or constant mass flux and ramped wall temperature. The dimensionless governing coupled linear partial differential equations are solved using the Laplace transform technique. Two different solutions for the fluid velocity are obtained–one valid for the fluids of Schmidt numbers different from unity, and the other for which the Schmidt number is unity. The effects of Prandtl number (Pr), Schmidt number (Sc), time (t) and mass to thermal buoyancy ratio parameter (N) for both aiding and opposing buoyancy effects on the velocity and skin-friction are studied. Also, the heat and mass transfer effects on the flow near a ramped temperature plate have been compared with the flow near a plate with constant temperature.
1. Introduction
Free convection flows past a vertical surface or plate have been studied extensively in the literature due to applications in engineering and environmental processes. Several investigations were performed using both analytical and numerical methods under different thermal conditions which are continuous and well-defined at the wall. Practical problems often involve wall conditions that are non-uniform or arbitrary. To understand such problems, it is useful to investigate problems subject to step change in wall temperature. For example in the fabrication of thin-film photovoltaic devices ramped wall temperatures may be employed to achieve a specific finish of the system [1]. Periodic temperature step changes are also important in building heat transfer applications, for example in air conditioning, where the conventional l assumption of periodic outdoor conditions may lead to considerable errors in the case of a significant temporary deviation of the temperature from periodicity, as elaborated by Antonopoulos and Democritou [2]. Other examples include nuclear heat transfer control, materials processing, turbine blade heat transfer, electronic circuits and sealed gas-filled enclosure heat transfer operations [3]. Schetz [4] presented one of the earliest analytical studies for free convection flow from a vertical plate with discontinuous wall temperature conditions. Several investigations were continued on this problem using an experimental technique [5], numerical methods [6], and by using series expansions [7,8]. Lee and Yovanovich [9] presented a new analytical model for the laminar natural convection from a vertical plate with step change in wall temperature. The validity and accuracy of the model is demonstrated by comparing with the existing results. Chandran et al. [10] have presented an analytical solution to the unsteady natural convection flow of an incompressible viscous fluid near a vertical plate with ramped wall temperature and they have compared the results with constant temperature. Recently, Saha et al. [11] investigated the natural convection boundary layer adjacent to an inclined semi-infinite flat plate subjected to ramp heating. The flow development from the start-up to an eventual steady state has been described based on scaling analysis and verified by numerical simulations. Chaudhary and Jain [12] developed closed-form solutions to the unsteady free convection flow past an infinite vertical oscillating plate for the scenario where the bounding plate has a ramped temperature profile using the Laplacetransform technique.
Free convection flows occur not only due temperature difference, but also due to concentration difference or the combination of these two. The study of combined heat and mass transfer play an important role in the design of chemical processing equipment, nuclear reactors, formation and dispersion of fog etc. Both steady-state and transient double-diffusive convection flows are of importance. The effect of presence of foreign mass on the free convection flow past a semi-infinite vertical plate was first studied by Gebhart and Pera [13]. Chen et al. [14] studied the combined double-diffusive mixed convective boundary layer flow from vertical and inclined surfaces. Bég et al. [15] extended the study in [14] to consider the supplementary effects of chemical reaction and cross-diffusion (Soret and Dufour effects) on mixed convection heat and mass transfer flows from inclined plates, using a numerical method. Soundalgekar [16] has studied mass transfer effects on thermal convection flow past an impulsively started infinite isothermal vertical plate. Dass et al. [17] considered the mass transfer effects on flow past an impulsively started infinite isothermal vertical plate with constant mass flux. Muthucumaraswamy et al. [18] presented an exact solution to the problem of flow past an impulsively started infinite vertical plate in the presence of uniform heat and mass flux at the plate using Laplace transforms.
However, mass transfer effects on free convection flow past an infinite vertical plate subject to discontinuous or non-uniform wall temperature conditions have not been studied in the literature. Hence it is now proposed to study the effects of mass transfer on the free convection flow of an incompressible viscous fluid past an infinite vertical plate subject to ramped wall temperature for the cases of 1) foreign mass and 2) constant mass flux at the plate. In section 2 the mathematical analysis is presented. In section 3 exact solutions to the non-dimensional coupled linear partial differential equations are derived by the Laplace transform method.
2. Mathematical Model
Consider the flow of a viscous incompressible fluid past an infinite vertical plate. The  - axis is taken along the plate in the vertically upward direction, and the
- axis is taken along the plate in the vertically upward direction, and the 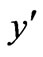 - axis is taken normal to the plate. Initially, for time
- axis is taken normal to the plate. Initially, for time , both the plate and the fluid are assumed to be at the same temperature
, both the plate and the fluid are assumed to be at the same temperature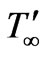 , concentration
, concentration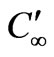 , and stationary. At time
, and stationary. At time , the temperature of the plate is raised or lowered to
, the temperature of the plate is raised or lowered to 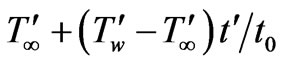 when
when , and thereafter, i.e. for
, and thereafter, i.e. for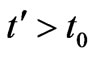 , is maintained at the constant temperature
, is maintained at the constant temperature 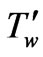 and the concentration level at the plate is raised to
and the concentration level at the plate is raised to  or concentration is supplied at a constant rate to the plate. Then under usual Boussinesq’s approximation, the unsteady flow past an infinite vertical plate is governed by the following equations [16-18]:
or concentration is supplied at a constant rate to the plate. Then under usual Boussinesq’s approximation, the unsteady flow past an infinite vertical plate is governed by the following equations [16-18]:
 (1)
(1)
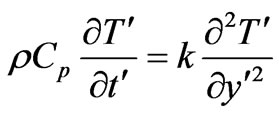 (2)
(2)
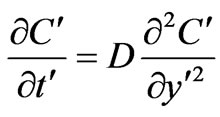 (3)
(3)
subject to the following initial and boundary conditions:
 (4)
(4)
As the plate is assumed to be infinite in length, the physical variables are functions of 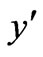 and
and 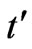 only. Here
only. Here 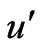 is the velocity in the
is the velocity in the 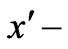 direction,
direction, 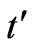 the time,
the time, 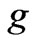 the acceleration due to gravity,
the acceleration due to gravity,  the volumetric coefficient of thermal expansion,
the volumetric coefficient of thermal expansion, 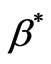 the volumetric coefficient of expansion for concentration,
the volumetric coefficient of expansion for concentration, 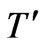 the temperature of the fluid near the plate,
the temperature of the fluid near the plate, 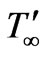 the temperature of the fluid far away from the plate,
the temperature of the fluid far away from the plate,  the species concentration near the plate,
the species concentration near the plate, 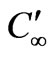 the species concentration in the fluid far away from the plate,
the species concentration in the fluid far away from the plate,  the plate temperature,
the plate temperature, 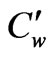 the species concentration at the plate,
the species concentration at the plate, 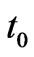 the characteristic time,
the characteristic time, 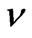 the kinematic viscosity,
the kinematic viscosity, 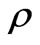 the density,
the density,  the specific heat at constant pressure,
the specific heat at constant pressure,  the thermal conductivity of the fluid,
the thermal conductivity of the fluid, 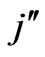 the mass flux per unit area at the plate and D is the mass diffusion coefficient. To facilitate analytical solutions we introduce the following non-dimensional quantities (see Equation (5)):
the mass flux per unit area at the plate and D is the mass diffusion coefficient. To facilitate analytical solutions we introduce the following non-dimensional quantities (see Equation (5)):
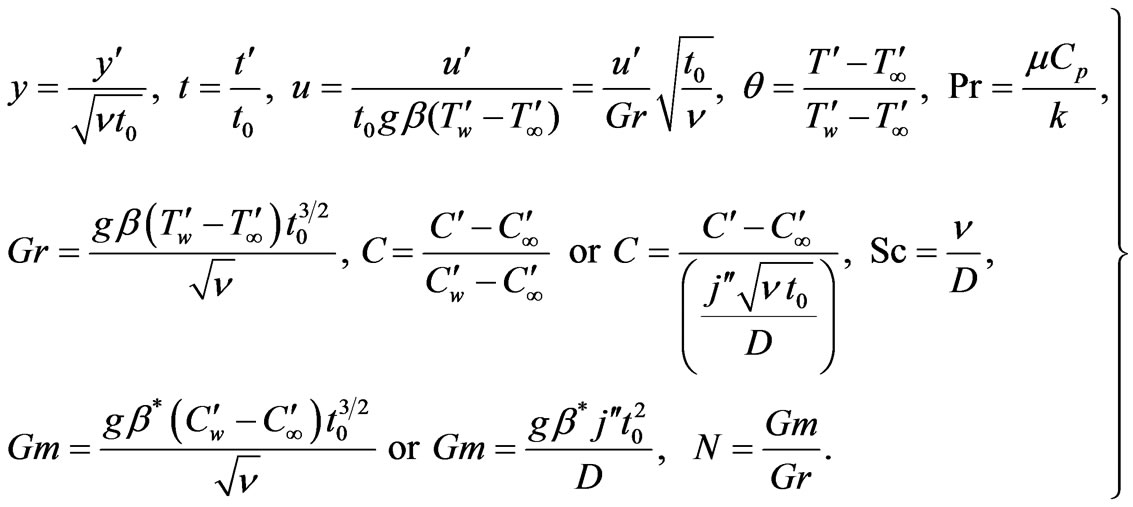 (5)
(5)
Implementation of the non-dimensional variables (5) in Equations (1) - (4), leads to the following group of linear, second order, first degree, coupled partial differential equations for momentum, heat and species diffusion conservation:
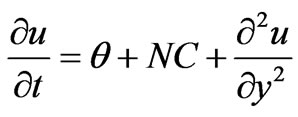 (6)
(6)
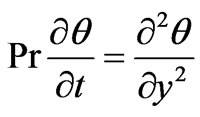 (7)
(7)
 (8)
(8)
where u the dimensionless velocity, y the dimensionless coordinate axis normal to the plate, t the dimensionless time, θ the dimensionless temperature, C the dimensionless concentration, Gr thermal Grashof number, Gm mass Grashof number, Pr the Prandtl number, μ the coefficient of viscosity, Sc the Schmidt number, and N is the buoyancy ratio parameter. According to the above nondimensionalisation process, the characteristic time 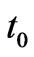 can be defined as:
can be defined as:
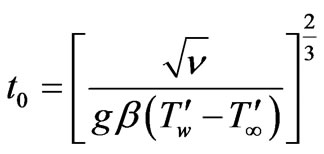 (9)
(9)
The corresponding initial and boundary conditions in dimensionless form are shown in Equation (10):
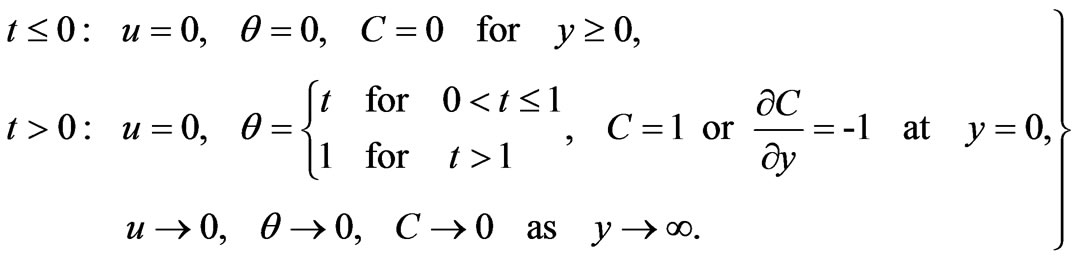 (10)
(10)
3. Analytical Laplace Transform Solutions
These equations (6) - (8) are a strongly coupled linear system of equations, which can be solved by the Laplace transform technique subject to the initial and boundary conditions (10). The solutions are readily yielded as:
Case I: 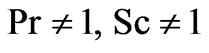
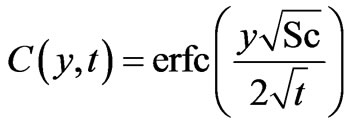 (Foreign mass)(11a)
(Foreign mass)(11a)
 (Constant mass flux) (11b)
(Constant mass flux) (11b)
 (12)
(12)
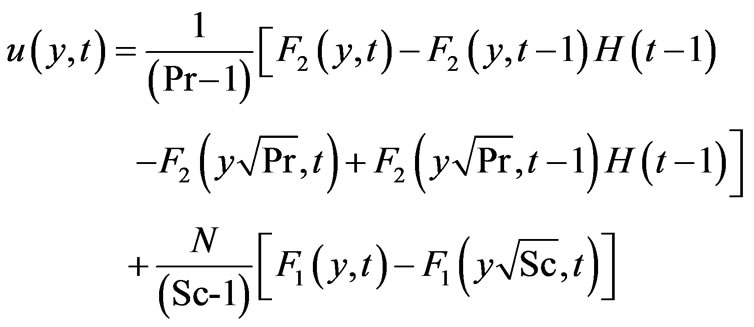
(Foreign mass)(13a)
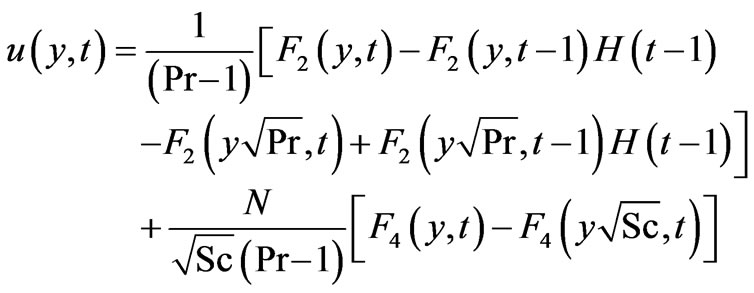
(Constant mass flux)(13b)
Case II: 
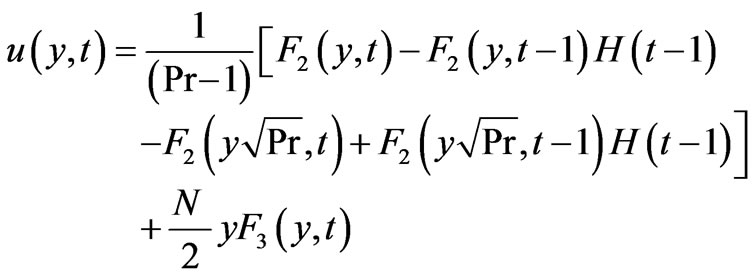
(Foreign mass) (14a)

(Constant mass flux)(14b)
where


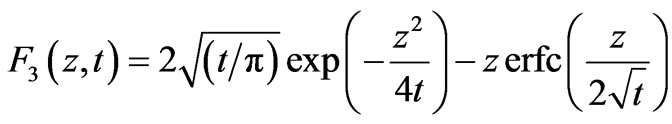
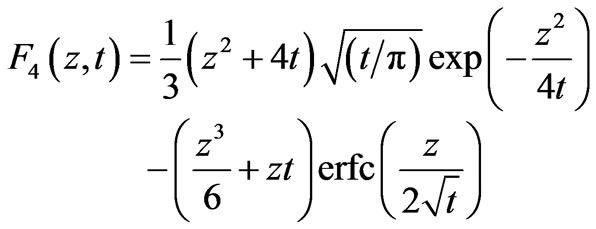 (14c)
(14c)
where 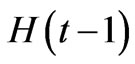 is the unit step function defined, in general, by:
is the unit step function defined, in general, by:
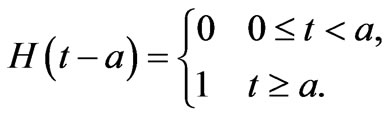 (15)
(15)
Here a is a constant, z is a dummy variable and 

 are functions of dummy variable. Moreover, concentration [10,12] and temperature [7] profiles given by Equations (11) and (12) respectively, are well known. Equations (11), (12) and (13) give analytical expressions for the concentration, temperature and velocity variables for flow near a vertical plate with ramped temperature. In order to highlight the effect of the ramped temperature distribution of the boundary on the flow, it may be worthwhile to compare such a flow with the one near a plate with constant temperature. Under the assumptions employed in this paper, it can be shown that the temperature and velocity variables for the flow near a plate with constant temperature can be expressed as
are functions of dummy variable. Moreover, concentration [10,12] and temperature [7] profiles given by Equations (11) and (12) respectively, are well known. Equations (11), (12) and (13) give analytical expressions for the concentration, temperature and velocity variables for flow near a vertical plate with ramped temperature. In order to highlight the effect of the ramped temperature distribution of the boundary on the flow, it may be worthwhile to compare such a flow with the one near a plate with constant temperature. Under the assumptions employed in this paper, it can be shown that the temperature and velocity variables for the flow near a plate with constant temperature can be expressed as
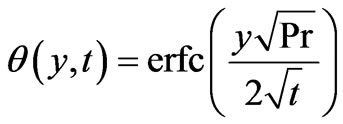 (16)
(16)
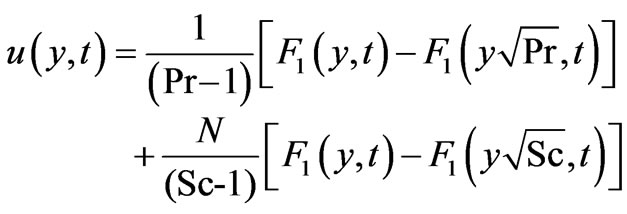
(Foreign mass)(17a)
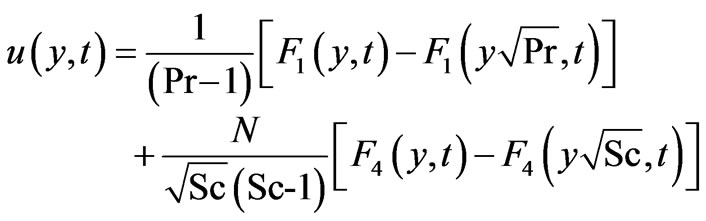
(Constant mass flux)(17b)
Equation (16) is valid only in the case of 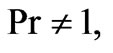
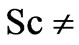 1; for the case
1; for the case 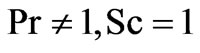 the velocity can be expressed as
the velocity can be expressed as

(Foreign mass)(18a)

(Constant mass flux)(18b)
and there is no change in the expression for concentration variable . From the velocity field, it is now proposed to study the effects of mass transfer on the skin-friction, the latter being defined in non-dimensional form as:
. From the velocity field, it is now proposed to study the effects of mass transfer on the skin-friction, the latter being defined in non-dimensional form as:
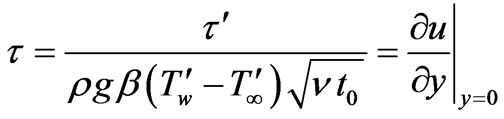 (19)
(19)
We obtain for the case of a ramped temperature plate:
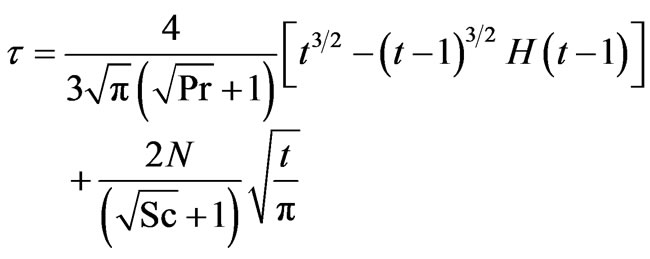
(Foreign mass) (20)
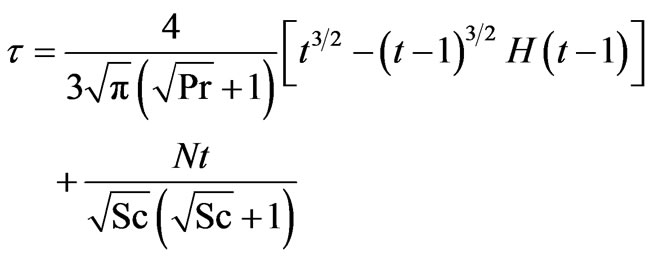
(Constant mass flux)(21)
and for the constant temperature (isothermal) plate,
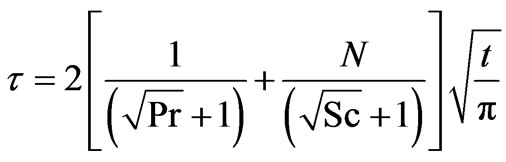 (Foreign mass)(22)
(Foreign mass)(22)
 (Foreign mass)(23)
(Foreign mass)(23)
It is seen that the expressions for 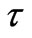 is valid for all values of Pr and Sc in both the cases. Also, we can see that
is valid for all values of Pr and Sc in both the cases. Also, we can see that 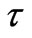 varies inversely with
varies inversely with  and
and  in both cases.
in both cases.
4. Results and Discussion
In order to get physical insight into the problem, the numerical values of the velocity and skin-friction are computed as functions of time for different values of the system parameters such as Pr, Sc and N. In the present analytical solutions, we have only considered 2 values of Pr i.e. 0.71 and 7.0. The two most frequently encountered fluids in engineering are air and water and these values of Pr correspond to these two cases, respectively. This approach was established by Ostrach at NASA [19] in the early 1950s. It has subsequently been implemented by many leading researchers working in analytical thermosciences. Other examples of this approach, which have subsequently been used for numerical benchmarking, are the works of Takhar and Perdikis [20], Takhar and Ram [21]. Furthermore, even in some very recent numerical (and experimental) studies, Pr has been fixed, since when many parameters are involved e.g. Grashof number, Schmidt number etc, it is more worthwhile to fix the only parameter which is a “physical property” of a fluid i.e. Pr and to parametrically study other parameters. Vallis [22], one of the leading atmospheric fluid dynamicists in the world, of Princeton University’s Geophysical Fluid Dynamics Laboratory (GFDL) has as very recently expounded the benefit of studying single Prandtl number thermal convection flows. In [22] it is stated: “In most of our experiments we change the Rayleigh number by changing the diffusivity and viscosity, keeping the Prandtl number fixed.” Reference [22] used a single Pr = 10. Similarly other leading mathematicians working in analytical thermal convection have used a single Prandtl number. An example is the work of Siggers et al. [23].
The buoyancy ratio parameter, N, represents the ratio between mass and thermal buoyancy forces. When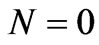 , there is no mass transfer and the buoyancy force is due to the thermal diffusion only.
, there is no mass transfer and the buoyancy force is due to the thermal diffusion only.  implies that mass buoyancy force acts in the same direction of thermal buoyancy force i.e. the buoyancy-assisted case, while
implies that mass buoyancy force acts in the same direction of thermal buoyancy force i.e. the buoyancy-assisted case, while 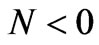 means that mass buoyancy force acts in the opposite direction i.e. the buoyancy-opposed. The present results for the case of the ramp heating of the plate include the results of Chandran et al. [10] in the case of the absence of the buoyancy ratio parameter N.
means that mass buoyancy force acts in the opposite direction i.e. the buoyancy-opposed. The present results for the case of the ramp heating of the plate include the results of Chandran et al. [10] in the case of the absence of the buoyancy ratio parameter N.
The velocity profiles for different values of buoyancy ratio parameter (N) for both aiding and opposing effects of mass transfer are shown in figures 1 and 3 for both ramped and isothermal plate temperature boundary conditions in the presence of foreign mass and constant mass flux respectively. It is observed that the velocity increases in the presence of aiding flows 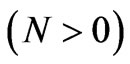 whereas it decreases in the presence of opposing flows
whereas it decreases in the presence of opposing flows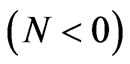 . Reverse flow is observed near the plate as the opposing buoyancy forces become dominant. It is also clear that the velocity near the plate is augmented with increasing time. Close observation of the curves for aiding flows from both figures reveals that the velocity is greater in the presence of foreign mass than that in the presence of constant mass flux. Foreign mass injection therefore accelerates the flow.
. Reverse flow is observed near the plate as the opposing buoyancy forces become dominant. It is also clear that the velocity near the plate is augmented with increasing time. Close observation of the curves for aiding flows from both figures reveals that the velocity is greater in the presence of foreign mass than that in the presence of constant mass flux. Foreign mass injection therefore accelerates the flow.
In figures 2 and 4 the velocity profiles are shown for different values of the Schmidt number (Sc) for aiding flows in the presence of foreign mass and constant mass flux respectively. It is observed that the velocity decreases with increasing Schmidt number. An increasing Schmidt number implies that viscous forces dominate over the diffusional effects. Schmidt number in free convection flow regimes, in fact represents the relative effectiveness of momentum and mass transport by diffusion in the velocity (momentum) and concentration (species) boundary layers. Smaller Sc values correspond to
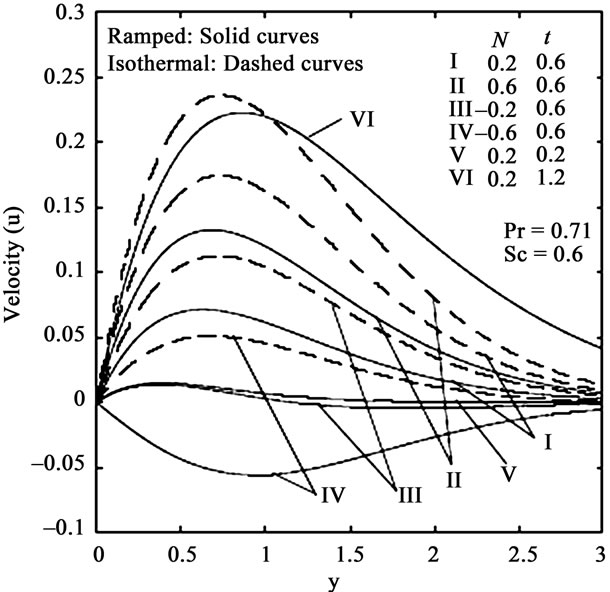
Figure 1. Velocity profiles for different N and t (Foreign mass).
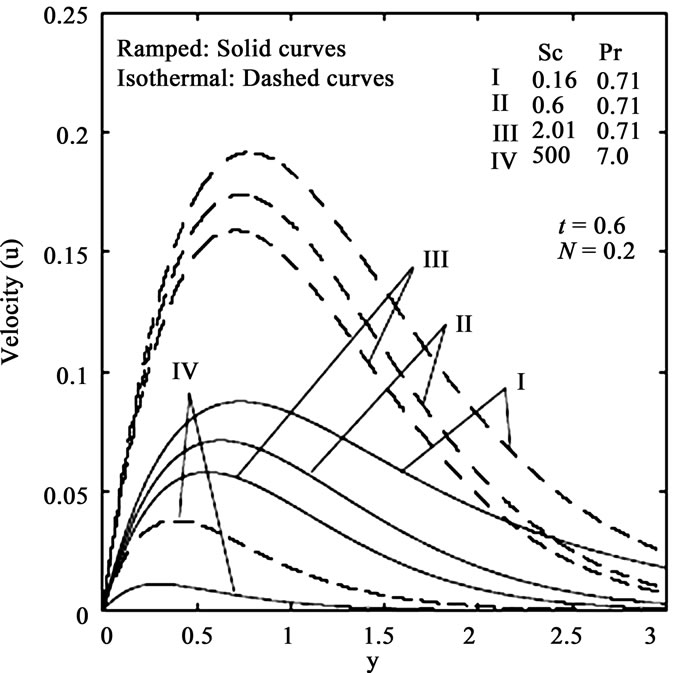
Figure 2. Velocity profiles for different Sc (Foreign mass).
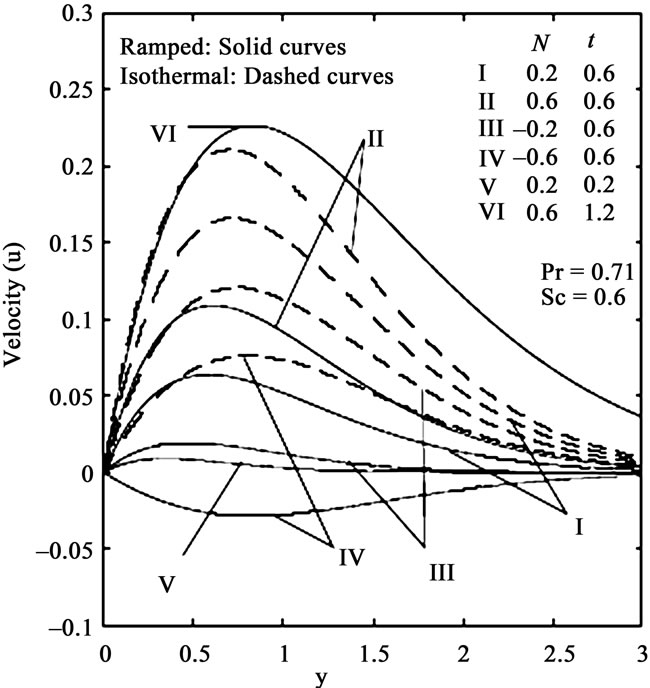
Figure 3. Velocity profiles for different N and t (Constant mass flux).
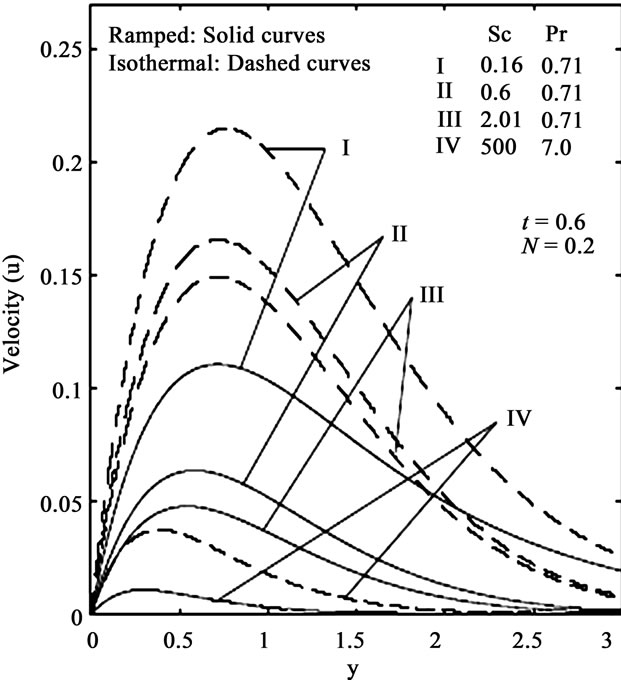
Figure 4. Velocity profiles for different Sc (Constant mass flux).
lower molecular weight species’ diffusing e.g. Hydrogen in air (Sc ~ 0.16) and higher values to denser hydrocarbons diffusing in air e.g. Ethyl benzene in air (Sc ~ 2.0). Effectively therefore an increase in Sc will counteract momentum diffusion since viscosity effects will increase and molecular diffusivity will be reduced. The flow will therefore be decelerated with a rise in Sc as testified to by figures 2 and 4. It is also important to note that for Sc ~ 1, the velocity and concentration boundary layers will have the same thickness. For Sc < 1 species diffusion rate greatly exceeds the momentum diffusion rate and vice versa for Sc > 1. Inspection of figures 1 to 4 also indicates that the fluid velocity is greater in the case of an isothermal plate than for the case of ramped temperature at the plate. This is expected since in the case of ramped wall temperature the heating of the fluid takes place more gradually than in the isothermal plate case. This feature is important in for example achieving better flow control in nuclear engineering applications, since ramping of the enclosing channel walls can help to decrease velocities. The distribution of dimensionless surface shear stress i.e. skin-friction with time is depicted in figures 5 and 6 for different values of buoyancy ratio parameter (N) and Schmidt number (Sc) in the presence of foreign mass and constant mass flux respectively. It is observed that the skin friction is enhanced for the case of aiding flows  but is reduced in the case of opposing flows
but is reduced in the case of opposing flows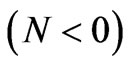 . Our results also indicate that skin friction is suppressed with increasing species concentration for the case of aiding flows. From figures 5 and 6 we also infer that the skin friction is greater in the case of an isothermal plate than in the case of ramped temperature of the plate, in consistency with the discussion earlier for figures 1 to 4, since ramping decelerates the flow and lowers skin friction. It is also noted that for small values of t (i.e, t < 1), there is a sharp ascent in the skin friction in the case of an isothermal plate whereas the friction increases more gradually with increasing time for the case of ramped temperature at the plate. That is, the friction curves assume parabolic shapes for the time
. Our results also indicate that skin friction is suppressed with increasing species concentration for the case of aiding flows. From figures 5 and 6 we also infer that the skin friction is greater in the case of an isothermal plate than in the case of ramped temperature of the plate, in consistency with the discussion earlier for figures 1 to 4, since ramping decelerates the flow and lowers skin friction. It is also noted that for small values of t (i.e, t < 1), there is a sharp ascent in the skin friction in the case of an isothermal plate whereas the friction increases more gradually with increasing time for the case of ramped temperature at the plate. That is, the friction curves assume parabolic shapes for the time . Ramping therefore acts to stabilize the skin friction response and again this characteristic is important in industrial transient heat transfer control systems.
. Ramping therefore acts to stabilize the skin friction response and again this characteristic is important in industrial transient heat transfer control systems.
Figures 2, 4 and 5, 6 also include various computations for different Prandtl numbers, namely Pr = 0.71 and Pr = 7; the former corresponds to air, the latter to water. In all cases a noticeable reduction in skin friction is identified with an increase in Pr. Prandtl number quantifies the relative effectiveness of momentum and energy transport by diffusion in the velocity and thermal boundary layers. For Pr < 1, energy i.e. heat diffuses faster than momentum. For Pr > 1, momentum diffuses faster than heat. For the special case of Pr = 1, the momentum and thermal boundary layers will have the same thickness. In consistency with this we observe that in figures 2 and 4 velocity is decreased (profiles I and IV) and in figures 5 and 6 skin friction is reduced with an increase in Pr from 0.71 to 7 (profiles I and VI i.e. weakly buoyancy-aided flows with N = 0.2) since higher Pr fluids will possess greater viscosities and this will serve to reduce velocities, thereby lowering the skin friction.
The present analytical (Laplace transform) solutions provide other researchers with solid benchmarks for numerical comparisons. The authors have used this method in other articles where they have benchmarked numerical methods against analytical (Laplace transform) solutions
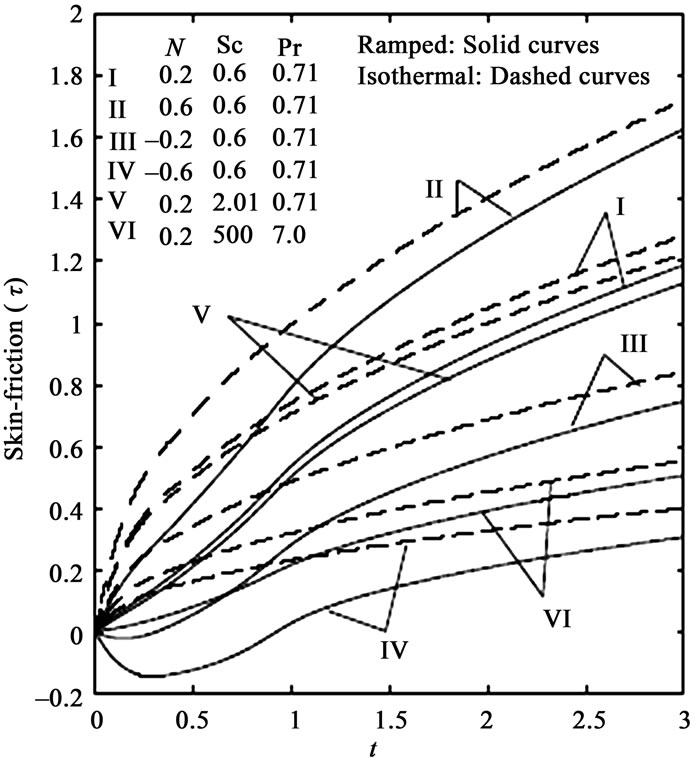
Figure 5. Skin-friction for different N and Sc (Foreign mass).
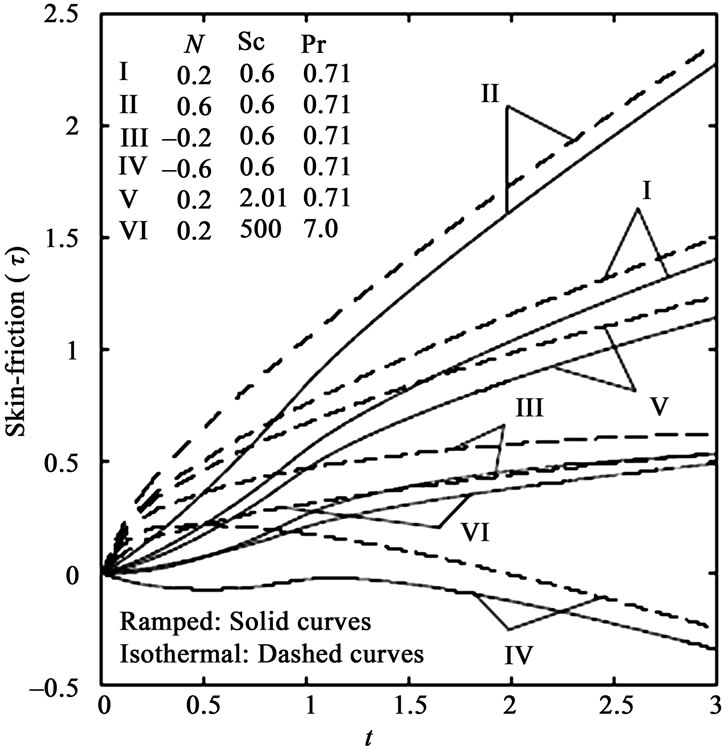
Figure 6. Skin-friction for different N and Sc (Constant mass flux).
in the same article [24-28]. Various techniques have been used to confirm the accuracy of Laplace transform solutions in these complex multi-physical and geophysical fluid dynamics problems by the authors, including asymptotic analysis [24], complex variables [25,26] and electrical network simulation computational techniques based on the PSPICE software [27,28]. There is therefore great confidence in our solutions presented, based on Laplace transforms.
5. Conclusions
A general analytical solution for the problem of the unsteady free convection flow past an infinite vertical plate subjected to a ramped wall temperature in the presence of i) foreign mass and ii) constant mass flux at the plate has been determined without any restrictions. The dimensionless governing equations are solved by the Laplace transform technique. The effects of the governing thermophysical parameters i.e. buoyancy ratio parameter (N), Schmidt number (Sc), Prandtl number (Pr) and time (t) on the velocity field and skin-friction has been discussed. Our computations have shown that:
I) velocity increases in the presence of aiding flows and it decreases with opposing flows.
II) velocity decreases with increasing values of the Schmidt number for aiding flows.
III) velocity increases with increasing time.
IV) velocity is greater in the presence of foreign mass than with constant mass flux.
V) skin-friction is increased for assisted flows and diminished for opposing flows.
VI) skin friction is reduced with increasing species concentration for aiding flows.
VII) skin friction is reduced with an increase in Prandtl number for aiding flows.
The fluid velocity and skin-friction in the present case has also been compared with that for the case of an isothermal plate. For this scenario our solutions indicate that velocity and skin-friction are greater in the case of isothermal plate than in the case of ramped temperature at the plate. The present results are useful in further elucidating the important class of flows in which the driving force is induced by a combination of the thermal and chemical diffusion effects. Such results have immediate relevance in industrial thermofluid dynamics, transient energy systems and also buoyancy-driven geophysical and atmospheric vertical flows.
6. Acknowledgements
The authors wish to express their gratitude to the reviewer for his useful comments which have helped to improve the present article.
REFERENCES
- C. P. Malhotra, R. L. Mahajan, W. S. Sampath, K. L. Barth and R. A. Enzenroth, “Control of Temperature Uniformity during the Manufacture of Stable Thin-Film PhoTovoltaic Devices,” International Journal of Heat and Mass Transfer, Vol. 49, No. 17-18, 2006, pp. 2840- 2850. doi:10.1016/j.ijheatmasstransfer.2006.02
- K. A. Antonopoulos and F. Democritou, “Experimental and Numerical Study of Unsteady Non-periodic Wall Heat Transfer under Step, Ramp and Cosine Temperature Perturbations,” International Journal of Energy Research, Vol. 18, No. 6, 1994, pp. 563-579. doi:10.1002/er.4440180602
- M. A. Kuczmarski and S. A. Gokoglu, “Buoyancy Suppression in Gases at High Temperatures,” International Journal of Heat Fluid Flow, Vol. 28, No. 3, 2007, pp. 496-511.doi:10.1016/j.ijheatfluidflow.2006.07.006
- J. A. Schetz, “On the Approximate Solution of Viscous-Flow Problems,” ASME Journal of Applied Mechanics, Vol. 30, 1963, pp. 263-268.
- J. A. Schetz and R. Eichhorn, “Unsteady Natural Convection in the Vicinity of a Doubly Infinite Vertical Plate,” Journal of Heat Transfer, Vol. 84, 1962, pp. 334-338.
- A. A. Hayday, D. A. Bowlus and R. A. McGraw, “Free Convection from a Vertical Flat Plate with Step Discontinuities in Surface Temperature,” ASME Journal of Heat Transfer, Vol. 89, 1967, pp. 244-250.
- M. Kelleher, “Free Convection from a Vertical Plate with Discontinuous Wall Temperature,” ASME Journal of Heat Transfer, Vol. 93, 1971, pp. 349-356. doi:org/10.1115/1.3449830
- T. T. Kao, “Laminar Free Convective Heat Transfer Response along a Vertical Flat Plate with Step Jump in Surface Temperature,” Letters of Heat Mass Transfer, Vol. 2, No. 5, 1975, pp. 419-428. doi:org/10.1016/0094-4548(75)90008-9
- S. Lee and M. M. Yovanovich, “Laminar Natural Convection from a Vertical Plate with a Step Change in Wall Temperature,” ASME Journal of Heat Transfer, Vol. 113, 1991, pp. 501-504. doi:org/10.1115/1.2910591
- P. Chandran, N. C. Sacheti and A. K. Singh, “Natural con-Vection near a Vertical Plate with Ramped Wall Temperature,” Heat Mass Transfer, Vol. 41, No. 5, 2005, pp. 459-464. doi:org/10.1007/s00231-004-0568-7
- S. C. Saha, C. Lei and J. C. Patterson, “On the Natural Convection Boundary Layer Adjacent to an Inclined Flat Plate Subject to Ramp Heating,” 16th Australian Fluid Mechanics Conference, Crown Plaza, Gold Coast, Australia, 2007, pp. 121-124.
- R. C. Chaudhary and P. Jain, “Transient Free Convection Flow along an Infinite Vertical Oscillating Plate with a Step Change in Wall Temperature,” Acta Technica ČSAV, Vol. 52, 2007, pp. 187-204.
- B. Gebhart and L. Pera, “The Nature of Vertical Natural Convection Flows Resulting from the Combined Buoyancy Effects of Thermal and Mass Diffusion,” International Journal of Heat and Mass Transfer, Vol. 14, No. 12, 1971, pp. 2025-2050. doi:org/10.1016/0017-9310(71)90026-3
- T. S. Chen, C. F. Yuh and A. Moustsoglou, “Combined Heat and Mass Transfer in Mixed Convection along Vertical and Inclined Plates,” International Journal of Heat and Mass Transfer, Vol. 23, No. 4, 1980, pp. 527-537. doi:org/10.1016/0017-9310(80)90094-0
- O. Anwar Bég, Tasveer A. Bég, A. Y. Bakier and V. R. Prasad, “Chemically-Reacting Mixed Convective Heat and Mass Transfer along Inclined and Vertical Plates with Soret and Dufour Effects: Numerical Solutions,” International Journal of Applied Mathematics Mechanics, Vol. 5, No. 2, 2009, pp. 39-57.
- V. M. Soundalgekar, “Effects of Mass Transfer and Free Convection on the Flow Past an Impulsively Started Vertical Plate,” ASME Journal of Applied Mechanics, Vol. 46, No. 4, 1979, pp. 757-760. doi:org/10.1115/1.3424649
- U. N. Dass, S. N. Ray and V. M. Soundalgekar, “Mass Transfer Effects on Flow Past an Impulsively Started Infinite Vertical Plate with Constant Mass Flux–an Exact Solution,” Heat and Mass transfer, Vol. 31, No. 3, 1996, pp. 163-167. doi:10.1007/bf02333314
- R. Muthucumaraswamy, P. Ganesan and V. M. Soundalgekar, “Heat and Mass Transfer Effects on Flow Past an Impulsively Started Vertical Plate,” Acta Mechanica, Vol. 146, No. 1-2, 2001, pp. 1-8. doi:org/10.1007/BF01178790
- S. Ostrach, “An Analysis of Laminar Free Convection Flow and Heat and Mass Transfer about a Flat Plate Parallel to the Direction of the Generating Body Force,” NACA 1111, Technical Report, 1952.
- H. S. Takhar and C. P. Perdikis, “Forced and Free Convective Flow of Water at 4˚C through a Porous Medium,” International Communications in Heat and Mass Transfer, Vol. 21, 1986, pp. 605-609. doi:org/10.1016/0735-1933(94)90005-1
- S. Takhar and P. C. Ram, “Magnetohydrodynamic Free Convection Flow of Water at 4˚C through a Porous Medium,” International Communications in Heat and Mass Transfer, Vol. 21, No. 3, 1994, pp. 371-376.
- M. Ilicak and G. K. Vallis, “Simulations and Scaling of Horizontal Convection,” Tellus, under review, May 25th 2011.
- J. H. Siggers, R. R. Kerswell and N. J. Balmforth, “Bounds on Horizontal Convection,” Journal of Fluid Mechanics, Vol. 517, 2004, pp. 55-70. doi:org/10.1017/S0022112004000497
- S. K. Ghosh, O. Anwar Bég and M. Narahari, “Hall Effects on MHD Flow in a Rotating System with Heat Transfer Characteristics,” Meccanica Journal, Vol. 44, No. 6, 2009, pp. 741-765. doi:org/10.1007/s11012-009-9210-6
- S. K. Ghosh, O. Anwar Bég and J. Zueco, “Hydromagnetic Free Convection Rayleigh Flow with Induced Magnetic Field Effects,” Meccanica, Vol. 45, No. 2, 2010, pp. 175-185. doi:org/10.1007/s11012-009-9235-x
- S. K. Ghosh, S. Rawat, O. Anwar Bég and Tasveer A. Bég, “Thermal Radiation Effects on Unsteady Hydromagnetic Gas Flow Along an Inclined Plane with Indirect Natural Convection,” International Journal of Applied Mathematics and Mechanics, Vol. 6, No. 13, 2010, pp. 41-57.
- S. K. Ghosh, O. Anwar Bég, J. Zueco and Prasad V. R., “Transient Hydromagnetic Flow in a Rotating Channel Permeated by an Inclined Magnetic Field with Magnetic Induction and Maxwell Displacement Current Effects,” ZAMP: Journal of Applied Mathematics and Physics, Vol. 61, No. 1, 2010, pp. 147-169. doi:org/10.1007/s00033-009-0006-2
- O. Anwar Bég, J. Zueco, S. K. Ghosh and A. Heidari, “Unsteady Magnetohydrodynamic Heat Transfer in A Semi-Infinite Porous Medium with Thermal Radiation Flux: Analytical and Numerical Study,” Advances in Numerical Analysis, Vol. 2011, 2011, pp. 1-17.

