ABSTRACT

The nineteenth century’s quest for the missing matter (Vulcan) ended with the publication of Einstein’s General Theory of Relativity. We contend that the current quest for the missing matter is parallel in its perseverance and in its ultimate futility. After setting the search for dark matter in its historic perspective, we critique extant dark matter models and offer alternative explanations—derived from a Lorentz-invariant Lagrangian—that will, at the very least, sow seeds of doubt about the existence of dark matter.

Keywords:Gravitons, Dark Matter, Dark Energy

1. Two Centuries of Searching for Dark Matter

1.1. The Nineteenth Century

The most puzzling and, perhaps, the most important problem of contemporary physics is finding a persuasive explanation of the supposed astronomical evidence for dark matter—invisible matter that is only “observed” through its gravitational effects on visible matter. This enigma is only the latest chapter of a story of perceived conflict between gravitational theory and astronomic observations. The first chapter started soon after the publication of Isaac Newton’s Principia in 1686. Astronomers had long known of various inequalities (departures from an undisturbed elliptical orbit) in the Moon’s motion. Hipparchus, for example, had discovered the evection about 1800 years before the Principia. Newton’s deceptively simple gravitational theory did not at first seem potent enough to explain the complex orbit of the Moon. Actually, it was the mathematics of lunar theory that was complex, and when worked out in detail in the eighteenth century, the validity of Newtonian theory was established. Further tests in planetary theory and in predicting the return of Halley’s comet in 1759 placed Newton’s theory on a pedestal of perfection; it was elegant and inviolable.

In the nineteenth century, minor inconsistencies between Newtonian based planetary theory and the orbit of Mercury became apparent. Mercury’s line of apsides was observed to advance by 565'' per century, but that was about seven percent larger than planetary theory predicted. Since Newtonian physics was inviolable, the search for Vulcan (or some other missing masses) began [1] . Led by Urbain J. J. Le Verrier starting around 1840, this futile search involved many observers through the rest of the century. Five years after Le Verrier’s inspired search for Vulcan began, longstanding inconsistencies in the orbit of Uranus were addressed with the search for Neptune. The planet was found relatively quickly, and this reinforced the belief that Newtonian theory was perfect. Discrepancies in Mercury’s orbit were assuredly due to Vulcan or to some other missing matters.

In 1873, Joseph L. F. Bertrand [2] proved that the only two central force laws that result in closed orbits are the linear and inverse square laws; otherwise, the line of apsides of a lone planet revolving about the Sun would precess. Applying Bertrand’s theory, Asaph Hall [3] in 1894 had the temerity to suggest that the exponent in Newtonian gravity was not −2 precisely, but −2.00000016. This would explain the anomalous secular motion of the perihelion of Mercury. It was not the correct solution, but it was, finally, a challenge to Newtonian theory. It was no longer just a question of missing masses; perhaps the theory was not quite perfect.

Indeed, Newtonian theory was not quite perfect, and Albert Einstein, as we all now know, finally resolved the dilemma in 1915 with GTR, his General Theory of Relativity [4] . GTR also predicted other subsequently verified effects such as the deflection of starlight passing close to the Sun and the gravitational red shift which is detectable in laboratories as the Mossbauer effect. Einstein’s theory replaced Newton’s on the pedestal of perfection; it was elegant and inviolable. There finally was no conflict between gravitational theory and astronomical observations, but this brief period of harmony lasted less than two decades.

1.2. The Twentieth Century

In the 1930’s, discrepancies between gravitational theory and astronomic observations began to resurface, this time for models of galactic scale where Newtonian gravity is in accord with GTR. In 1932 Jan H. Oort could not reconcile the density of Galactic disk matter in the vicinity of the Sun with the dynamics of tracer stars; in 1933 Fritz Zwicky applied the virial theorem to the observed radial velocities of Coma cluster galaxies and found that its mean mass density was many times larger than its luminous density would imply; and in 1939 Horace W. Babcock found that the high rotational velocities of the Andromeda Galaxy indicated a mass density appreciably higher than its luminous density would imply. For the appropriate references and authoritative discussions of these discoveries and some follow-on studies, please refer to [5] -[7] . Note that although the title of van den Bergh’s 1999 paper is The Early History of Dark Matter, the century long search for Vulcan is entirely overlooked. The most recent purported evidence for dark matter, starting in the last decade of the twentieth century and continuing vigorously today, comes from detailed surveys and analyses of Type Ia supernovae (SNe Ia) [8] - [13] and cosmic microwave background (CMB) anisotropies [7] .

Tens of thousands of research papers have been published in this second search for dark matter. For the most part they have consisted of speculations, and the true nature of dark matter—if indeed it exists at all—remains elusive. There is one exception: after numerous papers supporting and refuting Oort’s hypothesis, the current consensus is that there is no missing matter in the Galactic disk. Still, the stabilities of globular and galaxy clusters and the rotations of galaxies provide purportedly strong evidence for dark matter. Especially compelling evidence comes from the flat rotation curves of spiral galaxies. The orbital velocity of a planet in the Solar System falls off with its distance 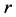from the Sun as, whereas the orbital velocity of a star revolving about the central bulge of a typical spiral galaxy is more or less independent of its distance from the center. If Newtonian gravity applies, then the explanation for this is that there must be a profusion of unseen galactic matter; moreover, the distribution of this invisible matter, supposedly in a spherical halo, is closely linked to the distribution of the visible matter in the disk. This linkage is a bothersome “conspiracy” that impairs the credibility of the hidden mass hypothesis (HMH). The SNe Ia observations have been interpreted as evidence for dark energy as well as dark matter because the expansion rate of the universe appears to be accelerating. The CMB evidence for dark matter is impressive on its own, but HMH is not a robust hypothesis; so if we cannot explain shortcomings on galactic scales we should be wary of accepting the CMB evidence for dark matter without considering one or more alternative hypotheses that might be robust at all scales.

An approach for resolving this enigma is to question the applicability of Newtonian gravity at galactic scales—and beyond—and, therefore, to question GTR itself. As firmly established as GTR is, not being allowed to challenge it makes the theory unfalsifiable, and GTR thereby loses its solid scientific foundation. Whether it is universally valid or not, GTR then becomes another theory that Karl Popper [14] would consider to be nonscientific, like astrology and the Marxist theory of history. Newton stands tall even after Einstein’s profound adjustments to his gravitational theory, and Einstein’s high repute would not suffer in the least if emendations to his theory resolved these discrepancies of galactic and cosmic scales. In 1983 Mordehai Milgrom wrote “the time is ripe for considering alternatives to the HMH” [15] and proposed an alternative, MOND, Modified Newtonian Dynamics. With a simple algorithm, MOND models the flat rotation curves of galaxies very well [16] , but its associated Lagrangian density is not Lorentz-invariant [17] , which is a serious defect. MOND is a clever mathematical artifice, but its physical foundation is unconvincing. It is analogous to Asaph Hall’s tinkering with the inverse square exponent 100 years earlier. Both approaches are simple. Both are phenomenologically successful, but neither has substantial physical underpinnings.

2. Extending Newtonian Gravity

A generalized Lorentz-invariant Lagrangian 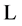for extending the potential of a centrally symmetric gravitational field beyond the Newtonian form is

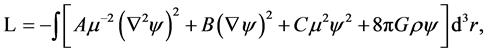(1)

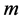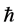where are dimensionless parameters; and, is the reduced Compton wavelength of the graviton which has the mass, is the speed of light, is the reduced Planck constant, 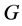is the Newtonian gravitational constant, and is the mass density. The solution to is

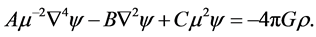(2)

For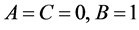, Equation (2) becomes Poisson’s equation,

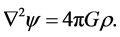(3)

For a point mass at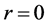, the solution is the Newtonian potential

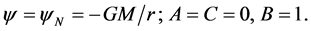(4)

For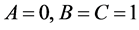, Equation (2) becomes

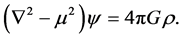(5)

For a point mass at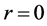, the solution is the Yukawa potential

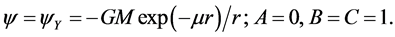(6)

For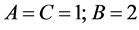, Equation (2) becomes

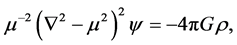(7)

For a point mass 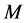at, the solution is the exponential potential

(8)

where 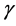is a dimensionless constant that is required when 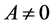so that 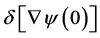(as well as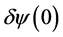) can be conceptually set to zero in solving by the calculus of variations.

For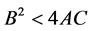, the Yukawa potential (Equation (6)) is modulated by the factor. This results in multiple concentric potential wells, but none at the origin—an interesting solution form for a physical problem that does not (yet?) exist.

3. The Expanding Universe

At scales larger than that of the solar system (say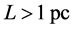), gravitational fields are weak, so GTR simplifies to Newtonian theory: gravitational attraction obeys the inverse-square law. Then, Newton’s shell theorem applies: a spherical shell attracts body outside of the shell as though all of the shell mass is at the center of the sphere, and there is no gravitational attraction by the shell on any body anywhere inside the shell. Smoothed over cosmological scales (say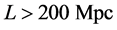), the mass density of the universe is approximately constant. Take any two points, and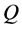, in such a uniform density universe, and set one of them at the center of a sphere and the other on its outer surface. The radius of this sphere is 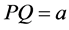and its mass is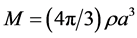. All matter outside of the sphere can be ignored, so the specific force between and 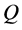is proportional to. They will accelerate toward each other at a rate (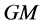remains constant as the sphere shrinks), so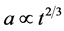; that is,. The entire universe will contract accordingly; this is the Einsteinde Sitter Universe. But our universe is expanding, not contracting. This suggests that the universe was given an initial impetus to expand, but that the expansion rate is decelerating and will eventually reverse itself and ultimately contract toward a “big crunch”. But this is incompatible with the SNe Ia analyses which conclude that the Einstein-de Sitter model must be supplemented by the addition of substantial braking cold dark matter (CDM) and opposing expansionary dark energy (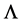, the cosmological constant) forces.

Two teams of scientists [8] -[13] found discrepancies between the distances to high redshift 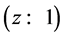type Ia supernovae (considered to be well understood “standard candles”) when the SNe Ia distances are determined by their apparent magnitudes versus when they are determined by their redshifts for a flat universe without a cosmological constant. The SNe Ia brightnesses appear to be about 25% weaker than expected, and so their distances are correspondingly greater than their redshifts would indicate. To phrase it another way, the SNe Ia redshifts are lower than their magnitudes would indicate, and so 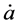in the past appears to be less than it is today; that is, 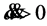and the expansion rate of the universe is accelerating. Actually, however, the acceleration satisfies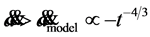, if the model is that of GTR for a flat universe with 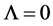and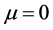. Although is not necessarily greater than zero at present, there still is an unmodeled effect, a repulsive force that has been ascribed to a mysterious ad hoc construct called “dark energy” that enters the GTR field equations as a cosmological constant,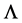. The only reason this term has recently been resurrected from the dustbin of rejected ideas has been to concoct a mathematical model that is consistent with astrophysical observations when they are interpreted by using what is, by choice, an immutable model: GTR with massless gravitons. Like a rabbit pulled out of a magician’s hat of tricks, this term’s reappearance is a matter of legerdemain, not science. Theoretical physicists consider a non-zero 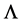to be exceedingly problematic and highly improbable (see, for example, [18] ). They countenance the concept of a non-zero cosmological constant only because they can conceive of no alternative, and more credible, explanation for an extant body of astrophysical observations, especially observations of type Ia supernovae. Although widely accepted, the LCDM model “staggers under the burden of its unnaturalness” [18] because of its dark energy component.

There is, however, a simple alternative explanation: for, the Newtonian potential is replaced by the Yukawa potential (see Equation (6)) and the Einstein-de Sitter Universe is replaced by the Milne Universe. And the Milne Universe is in total accord with SNe Ia observations without the need for dark matter or dark energy [19] . The Milne Universe is not especially sensitive to the value of 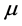chosen, just as long as it is greater than zero; but by choosing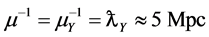 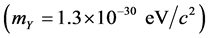, the Yukawa potential then also explains the separation scale of CMB peaks, the dimensions and stabilities of galaxy superclusters, and their spongiform groupings; the 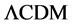model does not.

4. Spiral Galaxy Rotation Rates

The orbital velocity of a planet in the Solar System falls off with its distance from the Sun as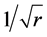, whereas the orbital velocity of a star revolving about the central bulge of a typical spiral galaxy is more or less independent of its distance from the center: the velocity profiles of disk stars in all spiral galaxies are “flat”. If Newtonian gravity applies, then the accepted explanation for the flat profiles is that the source of the gravitational field in the disk of a spiral galaxy is predominantly a spheroidal halo of dark matter. To support the observed flat velocity profiles, the mass of the halo must dwarf that of visible matter, and its density 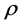must vary as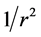, the same as a self-gravitating isothermal sphere [20] . Each concentric shell with the same thickness would have the same mass, so, without an outer boundary, the halo would necessarily have infinite mass. But there is no outer boundary, so such a halo would be unstable and rapidly dissipate. Alternative models of dark matter halos have been derived using gravitational N-body simulations which lead to ostensibly stable halos. However the densities of these halos do not vary as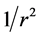, so they do not explain the flat velocity profiles. The simulation forces are all gravitational and there are no collisions (particles are allowed to pass through each other), so no matter how long the simulations last, isothermal halos will not materialize. Isothermal dark matter halo models that explain the flat velocity profiles are unstable, and N-body simulation models that are stable do not explain the velocity profiles. So, like Milgrom, we propose a modification of Newtonian theory, but one that is founded on the Lagrangian of Section 2.

The Yukawa potential 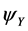(Equation (6)) with 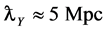is indistinguishable from the Newtonian potential 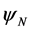(Equation (4)) at galactic scales. It cannot be ignored, so it is supplemented by another gravitational potential. Combining the exponential potential (Equation (8)) with the quasi-Newtonian 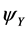results in uniformly excellent fits to the flat profiles of the rotational velocities of all twelve spiral galaxies that we have examined [21] , determining only two parameters, 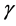and 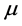that apply to all fits. The exponential potential 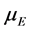is different from that of the Yukawa potential:.

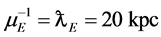5. Solar System and Geophysical Scales

For the weak gravitational fields of geophysics and most aspects of celestial mechanics (yes, the orbit of Mercury is an exception), the Yukawa potential is the only one to consider, and at those scales it is no different than the conventional Newtonian potential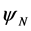. The exponential potential 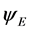at those scales dwindles to cause only an unobservable Rindler acceleration [22] .

6. Conclusion

Positing the existence of dark matter is the same as changing the facts. In the nineteenth century that approach failed to explain an irregularity in Mercury’s orbit; the theory had to be changed instead. Similarly, dynamic irregularities at cosmic scales are nowadays explained away—but not convincingly—by changing the facts. We maintain that the theory should be changed. We have presented alternate theoretical approaches of our own, which we advocate, but we are not averse to entertaining others. What we are averse to is changing the facts, because that leads to further discrepancies and a “preposterous universe” [18] .

References

NOTES

^*Corresponding author.