Advances in Linear Algebra & Matrix Theory
Vol.3 No.2(2013), Article ID:33062,6 pages DOI:10.4236/alamt.2013.32003
Jordan Semi-Triple Multiplicative Maps on the Symmetric Matrices*
Department of Mathematics, Taiyuan University of Technology, Staff Education and Training Center of Taiyuan Iron and Steel (Group) Co., Ltd., Taiyuan, China
Email: runlingan@yahoo.com.cn
Copyright © 2013 Xiaoning Hao et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 16, 2013; revised April 20, 2013; accepted April 28, 2013
Keywords: Symmetric matrices; Orthogonal matrix; Jordan homomorphism
ABSTRACT
In this paper, we show that if an injective map  on symmetric matrices
on symmetric matrices 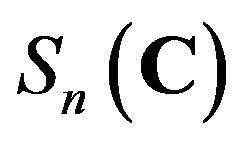 satisfies
satisfies 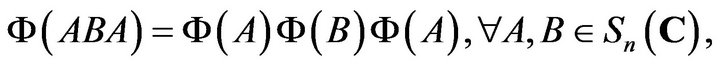 then
then 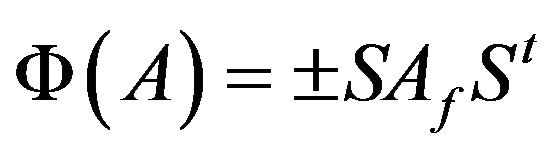 for all
for all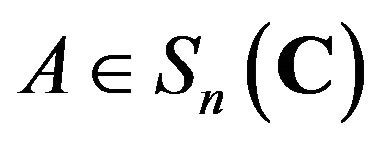 , where
, where 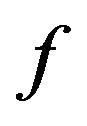 is an injective homomorphism on
is an injective homomorphism on ,
, 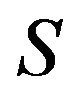 is a complex orthogonal matrix and
is a complex orthogonal matrix and 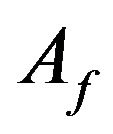 is the image of
is the image of  under
under 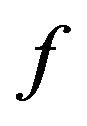 applied entrywise.
applied entrywise.
1. Introduction
It is an interesting problem to study the interrelation between the multiplicative and the additive structure of a ring or an algebra. Matindale in [1] proved that every multiplicative bijective map from a prime ring containing a nontrivial idempotent onto an arbitrary ring is additive. Thus, the multiplicative structure determines the ring structure for some rings. This result was utilized by P. Šemrl in [2] to describe the form of the semigroup isomorphisms of standard operator algebras on Banach spaces. Some other results on the additivity of multiplicative maps between operator algebras can be found in [3,4]. Besides ring homomorphisms between rings, sometimes one has to consider Jordan ring homomorphisms. Note that, Jordan operator algebras have important applications in the mathematical foundations of quantum mechanics. So, it is also interesting to ask when the Jordan multiplicative structure determines the Jordan ring structure of Jordan rings or algebras.
Let 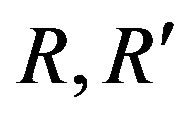 be two rings and let
be two rings and let  be a map. Recall that
be a map. Recall that  is called a Jordan homomorphism if
is called a Jordan homomorphism if
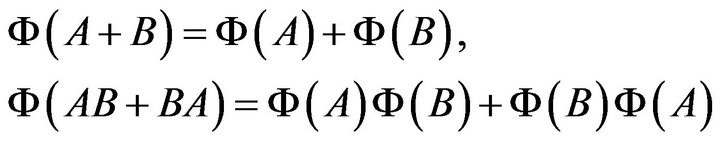
for all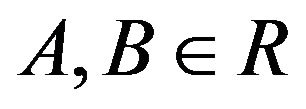 . There are two basic forms of Jordan multiplicative maps, namely1)
. There are two basic forms of Jordan multiplicative maps, namely1)  (Jordan semi-triple multiplicative map) for all
(Jordan semi-triple multiplicative map) for all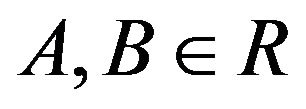 2)
2) 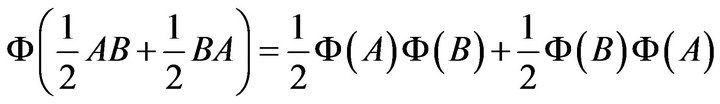
(Jordan multiplicative map) for all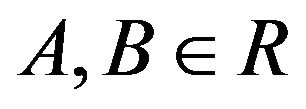 . It is clear that, if
. It is clear that, if  is unital and additive, then these two forms of Jordan multiplicative maps are equivalent. But in general, for a unital map, we do not know whether they are still equivalent without the additivity assumption.
is unital and additive, then these two forms of Jordan multiplicative maps are equivalent. But in general, for a unital map, we do not know whether they are still equivalent without the additivity assumption.
The question of when a Jordan multiplicative map is additive was investigated by several authors. Let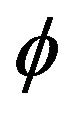 be a bijective map on a standard operator algebra. Molnár showed in [5] that if
be a bijective map on a standard operator algebra. Molnár showed in [5] that if 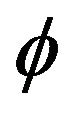 satisfies
satisfies

then 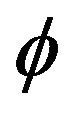 is additive. Later, Molnár in [5] and then Lu in [6] considered the cases that
is additive. Later, Molnár in [5] and then Lu in [6] considered the cases that 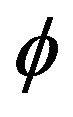 preserve the operation
preserve the operation
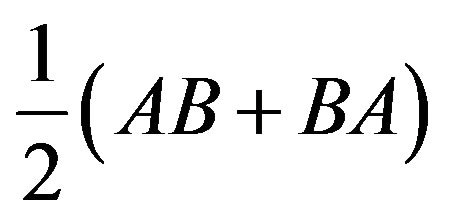 and
and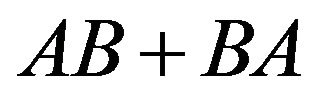 , respectively, and proved that such
, respectively, and proved that such 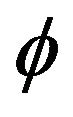 is also additive. Thus, the Jordan multiplicative structure also determines the Jordan ring structure of the standard operator algebras. Later, in [7] we proved these Jordan multiplicative maps on the space of selfadjoint operators space are Jordan ring isomorphism and thus are equivalent. In this paper, we consider the same question and give affirmative answer for the case of Jordan multiplicative maps on the Jordan algebras of all symmetric matrices. In fact, we study injective Jordan semi-triple multiplicative maps on the symmetric matrices
is also additive. Thus, the Jordan multiplicative structure also determines the Jordan ring structure of the standard operator algebras. Later, in [7] we proved these Jordan multiplicative maps on the space of selfadjoint operators space are Jordan ring isomorphism and thus are equivalent. In this paper, we consider the same question and give affirmative answer for the case of Jordan multiplicative maps on the Jordan algebras of all symmetric matrices. In fact, we study injective Jordan semi-triple multiplicative maps on the symmetric matrices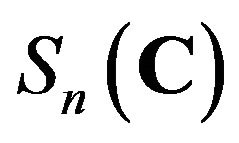 , and show that such maps must be additive, and hence are Jordan ring homomorphisms.
, and show that such maps must be additive, and hence are Jordan ring homomorphisms.
Let us recall and fix some notations in this paper. Recall that 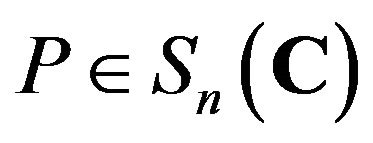 is called an idempotent if
is called an idempotent if . We define the order
. We define the order between idempotents as follows:
between idempotents as follows:  if and only if
if and only if 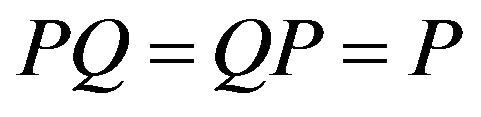 for any idempotents
for any idempotents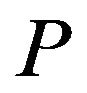 ,
, . For any
. For any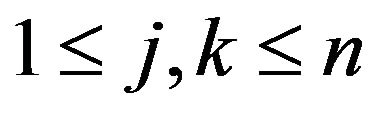 , let
, let  be the matrix with 1 in the position
be the matrix with 1 in the position  and zeros elsewhere, and
and zeros elsewhere, and 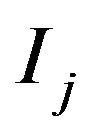 be the unit of
be the unit of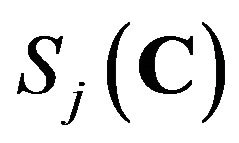 .
.
2. Main Results and Its Proof
In this section, we study injective Jordan semi-triple multiplicative maps on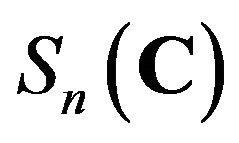 , the following is the main result.
, the following is the main result.
Theorem 2.1. An injective map
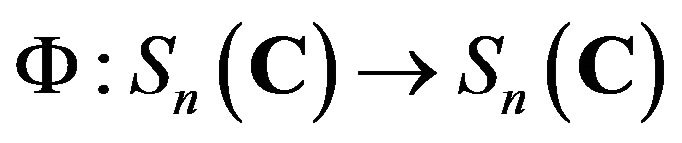
is a Jordan semi-triple multiplicative map, that is
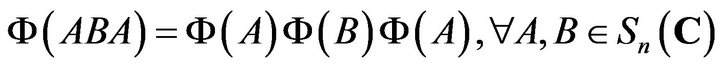 (2.1)
(2.1)
if and only if there is an injective homomorphism  of
of  and a complex orthogonal matrix
and a complex orthogonal matrix 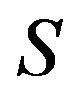 such that
such that
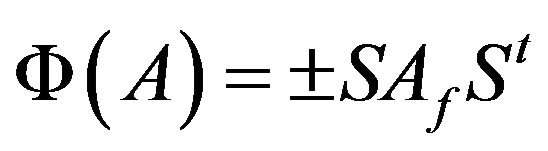 for all
for all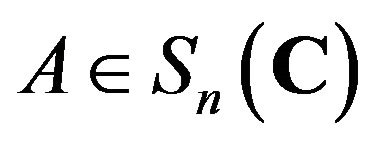 .
.
Firstly, we give some properties of injective Jordan semi-triple multiplicative maps on .
.
Lemma 2.2. Let 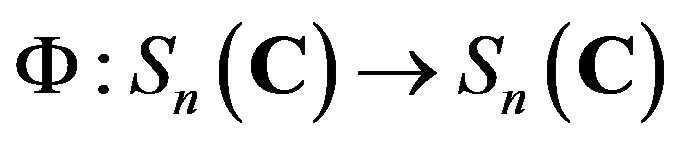 be an injective Jordan semi-triple multiplicative map. Then
be an injective Jordan semi-triple multiplicative map. Then  sends idempotents to tripotents and moreover1)
sends idempotents to tripotents and moreover1) 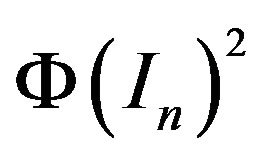 is an idempotent and
is an idempotent and
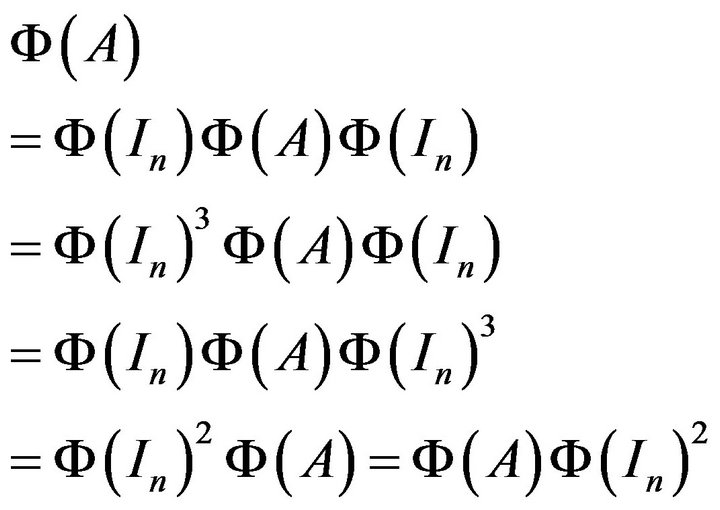
for all , in particular
, in particular
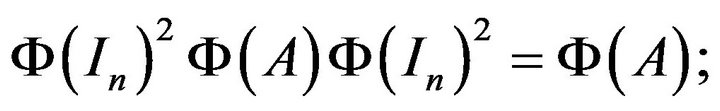
2)  commutes with
commutes with  for every
for every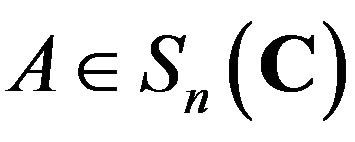 ;
;
3) 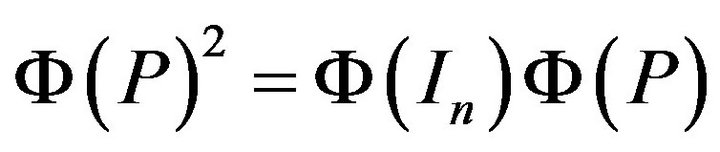 is an idempotent for each idempotent
is an idempotent for each idempotent ;
;
4) A map 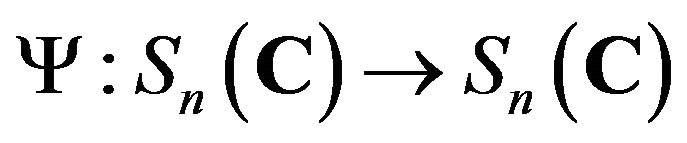 defined by
defined by
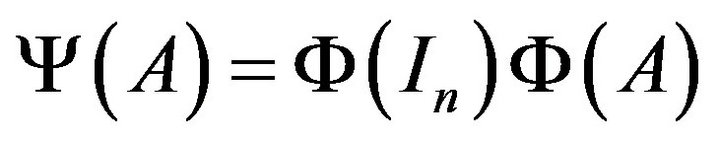
for all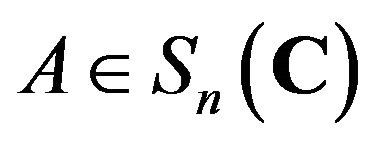 , is a Jordan semi-triple multiplicative map, which is injective if and only if
, is a Jordan semi-triple multiplicative map, which is injective if and only if  is injective.
is injective.
For  defined in Lemma 2.2, we can see that
defined in Lemma 2.2, we can see that

and  for any idempotents
for any idempotents
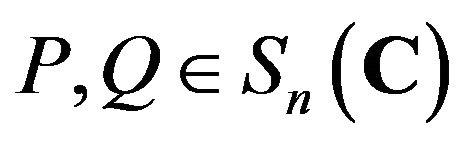 . Therefore, we have Corollary 2.3. Let
. Therefore, we have Corollary 2.3. Let 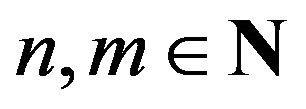 and
and
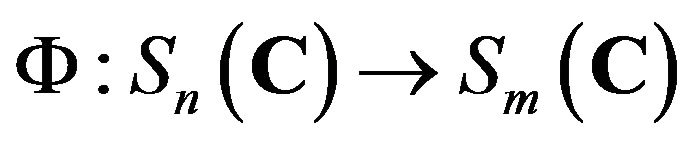
be an injective Jordan semi-triple multiplicative map. Then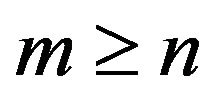 . In the case
. In the case , for each idempotent
, for each idempotent  the rank of
the rank of 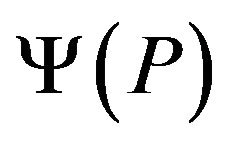 is equal to the rank of
is equal to the rank of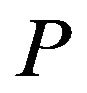 . In particular,
. In particular,

and

Now we give proof of Theorem 2.1. The main idea is to use the induction on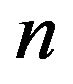 , the dimension of the matrix algebra, after proving the result for
, the dimension of the matrix algebra, after proving the result for  matrices.
matrices.
Proof of Theorem 2.1. In order to prove Theorem 2.1, it suffices to characterize . Note if
. Note if

then
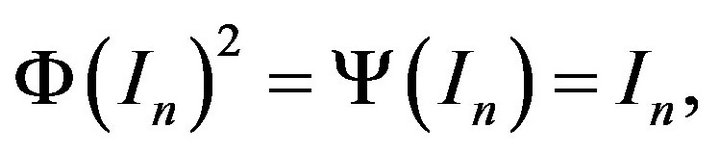
that is 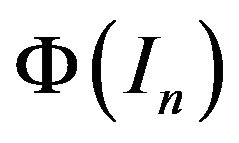 is invertible and
is invertible and
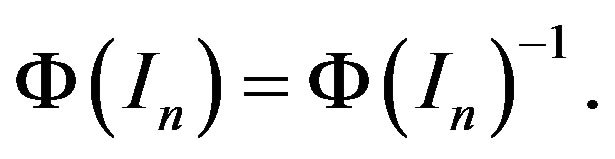
By Lemma 2.1, 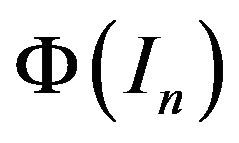 commutes with
commutes with 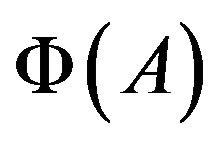 for all
for all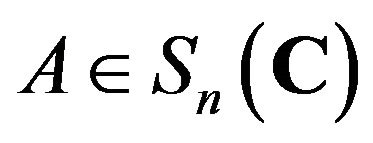 . It follows that
. It follows that 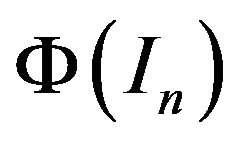 commutes with
commutes with  for all
for all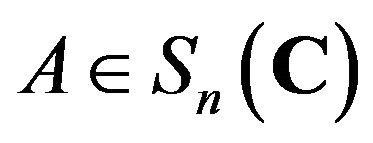 . Therefore, if
. Therefore, if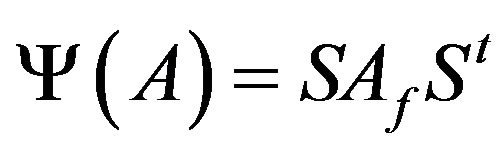 ,
, 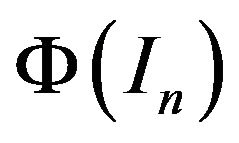 must be a scalar matrix. As
must be a scalar matrix. As 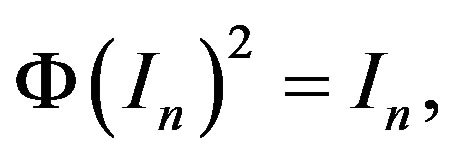
 and hence
and hence has the desired form.
has the desired form.
Therefore, we mainly characterize . The proofs are given in two steps.
. The proofs are given in two steps.
Step 1. The proof for .
.
The matrix  is an idempotent of rank one. By Corollary 2.3,
is an idempotent of rank one. By Corollary 2.3, 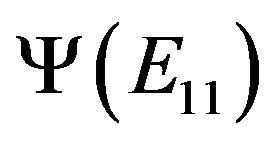 is a rank one idempotent. It is well known that every idempotent matrix in
is a rank one idempotent. It is well known that every idempotent matrix in 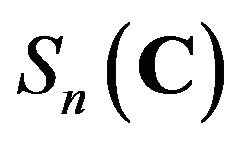 can be diagonalizable by complex orthogonal matrix. Thus, there exists a
can be diagonalizable by complex orthogonal matrix. Thus, there exists a 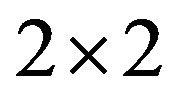 orthogonal matrix
orthogonal matrix 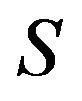 such that
such that
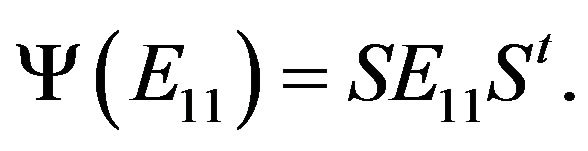
Without loss of generality, we may assume that
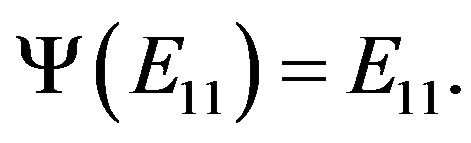
By Corollary 2.3 and from the following fact
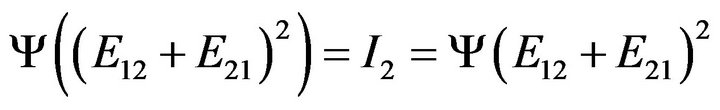
and
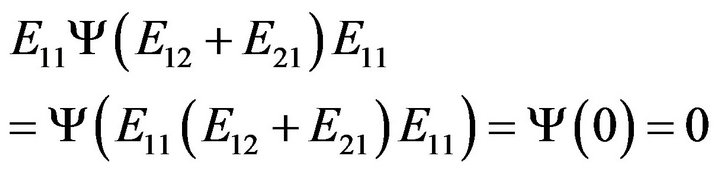
we conclude that
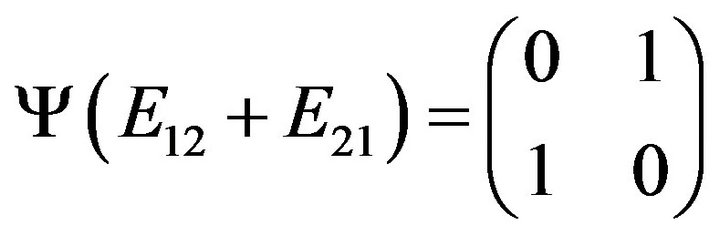
or
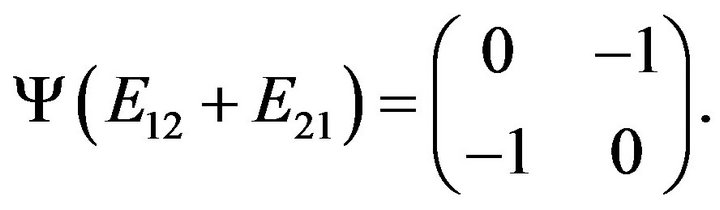
Let , by replacing
, by replacing  with
with 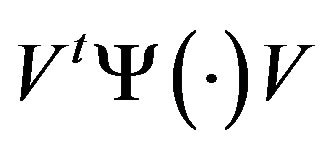 if necessary, we may assume that
if necessary, we may assume that
 .
.
For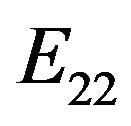 , since
, since  is a rank one idempotent and satisfying
is a rank one idempotent and satisfying 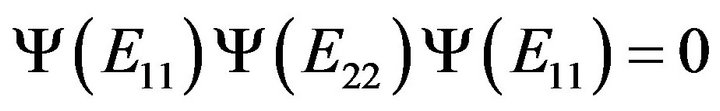 and
and
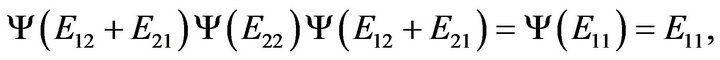
we have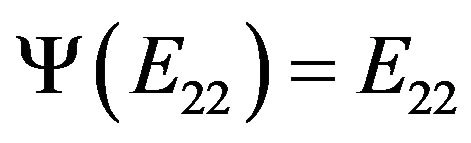 . Now for any
. Now for any
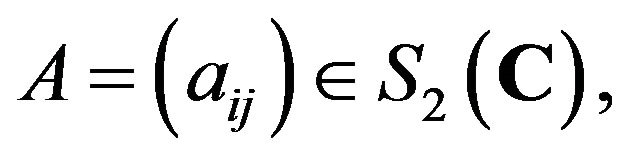
let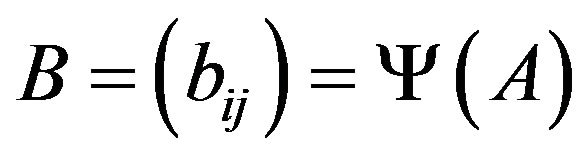 . Then
. Then
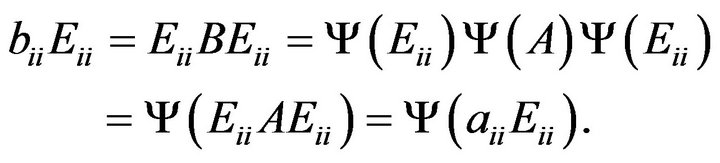
Thus, the entry of
entry of 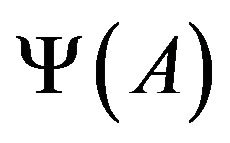 depends on the
depends on the 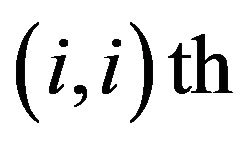 entry of
entry of only. Therefore, there exist injective functionals
only. Therefore, there exist injective functionals such that
such that  satisfy respectively
satisfy respectively 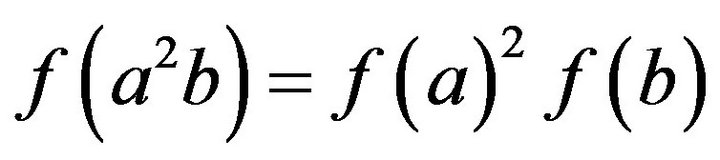 and
and
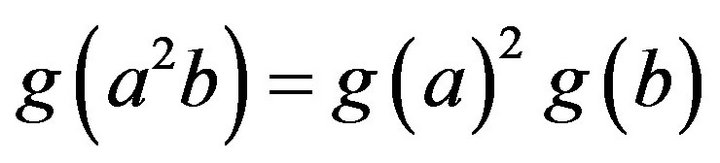 and
and
 .
.
From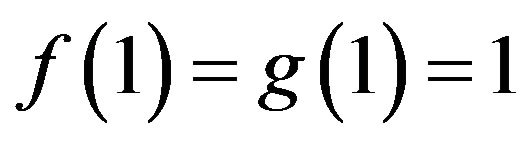 , it is easy to verify that
, it is easy to verify that 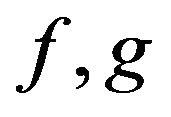 is multiplicative. Next we prove that
is multiplicative. Next we prove that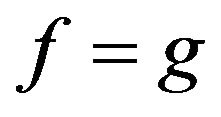 . Let
. Let
 since
since 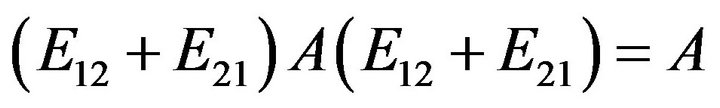
A and , we have
, we have
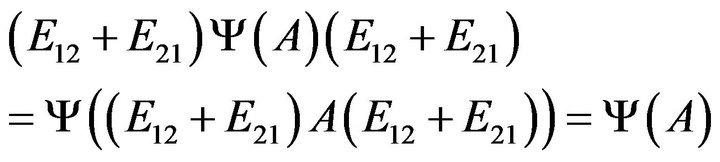
and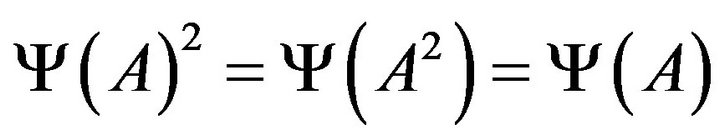 , hence
, hence 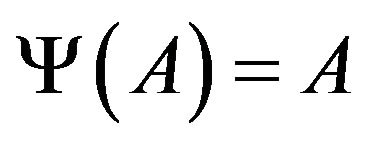 or
or
 with
with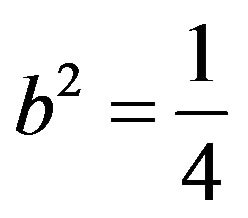 .
.
Thus,  and
and 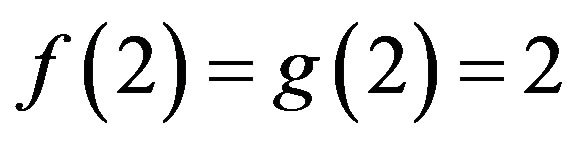 since
since
 is multiplicative. Let
is multiplicative. Let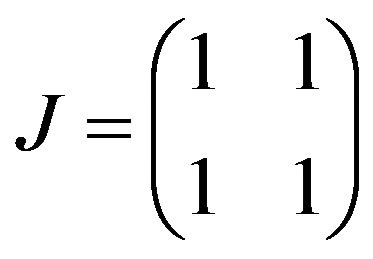 , then
, then
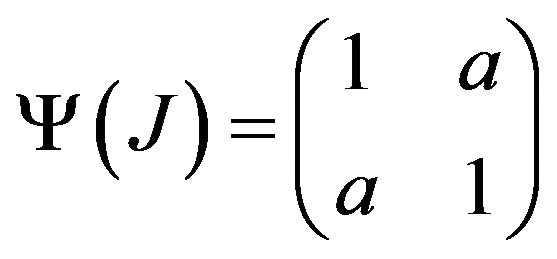 . Note that
. Note that 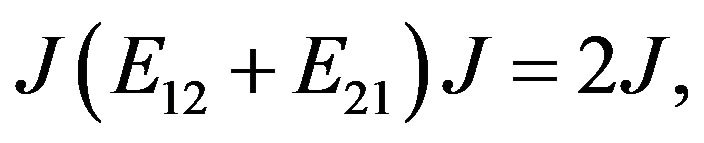 and
and
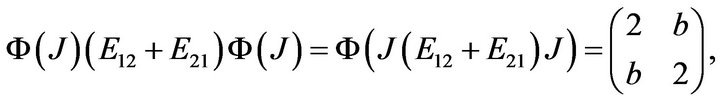
that is
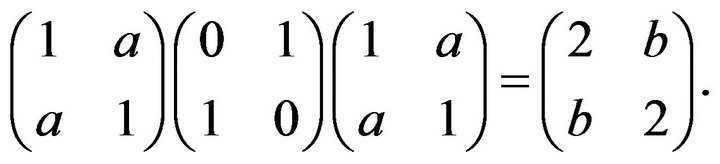
This implies 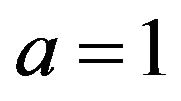 and
and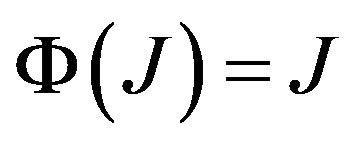 . Now by the fact
. Now by the fact  and
and , we get
, we get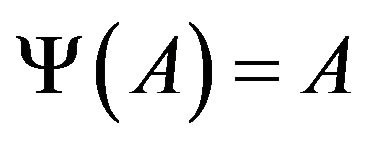 . For any
. For any , since
, since

thus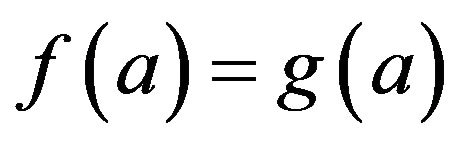 .
.
Next we prove that  is additive. Since
is additive. Since
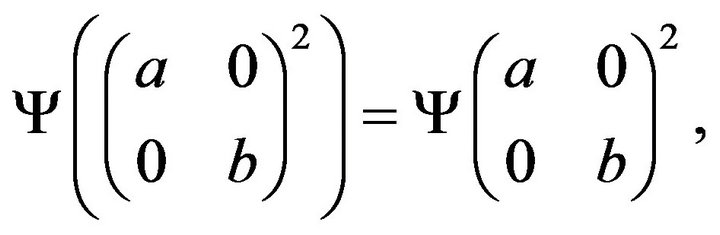 and thus we have
and thus we have
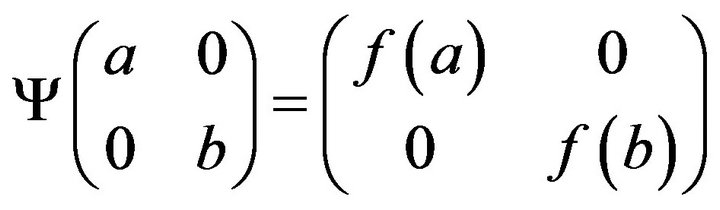
for any . Moreover by the fact
. Moreover by the fact 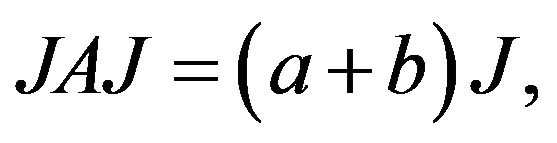 one can get that
one can get that
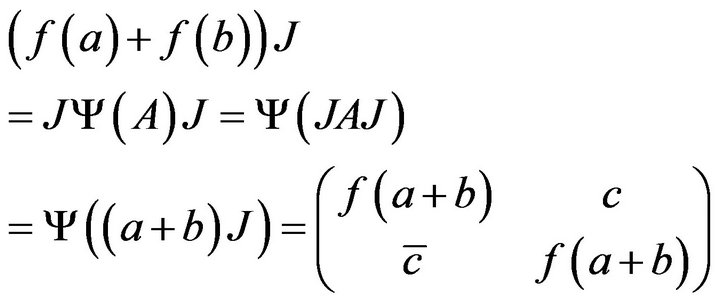
and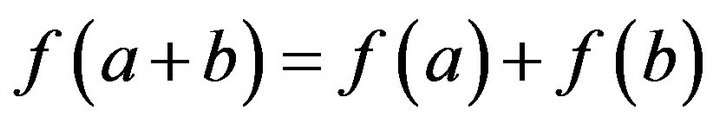 .
.
Finally, we prove
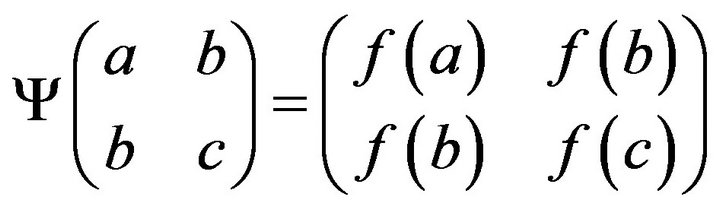
for any . Let
. Let
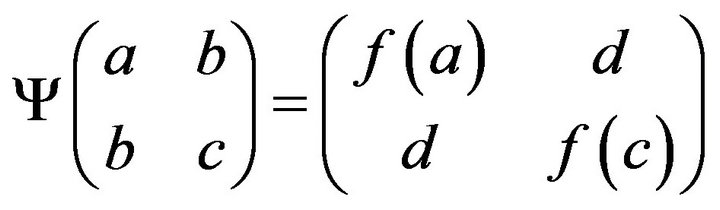 .
.
By the fact that 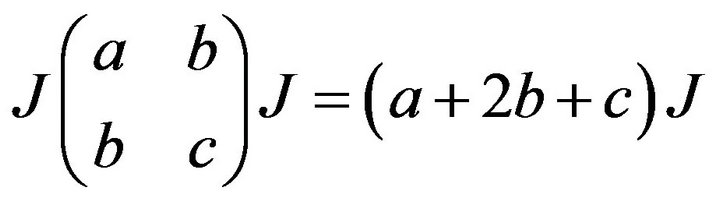
and
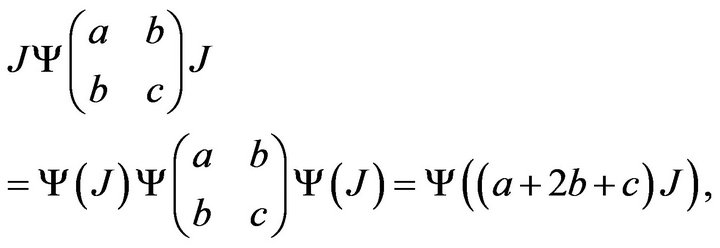
we get 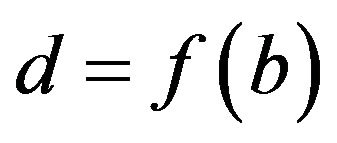 and
and 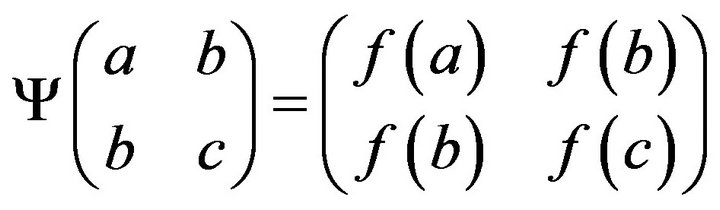 for any
for any .
.
Step 2. The induction.
Let
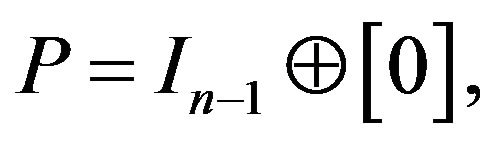
then  is a rank
is a rank 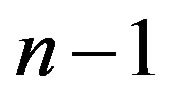 idempotent, so is
idempotent, so is 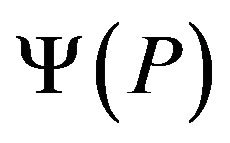 by Corollary 2.3. Therefore, there exists a orthogonal matrix
by Corollary 2.3. Therefore, there exists a orthogonal matrix 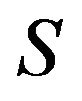 such that
such that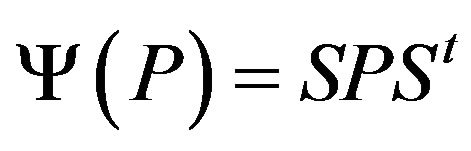 . Replacing
. Replacing  by the map
by the map 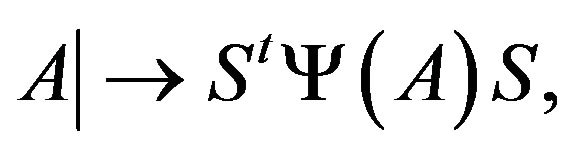 we may assume that
we may assume that .
.
For any 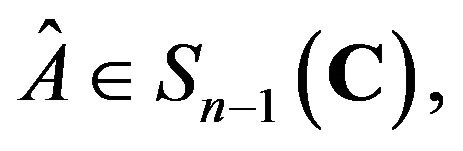 let
let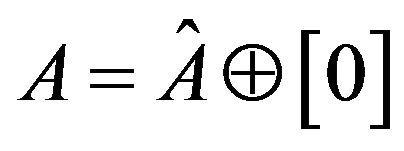 . Then
. Then 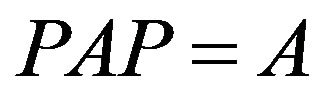 implies
implies
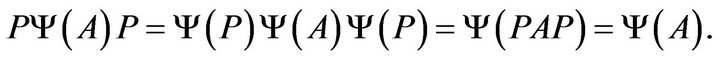
It follows that  for some matrix
for some matrix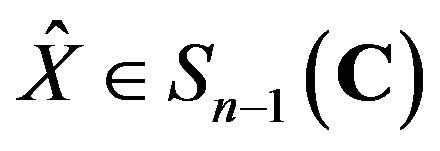 . Define the map
. Define the map  on
on 
by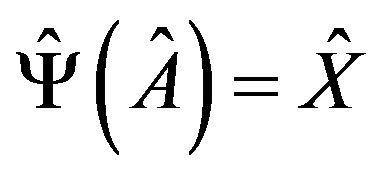 . It is easy to check that
. It is easy to check that  is an injective Jordan semi-triple multiplicative map on
is an injective Jordan semi-triple multiplicative map on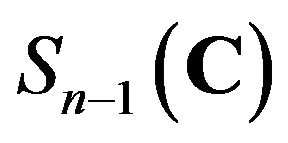 . Furthermore,
. Furthermore,  implies that
implies that . By the induction hypothesis there is a
. By the induction hypothesis there is a 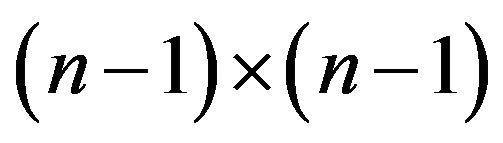 orthogonal matrix
orthogonal matrix 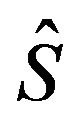 and an injective homomorphism
and an injective homomorphism 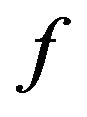 on
on  such that
such that 
Let 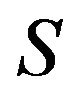 be the matrix
be the matrix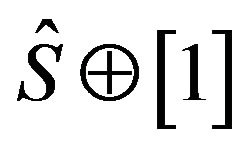 . Without loss of generality, we assume that
. Without loss of generality, we assume that 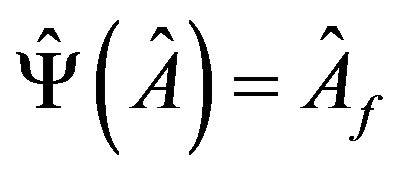 for all
for all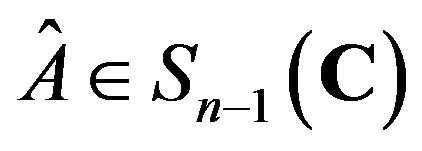 . This is equivalent to
. This is equivalent to . For any
. For any
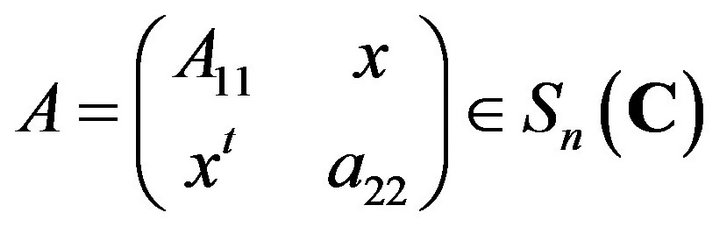 with
with 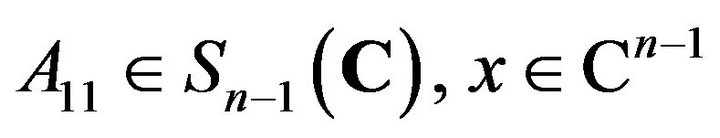
and , we have
, we have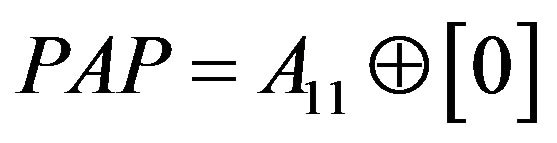 .
.
Thus,
 (*)
(*)
Let us define matrices 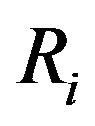 for each
for each  by
by

For an arbitrary , From (*) we have
, From (*) we have
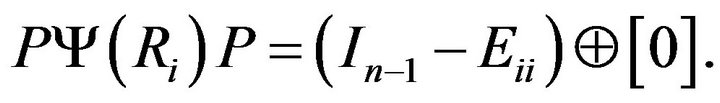
Then there exists 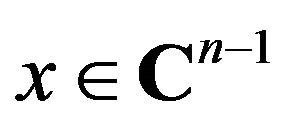 and
and  such that
such that
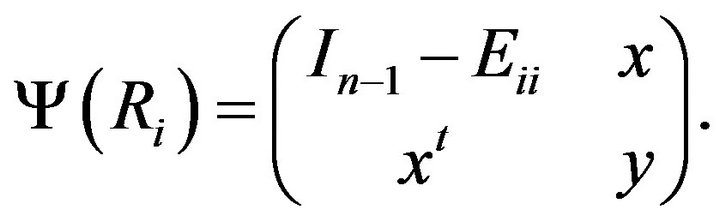
From the equality  we get that
we get that 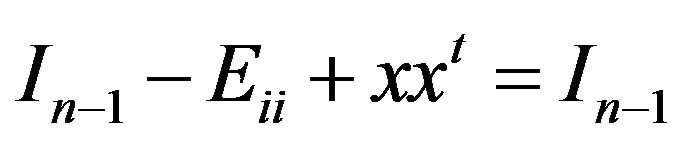 and
and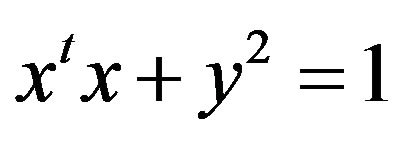 . These equality implies that
. These equality implies that  and
and
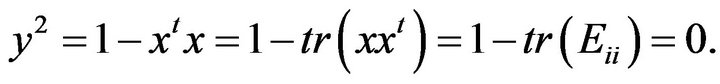
Hence only the  entries
entries 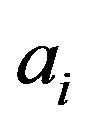 of
of 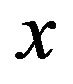 are nonzero and
are nonzero and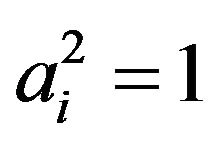 . It follows that
. It follows that

Next, take any two distinct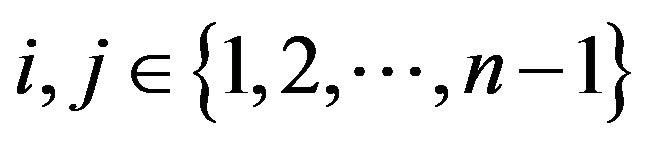 . From
. From
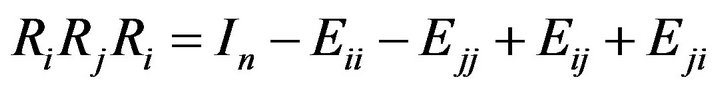
and using (*) , we get
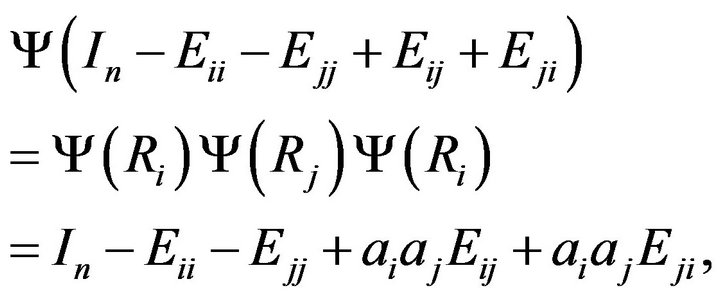
which implies that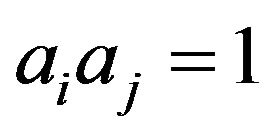 . Let
. Let , then
, then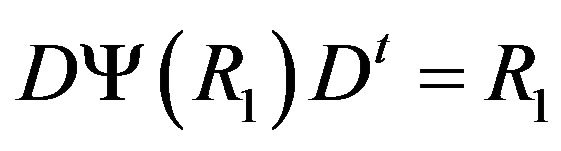 , so we may assume that
, so we may assume that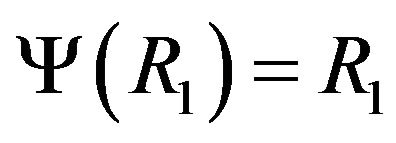 . Furthermore by the equality
. Furthermore by the equality
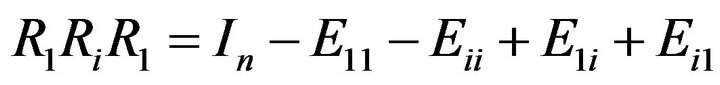
and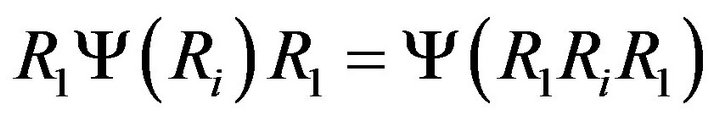 , we obtain
, we obtain 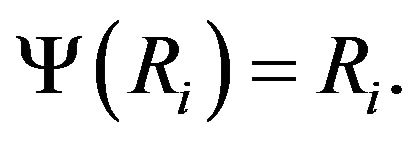
Next we prove that 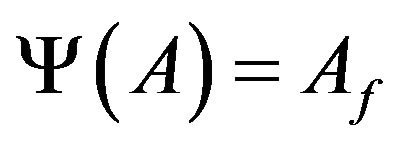 for any
for any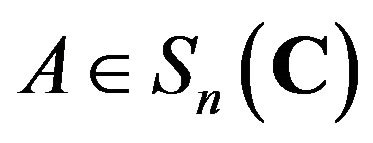 .
.
Let us fix some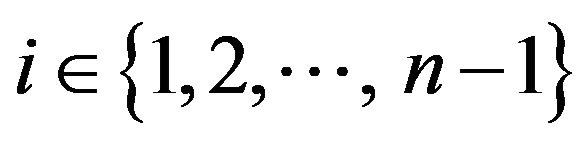 . As
. As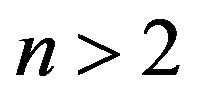 , there is another
, there is another  such that
such that

Then for any ,
,
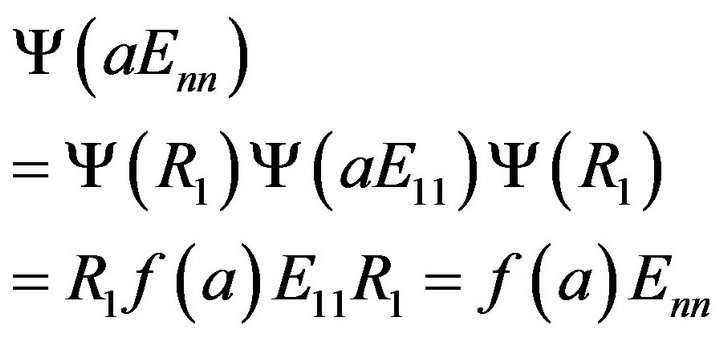
and
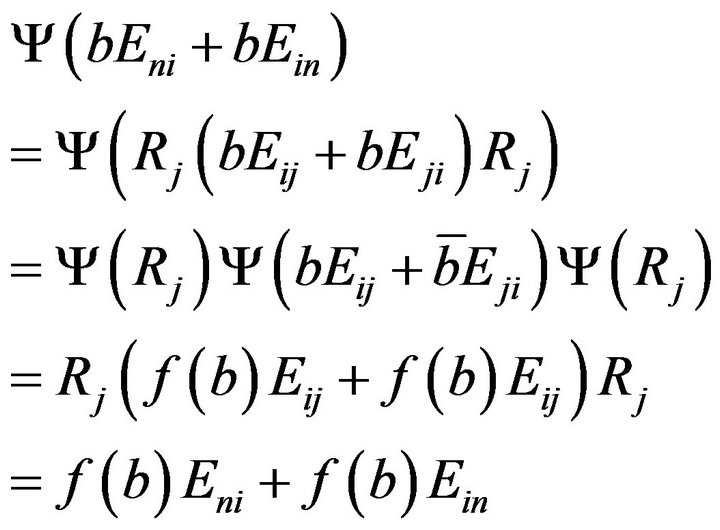 .
.
Thus, for any
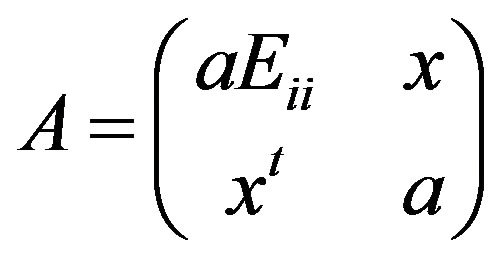
where 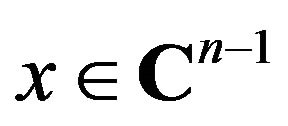 has only one nonzero entry in the
has only one nonzero entry in the  position, we have
position, we have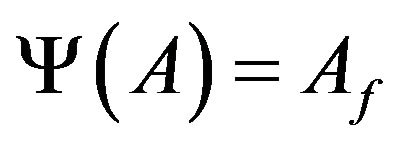 . For any
. For any , let
, let
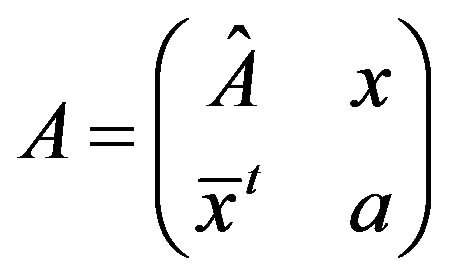
and
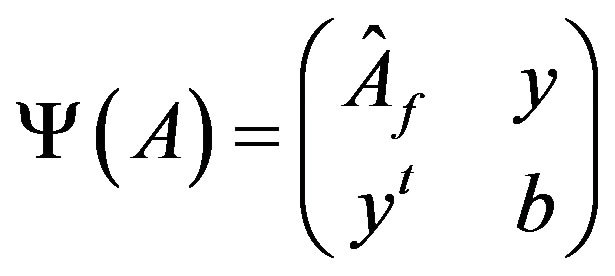 .
.
From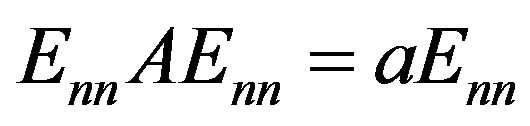 , we have
, we have
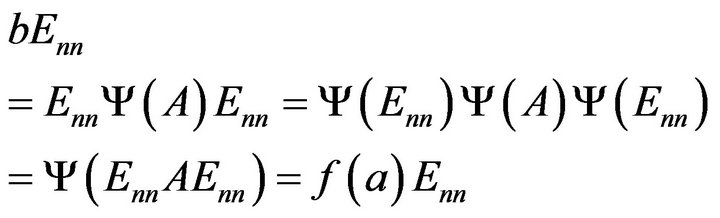
And . For any
. For any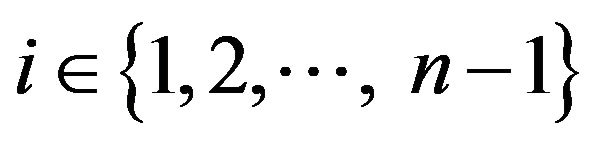 , since
, since

where  and
and  have only one nonzero entry
have only one nonzero entry  and
and 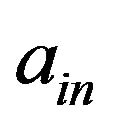 in the
in the 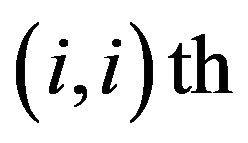 and
and 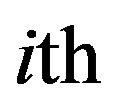 position respectively,
position respectively,  is equal to the
is equal to the 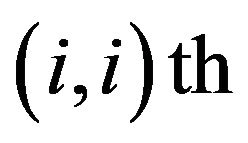 entry of
entry of , thus we have
, thus we have
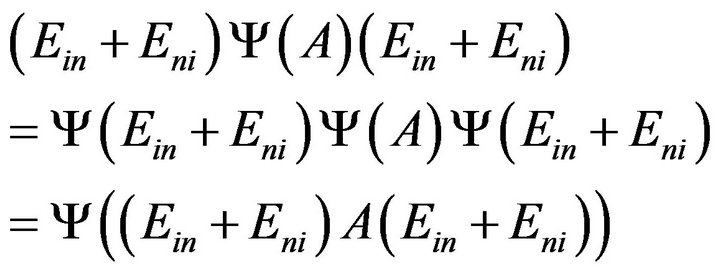
and so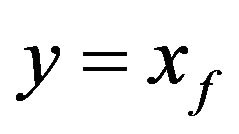 . The proofs are complete.
. The proofs are complete.
By Theorem 2.1, we can characterize another two forms of Jordan multiplicative maps on .
.
Theorem 2.4. An injective map

satisfies
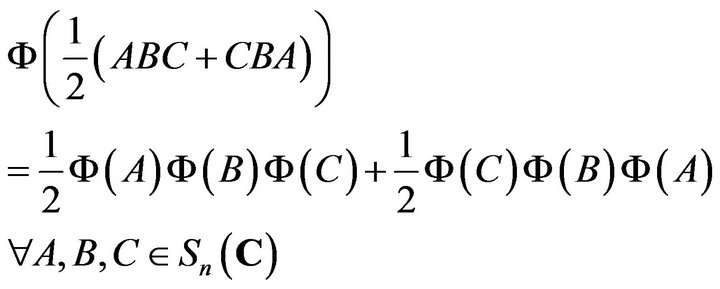 (2.2)
(2.2)
if and only if there is an injective homomorphism 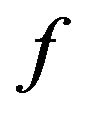 on
on  and a complex orthogonal matrix
and a complex orthogonal matrix 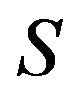 such that
such that
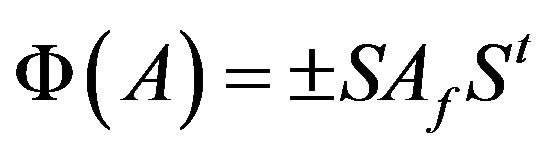 for all
for all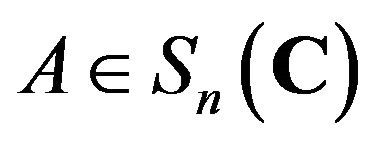 .
.
Proof. Let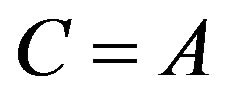 in Equation (2.2), we get
in Equation (2.2), we get
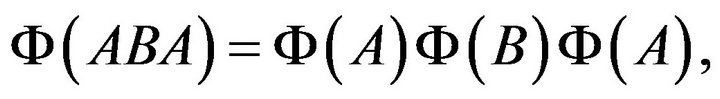
that is,  is a Jordan semi-triple multiplicative map. Consequently,
is a Jordan semi-triple multiplicative map. Consequently,  has the desired form by Theorem 2.1.
has the desired form by Theorem 2.1.
Since every ring homomorphism on is an identity map, thus by Theorem 2.1, Theorem 2.4, we get Corollary 2.5. Let
is an identity map, thus by Theorem 2.1, Theorem 2.4, we get Corollary 2.5. Let 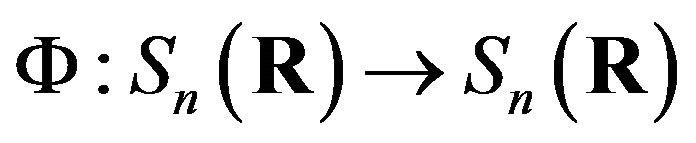 be an injective map. Then the following condition are equivalent1)
be an injective map. Then the following condition are equivalent1) 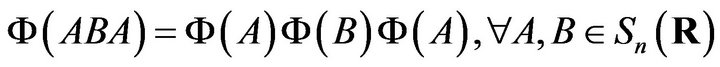
2) 

3) there is a real orthogonal matrix such that
such that
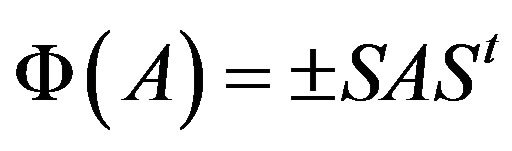 for all
for all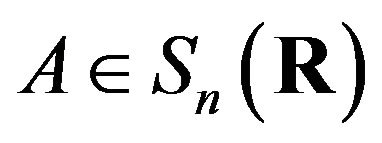 .
.
At the end of this section, we characterize bijective maps on 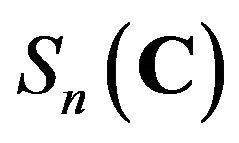 preserving
preserving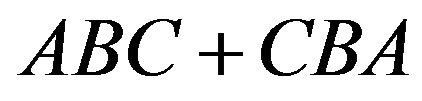 .
.
Theorem 2.6. A bijective map  satisfies
satisfies
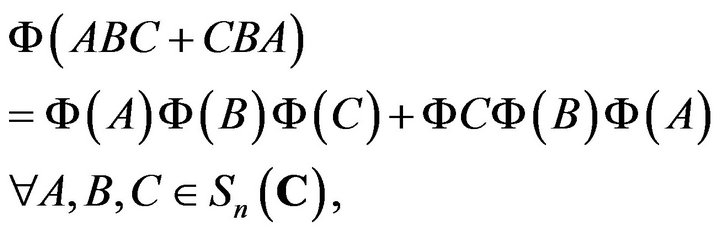 (2.3)
(2.3)
if and only if there is a ring isomorphism  on
on  and a complex orthogonal matrix
and a complex orthogonal matrix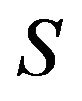 such that
such that
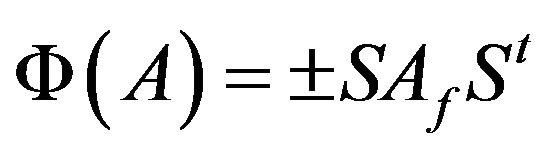 for all
for all 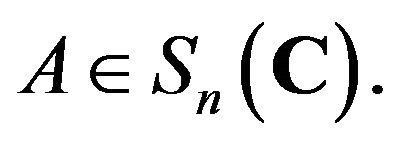
Proof. It is enough to check the “only if” part. Letting in Equation (2.3), we get
in Equation (2.3), we get

Taking 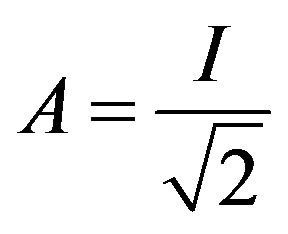 and
and , we get
, we get  and thus
and thus
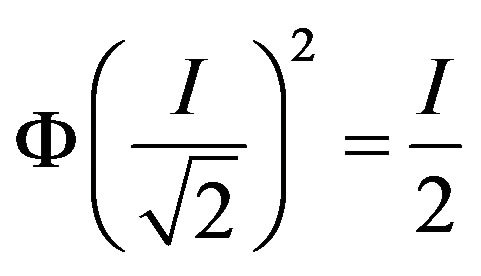 (2.4)
(2.4)
Letting 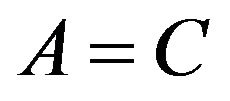 in Equation (2.3), we get
in Equation (2.3), we get
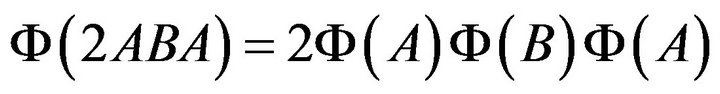 .
.
Taking , we get
, we get
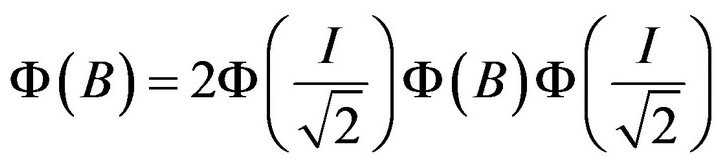 .
.
Multiplying this equality by 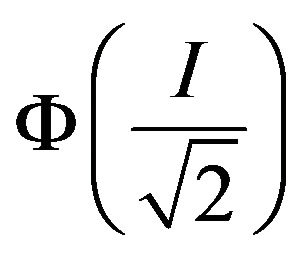 from the left side, by Equation (2.4) we get
from the left side, by Equation (2.4) we get
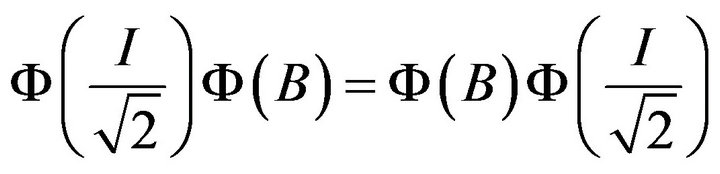
for any , and hence
, and hence 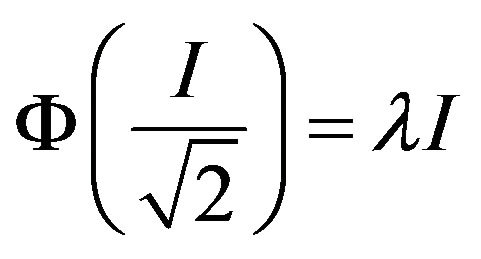 for some scalar
for some scalar . By Equation (2.4), we obtain
. By Equation (2.4), we obtain 
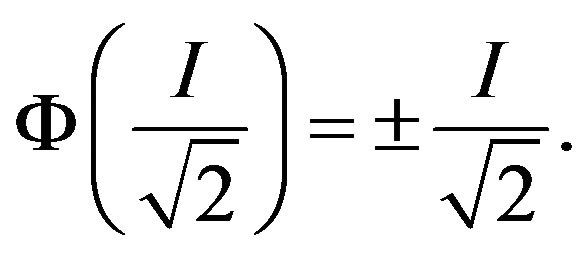
If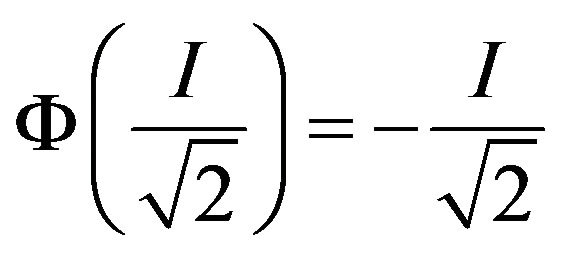 , let
, let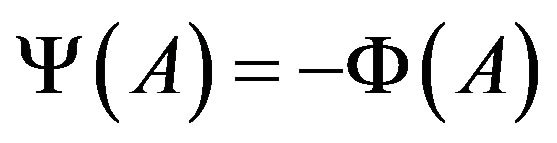 , then
, then  also meets Equation (2.3) and
also meets Equation (2.3) and . So without loss of generality, we assume
. So without loss of generality, we assume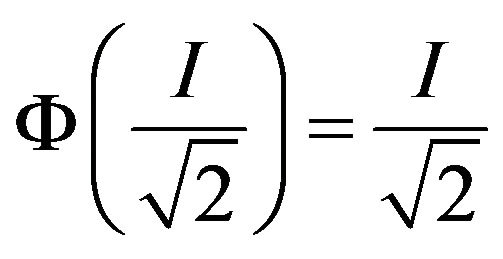 . By letting
. By letting 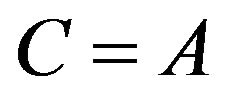 and
and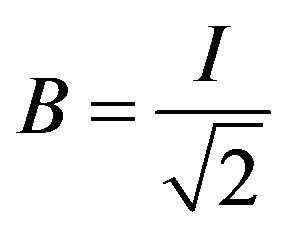 in Equation (2.3), we get
in Equation (2.3), we get
 and
and  for all
for all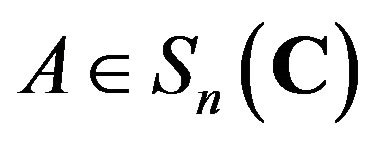 . Consequently
. Consequently
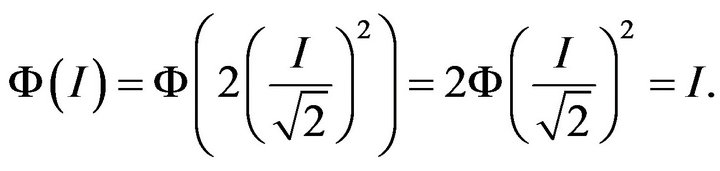
Now letting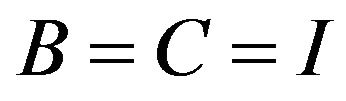 in Equation (2.3) we get
in Equation (2.3) we get
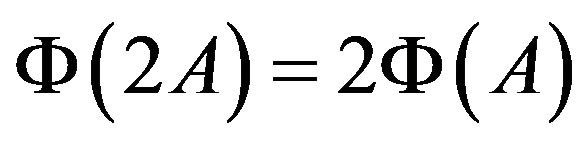 .
.
Thus, 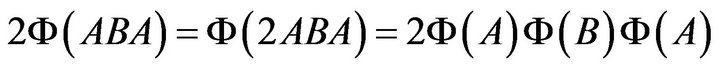
and 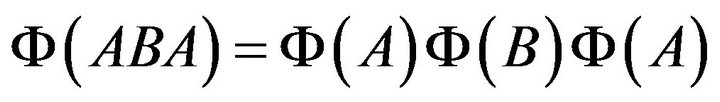 by taking
by taking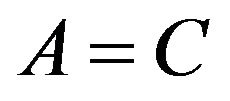 in Equation (2.3). Therefore,
in Equation (2.3). Therefore,  has desired form by surjectivity of
has desired form by surjectivity of  and Theorem 2.1.
and Theorem 2.1.
In particular, we have Corollary 2.7. A bijective map  satisfies
satisfies
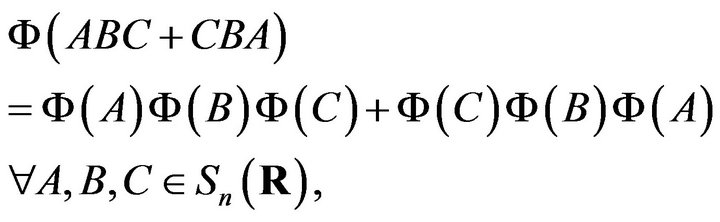
if and only if there is a real orthogonal matrix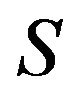 such that
such that
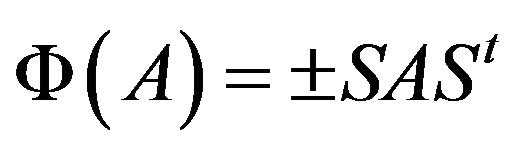 for all
for all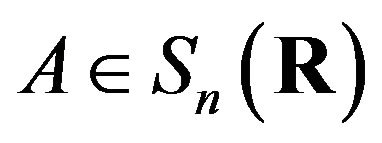 .
.
Remark 2.8. We do not know whether the surjective assumption in Theorem 2.6 and Corollary 2.7 can be omitted.
REFERENCES
- W. S. Matindale III, “When Are Multiplicative Mappings Additive?” Proceedings of the American Mathematical Society, Vol. 21, No. 3, 1969, pp. 695-698. doi:10.1090/S0002-9939-1969-0240129-7
- P. Šemrl, “Isomorphisms of Standard Operator Algebras,” Proceedings of the American Mathematical Society, Vol. 123, No. 6, 1995, pp. 1851-1855.
- L. Molnár, “On Isomorphisms of Standard Operator Algebras,” Studia Mathematica, Vol. 142, 2000, pp. 295- 302.
- J. Hakeda, “Additivity of *-Semigroup Isomorphisms among *-Algebra,” Bulletin of the London Mathematical Society, Vol. 18, No. 1, 1986, pp. 51-56. doi:10.1112/blms/18.1.51
- L. Molnár, “Jordan Maps on Standard Operator Algebras,” In: Z. Daroczy and Z. Páles, Eds., Functional Equations-Results and Advances, Kulwer Academic Publishers.
- F. Lu, “Additivity of Jordan Maps on Standard Operator Algebras,” Linear Algebra and its Applications, Vol. 357, No. 1-3, 2002, pp. 123-131. doi:10.1016/S0024-3795(02)00367-1
- R. L. An and J. C. Hou, “Additivity of Jordan Multiplicative Maps on Jordan Operator Algebras,” Taiwanese journal of mathematics, Vol. 10, No. 1, 2006, pp. 45-64.
NOTES
*The author is support by a grant from National Natural Foundation of China (11001194).

