Received 20 February 2015; accepted 9 March 2015; published 11 March 2015

ABSTRACT

Ab initio calculations of the band structure, total and partial densities of states and the spatial distribution of the electron charge density of crystalline Na₂GeS₃ are performed in the framework of density functional theory in the local density approximation for an exchange-correlation poten- tial. According to the calculation results, sodium thiogermanate is a direct-gap crystal with the top of the valence band and the bottom of the conduction band at the G point of the Brillouin zone. The calculated band gap is E_g = 2.51 eV. The nature of the components of the electronic states in different subbands of the valence band is determined. The calculated total density of states in the valence band of the crystal is compared with the known experimental X-ray photoelectron spec- trum of Na₂GeS₃ glass. Based on the maps of the electron density distribution, the nature of the chemical bonds and high mobility of Na⁺ ions in Na₂GeS₃ crystal is analyzed.

Keywords:

Sodium Thiogermanate, Electronic Structure, Density of States, Electron Charge Density

1. Introduction

In the recent years, an intense work is underway to search for electrode materials for sodium-ion batteries that could in future replace lithium-ion power sources [1] . A significant advantage of the sodium-ion batteries compared with the lithium-based ones is that abundance of sodium on the Earth is substantially larger than that of lithium; therefore, sodium batteries could be cheaper. Solid electrolytes are required to produce sodium batteries. Silicon and germanium dichalcogenide glasses modified by sodium chalcogenides are promising materials with high room-temperature ionic conductivity due to the sodium cation motion [2] - [5] .

Investigation of the phase diagram of GeS₂-Na₂S system by differential thermal analysis and X-ray diffraction analysis showed that in this system (depending on the GeS₂/Na₂S ratio), three crystalline phases―Na₂GeS₃, Na₄Ge₄S₁₀, and Na₆Ge₂S₇―could be formed [2] [6] . In addition, germanium disulfide forms stable glassy alloys with sodium sulfide (Na₂S) in a wide compositional range from 100 to 40 mol% GeS₂, including a ternary compound Na₂GeS₃ [2] - [5] . Even though physical and chemical properties, including the ionic conductivity, of glassy and crystalline Na₂GeS₃ are studied rather well [2] - [7] , the knowledge of such important characteristics as optical, vibrational, and mechanical ones is still quite limited. One of the main reasons for the lack of such data is high hygroscopicity of this material. In such situation, theoretical methods, above all the calculations of Na₂GeS₃ electronic structure, seem to play an increasing role because the important properties of ionic crystals are determined by the peculiarities of their crystal and electronic structure. So far, the electronic structure was experimentally investigated only for the glassy phase of Na₂GeS₃ by X-ray photoelectron spectroscopy (XPS) [8] [9] . The knowledge of the electronic structure will help one to determine the nature of the Na-S chemical bonds required for a better understanding of the glass local structure and the mechanism of the ionic conductivity.

In this paper, we report on the density functional theory (DFT) calculations of the energy band structure, total and partial local densities of states and the spatial distribution of the electron density for crystalline Na₂GeS₃. The calculated total density of electronic states of the crystal is compared with the experimental X-ray photoelectron spectrum (XPS) of Na₂GeS₃ glass taken from [8] .

2. Сrystal Structure

Sodium thiogermanate crystallizes in the monoclinic structure, which symmetry is described by the space group P2₁/c with the lattice parameters а = 6.952 Å, b = 15.230 Å, c = 5.720 Å, b = 115.24^°, Z = 4 [7] . The crystal

structure is composed of endless 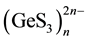chains extended along the c axis. The chains are built by transla-

tion of two [GeS₄] tetrahedra linked by shared vertices having a-cis relative orientation (Figure 1(a)). Similar tetrahedral chains can be found in the structures of oxogermanates Na₂GeO₃ and BaGeO₃. The unit cell contains two types of nonequivalent chains twisted in opposite directions. The interatomic distances in the chains are 2.22 Å - 2.25 Å for Ge-S (bridging), 2.14 Å - 2.17 Å for Ge-S (non-bridging), and 3.73 Å for Ge-Ge, the S-Ge-S bond angle is 96.5˚ - 120.1˚. Alloying of GeS₂ and Na₂S binary compounds in the 1:1 ratio results in the breakdown of the [Ge₂S₆] doubled tetrahedra, characteristic for the high-temperature phase of germanium disulphide [10] , where these doubled tetrahedra link the endless tetrahedral chains into three-layered packets. This eventually leads to the formation of the exclusively chain structure of Na₂GeS₃ (Figure 1(a)). The bond between the adjacent chains in sodium thiogermanate is formed by weak van der Waals forces. In van der Waals space between the chains, Na atoms are located in two nonequivalent positions: the octahedral one (NaI in Figure 1(b)) and the seven-vertex one (NaII). The average distance is 2.91 Å for NaI-S and 3.19 Å for NaII-S.

3. Calculation Method

Calculations of the energy band structure are performed within the density functional theory [11] [12] in the

local density approximation (LDA) in order to the exchange and correlation effects to be taken into account [13] [14] , using the SIESTA software [15] [16] . Linear combinations of atomic orbitals are used as the fundamental calculation basis. The periodic crystal structure was taken into account by the boundary conditions at the unit cell boundaries. The first-principle norm-conserving atomic pseudopotentials [17] [18] were used for the following electronic configurations of atoms: Ge-[Ar] 4s²4p², S-[Ne] 3s²3p⁴ and Na-[Ne] 3s¹. Marked states related to the valence shells, [Аr], [Ne]―to the core.

The cut-off energy E_cut = 200 Ry for the atomic orbitals for the self-consistent calculation was chosen to obtain a convergence in the cell total energy not worse than 0.001 Ry/atom. The basis had about 22320 atomic orbitals. The density of the k-point grid in the reciprocal space for the self-consistent calculation was selected from the same reasons. The electron density was calculated by interpolation between the sites of the 5 × 3 × 6 grid in the reciprocal space. The total and partial electron densities of states were determined by the modified tetrahedra method, for which the energy spectrum and wave functions were calculated on a k-grid containing 90 points. Integration over the irreducible part of the Brillouin zone was performed using the method of special k-points [19] [20] .

4. Results and Discussion

4.1. Electronic Structure and the Nature of Electronic States

Calculation of the band structure of Na₂GeS₃ crystal was performed for the high-symmetry points Г, B, D, Z, C, Y, A, E and along the lines between them in the Brillouin zone (Figure 2). The band structure of Na₂GeS₃ calculated without the account of the spin-orbit interaction is shown in Figure 3. The energy scale origin was put in the valence band top located in the center of the Brillouin zone (G point). The bottom of the conduction band is also in the Brillouin zone center, hence sodium thiogermanate is a direct-gap crystal with the calculated band gap E_g = 2.51 eV.

The valence bands have a weak dispersion and consist of three energy separated band bunches of (VBI, VBII, VBIII, numbering from the top subband), which correspond to discrete bands in the density of states N(E) spectra. The profiles of the total density of states for Na₂GeS₃ as well as the contributions from the individual states for different atoms are presented in Figure 4. The analysis of the energy distribution of the local partial densities of states of sodium, germanium and sulfur shows that in each of three filled bands the s- and p-states give unequal contributions, differing in value. The contributions of the electronic states of sulfur and germanium atoms dominate in the whole energy range. The lowest energy bunch of the valence bands (located in the energy range from −13.73 to −10.99 eV) are formed mainly by 3s-states of sulfur atoms. Despite the predominant character of the sulfur 3s-states, for this valence subband (VBIII) hybridization effects of Ge and S atom states are noticeable, leading to the appearance of the contribution of Ge4s-states, mainly localized in the energy range of the lower 4 branches, and contributions of Ge4p-states in the next bunch of 6 branches which have a weak dispersion.

The average occupied subband VBII (from −7.79 to −5.07 eV) is of hybrid character and is formed by an overlap of the Ge4s- and S3p-states, playing thus a prominent role in the formation of Ge-S covalent bonds in the [GeS₄] tetrahedral forming the endless chains.

The upper valence subband (VBI) can be conditionally divided into two parts: the lower one (from −4.42 to −2.18 eV) of 12 filled branches is mixed with the hybridized 3p-states of sulfur and 4p-states of germanium with the insignificant contribution of s- and p-states of sodium; the upper one (from −2.08 eV to the valence band top) consisting of 20 dispersive branches is formed mainly by the p-states of the lone pair of sulfur atoms which are mixed with the germanium d-states and the alkali metal s-, p-states. The top of the valence band at the Г point is formed exclusively by p_z-atomic orbitals of sulfur.

The low-energy electronic structure of unoccupied electronic states of sodium thiogermanate is formed mainly by “mixing” of free states of p-electrons of sulfur atoms as well as s-and p-electrons of germanium and sodium atoms.

The energy spectrum of the valence electrons directly determines such an important characteristic of the crystal as the spectral dependence of the absorption coefficient. However, no papers on the experimental measurement of the intrinsic absorption edge of crystalline or glassy Na₂GeS₃ have been published so far. The lack of the absorption edge data does not enable us to compare the calculated band gap value for Na₂GeS₃ with the experimental E_g.

Meanwhile, the calculations of total and partial densities of states significantly facilitate the interpretation of the experimental X-ray photoelectron spectra (XPS) which reflect the distribution of the total density of states in the valence band. In Figure 5 the XPS spectrum of glassy Na₂GeS₃ taken from [8] and the spectrum of the calculated total density of states in the valence band of the crystal are shown in the same energy scale. The origin of the energy scale is put at the top of the valence band. Since experimentally measured XPS spectra are always slightly smeared in energy compared to the band structure calculation data, in order to compare the XPS spectrum with the calculated total density of states N(E), the latter was smeared artificially by a Gaussian curve with a half-width of 0.2 eV. As one can see from Figure 5, the distribution profiles of the total density of states of the crystal and the XPS spectra of the glass are quite similar and the energy positions of the main peaks in the N(E) curve and the experimental XPS peaks of the glass generally correlate well. The loss of long-range order at the transition from the crystalline to the glassy state should seem to affect the electron spectrum. However, as can be seen from Figure 5, one does not observe large difference in N(E) spectra of the crystal and XPS of the glass. The observed differences in the widths of the experimental and calculated peaks may be due to the finite hole lifetime at the core levels resulting in the broadening of the experimental peaks. The studies of the structure

of glassy sodium thiogermanate by vibrational spectroscopy [3] [4] , give clear evidence that the glass preserves the structural and chemical short-range order characteristic for the crystal. Consequently, one may conclude that the main factor determining the band structure and the energy distribution of the density of states and thereby the X-ray photoelectron spectra of the crystalline and glassy Na₂GeS₃, is the short-range order in the arrangement of atoms.

We identify the nature of the peaks observed in the experimental XPS spectrum of the glass (curve 2 in Figure 5) using the calculation data for the local partial densities of states of the crystal (Figure 4). From this comparison one can ascribe the D maximum at the bottom of the valence band mainly to the s-states of sulfur. Germanium 4s-states hybridized with sulfur 3p-states localized in the energy interval from −7.79 to −5.72 eV determine the position of the C peak in the XPS spectrum. The electronic states of p-type symmetry of germanium and sulfur with admixing s-states of sodium located in the energy range from −4.42 to −2.18 eV are responsible for the formation of the В maximum in the photoelectron spectrum. The shape of the XPS spectrum near the top of the valence band is determined predominantly by the p-states of sulfur which correspond to the intense A peak.

4.2. Spatial Distribution of the Electron Charge Density

Investigation of the distribution of the total charge density of the valence electrons r(r) in the form of contour maps provides helpful information about the nature of both intra-chain and inter-chain chemical bonds in Na₂GeS₃ which is rather difficult to be obtained experimentally for such a complex crystal structure. Besides, from the contour maps of the electron density one can obtain additional information about the character of the ionic conductivity.

The choice of suitable sectional planes is crucial for the construction of the electron density contour maps for a crystal. The tetrahedral short-range structure of Na₂GeS₃ encumbers there presentation of the contour maps in a 2D format. In this case, it is most convenient to represent the electronic configurations for a single [GeS₄] tetrahedron in the plane passing through two sulfur atoms and one germanium atom, i.e. in the plane along the S-Ge-S bond lines. Since the [GeS₄] tetrahedra linked in the chain contain two bridged (S-Ge-S) and two non- bridged (end-point) (Ge-S) sulfur atoms, it is reasonable to built two planes: one through the germanium atom and the two bridging sulfur atoms, and the second one through the germanium atom and the two non-bridged sulfur atoms. The distribution of the electron density r(r) over the germanium atom and the two non-bridged and bridged sulfur atoms belonging to the same [GeS₄] tetrahedron is illustrated by the electron density maps shown in Figure 6(a) and Figure 6(b), respectively. From the comparison of the contour maps in Figure 6(a) and Figure 6(b), it follows that the maximum of the electron density r(r) is concentrated in the [GeS₄] tetrahedra near the sulfur atom positions. In both planes one can see common r(r) contours covering the electron density maxima on the sulfur and germanium atoms. The only difference is that for the plane passing through the non-bridged sulfur atoms one observes only the contours, common for two sulfur atoms and the same germanium atom, these contours extending from each sulfur atom along only one Ge-S bond line (Figure 6(a)). Mean- while, in the plane containing two bridged sulfur atoms (Figure 6(b)) one can see common contours covering the same bridging sulfur atom of one tetrahedron [GeS₄] and two germanium atoms which belong to two neighboring

tetrahedra. As a result, specific chains of 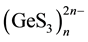are formed, mainly due to the overlap of the electron clouds of the bridging sulfur and germanium atoms.

The common contours, encompassing the maxima of the electron density on the Ge and S atoms, characterize the covalent component of the chemical bond. The deformation of contours towards the germanium and sulfur atoms indicates these directions as being capable of formation of sp³-hybrid bonding orbitals. Besides the covalent component of the chemical bonding, Na₂GeS₃ is characterized by ionic and weak van der Waals bonding components. The ionic component is determined by partial transfer of the charge density from the germanium and sodium atoms to the more electronegative sulfur atoms.

The ionic component of the chemical bond is characterized by charges localized on the atoms themselves, an asymmetry (polarization) of the covalent bond which is revealed in the charge shift at the Ge-S bond, and deformation of electron density contours. Since the distribution of the total charge in one (isolated) chain forms an almost closed shell (Figure 6(c)), this indicates a weak bonding between the neighboring chains. Thus, the spatial distribution of the valence charge density shows that there is strong ion-covalent bond between the germanium and sulfur atoms within the same chain while the atoms belonging to the two neighboring chains interact extremely weakly.

Sodium atoms localized the in inter-chain space, have no common contours of the electron density r(r) with the neighboring anions (sulfur atoms). From the contour maps of the electron density of Na₂GeS₃ crystal (Figure 6(c) and Figure 6(d)) it can be seen that between the endless chains of the [GeS₄] tetrahedra linked by shared vertices there are “tunnels” of minimum electron density, which can serve as channels for the motion of Na⁺ ions. Thus, the weak participation of the sodium atoms in the formation of the electron states (the small charge density around the

Na⁺ ions) and the presence of pass-through “tunnels” between the 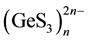infinite chains with a very low

charge density along the c axis indicate the direct participation of sodium ions in the ionic conductivity providing high conductivity of the sodium ions along these channels and, as a consequence high ionic conductivity.

5. Conclusions

Ab initio DFT calculations based on the linear combination of atomic orbitals are performed using the SIESTA software to obtain the electron energy spectrum and the density of states of sodium thiogermanate. Analysis of the total and local partial densities of electronic states of atoms contained in Na₂GeS₃ enabled us to determine the genesis of the components of the electronic states in different subbands of the valence band.

It is determined that Na states give a negligible contribution to the formation of the valence band of crystalline Na₂GeS₃ while the major contribution comes from the 3s-states of sulfur in the valence band lower part as well as hybridized Ge4s-, 4p- and S3р-states in other filled subbands. The top of the valence band of Na₂GeS₃ is formed exclusively by lone pair sulfur states while the bottom of the conduction band results from mixing of free S3p-, Ge4s- and Na3s-, 3p-states.

The calculated total density of electronic states of the crystal is compared with the known experimental X-ray photoelectron spectrum of the glass. The similarity of the shape of the N(E) spectrum of the crystal and the XPS spectrum of glass shows that the short-range order is preserved at the crystal-to-glass transition in sodium thiogermanate.

From the maps of the electron density distribution of Na₂GeS₃ crystal, it follows that the chemical bond between

the cation (germanium) and the anion (sulfur) in the endless chains is of ion-covalent character while

the chains are linked together by weak van der Waals forces. The negligible charge density around Na⁺ ions and the presence of pass-through “tunnels” between the infinite chains provide a considerable mobility of sodium ions along these channels and, as a consequence, high ionic conductivity of the crystal and glass.

References