ABSTRACT

In this paper, we consider the problem for determining an unknown source in the heat equation. The Tikhonov regularization method in Hilbert scales is presented to deal with ill-posedness of the problem and error estimates are obtained with a posteriori choice rule to find the regularization parameter. The smoothness parameter and the a priori bound of exact solution are not needed for the choice rule. Numerical tests show that the proposed method is effective and stable.

Keywords:Ill-Posed Problem; Unknown Source; Heat Equation; Regularization Method; Discrepancy Principle in Hilbert Scales

1. Introduction

In this paper, we consider the following problem for determining the unknown source in the heat equation 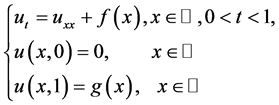[1]:

(1.1)

where 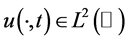represents state variable. Our purpose is to identify the source term 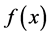from the data. This problem is called the inverse source problem. In practice, the data at 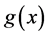are often obtained on the basis of reading of physical instrument. So only the perturbed data 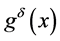can be obtained. We assume that the exact and measured data satisfy

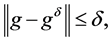(1.2)

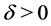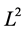where denotes the noisy level, denotes the -norm.

A variety of important problems in science and engineering involve the inverse source problems, e.g. heat conduction, crack identification electromagnetic theory, geophysical prospecting and pollutant detection. These problems are well known to be ill posed (the solution, if it exists, does not depend continuously on the data). Thus, the numerical simulation is very difficult and some special regularization is required. A few papers have presented the mathematical analysis and effective algorithms of these problems. The uniqueness and conditional stability results for these problems can be found in [2-7]. Some numerical reconstruction schemes can be found in [1,8-17].

In [1], the optimal error bound of the problem (1.1) has been obtained and a Fourier regularization method with an a prior parameter choice rule has been presented. It is well known that the ill posed problem is usually sensitive to the regularization parameter and the a priori bound is difficult to be obtained precisely in practice. In [18], we have used a modified Tikhonov regularization method with an a posteriori choice to solve the problem. But the smoothness parameter (which is usually unknown) is needed for that method. In this paper, we will use the method of Tikhonov regularization in Hilbert scales to solve the problem. We will show that the regularization parameter can be chosen by a discrepancy principle in Hilbert scales which is proposed by Neubauer [19]. The smoothness parameter and the a priori bound of exact solution are not needed for the new method.

This paper is organized as follows. In Section 2, we will give the method of Tikhonov regularization in Hilbert scales for the problem (1.1). The choice of regularization parameter and corresponding convergence results will be found in Section 3. Some numerical results are given in Section 4 to show the effectiveness of the new method.

2. The Method of Tikhonov Regularization in Hilbert Scales for the Problem (1.1)

Let 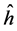denote the Fourier transform of 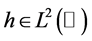defined by

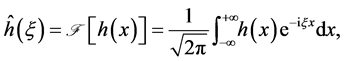(1.3)

and 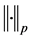denotes the norm in Sobolev space 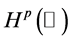defined by

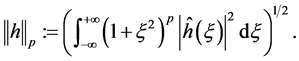(1.4)

When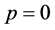, 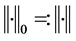denotes the 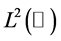norm.

Application of the Fourier transform technique to problem (1.1) with respect to the variable yields the following problem in the frequency space:

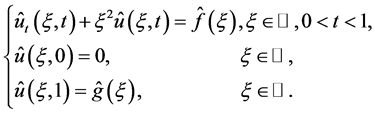(1.5)

It is easy to see that the solution of problem (1.5) is

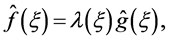(1.6)

where

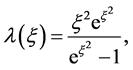(1.7)

or equivalently, the solution of problem (1.1) is given by

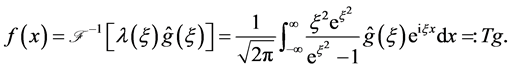(1.8)

It is apparent that the exact data must decay faster than the rate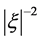. However, in general, the measured data 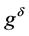does not possess such a decay property. In the following, we apply the Tikhonov regularization method to reconstruct a new function 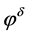from the perturbed data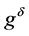. 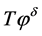will give a reliable approximation of. Before doing that, we impose an a priori bound on the unknown source

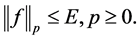(1.9)

In this case, we let 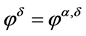be the minimizer of the Tikhonov functional

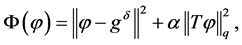(1.10)

where is a regularization parameter and 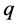is a positive real number. It can be verified that 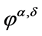is the solution of the following equation [20]

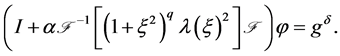(1.11)

So we can get

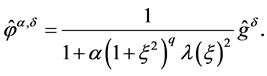(1.12)

That is to say

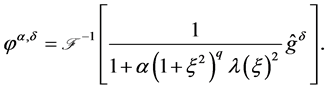(1.13)

By, we can give an approximation of as follows:

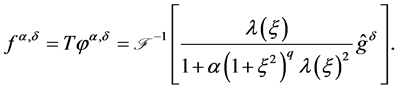(1.14)

Lemma 1 For any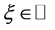, we have

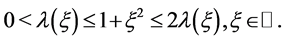(1.15)

Lemma 2 [21] For, we have

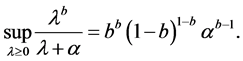(1.16)

Lemma 3

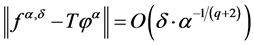(1.17)

where 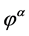is the unique minimizer of (1.10) with instead of.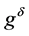

Proof 1 Due to Parseval formula and Lemma 1

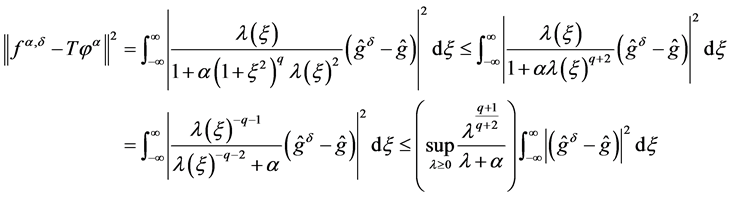(1.18)

The proposition follows by applying (1.16) with replaced by.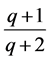

Lemma 4

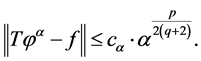(1.19)

where 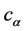is defined by

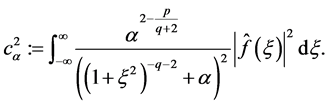(1.20)

Proof 2 With the representation

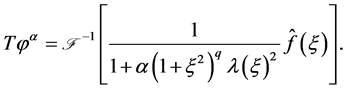(1.21)

and Lemma 1, we have

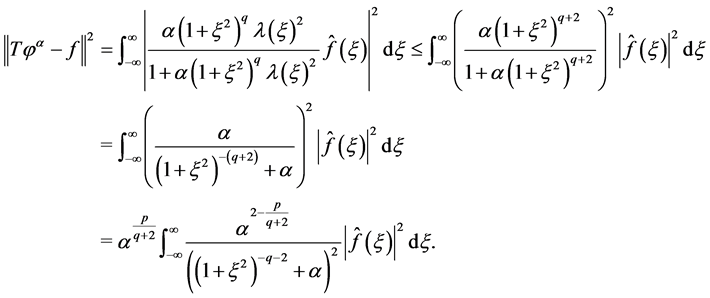(1.22)

3. The Choice of Regularization Parameter α and Convergence Results

For any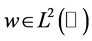, we define

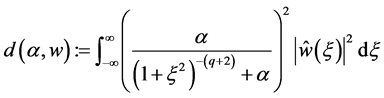(1.23)

It is apparent that the function 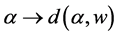is continuous and strictly increasing on 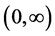and

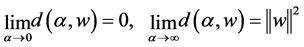(1.24)

So we can get the following lemma.

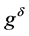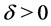Lemma 5 Let, and satisfy (1.2) and

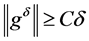(1.25)

for some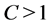. Then there is a unique 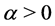such that

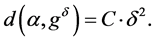(1.26)

In the following, we denote the unique determined in (1.26) by. In the next lemma we consider the behavior of.

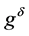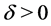Lemma 6 Let, and satisfy (1.2) and (1.25) for a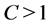, then 1)

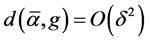(1.27)

2)

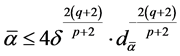(1.28)

where

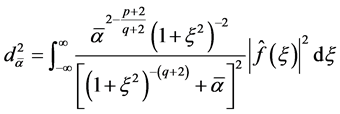(1.29)

Proof 1) Let

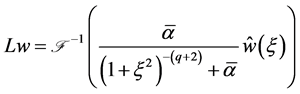(1.30)

then

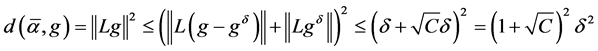(1.31)

2)

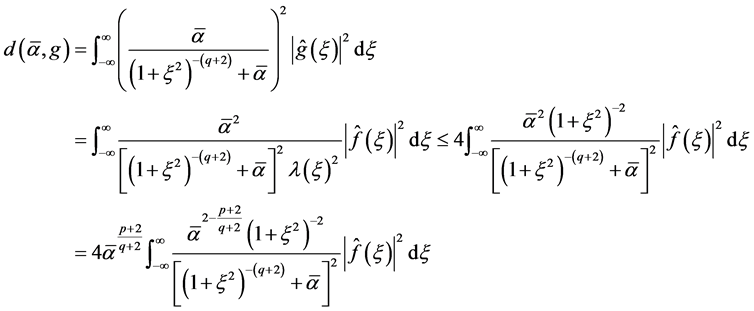(1.32)

The rest follows from 1).

Now we can prove the main result of this paper.

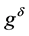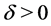Theorem 1 Let, and satisfy (1.2) and (1.25) for a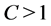,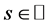. 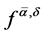is defined by (1.14) with the regularization parameter chosen in (1.26), then

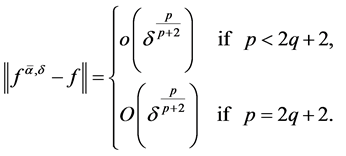(1.33)

Proof 4 With Lemma 3, Lemma 4, Lemma 6, we obtain

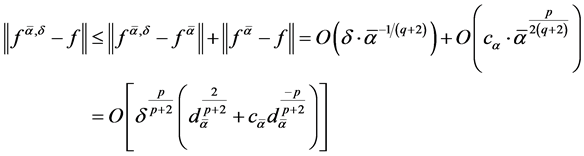(1.34)

Using the Hölder inequality, (1.20) and (1.29) we get 

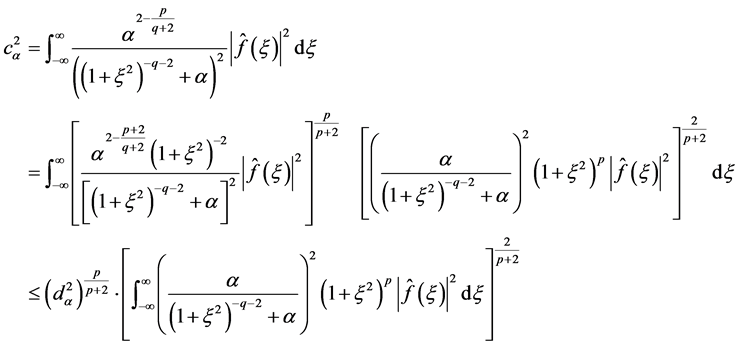(1.35)

Combining (1.34) and (1.35), we obtain

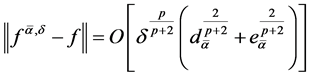(1.36)

where 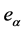is defined by

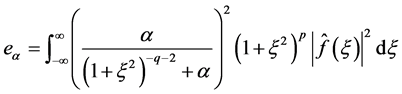(1.37)

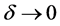Since for and

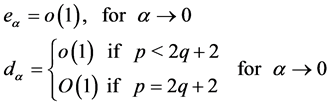(1.38)

The theorem is proved.

4. Numerical Examples

The proposed method can be easily implemented numerically by the fast Fourier transform. We consider the following example.

Example[1] It is easy to verify that the pair of functions

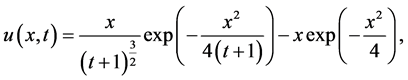(1.39)

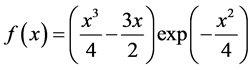(1.40)

is the exact solution of problem (1.1) with data

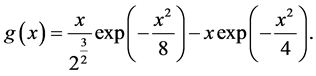(1.41)

Since 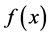approaches zero as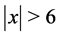, we always fix the interval 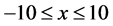in the numerical experiment. Let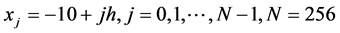. The perturbed data are given by

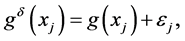(1.42)

where 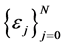are generated by Function 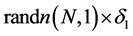in Matlab.

In the following, we present numerical results to check the efficiency of the method. In the following, we present numerical results of some examples to check the efficiency of the method and we will also compare the method (M1) with the method in [18] (M2, notate the approximate function as).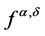

It is obvious that the condition (1.9) holds for any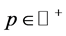. So we have 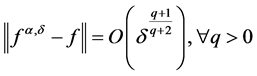for M1 and 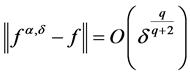for M2. The relative error has been displayed in Table 1, we can see that when

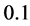decreases from to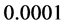, the errors 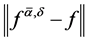become smaller and the results of M1 are better than M2.

5. Conclusion

In this paper, we present a modified Tikhonov regularization method for identifying an unknown source in the heat equation and the theoretical results show that the method is Order optimal. The numerical example also verified the efficiency and accuracy of the method.

Acknowledgements

The project is supported by the National Natural Science Foundation of China (No.11201085).

REFERENCES