Open Journal of Philosophy
Vol.05 No.06(2015), Article ID:58397,7 pages
10.4236/ojpp.2015.56040
From Fusion Algebra to Cold Fusion or from Pure Reason to Pragmatism
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 July 2015; accepted 26 July 2015; published 29 July 2015
“Das Bild Ist Ein Modell der Wirklichkeit”
(Ludwig Wittgenstein―TractatusLogico-Philosophicus)
ABSTRACT
The paper utilizes some fundamental results obtained in the context of topological quantum field theory, hyper finite sub-factors, Turaev-Viro machine and four dimensional fusion algebra to shed mathematical, physical and philosophical light on the major problem of cold fusion reactors. In particular, we develop a picture model for the quantum vacuum by using modern transfinite quantum field theory but also guided by philosophical ideas about the picture of the space of logic and reality.
Keywords:
Fusion Algebra, Topological Quantum Field, Cold Fusion, E-Infinity, the Philosophy of Pure Mathematics, Wittgenstein Picture Theory, William James Pragmatism

1. Introduction
The present work is mainly a continuation of the author’s philosophical thesis that all consistent and correct results obtained in pure mathematics represent correct and consistent facts in the physical world (Figure 1 and Figure 2) [1] [2] . This is particularly true the more we dig deeper and deeper into quantum physics [3] -[36] . The controversy surrounding cold fusion calls for a discussion in the mould of the above. There are many opponents of cold fusion [12] -[15] . However, there are also people of the stature of Nobel Laureate J. Shwinger (Figure 3) who resigned from the American Institute of Physics in protest of the censoring of research on cold fusion in which he strongly believed [14] [20] .
This paper is an attempt at a pure mathematical foundation of cold fusion using four dimensional fusion algebra
Figure 1. The quantum spacetime E-infinity hierarchy [12] [13] . It consists of three main layers [41] -[45] . We have first an infinite number of zero and empty sets with an average bi-dimension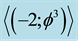 . This is the outer circle representing quantum spacetime. Inside this we have the quantum wave given by the bi-dimension
. This is the outer circle representing quantum spacetime. Inside this we have the quantum wave given by the bi-dimension 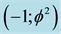 which is the empty set. Finally inside the quantum wave as its inner eye, we have the zero set quantum particle with the bi-dimension
which is the empty set. Finally inside the quantum wave as its inner eye, we have the zero set quantum particle with the bi-dimension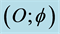 . The above picture also gives us an almost trivial resolution for quantum wave collapse. This is so because to “locate” QP we must somehow penetrate QW. Since QW is the empty set, the slightest touch would convert it to a non-empty set. Consequently QW disappears and metamorphose into QP. This is the observed mysterious state vector reduction which as the reader sees is not mysterious at all within this topological set theoretical picture.
. The above picture also gives us an almost trivial resolution for quantum wave collapse. This is so because to “locate” QP we must somehow penetrate QW. Since QW is the empty set, the slightest touch would convert it to a non-empty set. Consequently QW disappears and metamorphose into QP. This is the observed mysterious state vector reduction which as the reader sees is not mysterious at all within this topological set theoretical picture.
Figure 2. Banach-Tarski sphere decomposition Cantorian spacetime of E-infinity theory that is considered here to model our actual spacetime may be envisaged advantageously as in this artist impression. This is basically a two dimensional projection in which each of the larger balls (circles) are a zero set  representing the quantum particle while the surface (circumference) represents the empty set
representing the quantum particle while the surface (circumference) represents the empty set 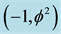 which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set
which in turn represents the quantum wave [1] [17] . This wave is then surrounded by an infinite hierarchy of smaller (fractal) spheres (surfaces), which may be seen as the emptier set , i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value equal
, i.e. the surface of the empty set quantum wave. Remarkably the average set of all zero and empty sets is an expectation value equal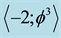 . In other words
. In other words 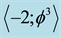 is our quantum spacetime, which is the cobordism of the quantum wave, which in turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that
is our quantum spacetime, which is the cobordism of the quantum wave, which in turn is the cobordism of the quantum particle, floating and propagating with the help of its wave in our Cantorian E-infinity spacetime [1] [2] [10] [11] . It is likewise remarkable that 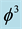 is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime. Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to find first the topological energy density by adding Kaluza-Klein D = 5 to
is simultaneously equal to the topological Casimir force as well as the topological mass of the ordinary energy of spacetime. Thus all matter and energy manifestations in our cosmos are essentially a manifestation of the zero point energy of the vacuum of spacetime. To obtain Einstein maximal energy density we just need to find first the topological energy density by adding Kaluza-Klein D = 5 to 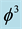 of the spacetime vacuum and find the fractal Kaluza-Klein dimension
of the spacetime vacuum and find the fractal Kaluza-Klein dimension 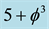 then multiply this with the average Cantorian interval speed of light
then multiply this with the average Cantorian interval speed of light  squared. The result is
squared. The result is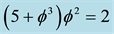 . Inserting in Newton’s kinetic energy one finds
. Inserting in Newton’s kinetic energy one finds 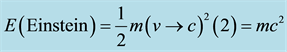 exactly as should be. The preceding explanation amounts to a paradigm shift in physics where the totally empty vacuum of spacetime is taken as fundamental and everything else is derivable from it. To prove this point was a dream of Serbian American inventor N. Tesla who died in 1943 as well as Soviet physicist A. Zakharov. In fact in his later years Nobel Laureate J. Schwinger was a champion of cold fusion [12] which comes very near to our present concept of a Casimir-nano energy reactor [10] [11] . We also stress that we are making tacit use of the Banach-Tarski decomposition theorem as a Schwinger-like source [18] [21] [34] .
exactly as should be. The preceding explanation amounts to a paradigm shift in physics where the totally empty vacuum of spacetime is taken as fundamental and everything else is derivable from it. To prove this point was a dream of Serbian American inventor N. Tesla who died in 1943 as well as Soviet physicist A. Zakharov. In fact in his later years Nobel Laureate J. Schwinger was a champion of cold fusion [12] which comes very near to our present concept of a Casimir-nano energy reactor [10] [11] . We also stress that we are making tacit use of the Banach-Tarski decomposition theorem as a Schwinger-like source [18] [21] [34] .
Figure 3. Julian Schwinger, Nobel Laureate in Physics and an extraordinary proponent of cold fusion. Prof. Schwinger went as far as resigning from the American Physical Society in defence of scientific freedom [12] . In the resignation letter of Prof. Schwinger he lamented what he considered censorship of science exemplified by Editors of famous mainstream journals rejecting papers based upon pretentious and unfair reports by anonymous referees. On the whole Prof. Schwinger was a careful thinker and superior mathematician compared to his colleagues and co-Nobel Prize winner of the same year, the equally extraordinary Richard Feynman. The usual cheap shots like crackpot and old wood or numerologist could never be applied to this extraordinarily intelligent and super rational thinker. By being open minded like he was, Prof. Schwinger may have provoked conventional thinkers because he did not think very highly of the extensive use of Feynman’s diagrams and by introducing an alternative theory to quantum field theory known as source theory [19] which he applied similar to the present work to the Casimir effect. In fact our Banach-Tarski theorem plays in our theory the role of a Schwinger source [18] [21] .
[26] . The author has taken the liberty of indulging in the philosophy of W. James as well as that of Wittgenstein [37] -[39] and the philosophy of pure mathematics although he by no means considers himself to be a specialist in these subjects. However, these subjects are too important to leave only to the specialists [37] -[39] . Although the work is mainly concerned with basic questions in mathematical physics and fundamental technologies related to vital energy gaining problems, we do vacillate among physics [1] -[36] , philosophy [37] -[39] and technology [40] -[45] . Nevertheless in essence we start with philosophy of science [1] and ends with general philosophy [46] -[56] . In fact, we could have started this work by paraphrasing a famous line of Wittgenstein [37] [47] [52] [54] “What (mathematics) fail to express, their application shows. What (mathematics) slur over, their application says clearly”. Here we exchanged Wittgenstein’s original word “signs” by our word “mathematics”. We could also proceed in the spirit of the Tractatus and illustrate the intention of the present short paper with the memorable Wittgenstein’s (see Figure 4) sentences of the breathtaking following quotations [37] :
1) Logical pictures can depict the world.
2) A picture is a model of reality.
3) A picture presents a situation in logical space, the existence and non-existence of states of affairs.
The present paper does in fact present two complimentary pictures in Figure 1 and Figure 2 and we leave it to the reader to judge if these pictures and the accompanying analysis present the complete mental picture needed to grasp the essence of our thesis that without philosophy there can be no fundamental science. In fact, the founder of set theory, G. Cantor, always refers to the foundation of science as “metaphysics”.
Figure 4. Ludwig Wittgenstein is one of the most important philosophers of the twentieth century [47] [52] [54] . His analysis of language and meaning as well as this theory of picture is central to modern philosophy as it was an inspiration for the pre- sent work.
2. Four Dimensional Fusion Algebra for Cold Fusion Nano Reactors
If we follow an admittedly relatively long road from sub-factors to a topological quantum field theory, then our trip will be rewarded by an encounter of the first, second and third type, namely a four dimensional fusion algebra [26] with highly structured golden mean rings flowing in the direction of a cold fusion-Casimir energy type nano reactor [40] -[45] . Having decided to go this road, let us start the journey which we will divide into three main stages. The final result is summarized pictorially in a mathematical philosophical picture shown in Figure 1 and an artistic imaginative but logical picture reproduced in Figure 2.
3. The Four Dimensional Fusion Algebra [26]
The notion of dimensional function was repeatedly encountered in connection with von Neumann-Connes’ work on continuous geometry and more so in noncommutative geometry leading to the bi-dimensions [10] [19]
where 



sion function, which can play a similar important role is that encountered in topological quantum field theory as seen from the view point of the theory of sub-factors. This subject is known as the four dimensional fusion algebra. The dimension function in this case is given by [26]
It is interesting to see that the union of four quasi “Eigenvalues” of the “Eigen function” leads directly to the five dimensional fractal Kaluza-Klein spacetime or equivalently a fractal de Sitter space which is not directly
obtainable from
The Casimir or ordinary energy density is consequently given by [12] [13] [41] -[44]
exactly as reasoned in previous work using different methods. At this point we should maybe recall that the reason for not being able to measure that dark energy is that it is related to the quantum wave as modelled by the
empty set

is what we perceive as wave collapse. For the sake of completeness we should mention the intimate relation between the adjoint matrix of the Coxeter diagram A4 and 4D-fusion algebra [26] . This leads to the obvious conclusion that the same deep relation is present for our most fundamental exceptional Lie symmetry group E8. In turn this link will exist for the sub E8 group, namely E6. We stress however that the above is not valid for various sub groups of E8, notably E7 [26] .
4. The Casimir Energy Density and Relations to Ordinary Energy and Dark Energy Density
This section could just have well been entitled “many names for essentially the same energy density”. To see why let us start with the topological Casimir force acting upon the two Casimir uncharged but perfectly conducting
plates. Since the plates are so close that the nano gap may be regarded as almost an empty set 



time including spin ½ dimensionality and fractal gaps in it. This means 

Now we are used to meeting surprizing results in this field which upon reflection steadily turn out to be not surprizing and this result, which is identical to the density of ordinary energy [19]
belongs to this category of results which we could call ‘wonder and yet no wonder’. The point is that 
i.e.


the energy concentrated at the edge of the universe as per Dvoretzky’s theorem [17] or the accumulation of Casimir energy at the one sided Möbius-like limit of the universe which is essentially the same end result and rationale. We conclude that Casimir energy, ordinary energy and dark energy are different labels for essentially the same physics [40] -[45] . In particular, a little contemplation would immediately reveal that the local nano scale Casimir energy must be simply the Witten T-duality transformation [27] of the large Hubble scale dark energy. We end this section by inviting all those who firmly believe in scientific philosophy to read what J.P. Sartre [50] wrote about Nothingness [56] and contrast this with what we understood from our confrontation with the zero set and the empty set [6] -[15] .
5. Entanglement, Self Entanglement and Intrinsic Entanglement Energy
The fundamental importance of Hardy’s generic quantum entanglement 
where n is the number of entangled quantum particles. Setting n = 2 we find the well known Hardy quantum entanglement probability 

which gives our E-infinity quantum spacetime core Hausdorff dimension 


does not mean P = 0 but gives us an intrinsic topological energy which we recognize as the Casimir topological energy discussed earlier on. It is only when we assume that n is practically infinite that 
6. Just in Case We Are Permitted to Say Something Philosophical
In view of the Vienna circle [47] [54] and as repeatedly mentioned by P. Dirac in informal discussions with Niels Bohr and Werner Heisenberg: “philosophy is the systematic misuse of a nomenclature devised specifically for this purpose” [37] . As witty and penetrating this memorable quotation may be and as justified in certain extreme situations in general, we could not agree with it. In our view theoretical-mathematical physics and pure mathematics are highly successful philosophy that shows the right way to deal with all fields of human endeavour and inquiry. Apart of all that, the author full heartedly agrees with William James, one of the main founders of pragmatic philosophy [38] that a mind that is not permitted to philosophize, i.e. not permitted to love the science of “wisdom” will sink into deep intellectual depression and emotional incomprehensibility [37] -[39] . Thus if the author may be permitted to come to the point of making the above case reasonably acceptable, then he would say that it is impossible to think of any “mechanism” of creation without having an abstract idea first and even if temporal order was not created yet, it is not possible to insist that the act of an abstract idea of ‘being’can only come about with a hot explosion. We have many mechanisms of creation without hot bangs in mathematical marvels like the Banach-Tarski decomposition and the related two dimensional hyperbolic examples [23] . It is clear that von Neumann-Connes’ dimensional function [34] and our way of dealing with four dimensional fusion runs pretty much in the same direction [26] . From all the above we would like to rhetorically ask if the entire universe was created from the totally empty set with fire, why could be not achieve a cold fusion? With this question and the self evident answer, we rest our case.
7. Conclusions
The present paper is a testament to the author’s deep belief that when it comes to deep questions pertaining to quantum physics, then what is pure mathematics and pure scientific philosophy is basically indistinguishable from pure real physics and its pragmatic implications. The paper argues that the implications of von Neumann- Connes’ dimensional function, as well as the dimensional function of 4 dimensional fusion algebra that makes cold fusion a real pragmatic physical possibility [38] .
In conclusion of our conclusion we wish to salute the late Nobel Laureate J. Schwinger (see Figure 3) for his unwavering stance towards the indispensible scientific freedom, which basically makes the present paper as well as many papers before it and hopefully many papers after it by many authors all over the world possible.
Cite this paper
Mohamed S. ElNaschie, (2015) From Fusion Algebra to Cold Fusion or from Pure Reason to Pragmatism. Open Journal of Philosophy,05,319-326. doi: 10.4236/ojpp.2015.56040
References
- 1. El Naschie, M.S. (2015) From Kantian-Reinen Vernunft to the Real Dark Energy Density of the Cosmos via the Measure Concentration of Convex Geometry in Quasi Banach Spacetime. Open Journal of Philosophy, 5, 123-130. http://dx.doi.org/10.4236/ojpp.2015.51014
- 2. El Naschie, M.S. (2014) From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos. Advances in Pure Mathematics, 4, 641-648. http://dx.doi.org/10.4236/apm.2014.412073
- 3. He, J.-H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718. http://dx.doi.org/10.1007/s10773-014-2123-8
- 4. Auffray, J.-P. (2014) Quantum Meteorites: An Extemporaneous Description of the System of the World. Journal of Modern Physics, 6, 878-889. http://dx.doi.org/10.4236/jmp.2015.67092
- 5. Nottale, L. (1996) Scale Relativity and Fractal Spacetime: Application to Quantum Physics, Cosmology and Chaotic Systems. Chaos, Solitons & Fractals, 7, 877-938. http://dx.doi.org/10.1016/0960-0779(96)00002-1
- 6. El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- 7. El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter—A General Physical and Topological Interpretation. Gravitation and Cosmology, 19, 151-155. http://dx.doi.org/10.1134/S0202289313030031
- 8. May, J.P. (1977) E-Infinity Ring Spaces and E-Infinity Spectra. Lecture Notes in Mathematics, Springer, Berlin.
- 9. Witten, E. (1998) D-Branes and K-Theory. Journal of High Energy Physics, 12, 1-35. http://dx.doi.org/10.1088/1126-6708/1998/01/001
- 10. Connes, A. (2000) Noncommutative Geometry Year 2000. In: Alon, N., Bourgain, J., Connes, A., Gromov, M. and Milman, V., Eds., Visions in Mathematics: Geometric and Functional Analysis, Special Volume, Part II, Birkhauser, Basel, 481-599. http://dx.doi.org/10.1007/978-3-0346-0425-3_3
- 11. Penrose, R. (2004) The Road to Reality. Jonathan Cape, London.
- 12. El Naschie, M.S. (2015) Kerr Black Hole Geometry Leading to Dark Matter and Dark Energy via E-Infinity Theory and the Possibility of Nano Spacetime Singularity Reactor. Natural Science, 7, 210-225. http://dx.doi.org/10.4236/ns.2015.74024
- 13. El Naschie, M.S. (2015) The Casimir Topological Effect and a Proposal for a Casimir-Dark Energy Nano Reactor. World Journal of Nano Science & Engineering, 5, 26-33. http://dx.doi.org/10.4236/wjnse.2015.51004
- 14. Schwinger, J. (1994) Cold Fusion Theory: A Brief History of Mine. A Talk Read in an Evening Session b Eugene Mallove at the Fourth International Conference on Cold Fusion ICCF4, Maui, Hawaii, December 1994. Printed Online by Infinity Energy—The Magazine of New Energy Science & Technology (2014-2015). http://www.infinite-energy.com/iemagazine/issue1/colfusthe.html
- 15. Jiang, X.L., Zhou, X.P. and Peng, W.M. (2014) Extraction of Clean and Cheap Energy from Vacuum. Materials for Renewable Energy & Environment, 2, 467-471.
- 16. El Naschie, M.S. (1999) From Implosion to Fractal Spheres. A Brief Account of the Historical Development of Scientific Ideas Leading to the Trinity Test and Beyond. Chaos, Solitons & Fractals, 10, 1955-1965. http://dx.doi.org/10.1016/s0960-0779(99)00030-2
- 17. El Naschie, M.S. (2015) Banach Spacetime-Like Dvoretzky Volume Concentration as Cosmic Holographic Dark Energy. International Journal of High Energy Physics, 2, 13-21. http://dx.doi.org/10.11648/j.ijhep.20150201.12
- 18. El Naschie, M.S. (2005) On 336 Kissing Spheres in 10 Dimensions, 528 P-Brane States in 11 Dimensions and the 60 Elementary Particles of the Standard Model. Chaos, Solitons & Fractals, 24, 337-457. http://dx.doi.org/10.1016/j.chaos.2004.09.071
- 19. El Naschie, M.S. (2014) From E = mc2 to E = mc2/22—A Short Account of the Most Famous Equation in Physics and Its Hidden Quantum Entanglement Origin. Journal of Quantum Information Science, 4, 284-291. http://dx.doi.org/10.4236/jqis.2014.44023
- 20. Schwinger, J. (1975) Casimir Effect in Source Theory. Letters in Mathematical Physics, 1, 43-47. http://dx.doi.org/10.1007/BF00405585
- 21. Finkelstein, D. (1996) Quantum Relativity. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-60936-7
- 22. ‘tHooft, G. (2014) The Cellular Automata Interpretation of Quantum Mechanics. A View on the Quantum Nature of Our Universe, Compulsory or Impossible? http://arxiv.org/abs/1405.1548
- 23. El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Micro Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508. http://dx.doi.org/10.1016/0960-0779(95)00052-6
- 24. El Naschie, M.S. (2009) Wild Topology, Hyperbolic Geometry and Fusion Algebra of High Energy Particle Physics. Chaos, Solitons & Fractals, 13, 1935-1945.
- 25. Gillet, H. (1981) Riemann-Roch Theorem for Higher Algebraic K-Theory. Advances in Mathematics, 40, 203-289. http://dx.doi.org/10.1016/s0001-8708(81)80006-0
- 26. Kodiyalam, V. and Saunder, V. (2001) Topological Quantum Field Theories from Subfactors. Chapman & Hall/CRC, Boca Raton and London.
- 27. Witten, E. (1988) Topological Quantum Field Theory. Communications in Mathematical Physics, 117, 353-386. http://dx.doi.org/10.1007/bf01223371
- 28. Baez, J.C. and Dolan, J. (1988) Higher-Dimensional Algebra III: N-Categories and the Algebra of Opetopes. Advances in Mathematics, 135, 145-206.
- 29. May, J.P. (2009) What Precisely Are E-Infinity Rings and E-Infinity Spectra. http://arxiv.org/abs/0903.2813
- 30. Ketov, S.V. (1995) Conformal Field Theory. World Scientific, Singapore.
- 31. Duplantier, B. and Rivasseau, V., Eds. (2003) Poincaré Seminar 2002. Vacuum Energy—Renormalization. Birkhauser, Basel. http://dx.doi.org/10.1007/978-3-0348-8075-6
- 32. Saller, H. (2006) Operational Quantum Theory I and II. Springer, Heidelberg.
- 33. Milonni, P.W. (1994) The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Academic Press, Boston. http://dx.doi.org/10.1119/1.17618
- 34. Connes, A. and Marcolli, M. (2008) Noncommutative Geometry, Quantum Fields and Motives. American Mathematical Society, Providence and Hindustan Book Agency, New Delhi.
- 35. Stephenson, K. (2005) Introduction to Circle Packing. Cambridge University Press, Cambridge.
- 36. Fried, H.M. (2014) Modern Functional Quantum Field Theory. World Scientific, Singapore. http://dx.doi.org/10.1142/8544
- 37. Wittgenstein, L. (1922) Tractatus Logico-Philosophious, with Introduction by B. Russell. Kegan Paul, Trench, Trubner and. Co., Ltd., London and Harcourt, Brace and Company, Inc., New York.
- 38. James, W. (1911) Some Problems of Philosophy. Longmans, Green, New York.
- 39. Heisenberg, W. (1969) Der Teil und das Ganze. Piper-Verlag, Munich.
- 40. El Naschie, M.S. (2015) Do You Feel with Me That This 21st Century Is the Nano-Tech and Quantum Information Century? Researchgate.net, February 7th, 2015.
- 41. El Naschie, M.S. (2015) The Cantorian Monadic Plasma Behind the Zero Point Vacuum Spacetime Energy. American Journal of Nano Research and Application, 3, 66-70.
- 42. El Naschie, M.S. (2015) A Cold Fusion-Casimir Energy Nano Reactor Proposal. World Journal of Nano Science and Engineering, 5, 49-56. http://dx.doi.org/10.4236/wjnse.2015.52007
- 43. El Naschie, M.S. (2015) A Casimir-Dark Energy Nano Reactor Design—Phase One. Natural Science, 7, 287-298. http://dx.doi.org/10.4236/ns.2015.76032
- 44. El Naschie, M.S. (2015) On a Non-Perturbative Quantum Relativity Theory Leading to a Casimir-Dark Energy Nanotech Reactor Proposal. Open Journal of Applied Sciences, 5, 313-324. http://dx.doi.org/10.4236/ojapps.2015.57032
- 45. El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53.
- 46. Whitehead, A.N. and Russell, B. (1980) Principia Mathematica. Cambridge University Press, Cambridge.
- 47. Storig, H.J. (1969) Kleine Welt-geschichte der philosophie, Volume 1 & 2. Fischer Bücherei, Hamburg.
- 48. Ayer, S.A.J. (1959) Logical Positivism. Greenwood Press, West Port.
- 49. Ayer, S.A.J. (1973) The Central Questions of Philosophy. Penguin Books, Markham.
- 50. Sartre, J.-P. (1968) Die Worter. Rowohlt Verlag, Hamburg.
- 51. Ayer, S.A.J. (1952) Language, Truth and Logic. Dover Publications, New York.
- 52. Wittgenstein, L. (1958) Philosophical Investigations. Basil Blackwell, Oxford.
- 53. James, W. (1907) Pragmatism and Four Essays from the Meaning of Truth. New American Library, New York.
- 54. Schischkoff, G., Ed. (1978) Philosophisches Worterbuch. A. KronerVerlag, Stuttgart.
- 55. Whithead, A.N. (1982) An Enquiry Concerning the Principles of Natural Knowledge. Dover Publications, New York.
- 56. Sartre, J.-P. (1952) Das Sein und das Nichts. Rowohlt Verlag, Hamburg.













