Received 14 February 2015; accepted 3 April 2015; published 13 April 2015

ABSTRACT

Conflicting views had greeted the use of systematic sampling for sample selection and estimation in stratified sampling in terms of the precision of the population mean base on the inherent characteristics of the population. These conflicting views were analyzed using Cochran data (1977, p. 211) [1] . When the population units are ordered, variance of systematic sampling for all possible systematic samples provides equal, non-negative and most precise estimates for all the variance functions considered i.e.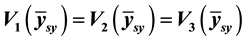, unlike when a single systematic sample is used and when variance of simple random sampling is used to estimate selected systematic samples.

Keywords:

Precision, Systematic Sampling, Stratified Systematic Sampling, Systematic Random Estimator

1. Introduction

Cochran (1977) [1] describes systematic sampling thus: suppose that N units in the population are numbered 1 to N in some order. To select a sample of n units, we take a unit at random from the first k units and every k^th unit thereafter. The selection of the first k^th units determined the whole sample. This is called an every k^th systematic sample.

Murthy (1967) [2] states that systematic sampling is operationally more convenient and at the same time saves time while ensuring equal probability of inclusion of each unit in the sample. He describes technique of systematic sampling as consisting of selecting every k^th unit starting with the unit corresponding to a number r chosen at random from 1 to k, where k is taken as the integer nearest to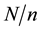. The random number r chosen from 1 to k is known as random start and the constant k is termed the sampling interval.

A sample selected by this procedure is termed a systematic sample with a random start r. Therefore, the value of r determines the whole sample. In other words, this procedure amounts to selecting with equal probability one of the k possible groups of units (samples) into which the population can be divided in a systematic manner.

Same view was expressed by Raj and Chandhok (1998) [3] . They described systematic sampling as a more convenient method of sample selection when the units were serially numbered from 1 to N with the assumption that N = nk, where n is the sample size desired, and k is an integer. A number is taken at random from the numbers 1 to k (using a table of random number/random number generator). Suppose the random number is i, then the sample contains n units with serial numbers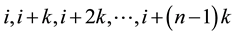. Thus, the sample consists of the first unit selected at random and every k^th unit thereafter. It is therefore called a 1-in-ksystematic sample.

Early studies on the development of theory of systematic sampling was as reported by Murthy (1967, p.134) [2] while Cochran (1977) [1] reported that Madow (1953) [4] had carried systematic sampling to its logical conclusion with his recommendation that a systematic sample be chosen at or near the center of the interval, i.e. instead of starting the sequence by a random number chosen between 1 and k, we take the starting number as 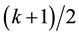if k is odd and eithe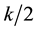r or 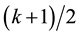if k is even.

Guatschi (1957) [5] investigated the efficiency of single and multiple random start systematic sampling in population exhibiting different characteristics and reported that when the population was in random order and for a population with linear trend, while in a periodic population

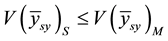equality results when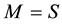. He, however, concluded that, with an exponential correlelo-

gram, single random start 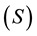was more precise than multiple random starts.

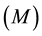Murthy (1967) [2] , Cochran (1977) [1] , Raj and Chandhok (1998) [3] and Okafor (2002) [6] have all mentioned that systematic sampling can be looked into in another way in relation to cluster sampling. They explained that in a population with N = nk, the population can be divided into k large systematic sampling units each containing n of the original n units. The operation of choosing a randomly located systematic sample is just the operation of choosing one of these large sampling units at random. Thus, systematic sampling amounts to selecting of a simple random sample of one cluster unit from a population of k cluster units with probability.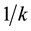

Thus for a population of Y units 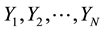divided into k possible clusters, the k possible samples with their means are as shown in Table 1 below.

Considering all the k possible samples, the sample mean 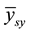is obtained thus:

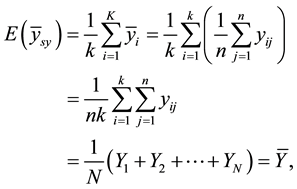(1)

Showing that when N = nk, is unbiased for. It should also be noted that systematic sampling has no repetition of sampling unit and therefore related to simple random sampling without replacement (SRSWOR).

Above is the applicable systematic sampling in a situation in which N = nk. In practice, it is common to encounter situations in which, and various suggestions have been made on how to handle such a situation.

2. Approaches When

2.1. Circular Systematic Sampling (CSS)

Lahiri (1952) [7] suggests the Circular Systematic Sampling (CSS) which consists of taking a random number from 1 to N and selecting the unit corresponding to this random start and every unit thereafter in a cyclical manner until a sample of n units is obtained, k being the nearest integer to, i.e. If r is a random number selected from 1 to N, the sample consists of the units corresponding to the number.

(2)

for

It implies from CSS, therefore, that the usual procedure of selecting a random start r from 1 to k and including in the sample the units corresponding to for reflected above may be termed Linear Systematic Sampling (LSS).

2.2. Murthy’s Approach

Murthy (1967) [2] suggested that when, i.e., the population units N cannot be divided into k clusters of equal size, therefore we choose the interval k to be the nearest integer to resulting in which may not necessarily be equal to n, the required sample size. He stated further that if, if q and were the quotient and remainder obtained respectively on dividing, then, N can be written as and the sampling interval k can be taking as:

Then, the units’ that can be expected in the sample would be given by:

This approach is suitable in situations in which the sample size n is not fixed or predetermined and the sampler is free to adjust the sample to suit the above application. Therefore, Murthy’s approach to handle is not suitable for fixed sample size or when stratum sample sizes are determined using the standard procedures for allocating samples into the strata.

2.3. Fractional Interval Approach

Another approach when is the use of fractional interval reported by Murthy (1967) [2] . This approach called for taking as k without rounding it off to the nearest integer, i.e., the unit is selected in the sample if for any. It is equivalent to associating different numbers with each unit such that the first gets the number 1 to n, the second gets from to 2n and so on and thus selecting units corresponding to a LSS sample of n numbers selected from 1 to Nn with N as the sampling interval. This approach involves a long process of iteration to satisfy the equation; hence it wastes time.

2.4. New Partially Systematic Sampling (NPSS)

Leu and Tsui (1996) [8] developed the New Partially Systematic Sampling (NPSS) in order to derive an unbiased estimator of the variance of systematic sampling. The population size N need not be a multiple of sample size n; therefore, it is a suitable procedure when. The procedure entails selection of SRS of size a and the remaining sample of size (n-a) systematically, these samples are combined to derive an unbiased estimate of. Thus, NPSS combines SRS with systematic sample to obtain its estimates thereby deviating from the objective of this study as we intend to observe performances when systematic sampling is employed as a choice scheme within strata and not when SRS is combined with systematic samples.

2.5. Remainder Linear Systematic Sampling (RLSS)

Also reviewed in this section is Remainder Linear Systematic Sampling (RLSS) due to Chang and Huang (2000) [9] . This procedure is a modification of the LSS. It is developed for situation when, and depends only on the remainder. It involves dividing the population into two strata, the sampling interval k is taken as the nearest integer to such that, where r is the remaining population units, where; N, n, k, and rare integers. When the remainder r is zero, the procedure reduces to LSS. Procedures for the RLSS are:

a) Divide the population units into two strata with the first stratum containing the front units and second stratum housing the remaining units. From stratum I, a random start is selected from the interval 1 to k and every units thereafter, from the group of units forming stratum I. Thus samples from stratum I contained in a sample space are:

;

b) From stratum II, random start is taken from interval 1 to, starting with units and every units thereafter from the r group forming the second stratum. Samples from stratum II are contained in the sample space are:

Sample of size n is the combination of and units.

Therefore, in stratified systematic sampling when, competing methods are: CSS, NPSS, and RLSS. Due to its greater efficiency over the CSS and NPSS as reported by Chang and Huang (2000) [9] , RLSS was used by Kareem et al (2015) [10] in stratum where. The mean and variance of RLSS is as given below (see relation 2.2 and 2.3, p. 251 of Chang and Huang (2000) [9] ).

3. Estimation Procedures in Systematic Sampling

Estimation of the population mean of a systematic sample over all possible samples is as given by relation (1). For the variance of the population mean, Murthy (1967) [2] , while assuming for a sample of size n and k sampling interval, states that there are k possible samples and be the sample mean of possible sample. The sampling variance of the systematic sample is given as:

(3)

where

Equivalent to

It is simplified as

where is the sum of systematic sample in the group, is the variate of the systematic sample.

Note that is the population variance of SRS and can be written as the sum of

and, which are the between and the within sample variances, respectively.

Therefore which is can be expressed as

(4)

where,.

Other expressions for the estimation of variance of the mean of systematic samples by various authors are reported by Murthy (1967, Section 5.8, pp. 153-155) [2] and Cochran (1977, pp. 213-226) [1] . Cochran, however, remarked “that no dearth of formulae for the estimated variance, but all appeared to have limited applicability”.

On the efficiency of systematic sampling in relation to other sampling scheme, literature agreed that efficiency of systematic sampling was strongly anchored on the arrangement of the population units. Cochran (1977) [1] stated that it greatly depended on the properties of the population. For some population, systematic sampling is extremely precise and for others, SRS is more precise than systematic sampling, not even with increase in sample size n. Thus, it is difficult to give general advice about the situation in which systematic sampling is to be recommended. However, the knowledge of the population structure is necessary for its most effective use.

Same view was expressed by Murthy (1967) [2] , that a good arrangement of the population units may yield a better estimate while a bad arrangement may lead to inefficient estimate and therefore, warned that one had to be careful with the use of systematic sampling and to ensure first, that the existing arrangement did not lead to inefficient estimates before using it. One way suggested is to ensure that the units are arranged either in increasing or decreasing order and this directly suits our investigation in this study, since application of methods of strata construction requires that the population units be arranged in order of magnitude to avoid overlapping of units.

Cochran (1977) [1] stated that several formulae had been developed for. Three of such formulae given by Cochran under the assumption that and could be applied to any kind of cluster sampling in which the clusters contain n elements, and the sample consists of one cluster, are stated below.

1) The variances of the mean of systematic sample given by Cochran are:

(5)

where

(6)

This can further be expressed as

which is the weighted variance over all possible systematic samples generated by random start. It implies therefore from relation (4)

(4)

while

hence, relation (5) above.

2) The second one is given as

(7)

where is the correlation coefficient between pairs of units that are in the same systematic sample, other references referred to it as intra-class correlation coefficient and denoted by

where the numerator is averaged overall distinct pairs, and the denominator over all N values of. Since the denominator is, this gives

(8)

The two expressions of above are expressed in terms of, hence it relates to the variance of SRS.

3) The third is expressed in terms of variance of stratified random sample in which the strata are composed of the first k units, the second k units and so on.

The subscript j in denotes the stratum and the stratum mean is written as.

(9)

where

This is the variance among units that lie in the same stratum. The divisor is used because each of the strata contributes degrees of freedom and

This quantity is the correlation between the deviations from the stratum means of pairs of units that are in the same systematic sample.

(10)

It implies therefore from relation (9) above that a systematic sample has the same precision as that of a stratified random sampling sample with one unit per stratum if, thus relation (9) reduces to

(11)

Thus, we have examined systematic sampling in terms of procedure and estimation process. But our concern is taking a systematic sample of fixed sample size n from each stratum for estimation purpose.

3.1. Estimation in Stratified Systematic Sampling

Much have been said in Section 2 on the significance of the arrangement of the population units on the precision, while Cochran (1977, p. 208) [1] has given a corollary that the mean of a systematic sample will be more precise than that of SRS if and only if, where is the weighted variance of all possible systematic samples as defined by relation (6) above and is the variance of the population mean.

Notations

Cochran (1977, p. 91) [1] has stated that expressions for the mean and variance of stratified sampling applied generally to all classes of stratified sampling and are not restricted to stratified random sampling. Therefore, all notations in Cochran (1977, p. 90) [1] are also valid for stratified systematic sampling.

The subscript h denotes the stratum and i the unit within the stratum.

The subscript “sy” in this section denotes systematic sample.

(12)

is the mean of systematic sample in stratum h, equivalent to relation (1).

(13)

is the population mean of the stratified systematic sample.

(14)

is the variance of stratified systematic samples in stratum h when.

Therefore, variance of systematic samples given by Cochran in relation (5) above when, is adopted for our sample estimation and modified for the stratified systematic samples as shown in relation (14) above. However, it should be noted that each of, , and would yield the same estimates when.

(15)

is the variance of the population mean of stratified systematic samples.

(16)

is the MSE of the population mean of stratified systematic samples.

The mean and the variance of RLSS are given below (see relation 2.2 and 2.3, p. 251 of Chang and Huang (2000) [9] ).

(17)

(18)

To suite our applications, expression (17) and (18) are modified as follows:

(19)

(20)

It should be noted that that expressions and in relation (20) are equivalent to relation (3) above, i.e..

3.2. Empirical Investigation

Systematic samples are easy to draw and to execute but may not be simple in term of estimation as there are competing estimators. This drew our attention for an empirical investigation to ensure the right choice of estimator in the face of conflicting reports. Murthy (1967, section 5.8, p. 153) [2] stated that “it is not possible to estimate unbiasedly the variance of the population mean and total on the basis of a single sample, but it is possible to build up some biased but useful variance estimators on the basis of systematic samples”. Same view was expressed by Mendenhall et al. (1971, p. 151) [11] that “an unbiased estimate of cannot be obtained using data from only one systematic sample and that for random population, systematic sampling is equivalent to SRS”, i.e. is approximately equal to. This is referred to as conservative estimator of by them, but referred to as Systematic Random Estimator (SRE) in this study, i.e. when is used to estimate.

Raj and Chandhok (1998) [3] stated that “when units are deliberately ordered, the formula for estimating variance of SRS will not apply to systematic sampling”. However, Cochran (1977, p. 227) [1] stated that if there were many strata, one systematic sample can be used in most of them.

In view of the above, the question is: should a single systematic sample be used to estimate or all possible systematic samples? To reach a conclusion, we explore Table 8.3, p. 211 of Cochran (1977) [1] . When all possible systematic samples are considered, , as obtained by Cochran.

Empirical investigation reveals that when we select a single systematic sample, the result is as shown in Table 2 below.

Since the efficiency of systematic sampling depends on the arrangement of the population units, an attempt is also made to rearrange Cochran (1977) [1] data (Table 8.3, p. 211), in order of magnitude; same sample of size was taking, and. With this arrangement, for all possible systematic samples our estimates are:

while and.

Table 3 below gives the estimates for single systematic samples when the units are arranged in order of magnitude before sample selection.

4. Conclusion

This analysis brings to the lime light the caution by Murthy (1967, p. 145) [2] in the application of systematic sampling that “one has to be careful in using systematic sampling and should at least ensure that the existing arrangement do not lead to inefficient estimates”. From the empirical investigation, it could be observed that when population units are arranged in order of magnitude, a more precise estimate is obtained for and when compared with the use of SRS estimator. It also reveals that, even when units are not in order of magnitude, it may be more precise than that of SRS, i.e. as shown in Table 2. Furthermore, while for all possible systematic samples, this is not true for single systematic samples as and in some instances reporting negative variances as

*In Table 2, g₅ indicates the center for systematic sample estimates when Madow’s procedure is used while the subscript i = 1, ・・・, k = 10 is the random start in the interval 1 to 10.

*In Table 3, g₅ indicates the center for systematic sample estimates when Madow’s procedure is used while the subscript i = 1, ・・・, k = 10 is the random start in the interval 1 to 10.

shown in Table 2 and Table 3 above. Therefore, when systematic sampling is the choice design within strata, estimates for all possible systematic samples should be used and the sampling units arranged in order of magnitude within the stratum. Kareem et al. (2015) [10] used this procedure and reported higher efficiency of systematic sampling within stratum over the popularly used SRS. It is hereby recommended that given by Cochran (1977) [1] should be used for estimation purpose when and that of Chang and Huang (2000) [9] when when systematic sampling is employed within strata.

References