Open Journal of Microphysics
Vol.2 No.3(2012), Article ID:21693,13 pages DOI:10.4236/ojm.2012.23005
Fractal Approximation of Motion and Its Implications in Quantum Mechanics
1Physics Department, Faculty of Machine Manufacturing and Industrial Management, “Gheorghe Asachi” Technical University, Iasi, Romania
2Lasers, Atoms and Molecules Physics Laboratory, University of Science and Technology, Lille, France
3Physics Department, “Al. I. Cuza” University, Iasi, Romania
4Department of Natural and Synthetic Polymers, Faculty of Chemical Engineering and Environmental Protection, “Gheorghe Asachi” Technical University, Iasi, Romania
Email: m.agop@yahoo.com
Received February 20, 2012; revised April 15, 2012; accepted May 10, 2012
Keywords: Fractals; Quantum Mechanics; Gravitational Models
ABSTRACT
Inconsistencies of some standard quantum mechanical models (Madelung’s, de Broglie’s models) are eliminated assuming the micro particle movements on continuous, but non-differentiable curves (fractal curves). This hypothesis, named by us the fractal approximation of motion, will allow an unitary approach of the phenomena in quantum mechanics (separation of the physical motion of objects in wave and particle components depending on the scale of resolution, correlated motions of the wave and particle, i.e. wave-particle duality, the mechanisms of duality, by means of both phase wave-particle coherence and wave-particle incoherence, the particle as a clock, particle incorporation into the wave and the implications of such a process). Moreover, correspondences with standard gravitational models (Einstein’s model, string theory) can be also distinguished.
1. Introduction
We perform a critical analysis of some quantum mechanical models such as the hydrodynamic model (Madelung’s model), de Broglie’s theory of double solution etc., specifying both mathematical and physical inconsistencies that occur in their construction.
These inconsistencies are eliminated by means of the fractal approximation of motion (physical objects moving on continuous and non-differentiable curves, i.e. fractal curves) developed in the framework of Scale Relativity (SR) [1-7]. The following original results are obtained: 1) Separation of the physical motion of objects in wave and particle components depending on the scale of resolution (differentiable as waves and non-differentiable as particles)—see Sections 5-7; 2) Correlated motions of the wave and particle (wave-particle duality)—see Section 8; 4) The mechanisms of duality (in phase wave-particle coherence, Sections 9 and 10; and 5) Wave-particle incoherence, see Section 11; 6) The particle as a clock, its incorporation into the wave and the implications of such a process—see Sections 12 and 13.
The original results of this work are published in references [8-12]. Explicitly, Eulerian’s approximation of motions on fractal curves is presented in [11,12], the hydrodynamic model in a second order approximation of motion in [8], wave-particle duality for “coherent” fractal fluids with the explanation of the potential gap in [9], the physical self-consistence of wave-particle duality in various approximations of motion and for various fractal curves in [11,12]. A unitary treatment of both the problems listed above and their various mathematical and physical extensions are developed in [10].
2. Hydrodynamic Model of Quantum Mechanics (Madelung’s Model)
Quantum mechanics is substantiated by the Schrődinger wave equation [13-16]
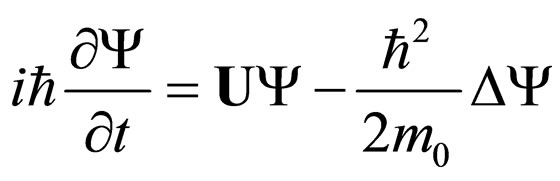 (1)
(1)
where 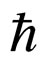 is the reduced Planck’s constant,
is the reduced Planck’s constant, 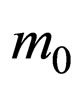 the rest mass of the test particle, U the external scalar field and
the rest mass of the test particle, U the external scalar field and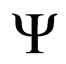 the wave-function associated to the physical system. This differential equation is linear and complex.
the wave-function associated to the physical system. This differential equation is linear and complex.
Starting from this equation, Madelung [17,18] constructed the following model. One separates real and imaginary parts by choosing 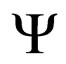 of the form:
of the form:
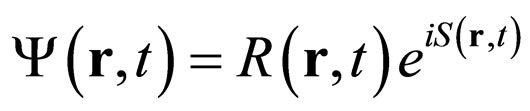 (2)
(2)
which induces the velocity field:
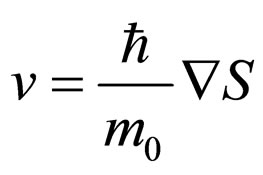 (3)
(3)
and the density of the probability field:
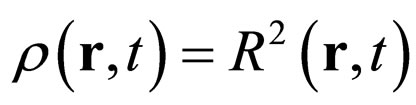 (4)
(4)
Using these fields one gets the hydrodynamic version of quantum mechanics (Madelung’s model)
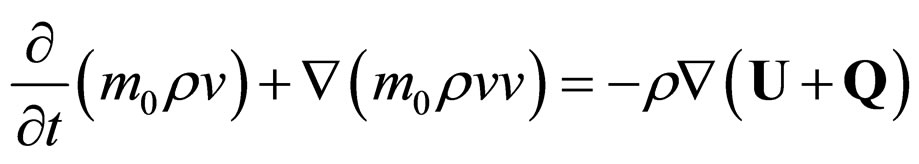 (5)
(5)
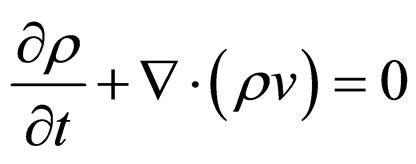 (6)
(6)
where
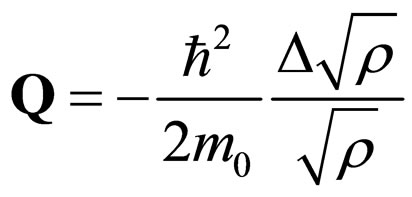 (7)
(7)
is called the quantum potential. Equation (5) corresponds to the momentum conservation law and Equation (6) to the conservation law of the probability’s density field (quantum hydrodynamics equations).
We have the following:
1) Any micro-particle is in constant interaction with an environment called “sub-quantum medium” through the quantum potential Q;
2) The “sub-quantum medium” is identified with a non-relativistic quantum fluid described by the equations of quantum hydrodynamics. In other words, the propagation of the Ψ field from wave mechanics is replaced by a fictitious fluid flow having the density 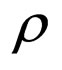 and the speed v, the fluid being in a field of forces
and the speed v, the fluid being in a field of forces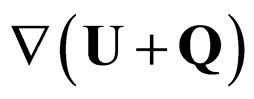 . Moreover, the following model of particle states [19-26], Madelung type fluid in “interaction” with its own “shell” (there is no space limitation of the fluid, though of the particle).
. Moreover, the following model of particle states [19-26], Madelung type fluid in “interaction” with its own “shell” (there is no space limitation of the fluid, though of the particle).
3. De Broglie’s Theory of Double Solution. The Need for Introducing the Model of Bohm and Vigier
One of the key observations that de Broglie left in the development of quantum mechanics, is the difference between the relativistic transformation of the frequency of a wave and that of a clock’s frequency [27-32]. It is well known that, if 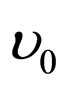 is the frequency of a clock in its own framework, the frequency conferred by an observer who sees it passing with the speed
is the frequency of a clock in its own framework, the frequency conferred by an observer who sees it passing with the speed 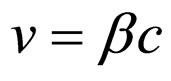 is
is
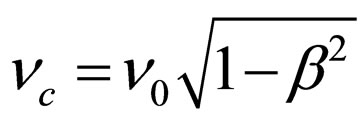
This is what is called the phenomenon of “slowing down of horologes”. This phenomenon takes place due to the relative motion of horologes. On the contrary, if a wave within a certain reference system is a stationary one, with frequency 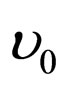 and is noticed in a reference system animated with speed
and is noticed in a reference system animated with speed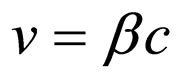 , as compared with the first one, it will appear as a progressive wave that propagates in the sense of the relative motion, with frequency
, as compared with the first one, it will appear as a progressive wave that propagates in the sense of the relative motion, with frequency
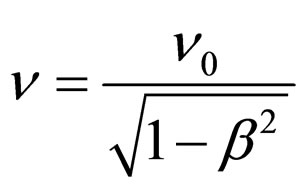
and with the phase speed
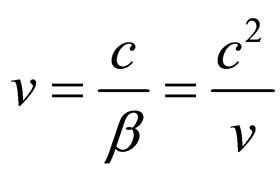
If the corpuscle, according to relation W = hv, is given an internal frequency
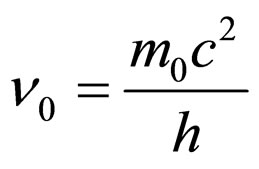
and if we admit that within the appropriate system of the corpuscle the associated wave is a stationary one, with frequency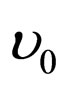 , all the fundamental relations of wave mechanics and in particular
, all the fundamental relations of wave mechanics and in particular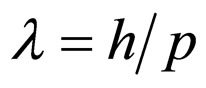 , in which p is the impulse of the corpuscle, are immediately obtained from the previous relations.
, in which p is the impulse of the corpuscle, are immediately obtained from the previous relations.
Since de Broglie considers that the corpuscle is constantly located in the wave, he notices the following consequence: the motion of the corpuscle has such a nature that it ensures the permanent concordance between the phase of the surrounding wave and the internal phase of the corpuscle considered as a small horologe. This relation can be immediately verified in the simple case of a corpuscle in uniform motion, accompanied by a monochromatic plain wave. Thus, when the wave has the general form
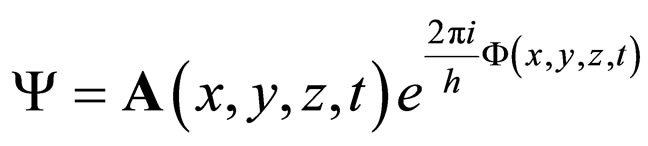
in which A and Φ are real, the phase concordance between the corpuscle and its wave requires that the speed of the corpuscle in each point of its trajectory be given by the relation
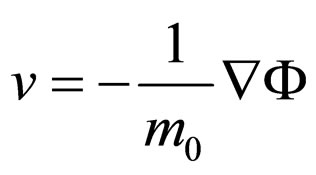
Nevertheless it was not enough to superpose the corpuscle with the wave, imposing it to be guided by the propagation of the wave: the corpuscle had to be represented as being incorporated in the wave, i.e. as being a part of the structure of the wave. De Broglie was thus directed to what he himself called the theory of “double solution”. This theory admits that the real wave is not a homogeneous one, that it has a very small area of high concentration of the field that represents the corpuscle and that, besides this very small area, the wave appreciably coincides with the homogeneous wave as formulated by the usual wave mechanics.
The phenomenon of guiding the particle by the surrounding wave field results from the fact that the equations of the field are not linear ones and that this lack of linearity, that almost exclusively shows itself in the corpuscular area, correlating the motion of the particle with the propagation of the surrounding wave [30-33].
Nevertheless there is a consequence of “guidance” upon which we should insist. Even if a particle is not submitted to any external field, if the wave that surrounds it is not an appreciably plain and monochromatic one (therefore if this wave has to be represented through a superposition of monochromatic plain waves) the motion that the guidance formula imposes is not rectilinear and uniform. The corpuscle is subjected by the surrounding wave, to a force that curves its trajectory: this “quantum force” equals the gradient with the changed sign of the quantum potential Q given by (7). Therefore, the uniform motion of the wave has to be superposed with a “Brownian” motion having random character that is specific to the corpuscle.
Under the influence of Q, the corpuscle, instead of uniformly following one of the trajectories that are defined by the guidance law, constantly jumps from one of these trajectories to another, thus passing in a very short period of time, a considerably big number of sections within these trajectories and, while the wave remains isolated in a finite area of the space, this zigzag trajectory hurries to explore completely all this region. In this manner, one can justify that the probability of the particle to be present in a volume element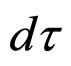 of the physical space is equal to
of the physical space is equal to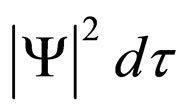 . This is what Bohm and Vigier did in their statement: therefore they showed that the probability of repartition in
. This is what Bohm and Vigier did in their statement: therefore they showed that the probability of repartition in 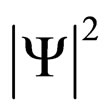 must take place very quickly. The success of this demonstration must be correlated with the characteristics if “Markov’s chains” [19,34-36].
must take place very quickly. The success of this demonstration must be correlated with the characteristics if “Markov’s chains” [19,34-36].
4. Comments
In his attempt to built the theory of the double solution, de Broglie admits certain assertions [27-32]: 1) The frequency of the corpuscle that is assimilated to a small horologe must be identified with the frequency of the associated progressive wave; 2) The coherence of the inner phase of the corpuscle-horologe with the phase of the associated wave; 3) The corpuscle must be “incorporated” into the progressive associated wave through the “singularity” state. Thus, the motion of the corpuscle “correlates” with the propagation of the associated progressive wave. Nevertheless, once we admit these statements, de Broglie’s theory does not answer a series of problems, such as, for example: 1) What are the mechanisms through which either the wave feature or the corpuscular one impose, either both of them in the stationary case as well as in the non stationary one? 2) The limits in the wave-corpuscle system of the corpuscular component as well as the wave one and their correspondence; 3) How is the “solidarity” between the motion of the corpuscle and the one of the associated progressive wave naturally induced? 4) What are the consequences of this “solidarity”? Others discrepancies are mentioned in [27- 32].
Moreover, Madelung’s theory [17,18] brings new problems. How can we built a pattern of a corpuscle (framework + Madelung liquid) endlessly extended in space?
Here are some of the “drawbacks” of the patterns in Sections 2 and 3 which we shall analyze and remove by means of introducing the fractal approximation of the motion.
5. The Motion Equation of the Physical Object in the Fractal Approximation of Motion. The Eulerian Separation of Motion on Resolution Scales
The fractal approximation of motion refers to the movement of physical objects (wave + corpuscle) on continuous and non differentiable curves (fractal curves). This approximation is based on the scale Relativity theory (RS) [1-7]. Thus, the fractal differential operator can be introduced
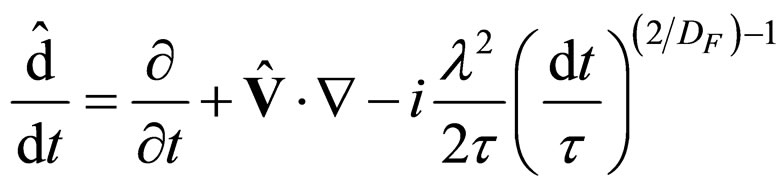 (8)
(8)
where  is the complex speed field
is the complex speed field
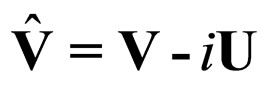 (9)
(9)
λ is the scale length, dt is the temporary resolution scale, 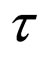 is the specific time to fractal-non fractal transition, and DF is the arbitrary and constant fractal dimension. Regarding the fractal dimension, we can use any of Hausdorff-Bezicovici, Minkowski-Bouligand or Kolmogoroff dimensions, etc. [3,5-7,36-46]. The only restriction refers to the maintaining of the same type of fractal dimension during the dynamic analysis. The real part of the speed field
is the specific time to fractal-non fractal transition, and DF is the arbitrary and constant fractal dimension. Regarding the fractal dimension, we can use any of Hausdorff-Bezicovici, Minkowski-Bouligand or Kolmogoroff dimensions, etc. [3,5-7,36-46]. The only restriction refers to the maintaining of the same type of fractal dimension during the dynamic analysis. The real part of the speed field  is differentiable and independent as compared with the resolution scale, while the imaginary scale
is differentiable and independent as compared with the resolution scale, while the imaginary scale is non differentiable (fractal) and depends on the resolution scale.
is non differentiable (fractal) and depends on the resolution scale.
Now we can apply the principle of scale covariance by substituting the standard time derivate 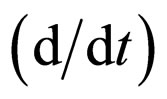 with the complex operator
with the complex operator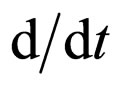 . Accordingly, the equation of fractal space-time geodesics (the motion equation in second order approximation, where second order derivates are used) in a covariant form:
. Accordingly, the equation of fractal space-time geodesics (the motion equation in second order approximation, where second order derivates are used) in a covariant form:
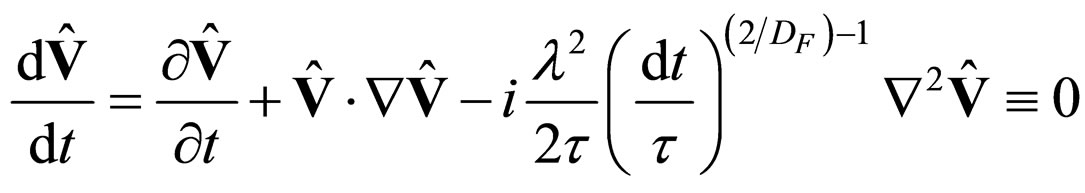 (10)
(10)
This means that the sum of the local acceleration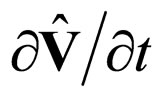 , convection
, convection 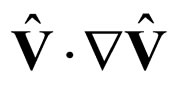 and “dissipation”
and “dissipation” 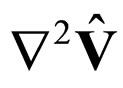 reciprocally compensate in any point of the arbitrarily fractal chosen trajectory of a physical object.
reciprocally compensate in any point of the arbitrarily fractal chosen trajectory of a physical object.
Formally, (10) is a Navier-Stokes type equation, with an imaginary viscosity coefficient,
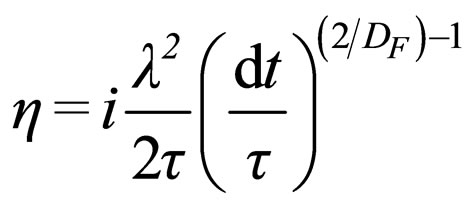 (11)
(11)
This coefficient depends on two temporary scales, as well as on a length scale. The existence of a pure imaginary structured coefficient specifies the fact that “the environment” has rheological features (viscoelastic and hysteretic ones [47-49].
For
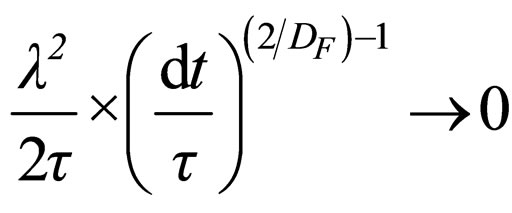 (12)
(12)
Equation (10) reduces to Euclidian form [10-12]:
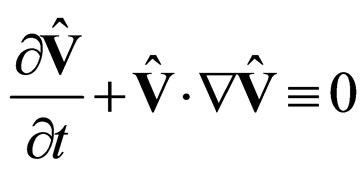 (13)
(13)
and, hence, separating the real part from the imaginary one
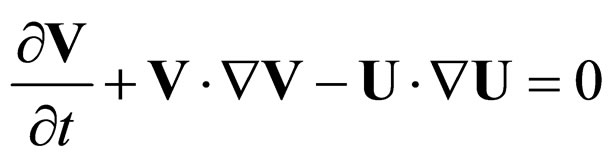 (14a)
(14a)
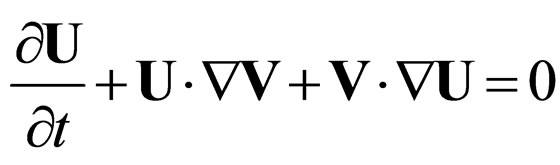 (14b)
(14b)
Equation (14a) corresponds to the law of the impulse conservation at differentiable scale (the undulatory component), while (14b) corresponds to the same law, but at a non differentiable scale (corpuscular component). As we will later show, in the case of irrotational movements (14) it will be assimilated to the law of mass conservation.
6. Rotational Motions and Flow Regimes of a Fractal Fluid
For rotational motions, 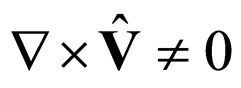 relation (10) with (9) through separating the real part from the imaginary one, i.e. through separating the motions at a differential scale (undulatory characteristic) and non differential one (corpuscular characteristic), results [10].
relation (10) with (9) through separating the real part from the imaginary one, i.e. through separating the motions at a differential scale (undulatory characteristic) and non differential one (corpuscular characteristic), results [10].
 (15a)
(15a)
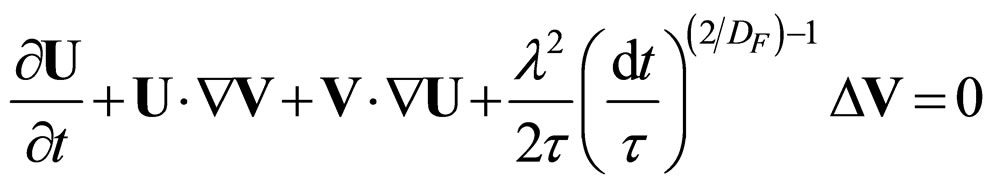 (15b)
(15b)
According to the operator relations
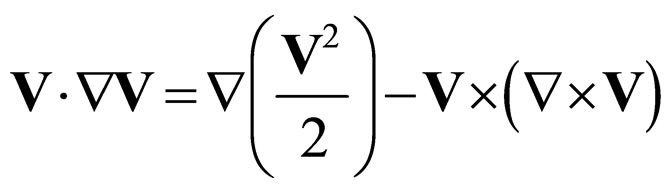 (16a)
(16a)
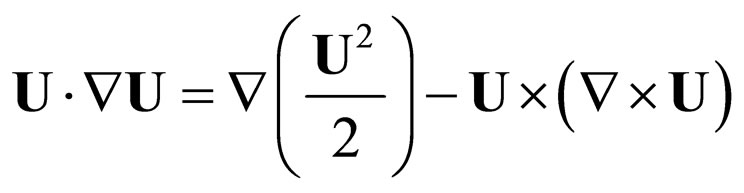 (16b)
(16b)
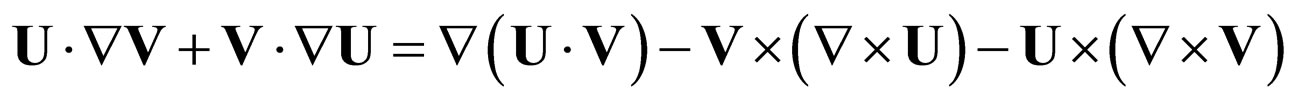 (16c)
(16c)
Equations (15) take equivalent forms
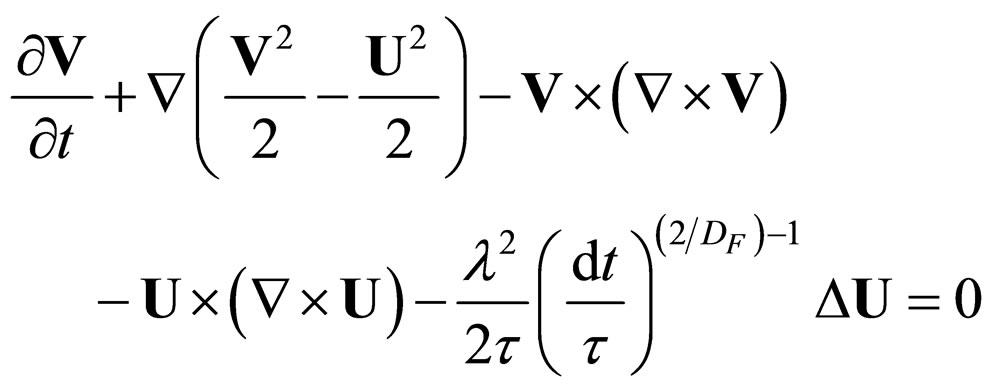 (17a)
(17a)
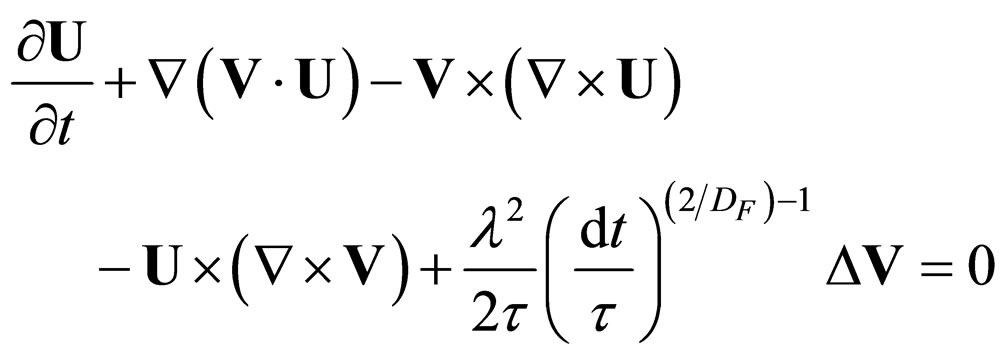 (17b)
(17b)
We can now characterize the flow regimes of the fractal fluid at different scales, using some classes of Reynolds numbers. At a differential scale we have
 (18)
(18)
 (19)
(19)
with
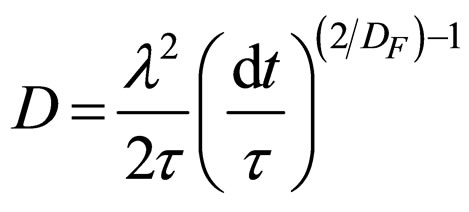 (20)
(20)
and at nondifferential scale.
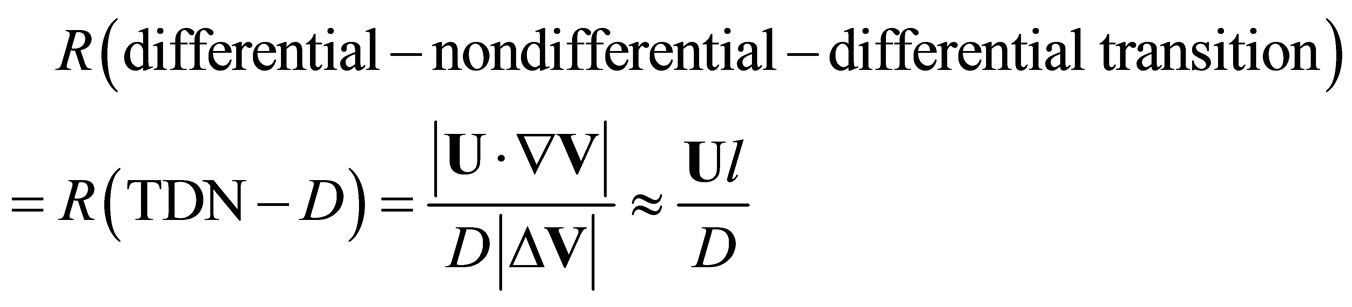 (21)
(21)
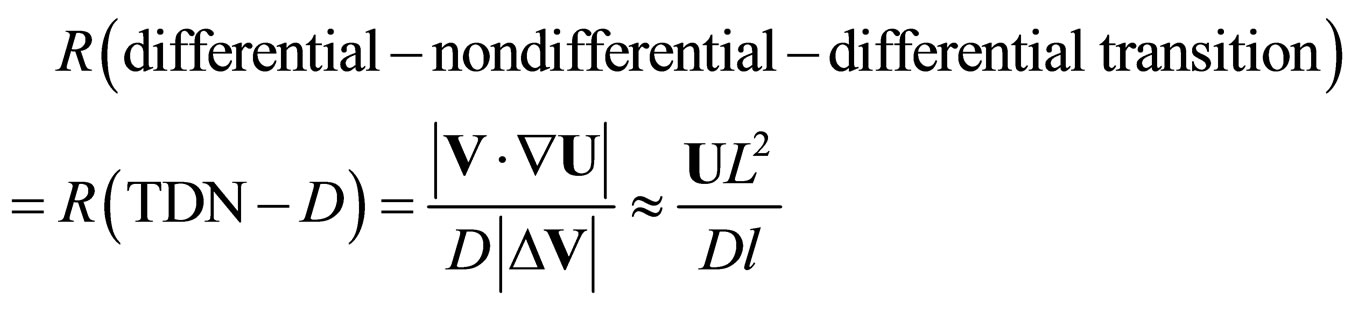 (22)
(22)
In previous relations V, L, D, are the specific parameters, while U, l, D are the parameters of the nondifferential scale. The parameters V, U are specific speeds, L, l specific lengths and D is a viscosity coefficient. Moreover, the common “element” for R(D N), R(N
N), R(N N), R(TDN
N), R(TDN D) and R(TND
D) and R(TND D) is the “viscosity” which, through (20) is imposed by the resolution scale.
D) is the “viscosity” which, through (20) is imposed by the resolution scale.
Equations (15) are simplified in the case of the stationary motion for small Reynolds numbers. Thus, Equation (15) for small R(D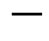 N) becomes
N) becomes
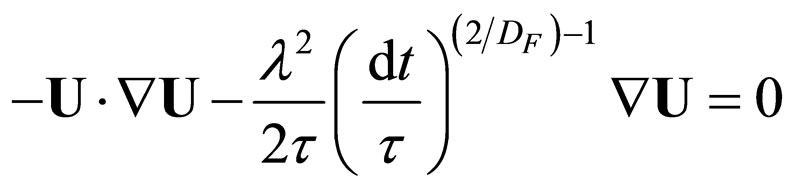 (23)
(23)
and for small R(N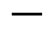 N)
N)
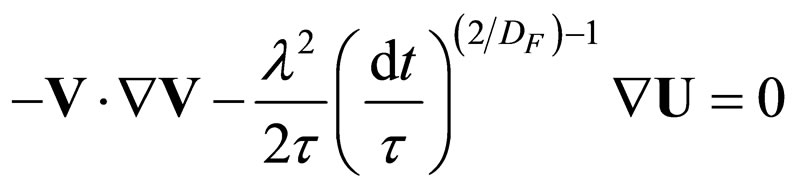 (24)
(24)
Equation (15b) for small R(TDN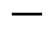 D) takes the form
D) takes the form
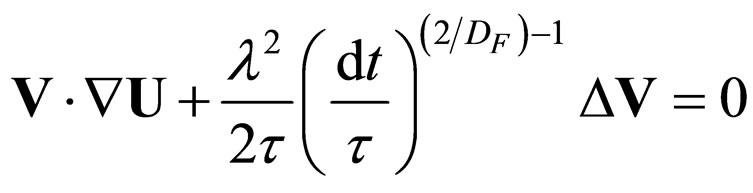 (25)
(25)
and for small R(TND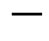 D)
D)
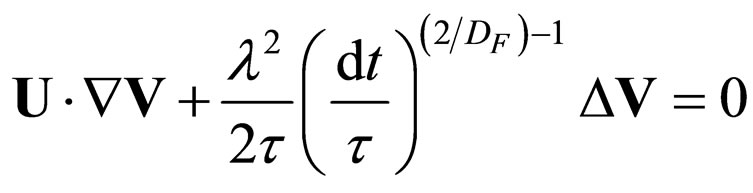 (26)
(26)
7. Irotational Motions of a Fractal Fluid. The Incorporation of the Associate Wave Corpuscle through the Solidarity of Movements and Generation of Schrodinger Equation
For irrotational motions
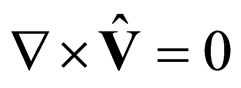 (27)
(27)
which implies
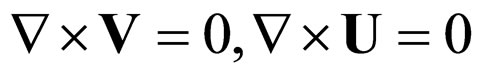 (28)
(28)
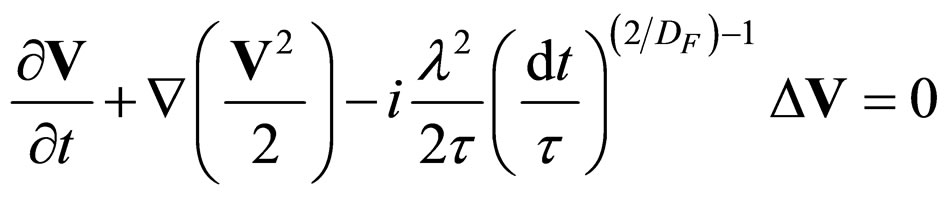 (29)
(29)
Since through (27) the complex speed field is expressed by means of a scalar function gradient F,
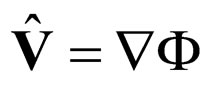 (30)
(30)
Equation (29) taking into account the operator identities
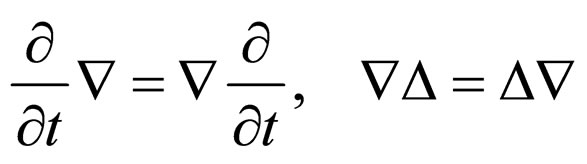 (31)
(31)
takes the form
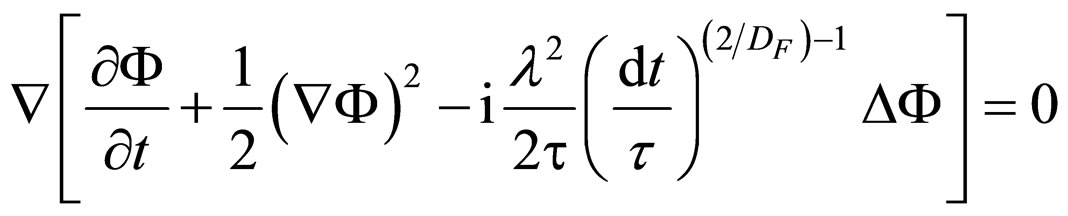 (32)
(32)
or furthermore, through integration
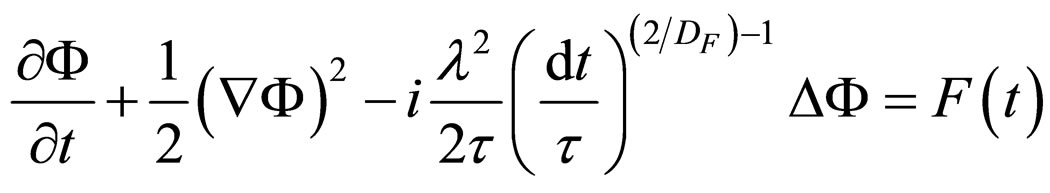 (33)
(33)
where F(t) is an arbitrary function depending only on time.
In particular, for F having the form
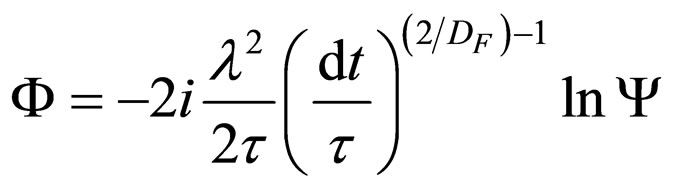 (34)
(34)
where Y is a new complex scalar function, Equation (46), with the operator identity
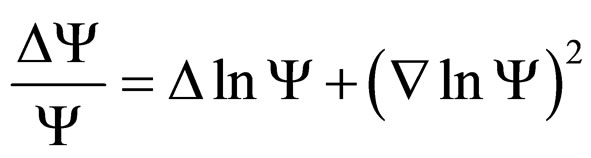 (35)
(35)
takes the form:
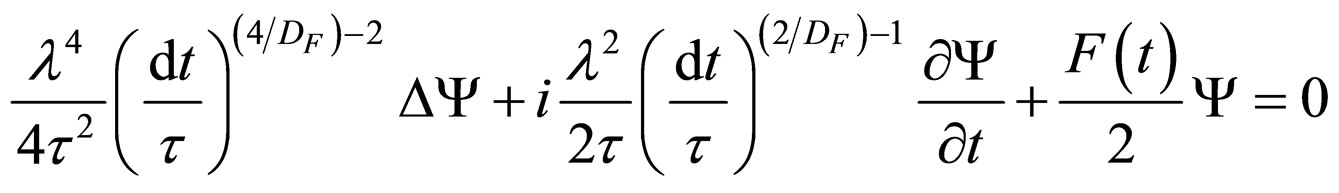 (36)
(36)
The Schrodinger “geodesics” can be obtained as a particular case of Equation (36), based on the following hypothesis (conditions of solidarity of the motion, incorporating the associated wave corpuscle): 1) The motions of the micro-particles take place on fractal curves with the fractal dimension DF = 2, i.e. the Peano curves [3,5]; 2) 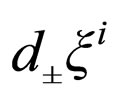 are the Markov-Wiener type stochastic variables [3,5] that satisfy the rule
are the Markov-Wiener type stochastic variables [3,5] that satisfy the rule
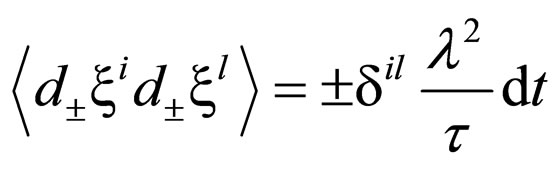 (37)
(37)
3) Space scale l and temporary one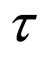 are specific for the Compton scale
are specific for the Compton scale
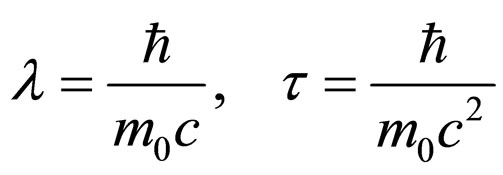 (38)
(38)
with m0 the rest mass of the microparticle, c the speed of light in vacuum and 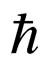 the reduced Planck constant. The parameters (38) should not be understood as “structures” of the standard space-time, but as standards of scale space-time; 4) Function F(t) from (36) is null. Under these circumstances, (36) is reduced to the standard form of Schrodinger’s Equation [13,15]
the reduced Planck constant. The parameters (38) should not be understood as “structures” of the standard space-time, but as standards of scale space-time; 4) Function F(t) from (36) is null. Under these circumstances, (36) is reduced to the standard form of Schrodinger’s Equation [13,15]
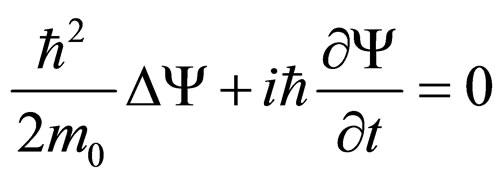 (39)
(39)
In such a context, the scale potential of the complex speeds plays the role of the wave function.
8. Extended Hydrodynamic Model of Scale Relativity and Incorporation of Associated Wave Corpuscle through Fractal Potential. The Correspondence with Madelung Model
Substituting the complex speed (9) with the restriction (27) and separating the real part with the imaginary one, we obtain the set of differential Equations [10]
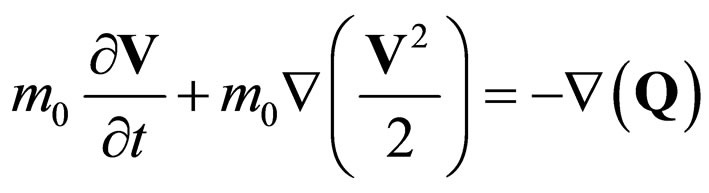 (40a)
(40a)
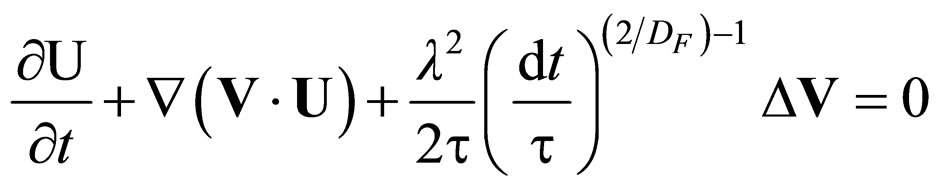 (40b)
(40b)
where Q is the fractal potential, expressed as follows:
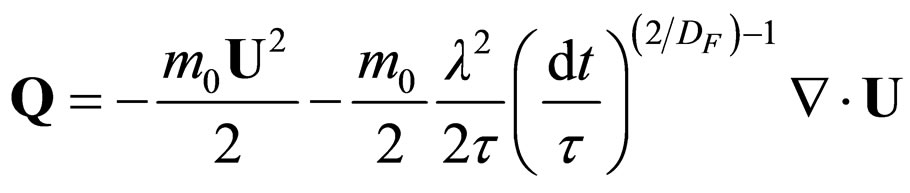 (41)
(41)
For
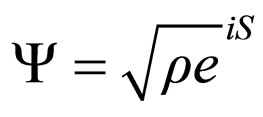 (42)
(42)
with 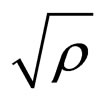 an amplitude and S a phase, then (34) under the form
an amplitude and S a phase, then (34) under the form
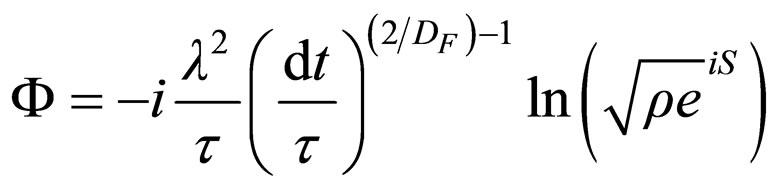
implies the complex speed fields of components
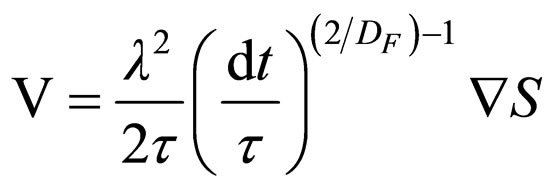 (43a)
(43a)
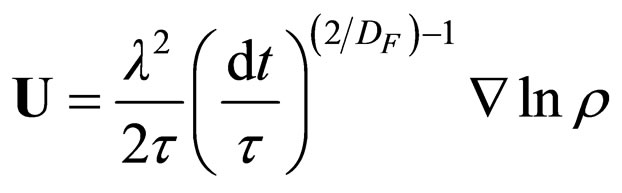 (43b)
(43b)
From the perspective of Equation (43), the Equation (40) keeps its form, and the fractal potential is given by the simple expression
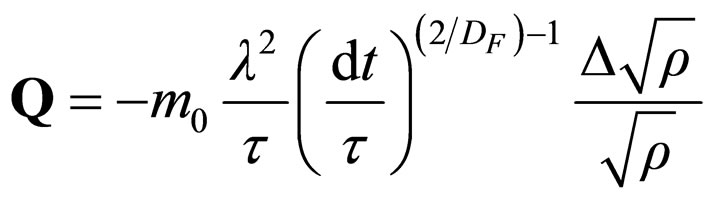 (44)
(44)
Again through Equations (43), Equation (40b) takes the form:
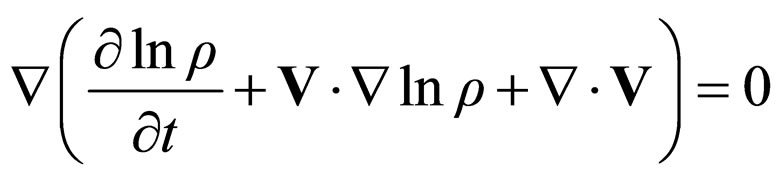
or, still, through integration with 
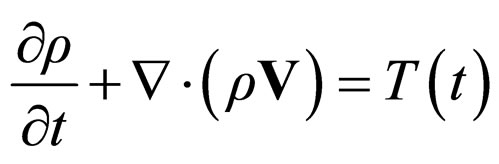 (45)
(45)
with T(t), an exclusively time dependent function Equation (40) corresponds to the impulse conservation law at differential scale (the classical one), while the impulse conservation law at non differential scale is expressed through (45) with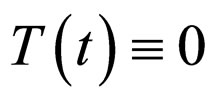 , as a probability density conservation law.
, as a probability density conservation law.
Therefore, equations
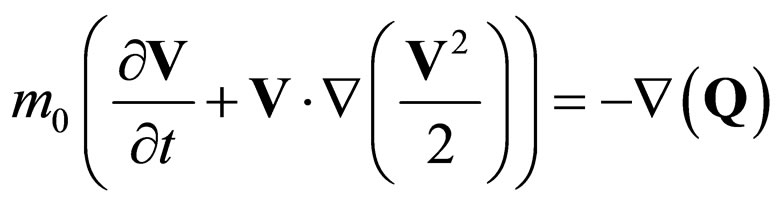 (46a)
(46a)
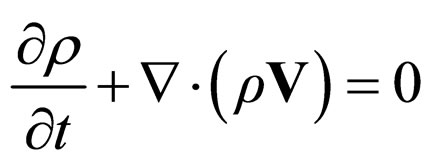 (46b)
(46b)
with Q given by (41) or (44) forms the set of equations of scale relativity extended hydrodynamics in fractal dimension DF. We mention that in references [3,5-7] the model has been extended only for DF = 2. The fractal potential (41) or (44) is induced by the non differentiability of space-time.
In an external scalar field U, the system of Equation (46) modifies as follows:
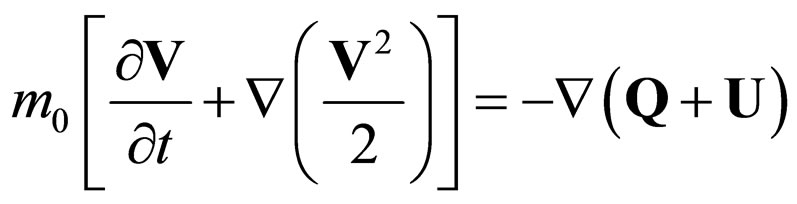 (47a)
(47a)
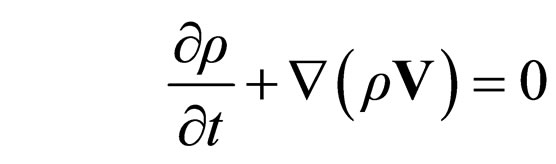 (47b)
(47b)
Now the quantum mechanics in hydrodynamic formula (Madelung’s model [17]) is obtained as a particular case of relations (47), using the following hypothesis: 1) The motion of the micro-particles takes place on Peano curves with DF = 2; 2) 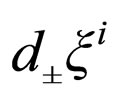 are the Markov-Wiener variables [3,5-7]; 3) The time space scale is a Compton one. Then, (38) have the expressions
are the Markov-Wiener variables [3,5-7]; 3) The time space scale is a Compton one. Then, (38) have the expressions
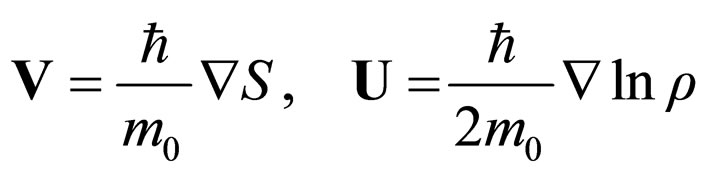 (48)
(48)
and (41),
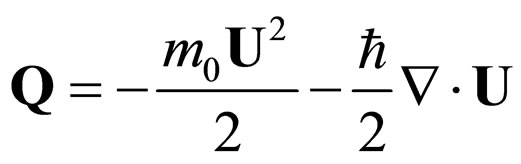 (49)
(49)
9. “Mechanisms” of Duality through Coherence in Corpuscle-Wave Phase
In the stationary case, the system of Equations (46(a) and (b)) become [10]
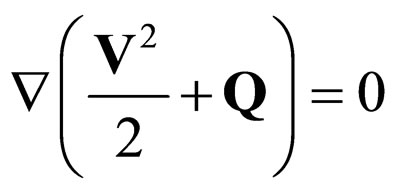 (50a)
(50a)
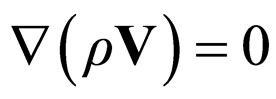 (50b)
(50b)
or, still, through integration
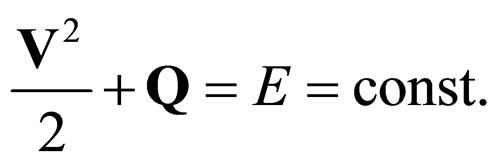 (51a)
(51a)
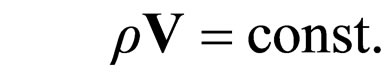 (51b)
(51b)
Let us choose the null power density in (51b). Then there is no impulse transport at differential scale between corpuscle and wave. Moreover, for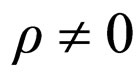 .
.
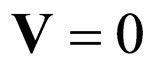 (52)
(52)
which implies through relation (43)
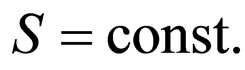 (53)
(53)
In other words, the fluid becomes coherent (the fluid particles have the same phase). Such a state is specific for quantum fluids [50,51], such as superconductors, super-fluids, etc. [14,52]. Under such circumstances, the phase of the corpuscle considered as a small horologe equals the phase of the associated wave (coherence in corpuscle-wave phase).
At non-differential scale, Equation (51), with restriction (52) takes the form
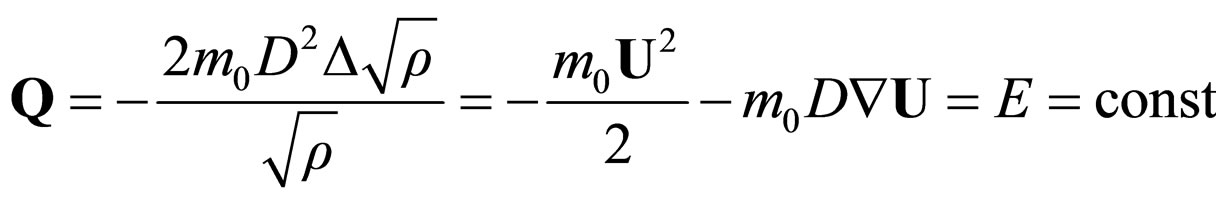 (54a)
(54a)
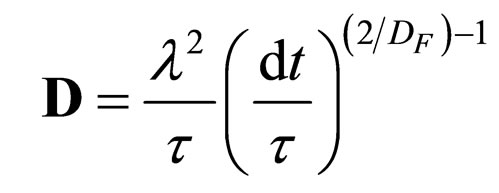 (54b)
(54b)
or, still, by applying the gradient operator
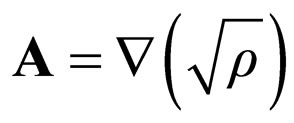 (55)
(55)
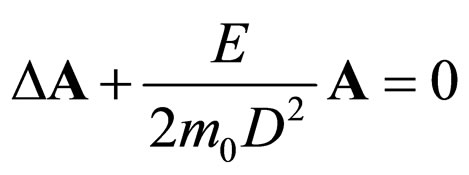 (56)
(56)
We distinguish the following situations:
1) For E > 0 and with substitution
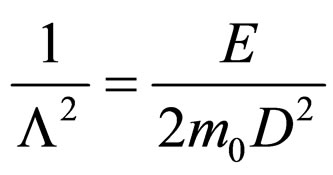 (57)
(57)
Equation (56) becomes
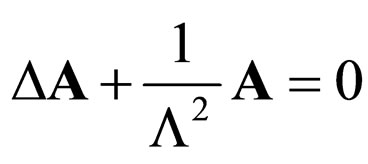 (58)
(58)
Therefore: a) The space oscillations of field A and, therefore the space associated with the motion of coherent fluid particles is endowed with regular non homogeneities (of lattice type). In other words, the field A crystallizes the space. The one dimensional space “crystal” has the constant of the network
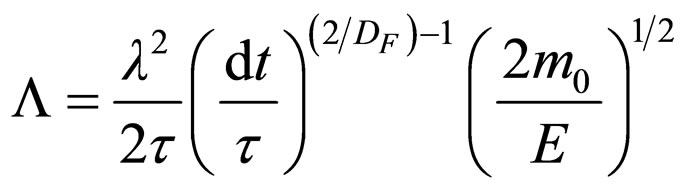 (59)
(59)
that depends both on the “viscosity” – iη given by (11) and on the energy of the particle; b) The one dimensional geodesics of the “crystallized” space given by the expression
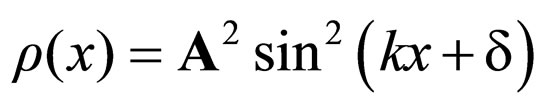 (60)
(60)
implies both fractal speed
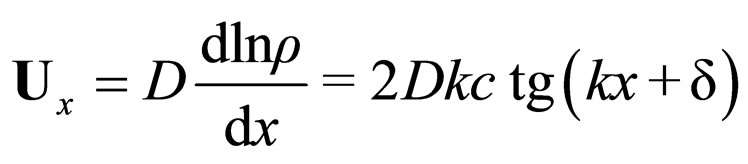 (61)
(61)
and fractal potential
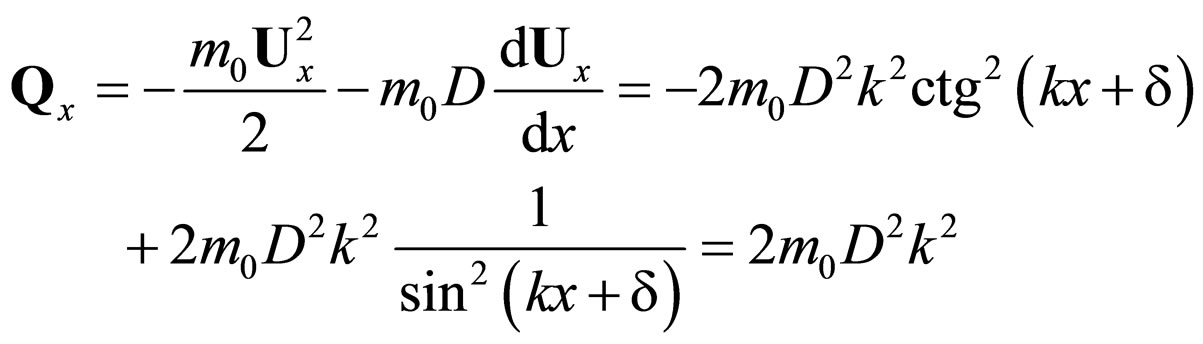 (62)
(62)
with A and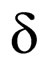 , the integration constants
, the integration constants
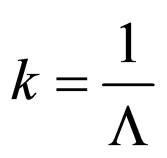 (63)
(63)
c) For the movements of micro particles on Peano curves (DF = 2) at Compton scale
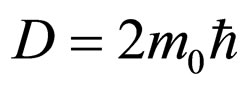
Therefore, through (62), under the form
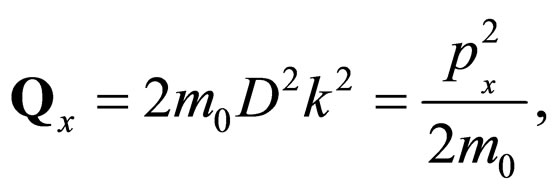 (64a)
(64a)
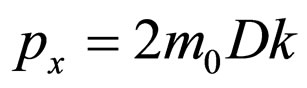 (64b)
(64b)
De Broglie “quantum” impulse is found
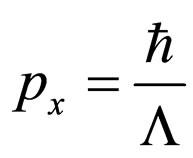 (65)
(65)
d) The dominant of the wave characteristic is achieved by the “self diffraction” mechanism of the fractal field, ρ, on the one dimensional space “crystal” of constant Λ induced by the same field. Indeed, relation (61) with notations
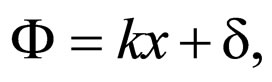 (66a)
(66a)
 (66b)
(66b)
In approximation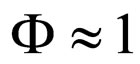 , i.e. for
, i.e. for 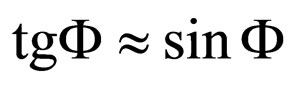 and using Nottale’s relation [1-7]
and using Nottale’s relation [1-7] 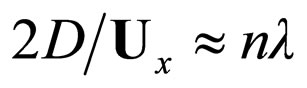 it takes the common form (Bragg’s relation)
it takes the common form (Bragg’s relation)
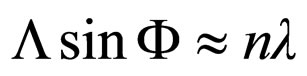 (67)
(67)
This result is in concordance with the recently expressed opinion in [53-55]; e) There is impulse transfer on the fractal field between the corpuscle and the wave; f) According to Taylor’s criterion [56] self-organization (crystallization and self diffraction of the space) appears when the energy of the system is minimal. This can be immediately verified using relation (51a).
2) For E = 0, Equations (51a) and (56) have the same form
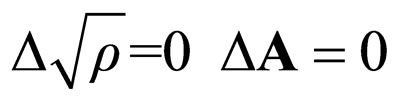 (68)
(68)
It follows that: a) The geodesics are expressed through harmonic functions and the particle finds itself in a critical state, i.e. the one that corresponds to the wave-corpuscle transition; b) In the one dimensional case, the geodesics have the form
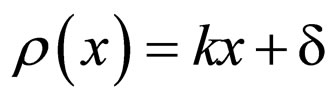 (69)
(69)
which induces the fractal speed field
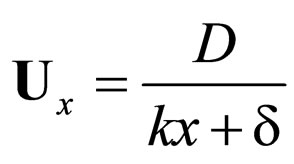 (70)
(70)
namely the null value of the fractal potential
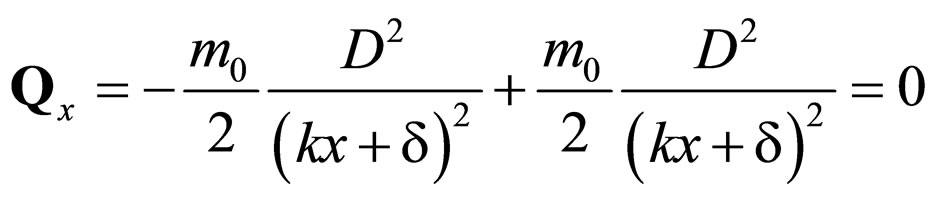 (71)
(71)
c) Although the energy is null, there is impulse transfer between corpuscle and wave on the fractal component of the speed field.
3) For E < 0 and with notations
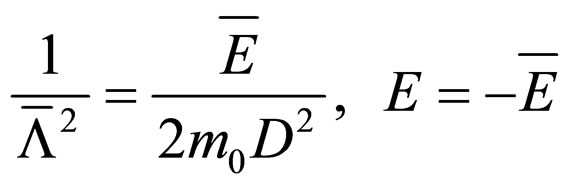 (72)
(72)
Equation (56) takes the form
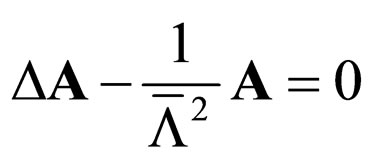 (73)
(73)
The following aspects result: a) Field A is expelled from the structure, its penetration depth being
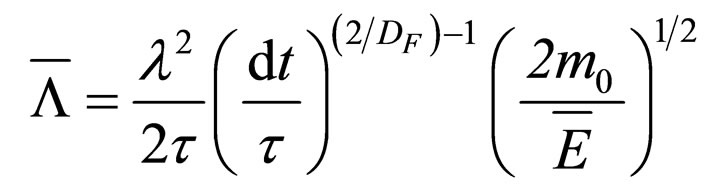 (74)
(74)
b) The one-dimensional geodesics of the space are described through function
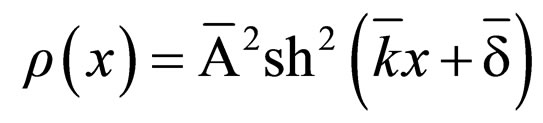 (75)
(75)
and lead to the fractal speed
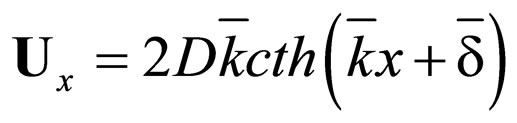 (76)
(76)
the fractal potential respectively
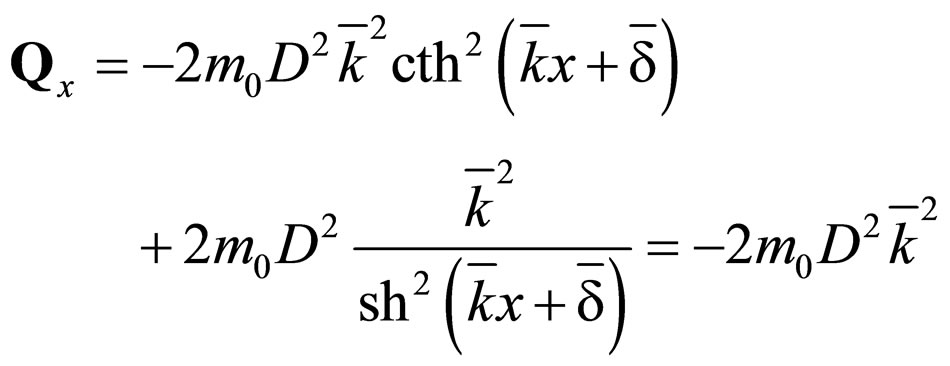 (77)
(77)
where 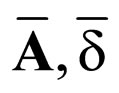 are two integration constants
are two integration constants
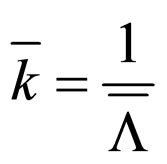 (78)
(78)
c) The dominant of the corpuscular characteristic is accomplished by means of “self-expulsion” mechanism of the fractal field from its own structure that it generates (that is the corpuscle), the penetration depth being . The identification
. The identification
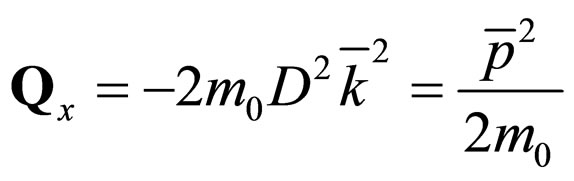 (79)
(79)
implies the purely imaginary impulse
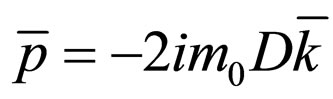 (80)
(80)
that suggests ultra rapid virtual states (ultra rapid motions in the wave field, resulting in the “singularity” of the field, i.e. the corpuscle). As a matter of fact, if we consider de Broglie’s original theory (motions on Peano curves with DF = 2, at Compton’s scale), singularity (the corpuscle) moves “suddenly” and chaotically in the wave field, the wave-corpuscle coupling being accomplished through the fractal potential. The corpuscle “tunnels” the potential barrier imposed by the field of the associate progressive wave, generating particle-antiparticle type pairs (ghost type fields (Bittner E.R., 2000)). Nevertheless this model cannot specify the type of the physical process by means of which we reach such a situation: it is only the second quantification that can do this [50, 51,54-57]; d) There is an impulse transfer between the corpuscle and the wave on the fractal component of the speed field, so that all the attributes of the differential speed could be transferred on the fractal speed.
All the above results indicate that wave-particle duality is an intrinsic property of space and not of the particle.
10. Wave-Corpuscle Duality through Flowing Stationary Regimes of a Coherent Fractal Fluid in Phase. The Potential Well
According to the previous paragraph, let us study the particle in a potential well with infinite width and walls. Then the speed complex field has the form [8-12]
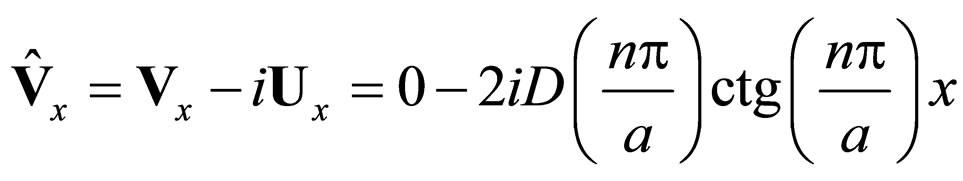 (81)
(81)
and generates the fractal potential (the energy of the structure) under the form of the noticeable
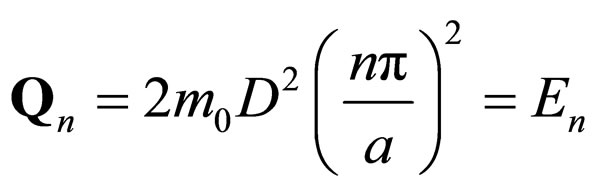 (82)
(82)
The last relation (82) allows the implementation of Reynold’s criterion
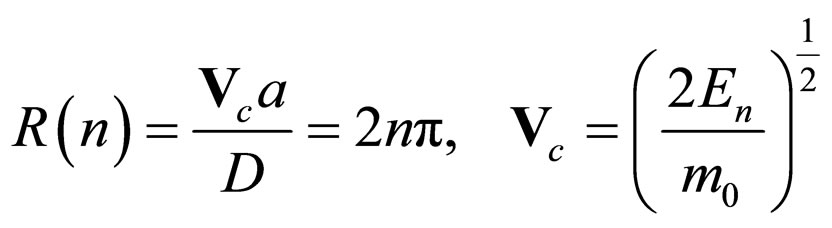 (83)
(83)
For movements on Peano curves (DF = 2) at Compton scale 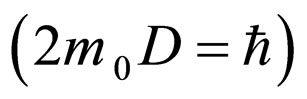 (83) with substitutions
(83) with substitutions
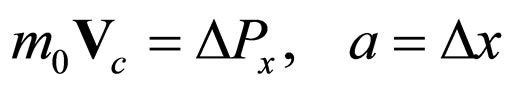 (84)
(84)
and n = 1 reduces to Heinsenberg’s relation of uncertainty under equal form
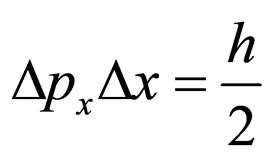 (85)
(85)
while for 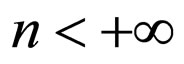 it implies a Ruelle-Takens’ type criterion of evolution towards chaos [58,59]. Therefore, the wave-corpuscle duality is accomplished through the flowing regimes of a fractal fluid that is coherent in phase. Thus, the laminar flow (small n) induces a dominant ondulatory characteristic, while the turbulent flow (big n) induces a dominant corpuscular characteristic.
it implies a Ruelle-Takens’ type criterion of evolution towards chaos [58,59]. Therefore, the wave-corpuscle duality is accomplished through the flowing regimes of a fractal fluid that is coherent in phase. Thus, the laminar flow (small n) induces a dominant ondulatory characteristic, while the turbulent flow (big n) induces a dominant corpuscular characteristic.
11. Wave-Corpuscle Duality through Non-Stationary Regimes of an Incoherent Fractal Fluid
In the one dimensional case the equations of hydrodynamics (46) take the form
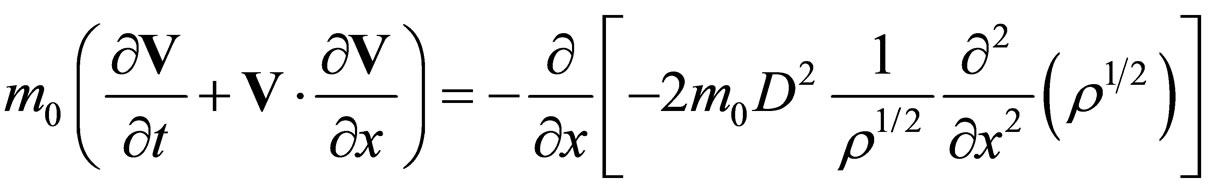 (86a)
(86a)
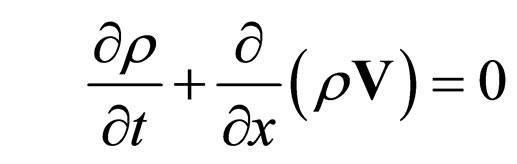 (86b)
(86b)
Imposing the initial conditions
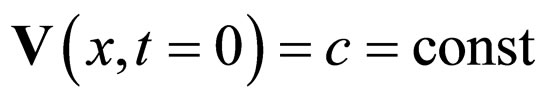 (87a)
(87a)
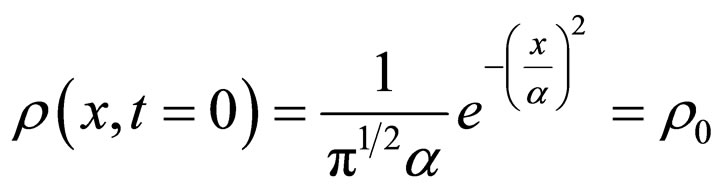 (87b)
(87b)
and on the frontier
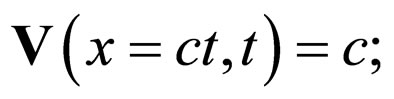 (88a)
(88a)
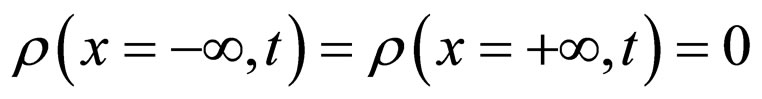 (88b)
(88b)
The solutions of the system (86), using the method in [60], have the expressions
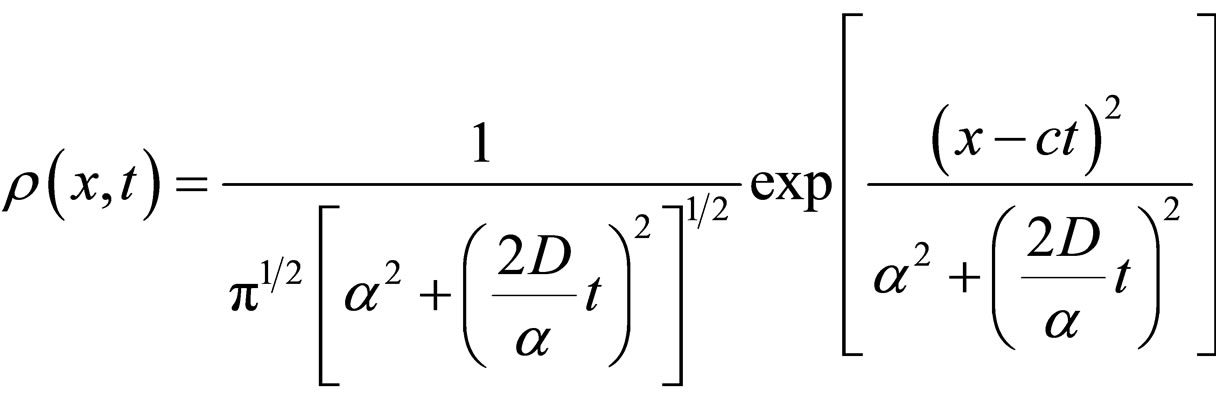 (89a)
(89a)
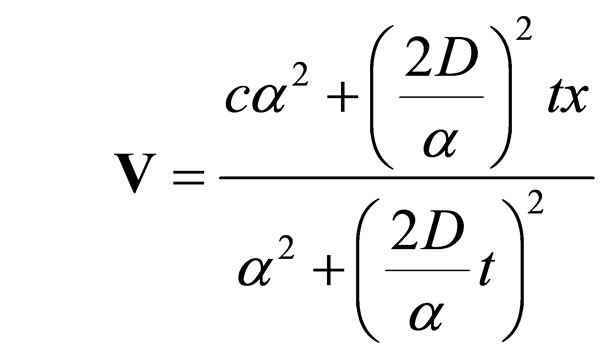 (89b)
(89b)
The complex speed field is obtained
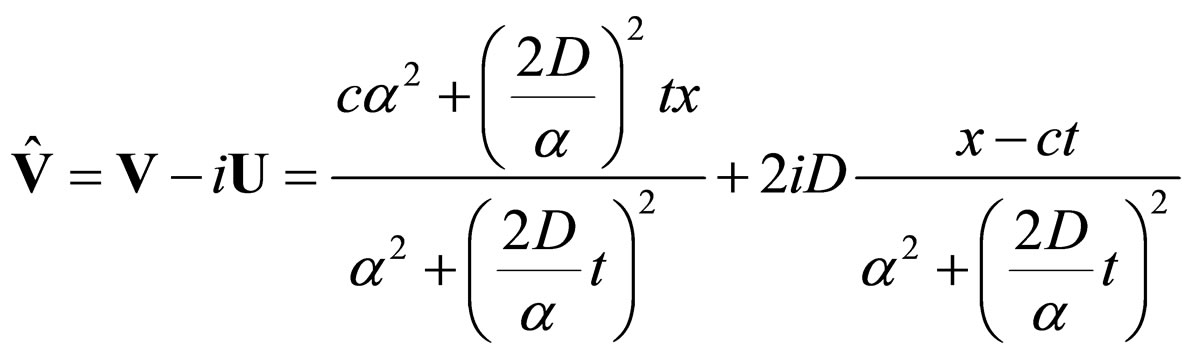 (90)
(90)
and the field of fractal forces
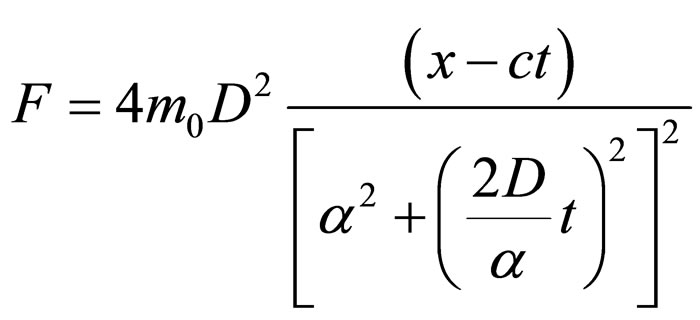 (91)
(91)
Therefore: 1) Both differential scale speed V and nondifferential one U are not homogeneous in x and t. Under the action of fractal force F, the corpuscle is assimilated to the wave, is a part of its structure, so that it joins the movement of the corpuscle with the propagation of the associated progressive wave; 2) The timing of the movements at the two scales, V = U implies the space-time homographic dependence
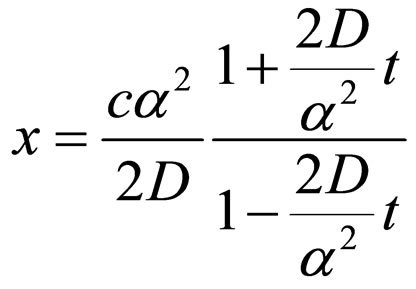 (92)
(92)
in the field of forces
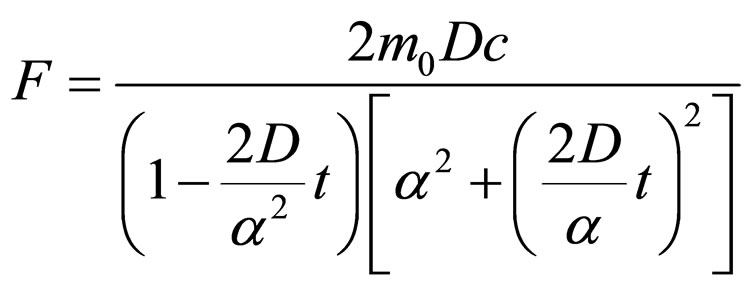 (93)
(93)
Considering that the type (92) changes are implied in gravitational interaction [61,62], it follows that the solidarity of the corpuscle movement with the movement of the associated progressive wave is accomplished by means of the appropriate gravitational field of the physical object; 3) The uniform movement V = c is obtained for null fractal force F = 0 and fractal speed U = 0, using condition x = ct. The fractal forces in the semi space. 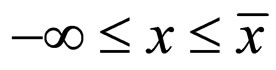 and
and 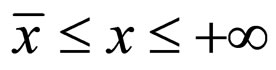 are reciprocally compensated.
are reciprocally compensated.
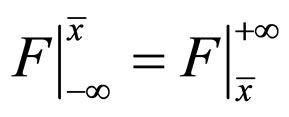
This means that the corpuscle in “free” motion simultaneously polarizes the “environment” of the wave behind x ≤ ct and in front of x ≥ ct, in such a manner that the resulting force has a symmetrical distribution as compared with the plane that contains the position of the noticeable object x = ct at any time moment t. Under such circumstances, the physical object uniformly moves (the corpuscle is located in the field of the associated wave).
12. The Corpuscle as a Horologe and Its Incorporation in the Associated Wave. Implications
According to de Broglie’s theory, the corpuscle must be associated to a horologe having the frequency equal to that of the associated progressive wave. Mathematically we can describe such an oscillator through the differential equation
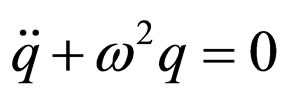 (94)
(94)
where ω defines the natural frequency of the oscillator as it is dictated by the environment (the wave), and the point above the symbol refers to the differential as compared with time. The most general solution of Equation (94) generally depends not on two arbitrary constants, as it is usually considered, but on three: the initial relevant coordinate, the initial speed and the phase of the harmonic oscillatory within the ensemble that structurally represents the environment (the isolated oscillator is an abstraction). Such a solution gives the relevant co-ordinate
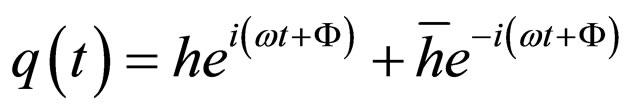 (95)
(95)
where 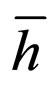 refers to the complex conjugate of h and
refers to the complex conjugate of h and  is an initial phase specific to the individual movement of the oscillator. Such a notation allows us to solve a problem that we could name “the oscillators with the same frequency”, such as Planck’s resonators’ ensemble—the basis of the quantum theory arguments in their old shape. That is, given an ensemble of oscillators having the same frequency in a space region, which is the relation between them?
is an initial phase specific to the individual movement of the oscillator. Such a notation allows us to solve a problem that we could name “the oscillators with the same frequency”, such as Planck’s resonators’ ensemble—the basis of the quantum theory arguments in their old shape. That is, given an ensemble of oscillators having the same frequency in a space region, which is the relation between them?
The mathematical answer to this problem can be obtained if we note that what we want here is to find a mean to pass from a triplet of numbers—the initial conditions—of an oscillator towards the same triplet of another oscillator with the same frequency. This process (passing) implies a simple transitive continuous group with three parameters that can be built using a certain definition of the frequency. We start from the idea that the ratio of two fundamental solutions of Equation (94) is a solution of Schwarts’ non linear equation [63-65]
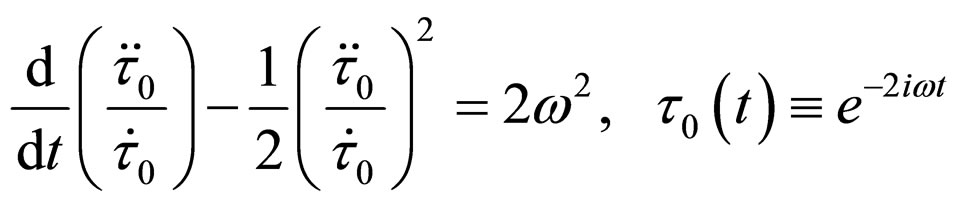 (96)
(96)
This equation proves to be a veritable definition of frequency as a general characteristic of an ensemble of oscillators that can be scanned through a continuous group of three parameters. Indeed Equation (96) is invariant to the change of the dependent variable
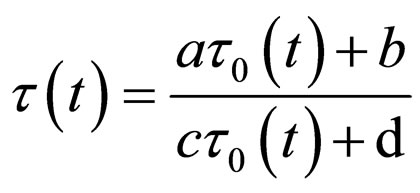 (97)
(97)
which can be verified through direct calculation. Thus, 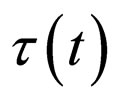 characterizes another oscillator with the same frequency which allows us to say that, starting from a standard oscillator we can scan the whole ensemble of oscillators of the same frequency when we let loose the three ratios a:b:c:d in Equation (97). We can make a more precise correspondence between a homographic change and an oscillator, by means of associating to each oscillator a personal
characterizes another oscillator with the same frequency which allows us to say that, starting from a standard oscillator we can scan the whole ensemble of oscillators of the same frequency when we let loose the three ratios a:b:c:d in Equation (97). We can make a more precise correspondence between a homographic change and an oscillator, by means of associating to each oscillator a personal 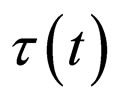 through equation
through equation
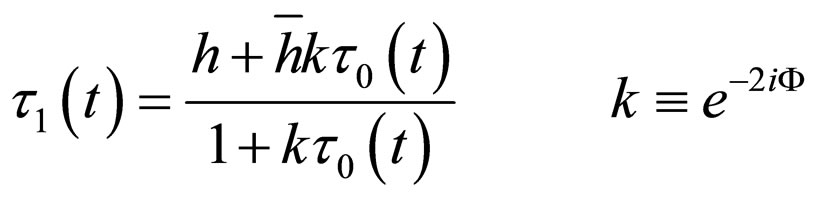 (98)
(98)
Let us notice that 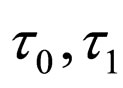 can be freely used one instead the other, which leads to the next group of changes for the initial conditions
can be freely used one instead the other, which leads to the next group of changes for the initial conditions
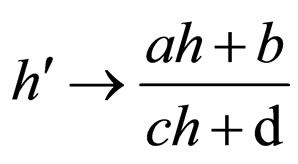 (99a)
(99a)
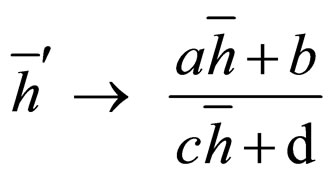 (99b)
(99b)
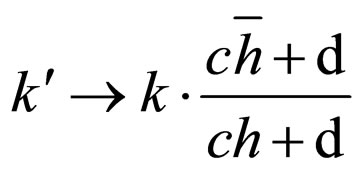 (99c)
(99c)
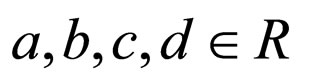 (99d)
(99d)
This is a simple transitive group: one and only one change of the group (the Barbilian group [63,64]) corresponds to a given set of values (a/c, b/c, d/c).
This group admits the 1-differential forms, absolutely invariant through the group [63]
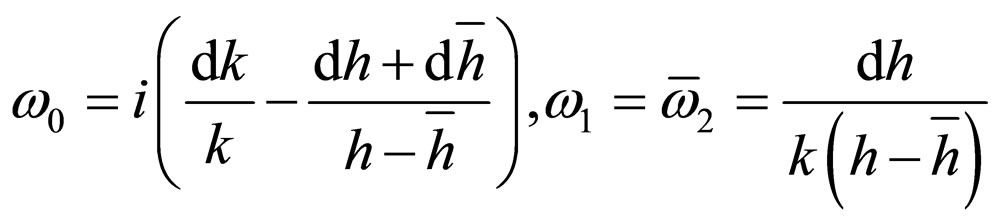 (100)
(100)
and the 2-differential form
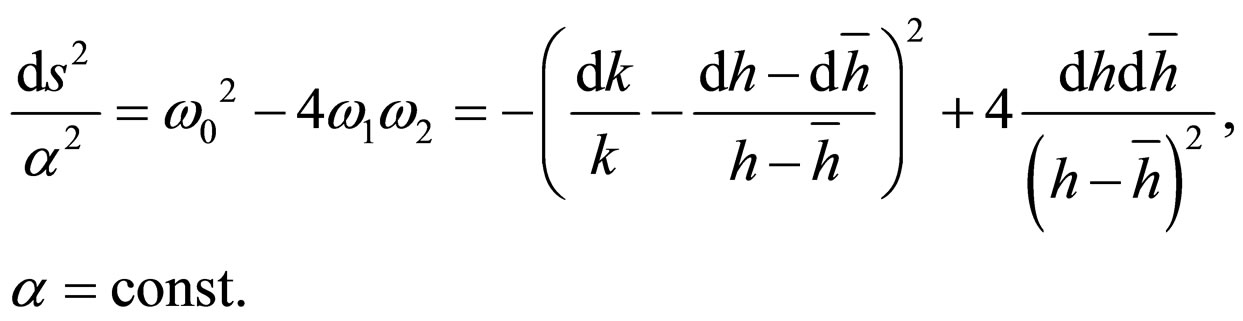 (101)
(101)
respectively.
If we restrict the definition of a parallelism of directions in Levi-Civita manner [63]
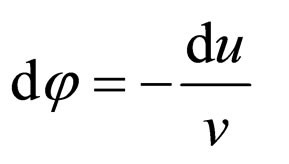 (102)
(102)
with
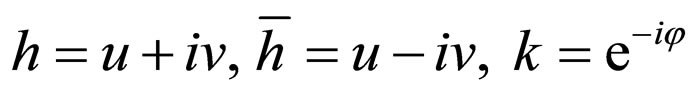 (103)
(103)
Barbilian’s group invariates the metrics of Lobacevski’s plane [63],
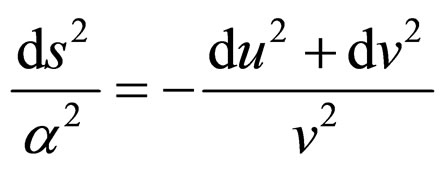 (104)
(104)
Metrics (104) coincides with the differential invariant that is built with the complex scalar field of the speed,
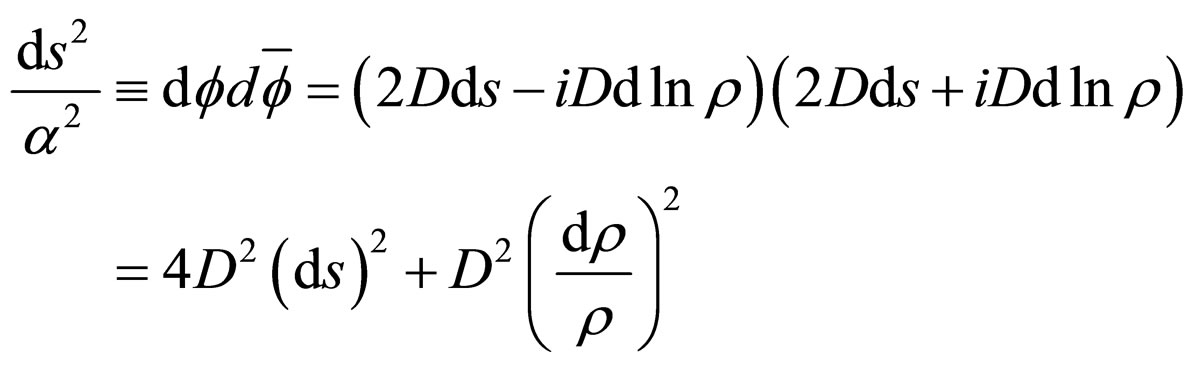 (105)
(105)
which admits the identities
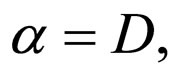 (106a)
(106a)
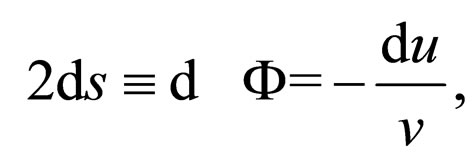 (106b)
(106b)
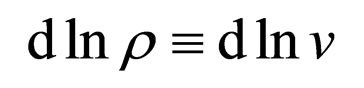 (106c)
(106c)
Now, through a Matzner-Misner type principle one can obtain Ernst’s principle of generating the symmetrical axial metrics [61,62]
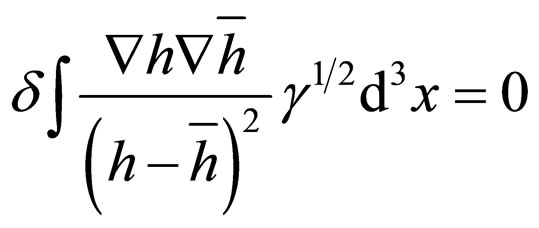 (106d)
(106d)
where g = det gab with gab the metrics of the “environment”.
Therefore, the incorporation of the corpuscle in the wave, considering that it functions as a horologe with the same frequency as that of the associated progressive wave, implies gravitation through Einstein’s vacuum equations (equivalent to Ernst’s principle (106d)). On the contrary, when the frequencies do not coincide, there is an induction of Stoler’s group from the theory of coherent states (the parameter of the change is the very ratio of frequencies when creation and annihilation operators refer to a harmonic oscillator [63]
Let us note that the homographic changes (99) generalize the result (92). Moreover, if 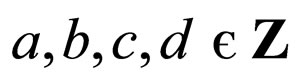 then the Ernst type equations describe super-gravitation N = 1 [65].
then the Ernst type equations describe super-gravitation N = 1 [65].
13. Conclusions
Finally we can display the conclusions of this chapter as follows:
- A critical analysis of the hydrodynamic model of Madelung and of the double solution theory of de Broglie’s theory of double solution was performed—departing from here, we built a fractal approximation of motion;
- We got the equation of motion of the physical object in the fractal approximation and the Eulerian case was studied;
- The flowing regimes of a rotational fractal fluid were studied;
- We studied the irrotational regime of a fractal fluid and the incorporation of the particle into the associated wave by generating a Schrödinger equation;
- The extended hydrodynamic model of scale relativity was built and the role of the fractal potential in the process of incorporation of the particle into the wave, specified;
- We indicated the mechanisms of wave-particle duality by their in phase coherences;
- We studied the wave-particle duality by stationary flow regimes of a fractal fluid which is coherent in phase, and by non-stationary flow regimes of an incoherent fractal fluid by means of a “polarization” type mechanism;
- Considering the particle as a singularity in the wave, we showed that its incorporation into the associated wave resulted in Einstein’s equations in vacuum—contrary, its non-incorporation led to the second quantification;
14. Acknowledgements
This paper was supported by the project POSDRU/88/1.5/ S/47646 of The European Social Fund and the project PERFORM-ERA “Postdoctoral Performance for Integration in the European Research Area” (ID-57649), financed by the European Social Fund and the Romanian Government.
REFERENCES
- L. Nottale and J. Schneider, “Fractals and Non-Standard Analysis,” Journal of Mathematical Physics, Vol. 25, No. 12, 1984, pp. 96-300.
- L. Nottale, “Fractals and the Quantum Theory of SpaceTime,” International Journal of Modern Physics, Vol. A4, No. 50, 1989, pp. 47-117.
- L. Nottalle, “Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity,” World Scientific, Singapore, 1993.
- L. Nottale, “Scale Relativity and Fractal Space-Time: Applications to Quantum Physics, Cosmology and Chaotic Systems,” Chaos, Solitons & Fractals, Vol. 7, No. 6, 1996, pp. 877-938.
- L. Nottale, “The Theory of Scale Relativity: Non-Differentiable Geometry, Fractal Space-Time and Quantum Mechanics,” Computing Anticipatory Systems: CASYS’ 03- 33 Sixth International Conference, Liège, 11-16 August 2003, pp. 68-95.
- J. Chaline, L. Nottale and P. Grou, “The Trees of Evolution: Universe S,” Life Companies Societies, Paris, 2000.
- J. Chaline, L. Nottale and P. Grou, “Flowers for Scrodinger Sscale Relativity and Its Applications,” Editure Ellipses Marketing, Paris, 2009.
- A. Harabagiu and M. Agop, “Hydrodyamic Model of Scale Relativity Theory,” Bulletin of the Polytechnic Institute of Iasi, Vol. LV, No. 3-4, 2005, pp. 77-82.
- A. Harabagiu, O. Niculescu, M. Colotin, T. D. Bibere, I. Gottlieb and M. Agop, “Particle in a Box by Means of Fractal Hydrodynamic Model,” Romanian Reports in Physics, Vol. 61, No. 3, 2009, pp. 395-400.
- A. Harabagiu, D. Magop and M. Agop, “Fractality and Quantum Mechanics,” Ars Longa Publishing House, Iaşi, 2010.
- M. Agop, L. Chicoş, P. Nica and A. Harabagiu, “Euler’s Fluids and Non-Differentiable Space-Time,” Far East Journal of Dynamical Systems, Vol. 10, No. 1, 2008, pp. 93-106.
- M. Agop, A. Harabagiu and P. Nica, “Wave-Particle Duality through a Hydrodynamic Model of the Fractal Space Time Theory,” Acta Physica Polonica A, Vol. 113, No. 6, 2008, pp. 1557-1574.
- S. Ţiţeica, “Quantum Mechanics,” Academiei Publishing House, Bucureşti, 1984.
- B. Felsager, “Geometry, Particles and Fields,” Odense University Press, Odense, 1981.
- A. Peres, “Quantum Theory: Concepts and Methods,” Kluwer Academic Publishers, Boston, 1993.
- J. J. Sakurai and T. S. Fu, “Modern Quantum Mechanics,” Addison-Wesley, Boston, 1994.
- F. Halbwacs, “Theorie Relativiste Des Fluids a Spin,” Gauthier-Villars, Paris, 1960.
- R. Madelung, “A Hydrodynamic Interpretation of Quantum Mechanics,” Journal for Physics, Vol. 40, No. 3-4, 1927, pp. 322-326.
- D. Bohm and B. J. Hiley, “The Undivided Universe: An Ontological Interpretation of Quantum Theory,” Routledge and Kegan Paul, London, 1993.
- D. Dϋrr, S. Goldstein and N. Zanghi, “Quantum Mechanics, Randomness and Deterministic Reality,” Physics Letters A, Vol. 172, No. 1-2, 1992, pp. 6-12. doi:10.1016/0375-9601(92)90181-K
- D. Dϋrr, S. Goldstein and N. Zanchi, “A Global Equilibrium as the Foundation of Quantum Randomness,” Foundations of Physics, Vol. 23, 1993, pp. 712-738.
- D. Z. Albert, “Bohm’s Alternative to Quantum Mechanics”, Scientific American, Vol. 270, No. 2, 1994, pp. 32- 39. doi:10.1038/scientificamerican0594-58
- J. S. Bell, “Speakable and Unspeakable in Quantum Mechanics,” Cambridge University Press, Cambridge, 1987.
- K. Berndl, D. Dϋrr, S. Goldstein, G. Peruzzi and N. Zanchi, “Existance of Trajectories for Bohmian Mechanics,” International Journal of Theoretical Physics, Vol. 32, No. 12, 1993, pp. 2245-2251. doi:10.1007/BF00672996
- K. Berndl, D. Dϋrr, S. Goldstein, N. Zanchi, “Selfadjointness and the Existance of Deterministic Trajectories in Quantum Theory,” In: M. Fannes, C. Maes and A. Verbeure, Eds., On Three Levels: Micro-, Meso-, and Macroscopic Approches in Physics, (NATO ASI Series B: Physics), Plenum, New York, 1994, pp. 429-434.
- P. R. Holland, “The Quantum Theory of Motion,” Cambridge University Press, Cambridge, 1993. doi:10.1017/CBO9780511622687
- L. de Broglie, “Causal Interpretation Attempt and NonLinear Wave Mechanics: The Theory of Double Solution,” Gauthier-Villars, Paris, 1956.
- L. de Broglie, “The Measure Theory in Wave Mechanics,” Gauthier-Villars, Paris, 1957.
- L. de Broglie, “Wave Mechanics Interpretation,” Journal of Physics Radium, Vol. 20, No. 12, 1959, pp. 963-979. doi:10.1051/jphysrad:019590020012096300
- L. de Broglie, “Critical Study of the Current Foundations Interpretation of Wave Mechanics,” Gauthier-Villars, Paris, 1963.
- L. de Broglie, “Thermodynamics of Isolated Particle (Hidden Thermodynamics of Particles),” Gauthier-Villars, Paris, 1964.
- L. de Broglie, “Certainity and Uncertainity in Science,” Politică Publishing House, Bucureşti, 1980.
- D. Bohm, “A Suggested Interpretation of Quantum Theory in Terms of ‘Hidden’ Variables I,” Physical Review, Vol. 85, No. 2, 1952, pp. 166-179. doi:10.1103/PhysRev.85.166
- D. Bohm, “A Suggested Interpretation of Quantum Theory in Terms of ‘Hidden Variables’: Part II,” Physical Review, Vol. 85, No. 2, 1952, pp. 180-193. doi:10.1103/PhysRev.85.180
- D. Bohm, “Proof that Probability Density Approaches
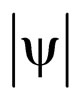 in Causal Interpretation of Quantum Theory,” Physical Review, Vol. 89, No. 2, 1953, pp. 458-466. doi:10.1103/PhysRev.89.458
in Causal Interpretation of Quantum Theory,” Physical Review, Vol. 89, No. 2, 1953, pp. 458-466. doi:10.1103/PhysRev.89.458 - L. Budei, “Fractal Models: Applications in Enviroment Arhitecture,” Publishing House University, Gh. Asachi, Iaşi, 2000.
- M. Barnsley, “Fractals Everywhere: The First Course in Deterministic Fractal Geometry,” Academic Press, Boston, 1988.
- A. Le Mehante, “Les Geometries Fractales,” Hermes, Paris, 1990.
- A. Heck and J. M. Perdang, “Applying Fractals in Astronomy,” Springer Verlag, Berlin, 1991.
- J. Feder and A. Aharony, “Fractals in Physics,” NorthHolland, Amsterdam, 1990.
- P. Berge, Y. Pomeau and C. Vidal, “The Order in Chaos,” Wiley, New York, 1984.
- J. F. Gouyet, “Physical Structures and Fractals,” Masson, Paris, 1992.
- M. S. El Naschie, O. E. Rössler and I. Prigogine, “Quantum Mechanics, Diffusion and Chaotic Fractals”, Elsevier, Oxford, 1995.
- P. Weibel, G. Ord and O. E. Rössler, “Space Time Physics and Fractality: Festschroft in Honer of Mohamad El Naschie Vienna,” Springer, New York, 2005.
- E. Nelson, “Quantum Fluctuations,” Princeton University Press, Princeton, 1985.
- M. Agop, M. Colotin and V. Păun, “Haoticity, Fractality and Fields: Elements of Fractal Theory,” Publishing House ArsLonga, Iaşi, 2009, pp. 12-46.
- V. Chioroiu, L. Munteanu, P. Ştiucă and S. Donescu, “Introduction in Nanomechanics,” Publishing House Academiei Române, Bucureşti, 2005.
- D. K. Ferry and S. M. Goodnick, “Transport in Nanostructures,” Cambridge University Press, Cambridge, 2001.
- Y. Imry, “Introduction to Mesoscopic Physics,” Oxford University Press, Oxford, 2002.
- D. Benoit, “Physics of Semiconductor Microcavities from Fundamentals to Nano-Scale Decretes,” Wiley-VCH Verlag GmbH, Weinheim, 2007.
- C. Ciuti and I. Camsotto, “Quantum Fluids Effects and Parametric Instabilities in Microcavities,” Physica Status Solidi B, Vol. 242, No. 11, 2005, p. 2224.
- C. P. Poole, K. A. Farach and R. Creswick, “Super-Conductivity,” Academic Press, San Diego, 1995.
- G. Grössing, “Diffusion Waves in Sub-Quantum Thermodynamics: Resolution of Einstein’s ‘Particle-in-a-Box’ Objection,” 2008. http://arxiv.org/abs/0806.4462
- A. Mandelis, L. Nicolaides and Y. Chen, “Structure and the Reflectionless/Refractionless Nature of Parabolic Diffusion-Wave Fields, “ Physical Review Letters, Vol. 87, No. 2, 2001, 4 pages. doi:10.1103/PhysRevLett.87.020801
- A. Mandelis, “Diffusion Waves and Their Uses,” Physics Today, Vol. 53, No. 8, 2000, p. 29. doi:10.1063/1.1310118
- S. Popescu, “Actual Issues in Self-Structuring Systems,” Publishing House Tehnopress, Iasi, 2004.
- E. R. Bittner, “Quantum Tunneling Dynamics Using Hydrodynamic Trajectories,” Journal of Chemical Physics, Vol. 112, No. 22, 2000, p. 9703. doi:10.1063/1.481607
- D. Ruelle and F. Takens, “On the Nature of Turbulence,” Communications in Mathematical Physics, Vol. 20, No. 23, 1971, pp. 167-192,
- D. Ruelle, “Strange Attractors,” The Mathematical Intelligencer, Vol. 2, No. 3, 1979, pp. 126-137.
- C. V. Munceleanu, D. Magop, C. Marin and M. Agop, “Fractal Models in Polymer Physics,” Ars Longa Publishing House, Iasi, 2010.
- F. J. Ernst, “New Formulation of the Axially Symemetric Gravitational Fielf Problem I,” Physical Reviews, Vol. 167, No. 5, 1968, pp. 1175-1178. doi:10.1103/PhysRev.167.1175
- F. J. Ernst, “Exterior Algebraic Derivation of Einstein Field Equation Employing a Generalized Basis,” Journal of Mathematical Physics, Vol. 12, No. 11, 1971, pp. 2395-2398. doi:10.1063/1.1665549
- M. Agop and N. Mazilu, “Fundaments of Modern Physics,” Junimea Publishing House, Iasi, 1989.
- M. Agop and N. Mazilu, “The Crossroads of the Theories between Newton and Einstein Barbilian’s Univers,” Ars Longa, Iaşi, 2010.
- M. B. Green, J. H. Schwarz and E. Witten, “Superstring Theory,” Cambridge University Press, Cambridge, 1998.

