Received 27 October 2015; accepted 29 November 2015; published 2 December 2015

ABSTRACT

This article examines a fifth order critically damped nonlinearsystem in the case of small equal eigenvalues and tries to find out an asymptotic solution. This paper suggests that the solutions obtained by the perturbation techniques based on modified Krylov-Bogoliubov-Mitropoloskii (KBM) method is consistent with the numerical solutions obtained by the fourth order Runge-Kutta method.

Keywords:

KBM, Eigenvalues, Critically Damped System, Nonlinearity, Asymptotic Solution, Runge-Kutta Method

1. Introduction

The Krylov-Bogoliubov-Mitropoloskii ([1] [2] ) method, known as KBM method, is one of the most used methods for analysing nonlinear oscillatory and non-oscillatory differential systems with small nonlinearities. Krylov and Bogoliubov [1] first developed this method to find the periodic solutions of second order nonlinear differential systems with small nonlinearities. However, the method was later improved and justified mathematically by Bogoliubov and Mitropolskii [2] . It was then extended by Popov [3] to damped oscillatory nonlinear systems. The Popov results were rediscovered by Mendelson [4] because of the physical importance of the damped oscillatory systems. In the meantime, Murty et al. [5] developed an asymptotic method based on the theory of Bogoliubov to obtain the response of over damped nonlinear systems. Later, Murty [6] offered a unified KBM method, which was capable to cover the damped and over-damped cases. Sattar [7] also examined an asymptotic solution for a second order critically damped nonlinear system. Alam [8] proposed a new asymptotic solution for both over-damped and critically damped nonlinear systems. Akbar et al. [9] propounded an asymptotic method for fourth order over-damped nonlinear systems, which was straightforward as well as easier than the method put forward by Murty et al. [5] . Later, Akbar et al. [10] extended the method for fourth order damped oscillatory systems. Akbar et al. [11] also suggested a technique for obtaining over-damped solutions of n-th order nonlinear differential systems. Recently, Rahaman and Rahman [12] have found analytical approximate solutions of fifth order more critically damped systems in the case of smaller triply repeated roots. Besides, Rahaman and Kawser [13] have also proposed asymptotic solutions of fifth order critically damped nonlinear systems with pair wise equal eigenvalues and another is distinct. Further, Islam et al. [14] suggested an asymptotic method of Krylov-Bogoliubov-Mitropolskii for fifth order critically damped nonlinear systems. Furthermore, Rahaman and Kawser [15] expounded analytical approximate solutions of fifth order more critically damped nonlinear systems.

This study seeks to find solutions of fifth order critically damped nonlinear systems where two of the eigenvalues are equal and smaller than the other three distinct eigenvalues. This paper shows that the obtained perturbation results show good coincidence with the numerical results for different sets of initial conditions and eigenvalues.

2. The Method

Consider a fifth order weakly nonlinear ordinary differential system

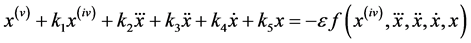(1)

where 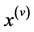and 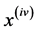denote the fifth and fourth derivatives respectively and over dots represent the first, second and third derivatives of x with respect to t; 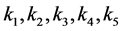are constants, 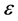is a sufficiently small and positive

parameter and 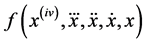is the given nonlinear function. Let us choose that the characteristic equation of

the linear equation of (1) has five eigenvalues, where two of the eigenvalues are equal and other three are distinct. Suppose the eigenvalues are 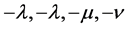and.

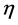When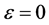, the solution of the corresponding linear equation of (1) is

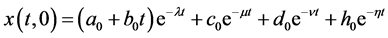(2)

where 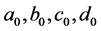and 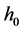are integral constants.

When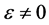, following Alom [16] , an asymptotic solution of (1) is found in the form

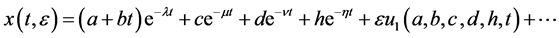(3)

where 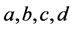and h are functions of t and they satisfy the first order differential equations

(4)

In order to determine the unknown functions and we differentiate the proposed solution (3) fifth times with respect to t, substituting the value of x and the derivatives in the original equation (1), utilizing the relation presented in (4) and finally equating the coefficients of, we obtain

(5)

where

and.

In this investigation, we have expanded the function in the Taylor’s series (see also Murty et al. [5] for details) about the origin in powers of t. Therefore, we obtain

(6)

Here the limits of and m are from 0 to. But for a particular problem they have some definite values. Therefore, using (6) in (5), we obtain

(7)

Following the KBM method, Sattar [7] , Alam [17] , Alam and Sattar ( [18] [19] ) imposed the condition that does not contain the fundamental terms of. Therefore, Equation (7) can be separated in the following way:

(8)

(9)

Now, equating the coefficients of and from both sides of Equation (8), we obtain

(10)

(11)

Solution of Equation (10) is

(12)

where

Substituting the value of from Equation (12) into Equation (11), we obtain

(13)

Different authors imposed different conditions according to the behavior of the systems, such as Alam ( [20] , [21] ) imposed the condition Consequently, we have investigated the solutions for the case. Thus, we shall be able to separate the Equation (13) for the unknown functions and; and solving them. Thus, substituting the values of and into the Equation (4) and integrating, we shall obtain the values of and h. Equ- ation (9) is a fifth order inhomogeneous linear differential equation. Therefore, it can be solved for by the well-known operator method. Hence, the determination of the first order approximate solution is completed.

3. Example

As an example of the above method, we consider the weakly nonlinear differential system

(14)

Comparing (14) and (1), we obtain

(15)

Now, comparing Equations (6) and (15), we obtain

(16)

For Equation (14), the Equations (9) to (11) respectively become

(17)

(18)

(19)

The solution of the Equation (18) is

(20)

where

Putting the value of from Equation (21) into Equation (20), we obtain

(21)

Since the relation among the eigenvalues, so the Equation (21) can be separated for the unknown functions and in the following way:

(22)

Solving Equation (22), we obtain

(23)

where ,

(24)

where

(25)

where

(26)

where ,

And the solution of the Equation (18) is

(27)

where

Substituting the values of and from Equations (23), (20), (24), (25) and (26) into Equation (4), we obtain

(28)

Here the equations of (28) have no exact solutions, but since and are proportional to the small parameter, so they are slowly varying functions of time t. Therefore, it is possible to replace and h by their respective values obtained in linear case in the right hand side of Equation (28). Murty and Deekshatulu [22] and Murty et al. [5] first made such type of amendment to solve similar type of nonlinear equations. Thus, the solution of (28) is

(29)

We, therefore, obtain the first approximate solution of the Equation (14) as

(30)

where and h are given by the Equation (29) and is given by (27).

4. Results and Discussion

Generally, the perturbation solution is compared to the numerical solution in order to test the accuracy of the approximate solution obtained by a certain perturbation method. First, we have considered the eigenvalues and. We have then computed using (30), in which and h are obtained from (30) and is calculated from Equation (27) together with initial conditions and when. Throughout the paper all the figures (Figures 1-3) represent the perturbation results which are displayed by the continuous line and the corresponding numerical results have been computed by fourth-order Runge-Kutta method, which are plotted by a discrete line.

Again, we have computed from (30) by considering and. We have computed using (30), in which and h are obtained from (30) and is calculated from Equation (27) together with initial conditions and when

Finally, we have computed from (30) by considering and We have computed using (30), in which and h are obtained from (30) and is calculated from Equation (27) together with initial conditions and when

5. Conclusion

In this paper, we have obtained an analytical approximate solution based upon the KBM method of fifth order critically damped nonlinear systems. Moreover, we have shown in this paper that the results obtained by the proposed method correspond satisfactorily to the numerical results obtained by the fourth order Runge-Kutta method.

Acknowledgements

The authors appreciate the precious comments of Mr. Md. Mizanur Rahman, Associate Professor, Department of Mathematics, Islamic University, Bangladesh, on the earlier draft of this article. Special thanks are due to Mr. Md. Imamunur Rahman who has assisted the authors in editing this paper.

Cite this paper

Md. FirojAlam,M. AbulKawser,Md. MahafujurRahaman, (2015) Asymptotic Solutions for the Fifth Order Critically Damped Nonlinear Systems in the Case for Small Equal Eigenvalues. American Journal of Computational Mathematics,05,414-425. doi: 10.4236/ajcm.2015.54036

References