American Journal of Computational Mathematics
Vol. 1 No. 1 (2011) , Article ID: 4448 , 4 pages DOI:10.4236/ajcm.2011.11002
An O(k2+kh2+h4) Accurate Two-level Implicit Cubic Spline Method for One Space Dimensional Quasi-linear Parabolic Equations
1Department of Mathematics, Faculty of Mathematical Sciences, University of Delhi, Delhi, India
2Department of Mathematics, Deenbandhu Chhotu Ram University of Science & Technology, Murthal, India
E-mail: rmohanty@maths.du.ac.in, vijay_15dahiya@yahoo.com
Received February 23, 2011; revised March 6, 2011; accepted March 6, 2011
Keywords: Quasi-Linear Parabolic Equation, Implicit Method, Cubic Spline Approximation, Diffusion-Convection Equation, Singular Equation, Burgers’ Equation, Reynolds Number
Abstract
In this piece of work, using three spatial grid points, we discuss a new two-level implicit cubic spline method of O(k2 + kh2 + h4) for the solution of quasi-linear parabolic equation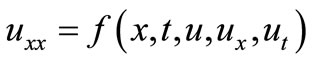 , 0< x <1, t > 0 subject to appropriate initial and Dirichlet boundary conditions, where h > 0, k > 0 are grid sizes in space and time-directions, respectively. The cubic spline approximation produces at each time level a spline function which may be used to obtain the solution at any point in the range of the space variable. The proposed cubic spline method is applicable to parabolic equations having singularity. The stability analysis for diffusionconvection equation shows the unconditionally stable character of the cubic spline method. The numerical tests are performed and comparative results are provided to illustrate the usefulness of the proposed method.
, 0< x <1, t > 0 subject to appropriate initial and Dirichlet boundary conditions, where h > 0, k > 0 are grid sizes in space and time-directions, respectively. The cubic spline approximation produces at each time level a spline function which may be used to obtain the solution at any point in the range of the space variable. The proposed cubic spline method is applicable to parabolic equations having singularity. The stability analysis for diffusionconvection equation shows the unconditionally stable character of the cubic spline method. The numerical tests are performed and comparative results are provided to illustrate the usefulness of the proposed method.
1. Introduction
The use of cubic splines for the numerical solution of linear two point boundary value problems has been discussed by Bickley [1], Fyfe [2], Albasiny and Hoskins [3] and Rubin and Khosla [4]. Later, Chawla et al [5,6] have developed fourth order accurate cubic spline methods for singular two point boundary value problems. In 1983, Jain and Aziz [7] have derived fourth order cubic spline method for the solution of general two point non-linear boundary value problems. Khan and Aziz [8] have used parametric cubic spline approach for the solution of a system of second order boundary value problems. Recently, Monoj Kumar et al [9-11], and Rashidinia et al [12-13] have discussed higher order cubic spline finite difference method for singular two point boundary value problems. A cubic spline technique for the solution of 1D heat equation was discussed by Papamichael and Whiteman [14]. This technique was extended by Fleck Jr [15] and Raggett and Wilson [16] for solving one-dimensional wave equation. Archer [17] has developed a fourth order collocation method for quasi-linear parabolic equation. Jain and Lohar [18] have solved non-linear parabolic equations by using second order cubic spline method. Recently, Rashidinia et al [19] have studied nonpolynomial cubic spline methods for the solution of parabolic equations. High order finite difference methods for the solution of non-linear parabolic equations have been discussed by Jain et al [20] and Mohanty et al [21-22]. In the present paper, using three spatial grid points (see Figure 1), a new cubic spline technique similar to that of Jain and Aziz [7] is developed for the solution of one dimensional general quasi-linear parabolic equation. We use the cubic spline approximation in the space direction together with a finite difference approximation in the time direction. This approximation produces at each time level a cubic spline function, which may be used to obtain the solution at any point in the range of the space variable. In next section, we discuss the cubic spline method. In Section 3, we give the complete derivation of the method. Stability of a linear difference scheme, which is consistent with diffusionconvection equation, is discussed in Section 4 and it is shown that the linear scheme is unconditionally stable. Difficulties were experienced in the past for the high order cubic spline solution of parabolic equations with
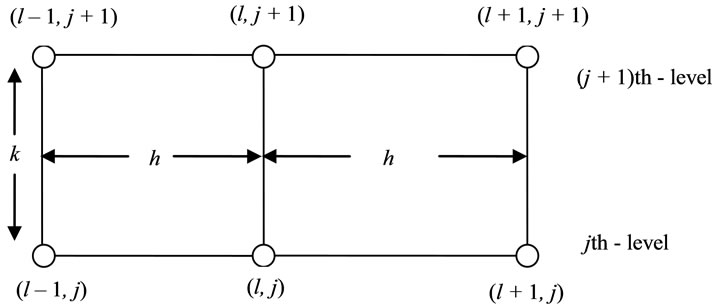
Figure 1. (Schematic representation of two-level scheme).
singular coefficients. The solution usually deteriorates in the vicinity of the singularity. In this paper, we refine our technique in such a way that the solution retains its order and accuracy everywhere in the solution region. In Section 5, we compared the proposed cubic spline method with the corresponding finite difference methods discussed in [20-22]. Finally, concluding remarks are given in Section 6.
2. The Two Level Implicit Cubic Spline Method
Consider the quasi-linear parabolic equation in which the function u(x,t) satisfies
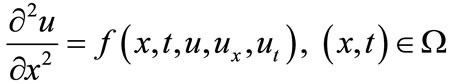 (1)
(1)
where the solution space is defined by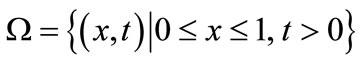 .
.
The initial condition is given by
 (2)
(2)
and the boundary conditions are given by
 (3)
(3)
where 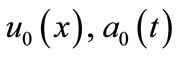 and
and  are given smooth functions.
are given smooth functions.
The region 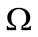 is covered in the usual manner by a rectangular net
is covered in the usual manner by a rectangular net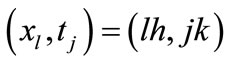 ,
, 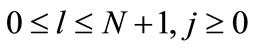 , where (N + 1)h = 1, and h > 0 and k > 0 are grid sizes in xand t-directions, respectively. The mesh ratio parameter is given by
, where (N + 1)h = 1, and h > 0 and k > 0 are grid sizes in xand t-directions, respectively. The mesh ratio parameter is given by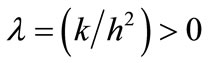 . Let
. Let  be the exact solution value of u(x,t) and
be the exact solution value of u(x,t) and 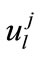 denotes a discrete approximation to u(x,t) at the grid point
denotes a discrete approximation to u(x,t) at the grid point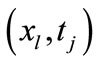 .
.
We let 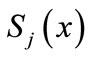 denote the cubic spline interpolating the value
denote the cubic spline interpolating the value 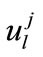 at the jth time level, and is given by
at the jth time level, and is given by
 (4)
(4)
which satisfies at jth-level the following properties:
1) 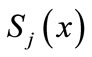 coincides with a polynomial of degree three on each
coincides with a polynomial of degree three on each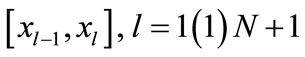 , j > 0
, j > 0
2)  and
and
3) 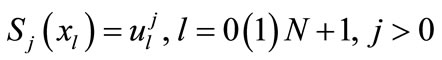 ,
,
and where
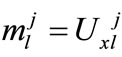 and
and

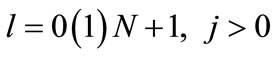 .
.
We consider the following approximations:
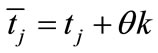 (5)
(5)
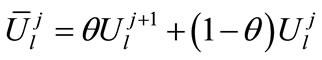 (6a)
(6a)
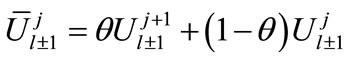 (6b)
(6b)
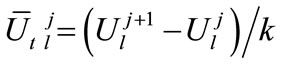 (7a)
(7a)
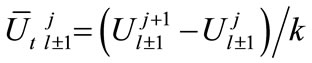 (7b)
(7b)
 (8a)
(8a)
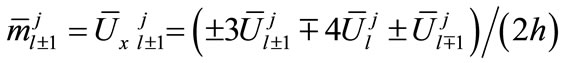 (8b)
(8b)
 (9a)
(9a)
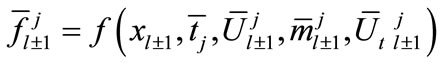 (9b)
(9b)
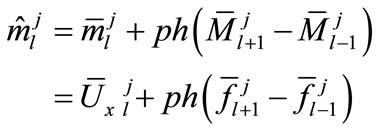 (10a)
(10a)
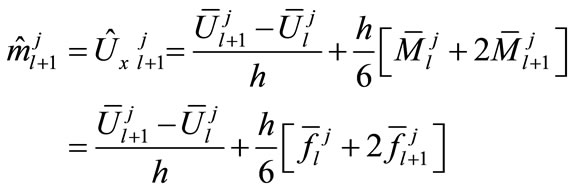 (10b)
(10b)
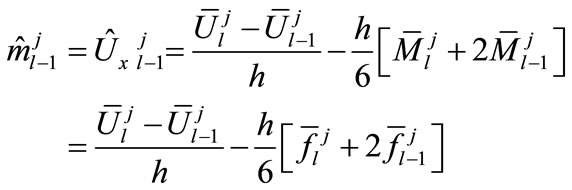 (10c)
(10c)
where
 etc.
etc.
Further, we define
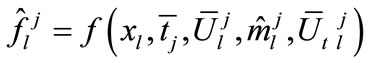 (11a)
(11a)
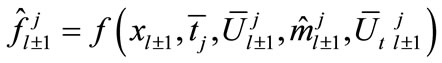 (11b)
(11b)
Then at each grid point , the cubic spline method with accuracy of O(k2 + kh2 + h4) for the solution of differential Equation (1) may be written as
, the cubic spline method with accuracy of O(k2 + kh2 + h4) for the solution of differential Equation (1) may be written as
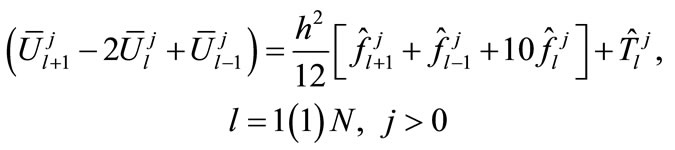 (12)
(12)
where  for
for 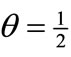 and
and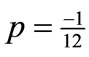 .
.
Note that, the initial and Dirichlet boundary conditions are given by (2) and (3), respectively. Incorporating the initial and boundary conditions, we can write the cubic spline method (12) in a tri-diagonal matrix form. If the differential Equation (1) is linear, we can solve the linear system using a tri-diagonal solver; in the non-linear case, we can use generalized Newton-Raphson method to solve the non-linear system (see Kelly [23], and Hageman and Young [24]).
3. Derivation of the Cubic Spline Method
For the derivation of the cubic spline method (12) for the solution of the quasi-linear parabolic Equation (1), we simply follow the approaches given by Jain and Aziz [7].
At the grid point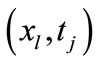 , let us denote
, let us denote
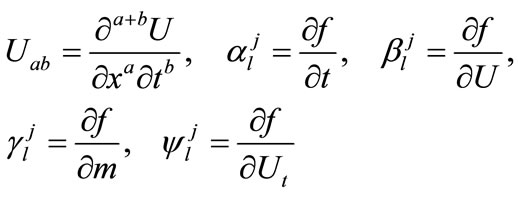 (13)
(13)
Further at the grid point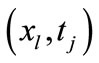 , we may write the differential Equation (1) as
, we may write the differential Equation (1) as
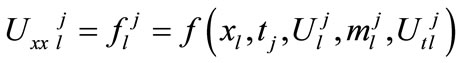 (14a)
(14a)
Similarly,
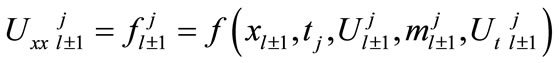 (14b)
(14b)
A difference method of accuracy of 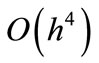 for the differential Equation (1) in the absence of first derivative terms may be written as
for the differential Equation (1) in the absence of first derivative terms may be written as
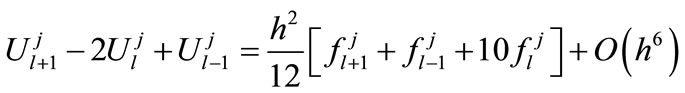 (15)
(15)
By the help of the notations (13) and simplifying (5)-(8b), we obtain
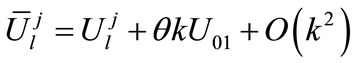 (16a)
(16a)
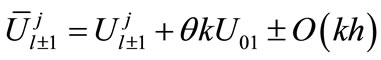 (16b)
(16b)
 (17a)
(17a)
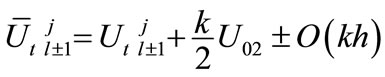 (17b)
(17b)
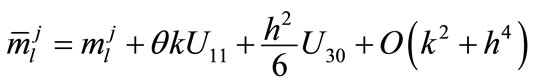 (18a)
(18a)
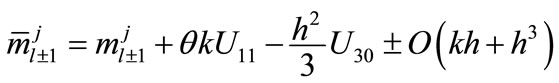 (18b)
(18b)
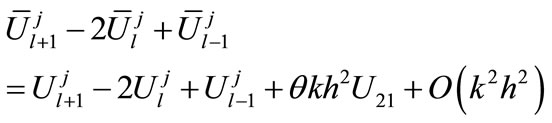 (19)
(19)
With the help of the approximations (5), (16a)-(18b), from (9a) and (9b), we obtain
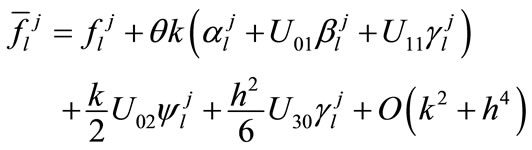 (20a)
(20a)
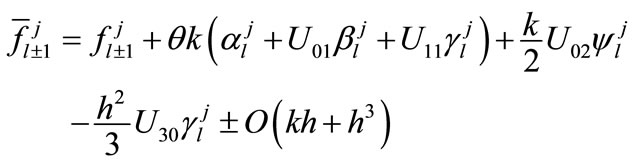 (20b)
(20b)
Using the approximations (18a), (18b), (20a), (20b) and simplifying (10a), we get
 (21)
(21)
From (21), it is easy to verify that for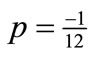 , we have
, we have
 (22a)
(22a)
Similarly, from (10b) and (10c), we have
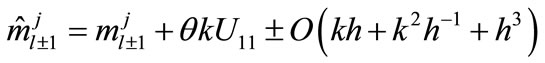 (22b)
(22b)
Finally, by the help of the approximations (5), (16a)-(17b), (22a)-(22b), from (11a) and (11b), we get
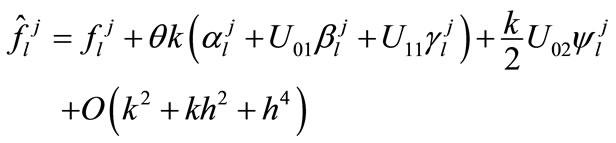 (23a)
(23a)
 (23b)
(23b)
Now differentiating the differential Equation (1) with respect to ‘t’ at the grid point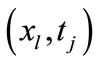 , we obtain a relation of the form
, we obtain a relation of the form
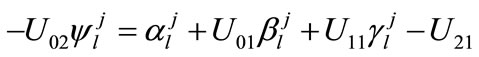 (24)
(24)
Using the approximations (19), (23a), (23b) and by the help of the relation (24), from (12) and (15), we obtain the local truncation error
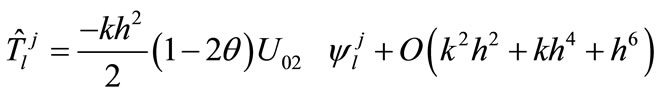 (25)
(25)
The proposed cubic spline method (12) to be of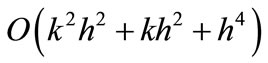 , the coefficient of
, the coefficient of 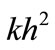 in (25) must be zero. Thus we obtain the value of
in (25) must be zero. Thus we obtain the value of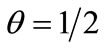 , for which
, for which .
.
4. Cubic Spline Scheme for Parabolic Equation with Singular Coefficients
Consider the linear parabolic equation of the form
 (26)
(26)
subject to appropriate initial and Dirichlet boundary conditions are prescribed by (2) and (3), respectively. Assume that the functions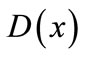 ,
, 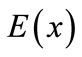 and
and 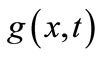
 .
.
For 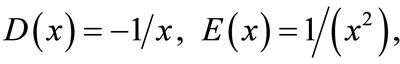 the equation above represents linear parabolic equation with singular coefficients. For
the equation above represents linear parabolic equation with singular coefficients. For 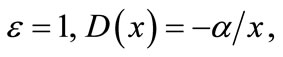
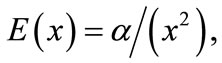 the above parabolic equation becomes a cylindrical and spherical problem for
the above parabolic equation becomes a cylindrical and spherical problem for 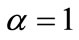 and 2, respectively.
and 2, respectively.
Applying the formula (12) to the differential Equation (26), we get
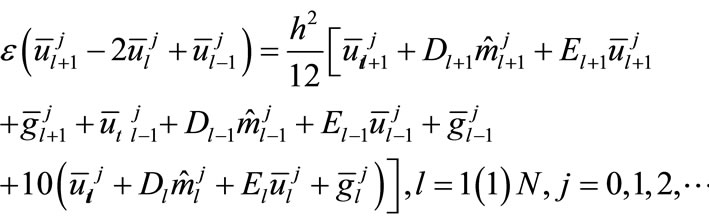 (27)
(27)
where
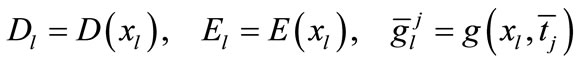 ,
,
 etc.
etc.
At the grid point , let us denote
, let us denote
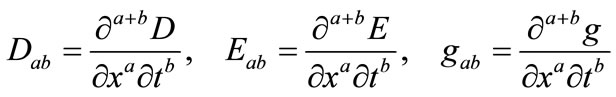 (28)
(28)
Note that, the cubic spline sheme (27) is of 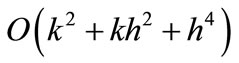 accuracy for the approximate solution of Equation (26). However, the scheme (27) fails to compute at l = 1 when the coefficients
accuracy for the approximate solution of Equation (26). However, the scheme (27) fails to compute at l = 1 when the coefficients 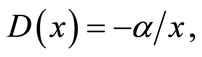
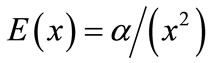 etc. In order to get a meaningful cubic spline scheme of
etc. In order to get a meaningful cubic spline scheme of 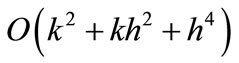 accuracy in compact operator form, we need the following approximations:
accuracy in compact operator form, we need the following approximations:
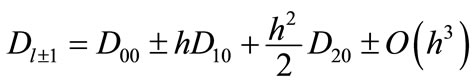 (29a)
(29a)
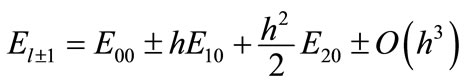 (29b)
(29b)
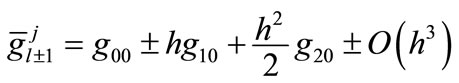 (29c)
(29c)
where
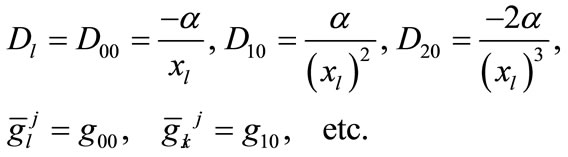
Now, by the help of the approximations (5)-(10c) and (29a)-(29c), neglecting high order terms, we can re-write the scheme (27) as a two-level implicit cubic spline scheme in operator compact form
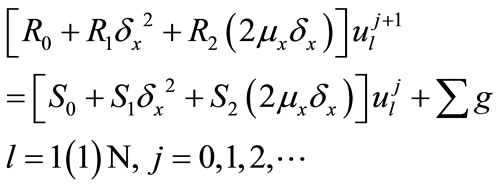 (30)
(30)
where
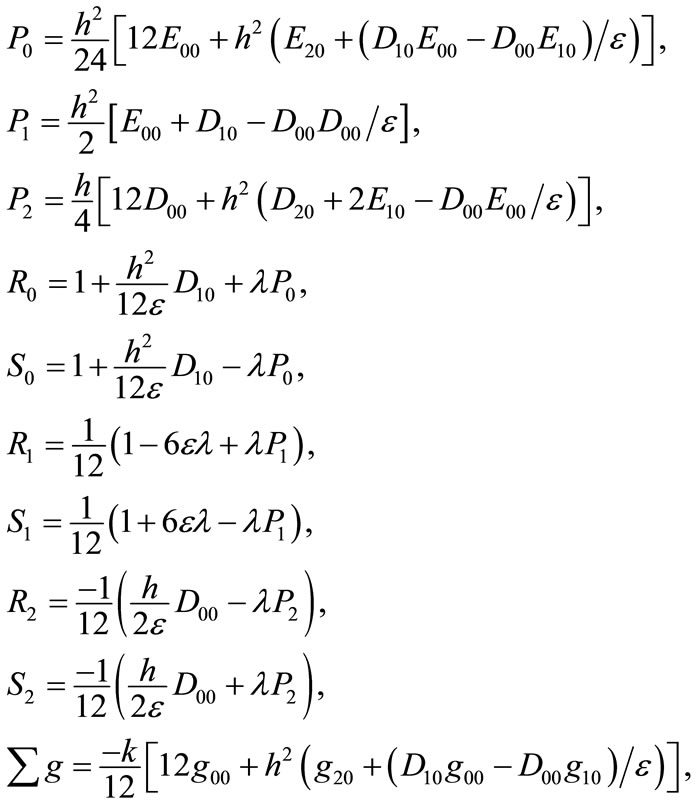
and
 and
and 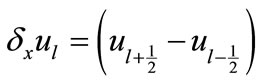
are averaging and central difference operators with respect to x-direction etc. The cubic spline scheme (30) has a local truncation error of  and is free from the terms
and is free from the terms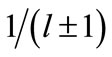 , and hence, it can be solved for l = 1(1)N in the region 0 < x < 1, t > 0.
, and hence, it can be solved for l = 1(1)N in the region 0 < x < 1, t > 0.
Now consider the linear singular parabolic equation
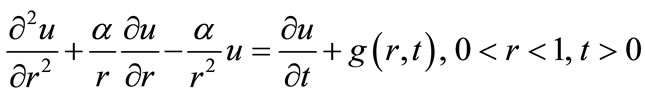 (31)
(31)
For  and 2, the equation above represents the parabolic equation in cylindrical and spherical coordinates respectively. Replacing the variable x by r and substituting
and 2, the equation above represents the parabolic equation in cylindrical and spherical coordinates respectively. Replacing the variable x by r and substituting 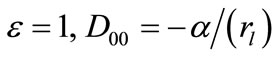
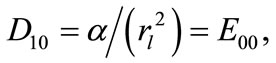
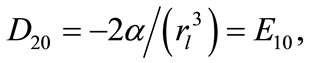
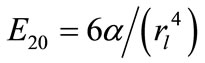 etc. in Equation (30), we can get a two level implicit cubic spline scheme of
etc. in Equation (30), we can get a two level implicit cubic spline scheme of 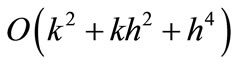 for the solution of linear singular parabolic Equation (31).
for the solution of linear singular parabolic Equation (31).
Now, consider the linear diffusion-convection parabolic equation
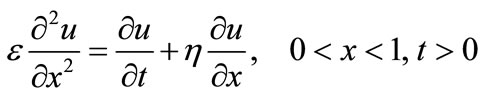 (32)
(32)
The constant terms 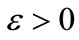 and
and 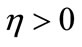 are called the diffusivity and convective terms, respectively. For
are called the diffusivity and convective terms, respectively. For , the problem is said to be convection dominated problem. Substituting
, the problem is said to be convection dominated problem. Substituting 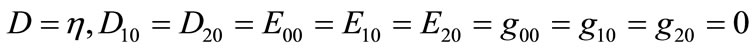 in the formula (30), we obtain a two-level implicit cubic spline scheme
in the formula (30), we obtain a two-level implicit cubic spline scheme
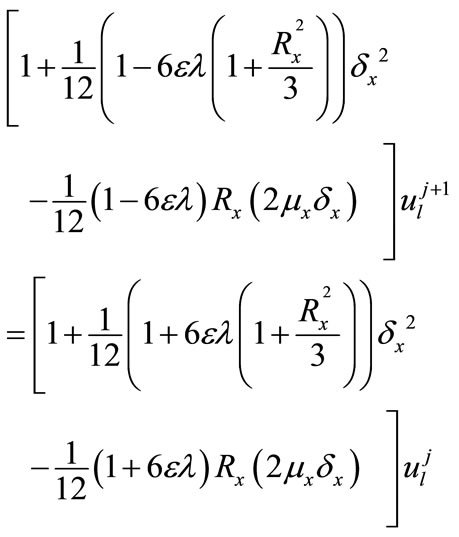 (33)
(33)
where 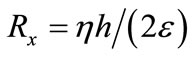 represents the cell-Reynolds number. The scheme (33) is of
represents the cell-Reynolds number. The scheme (33) is of 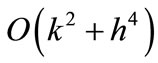 and consistent with the differential Equation (32). Further note that, the scheme (33) is identical with the scheme discussed by Jain et al [20]. It has been shown that, the scheme (33) is unconditionally stable and using this scheme computational result for the solution of Equation (32) is reported in [20].
and consistent with the differential Equation (32). Further note that, the scheme (33) is identical with the scheme discussed by Jain et al [20]. It has been shown that, the scheme (33) is unconditionally stable and using this scheme computational result for the solution of Equation (32) is reported in [20].
5. Numerical Results
In order to demonstrate the application of the proposed cubic spline method, we have solved the following four problems whose analytical solutions are known to us. The right-hand side homogeneous functions, initial and boundary conditions can be obtained using the exact solution as a test procedure. We have also compared the proposed cubic spline method with the corresponding finite difference method of 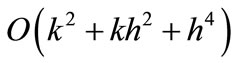 discussed in [20-22]. We have solved the system of linear difference equations using a tri-diagonal solver and the system of non-linear difference equations by Newton-Raphson method (see Kelly [23], and Hageman and Young [24]). All computations were performed using double length arithmetic.
discussed in [20-22]. We have solved the system of linear difference equations using a tri-diagonal solver and the system of non-linear difference equations by Newton-Raphson method (see Kelly [23], and Hageman and Young [24]). All computations were performed using double length arithmetic.
Example 1: (Linear parabolic equation with singular coefficients)
 (34)
(34)
The exact solution is given by u(x,t) = exp(-εt) sinh x. The root mean square (RMS) errors at t = 1.0 are tabulated in Table 1 for 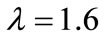 and small values of ε > 0.
and small values of ε > 0.
Example 2: The Equation (31) is solved whose exact solution is u(r,t)=exp(-t) cosh r. The RMS errors at t = 1.0 are tabulated in Table 2 for α = 1 and 2 for a fixed value of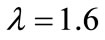 .
.
Example 3: (Burgers’ Equation )
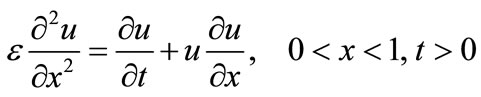 (35)
(35)
The exact solution is given by
 , where
, where 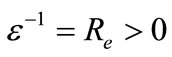
is termed as a Reynolds number. The RMS errors at t = 1.0 are tabulated in Table 3 for different values of Re and for a fixed value of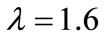 .
.
Example 4: (Non-linear Parabolic Equation )
 (36)
(36)
The exact solution is given by u(x,t)=exp(-t) sin(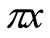 ). The RMS errors at t = 1.0 are tabulated in Table 4 for various values of α for a fixed parameter value of
). The RMS errors at t = 1.0 are tabulated in Table 4 for various values of α for a fixed parameter value of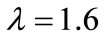 .
.

Table 1. Example 1: The RMS errors.
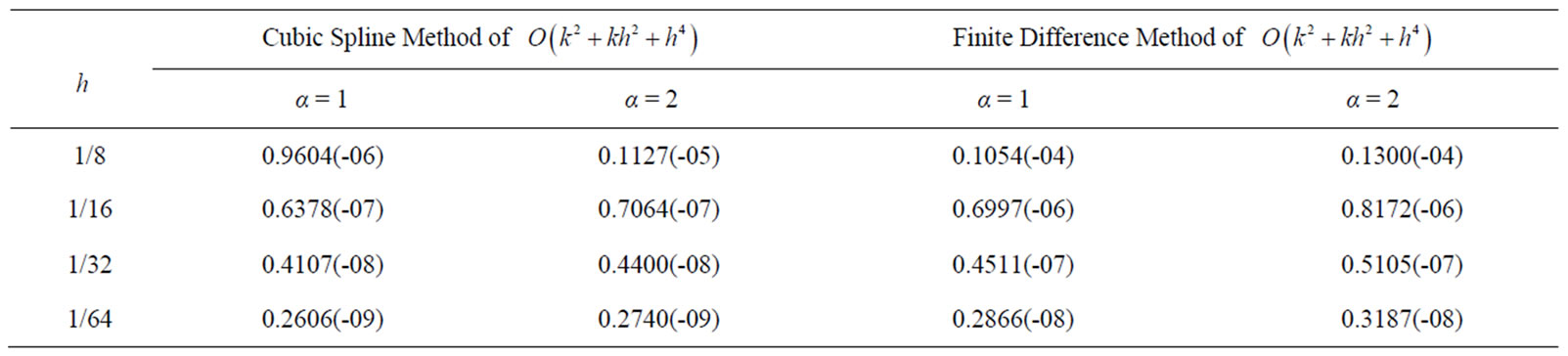
Table 2. Example 2: The RMS errors.

Table 3. Example 3: The RMS errors.

Table 4. Example 4: The RMS errors.
6. Final Remarks
We presented a new cubic spline discretization strategy of 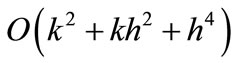 for the solution of one-space dimensional quasi-linear parabolic partial differential equations. The proposed method with a little modification is applicable to singular parabolic problems. For singular problems, our numerical results show that the new cubic spline method may be advantageous compared with the corresponding finite difference method discussed in [20-22]. Numerical results for non-linear problems also show better as compared to the method discussed in [20-22], and numerical oscillation do not appear for high Reynolds number.
for the solution of one-space dimensional quasi-linear parabolic partial differential equations. The proposed method with a little modification is applicable to singular parabolic problems. For singular problems, our numerical results show that the new cubic spline method may be advantageous compared with the corresponding finite difference method discussed in [20-22]. Numerical results for non-linear problems also show better as compared to the method discussed in [20-22], and numerical oscillation do not appear for high Reynolds number.
7. Acknowledgement
The authors thank the reviewers for their valuable suggestions, which substantially improved the standard of the paper.
8. References
- W. G. Bickley, “Piecewise Cubic Interpolation and Two Point Boundary Value Problems,” Computer Journal, Vol. 11, No. 2, 1968, pp. 206-208.
- D. J. Fyfe, “The Use of Cubic Splines in the Solution of Two Point Boundary Value Problems,” Computer Journal, Vol. 12, No. 2, 1969, pp. 188-192. doi:10.1093/comjnl/12.2.188
- E. L. Albasiny and W. D. Hoskins, “Increased Accuracy Cubic Spline Solutions to Two Point Boundary Value Problems,” Journal of the Institute of Mathematics and its Applications, Vol. 9, No.1, 1972, pp. 47-55. doi:10.1093/imamat/9.1.47
- S. G. Rubin and P. K. Khosla, “Higher Order Numerical Solutions Using Cubic Splines,” American Institute of Aeronautics and Astronautics Journal. Vol. 14, No.7, 1976, pp. 851-858.
- M. M. Chawla and R. Subramanian, “A New Spline Method for Singular Two Point Boundary Value Problems,” International Journal of Computer Mathematics, Vol. 24, No. 3-4, 1988, pp. 291-310. doi:10.1080/00207168808803650
- M. M. Chawla, R. Subramanian and H. L. Sathi, “A Fourth Order Spline Method for Singular Two Point Boundary Value Problems,” Journal of Computational and Applied Mathematics, Vol. 21, No. 2, 1988, pp. 189-202. doi:10.1016/0377-0427(88)90267-1
- M. K. Jain and T. Aziz, “Cubic Spline Solution of Two Point Boundary Value Problems with Significant First Derivatives,” Computer Methods in Applied Mechanics and Engineering, Vol. 39, No. 1, 1983, pp. 83-91. doi:10.1016/0045-7825(83)90075-0
- A. Khan and T. Aziz, “Parametric Cubic Spline Approach to the Solution of a System of Second Order Boundary Value Problems,” Journal of Optimization Theory and Applications, Vol. 118, No. 1, 2003, pp. 45-54. doi:10.1023/A:1024783323624
- Manoj Kumar, “A Fourth Order Spline Finite Difference Method for Singular Two Point Boundary Value Problems,” International Journal of Computer Mathematics, Vol. 80, No.12, 2003, pp. 1499-1504. doi:10.1080/0020716031000148179
- Manoj Kumar, “Higher Order Method for Singular Boundary Value Problems by Using Spline Function,” Applied Mathematics and Computations, Vol. 192, No.1, 2007, pp. 175-179. doi:10.1016/j.amc.2007.02.156
- Manoj Kumar and P. K. Srivastava, “Computational Techniques for Solving Differential Equations by Cubic, Quintic and Sextic Spline,” International Journal for Computational Methods in Engineering Science and Mechanics, Vol. 10, No. 1, 2009, pp. 108-115. doi:10.1080/15502280802623297
- J. Rashidinia, R. Mohammadi and M. Ghasemi, “Cubic Spline Solution of Singularly Perturbed Boundary Value Problems with Significant First Derivatives,” Applied Mathematics and Computations, Vol. 190, No. 2, 2007, pp. 1762-1766.
- J. Rashidinia, R. Mohammadi, R. Jalilian and M. Ghasemi, “Convergence of Cubic Spline Approach to the Solution of a System of Boundary Value Problems,” Applied Mathematics and Computations, Vol. 192, No. 2, 2007, pp. 319-331. doi:10.1016/j.amc.2007.03.008
- N. Papamichael and J. R. Whiteman, “A Cubic Spline Technique for the One-dimensional Heat Equation,” IMA Journal of Applied Mathematics, Vol. 11, No. 1, 1973, pp. 111-113. doi:10.1093/imamat/11.1.111
- J. A. Fleck Jr., “A Cubic Spline Method for Solving the Wave Equation of Non-linear Optics,” Journal of Computational Physics, Vol. 16, No. 4, 1974, pp. 324-341. doi:10.1016/0021-9991(74)90043-6
- G. F. Raggett and P. D. Wilson, “A Fully Implicit Finite Difference Approximation to the One-dimensional Wave Equation Using a Cubic SplineTechnique,” Journal of the Institute of Mathematics and its Applications, Vol. 14, No. 1, 1974, pp. 75-77. doi:10.1093/imamat/14.1.75
- D. Archer, “An O(h4) Cubic Spline Collocation Method for Quasi-linear Parabolic Equation,” SIAM Journal of Numerical Analysis, Vol. 14, No. 4, 1977, pp. 620-637. doi:10.1137/0714042
- P. C. Jain and B. L. Lohar, “Cubic Spline Technique for Coupled Non-linear Parabolic Equations,” Computers & Mathematics with Applications, Vol. 5, No. 3, 1979, pp. 179-195. doi:10.1016/0898-1221(79)90040-3
- J. Rashidinia and R. Mohammadi, “Non-polynomial Cubic Spline Methods for the Solution of Parabolic Equations,” International Journal of Computer Mathematics, Vol. 85, No.5, 2008, pp. 843-850. doi:10.1080/00207160701472436
- M. K. Jain, R. K. Jain and R. K. Mohanty, “A Fourth Order Difference Method for the One-dimensional General Quasi-linear Parabolic Partial Differential Equation,” Numerical Methods for Partial Differential Equations, Vol. 6, No.4, 1990, pp. 311-319. doi:10.1002/num.1690060403
- R. K. Mohanty, “An O(k2 + h4) Finite Difference Method for One Space Burgers’ Equation in Polar Coordinates,” Numerical Methods for Partial Differential Equations, Vol. 12, No. 5, 1996, pp. 579-583. doi:10.1002/(SICI)1098-2426(199609)12:5<579::AID-NUM3>3.0.CO;2-H
- R. K. Mohanty and M. K. Jain, “Single Cell Finite Difference Approximations of O(kh2 + h4) for (
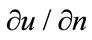 ) for one Space Dimensional Non-linear Parabolic Equations,” Numerical Methods for Partial Differential Equations, Vol. 16, No.4, 2000, pp. 408-415. doi:10.1002/1098-2426(200007)16:4<408::AID-NUM5>3.0.CO;2-J
) for one Space Dimensional Non-linear Parabolic Equations,” Numerical Methods for Partial Differential Equations, Vol. 16, No.4, 2000, pp. 408-415. doi:10.1002/1098-2426(200007)16:4<408::AID-NUM5>3.0.CO;2-J - C. T. Kelly, “Iterative Methods for Linear and Non-linear Equations,” SIAM Publication, Philadelphia, 1995.
- L. A. Hageman and D. M. Young, “Applied Iterative Methods,” Dover Publication, New York, 2004.

