World Journal of Nuclear Science and Technology
Vol.3 No.2A(2013), Article ID:33246,10 pages DOI:10.4236/wjnst.2013.32A002
Fukushima Plutonium Effect and Blow-Up Regimes in Neutron-Multiplying Media
1Department of Theoretical and Experimental Nuclear Physics, Odessa National Polytechnic University, Odessa, Ukraine
2State Ecological Academy for Postgraduate Education, Kiev, Ukraine
Email: *siiis@te.net.ua
Copyright © 2013 V. D. Rusov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 27, 2013; revised May 29, 2013; accepted June 11, 2013
Keywords: Nuclear Burning Wave; Temperature Blow-Up Regimes; Fukushima Plutonium Effect
ABSTRACT
It is shown that the capture and fission cross-sections of 238U and 239Pu increase with temperature within 1000 K - 3000 K range, in contrast to those of 235U, that under certain conditions may lead to the so-called blow-up modes, stimulating the anomalous neutron flux and nuclear fuel temperature growth. Some features of the blow-up regimes in neutronmultiplying media are discussed.
1. Introduction
It is known that after the loss of coolant at three nuclear reactors during Fukushima nuclear accident its nuclear fuel melted. It means that the temperature in the active zone at some moments reached the melting point of uranium-oxide fuel1, i.e. ~3000˚C.
Surprisingly enough, scientific literature today contains absolutely no either experimental or even theoretically calculated data on behavior of the 238U and 239Pu capture and fission cross-sections depending on temperature at least in 1000˚C - 3000˚C range. At the same time there are serious reasons to believe that the crosssection values of the mentioned elements increase with temperature. At least we may point, for example, to the qualitative estimates by Ukraintsev [1], Obninsk Institute of Atomic Energetics (Russia), that confirm the possibility for 239Pu cross-sections growth in 300˚C - 1500˚C range.
Obviously, such anomalous temperature dependence of 238U and 239Pu capture and fission cross-sections may change the neutron and heat kinetics of nuclear reactors drastically. This is also true for the perspective new generation fast reactors (uranium-plutonium of Feoktistov [2] and thorium-uranium of Teller [3] type), that we classify as fast TWR reactors. Hence it is very important to know the anomalous temperature behavior of 238U and 239Pu capture and fission cross-sections, and furthermore it becomes critically important to know their influence on the heat transfer kinetics, since it may become a reason of the positive feedback2 (PF) with neutron kinetics leading to undesirable solution stability loss (the nuclear burning wave) as well as to a trivial reactor runaway with a subsequent nontrivial catastrophe.
A special case of PF is a non-linear PF, which leads to the system evolution in so-called blow-up mode [4-9], or in other words, in such a dynamic mode when one or several modeled values (e.g. temperature and neutron flux) grows to infinity at a finite time. In reality, a phase transition is observed instead of the infinite values in this case, and this can in its turn become a first stage or a precursor of the future technogenic disaster.
Investigation of the temperature dependence of 238U and 239Pu capture and fission cross-sections in 300˚C - 3000˚C range, and correspondingly, the heat transfer kinetics and its influence on neutron kinetics in TWR, is the main goal of the present paper.
2. Temperature Blow-Up Regimes in Neutron-Multiplying Media
Heat transfer equation for uranium-plutonium fissile medium is:
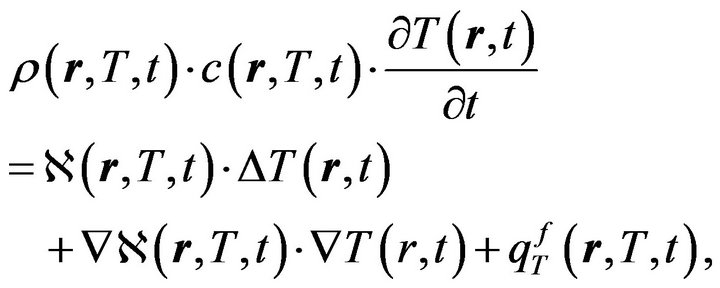 (1)
(1)
where the effective medium density is
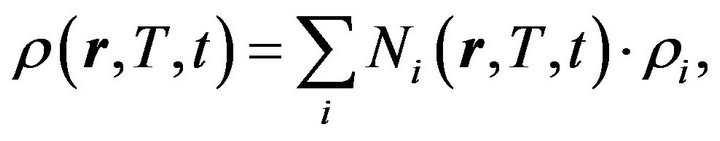 (2)
(2)
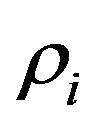 are tabulated values,
are tabulated values, 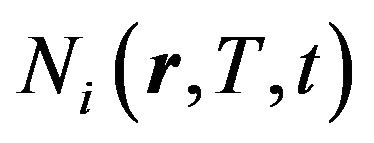 are the concentrations of the medium components, while the effective specific heat capacity (accounting for the medium components heat capacity values ci) and fissile material heat conductivity coefficient (accounting for the medium components heat conductivity coefficients
are the concentrations of the medium components, while the effective specific heat capacity (accounting for the medium components heat capacity values ci) and fissile material heat conductivity coefficient (accounting for the medium components heat conductivity coefficients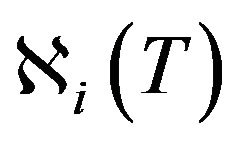 ) respectively are:
) respectively are:
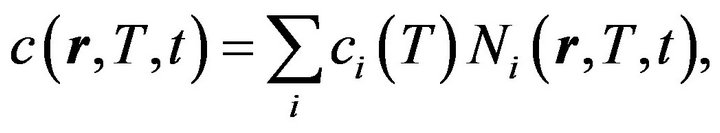 (3)
(3)
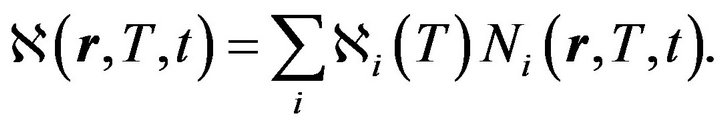 (4)
(4)
Here 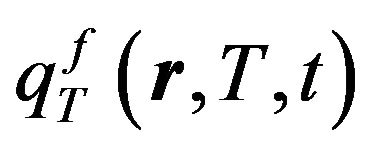 is the heat source density produced by nuclear fissions Ni of fissile metal components which vary in time.
is the heat source density produced by nuclear fissions Ni of fissile metal components which vary in time.
Theoretical temperature dependence of heat capacity c(T) for metals is known: at low temperatures c(t) ~ T3, and at high temperatures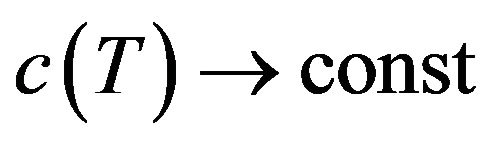 , where the constant value (const ≈ 6 Cal/(mol∙deg)) is determined by Dulong-Petit law. At the same time it is known that thermal expansion coefficient is small for metals, therefore the specific heat capacity at constant volume cv almost equals to the specific heat capacity at constant pressure cp. On the other hand, the theoretical dependence of heat conductivity
, where the constant value (const ≈ 6 Cal/(mol∙deg)) is determined by Dulong-Petit law. At the same time it is known that thermal expansion coefficient is small for metals, therefore the specific heat capacity at constant volume cv almost equals to the specific heat capacity at constant pressure cp. On the other hand, the theoretical dependence of heat conductivity 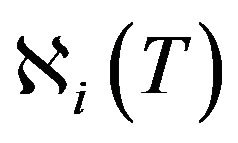 at high temperature of “fissile” metals is not known, while it is experimentally determined that the heat conductivity coefficient
at high temperature of “fissile” metals is not known, while it is experimentally determined that the heat conductivity coefficient 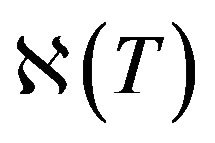 of fissile medium is a non-linear function of temperature (e.g. see [10], where heat conductivity coefficient is given for α-uranium 238 and for metallic plutonium 239, and also [11]).
of fissile medium is a non-linear function of temperature (e.g. see [10], where heat conductivity coefficient is given for α-uranium 238 and for metallic plutonium 239, and also [11]).
Further for solving thermal conductivity equation we used the following initial and boundary conditions:
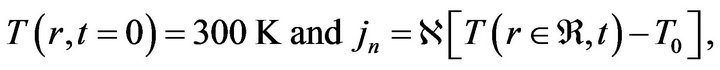 (5)
(5)
where jn is the normal (to the fissile medium boundary) heat flux density component, 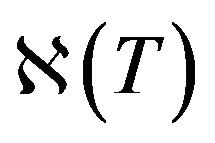 is the thermal conductivity coefficient,
is the thermal conductivity coefficient, 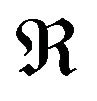 is the fissile medium boundary, T0 is the temperature of the medium adjacent to the active zone.
is the fissile medium boundary, T0 is the temperature of the medium adjacent to the active zone.
Obviously, if the cross-sections of some fissile nuclides increase with temperature, then due to exothermic nature of the nuclei fission reaction, the significantly non-linear kinetics of mother and daughter nuclides in the nuclear reactor will immediately result in an autocatalytic increase of generated heat, just like in the autocatalytic processes of exothermic chemical reactions. The heat source density 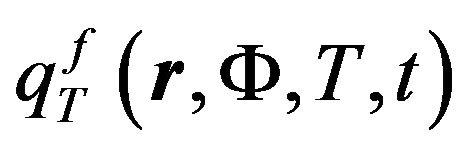 which characterizes the amount of generated heat in this case will be:
which characterizes the amount of generated heat in this case will be:
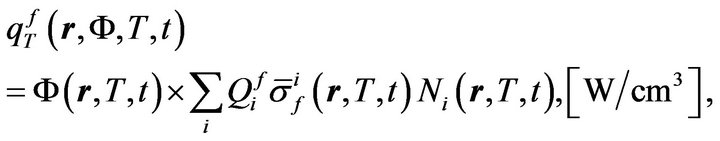 (6)
(6)
where
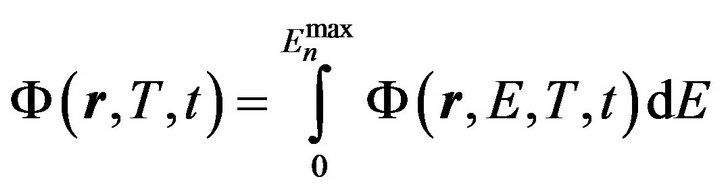
is the total neutron flux density; 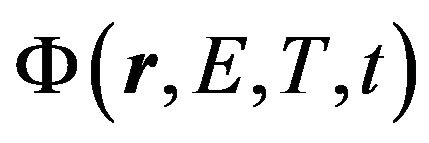 is the density of a neutron flux with energy
is the density of a neutron flux with energy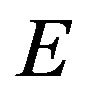 ;
; 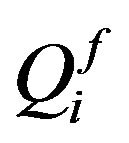 is the mean heat released in one fission event of the i-th nuclide;
is the mean heat released in one fission event of the i-th nuclide;
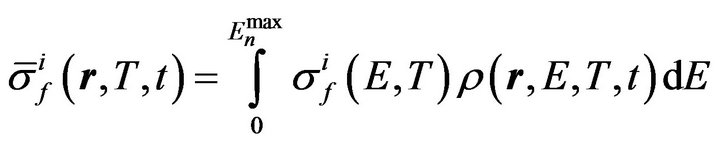
is the fission cross-section of the i-th nuclide averaged over the neutron spectrum;
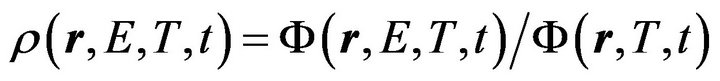
is the probability density function of the neutron energy distribution; 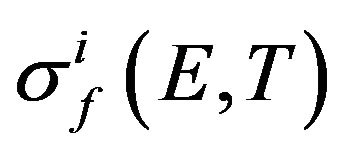 is the microscopic fission crosssection of the i-th nuclide, which is known to depend on the neutron energy and fissile medium temperature (Doppler effect [12]);
is the microscopic fission crosssection of the i-th nuclide, which is known to depend on the neutron energy and fissile medium temperature (Doppler effect [12]); 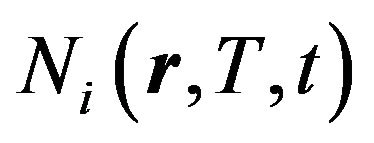 is the density of the i-th nuclide nuclei.
is the density of the i-th nuclide nuclei.
As follows from (6), in order to build a density function of the heat source, it is necessary to solve a problem related to the construction of a theoretical dependence of the cross-sections 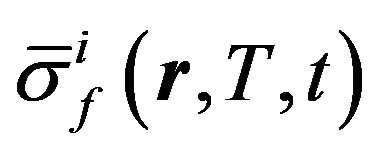 averaged over the neutron spectrum on the temperature of reactor fuel (fissile medium). As is known, the impact of the nuclei thermal motion in the medium comes to a broadening and lowering of the resonances. By optical analogy this phenomenon is usually referred to as Doppler effect [12]. Since the resonance levels in the low energy region are observed for heavy nuclei only, the Doppler effect is noticeable only during the interaction of neutrons with such nuclei. And the higher is the environment temperature, the stronger is the effect.
averaged over the neutron spectrum on the temperature of reactor fuel (fissile medium). As is known, the impact of the nuclei thermal motion in the medium comes to a broadening and lowering of the resonances. By optical analogy this phenomenon is usually referred to as Doppler effect [12]. Since the resonance levels in the low energy region are observed for heavy nuclei only, the Doppler effect is noticeable only during the interaction of neutrons with such nuclei. And the higher is the environment temperature, the stronger is the effect.
Therefore a program was developed using Microsoft Fortran Power Station 4.0 (MFPS 4.0) that allows at the first stage to calculate the cross-sections of the resonance neutron reactions depending on neutron energy taking into account the Doppler effect. The cross-sections dependence on neutron energy for reactor nuclides from ENDF/B-VII database [13] corresponding to 300 K environment temperature were taken as the input data for the calculations. For example, the results for radioactive neutron capture cross-sections dependence on neutron energy for 235U are given in Figure 1 for different temperatures of the fissile medium in 300 K - 3000 K temperature range. Using this program, the dependence of scattering, fission and radioactive neutron capture crosssections for essential reactor fuel nuclides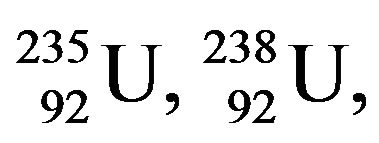
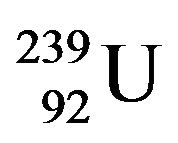 and
and 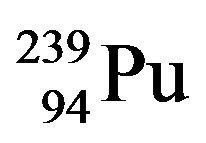 were obtained for different temperatures in 300 K - 3000 K range.
were obtained for different temperatures in 300 K - 3000 K range.
At the second stage a program was developed to calculate the dependence of the cross-sections 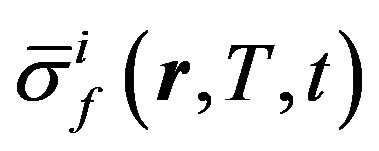 averaged over the neutron spectrum for main reactor nuclides and for main reactor nuclear neutron reactions for the specified temperatures. The averaging of neutron cross-sections for the Maxwell distribution was performed using the following expression:
averaged over the neutron spectrum for main reactor nuclides and for main reactor nuclear neutron reactions for the specified temperatures. The averaging of neutron cross-sections for the Maxwell distribution was performed using the following expression:

where Elim is the upper limit of neutrons thermalization, while for the procedure of neutron cross-sections averaging over Fermi spectrum the following expression was used:
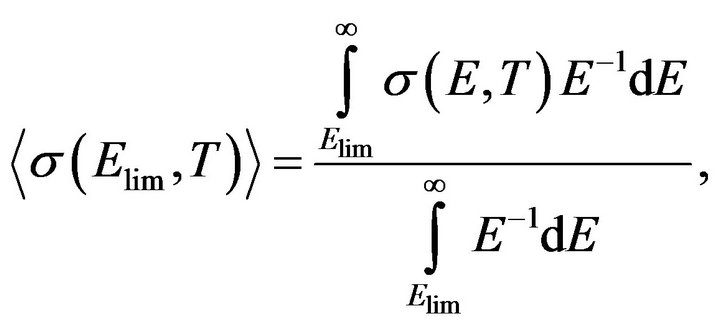
During further calculations in our programs we used the results obtained at the first stage i.e. the dependence of reaction cross-sections on neutron energy and medium temperature (Doppler effect). The neutron spectrum was specified in a combined way—below the limit of
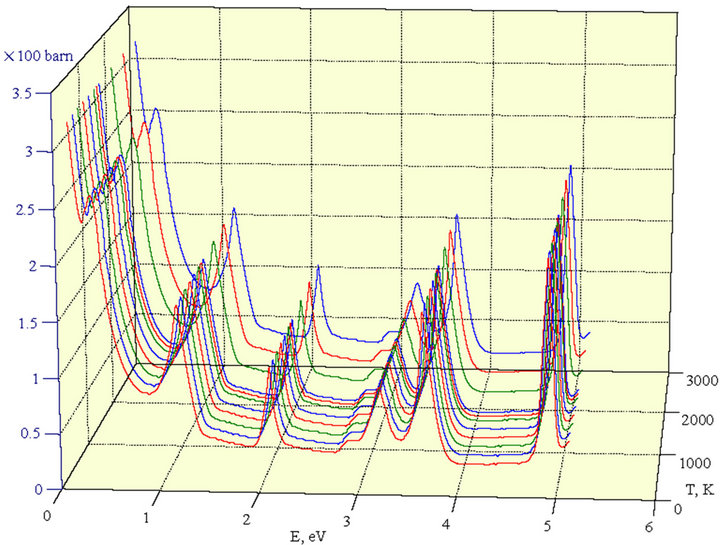
Figure 1. Calculated dependency of radioactive neutron capture reaction on its energy for 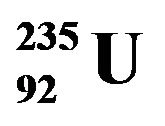 at different temperatures within 300 K to 3000 K.
at different temperatures within 300 K to 3000 K.
thermalization Elim the neutron spectrum was described by Maxwell spectrum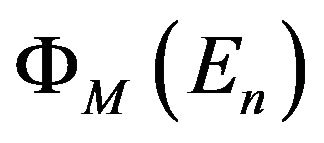 ; above Elim but below EF (upper limit for Fermi neutron energy spectrum) the neutron spectrum was described by Fermi spectrum
; above Elim but below EF (upper limit for Fermi neutron energy spectrum) the neutron spectrum was described by Fermi spectrum 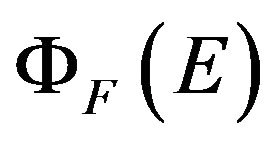 for a moderating medium with absorption; above EF, but below maximal neutron energy
for a moderating medium with absorption; above EF, but below maximal neutron energy 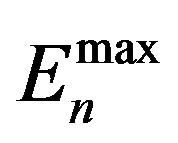 the spectrum was described by 239Pu fission spectrum [14,15]. Here the neutron gas temperature for Maxwell distribution was given by (7), described in [12]. According to this approach [12], the drawbacks of standard slowing-down theory for thermalization area may be formally reduced if a variable
the spectrum was described by 239Pu fission spectrum [14,15]. Here the neutron gas temperature for Maxwell distribution was given by (7), described in [12]. According to this approach [12], the drawbacks of standard slowing-down theory for thermalization area may be formally reduced if a variable 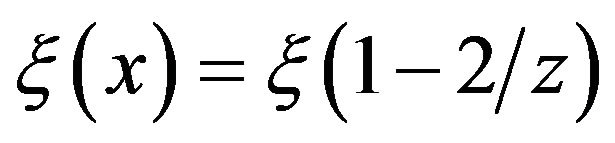 is introduced instead of the average logarithmic energy loss
is introduced instead of the average logarithmic energy loss , which is almost independent of neutron energy (as is known, for environment consisting of nuclei with A > 10 the statement
, which is almost independent of neutron energy (as is known, for environment consisting of nuclei with A > 10 the statement 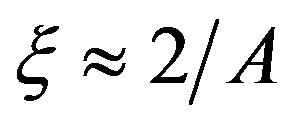 is true). Here
is true). Here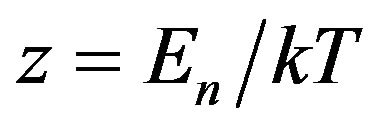 , En is the neutron energy, T is the environment temperature. Then within such a framework the following expression may be used for the temperature of the neutron gas in Maxwell spectrum of thermal neutrons3:
, En is the neutron energy, T is the environment temperature. Then within such a framework the following expression may be used for the temperature of the neutron gas in Maxwell spectrum of thermal neutrons3:
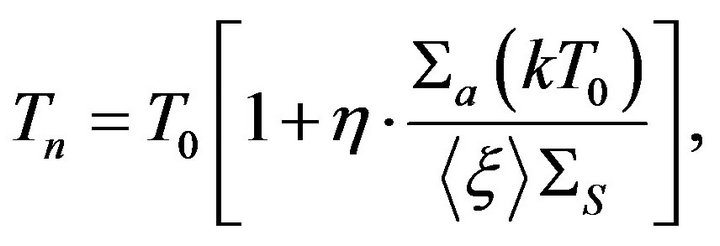 (7)
(7)
where T0 is the fuel medium temperature, 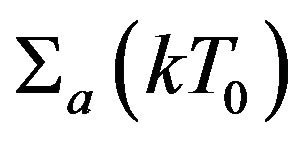 is the absorption cross-section for energy
is the absorption cross-section for energy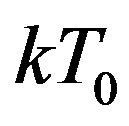 ,
, 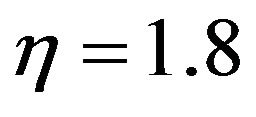 is the dimensionless constant,
is the dimensionless constant,  is averaged over the whole energy interval of Maxwell spectrum
is averaged over the whole energy interval of Maxwell spectrum 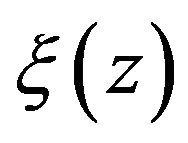 at kT = 1 eV.
at kT = 1 eV.
Fermi neutron spectrum for a moderating medium with absorption (we considered carbon as a moderator and 238U, 239Uand 239Pu as absorbers) was set in the form [12,16]:
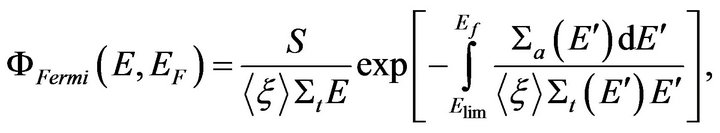 (8)
(8)
where S is the total volume neutron generation rate,
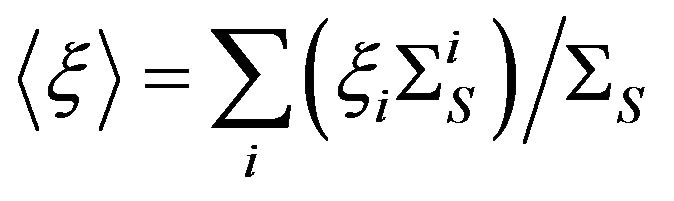 ,
, 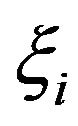 is the average logarithmic decrement of energy loss,
is the average logarithmic decrement of energy loss, 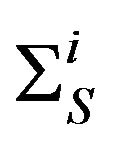 is the macroscopic scattering cross-section of the i-th nuclide,
is the macroscopic scattering cross-section of the i-th nuclide, 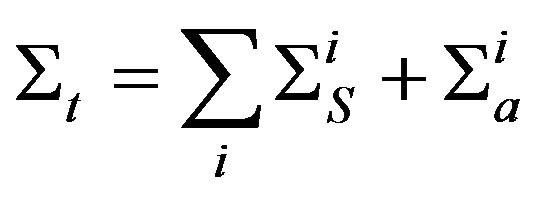 is the total macroscopic cross-section of the fissile material,
is the total macroscopic cross-section of the fissile material,
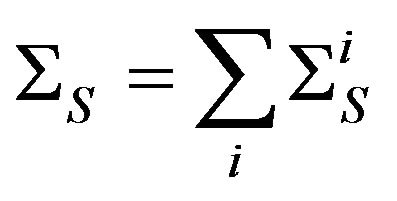 is the total macroscopic scattering crosssection of the fissile material,
is the total macroscopic scattering crosssection of the fissile material, 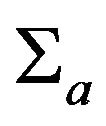 is the macroscopic absorption cross-section, EF is the upper neutron energy for Fermi spectrum.
is the macroscopic absorption cross-section, EF is the upper neutron energy for Fermi spectrum.
The upper limit of neutron thermalization Elim in our calculation was considered as a free parameter, setting the neutron fluxes of Maxwell and Fermi spectra at a common energy limit Elim equal:
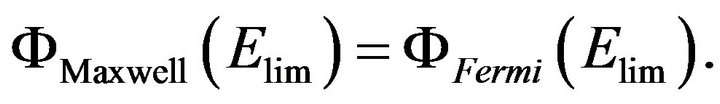 (9)
(9)
The high energy neutron spectrum part 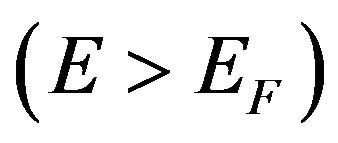 was defined by fission spectrum [16-18] in our calculations. Therefore for the total volume neutron generation rate S in the expression for the Fermi spectrum (8) the following expression may be written:
was defined by fission spectrum [16-18] in our calculations. Therefore for the total volume neutron generation rate S in the expression for the Fermi spectrum (8) the following expression may be written:
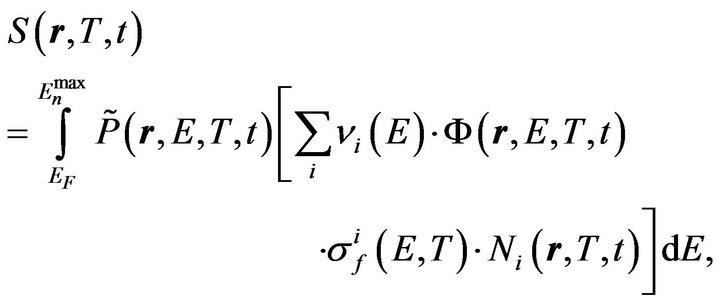 (10)
(10)
where 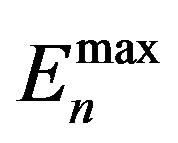 is the maximum energy of neutron fission spectrum (usually taken as
is the maximum energy of neutron fission spectrum (usually taken as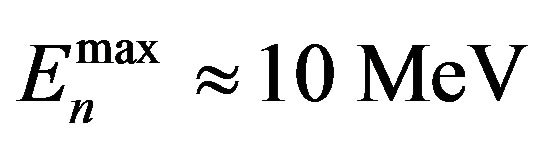 ), EF is the neutron energy, below which the moderating neutrons spectrum is described as Fermi spectrum (usually taken as EF ≈ 0.2 MeV);
), EF is the neutron energy, below which the moderating neutrons spectrum is described as Fermi spectrum (usually taken as EF ≈ 0.2 MeV);  is the probability for the neutron not to leave the boundaries of the fissile medium, which depends on the fissile material geometry and conditions at its border as well (e.g. presence of a reflector).
is the probability for the neutron not to leave the boundaries of the fissile medium, which depends on the fissile material geometry and conditions at its border as well (e.g. presence of a reflector).
The obtained calculation results show that the crosssections averaged over the spectrum may increase (Figure 2 for 239Pu and Figure 4 for 238U) as well as decrease
 (a)
(a)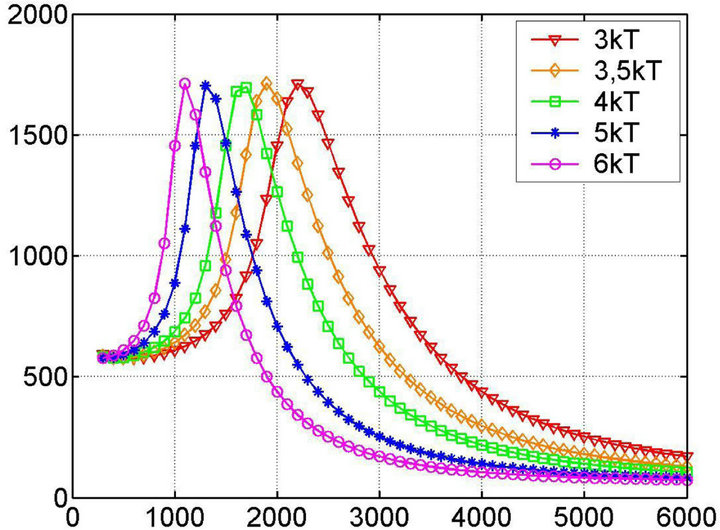 (b)
(b)
Figure 2. Temperature dependences for the fission crosssection (a) and radioactive capture cross-section (b) for 239Pu, averaged over the Maxwell spectrum, on the Maxwell and Fermi spectra joining energy and η = 1.8 (see (0.7)).
(Figure 3 for 235U) with fissile medium temperature increase. As follows from the obtained results, the arbitrariness in selection of the limit energy for joining Maxwell and Fermi spectra does not alter the character of these dependences evolution significantly.
This can be justified by the fact that 239Pu resonance region starts from significantly lower energies than that of 235U and with fuel temperature increase, the neutron gas temperature increases producing Maxwell's neutron distribution maximum shift to higher neutron energies. In other words, the neutron gas spectrum hardening, when more neutrons fit into resonance area of 239Pu, is the cause of the averaged cross-sections growth.
For 235U this process in not as significant because its resonance region is located at higher energies. As a result, the 235U neutron gas spectrum hardening related to fuel temperature increase (in the considered interval) does not result in a significant increase of the number of neutrons fitting into the resonance region. Therefore according to the known dispersion relations for 235U giving the neutron reactions cross-sections behaviour depending on their energy En for non-resonance areas, we observe a dependence for the averaged cross-sections 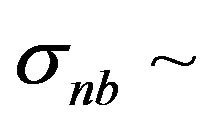
 .
.
 (a)
(a)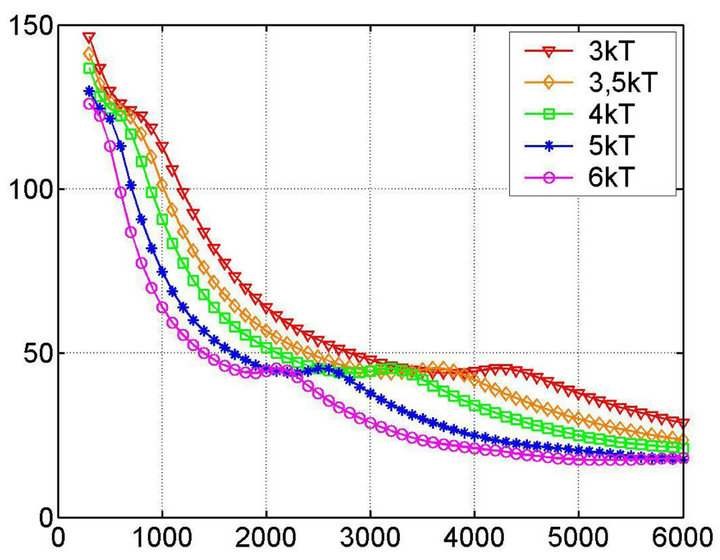 (b)
(b)
Figure 3. Temperature dependences for the fission crosssection (a) and radioactive capture cross-section (b) for 235U, averaged over the Maxwell spectrum, on the Maxwell and Fermi spectra joining energy and η = 1.8 (see (0.7)).
 (a)
(a)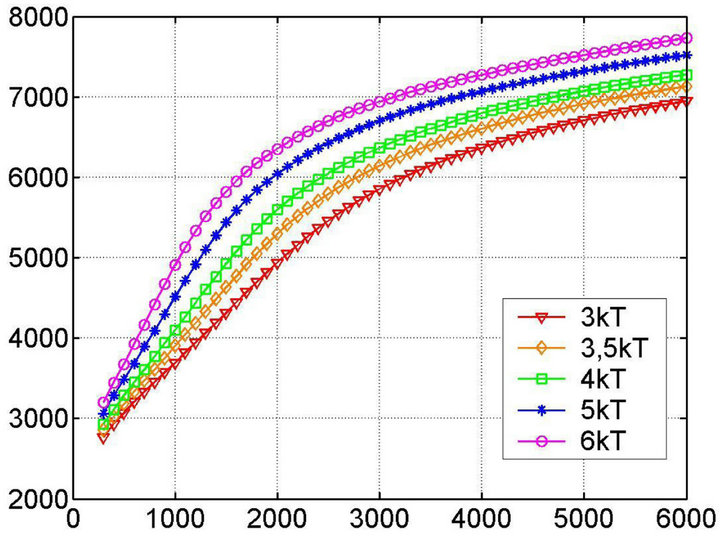 (b)
(b)
Figure 4. Temperature dependences for the fission crosssection (a) and radioactive capture cross-section (b) for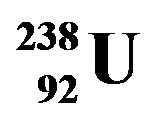 , averaged over the combined Maxwell and Fermi spectra depending on Maxwell and Fermi spectra joining energy and η = 1.8 (see (0.7)).
, averaged over the combined Maxwell and Fermi spectra depending on Maxwell and Fermi spectra joining energy and η = 1.8 (see (0.7)).
The data on the averaged fission and capture crosssections of 238U presented at Figure 4 show that the averaged fission cross-section for 238U is almost insensitive to the neutron spectrum hardening caused by the fuel temperature increase, because of the high fission threshold ~1 MeV (see Figure 4(a)). On the other hand, they confirm the dependence of the capture cross-section on temperature, because its resonance region is located as low as for 239Pu. Obviously, fuel enrichment with 235U essentially makes no difference in this case, because the averaged cross-sections for 235U, as described above, behave in a standard way.
And finally we performed a computer estimate of the heat source density dependence 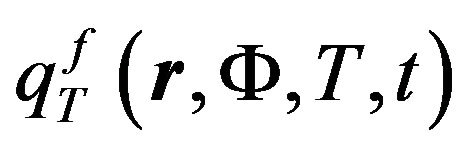 (6) on temperature for different compositions of uranium-plutonium fissile medium with a constant neutron flux density, presented at Figure 5. We used the dependences presented above at Figures 2-4 for these calculations. Let us note that our preliminary calculations were made not taking into account the change in composition and density of the fissile uranium-plutonium medium that is a direct consequence of the constant neutron flux assumption.
(6) on temperature for different compositions of uranium-plutonium fissile medium with a constant neutron flux density, presented at Figure 5. We used the dependences presented above at Figures 2-4 for these calculations. Let us note that our preliminary calculations were made not taking into account the change in composition and density of the fissile uranium-plutonium medium that is a direct consequence of the constant neutron flux assumption.
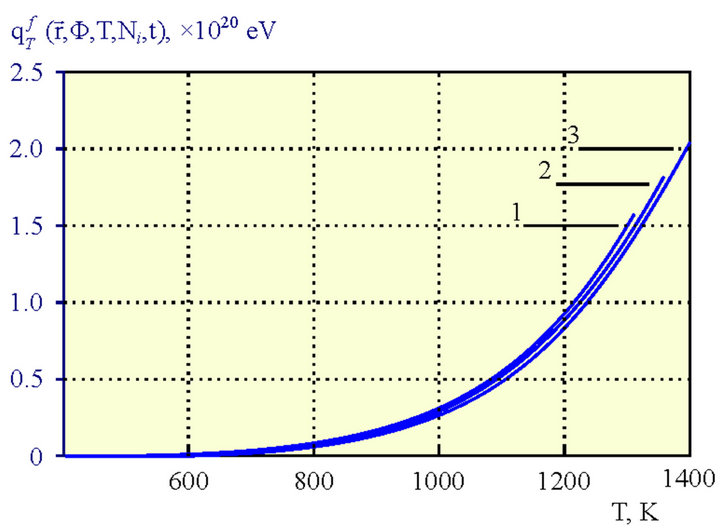
Figure 5. Dependence of the heat source density 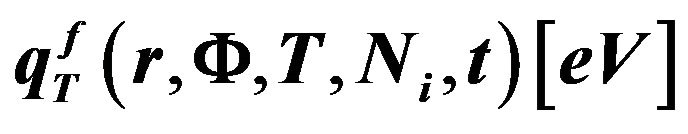 on the fissile medium temperature (300 K - 1400 K) for several compositions of uraniumplutonium medium (1% - 10% Pu; 2% - 5% Pu; 3% - 1% Pu) at a constant neutron flux density Φ = 1013 n/(cm2∙s).
on the fissile medium temperature (300 K - 1400 K) for several compositions of uraniumplutonium medium (1% - 10% Pu; 2% - 5% Pu; 3% - 1% Pu) at a constant neutron flux density Φ = 1013 n/(cm2∙s).
The necessity of such assumption is caused by the following. It is obvious that for a reasonable description of the neutron source density 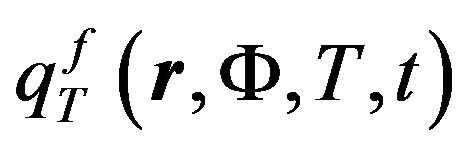 (6) dependence on temperature, a system of three equations must be solved. Two of them correspond to the neutron kinetics equation (flux and fluence) and to the system of equations for the parental and child nuclides nuclear density kinetics (e.g. see [19,20]), while the third equation corresponds to a heat transfer equation of (1) type. However, some serious difficulties arise at this point, associated with the limited computational capabilities available. And here is why.
(6) dependence on temperature, a system of three equations must be solved. Two of them correspond to the neutron kinetics equation (flux and fluence) and to the system of equations for the parental and child nuclides nuclear density kinetics (e.g. see [19,20]), while the third equation corresponds to a heat transfer equation of (1) type. However, some serious difficulties arise at this point, associated with the limited computational capabilities available. And here is why.
One of the principal physical peculiarities of TWR is the fact [21] that fluctuation residuals of plutonium (or 233U in Th-U cycle) over its critical concentration burn out for the time comparable with the reactor lifetime of a neutron 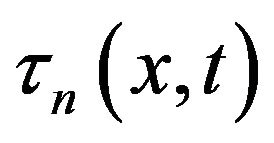 (not considering delayed neutrons), or at least comparable with the reactor period4
(not considering delayed neutrons), or at least comparable with the reactor period4 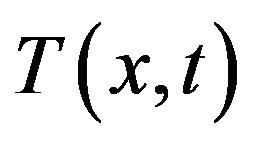 (considering delayed neutrons). Meanwhile, the new plutonium (or 233U in Th-U cycle) is formed in a few days (or a month) and not at once. It means [21] that numerical calculation must be performed with a temporal step around 10−6 - 10−7 for the case of not taking into account the delayed neutrons and ~10−1 - 100 otherwise. At first glance, taking into account the delayed neutrons, according to [21], really “saves the day”, however it is not always true. If the heat transfer equation contains a significantly non-linear source, then in the case of a blow-up mode, the temperature at some conditions may grow extremely fast and in 10 - 20 steps (with time step10−6 - 10−7 s) reaches the critical amplitude that may lead to (as a minimum) a solution stability loss or (as a maximum) blow-up bifurcation of the phase state, almost unnoticeable with a rough time step.
(considering delayed neutrons). Meanwhile, the new plutonium (or 233U in Th-U cycle) is formed in a few days (or a month) and not at once. It means [21] that numerical calculation must be performed with a temporal step around 10−6 - 10−7 for the case of not taking into account the delayed neutrons and ~10−1 - 100 otherwise. At first glance, taking into account the delayed neutrons, according to [21], really “saves the day”, however it is not always true. If the heat transfer equation contains a significantly non-linear source, then in the case of a blow-up mode, the temperature at some conditions may grow extremely fast and in 10 - 20 steps (with time step10−6 - 10−7 s) reaches the critical amplitude that may lead to (as a minimum) a solution stability loss or (as a maximum) blow-up bifurcation of the phase state, almost unnoticeable with a rough time step.
Here we should also mention that modern scientific literature has absolutely no theoretical or experimental data on heat capacity cp and heat conductivity  of the fissile material for the temperatures over 1500 K, which makes the further model calculations quite problematic.
of the fissile material for the temperatures over 1500 K, which makes the further model calculations quite problematic.
According to these remarks, and considering the goal and format of this paper, we didn't aim at finding the exact solution of some specific system of three joined equations described above. However, we found it important to illustrate—at the qualitative level—the consequences of the possible blow-up modes in case of nonlinear heat source existence in the heat transfer equation. As it was described above, we performed the estimate computer calculations of the heat source density 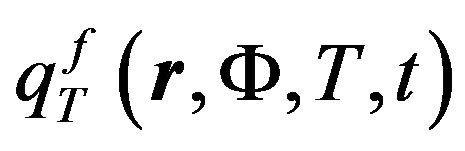 (6) dependence on temperature in 300 K - 1400 K range for selected compositions of uranium-plutonium fissile medium at a constant neutron flux (Figure 5).
(6) dependence on temperature in 300 K - 1400 K range for selected compositions of uranium-plutonium fissile medium at a constant neutron flux (Figure 5).
The obtained dependences for the heat source density 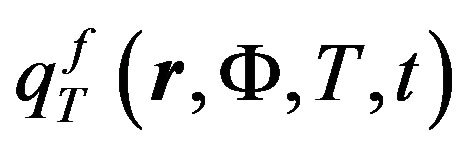 were successfully approximated by a power function of temperature with an exponent of 4 (Figure 5). In other words, we obtained a heat transfer equation with a significantly nonlinear heat source in the following form:
were successfully approximated by a power function of temperature with an exponent of 4 (Figure 5). In other words, we obtained a heat transfer equation with a significantly nonlinear heat source in the following form:
 (11)
(11)
where 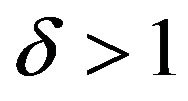 in the case of a non-linear heat conductivity dependence on temperature [4-8]. The latter means that the solutions of the heat transfer equation (0.1) describe the so-called Kurdyumov blow-up modes [4-9], i.e. such dynamic modes when one of the modeled values (e.g. temperature) turns into infinity for a finite time interval. As noted before, in reality instead of reaching infinite values, a corresponding phase transition is observed (a final phase of the parabolic temperature growth), that requires a separate model and is a basis for an entirely new problem.
in the case of a non-linear heat conductivity dependence on temperature [4-8]. The latter means that the solutions of the heat transfer equation (0.1) describe the so-called Kurdyumov blow-up modes [4-9], i.e. such dynamic modes when one of the modeled values (e.g. temperature) turns into infinity for a finite time interval. As noted before, in reality instead of reaching infinite values, a corresponding phase transition is observed (a final phase of the parabolic temperature growth), that requires a separate model and is a basis for an entirely new problem.
Mathematical modeling of blow-up modes was performed mainly using Mathematica 5.2 - 6.0, Maple 10, Matlab 7.0, utilizing multiprocessor calculations for effective application. Runge-Kutta method of 8th - 9th order and the numerical methods of lines [22] were also applied to the calculations. The numerical error estimate did not exceed 0.01%. The coordinate and temporal steps were variable and chosen by the program in order to fit the given error at every calculation step.
Below we give the solutions for the heat transfer Equation (1) with nonlinear exponential heat source (11) in uranium-plutonium fissile medium for the boundary and initial parameters corresponding to those of the technical reactors. The calculations were done for a cube of fissile material with different spatial size, boundary and initial temperature values. Since the temperature dependences of the heat source densities were obtained without account for changing composition and density of the uranium-plutonium fissile medium, different blow-up modes can take place (HS-mode, S-mode, LS-mode) depending on the ratio between the exponents of the temperature dependences of thermal conductivity and heat source according to [4-9]. Therefore we considered cases for 1st, 2nd and 4th temperature order sources. Here the power of the source also varied by varying the proportionality factor in (11) (const = 1.00 J/(cm3∙s∙K)) for 1st temperature order source; 0.10 J/cm3∙s∙K2, 0.15 J/cm3∙s∙K2 and 1.00 J/cm3∙s∙K2 for 2nd temperature order source; 1.00 J/cm3∙s∙K4 for 4th temperature order source). While calculating the heat capacity cp and thermal conductivity  (Figure 6) dependences on the fissile medium temperature in 300 K - 1400 K range, the specified parameters were given by the analytic expressions, obtained by approximation of the experimental data for 238U based on the polynomial progression:
(Figure 6) dependences on the fissile medium temperature in 300 K - 1400 K range, the specified parameters were given by the analytic expressions, obtained by approximation of the experimental data for 238U based on the polynomial progression:
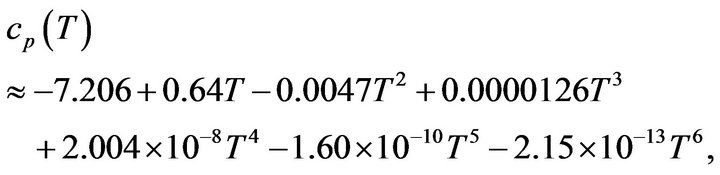 (12)
(12)
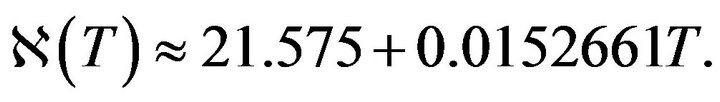 (13)
(13)
And finally a solution of the heat transfer equation (1) was obtained for the constant thermal conductivity (27.5 W/(m∙K)) and heat capacity (11.5 J/(K∙mol)) values, presented in Figure 7(a), as well as the solutions of the heat transfer equation considering their temperature dependences (Figures 7(b)-(d)).
Preliminary results point directly to a possibility of the local melting of the uranium-plutonium fissile medium, having melting temperature almost identical to that of 238U, that equals 1400 K (Figures 7(a)-(d)). Moreover,
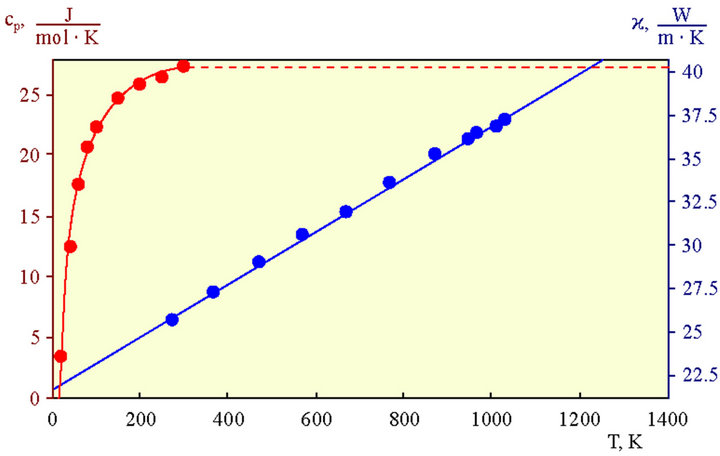
Figure 6. Temperature dependence of the fissile material heat capacity cp and thermal conductivity χ. Points represent the experimental values for the heat capacity and thermal conductivity of 238U.
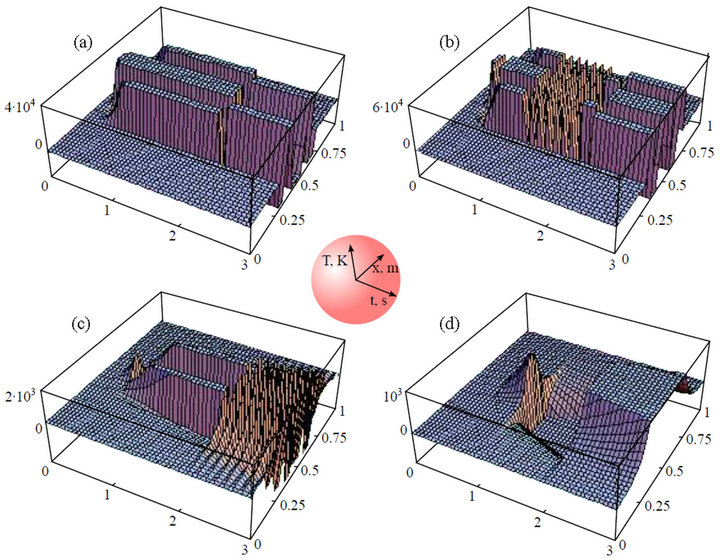
Figure 7. Heat transfer equation (0.1) solution for 3D case (crystal sizes 0.001 × 0.001 × 0.001 mm; initial and boundary temperatures equal to 100 K): (a) The source is proportional to the 4th order of temperature; const = 1.00 J/(cm3∙s∙K4), heat capacity and thermal conductivity are constant and equal to 11.5 J/(K∙mol) and 27.5 W/(m∙K) respectively; (b) the source is proportional to the 4th order of temperature; const = 1.00 J/(cm3∙s∙K4); (c) The source is proportional to the 2nd order of temperature; const = 1.00 J/(cm3∙s∙K2); (d) the source is proportional to the 2nd order of temperature; const = 0.10 J/(cm3∙s∙K2). Note: in cases (b)-(d) the heat capacity and thermal conductivity were determined by (0.12) and (0.13) respectively.
these regions of the local melting are not the areas of the so-called thermal spikes [23], and probably are the anomalous areas of the uranium surface melting observed by Laptev and Ershler [24] that were also mentioned in [25]. More detailed analysis of the probable temperature scenario associated with the blow-up modes is discussed below.
3. Physical Peculiarities of the Blow-Up Regimes in Neutron-Multiplying Media
Earlier we noted the fact that due to the coolant loss at nuclear reactors during Fukushima nuclear accident the fuel was melted, or in other words, temperature inside the active zone at some moment reached the melting temperature of the uranium-oxide fuel, i.e. ~3000˚C.
On the other hand, we already know that the coolant loss may become a cause of the nonlinear heat source formation inside the nuclear fuel and thus become a cause of the temperature and neutron flux blow-up mode occurrence. A natural question arises as to whether it is possible to use such blow-up mode (in terms of temperature and neutron flux) for the initiation of certain controlled physical conditions, under which the nuclear burning wave would regularly “experience” the so-called controlled blow-up regime. It is quite difficult to answer this question definitely, because such fast process has some physical vaguenesses, any of which can become experimentally unsurmountable for the its controlling.
Nevertheless such process is very elegant and beautiful from the physical point of view and therefore requires more detailed phenomenological description. Let us try to make it in short.
As one can see from the plots of the capture and fission cross-sections evolution for 239Pu (Figure 2), the blow-up mode may develop actively at ~1000 K - 2000 K (depending on the real value of Fermi and Maxwell spectra joining boundary), but it returns to almost the initial cross-sections values at temperatures over 2500 K - 3000 K. If we turn on some effective heat sink at that point, the fuel may return to its initial temperature state. However, while the blow-up mode develops, the fast neutrons already penetrate to the adjacent fuel areas, where the new fissile material starts accumulating and so on (see cycles (1) and (2)). After some time the similar blow-up mode will develop in this adjacent area and everything starts over again. In other words, such hysteresis blow-up mode, closely time-conjugated to a heat takeoff procedure, will appear against the background of a stationary nuclear burning wave in a form of the periodic impulse bursts.
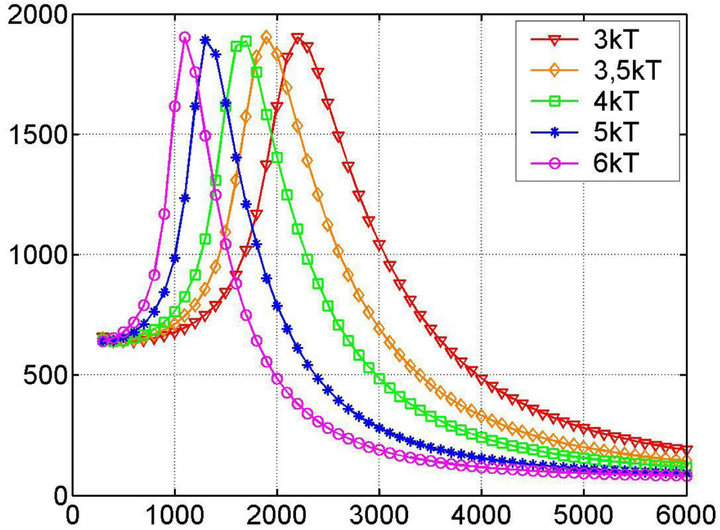
In order to demonstrate the marvelous power of such process, we investigated the heat transfer equation with non-linear exponential heat source in uranium-plutonium fissile medium with the boundary and initial parameters emulating the heat takeoff process. In other words, we investigated the blow-up modes in the fast Feoktistovtype uranium-plutonium reactor [2] where the temperature was deliberately fixed at 6000 K inside and outside the boundary.
This temperature is defined by the following important question: “Is it possible to obtain a solution, i.e. the spacio-temporal temperature distribution not in a form of a  -function at some local spatial area, but as some kind of a stationary and limited by amplitude solitary wave under such conditions (6000 K), which emulate the time-conjugated heat takeoff (see Figure 2)?” As shown below, such suggestion proved productive.
-function at some local spatial area, but as some kind of a stationary and limited by amplitude solitary wave under such conditions (6000 K), which emulate the time-conjugated heat takeoff (see Figure 2)?” As shown below, such suggestion proved productive.
Below we present some calculation characteristics and parameters. During these calculations we used the following expression for the heat conductivity coefficient:
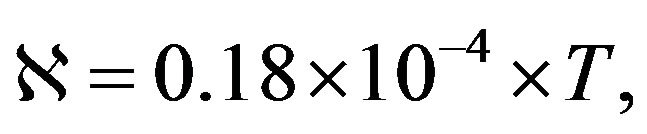
which was obtained using Wiedemann-Franz law and the data on electric conductivity of metals at temperature 6000 K [26]. Specific heat capacity at constant pressure was set to cp ≈ 6 cal/(mol∙deg) according to Dulong and Petit law.
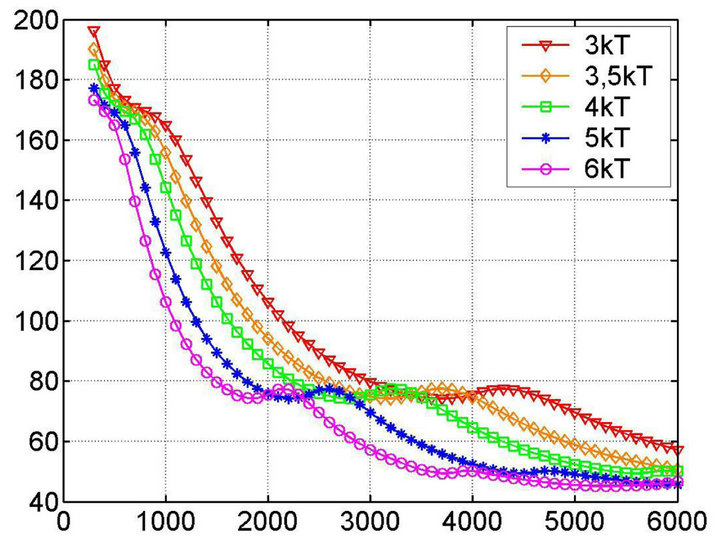
The fissile uranium-plutonium medium was modeled as a cube of the size 10.0 × 10.0 × 10.0 m (Figure 8) during the calculations. Here we used the 2nd order temperature dependence for the heat source (see (11)).
And finally Figures 8(a)-(d) present a set of solutions of the heat transfer Equation (1) with nonlinear exponential heat source (11) in uranium-plutonium fissile medium with boundary and initial conditions emulating such process of heat takeoff that initial and boundary temperatures remain constant and equal to 6000 K.
It is important to note here, that the solution set presented at Figure 8 demonstrates the temporal evolution of the solution to its “stationary” state quite clearly. This is achieved using the so-called “magnifying glass” approach when the solutions of the same problem are deliberately investigated at the different timescales. For example, Figure 8(a) shows the solution at the time scale , while Figure 8(b) describes the spatial solution of the problem (temperature field) for t = 10−6 s. The Figures 8(c) and (d) present the solution (the spatial temperature distribution) at t = 0.5 s and t = 50 s.
, while Figure 8(b) describes the spatial solution of the problem (temperature field) for t = 10−6 s. The Figures 8(c) and (d) present the solution (the spatial temperature distribution) at t = 0.5 s and t = 50 s.
As one can see, the solution (Figure 8(d)) is completely identical to the previous (Figure 8(c)), i.e. to the distribution established in the medium in 0.5 seconds, which allows us to make a conclusion about the temperature field stability, starting from some moment. It is
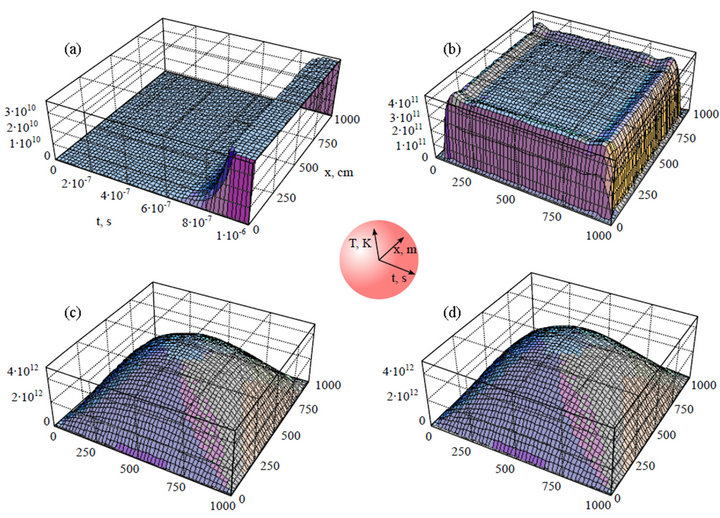
Figure 8. Heat transfer equation solution for a model reactor (source ~2nd order temperature dependence, const = 4.19 J/(cm3∙s∙K2); Initial and boundary temperatures equal to 6000 K; fissile medium is a cube 10 × 10 × 10 m. The presented results correspond to the following times of the temperature field evolution: (a) (1 - 10)∙10−7 s, (b) 10−6 s, (c) 0.5 s, (d) 50 s.
interesting that the established temperature field creates the conditions enough for thermonuclear synthesis reaction, i.e. reaching 108 K, and the time of such temperature field existence is not less than 50 s. These conditions are highly favorable for a stable thermonuclear burning given the necessary nuclei concentration to enter the thermonuclear synthesis reaction.
That said, one should remember that the results of the current chapter are only demonstrative, because their accuracy is very relative and requires careful investigations involving the necessary computational resources. However, qualitative peculiarities of these solutions should attract the researchers' attention to the nontrivial properties of the blow-up modes, at least, with respect to the obvious problem of internal TWR safety violation.
4. Conclusions
Below we give short conclusions stimulated by significant problems, that can be formulated in the following form.
1) The consequences of the anomalous 238U and 239Pu cross-sections behavior with temperature increase. It is shown that the capture and fission crosssections of 238U and 239Pu manifest a monotonous growth in 1000 K - 3000 K range. Obviously, such anomalous temperature dependence of 238U and 239Pu cross-sections changes the neutron and heat kinetics drastically in the nuclear reactors, and in TWR in particular. It becomes crucial to know their influence on kinetics of heat transfer because it may become the cause of a positive feedback with neutron kinetics, which may lead not only to undesirable loss of solution stability (the nuclear burning wave), but also to a trivial reactor runaway with a subsequent nontrivial disaster.
2) Blow-up modes and the problem of nuclear burning wave stability. One of the causes of a possible fuel temperature growth may lie, for instance, in a deliberate or spontaneous coolant loss, analogous to what happened during the Fukushima nuclear accident. As shown above, the coolant loss may become a cause of the nonlinear heat source formation in the nuclear fuel, and consequently emergence of the mode with the temperature and neutron flux blow-up. In our opinion, the preliminary investigation of the heat transfer equation with nonlinear heat source points to an extremely important phenomenon of the anomalous of the temperature and neutron flux blow-up modes behavior. This result poses a natural nontrivial problem of fundamental nuclear burning wave stability and, orrespondingly, of a physically reasonable application of Lyapunov method to this problem, which is a basis for the motion stability theory, and thus a reliable basis for justification of the Lyapunov functional minimum existence.
It is shown that some variants of solution stability loss are caused by anomalous nuclear fuel temperature evolution. They can be not only the cause of TWR internal safety loss, but can lead to a new stable mode when nuclear burning wave would periodically “experience” the so-called controlled blow-up regime through a bifurcation of states (which is very important!). At the same time, it is noted that such fast (blow-up regime) process has a number of physical vaguenesses, any of which may happen to be experimentally insurmountable for the control of such process.
3) On-line remote neutrino diagnostics of intrareactor processes. Due to the fact that a high-power TWR or a nuclear fuel transmutation reactor are the projects of the single-load and fuel burn-up with a subsequent burial of the reactor apparatus, there is an obvious necessity for remote system of neutrino monitoring of the neutronnuclear burning wave in normal operation mode and control of the neutron kinetics in emergency situation. The calculation of the spatio-temporal distribution of the isotope composition in the TWR active zone in the framework of the inverse problem of neutrino diagnostics of intra-reactor processes is presented in [27-29] in detail.
REFERENCES
- V. F. Ukraintsev, “Reactivity Effects in Energetic Installations (in Russian),” Handbook, Obninsk Institute for Nuclear Power Engineering, Obninsk, 2000.
- L. P. Feoktistov, “Neutron-Fissio Wave,” Doklady Akademii Nauk SSSR, Vol. 309, No. 1, 1989, pp. 4-7.
- E. Teller, M. Ishikawa, L. Wood, R. Hyde and J. Nuckolls, “Completely Automated Nuclear Reactors for LongTerm Operation Ii: Toward a Concept-Level Point-Design of a High-Temperature, Gas-Cooled Central Power Station System, Part ii,” Proceedings of the International Conference on Emerging Nuclear Energy Systems, ICENES’96, Obninsk, 1996, pp. 123-127.
- T. S. Akhromeeva, S. P. Kurdyumov, G. G. Malinetskii and A. A. Samarskii, “Non-Stationary Structures and Diffusive Chaos (in Russian),” Nauka, Moscow, 1992.
- A. A. Samarskii, V. A. Galaktionov, S. P. Kurdyumov and A. P. Mikhailov, “Blow-Up in Quasilinear Parabolic Equations,” Walter de Gruyter, Berlin, 1995. doi:10.1515/9783110889864
- “Blow-Up Modes. Evolution of the Idea. The Laws of Co-Evolution of Complex Systems,” Nauka, Moscow, 1999.
- S. P. Kurdyumov, “Blow-Up Modes,” Fizmatlit, Moscow, 2006.
- E. N. Knyazeva and S. P. Kurdyumov, “Synergetics: Nonlinearity of Time and Landscape of Co-Evolution,” KomKniga, Moscow, 2007.
- V. D. Rusov, V. A. Tarasov and S. A. Chernegenko, “Blow- Up Modes in Uranium-Plutonium Fissil Medium in Technical Nuclear Reactors and Georeactor (in Russian),” Problems of Atomic Science and Technology, Vol. 97, 2011, pp. 123-131.
- D. M. Skorov, Y. F. Bychkov and A. I. Dashkovskii, “Reactor Material Science (in Russian),” Atomizdat, Moscow, 1979.
- B. A. Nadykto, “Plutonium. Fundamental Problems (in Russian),” RFNC-Arepri, Sarov, 2003.
- G. G. Bartolomey, G. ABat’, V. D. Babaykov and M. S. Altukhov, “Basic Theory and Methods of Nuclear Power Installations Calculation,” Energoatomizdat, Moscow, 1989.
- “ENSDF/B-VI,” Los Alamos National Laboratory, 1998.
- V. N. Pavlovich, V. N Khotyaintsev and E. N. Khotyaintseva, “Physical Basics of the Nuclear Burning Wave Reactor. 2. Specifc Imodels,” Nuclear Physics and Energetics, Vol. 3, 2008, pp. 39-48.
- R. Hyde, M. Ishikawa, N. Myhrvold, J. Nuckolls and L. Wood, “Nuclear Fission Power for 21st Century Needs: Enabling Technologies for Large-Scale, Lowrisk, Affordable Nuclear Electricity,” Progress in Nuclear Energy, Vol. 50, No. 2-6, 2008, pp. 82-91. doi:10.1016/j.pnucene.2007.10.027
- S. V. Shirokov. “Nuclear Reactor Physics (in Russian),” Naukova Dumka, Kiev, 1992.
- N. D. Fedorov, “Short Reference Book for EngineerPhysicist. Nuclear Physics and Atomic Physics (in Russian),” State Publishing Company for Atomic Science and Technology Literature, Moscow, 1961.
- V. I. Vladimirov, “Practical Problems Onnuclear Reactors Operation (in Russian),” Energoatomizdat, Moscow, 1986.
- V. D. Rusov, E. P. Linnik, V. A. Tarasov, T. N. Zelentsova, I. V. Sharph, V. N. Vaschenko, S. I. Kosenko, M. E. Beglaryan, S. A. Chernezhenko, P. A. Molchinikolov, S. I. Saulenko and O. A. Byegunova, “Traveling Wave Reactor and Condition of Existence of Nuclear Burning Soliton-Like Wave in Neutron-Multiplying Media,” Energies, Vol. 4, No. 9, 2011, pp. 1337-1361. http://www.mdpi.com/1996-1073/4/9/1337 doi:10.3390/en4091337
- V. N. Pavlovich, V. N Khotyaintsev and E. N. Khotyaintseva, “Nuclear Burning Wave Reactor: Wave Parameter Control,” Nuclear Physics and Energetics, Vol. 11, 2010, pp. 49-56.
- V. N. Pavlovich, V. N Khotyaintsev and E. N. Khotyaintseva, “Physical Basics of the Nuclear Burning Wave Reactor. 1,” Nuclear Physics and Energetics, Vol. 2, 2008, pp. 39-48.
- A. A. SamarskiI and A. V. Gulin, “Numerical Methods in Mathematical Physics (in Russian),” Nauchnyimir, Moscow, 2003.
- G. H. Kinchin and R. S. Pease, “Displacement of Atoms in Solid by Radiation,” Reports on Progress in Physics, Vol. 18, No. 4, 1955, pp. 590-615.
- B. V. Ershler and F. S. Lapteva, “The Evaporation of Metals by Fission Fragments,” Journal of Nuclear Energy, Vol. 4, No. 4, 1954, pp. 471-474. http://www.sciencedirect.com/science/article/pii/089139195790075X. doi:10.1016/0891-3919(57)90075-X
- I. M. Lifshits, M. I. Kaganov and L. V. Tanatarov, “On the Theory of the Changes Produced in Metals by Radiation,” The Soviet Journal of Atomic Energy, Vol. 6, No. 4, 1960, pp. 261-270. doi:10.1007/BF01479732
- V. N. Zharkov, “The inner structure of Earth and planets,” Nauka, Moscow, 1983.
- V. D. Rusov, T. N. Zelentsova, V. A. Tarasov and D. A. Litvinov, “Inverse Problem of Remote Neutrino Diagnostics of Intrareactor Processes,” Journal of Applied Physics, Vol. 96, No. 3, 2004, pp. 1734-1739. doi:10.1063/1.1737803
- V. D. Rusov, V. N. Pavlovich, V. N. Vaschenko, V. A. Tarasov, T. N. Zelentsova, V. N. Bolshakov, D. A. Litvinov, S. I. Kosenko and O. A. Byegunova, “Geoantineutrino Spectrum and Slow Nuclear Burning on the Boundary of the Liquid and Solid Phases of the Earth’s Core,” Journal of Geophysical Research: Solid Earth, Vol. 112, No. B9, 2007, in press. doi:10.1029/2005JB004212
- V. D. Rusov, V. A. Tarasov and D. A. Litvinov, “Reactor Antineutrino Physics (in Russian),” URSS, Moscow, 2008.
NOTES
*Corresponding author.
1Let us note that the third block partially used MOX-fuel enriched with plutonium.
2Positive feedback is a type of feedback when a change in the output signal leads to the change in the input signal, which in its turn leads to a further deviation of the output signal from its original value. In other words, PF leads to instability and appearance of qualitatively new (often self-oscillation) systems.
3A very interesting expression revealing a hidden connection between the temperature of the neutron gas and the medium (fuel) temperature.
4The reactor period by definition equals to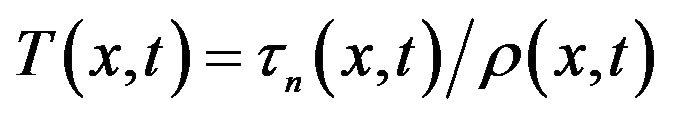 , i.e. is a ratio of the reactor neutron lifetime to reactivity.
, i.e. is a ratio of the reactor neutron lifetime to reactivity.

