American Journal of Operations Research
Vol. 2 No. 1 (2012) , Article ID: 17825 , 12 pages DOI:10.4236/ajor.2012.21002
Limited Re-Sequencing for Mixed-Models with Multiple Objectives, Part II: A Permutation Approach
Schools of Business, Wake Forest University, Winston-Salem, USA
Email: mcmullpr@wfu.edu
Received October 31, 2011; revised November 28, 2011; accepted December 13, 2011
Keywords: Permutation; Heuristic; Sequencing; Discrete Optimization
ABSTRACT
This research presents an approach to solving the limited re-sequencing problem for a JIT system when two objectives are considered for multiple processes. One objective is to minimize the number of setups; the other is to minimize the material usage rate [1]. For this research effort, each unique permutation of the problem’s demand structure is noted, and used as a mechanism for finding subsequent sequences. Two variants of this permutation approach are used: one employs a Monte-Carlo simulation, while the other employs a modification of Ant-Colony Optimization to find sequences satisfying the objectives of interest. Problem sets from the literature are used for assessment, and experimentation shows that the methodology presented here outperforms methodology from an earlier research effort [2].
1. Introduction
Prudent production scheduling has long been a means for enhancing the competitive position of the manufacturing firm. Effective scheduling can be used to enhance flexibility in a Just-in-time (JIT) system, as well as reduce the required number of setups associated with changeovers. These two entities (flexibility and required number of setups) are of paramount concern here. Many past research efforts have confirmed the fact that these two entities are inversely related to each other. In other words, a strong performance of one suggests a poor performance of the other.
Another caveat related to production sequencing relates to the fact that there are frequently several individual processes involved in the aggregate production function. For each individual process, it may be possible to “re-sequence” the production sequence used in the prior stage of production. This re-sequencing may, if properly done, induce some efficiencies that were not present before re-sequencing. Exploiting the multiple processes with the intent of performing well with regard to both number of setups and flexibility is a facet of production research that has not been explored to any reasonable degree.
This research addresses the production sequencing problem in a JIT environment where the number of setups and the flexibility of the sequences are simultaneously considered for multiple processes. Two heuristics are presented to accomplish the sequencing—both are rooted in a Monte-Carlo simulation selection process. The first employs a selection process rooted in performance potential, the second employs the same selection process as the first, but is also weighted in the spirit of Ant Colony Optimization [3]. For a set of problems from the literature, the performance of the heuristics is assessed against optimal, and against a search heuristic from a prior research effort [2].
Via development of a detailed example detailing the concept of limited re-sequencing and capturing the efficient frontier, the sequencing methodology is presented, an experiment is described, analyses of performance are made, and general observations are offered.
2. Sequencing and Limited Re-Sequencing
2.1. Setups vs. Flexibility
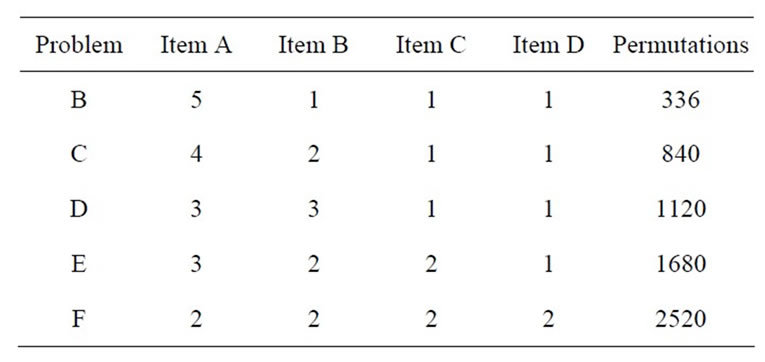
To better understand the idea of multiple objectives and multiple processes, consider a trivial problem that requires two units of item A, one item of item B, and one unit of item of C to be placed into a production sequence. On possible sequence is AABC. This sequence results in (3) changeovers, which is the minimum value possible. Unfortunately, this sequence does not propagate flexibility—there is an uneven flow of items through the sequence, in proportion to demand, resulting in a high usage rate (2.75) as presented by Miltenburg [1]. Although the usage rate is formally defined in the methodology section, an informal description is provided here. Consider a hypothetical situation where the two units of A, and single units of B and C are required for the customer’s to assemble. If the total number of demanded assemblies is 10,000 units, then 20,000 units of A would be required, with 10,000 units of both B and C required. Suppose the schedule is to produce the 20,000 units of A, followed by the 10,000 units of B, and finishing with the 10,000 units of C. This sequence would result in (3) setups—the minimum possible amount. Consider next, some sort of disaster, such as a massive power outage, occurring immediately after the 20,000 units of A were produced. These completed units of item A are of no value to the customer, because items B and C are unavailable and required for the assembly. This hypothetical scenario illustrates a lack of flexibility, underscoring the importance of “inter-mixing” the individual items as much as possible—an important feature of JIT systems.
One sequence that would better propagate flexibility is ABAC. This sequence has a better measure of usage (1.75) than does AABC. Unfortunately, this sequence requires (4) setups, more than the (3) associated with the AABC sequence. This scenario illustrates that a sequence boasting flexibility can result in more setups than a sequence involving less flexibility. This inverse relationship between required setups and flexibility (measured via Miltenburg’s usage rate) is a complicating force in production scheduling.
2.2. Multiple Processes
Another complicating force is the requirement of multiple processes. Consider the above example applied to multiple processes. For the purpose of this illustration, it is assumed that (10) processes are required. The AABC sequence would then require (30) setups in all, with an aggregate usage measure of 27.5. The ABAC sequence would require (40) setups, with an aggregate usage measure of 17.5. The AABC sequence provides desirable setups, but undesirable flexibility, while the ABAC sequence provides just the opposite returns.
2.3. Limited Re-Sequencing
It appears that the multiple processes further amplify the tradeoff between setups and flexibility. This need not be the case if one were to “re-sequence” items between the different processes. In this context, re-sequencing means that one item is taken out of the sequence, and re-inserted into a later part of the sequence. Consider the following example of re-sequencing, where item B (underlined) is re-inserted into a later part of the sequence.
AABC (Original Sequence)
AACB (Modified Sequence)
In the example above, item B was physically removed from the sequence, held in a buffer, and later re-inserted [4]. This type of re-sequencing suggests the assumption that there is physical space available that permits one to hold an item in a buffer until a later time. Specifically, this research does permit a buffer size of one unit, essentially meaning that one unit can be held and later re-inserted in the sequence. A side effect of this assumption is that units not held in buffer can move up no more than one sequence position. Below is an example of a forbidden sequence modification:
AABC (Original Sequence)
BCAA (Modified Sequence)
The above scenario is more permitted because both of the items A would have been held in buffer (exceeding the buffer size of one), causing the B and C to move up more than one position in the sequence. Finally, it is permitted to have more than one modifications made in a sequence, provided that there is never more than one unit held in buffer at a time. Here is an example of this:
The above sequence modification is permitted because there is at most one unit held in buffer at any time (it is item A in this example). The first item A is held in buffer and is re-inserted after item B. The second item A is held in buffer and is re-inserted after item C. Note that neither items B or C more up more than one sequence position. This re-sequencing preserves diversity in the continuum of feasibility [5].
2.4. Seeking an Efficient Frontier
As stated earlier, the minimum setups sequence is AABC, resulting in (3) setups and a usage rate of 2.75. Another sequence is ABAC, resulting in (4) setups and a usage rate of 1.75. Applied over (10) total processes, AABC yields 30 total setups and an aggregate usage of 27.5. The ABAC sequence, over (10) processes yields 40 total setups and an aggregate of usage of 17.5.
In the interest of multiple objectives, it is germane to seek sequences that find some “middle ground” between the extreme values of setups and usage rates. This “middle ground” can be found via an efficient frontier. In the context of this application, an efficient frontier is intended to describe the minimum usage rate for each unique number of setups for the total number of processes. For problems such as this, where one objective is of a discrete nature (number of required setups) and the other is continuous (the associated usage rate), an efficient frontier works well.
Finding this efficient frontier is a non-trivial task, and is, in effect, one of the main contributions of this research effort. In order to find the efficient frontier, one must find the set of sequences that yield the minimum total usage rate for their associated number of required setups/changeovers. For this research, the “trivial,” or “level-0” sequence will always be the one with the item As at the head of the sequence, followed by the items Bs, etc. For each process required, the prior level’s sequence is subjected to limited re-sequencing as described above. One of the candidate sequences is selected and this process continues until the desired number of levels has received proper attention.
There are essentially two general ways of capturing the efficient frontier. One way is via enumeration, the other way is via some heuristic search. The enumerative approach is guaranteed optimal, but expensive in terms of effort. The heuristic approach is not guaranteed optimal, but if wisely pursued, it can provide near-optimal results with a reasonable effort. For an enumerative effort, one must traverse a search tree, where the nodes are the parent sequence, and the branches are the feasible child sequences of the parent sequences. For the child sequences to be feasible, they must have their sequence members move up at most one position in the sequence. For example, the “level-0” sequence of AABC only has four feasible child sequences: AABC, AACB, ABAC and ABCA. Each of these child sequences then exist at level 1, and each of these are then considered parent sequences for level 2, etc.
Figure 1 shows cumulative usage and setups through each path of the traversal. While the required setups are easily understandable, usage rate is less so, and is discussed in the methodology section. For now, the usage rates and setups are shown in Table 1 for all twelve possible permutations of the AABC problem.
Also shown in Table 1 is information regarding feasibility of child sequences descending from parent sequences. A mark of “1” indicates feasibility from parent to child sequence, a mark of “0” indicates infeasibility. For example, the above elaboration of the feasible child sequences of AABC are noted with marks of “1” in Table 1 (shaded—“ID” tags must be referenced).
If the traversal process were continued through ten processes, the efficient frontier would appear as shown in Figure 2.
While inspection of Figure 2 shows the graphical relationship between setups and usage rate, Table 2 shows the specific sequences that make up the efficient frontier. Here, the interested reader can see the exact sequences that make up the efficient frontier. For example, the combinations of sequences that comprise the lowest usage for 39-setups are BAAC for Level 1, ABCA for Level 2, etc.
2.5. Combinatorial Explosion
Figure 1 shows the traversal details that are essentially required to find the efficient frontier through two levels. Even for two levels, the effort is consequential. Level 0 has a single node, Level 1 has four nodes, Level 2 has twenty-nodes. This illustrates a combinatorial explosion.
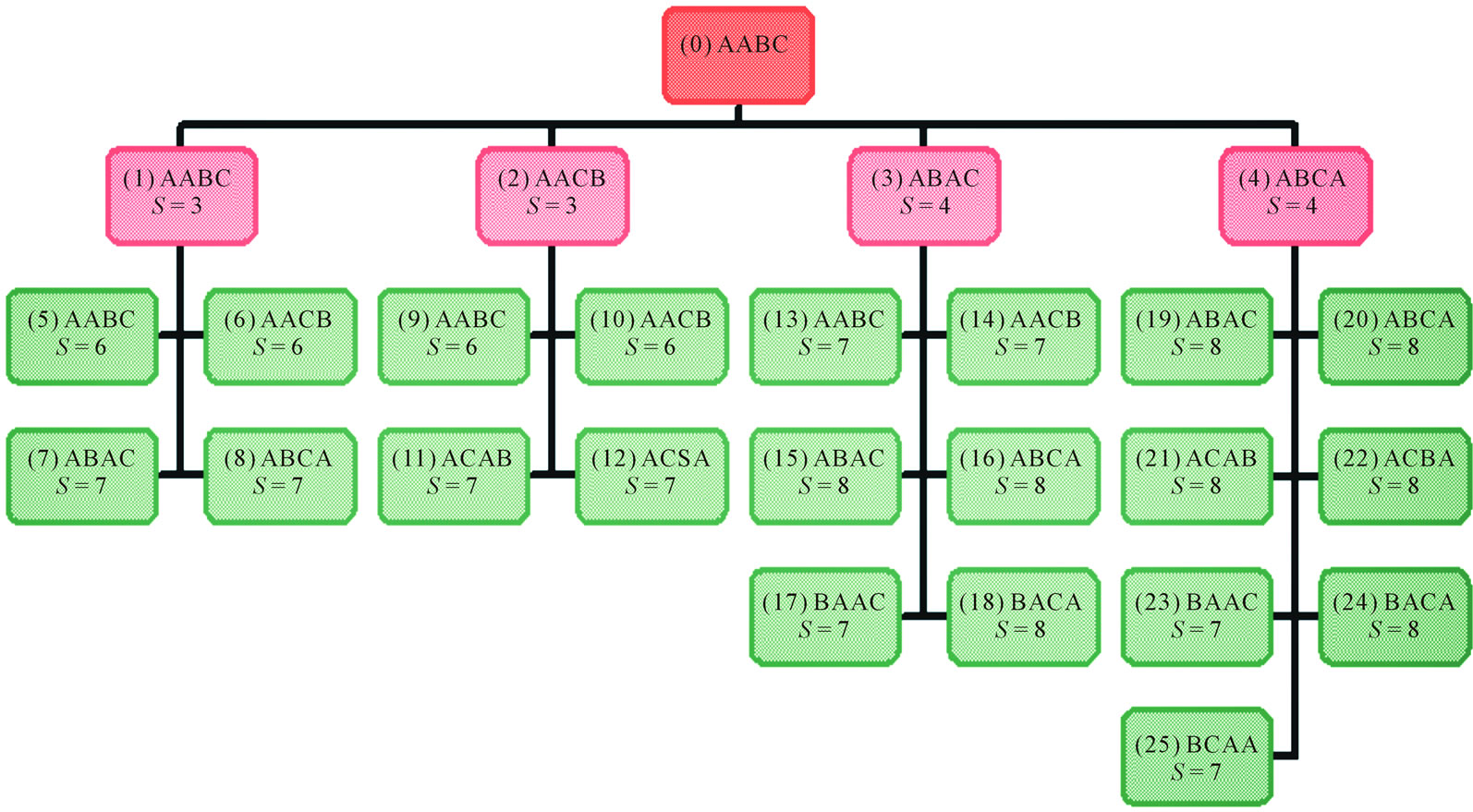
Figure 1. Tree diagram of AABC: Full enumeration through two processes (p = 2). Cumulative setups (S) and usage (U) are shown for each feasible sequence arrangement.
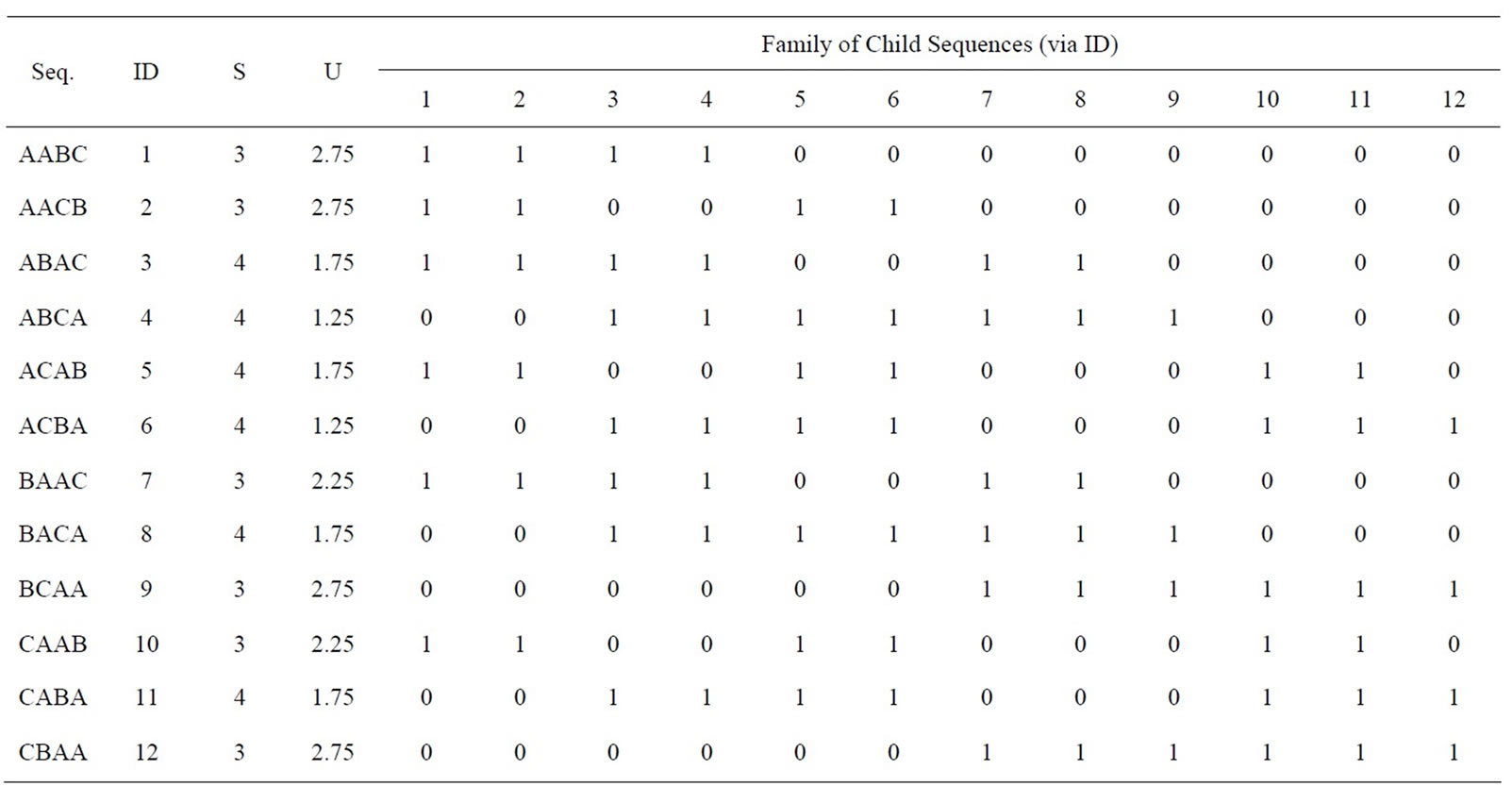
Table 1. Details of example problem.
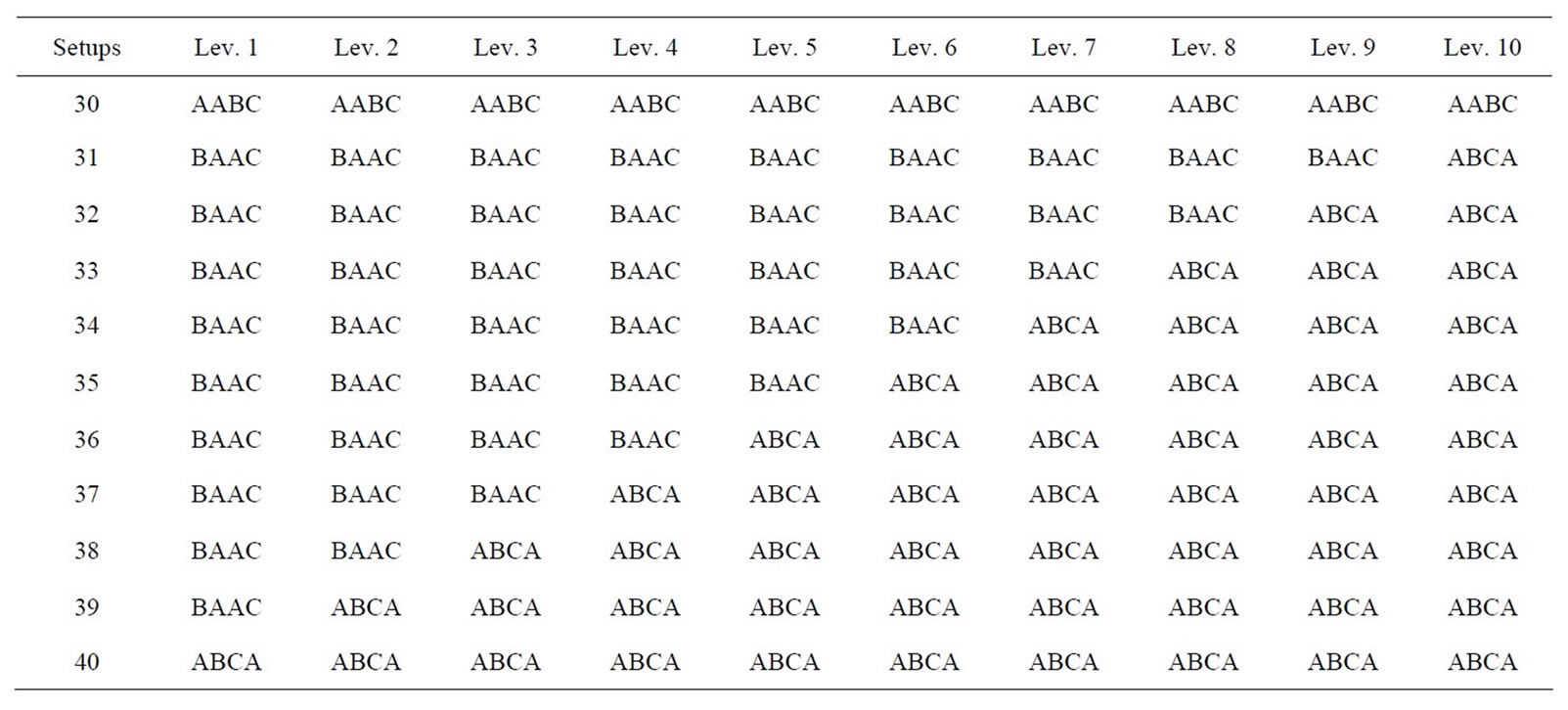
Table 2. Sequence details of example problem’s efficient frontier for ten levels.
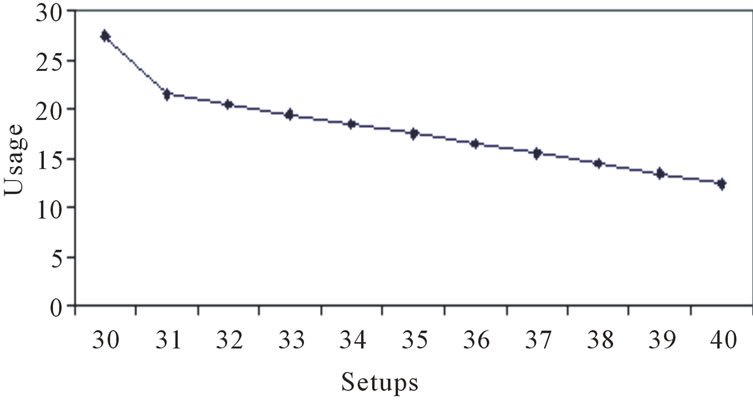
Figure 2. Efficient frontier for AABC through 10 processes.
If one were to enumerate in this nature to find the efficient frontier for ten levels, there would be 5,542,861 nodes at Level 10. Given such computational difficulty, enumeration cannot be effectively used to find optimal solutions for problems of any significant size. Because of this reality, the next section details the methodology used to obtain near-optimal solutions for several problem sets.
3. Methodology
Prior to a description of the methodology used to find solutions to multiple-level, re-sequencing problems involving objective of setups and usage, the following terminology is presented via Table 3. The objective of this problem is to find sequences that minimize the total usage rate (Usage) across all p processes (or levels) for each associated setup (Setup). From a mathematical programming standpoint, this can be stated as follows:
Min:
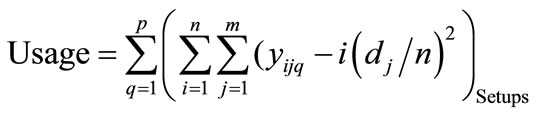 , (1)
, (1)


Table 3. Definitions used for methodology.
where
 , (2)
, (2)
and
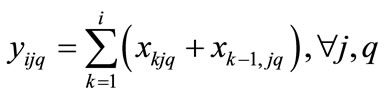 (3)
(3)
Subject to:
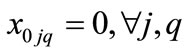 (4)
(4)
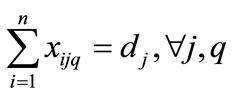 (5)
(5)
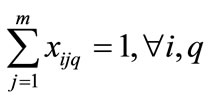 (6)
(6)
Equation (1) shows how Miltenburg’s usage rate is computed [1]. Equation (2) shows, from a mathematical standpoint, how Setups are determined in terms of the parameters of interest here. Equation (3) simply relates the decision variable xijq to the endogenous variable yijq. Equation (3) is not mandatory, but is included here with the intent of simplifying the objective function, Equation (1). Equation (4) initializes the 0th level of the decision variables to zero. Equation (5) mandates that the decision variables reflect the quantity demanded for each unique item. Equation (6) forces each sequence position to have exactly one item.
Although a mathematical programming formulation approach is presented above, conventional mathematical programming solution approaches are ineffective for a problem of this type. The reasoning for this essentially lies in the fact that the decision variables exclusively binary, and the objective function is linear. Models such as this are frequently referred to as Pure Integer Nonlinear Programming models (PINLP) and are considered difficult to solve to optimality by commercial solvers [6]. Given this unfortunate reality, a search heuristic must be employed to solve the problem.
3.1. Search Heuristic
To heuristically find sequences for minimal usage rates across the spectrum of feasible setups across multiple processes, several algorithmic steps must be taken. These steps are as follows:
3.1.1. Step 1: Initialization
The initial step in the search is to first initialize values of the total number of sequence positions (n), the number of unique items to be sequenced (m) and the number of processes required (p). Demand for each unique item must be stated (dj). The number of replications (r) is determined. All permutations for the test problem are generated—the number of permutations is set to TP, and each permutation is assigned an ID label. From these permutations, the pairwise relationships between all TP sequences are inspected. If sequence jj is a feasible child sequence of sequence ii, then the matrix value fii,jj is set to one. Otherwise, this value of fii,jj is set to zero. For all TP sequences, the usage (Uii) and setups (Sii) values are determined, along with the maximum usage (MaxU). Mathematically, Uii and Sii are as follows:
 (7)
(7)
 , (8)
, (8)
where aij represents the number of item j in the sequence through the ith position, and bij is one if item j is present in the ith sequence position, zero otherwise. Note that these two formulae are essentially the same as shown in Equations (1) and (2) respectively, with the difference being that these two formulae consider only one process, whereas the Equations (1) and (2) consider p processes. The parent sequence for the 0th level is always the trivial sequence—the sequence where all of the “As” are placed into the sequence, followed by the “Bs,” etc. It is noted that the permutation index values, values of Uii and Sii, and fii,jj values are shown for the example problem in Table 1.
3.1.2. Step 2: Candidate Sequence for Next Process
The sequence that was selected for the last process is now given status as the parent sequence. The value of q is set to the appropriate level. Each of the candidate sequences is given a probability of selection via a probabilistic mechanism. This probabilistic mechanism is a function of the candidate’s usage rate (Ujj). Lower usage rates are more attractive, as the lowest usage rate for each unique setup across all processes describes the efficient frontier. The probability of selecting candidate sequence jj when sequence ii is the parent sequence is as follows:
 , (9a)
, (9a)
If the researcher wishes to incorporate the concept of pheromone into the probability of selecting candidate sequence jj, P(Seljj) is calculated as follows:
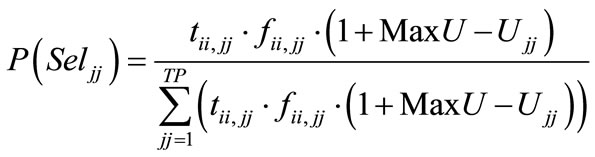 (9b)
(9b)
This is similar to Equation (9a), with the difference being that (9b) incorporates the transition matrix, tii,jj into the calculation, which increases the probability of transitioning from sequences ii to jj, which have historically been observed to result in strong performance in terms of the efficient frontier.
It should be noted that infeasible child sequences of sequence ii are excluded from these calculations, as their associated fii,jj values are zero, forcing nonexistent probabilities.
3.1.3. Step 3: Selection of Next Sequence via Monte-Carlo Simulation
For all selection candidates, a cumulative probability distribution table is constructed, based upon the probability values determined via Equation (9a) or (9b). A random number on the [0, 1) interval is then generated and matched with the appropriate child sequence candidate. This appropriate child sequence candidate is now classified as the selected sequence. The selected sequence for process q is noted as Sq.
3.1.4. Step 4: Iterate toward p
Steps 1 and 2 are repeated for each of the p processes.
3.1.5. Step 5: Objective Function and Efficient Frontier
For each of the p sequences selected via the three prior steps, their values of setups (Sjj) and usage (Ujj) are determined and summed, and determine the total setups (TS) and corresponding total usage rate (TUTS) for the p-sequence solution.
3.1.6. Step 6: Efficient Frontier
If the usage rate for the p-sequence solution (TUTS) is superior to that on the efficient frontier for the corresponding number of setups, than the p-sequence solution usage rate becomes part of the efficient frontier. In mathematical terms, this is as follows:
If TUTS < FTS, then FTS = TUTS(10)
If transition is used for seeking an optimal solution— that is, if Equation (9b) is used instead of Equation (9a), then the new efficient frontier results in the transition matrix being updated. Specifically, the values of the transition matrix that comprise the recent traversal/solution that resulted in the new efficient frontier value are incremented by one. This is done to reinforce, or encourage traversal through sequences that show relative promise. Mathematically, this is as follows:
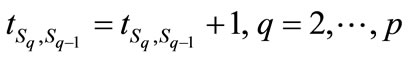 (11)
(11)
If transition is not used for seeking an optimal solution, Equation (11) is ignored.
3.1.7. Step 7: Iteration toward r
Steps (1)-(5) are repeated r times. Again, r is a userspecified parameter which dictates the number of iterations, or replications.
3.1.8. Step 8: Report Findings
At the end of the iterative process, the efficient frontier is reported, along with all information associated with performance.
3.2. Performance Measures
There are two performance measure of interest associated with this research effort. These performance measures are: relative inferiority to optimal; number of voids in the efficient frontier; and CPU time.
Relative Inferiority is the degree to which the searchbased solution is “above,” or inferior to, the optimal solution. If (FO)S is used to note the optimal frontier usage for some number of setups, and (FS)S is used to note the frontier usage associated with the search heuristic (for the same number of setups) described above, then the Relative Inferiority (RI) can be computed as follows:
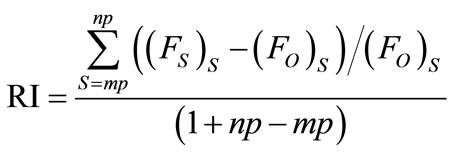 (11)
(11)
It is, of course, desired that the relative inferiority be minimized. Figure 3 provides an illustration of relative inferiority for the example problem.
The second performance measure of interest here is the number of frontier voids. A frontier void is a measure of the heuristic’s failure to span the gamut of the efficient frontier. This particular concern is a widely acknowledged problem in the world of multiple objective optimization, where (as is the case here) the researcher attempts to minimize some objective function (usage) across a variety of conditions (setups). The number of frontier voids is easily determined, as it is the number of times that the search heuristic fails to find a solution on the efficient frontier, where an optimal solution is known to exist. Figure 4 details this via the example problem. Here, one will notice that there is a single frontier void when there are eleven opportunities for voids. This frontier void resides at (36) setups. The optimal solution shows that sets of sequences exist for as few as (30) setups, and as many as (40) setups (eleven total unique setups). This means that the search heuristic failed on one occasion to find a full set of solutions. This frontier void performance can then be “standardized” to one out of eleven, or 9.09%. In the interest of full disclosure, it is appropriate to note that the example shown in Figure 3 resulted in zero frontier voids (0.0%).
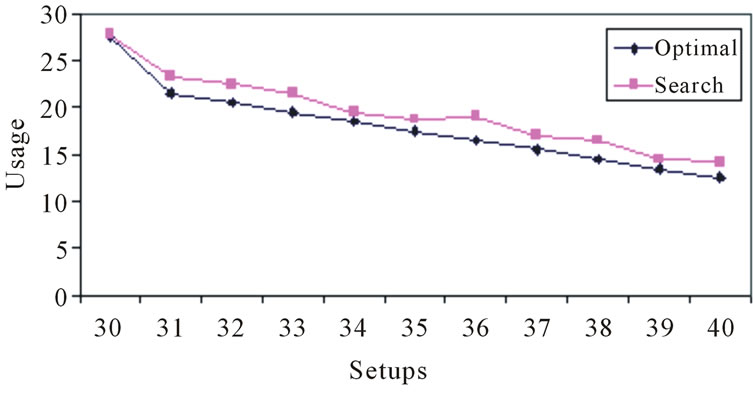
Figure 3. Relative inferiority of efficient frontier for example problem.

Figure 4. Illustration of single frontier void for example problem.
4. Experimentation
The methodology presented above is used on several test problem sets from the literature. These test problem sets contain items requiring sequencing, possessing varying degrees of item homogeneity. The five general problem sets are detailed on the Appendix. These problem sets are also used for a varying degree of processes (p)—all problems employ as few as two processes (p = 2), some employ as many as ten processes (p = 10). For each problem studied, the performance measures of relative inferiority, frontier voids and CPU time are determined and analyzed. The performance summary information is broken down into three categories. The first category is the search heuristic associated with not using transition, where the selection probability is governed by Equation (9a). The second category is the search heuristic associated with the use of transition, where the selection probability is governed by Equation (9b), and the transition matrix is updated via Equation (11). The third category is the result of a simulated annealing solution approach from a previous research effort. Each of these categories is hereafter referred to as search strategies. It is important to note that to make a fair comparison between these three strategies, each strategy exploited the same magnitude of search space. The magnitude of search space is dictated by the number of replications (r). In other words, the number of replications (r) was kept the same for each strategy for each of the fifty-five unique problems.
4.1. Research Questions
To make a determination of which strategies perform best on the problem sets, the following research questions are posed:
1) Does the strategy have an effect on relative inferiority? If so, which strategies are best? Do any of the strategies produce optimal results from the standpoint of statistical significance?
2) Does the strategy have an effect on the degree of frontier voids? If so, which strategies are best? Do any of the strategies produce optimal results from the standpoint of statistical significance?
The first two parts of each of these research questions will be addressed via single-factor ANOVA and appropriate pairwise comparison tests. The final part of each research question will be a single-sample t-test, with the following hypotheses:
H0: µ = 0 HA: µ > 0 Here, µ represents the population mean of the performance measure of interest (either relative inferiority or the frontier void ratio). The “0” represents optimality, either in the form of a relative inferiority of “0” or a frontier void ratio of “0”.
4.2. Computational Experience
The search heuristic described in the methodology section was coded using the Java Development Kit version 6, on the Microsoft Vista operating system with an AMD Turion 64 × 2 processor, having a CPU speed of 1.90 GHz. In all instances, efforts were made to maximize the computational efficiency of the algorithms.
5. Experimental Results
The research questions are first addressed, followed by a presentation of results for all problem sets and a discussion of CPU time.
5.1. Research Questions
For the first research question, it is clear that the strategy has an effect on relative inferiority performance (F = 43.73, p < 0.001). Means and standard deviations of relative inferiority are presented in Table 4. From inspection of Table 4, it is clear that in terms of relative inferiority, the two search heuristics presented here outperform the Simulated Annealing approach from a prior research effort. In fact, subsequent analysis shows that while the heuristic without transition does not statistically show optimality (mean inferiority of zero; t = 3.92, p = 0.0001), the heuristic with transition does statistically show optimality (t = 1.21, p = 0.12).
For the second research question, it is also clear that the heuristic strategy has an effect on the performance measure of frontier void ratio (F = 2.33, p = 0.10). While this p-value is higher than the one associated with the first research question, Table 5 does show that the results associated with the heuristic presented with this research are desirable to those associated with the research effort that presented the Simulated Annealing approach [2]. For frontier void ratio, the heuristics presented in the methodology section are roughly half to magnitude from the earlier research effort. While the heuristic with transition enjoys a slight advantage in terms of relative inferiority, the heuristic without transition enjoys a slight advantage in terms of frontier void ratio.
5.2. Problem Set Results
Tables 6(a)-(e) show results in terms of relative inferiority and frontier void ratio for each of the three strategies. Each table is dedicated to a unique problem set. As the five problem sets and their results are inspected, it becomes clear that the methodology presented with this research consistently outperforms the simulated annealing methodology from an earlier research effort [2], essentially validating the results shown in Tables 4 and 5.
5.3. CPU Time
For each of the fifty-five problems studied, CPU time was captured for the two heuristics presented here. Space limitations prevent presenting them on a by-problem basis, but means are summarized here: the heuristic that does not employ transition results in a mean CPU time of 90.6 seconds, while the heuristic that does employ transition results in a mean CPU time of 91.2 seconds. This slight

Table 4. Performance comparison of strategies for relative inferiority.

Table 5. Performance comparison of strategies for frontier void ratio.
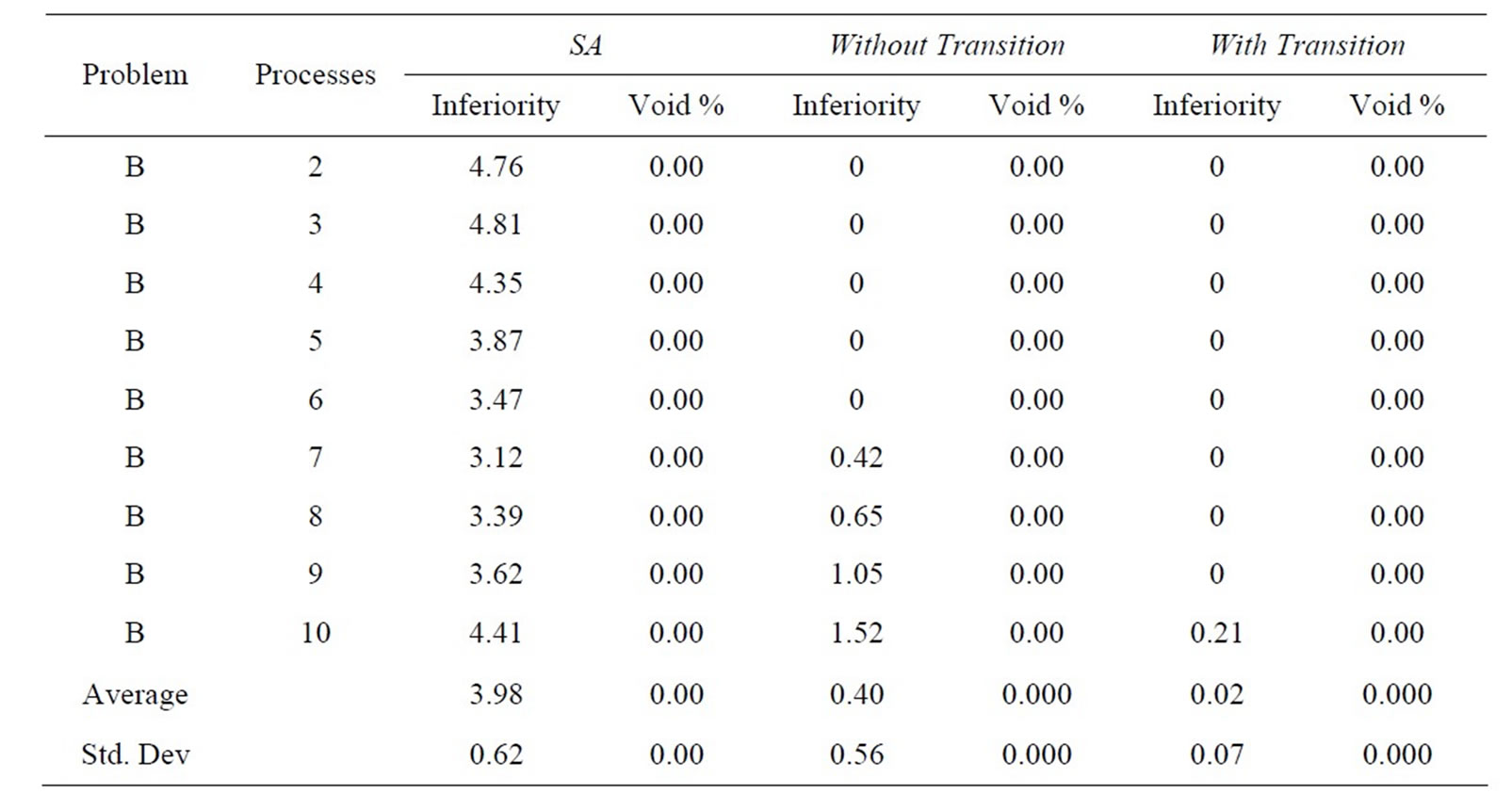 (a)
(a)  (b)
(b) 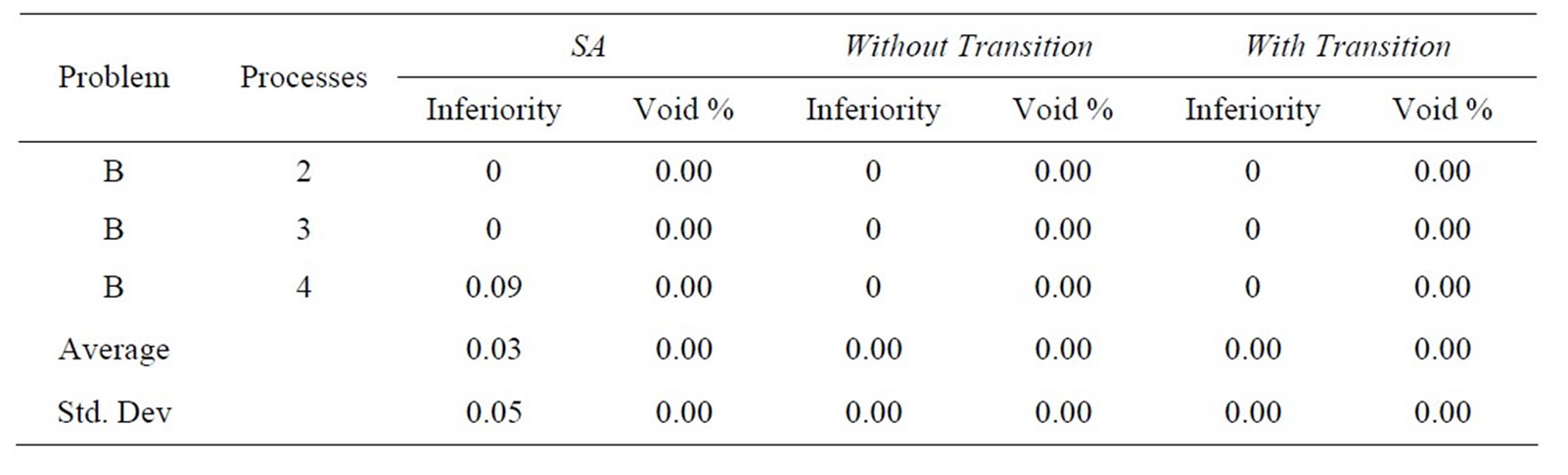 (c)
(c) 
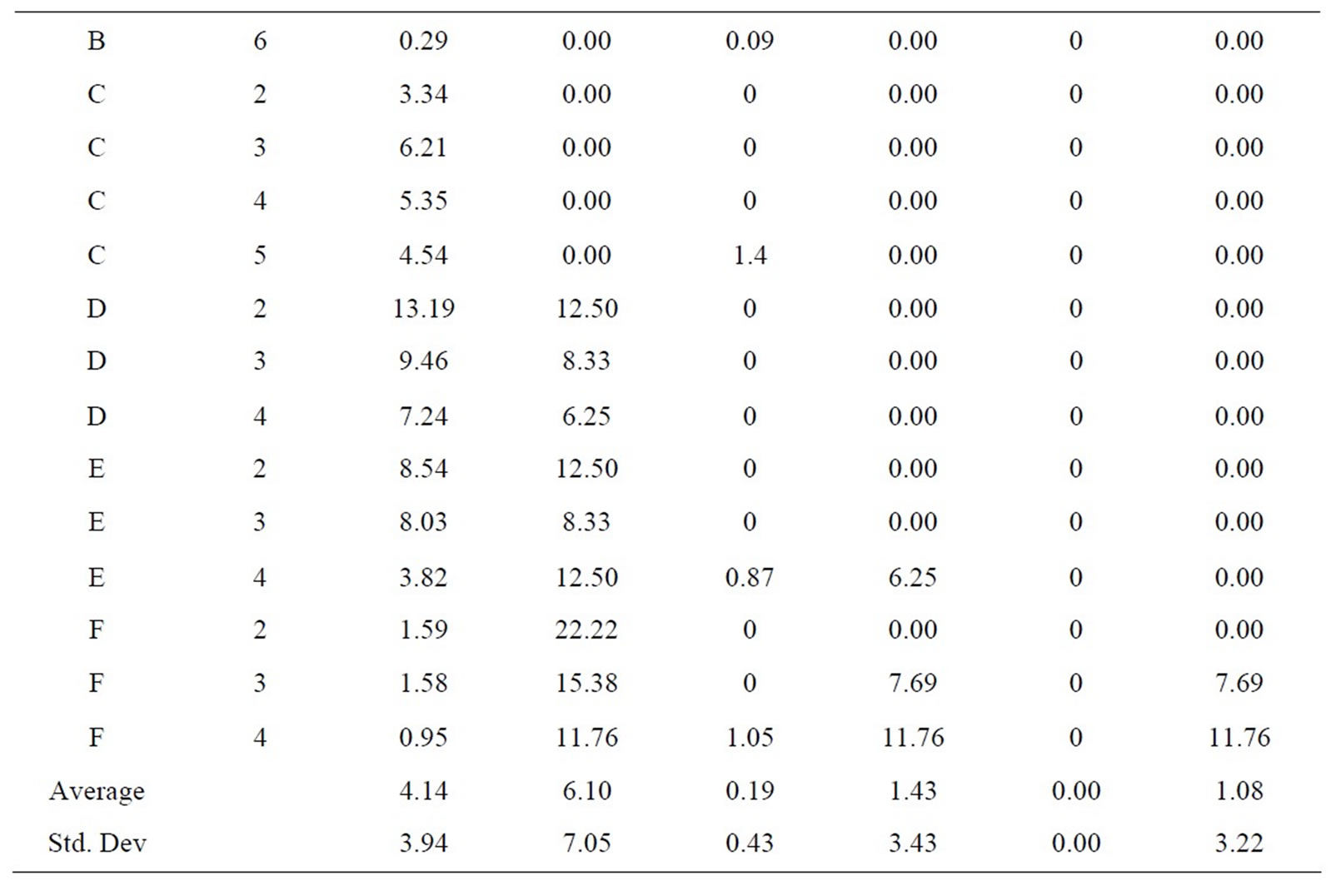 (d)
(d)
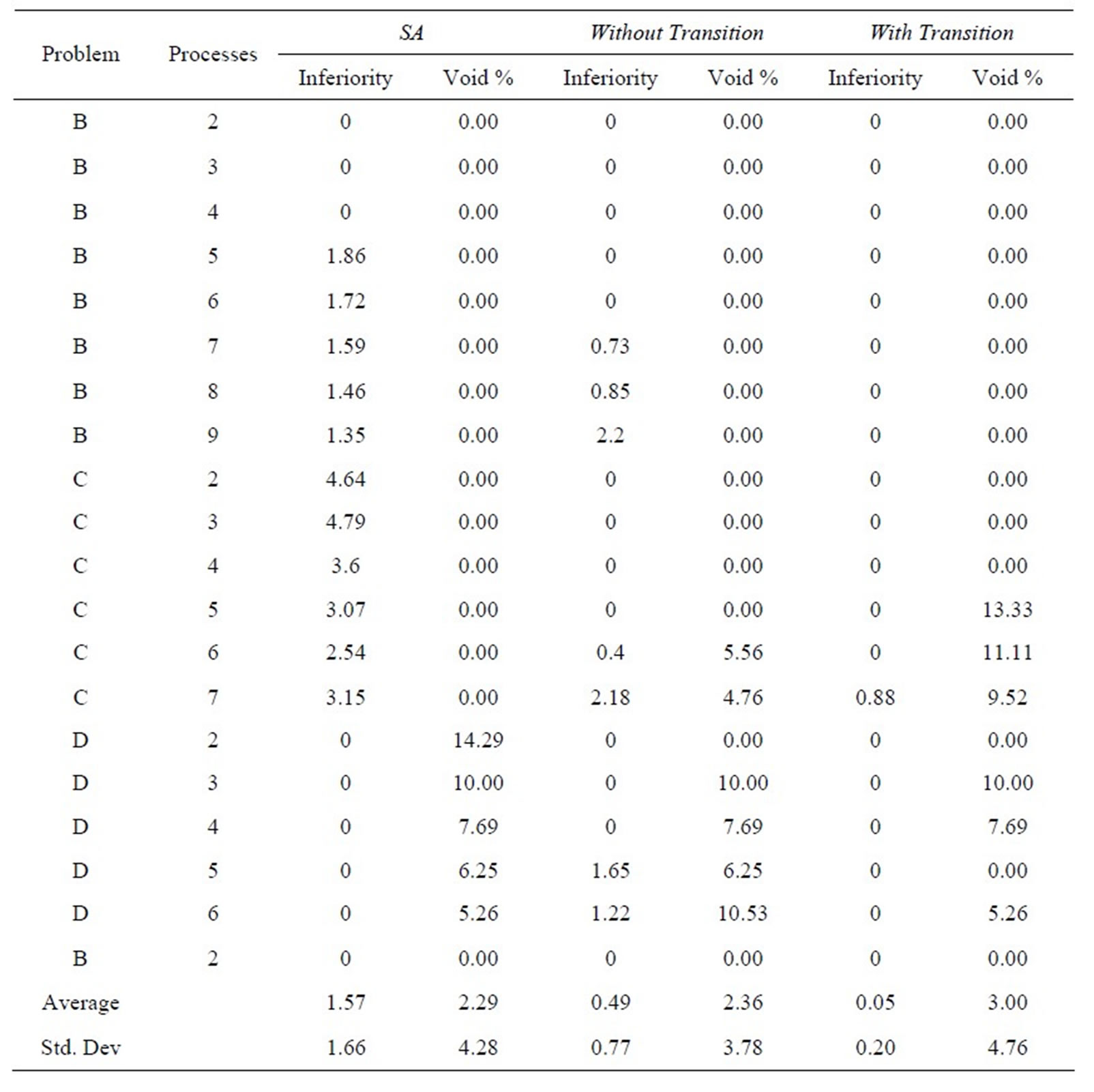 (e)
(e) Table 6. Results for problem. (a) set A0; (b) set A1; (c) set A2; (d) set A4; (e) set A5.
difference in CPU time can be explained by the extra computation involving tii,jj in Equation (9b) as compared to (9a), along with the extra step required to update tii,jj associated with transition in Equation (11). CPU times for the simulated annealing approach are much less than the CPU times for the two heuristic approaches presented here. CPU times never exceeded 10 seconds for any problem.
6. Limitations and Opportunities
This research presented a general approach to address the multiple-process sequencing problem with the objectives of setups and usage rate. Results were found to be a substantial improvement over an earlier effort involving simulated annealing. Despite this favorable outcome, there are some constraining issues that need mentioning.
6.1. Problem Breadth
The size of the problem is a constraining factor which dictates which problems can be solved to optimality. One will note that from Figure 1 that solving a problem to optimality is a cumbersome task—this even applies to very small problems. The problem shown in Figure 1 is essentially the smallest example imaginable, having just twelve unique permutations and only two levels. Nevertheless, the solution space becomes large. For larger problems with more permutations and more levels requiring processing, this issue only becomes more severe. Given this combinatorial explosion, comparing heuristic solutions to optimal solutions is only available for smaller problems.
6.2. Permutation-Based Approach
Another constraining factor is specific to the heuristic approach presented. One will notice that Equations (9a) and (9b) involve feasibilities (fii,jj). Capturing values for each of these endogenous variables involves enumerating through each of the TP permutations TP times so that the binary values of fii,jj can be captured. This endeavor is computationally intensive, contributing O(TP2) to CPU time and memory requirements [7]. Even with highspeed computing, along with Java’s ability to allocate memory to the heap, the O(TP2) issue limits the size of the problem that can be solved via the presented heuristic. This problem only gets worse as the number of feasible permutations grows (as TP increases). It is important to note that the author attempted to avoid a component of the O(TP2) order, but omission of this element led to a relatively weak list of candidate solutions, and a subsequent marginal heuristic performance. As such, this research effort has sacrificed some computational efficiency so that a near-optimal performance could be gained.
6.3. Buffer Size of One
As stated earlier, a pervasive assumption throughout this research is that there is a buffer size of one. This means that whenever re-sequencing is performed, an item can move forward in the sequence one position at most. It is possible to use buffer sizes of larger than one. If this were to be done, however, the breadth of the problem would increase (as there would be more feasible “resequences” because items would be permitted to move up more than one sequence position), further increasing computational efforts to find optimal or near-optimal solutions.
6.4. Future Research Opportunities
The limiting factors listed above, in one form or another, essentially all pertain to problem size and the difficulty of finding optimal solutions and/or good-quality heuristic-based solutions via a reasonable computational effort. Such limiting factors, of course, also present opportunities for subsequent research.
A salient opportunity for future research relates to finding a strong list of candidate solutions while bypassing the feasibility matrix (the values of fii,jj). When this happens, CPU performance will improve, along with reduced memory requirements, enabling the researcher to address problems of a larger size.
Another opportunity for future research applies to using a buffer-size of something larger than one. This, of course, is more computationally expensive, but with gains in computational resources, coupled with the point immediately above, this issue could be explored as well.
Yet another research opportunity relates to finding near-optimal solutions to these problems via exploitation of some of the other search heuristics (such as genetic algorithms [8], tabu search [9], etc.) that repeatedly show promise.
REFERENCES
- J. Miltenburg, “Level Schedules for Mixed-Model Assembly Lines in Just in Time Production Systems,” Management Science, Vol. 35, No. 2, 1989, pp. 192-207. doi:10.1287/mnsc.35.2.192
- P. R. McMullen, “Limited Re-Sequencing for Mixed Models with Multiple Objectives,” American Journal of Operations Research, Vol. 1, No. 4, 2011, pp. 220-228.
- M. Dorigo and L. M. Gambardella, “Ant Colonies for the Traveling Salesman Problem,” Biosystem, Vol. 43, No. 1, 1997, pp. 73-81. doi:10.1016/S0303-2647(97)01708-5
- M. Lahmar and S. Banjaafar, “Sequencing with Limited Flexibility,” IIE Transactions, Vol. 39, No. 10, 2007, pp. 937-955. doi:10.1080/07408170701416665
- M. Masin and Y. Bukchin, “Diversity Maximization Approach for Multiobjective Optimization,” Operations Research, Vol. 56, No. 2, 2008, pp. 411-424. doi:10.1287/opre.1070.0413
- L. A. Schrage, “LINGO: The Modeling Language and Optimizer,” Lindo Systems, Inc., Chicago, 2006.
- R. Sedgewick, “Algorithms in Java: Third Edition,” Addison-Wesley, Boston, 2003.
- J. H. Holland, “Adaptation in Natural and Artificial Systems,” First Edition, University of Michigan Press, Ann Arbor, 1975.
- F. Glover, “Tabu Search: A Tutorial,” Interfaces, Vol. 20, No. 1, 1990, pp. 74-94. doi:10.1287/inte.20.4.74
- P. R. McMullen, “An Ant Colony Optimization Approach to Addressing a JIT Sequencing Problem with Multiple Objectives,” Artificial Intelligence in Engineering, Vol. 15, No. 3, 2001, pp. 309-317. doi:10.1016/S0954-1810(01)00004-8
- P. R. McMullen, “A Kohonen Self-Organizing Map Approach to Addressing a Multiple Objective, Mixed Model JIT Sequencing Problem,” International Journal of Production Economics, Vol. 72, No. 1, 2001, pp. 59-71. doi:10.1016/S0925-5273(00)00091-8
Appendix: Problem Sets
The Appendix containing the problem set details used for this research. These problems were taken from the work of McMullen [10,11].