Applied Mathematics
Vol.06 No.02(2015), Article ID:54176,8 pages
10.4236/am.2015.62039
Generalized Spectrum of Steklov-Robin Type Problem for Elliptic Systems
Alzaki Fadlallah, Kwadwo Antwi-Fordjour, Marius N. Nkashama
Department of Mathematics, University of Alabama at Birmingham, Birmingham, USA
Email: zakima99@uab.edu, kantwi@uab.edu, nkashama@math.uab.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 January 2015; accepted 13 February 2015; published 17 February 2015
ABSTRACT
We will study the generalized Steklov-Robin eigenproblem (with possibly matrix weights) in which the spectral parameter is both in the system and on the boundary. The weights may be singular on subsets of positive measure. We prove the existence of an increasing unbounded sequence of eigenvalues. The method of proof makes use of variational arguments.
Keywords:
Steklov-Robin, Variational Arguments, Matrix Weights

1. Introduction
We study the generalized Steklov-Robin eigenproblem. This spectrum includes the Steklov, Neumann and Robin spectra. We therefore generalize the results in [1] -[4] .
Consider the elliptic system
 (1)
(1)
where ,
, 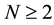 is a bounded domain with boundary
is a bounded domain with boundary  of class
of class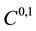 ,
,
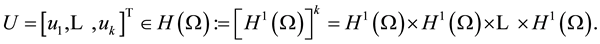 Throughout this paper all matrices are symmetric. The matrix
Throughout this paper all matrices are symmetric. The matrix
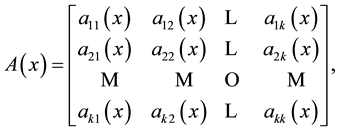
verifies the following conditions:
(A1) The functions 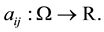
(A2)  is positive semidefinite a.e. on Ω with
is positive semidefinite a.e. on Ω with 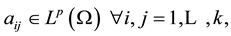 for
for 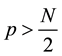 when
when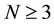 , and
, and  when
when 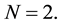
The matrix
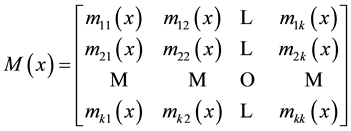
satisfies the following conditions:
(M1)  is positive semidefinite a.e. on Ω The functions
is positive semidefinite a.e. on Ω The functions 





verifies the following conditions:
(S1) The functions
(S2) 





and the matrix
(P1) 




We assume that 
Assumption 1. 1) 
2) 
3) 
4) 
Remark 2. Assumption 1 is equivalent to
Remark 3. Since 
where 




Remark 4. The weight matrices 

Definition 1. The generalized Steklov-Robin eigensystem is to find a pair 


Remark 5. Let 

Indeed, if 

We have that 





positive measure, and 



that 



Remark 6. If 




It is therefore appropriate to consider the closed linear subspace (to be shown below) of 
Now all the eigenfunctions associated with (2) must belong to the 







Therefore 
Since 
By setting 
Since 

that is, the vector 
or equivalently
Hence,
since 
Therefore 




Remark 7. 1) If 



2) If 




・ We shall make use in what follows the real Lebesgue space 

is well-defined, it is a Lebesgue integrable function with respect to Hausdorff 



and the associated norm by
(see [5] , [6] and the references therein for more details).
・ The trace mapping 

defines an inner product for

Now, we state some auxiliary result, which will be need in the sequel for the proof of our main result. Using the Hölder inequality, the continuity of the trace operator, the Sobolev embedding theorem and lower semicontinuity of


Definition 2. Define the functional
and
Lemma 1. Suppose (A2), (S2), (M1), (P1) are met. Then the functionals 

See [8] for the proof of Lemma 1.
Theorem 8. 

See [8] for the proof of Theorem 8.
2. Main Result
Theorem 9. Assume Assumption 1 as above, then we have the following.
1) The eigensystem (1) has a sequence of real eigenvalues
and each eigenvalue has a finite-dimensional eigenspace.
2) The eigenfunctions 





3) The normalized eigenfunctions provide a complete 



In addition,
Proof of Theorem 9. We will prove the existence of a sequence of real eigenvalues 
tions 

We show that 
Let 
the lower-semi-continuity of
Let 







so we have that
Therefore, this sequence is bounded in
which convergent weakly to 





There exists 





for all 


plies that 




Clearly,








Now we show the existence of higher eigenvalues.
Define
We know that the kernel of
Since W1 is the null-space of the continuous functional 

space of

we define
Since 

we know that the kernel of
Since W2 is the null-space of the continuous functional 



we define
Since 

is achieved at some
We let
and
Since 

is achieved at some
Proceeding inductively, in general we can define
we know that the kernel of
Since Wj is the null-space of the continuous functional 

of

In this way, we generate a sequence of eigenvalues
whose associated 

Claim 1 
Proof of claim 1. By way of contradiction, assume that the sequence is bounded above by a constant. Therefore, the corresponding sequence of eigenfunctions 



Since the 


which contradicts Equation (7). Thus, 

Claim 2
Each eigenvalue 
See [8] for the proof of claim 2.
We will now show that the normalized eigenfunctions provide a complete orthonormal basis of
so that
Claim 3
The sequence 


maximal 
Proof of Claim 3. By way of contradiction, assume that the sequence 




since



Since we know from Claim 1 that 











Now let
Therefore,
and
Claim 4
We shall show that
Proof of Claim 4.
Thus
References
- Auchmuty, G. (2012) Bases and Comparison Results for Linear Elliptic Eigenproblems. Journal of Mathematical Analysis and Applications, 390, 394-406. http://dx.doi.org/10.1016/j.jmaa.2012.01.051
- Mavinga, N. (2012) Generalized Eigenproblem and Nonlinear Elliptic Equations with Nonlinear Boundary Conditions. Proceedings of the Royal Society of Edinburgh: Section A Mathematics, 142, 137-153.
- de Godoi, J.D.B., Miyagaki, O.H. and Rodrigues, R.S. (2013) Steklov-Neumann Eigenvalue Problems for a Class of Elliptic System. SP-Brazil.
- Steklov, L.M.W. (1902) Sur les problèmes fundamentaux de la physique mathématique. Annali Scuola Norm. Sup. Pisa, 19, 455-490.
- Küfner, A., John, O. and Fučik, S. (1977) Function Spaces. Noordhoff International Publishing, Leyden.
- Nečas, J. (1967) Les Mèthodes directes en thèorie des equations elliptiques. Masson, Paris.
- Grisvard, P. (1985) Elliptic Problems in Nonsmooth Domains. Pitman, Boston.
- Fadlallah, A. (2015) Elliptic Equations and Systems with Nonlinear Boundary Conditions. Ph.D. Dissertation, University of Alabama at Birmingham (UAB), Birmingham.














































































