Theoretical Economics Letters
Vol.2 No.2(2012), Article ID:19328,5 pages DOI:10.4236/tel.2012.22039
A Preliminary Investigation of the Optimal Percentage Requirement in an Electricity Market with Tradable Green Certificates
1Oklahoma State University, Stillwater, USA
2University of Central Oklahoma, Edmond, USA
Email: Kevin.currier@okstate.edu, scurrier@UCO.edu
Received February 20, 2012; revised March 14, 2012; accepted March 22, 2012
Keywords: Renewable Energy; Tradable Green Certificates; Percentage Requirement; Renewable Portfolio Standard
ABSTRACT
Around the world, energy markets are being liberalized with the goal of achieving fully competitive markets while attaining environmental policy objectives. This paper considers a system of Tradable Green Certificates (TGCs)—a market based regulatory instrument designed to promote electricity generation from renewable energy sources. In a TGC program, the principal policy instrument is the “percentage requirement” which stipulates the percentage of total electricity generation that must be obtained from renewable sources. This paper provides a preliminary investigation of the socially optimal choice of the percentage requirement in a Cournot duopoly setting. The paper discusses the problem geometrically and considers some of the practical difficulties associated with the determination of the optimal percentage requirement. Several important avenues for generalization of the results are also discussed.
1. Introduction
Around the world, and particularly in the European Union, energy markets are being liberalized, with the goal of achieving (ideally) fully competitive energy markets while attaining environmental policy objectives. Many countries have introduced systems of Tradable Greenertificates (TGCs)—market based regulatory instruments designed to promote electricity generation from renewable energy sources, such as wind, solar, biomass etc. (See for example, Amundsen and Mortensen [1], Amundsen and Nese [2], Ford, Vogstad and Flynn [3] and Bohringer and Rosendahl [4]). Under the typical TGC program, targets for renewable output are set and generators of renewable energy are awarded TGCs in proportion to their output of “green” energy. Green energy targets can be met via buying and selling of TGCs, independently of electricity production (Dinica and Arentsen [5]). Proponents of TGC programs argue that TGCs promote investment in renewable generation as well as allowing renewable targets to be met at lower cost than under direct subsidization schemes such as the “feed-in tariff” (Tamas, Shrestha and Zhou [6], Bergek and Jacobsson [7]).
Total electricity generation is the sum of the electricity generated from renewable sources and fossil-fuel (“black”) sources. In a TGC program, a “percentage requirement” (i.e., a renewable portfolio standard) is stipulated which requires a specified percentage of total electricity generation to derive from renewable sources. The value selected by the regulator for the percentage requirement affects both black and green output levels, as well as TGC prices and the price of electricity paid by final consumers and is thus a policy instrument of central importance to the development and promotion of renewable electricity generation.
This paper considers a simple electricity duopoly consisting of one green producer and one black producer. The paper examines some equilibrium implications of variations in the stipulated percentage requirement and characterizes its welfare maximizing value. The analysis is illustrated with a simple example, providing a geometric characterization. Finally, the paper discusses some practical difficulties associated with the determination of the optimal percentage requirement and several directions in which this research could be further developed.
2. The Model
Consider an electric utilities industry served by two firms: a fossil-fuel producer of “black” electricity y and a renewable producer of “green” electricity x where 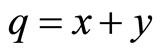 denotes total electricity. The demand for electricity is formed by the maximization of consumer surplus
denotes total electricity. The demand for electricity is formed by the maximization of consumer surplus 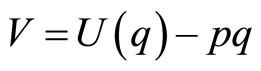 where
where 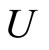 denotes total consumer utility and p denotes the price paid for electricity by final consumers. Inverse market demand is
denotes total consumer utility and p denotes the price paid for electricity by final consumers. Inverse market demand is 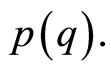 It is assumed that
It is assumed that 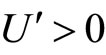 and
and 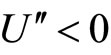 implying that
implying that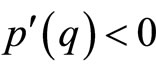 .
.
Black output and green output are produced under constant marginal costs 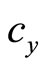 and
and  respectively, with
respectively, with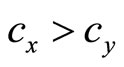 . In a TGC market, for each unit of black electricity supplied, the black producer must surrender
. In a TGC market, for each unit of black electricity supplied, the black producer must surrender ![]() TGCs which costs
TGCs which costs ![]() where
where 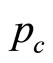 denotes the price of a TGC. Assuming Cournot behavior, the black producer selects y to maximize
denotes the price of a TGC. Assuming Cournot behavior, the black producer selects y to maximize 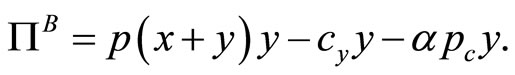 Each green producer also is required to surrender
Each green producer also is required to surrender ![]() TGCs per unit of x but receive
TGCs per unit of x but receive 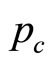 for each unit in addition to the price of electricity. Hence, the green producer selects x to maximize
for each unit in addition to the price of electricity. Hence, the green producer selects x to maximize

Obviously, the TGC program implies a transfer from the black producer to the green producer. It is assumed that both firms are price takers in the TGC market. The equilibrium price of a TGC is determined such that the percentage requirement 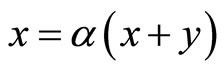 is satisfied (i.e., the TGC market clears), where
is satisfied (i.e., the TGC market clears), where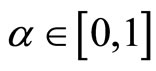 .
.
Finally, let 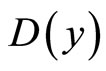 denote the environmental damage caused by the production of black electricity, where
denote the environmental damage caused by the production of black electricity, where 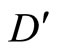 and
and 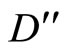 > 0. Social welfare W is defined to be the unweighted sum of consumer surplus and profits net of environmental damages:
> 0. Social welfare W is defined to be the unweighted sum of consumer surplus and profits net of environmental damages:
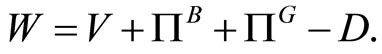
3. The Regulatory Problem
3.1. The Equilibrium Locus
Observe first that in the absence of a TGC market, the black firm maximizes 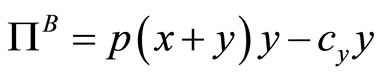 and the green firm maximizes
and the green firm maximizes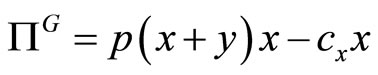 . Since the marginal cost of green electricity is assumed greater than that of black electricity (i.e.,
. Since the marginal cost of green electricity is assumed greater than that of black electricity (i.e.,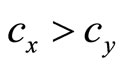 ), the Cournot equilibrium
), the Cournot equilibrium 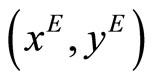 will be above the 45 degree line in
will be above the 45 degree line in  space. Profit maximization in the presence of the TGC market implies that for each value of
space. Profit maximization in the presence of the TGC market implies that for each value of![]() , there will be (an assumed unique) Cournot equilibrium
, there will be (an assumed unique) Cournot equilibrium 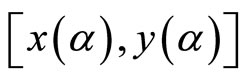 with corresponding equilibrium TGC price
with corresponding equilibrium TGC price 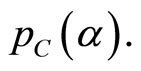 Note that these two problems are equivalent precisely when the value of
Note that these two problems are equivalent precisely when the value of ![]() is such that
is such that 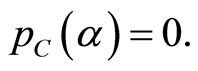 In this case,
In this case, 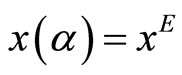 and
and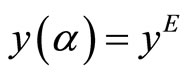 , implying that the value of
, implying that the value of ![]() must be
must be 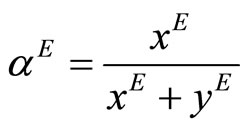 with the slope of the line from
with the slope of the line from 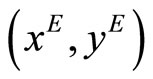 to the origin given by
to the origin given by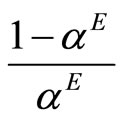 . As
. As ![]() increases from
increases from ![]() to 1, an equilibrium locus E of
to 1, an equilibrium locus E of 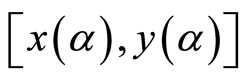 pairs is traced out with
pairs is traced out with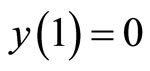 . The equilibrium locus E is the set of all intersection points of the firms’ reaction functions, when
. The equilibrium locus E is the set of all intersection points of the firms’ reaction functions, when 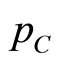 assumes its equilibrium value. If
assumes its equilibrium value. If 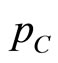 is not at its equilibrium value, the reactions functions intersect at a point that is not on E.
is not at its equilibrium value, the reactions functions intersect at a point that is not on E.
3.2. Welfare
To analyze the issue of determining the socially optimal value of![]() , the following Proposition is needed.
, the following Proposition is needed.
Proposition 1.
When the TGC market clears, social welfare may alternatively be expressed as
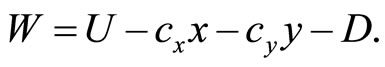
Proof.
As defined previously,
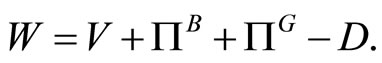
Using the definition of consumer surplus and profits,
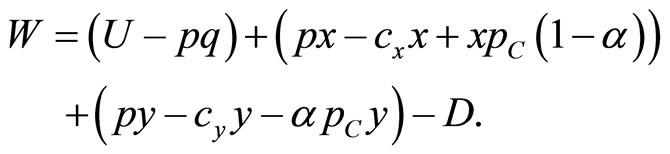
Now 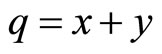 and
and 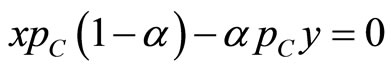 when the TGC market clears (since
when the TGC market clears (since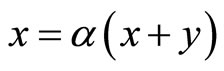 ) implying that
) implying that 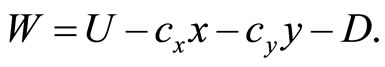
3.3. The Optimal Percentage Requirement
Observe that 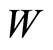 is strictly concave in
is strictly concave in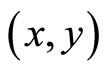 . However, only
. However, only  pairs along E are attainable under the existing market structure. Thus, the regulator’s objective is to determine the value of
pairs along E are attainable under the existing market structure. Thus, the regulator’s objective is to determine the value of![]() , say
, say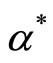 , that maximizes
, that maximizes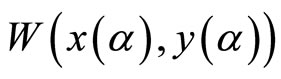 . Differentiation of
. Differentiation of  with respect to
with respect to ![]() implies that at this optimal point,
implies that at this optimal point,
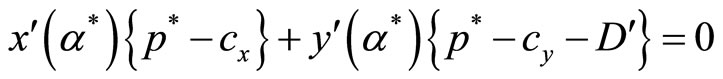
where 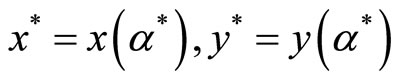 and
and 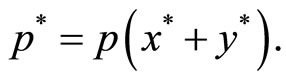 This is equivalent to determining the corresponding
This is equivalent to determining the corresponding 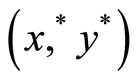 that maximizes
that maximizes  over the equilibrium locus E, in which case
over the equilibrium locus E, in which case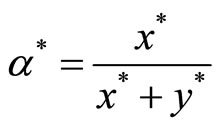 . It should be noted however that welfare comparisons between
. It should be noted however that welfare comparisons between 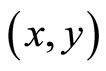 pairs not on E are not valid in the presence of a TGC market due to the failure of the TGC market to clear. In addition, it has been shown that increases in
pairs not on E are not valid in the presence of a TGC market due to the failure of the TGC market to clear. In addition, it has been shown that increases in ![]() do not necessarily lead to increases in green output and decreases in black output (Amundsen and Mortensen [1]). However, if
do not necessarily lead to increases in green output and decreases in black output (Amundsen and Mortensen [1]). However, if 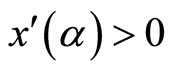 and y'(α) < 0 for all
and y'(α) < 0 for all![]() , then E slopes downward and at the optimum,
, then E slopes downward and at the optimum,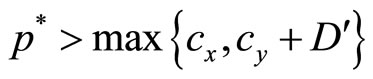 .
.
The following section provides an illustration of the equilibrium locus E and the determination of the socially optimal percentage requirement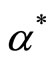 .
.
4. An Example
4.1. The Equilibrium Locus and Welfare Maximization
Assume that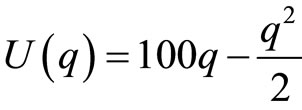 . Since
. Since 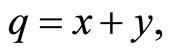 market demand is
market demand is 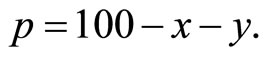 In addition, assume that marginal costs are cx = 6 and cy = 2 with environmental damage function
In addition, assume that marginal costs are cx = 6 and cy = 2 with environmental damage function 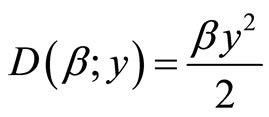 where
where 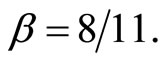 Under Cournot profit maximization, it is straightforward to show that
Under Cournot profit maximization, it is straightforward to show that 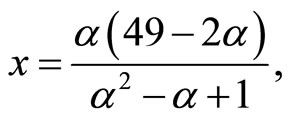
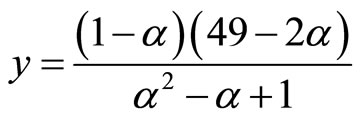 and
and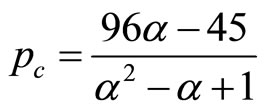 . The equilibrium locus is
. The equilibrium locus is
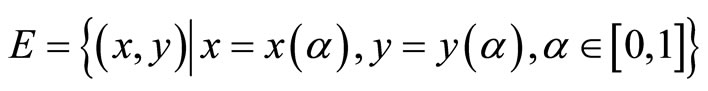 .
.
Note that 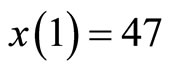 and
and 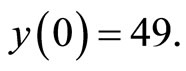 The unregulated Cournot equilibrium is
The unregulated Cournot equilibrium is  with implied percentage requirement
with implied percentage requirement 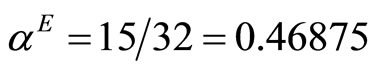 and
and 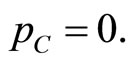 Welfare is
Welfare is
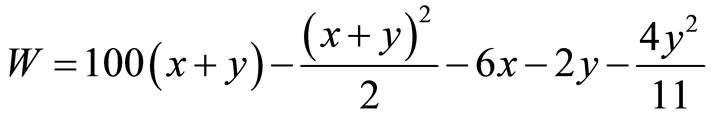
which attains its unconstrained global maximum at (88.5, 5.5). At the Cournot equilibrium,

As ![]() increases from
increases from  to 1, the equilibrium certificate price increases monotonically from 0 to 51. Social welfare is maximized when
to 1, the equilibrium certificate price increases monotonically from 0 to 51. Social welfare is maximized when 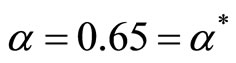 with resulting Cournot equilibrium
with resulting Cournot equilibrium 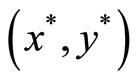 = (40, 21.80),
= (40, 21.80),
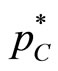 = 22.52 and welfare
= 22.52 and welfare 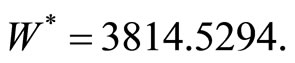 Figure 1 provides an illustration.
Figure 1 provides an illustration.
4.2. The Damage Function
As would be expected in general, the socially optimal green/black output combination, 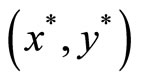 moves upward and to the left along E as the damage parameter
moves upward and to the left along E as the damage parameter  decreases, for
decreases, for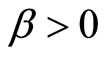 . When
. When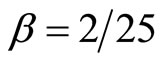 , the welfare maximizing percentage requirement is
, the welfare maximizing percentage requirement is 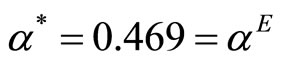 with resulting Cournot equilibrium
with resulting Cournot equilibrium
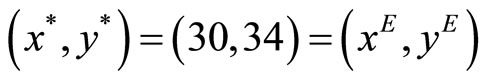 and
and 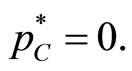 Thus,
Thus,
Proposition 2.
For the damage function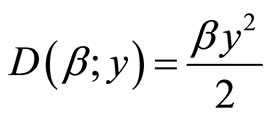 , there exists a “threshold” value
, there exists a “threshold” value 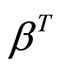 of the damage parameter such that, for
of the damage parameter such that, for 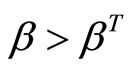 the TGP program with the percentage requirement chosen optimally, improves social welfare.
the TGP program with the percentage requirement chosen optimally, improves social welfare.
5. Conclusions
This paper has studied a simple electricity duopoly operated under a system of Tradable Green Certificates. TGC programs stipulate that a specified percentage of total energy production be derived from renewable sources. The analysis has demonstrated that the value selected for
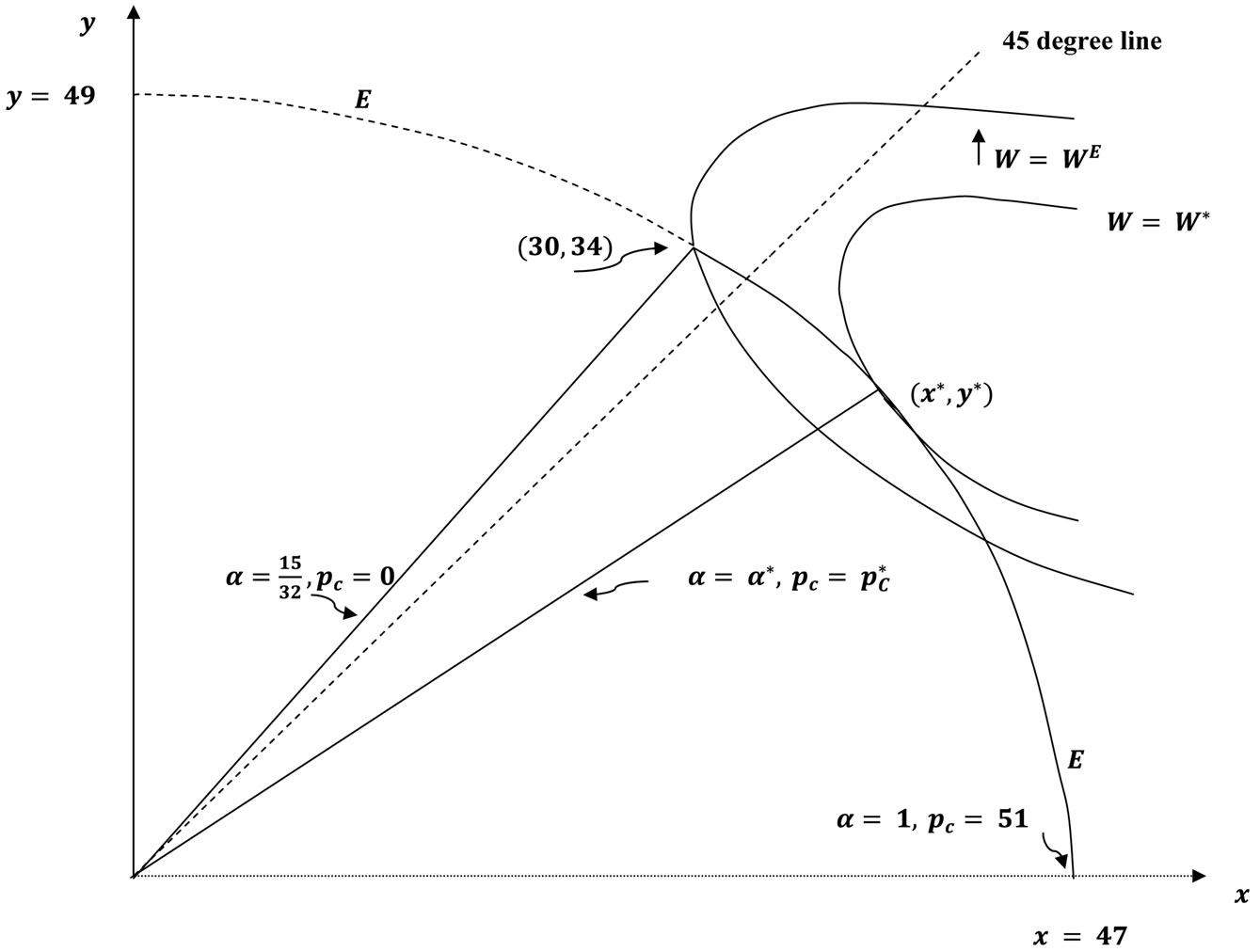
Figure 1. The equilibrium locus and the welfare maximizing percentage requirement.
the percentage requirement has endogenous effects on both black and green producers revenues and costs and hence, output levels. Thus, in terms of promotion of environmental objectives, the value that the regulator selects for the percentage requirement is a key policy instrument.
While a TGC program does in general promote the development of renewable electricity generation, given the status-quo, a small increase in the percentage requirement need not result in an increase in green and a decrease in black outputs. The paper has demonstrated that under standard Cournot behavior, variations in the percentage requirement generate an “equilibrium locus” E which represents the set of attainable green/black output levels for the market under the current market structure. The unconstrained social welfare maximum requires a larger amount of green output and a smaller amount of black output than that obtained in the absence of the TGC program. Therefore, from a policy perspective, the regulator’s objective will be to determine the value of the percentage requirement that maximizes social welfare given the existing market structure, i.e., the realized green/black output combination must lie on E. When the percentage requirement is selected optimally, the equilibrium price of a TGC will be such that the socially optimal green/black output combination on E is achieved as the Cournot equilibrium.
In practice, the regulator will possess limited information about production costs and consumer demand. Thus, it remains a significant challenge to devise a technique for determining the socially optimal percentage requirement under limited information. In the example provided, the equilibrium locus E is the outer boundary of a convex set, but in general this set need not be convex. The problem shares many features of standard non-convex economic planning problems and an adaptation of one of the well-known planning procedures (see for example, Heal [8], Weitzman [9] and Cremer [10]) suggest itself. In addition, electricity markets are currently fairly concentrated and full competition remains an ideal. While this paper has modeled a simple Cournot duopoly, the “equilibrium locus” approach suggests that the issue of the optimal percentage requirement could be similarly addressed with varying degrees of competition by assuming 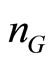 (identical) green firms and
(identical) green firms and 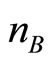 (identical) black firms and letting
(identical) black firms and letting  and/or
and/or 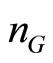 get large. In addition, an investigation into the sensitivity of the “threshold” value of the damage parameter (Proposition 2) to the underlying market structure would be useful. Moreover, the model could be generalized to accommodate strategic (price setting) behavior and/or price caps in the TGC market. A cap on the TGC price for example would restrict the regulator’s choice of the percentage requirement, thereby eliminating a subset of E as potential equilibria. Similarly, the use of “overlapping regulation” such as an overall emissions cap in conjunction with the TGC market (Bohringer, Koschel and Moslener [11]) could render subsets of E unattainable. Finally, this paper’s approach could be applied to a model which embodies banking of TGCs and/or an international market for TGCs (Amundsen, Baldursson and Mortensen [12], Neilsen and Jeppesen [13]). In such cases, the location and structure of the equilibrium locus may be investigated and its proximity to the unconstrained social optimum may be studied as competitive conditions and/or trade restrictions change. These and other related questions we hope to address in future research.
get large. In addition, an investigation into the sensitivity of the “threshold” value of the damage parameter (Proposition 2) to the underlying market structure would be useful. Moreover, the model could be generalized to accommodate strategic (price setting) behavior and/or price caps in the TGC market. A cap on the TGC price for example would restrict the regulator’s choice of the percentage requirement, thereby eliminating a subset of E as potential equilibria. Similarly, the use of “overlapping regulation” such as an overall emissions cap in conjunction with the TGC market (Bohringer, Koschel and Moslener [11]) could render subsets of E unattainable. Finally, this paper’s approach could be applied to a model which embodies banking of TGCs and/or an international market for TGCs (Amundsen, Baldursson and Mortensen [12], Neilsen and Jeppesen [13]). In such cases, the location and structure of the equilibrium locus may be investigated and its proximity to the unconstrained social optimum may be studied as competitive conditions and/or trade restrictions change. These and other related questions we hope to address in future research.
6. Acknowledgements
We wish to thank an anonymous referee for his/her comments and suggestions.
REFERENCES
- E. S. Amundsen and J. B. Mortensen, “The Danish Green Certificate System: Some Simple Analytical Results,” Energy Economics, Vol. 23, No. 5, 2001, pp. 489-509. doi:10.1016/S0140-9883(01)00079-2
- E. S. Amundsen and G. Nese, “Integration of Tradable Green Certificate Markets. What Can Be Expected?” Journal of Policy Modeling, Vol. 31, No. 6, 2009, pp. 903-922. doi:10.1016/j.jpolmod.2009.09.002
- A. Ford, K. Vogstad and H. Flynn, “Simulating Price Patterns for Tradable Green Certificates to Promote Electricity Generation from Wind,” Energy Policy, Vol. 35, 2007, pp. 91-111. doi:10.1016/j.enpol.2005.10.014
- C. Bohringer and K. E. Rosendahl, “Green Promotes the Dirtiest: On the Interaction between Black and Green Quotas in Energy Markets,” Journal of Regulatory Economics, Vol. 37, No. 3, 2010, pp. 316-325. doi:10.1007/s11149-010-9116-1
- V. Dinica and M. J. Arentsen, “Green Certificate Trading in the Netherlands in the Prospect of the European Electricity Market,” Energy Policy, Vol. 31, No. 7, 2003, pp. 609-620. doi:10.1016/S0301-4215(02)00146-5
- M. M. Tamas, S. O. B. Shrestha and H. Zhou, “Feed in Tarriff and Tradable Green Certificates in Oligopoly,” Energy Policy, Vol. 38, 2010, pp. 4040-4047. doi:10.1016/j.enpol.2010.03.028
- A. Bergek and S. Jacobsson, “Are Tradable Green Certificates a Cost—Efficient Policy Driving Technical Change or a Rent—Generating Machine? Lessons from Sweden 2003-2008,” Energy Policy, Vol. 38, No. 3, 2010, pp.1255-1271. doi:10.1016/j.enpol.2009.11.001
- G. Heal, “Planning, Prices and Increasing Returns,” Review of Economic Studies, Vol. 38, 1971, pp. 281-294. doi:10.2307/2296382
- M. Weitzman, “Iterative Multilevel Planning with Production Targets,” Econometrica, Vol. 38, No. 1, 1970, pp. 50-65. doi:10.2307/1909240
- J. Cremer, “A Quantity—Quantity Algorithm for Planning under Increasing Returns,” Econometrica, Vol. 45, No. 6, 1977, pp. 1339-1348. doi:10.2307/1912303
- C. Bohringer, H. Koschel and U. Moslener, “Efficiency Losses from Overlapping Regulation of EC Carbon Emissions,” Journal of Regulatory Economics, Vol. 33, No. 3, 2008, pp. 299-317. doi:10.1007/s11149-007-9054-8
- E. S. Amundsen, F. M. Baldursson and J. B. Mortensen, “Price Volatility and Banking in Green Certificate Markets,” Environmental and Resource Economics, Vol. 35, No. 4, 2006, pp. 259-287. doi:10.1007/s10640-006-9015-1
- L. Neilsen and T. Jeppesen, “Tradable Green Certificates in Selected European Countries—Overview and Assessment,” Energy Policy, Vol. 31, No. 1, 2003, pp. 3-14.

