Open Journal of Statistics, 2012, 2, 198-203
http://dx.doi.org/10.4236/ojs.2012.22023 Published Online April 2012 (http://www.SciRP.org/journal/ojs)
Asymmetry Index on Marginal Homogeneity for Square
Contingency Tables with Ordered Categories
Kouji Tahata, Kanau Kawasaki, Sadao Tomizawa
Department of Information Sciences, Faculty of Science and Technology, Tokyo University of Science,
Chiba, Japan
Received December 27, 2011; revised January 25, 2012; accepted February 10, 2012
ABSTRACT
For square contingency tables with ordered categories, the present paper considers two kinds of weak marginal homo-
geneity and gives measures to represent the degree of departure from weak marginal homogeneity. The proposed meas-
ures lie between –1 to 1. When the marginal cumulative logistic model or the extended marginal homogeneity model
holds, the proposed measures represent the degree of departure from marginal homogeneity. Using these measures,
three kinds of unaided distance vision data are analyzed.
Keywords: Marginal Homogeneity; Marginal Cumulative Logistic Model; Measure; Square Contingency Table
1. Introduction
Consider an square contingency table with or-
dered categories. Let ij denote the probability that an
observation will fall in the ith row and jth column of the
table (;). Also let
RRp
1, ,iR1, ,jR
X
and
denote the row and column variables, respectively. The
marginal homogeneity (MH) model ([1]) is defined by
Y
XY
ii
F
F1, ,1 for iR


1
ik
k
where
i
X
F
p
1
i
Y
ik
k
,
F
p


1
kkt
t
1
R
ksk
s
pp



1
1
1
RXY
ii
i
with
R
pp, .
When the MH model does not hold, we are interested
in applying the model that has weaker restriction than the
MH model. As such a model, for example, there are the
marginal cumulative logistic (ML) model ([2]) and the
extended marginal homogeneity (EMH) model ([3-5]).
We are also interested in considering the other structure
of weak MH. The measures to represent the degree of
departure from MH are given by, for example, [6,7].
When the structure of weak MH does not hold, we are
interested in measuring what degree the departure from
weak MH is.
The present paper considers two kinds of structures of
weak MH and proposes the measures to represent the
degree of departure from weak MH.
2. Weak Marginal Homogeneity I and
Measure
2.1. Submeasure I
Let
F
F


 


,
and
*
1
1
X
i
i
F
F

,

*
2
1
Y
i
i
F
F, for .

1, ,1iR
 


1**
12
11
R
ii
iFF


Note that


. Assuming that


0
XY
ii
FF , consider the submeasure defined by


 


11
**
112
1
4π
π4
R
i
ii
i
FF 



 





,
where
11
22
sin
Y
i
iXY
ii
F
FF









.
Noting that 1 0π2   11
11
i, we see that 1) 1
 ,
2)

 0
Y
i
F0
X
F
1, ,1R
if and only if and i
(i11), and 3) 0
X
F if and only if i



and (i
0
Y
i
F1,,1R


1
). When the MH model
holds,

equals zero.
C
opyright © 2012 SciRes. OJS

K. TAHATA ET AL. 199
2.2. Submeasure II
Let
1
ii
SF
XX1 YY
SF 1, ,1
XY
SS1, , 1
, for iR.
ii
The MH model may be expressed as
ii
for iR



1
1
RXY
ii
i
SS





.
Let
2

1, ,1iR 
,
and for ,

21
sin
i


22
X
i
XY
ii
S
SS






,

*
1
2
i
i
S
X
S

, *
2
2
Y
i
i
S
S
 

1**
12
1
R
ii
SS

2
.
Note that . Assuming that
1i


0
XY
ii
SS
, we shall define the submeasure

as
follows;
 


12
4π
4
R
i ii






**
212
1
πi
SS

 
.
Noting that 2
0π2
i
 
21 0
X
S
, we see that 1)
2; 2) if and only if i
11

and
(); and 3) if and only if
and (i). When the MH
model holds, equals zero.
0
Y
i
S1,i
0
Y
i
Si S

, 1R1
X1, 

0
XY
FF 0
XY
ii
SS
2

, 1R
0
2
2.3. Complete Measure
Assume that ii and

. Con-
sider a measure defined by

12
2
11 1
X
FX S0
Y
F1
Y
S
1


.
We see that 1) , 2) if and only if
i (then ) and (then i
10
i i

) for
all , and 3) if and only if 1, ,1iR1 0
X
i
F

(then ) and (then ) for all
. Thus, indicates that 1R
1
X
i
S
1, , 1iR
1
Y
i
F

0
Y
i
S
11p

and the other cell probabilities are zero (say, upper-right-
marginal inhomogeneity), and indicates that
1R and the other cell probabilities are zero (say,
lower-left-marginal inhomogeneity). When , we
shall refer to this structure as the weak marginal homo-
geneity I (WMH-I). We note that if the MH model holds
then the structure of WMH-I holds, but the converse does
not hold.
1
1 p
0


Therefore, using the measure , we can see whether
the structure of WMH-I departs toward the upper-right-
marginal inhomogeneity or toward the lower-left-margi-
nal inhomogeneity. As the measure approaches –1,
the departure from WMH-I becomes greater toward the
upper-right-marginal inhomogeneity. While as the

approaches 1, it becomes greater toward the lower-left-
marginal inhomogeneity.
3. Weak Marginal Homogeneity II and
Measure
Let

1
Pr
i
Xc
ik
k
TXiXYp



,

1
Pr
i
Yc
ik
k
TYiXYp




1, ,1iR
,
, where for


1
c
kkkk
ppp


,

1
c
kkkk
ppp


,
s
t
st
p 




XY
ii
TT1, ,1iR
1

1
.
The MH model may be expressed by
for .
We shall consider the submeasure which is de-

replaced

X
i
F
and fined by the submeasure


Y
i
F
by


X
i
T and


Y
i
T
1
XX
ii
UT 1
YY
ii
UT 1, ,1iR
XY
ii
UU1, ,1iR
2

2
, respectively.
Let
, for .
The MH model may be expressed by
for .
We shall consider the submeasure which is de-

replaced

and

X
i
S
fined by the submeasure


Y
i
S by


X
i
U and


Y
i
U, respectively.


0
XY
TT
ii


0
XY
ii
UU and Assume that


.
Consider a measure defined by

12
1
2


11
.
We see that

. Let c
pp

ij ij
j (i

). In a
similar way to

, 1 1
c
p
indicates that 1R


and
the other ij are zero (i
c
pj

) (say, conditional upper-
right-marginal inhomogeneity), and indicates that
1 R
1
1
c
p

and the other ij are zero () (say, condi-
tional lower-left-marginal inhomogeneity). When
c
pij
0

,
we shall refer to this structure as the weak marginal ho-
mogeneity II (WMH-II). We note that if the MH model
holds then the structure of WMH-II holds, but the con-
verse does not hold.

K. TAHATA ET AL.
200
 
XY
LL 1, ,1
4. Relationships between Measures and
Models
We shall consider the relationship between the measure
(or ) and the ML model. The ML model is given
by
ii for iR,
where
log 1
X
iX
i
F
F




X
i
L, log 1
Y
Yi
iY
i
F
LF




0

.
A special case of this model obtained by putting
is the MH model. The ML model may also be
expressed as

exp
1exp
i
X
i
F
i





, exp
1exp
i
Y
ii
F




1R
0

XY
ii
,
for . Therefore, when the ML model holds, 1, ,i
1) if and only if
F
F0
, 2) if and
only if

XY
ii
F
F

Y
i
, and 3) if and only if 0

X
i
F
F
0 0 0
0 0 0
0
0 0
 
 
12ii
GG
. We obtain the following theorem.
Theorem 1. When the ML model holds,
1) if and only if (),
2) if and only if (),
3) (i.e., the MH model holds) if and only if
().
Next, we shall consider the relationship between the
measure (or ) and the EMH model, defined by

1, ,1iR

1
11
iR
for ,
where
s
t isti
Gp



2
11
Ri
,

s
t isi t
Gp
 

1
.

A special case of this model obtained by putting

is the MH model. Noting that
 
12
XY
ii
ii
GG FF
1, ,1R (i
1
), we obtain the following theorem.

Theorem 2. When the EMH model holds,
0 if and only if 1)


0
1
(),

if and only if 2) 0


0
1
(),

(i.e., the MH model holds) if and only if 3)

00 (

).

Thus, when the ML (EMH) model holds, the measures

and

are adequate to represent the degree of
departure from MH.
5. Approximate Confidence Interval for
Measures
Let ij denote the observed frequency in the ith row and
jth column of the table (;). As-
suming that a multinomial distribution applies to the
n
1, ,iR1, ,jR
RR

table, we shall consider an approximate standard
error and large-sample confidence interval for the meas-
ure

, using the delta method, as described by [8]. The
sample version of

, i.e., , is given by
ˆ


with


ˆij p, where


ij
p replaced by ˆij
ij nn
p
nn
and

ij
. Using the delta method, we obtain the fol-
lowing theorem.

Theorem 3.

ˆ
n


n
2ˆ

has asymptotically (as
) a normal distribution with mean zero and vari-
ance


, where



2
2
11
1
ˆ
4
RR
ij ijij
ij
abp 


 
  ,
with
  


 

  
11
1
22
1
21
4XY
RYX
kk
ijkk k
XY
kk
Rij
FF
aIjkIikF IjkF
FF


 


 





1
1
πk
Iik


,
  




  
12
22
1
2 2
21
4
π
XY
RYX
kk
ijkk k
XY
kkk
ij
SS
bIik IjkIikSIjkS
SS



 


 

 





2
  ,
and
I


1I
ˆ 


p
is the indicator function, if true, 0 if
not.
Also, the sample version of , i.e., , is given by
with

ij replaced by


ˆij
p. We obtain the fol-
lowing theorem.
Theorem 4.

ˆ
n
n
2ˆ

has asymptotically (as
) a normal distribution with mean zero and vari-


, where ance



2
2
11
1
ˆ
4
RR
ij ijij
ij
ji
cd p 




 ,
with


















13
22
1
3
1
1
3
4π
π4
1
,
XY
RXY XYYX
kk
ijkkkkkk k
XY
kkk
RXY
kk
k
TT
cIikTIjkT IikTTIjkTT
TT
IikTI jkT







 


 


 
 
 
 






1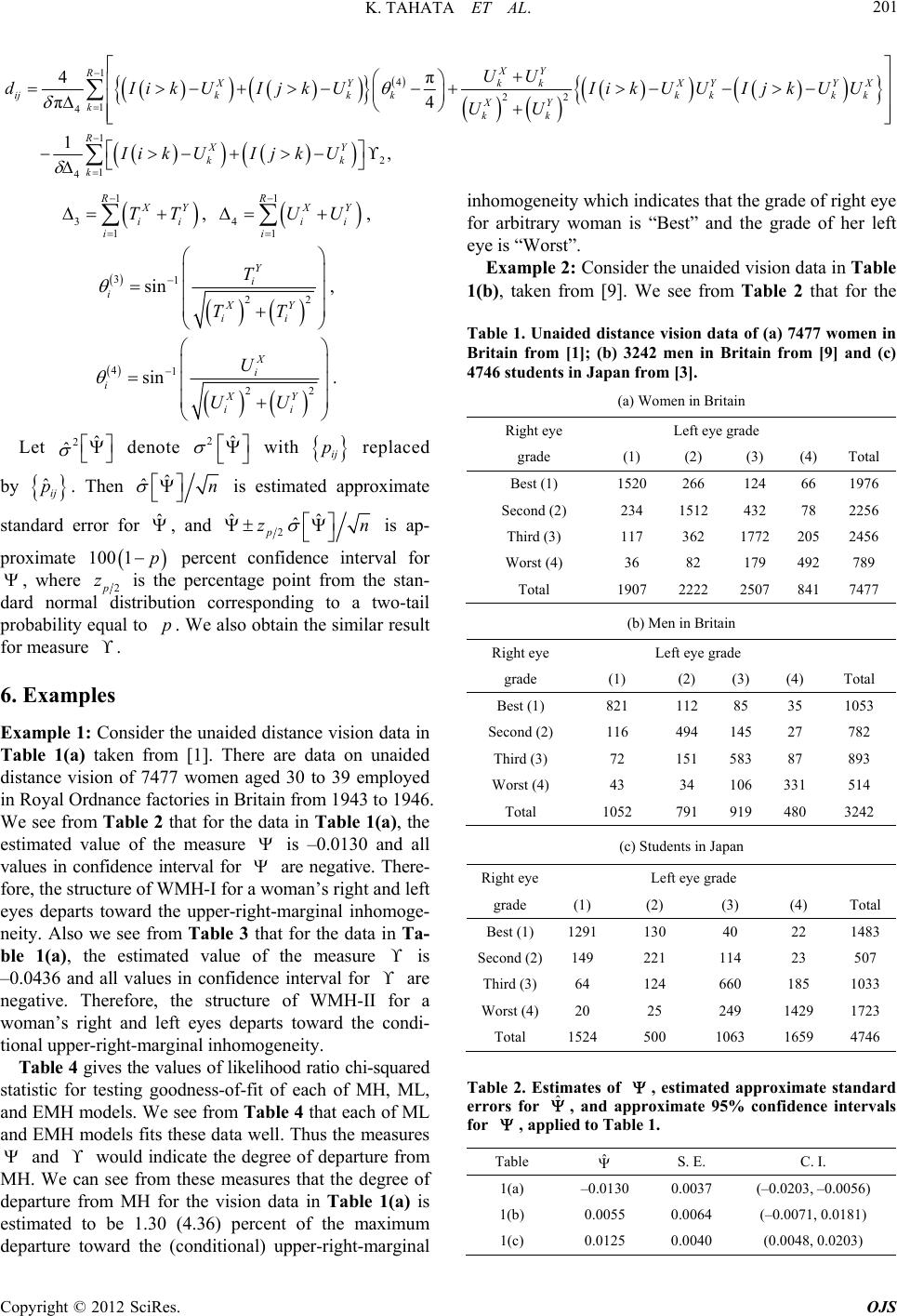

K. TAHATA ET AL. 201

 

 



 

 




14
22
1
4
1
2
1
4
4π
π4
1
,
XY
RXY XY
kk
ijkkkk k
XY
kkk
RXY
kk
k
UU
dIik UIjk UIik UUIj
UU
IikUI jkU










 


 








YX
k k
k UU





i

1
1
XY
ii
UU



,


1
1
RXY
ii
TT



, 4
R
i



3

31
sin
Y
i
i
T
22
XY
ii
TT






,





41
sin
i22
X
i
XY
ii
U
UU






.
Let 2
ˆ

denote



ˆ


 2ˆ




with

ij
p replaced
by

ˆij
p. Then ˆn


 is estimated approximate
ˆ
, and
ˆ

ror for standard er2
ˆˆ
ˆ
p
zn 

 
 is ap-
e

100 1p percent confidence interval for proximat
ere, wh2
p
zfrom
ibution co
o p. We a
les
m
7477 women aged 30 to 39 employed
in Royal Ordnance factories in Britain from 1943 to 1946.
ble 2 that for the data in Table 1(a), the
e measure  is –0.0130 and all
is the percentage point the stan-
dardmal distrrresponding to a two-tail
proby equal tlso obtain the similar result
for measure .
nor
abilit
6. Examp
Example 1: Consider the unaided distance vision data in
Table 1(a) taken fro [1]. There are data on unaided
distance vision of
We see from Ta
estimated value of th
values in confidence interval for  are negative. There-
fore, the structure of WMH-I for a woman’s right and left
eyes departs toward the upper-right-marginal inhomoge-
neity. Also we see from Table 3 that for the data in Ta-
ble 1(a), the estimated value of the measure

is
–0.0436 and all values in confidene interval for c

are
negative. Therefore, the structure of WMH-II for a
woman’s right and left eyes departs toward the condi-
tional upper-right-marginal inhomogeneity.
Table 4 gives the values of likelihood ratio chi-squared
statistic for testing goodness-of-fit of each of MH,L,
and EMH models. We see from Table 4 that each of ML
and EMH models fits these data well. Thus the measures
 and  would indicate the degree of departure from
MH. We can see from these measures that the de
M
gree of
de
inhomogeneity which indicates that the grade of right eye
for arbitrary woman is “Best” and the grade of her left
eye is “Worst”.
Example 2: Consider the unaided vision data in Table
1(b), taken from [9]. We see from Table 2 that for the
Br m
parture from MH for the vision data in Table 1(a) is
estimated to be 1.30 (4.36) percent of the maximum
departure toward the (conditional) upper-right-marginal
Table 1. Unaided distance vision data of (a) 7477 women in
itain fro [1]; (b) 3242 men in Britain from [9] and (c)
4746 students in Japan from [3].
(a) Women in Britain
Right eye Left eye grade
grade (1) (2) (3) (4)Total
Best (1) 1520 266 124 66 1976
Second (2) 234 1512 432 78 2256
Third (3) 117 362 1772 2052456
Worst (4) 36 82 179 492789
Total 1907 2222 2507 8417477
(b) Men in Britain
Right eye Left eye grade
grade (1
1)
) (4) Total
Best (821 35 1053
(2) (3)
112 85
Second (116 494 145 27
T72 151 583 87
W43 106 331
791 919 480 3242
2) 782
hird (3) 893
orst (4)
Total 1052
34 514
(c) Studeapa
Right eye
nts in Jn
Left eye grade
grade (1) (2(4) Total
Be 1291130 4
) (3)
st (1) 0 22 1483
Second (149 221 114
T64 124 660
W20 25 249 1429
1524500 1063
2)23 507
hird (3) 185 1033
orst (4)1723
Total 16594746
Table 2. Estimates of

, estimated approximate standard
errors for ˆ

, and
for approximate 95% confidence intervals , applied to Table
ˆ
1.

Table

S. E. I. C.
1(a) –0.0130 0037 (–0.0 –0.00.203,056)
1(b) 0.0055 0.0064 (–0.0071, 0.01
0040 (0.00.020
81)
1(c) 0.0125 0.048, 3)

K. TAHATA ET AL.
202
Table 3. Estim
p
ates of timateprox standard
erro ˆ 
for lie
, esd apimate
rs fo
, ap
r , and approximate 95%
d to Table confidence intervals 1.
Table ˆ
 S. E. C. I.
1(a) –0.0436 0.0126 (–0.0683, –0.0190)
1(0.0201 (–0.0222, 0.0566)
0.07 3 (0.0198, .0836)
b) 0.0172
1(c) 510.0160
Table 4. Values of likelihood i-sq
the ML, an modlied t
ratio ch
els appuared statistic for o Table 1. H, Md EMH
Applied Degrees of Table
models freedom 1(a) 1(b) 1(c)
H 3 M11.99* 3.68 11.18*
ML 2 0.39 3.16 .41
E0 2
1
MH 2 .005 .94 0.56
*Meanant at tvel.
data in Table 1(b) the estimated value of measure
s significhe 0.05 le

is
H-I in
the data in Table 1(b)se Table 3 that for
th Table 1(b), estima of measure
72 aor  includes
zero. So this mindicatthere structure of
WMH-II in the data in Tabl ).
Ee 3: C nsider tta inle 1(en
om [3,10]. We see from that for the data in
value of measure
0.0055 and the confidence interval for  includes zero.
So this may indicate that there is a structure of WM
. Also we
the
nfide
e from
ted value
terval fo
e data in
is 0.01nd the cnce in
ay e that is a
e 1(b
xampl ohe da
Table 2 Tab c) tak fr
Table 1(c), the estimated the

is
0.0125 and all values in confidence interval for

f
are
positive. Therefore, the structure of WMH-I for a stu-
dent’s right and left eyes departs toward the lower-left-
marginal inhomogeneity. Also we see from Table 3 that
for the data in Table 1(c), the estimated value of the
measure  is 0.0517 and all values in conidence in-
terval for  are positive. Therefore, the structure of
WMH-II for a student’s right and left eyes departs to-
ward the conditional lower-left-marginal inhomogeneity.
We see from Table 4 that each of ML and EMH mod-
els fits these data well. Thus the measures  and

would indicate the degree of departure from MH. We can
see from these measures that the degree of departure
from MH for the vision data in Table 1 (c) is estimated to
be 1.25 (5.17) percent of the maximum departure toward
the (conditional) lower-left-marginal inhomogeneity which
indicates tat the grade of right eye for arbitrary student
is “Worst” ad the grade of his/her left eye is “Best”.
7. Concluding Remarks
h
n
Fo
t H
r the analysis of square contingency tables with or-
dered categories, when the ML model, or he EM
model, or other asymmetry models, for example, [11]’s
conditional symmetry model (defined by ijji pp


for ij

) holds, the proposed measures  and

are
adequate to represent the degree of departure from the
MH model toward two maximum departures, i.e., toward
the (conditional) lower-left-marginal inhomogeneity or
toward the (conditional) upper-right-marginal inhomoge-
neity.
ity (i.e., the
r-lefhe-r
8. Discussion
[6,7] considered the measures to represent the degree of
departure from MH. The present paper has considered
two types of maximum marginal inhomogene
lowet-marginal inhomogeneity and t upperight-
marginal inhomogeneity). The measures in [6,7] take the
value 1 in two types of maximum marginal inhomoge-
neity. The measures

and  in the present paper
can distinguish these two kinds of maximum marginal
inhomogeneity by the values –1 or 1 although the meas-
ures in [6,7] cannot distinguish them. Also the proposed
esent the degree of departure from MH
toss
measures can repr
when the ML or the EMH models, or the other asym-
metry models hold. Therefore for the ordinal data, the
proposed measures rather than those in [6,7] may be
useful to represent the degree of departure from MH.
9. Acknowledgements
The authors would like expre their sincere thanks to
the editor and a referee for their helpful comments.
REFERENCES
[1] A. Stuart, “A Test for Homogeneity of the Marginal Dis-
tributions in a Two-Way Classification,” Biometrika, Vol.
42, No. 3-4, 1955, pp. 412-416.
doi:10.1093/biomet/42.3-4.412
[2] A. Agresti, “Analysis of Ordinal Categorical Data,” John
ds of Decompositions for the
[4] S. Tomizawa,e Marginal Homo-
geneity Modey Tables with Or-
tion to Marginal Equi-
pp. 295-311.
Wiley, New York, 1984.
[3] S. Tomizawa, “Three Kin
Conditional Symmetry Model in a Square Contingency
Table,” Journal of the Japan Statistical Society, Vol. 14,
No. 1, 1984, pp. 35-42.
“A Generalization of th
l for Square Contingenc
dered Categories,” Journal of Educational and Behav-
ioral Statistics, Vol. 20, 1995, pp. 349-360.
[5] K. Tahata and S. Tomizawa, “Generalized Marginal Ho-
mogeneity Model and Its Rela
moments for Square Contingency Tables with Ordered
Categories,” Advances in Data Analysis and Classifica-
tion, Vol. 2, No. 3, 2008,
doi:10.1007/s11634-008-0028-1
[6] K. Tahata, T. Iwashita and S. Tomizawa, “Measure of
Departure from Symmetry of Cumulative Marginal Pro-
babilities for Square Contingency Tables with Ordered
Categories,” SUT Journal of Mathematics, Vol. 42, 2006,

K. TAHATA ET AL.
203
y for
pp. 7-29.
[7] K. Tahata, T. Iwashita and S. Tomizawa, “Measure of
Departure from Conditional Marginal Homogeneit
Square Contingency Tables with Ordered Categories,”
Statistics, Vol. 42, No. 5, 2008, pp. 453-466.
doi:10.1080/02331880802190521
[8] Y. M. M. Bishop, S. E. Fienberg and P. W. Holland,
“Discrete Multivariate Analysis: Theor
The MIT Press, Cambridge, 1975
y and Pract
.
/2333101
ice,”
[9] A. Stuart, “The Estimation and Comparison of Strengths
of Association in Contingency Tables,” Biometrika, Vol.
40, 1953, pp. 105-110. doi:10.2307
etry,” Quantum Prob-
els for the
[10] K. Yamamoto, K. Tahata, N. Miyamoto and S. Tomizawa,
“Comparison between Several Square Tables Data Using
Models of Symmetry and Asymm
ability and White Noise Analysis: Quantum Bio-Infor-
matics, Vol. 21, 2007, pp. 337-349.
[11] P. McCullagh, “A Class of Parametric Mod
Analysis of Square Contingency Tables with Ordered
Categories,” Biometrika, Vol. 65, No. 2, 1978, pp. 413-
418. doi:10.1093/biomet/65.2.413