Int. J. Communications, Network and System Sciences, 2010, 3, 466-471
doi:10.4236/ijcns.2010.35062 Published Online May 2010 (http://www.SciRP.org/journal/ijcns/)
Particle Swarm Optimization Based Approach for
Resource Allocation and Scheduling in OFDMA Systems
Chilukuri Kalyana Chakravarthy1, Prasad Reddy2
1Department of Computer Science and Engineering, Maharaj Vijayaram Gajapathi Raj College of Engineering,
Vizianagaram, India
2Department of CS&SE, Andhra University, College of Engineering, Visakhapatnam, India
Received March 9, 2010; revised April 10, 2010; accepted May 11, 2010
Abstract
Orthogonal Frequency-Division Multiple Access (OFDMA) systems have attracted considerable attention
through technologies such as 3GPP Long Term Evolution (LTE) and Worldwide Interoperability for Micro-
wave Access (WiMAX). OFDMA is a flexible multiple-access technique that can accommodate many users
with widely varying applications, data rates, and Quality of Service (QoS) requirements. OFDMA has the
advantages of handling lower data rates and bursty traffic at a reduced power compared to single-user
OFDM or its Time Division Multiple Access (TDMA) or Carrier Sense Multiple Access (CSMA) counter-
parts. In our work, we propose a Particle Swarm Optimization based resource allocation and scheduling
scheme (PSORAS) with improved quality of service for OFDMA Systems. Simulation results indicate a
clear reduction in delay compared to the Frequency Division Multiple Access (FDMA) scheme for resource
allocation, at almost the same throughput and fairness. This makes our scheme absolutely suitable for han-
dling real time traffic such real time video-on demand.
Keywords: OFDMA, Resource Allocation, Scheduling, Quality of Service, Delay
1. Introduction
TDMA and FDMA used for distributing subcarriers in
OFDM systems form static subcarrier management sche-
mes. While in OFDM-TDMA, one of the users is as-
signed all the subcarriers for the entire scheduling inter-
val, in the OFDM-FDMA, each user is assigned prede-
termined number of subcarriers. However, neither of
these techniques is time or frequency efficient: TDMA is
a time hog and FDMA is a bandwidth hog. OFDMA is a
multi-user OFDM that allows multiple access on the
same channel (a channel being a group of evenly spaced
subcarriers, as discussed above). WiMAX uses OFDMA,
extended OFDM, to accommodate many users in the
same channel at the same time. In OFDMA, the OFDMA
subcarriers are divided into subsets of subcarriers, each
subset representing a subchannel (see Figure 1). Dy-
namic subcarrier allocation schemes which consider the
instantaneous channel conditions have been the main
area of research interest recently. The resource allocation
is usually formulated as a constrained optimization pro-
blem, to either 1) minimize the total transmit power with
a constraint on the user data rate [1,2] or 2) maximize the
total data rate with a constraint on total transmit power
[3-5]. The first objective is appropriate for fixed-rate
applications, such as voice, whereas the second is more
appropriate for bursty applications, such as data and
other IP applications.
In the downlink, a subchannel may be intended for
different receivers or groups of receivers; in the uplink, a
transmitter may be assigned one or more subchannels.
The subcarriers forming one subchannel may be adjacent
or not. The standard indicates that the OFDM symbol is
divided into logical subchannels to support scalability,
Figure 1. OFDMA frame structure.

C. K. CHAKRAVARTHY ET AL. 467
multiple access and advanced antenna array processing
capabilities. The multiple access has a new dimension
with OFDMA where in a downlink or an uplink user will
have a time and a subchannel allocation for each of its
communications.
The main motivation for adaptive subcarrier allocation
in OFDMA systems is to exploit multiuser Diversity. In
a K-user system in which the subcarrier of interest ex-
periences i.i.d. Rayleigh fading—that is, each user’s
channel gain is independent of the others, as the number
of users’ increases, the probability of getting a large
channel gain increases. Further, it was observed that ma-
jority of the gain is achieved from only the first few users.
Adaptive modulation is the means by which good chan-
nels can be exploited to achieve higher data rates.
WiMAX systems use adaptive modulation and coding
in order to take advantage of fluctuations in the channel.
The basic idea is quite simple: Transmit as high a data
rate as possible when the channel is good, and transmit at
a lower rate when the channel is poor, in order to avoid
excessive dropped packets. While Lower data rates are
achieved by using a small constellation, such as QPSK,
and low-rate error-correcting codes, such as rate convo-
lutional or turbo codes, the higher data rates are achieved
with large constellations, such as 64 QAM, and less ro-
bust error correcting codes; for example, rate convolu-
tional, turbo, or LDPC codes. However, a key challenge
in AMC is to efficiently control three quantities at once:
transmit power, transmit rate (constellation), and the
coding rate.
In theory, the best power-control policy from a capac-
ity standpoint is the so-called waterfilling strategy, in
which more power is allocated to strong channels and
less power allocated to weak channels [6]. In practice,
the opposite may be true in some cases. For example, in
regions of low gain, the transmitter would be well ad-
vised to lower the transmit power, in order to save power
and generate less interference to neighboring cells [7].
As mentioned earlier, OFDMA thus facilitates the ex-
ploitation of frequency diversity and multiuser diversity
to significantly improve the system capacity. In a multi-
user System, the optimal solution is not necessarily to
assign the best subcarriers seen by a single chosen user
since the best subcarrier of one user is also the best sub-
carrier for another user who has no other good subcarri-
ers. Hence, a different approach should be considered for
scheduling the best user. We consider the problem where
K users are involved in the OFDMA system to share N
subcarriers. Each user allocates non overlapping set of
subcarriers Sk where the number of subcarriers per user
is J(k). The allocation module of the transmitter assigns
subcarriers to each user according to some QoS criteria.
QoS metrics in the system are rate and BER. Each user’s
bit stream is transmitted using the assigned subcarriers
and adaptively modulated for the number of bits assigned
to the subcarrier. The power level of the modulation is
adjusted to meet QoS for given fading of the channel
(see Figure 2).
User 1
User 2
User 3
User N
OFDMA
TRANSCEIVER
SUB CARRIER
ALLOCATION
SUB Carrier
Information
DAT
A
OFDMA
TRANSCEIVER
SUBCARRIER
SELECTOR
SUBCARRIER
ALLOCATION
ALGORITHM
CHANNEL
ESTIMATOR
Channel
Stae
Channel State
Information
Subcarrier
Information
for User N
Figure 2. Downlink OFDMA System architecture.

C. K. CHAKRAVARTHY ET AL. 468
If k,n

is the indicator of allocating the nth subcarrier
to the kth user, the transmission power allocated to the
nth subcarrier of kth user can be expressed as
2
,, ,
= (, )/
knk knkkn
PfCBER  where

kk,n
fC is the re-
quired received power with unity channel gain for reli-
able reception of c bits per symbol. Therefore, the re-
source allocation problem with an imposed power con-
straint can be formulated as
,
N
,,,
n1
max, kn
knkkn kn
CγRCγ

 for all k
subject to KN ,
,max
2 k1 n1
(, )
α
kkn k
rkn
k,n
f CBER
PγP



The limit on the total transmission power is expressed
as max P for all {1, . . . ,}nN, {1, . . . ,}kK
and , {1, . . . ,}
kn
CM. The proposed method uses the
Particle Swarm Optimization for resource allocation and
scheduling in a multiuser scenario, considering the rate,
power and the subcarrier allocation constraints.
2. Particle Swarm Optimization
Particle Swarm Optimization (PSO) is motivated from the
simulation of social behavior of animals’. It was intro-
duced by Eberhart & Kennedy in 1995. In PSO, potential
solutions (particles) move dynamically in space. PSO is
similar to the other evolutionary algorithms in which the
system is initialized with a population of random solutions.
A list of Genetic algorithms is given in [8-12]. Each po-
tential solution, call particles, flies in the D-dimensional
problem space with a velocity which is dynamically ad-
justed according to the flying experiences of its own and
its colleagues. The location of the ith particle is repre-
sented as 1 (,,,,)
i iid iD
X
xx x. The best previous
position (which giving the best fitness value) of the ith
particle is recorded and represented asi P

1
(,, ,,)
iidiD
pp p , which is also called pbest. The in-
dex of the best pbest among all the particles is represented
by the symbol g. The location Pg is also called gbest. The
velocity for the ith particle is represented as
1
(,,,,)
i iid iD
Vv vv. The particle swarm optimization
concept consists of, at each time step, changing the veloc-
ity and location of each particle toward its pbest and gbest
locations. The particle swarm optimization concept con-
sists of, at each time step, changing the velocity and loca-
tion of each particle toward its pbest and gbest locations
according to the equations= wc1rand()
id id
vv 
 
c2 rand()
id idgd id
pxp x and xid +
id id
x
v re-
spectively.where w is inertia weight, c1 and c2 are ac-
celeration constants [13] which is responsible for keep-
ing the particle moving in the same direction, and rand()
is a random function in the range [0, 1]. For the first
equation, the first part represents the inertia of pervious
velocity; the second part is the “cognition” part, which
represents the private thinking by itself which causes the
particle to move to regions of higher fitness; the third
part is the “social” part, which represents the cooperation
among the particles [14]. Thus the social component
causes the particle to move to the best region the swarm
has found so far.
The PSO algorithm consists of just three steps, which
are repeated until some stopping condition is met [15]:
1) Evaluate the fitness of each particle
2) Update individual and global best fitnesses and po-
sitions
3) Update velocity and position of each particle
Further, velocity clamping is used to prevent the parti-
cle to move too much away from the search space, the
limits being confined to [–Vmax, Vmax ] if the search space
spans from [–Pmax, Pmax][16].
3. The Proposed System
In this work, we propose a Particle Swarm Optimization
(PSO) Approach combined with Credit based scheduling
to guarantee QOS in WiMAX.
Formal definition of our scheduling model:
1
i1
1
Minimize =
P
p
N
iik
kkK
ik
rx
ZD
x










Subject to 1,1
N
iik
itxuk K



 (1)
and
1,1,1 ;
N
ij ikj
ipxmj Mk K 
 (2)
where terms 1 and 2 refer to the time and power con-
straints during scheduling respectively.
xik are decision variables, where 1 ≤ i ≤ N and 1 ≤ k ≤
K, xik is 1 if a subcarrier has been allocated, 0 otherwise.
The decision of whether to grant the subchannel to the
subcarrier is based on whether the subcarrier lies within
the range of existing subcarriers for a subchannel. A cri-
teria such as rejection of the subcarrier if it is directly
adjacent to a previously allocated subcarrier within the
same subchannel and acceptance if not so is used. This
results in an improvement of SINR. N is the total number
of subcarriers per user and K total number of users, ri is
the rate of each allocated subcarrier, D is the target rate
for each user, ti is the allocation time for the subcarrier, u
is the allowable deadline for a user, pi is the power allo-
cation for each subcarrier, m is the maximum power al-
location for user. Ci is the maximum allowable credits for
a user. We define different penalty factors as follows: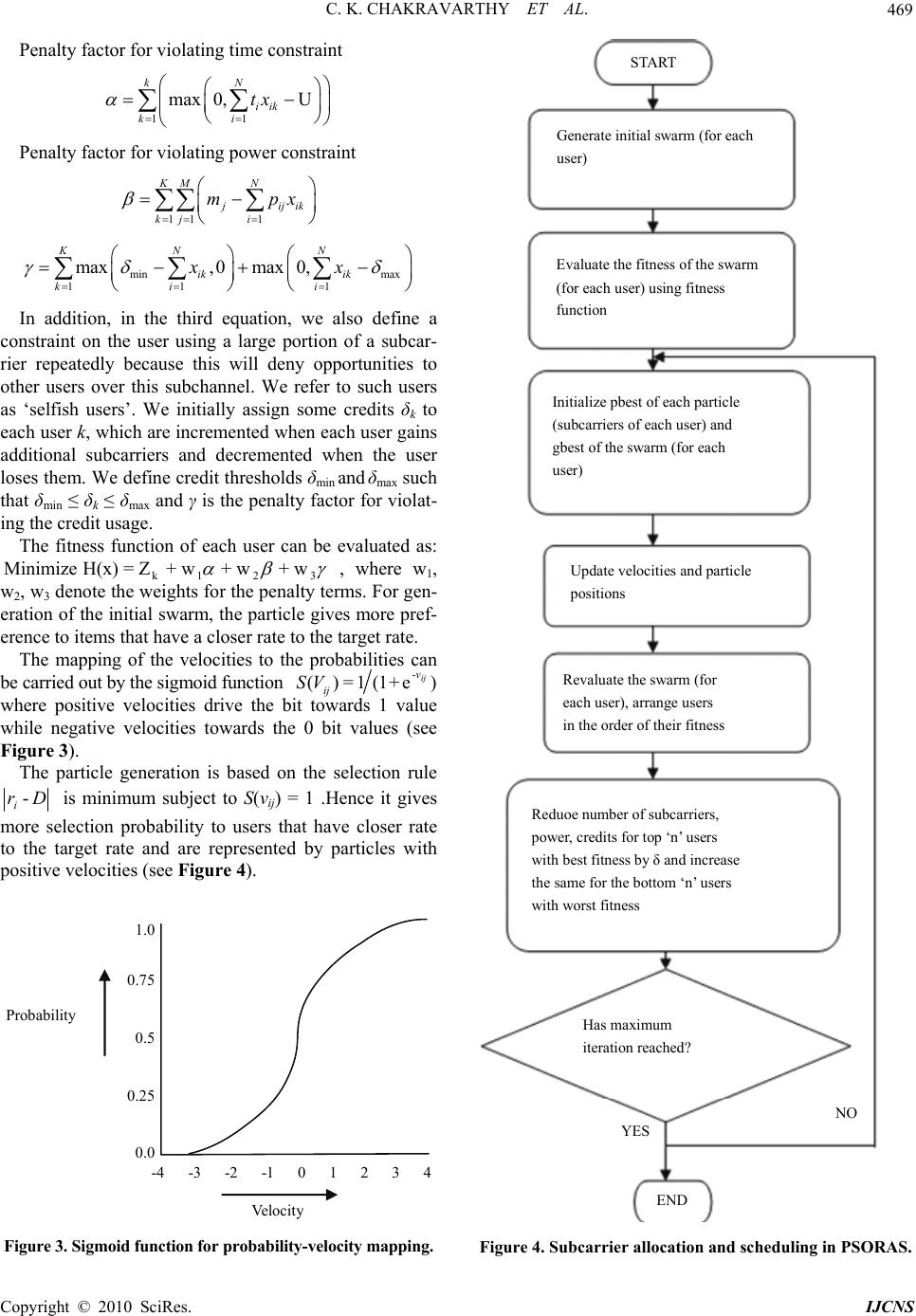

C. K. CHAKRAVARTHY ET AL. 469
Penalty factor for violating time constraint
11
max 0,U
kN
iik
ki
tx 











Penalty factor for violating power constraint
11 1
KM N
j
ij ik
kj i
mpx 





 
min max
11 1
max, 0max0,
KN N
ik ik
ki i
xx  
 

 


 
In addition, in the third equation, we also define a
constraint on the user using a large portion of a subcar-
rier repeatedly because this will deny opportunities to
other users over this subchannel. We refer to such users
as ‘selfish users’. We initially assign some credits δk to
each user k, which are incremented when each user gains
additional subcarriers and decremented when the user
loses them. We define credit thresholds δmin and δmax such
that δmi n ≤ δk ≤ δmax and γ is the penalty factor for violat-
ing the credit usage.
The fitness function of each user can be evaluated as:
k1 23
Minimize H(x) = Z + w + w + w

 , where w1,
w2, w3 denote the weights for the penalty terms. For gen-
eration of the initial swarm, the particle gives more pref-
erence to items that have a closer rate to the target rate.
The mapping of the velocities to the probabilities can
be carried out by the sigmoid function ()=1 (1+e)
ij
-v
ij
SV
where positive velocities drive the bit towards 1 value
while negative velocities towards the 0 bit values (see
Figure 3).
The particle generation is based on the selection rule
-
i
rD is minimum subject to S(vij) = 1 .Hence it gives
more selection probability to users that have closer rate
to the target rate and are represented by particles with
positive velocities (see Figure 4).
Velo cit y
Probabilit
y
1.0
0.75
0.5
0.25
0.0
-4 -3 -2 -1 0 1 2 3 4
Figure 3. Sigmoid function for probability-velocity mapping.
START
Generate initial swarm (for each
user)
Evaluate the fitness of the swarm
(for each user) using fitness
function
Initialize pbest of each particle
(subcarriers of each user) and
gbest of the swarm (for each
user)
Update velocities and particle
positions
Revaluate the swarm (for
each user), arrange users
in the order of their fitness
Reduoe number of subcarriers,
power, credits for top ‘n’ users
with best fitness by δ and increase
the same for the bottom ‘n’ users
with worst fitness
Has maximum
iteration reached?
END
YES
NO
Figure 4. Subcarrier allocation and scheduling in PSORAS.

C. K. CHAKRAVARTHY ET AL. 470
4. The Simulation Model and Results
We consider the downlink of an OFDMA system with N
subchannels and K users. The time axis is divided into
frames. A frame is further divided into S time slots, each
of which may contain one or several OFDM symbols.
The duration of a frame is set to be 5 ms, thus we can
assume that the channel quality remains constant within
a frame, but may vary from frame to frame. In our simu-
lation, there are 1024 subcarriers, 1 to 50 users in the IE-
EE 802.16 OFDMA system. Each user transmits 80 bits in
an OFDMA symbol. The modulation type in the OFDMA
system is confined to QPSK, 16-QAM, 64-QAM. (see
Figures 5-7)
Following are the simulation results for the variation
in average throughput, fairness index and the average
delay with the number of users. The results clearly indi-
cate a reduction in the delay with the proposed swarm
based approach compared to the Naïve allocation of
subcarriers, i.e. allocation on availability basis in FDMA
without considering variation in channel conditions. The
results have been evaluated for different sets of target
rates and target powers for the subcarriers and the priori-
ties of users are varied after every 5 ms based on the
Figure 5. Number of users Vs. Average Throughput.
Figure 6. Number of users Vs. Throughput Fairness Index.
Figure 7. Number of users Vs. Average Delay.
calculated fitness. The throughput fairness index has
been calculated as max minmin
=(- )/
n
τThThTh , where
min
Th and max Th are the minimum and maximum val-
ues of throughput of each user over ‘n’ frames measured
in bits.
5. Conclusions
Swarm optimization is increasingly finding its place in
multiuser downlink MIMO scheduling, smart Antenna
array systems etc. In our work, we have proposed a
PSO-based fair Resource allocation and scheduling algo-
rithm for the IEEE 802.16 System. We have compared
our results with the static FDMA algorithm and have
found it offers better delay characteristics with increasing
number of users while still maintaining the fairness and
throughput utilization. This makes the proposed scheme
absolutely useful for real-time applications.
6. References
[1] D. Kivanc, G. Li and H. Liu, “Computationally Efficient
Bandwidth Allocation and Power Control for OFDMA,”
IEEE Transactions on Wireless Communications, Vol. 2,
No. 6, 2003, pp. 1150-1158.
[2] C. Wong, R. Cheng, K. Letaief and R. Murch, “Multiuser
OFDM with Adaptive Subcarrier, Bit, and Power Alloca-
tion,” IEEE Journal on Selected Areas in Communica-
tions, Vol. 17, No. 10, 1999, pp. 1747-1758.
[3] J. Jang and K. Lee, “Transmit Power Adaptation for Mul-
tiuser OFDM Systems,” IEEE Journal on Selected Areas
in Communications, Vol. 21, No. 2, 2003, pp. 171-178.
[4] G. Li and H. Liu, “On the Optimality of the OFDMA
Network,” IEEE Communications Letters, Vol. 9, No. 5,
2005, pp. 438-440.
[5] C. Mohanram and S. Bhashyam, “A Sub-optimal Joint
Subcarrier and Power Aallocation Algorithm for Multi-
user OFDM,” IEEE Communications Letters, Vol. 9, No.
8, 2005, pp. 685-687.

C. K. CHAKRAVARTHY ET AL. 471
[6] G. Manimaran and C. Siva Ram Murthy, “A
Fault-Tolerant Dynamic Scheduling Algorithm for Mul-
tiprocessor Real-Time Systems and Its Analysis,” IEEE
Transactions on Parallel and Distributed Systems, Vol. 9,
No. 11, 1998, pp. 1137-1152.
[7] R. Chen, J. G. Andrews, R. W. Heath and A. Ghosh,
“Uplink Power Control in Multi-Cell Spatial Multiplex-
ing Wireless Systems,” IEEE Transactions on Wireless
Communications, Vol. 6, No. 7, 2007, pp. 2700-2711.
[8] A. J. Page and T. J. Naughton, “Framework for Task
Scheduling in Heterogeneous Distributed Computing
Using Genetic Algorithms,” 15th Artificial Intelligence
and Cognitive Science Conference, Ireland, 2004, pp.
137-146.
[9] A. J. Page and T. J. Naughton, “Dynamic Task Schedul-
ing Using Genetic Algorithms for Heterogeneous Dis-
tributed Computing,” Proceedings of the 19th IEEE/ACM
International Parallel and Distributed Processing Sym-
posium, Denver, 2005, pp. 1530-2075.
[10] A. S. Wu, H. Yu, S. Jin, K.-C. Lin and G. Schiavone, “An
Incremental Genetic Algorithm Approach to Multiproc-
essor Scheduling,” IEEE Transactions on Parallel and
Distributed Systems, Vol. 15, No. 9, 2004, pp. 824-834.
[11] A. Y. Zomaya and Y.-H. Teh, “Observations on Using
Genetic Algorithms for Dynamic Load-Balancing,” IEEE
Transactions on Parallel and Distributed Systems, Vol.
12, No. 9, 2001, pp. 899-911.
[12] E. S. H. Hou, N. Ansari and H. Ren, “A Genetic Algo-
rithm for Multiprocessor Scheduling,” IEEE Transactions
on Parallel and Distributed Systems, Vol. 5, No. 2, 1994,
pp. 113-120.
[13] R. Eberhart and Y. Shi, “Particle Swarm Optimization:
Developments, Applications and Resources,” IEEE In-
ternational Conference on Evolutionary Computation,
Seoul, 2001, pp. 81-86.
[14] J. Kennedy, “The Particle Swarm: Social Adaptation of
Knowledge,” IEEE International Conference on Evolu-
tionary Computation, Indianapolis, 1997, pp. 303-308.
[15] F. van den Bergh, “An Analysis of Particle Swarm Opti-
mizers,” PhD Thesis, University of Pretoria, 2001.
[16] J. Blondin, “Particle Swarm Optimization: A Tutorial,”
September 2009.