Journal of Modern Physics
Vol.5 No.6(2014), Article ID:45403,6 pages DOI:10.4236/jmp.2014.56058
Mass Creation from Extra Dimensions
Dao Vong Duc1, Nguyen Mong Giao2
1Institute of Physics, Hanoi, Vietnam
2Hung Vuong University, Ho Chi Minh City, Vietnam
Email: nmgiao2011@yahoo.com.vn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 March 2014; revised 29 March 2014; accepted 15 April 2014
ABSTRACT
In this work we consider a mechanism for mass creation based on the periodicity condition dictated from the compactification of extradimensions. It is shown that the existence and the compactification of extradimensions are the origin for creating particle mass in ordinary 4-dimensional space-time. Mass of Higgs particles themselves would be also originated from the geometric topology of extradimensions.
Keywords:Origin of Mass, Mass of Higg Particles, Extra Dimensions

1. Introduction
The existence of space-time extradimensions has been a subject of intensive research study during the last decades [1] -[3] .
The topology of extradimensions, especially their compactification, plays a crucial role in many physical aspects, mostly in the construction of various models of unified theory of interactions, such as superstring theory, extended general relativity, and so on [4] -[7] .
It is worth noting, on the other hand, that it is in such approaches the particle mass always remains a problem of actual characters.
In this work we propose a mechanism for mass creation through the compactification of spacetime extradimensions. The crucial argument is the proposed periodicity condition dictated from the compactification of extra dimensions.
The original field functions depend on all space-time coordinate components including those for extradimensions, the ordinary field functions, ordinary 4-dimensional space-time considered as effective field functions obtained by integration of the original ones over extra space-time.
In Section 2, we present some general principles related to the compactification of extradimensions.
In Section 3, a mechanism for mass creation is treated.
2. Periodicity Compactification Condition
For simplicity let us begin with the case of one extra dimension. Denote the 5-dimensional coordinate vector by xM with M =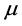 , 5. The Greek indices
, 5. The Greek indices ,
,  ,··· will be used as conventional 4-dimensional Lorentz indices (0, 1, 2, and 3). We do not directly care from the extra dimensions is topologically compactified, but instead a specific periodicity condition is put on the field functions depending on extra dimensions, namely
,··· will be used as conventional 4-dimensional Lorentz indices (0, 1, 2, and 3). We do not directly care from the extra dimensions is topologically compactified, but instead a specific periodicity condition is put on the field functions depending on extra dimensions, namely
 (1)
(1)
where 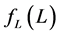 is some parameter function depending on the compactification length L.
is some parameter function depending on the compactification length L.
The condition (1) corresponds to the equation:
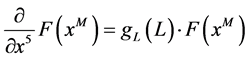 (2)
(2)
With the relations:
 (3)
(3)
In general we can put
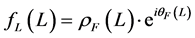 (4)
(4)
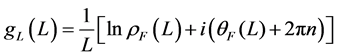
For neutral field, 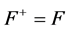 ,
, 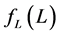 is to be real and therefore
is to be real and therefore 
The periodicity condition (1) can be generalized for the case of arbitrary number of extra dimensions in the following manner.
For convenience we denote the extra dimension coordinates  by
by 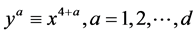 and write
and write
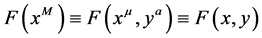 (5)
(5)
The periodicity condition (1) is now generalized to be:
 (6)
(6)
and the corresponding Equation (2) becomes:
 (7)
(7)
with the relations:
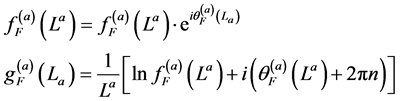 (8)
(8)
3. Effective Field Equation and Mass
The general procedure of our treatment is as follows. We start from the (4 + d) dimensional Lorentz invariant Kinetic Lagrangian L(x, y) and the action for the field F(x, y) defined as
 (9)
(9)
where  and the integral is performed over the whole extra space time.
and the integral is performed over the whole extra space time.
The principle of minimal action for S(y) then gives the Euler-Lagrange equation
 (10)
(10)
which in turn leads to the equation of Klein-Gordon type:

For the effective field defined as
 (11)
(11)
For illustration let us consider in more details the cases of scalar, spinor and vector fields.
3.1. Scalar Field
The free neutral scalar field 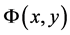 is described by the Lagrangian
is described by the Lagrangian
 (12)
(12)
where ,
, 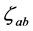 is a Minkonski metric for extra dimensions:
is a Minkonski metric for extra dimensions:
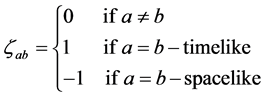
By inverting (7) into (12), we obtain:
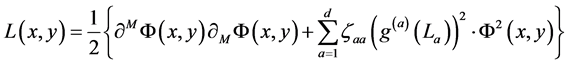 (13)
(13)
And from here the equation
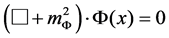 (14)
(14)
For the effective field

With
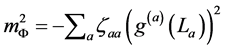 (15)
(15)
It is worth nothing that the squared mass  is positive if all the extra dimensions are space-live, and can be negative if there exist time-live extra dimensions.
is positive if all the extra dimensions are space-live, and can be negative if there exist time-live extra dimensions.
For change scalar field instead of (12) we take
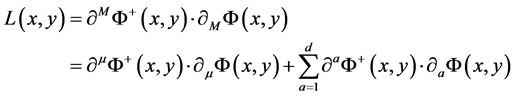 (16)
(16)
And instead of (13) we have:
 (17)
(17)
And from here the equation the same Equation as (14) with:
 (18)
(18)
3.2. Spinor Field
In (4 + d) dimensional space-time, the spinor field is described by a 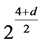 component function
component function  with the live Lagrangian
with the live Lagrangian
 (19)
(19)
where  denote (4 + d) Dirac
denote (4 + d) Dirac  matrices obeying the ant commutation relations:
matrices obeying the ant commutation relations:
 (20)
(20)
By inverting
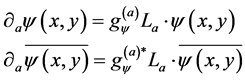 (21)
(21)
Into (19) we obtain:
 (22)
(22)
And from here the equation
 (23)
(23)
By acting from the left both sides of this equation by

And taking into account the relations (20) we have:
 (24)
(24)
And hence
 (25)
(25)
We note that  if all the extra dimensions are space-like,
if all the extra dimensions are space-like, 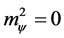 if all
if all 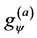 are real, and
are real, and 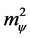 can be negative if there exists time-like extra dimension
can be negative if there exists time-like extra dimension
3.3. Vector Field
We restrict ourselves to the case d = l and consider the neutral vector field 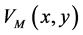 satisfying the periodicity condition
satisfying the periodicity condition
 (26)
(26)
And in correspondence
 (27)
(27)
The free vector field 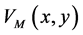 is described by the Lagrangian
is described by the Lagrangian
 (28)
(28)
where
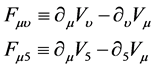
By inverting (27) into (28) we have:
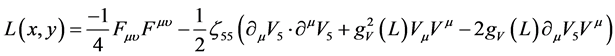 (29)
(29)
Now we define a new physical vector field  by putting
by putting
 (30)
(30)
Expressed in terms of , the Lagrangian (29) has the form:
, the Lagrangian (29) has the form:
 (31)
(31)
The Lagrangian (31) leads to the equation:
 (32)
(32)
which means that the effective vector field

Has squared mass
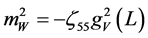 (33)
(33)
It’s positive or negative depending upon whether the extra dimension is space-like or time-like.
4. Conclusion and Discussion
In this work we have proposed a mechanism for the creation of particle mass. The key idea is that the mass is originated from the compactification of extra dimensions followed by the periodicity condition for the particle fields.
It is worth noting that according to the mechanism the existence of tachyon having negative squared mass is closely related to the existence of time-like extra dimensions.
In this work we have considered originality for mass creation, which is originated from the compactification of extradimensions. It is shown that the mass spectrum is completely determined by some functions of compactification length and closely related to the metric of extradimensions.
The key idea is that the existence and the compactification of extradimensions are the origin for creating particle mass in ordinary 4-dimensional space-time. In this connection one might think that the mass of Higgs particles themselves would be also originated from the geometric topology of extradimensions. The problem of whether there exists some mechanism allowing the extradimensions to create Higgs particles would be a problem of significant meaning. It might be also that the particles could acquire mass through different mechanisms, including those related to extradimensions. This could lead to thinking that the probability for experimentally finding Higgs particles is much smaller than the value theoretically obtained when Higgs mechanism is considered as the only one for mass creation.
References
- Cs’aki, C. (2004) TASI Lectures on Extradimensions and Branes. hep_ph 0404096.
- Randall, L. and Schwarz, M.D. (2001) Quantum Field Theory and Unification in Ad55. JHEP, 0111, 003.
- Sundrum, R. (2005) To the Fifth Dimension and Back. TASI.
- Green, M.B., Schwarz, J.H. and Witten, E. (1987) Superstring Theory. University Press, Cambridge.
- Brink, L. and Henneaux, M. (1988) Principles of String Theory. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4613-0909-3
- Carroll, S.M. (1997) Lecture Notes on General Relativity. University of California, Oakland.
- Furlan, G., et al. (1997) Superstrings, Super Gravity and Unified Theories World Scientific.

