Journal of Modern Physics
Vol.4 No.8A(2013), Article ID:36276,14 pages DOI:10.4236/jmp.2013.48A018
New Evidence, Conditions, Instruments & Experiments for Gravitational Theories
Interstellar Space Exploration Technology Initiative (iSETI) LLC, Denver, USA
Email: benjamin.t.solomon@iseti.us
Copyright © 2013 Benjamin T. Solomon. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 18, 2013; revised July 22, 2013; accepted August 16, 2013
Keywords: Relativity; Special Theory of Relativity; General Theory of Relativity; Entanglement; Baking Bread; Transverse Wave; Electromagnetism; Separation Vectors; Gamma Ray Burst; Quarks; Gravity Modification; Exotic Matter; Photons; Strings; Shielding; Cloaking; Invisibility; Near Field Gravity Probe; Wave Function; Gaussian
ABSTRACT
Two significant findings compel a rethink of physical theories. First, using a 7-billion-year-old gamma-ray burst, Nemiroff (2012) showed that quantum foam could not exists. And second, Solomon (2011) showed that gravitational acceleration is not associated with the gravitating mass, that gravitational acceleration g is determined solely by τ the change in time dilation over a specific height multiplied by c2 or g = τc2. Seeking consistency with Special Theory of Relativity, as means to initiate this rethink, this paper examines 12 inconsistencies in physical theories that manifest from empirical data. The purpose of this examination is to identify how gravitational theories need to change or be explored, to eliminate these 12 inconsistencies. It is then proposed that spacetime is much more sophisticated than just a 4-dimensional continuum. And, that the Universe consists of at least two layers or “kenos” (Greek for vacuous), the 4-dimensional kenos, spacetime (x, y, z, t) and the 3-dimensional kenos, subspace (x, y, z) that are joined at the space coordinates (x, y, z). This explains why electromagnetic waves are transverse, and how probabilities are implemented in Nature. This paper concludes by proposing two new instruments and one test, to facilitate research into gravitational fields, the new torsion-, tensionand stress-free near field gravity probe, the gravity wave telescope, and a non-locality test.
1. Introduction
1.1. Is There a Need?
Do we need a new theory on gravity? If so, why? Nemiroff [1] used photon arrivals from a 7-billion-year-old gamma-ray burst to show that quantum foam cannot exist. If corroborated this would require significant revisions to quantum theory. A new theoretical approach would then be required. But why wait?
1.2. Can a New Theory Provide New Insights?
Solomon [2] proposed a different formalism, schemas, for analyzing gravitational fields. A schema is an outline of a model of a complex reality to assist in explaining this reality. The work of various researchers [2] in the gravity field can be presented by the conceptual formalism referred to as source-field-effect schema. The sourcefield-effect schema corresponds to the mass-gravity-acceleration phenomenon, respectively. With this approach one can take out the source or mass and just consider the field-effect or gravitational-field-gravitational-acceleration.
One could rewrite [2,3] General Relativity’s separation vectors as a function of Ω, as follows,
 (1)
(1)
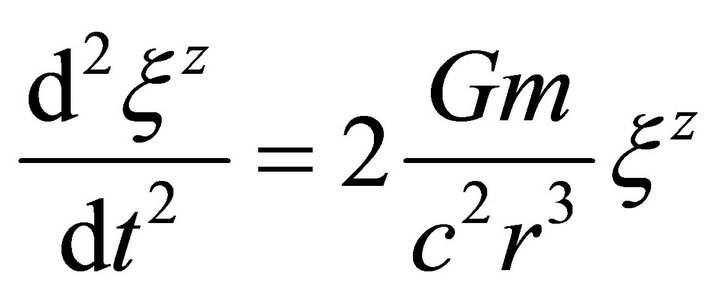 (2)
(2)
 (3)
(3)
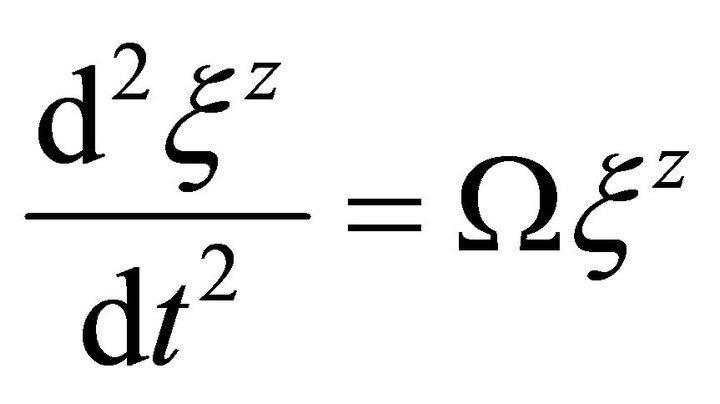 (4)
(4)
or,
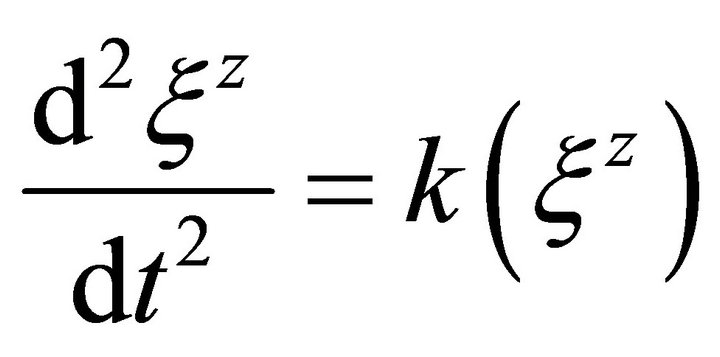 (5)
(5)
Equation (1) expresses gravitational acceleration g as a function j of the separation vectors. Equation (2) presents the standard z-direction separation vector as a function of gravitational mass m, and gravitational constant G at a distance r from the source. The mass source of the gravitational field can be replaced with an Ω function as defined by Equation (3). Therefore, Equation (2) can be rewritten as a function of Ω as Equation (4) or simply as a function k as in Equation (5). Solomon’s schema can be described as three parts, first the mass source or Equation (3), second the field or Equation (5), and third the field effect or acceleration, Equation (1).
Rewriting, Equation (1) gives Equation (6) that gravitational acceleration is primarily a field effect, and one does not really need to know what precisely is Ω as long as it is a function of matter.
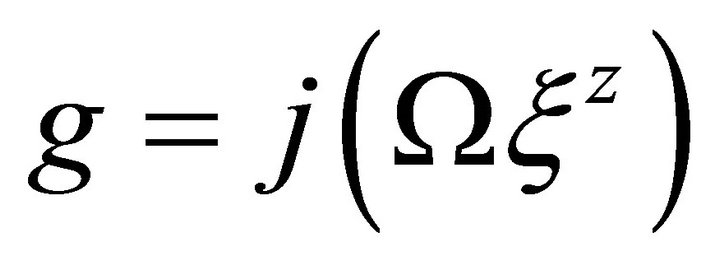 (6)
(6)
One could ask the question, what part of matter causes the gravitational field? Contemporary theories use mass as a measure of that matter. Matter, however, consists of at least two parts, mass and quarks. These are impossible to distinguish empirically with current technology. So if mass is a proxy for matter, could it be that the real source of a gravitational field is quark interaction, and not mass? We don’t know, and thus the need for a better theory for gravitational source to probe such questions. This separation vector approach support the premise that one could develop a field-effect relationship for gravitational acceleration per (1) that does not require a prior knowledge of the mass of the gravitating source.
1.3. New Inferences from Empirical Results?
Using the source-field-effect schema, and with extensive numerical modeling Solomon [2,4] discovered a new, elegantly simple formula for gravitational acceleration g that does not require one to have a prior knowledge of the mass of the gravitating source,
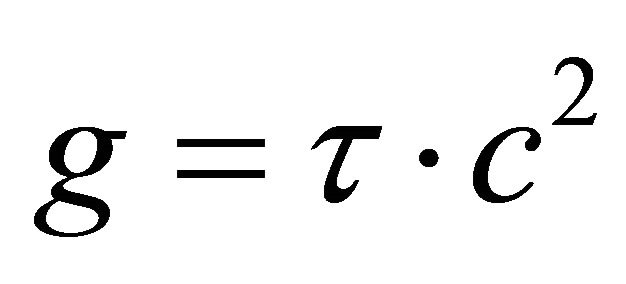 (7)
(7)
where gravitational acceleration g is defined by the velocity of light squared c2 multiplied by τ the change in time dilation divided by the height across this change in time dilation or a purely field effect. Note there is no mass source in this Equation (7). This is akin to knowing the frequency of a photon without having to know the properties of the photon source.
Equation (7) provide three inferences, first that gravitational acceleration is a 4-dimensional (x, y, z & t) problem. No further dimensions are required. The second, that the source-field-effect schema is correct as it is now possible to investigate the field-effect schema without taking into consideration the source component of the full source-field-effect schema. Similarly, one should be able to investigate the source-field schema without taking into consideration the effect component. And, third [2,4], that the gravitational effect on an elementary particle is independent of the internal structure of that particle. This independence suggests that any particle-based theory could in principle explain gravitational acceleration. That is, it need not be quantumor string-based particles. It could be something else, say, quantized compressive structures that contract with energy as opposed to string theory’s quantized tensile structures that expand with energy.
With three major gravitational theories (relativity, quantum & string) why would one need a fourth? Equation (7) provides an answer. All contemporary theories require mass in their calculations, while Equation (7) does not. One now has a means to evaluate gravitational acceleration without know the gravitating mass. This therefore, hints of new theoretical and technological approaches to modifying gravity without using mass.
1.4. Wasn’t Gravity Modification Disproved?
With respect to gravity modification, the literature reviews [2] point to inconclusive theoretical explorations and experimental results. The pertinent research is the work of Podkletnov [5,6], Solomon [7], Woods1, Cooke, Helme & Caldwell [8] and Hathaway, Cleveland & Bao [9]. Podkletnov [5,6] observed both gravity shielding or attenuation and amplification. Solomon [7] showed that any hypothesis on superconducting gravity shielding should eventually explain four observations, the stationary disc weight loss, spinning disc weight loss, weight loss increases along a radial distance and a weight increase. Woods, Cooke, Helme & Caldwell [8] attempted to reproduce Podkletnov’s [5,6] work without much success as (quoting the authors) “the tests have not fulfilled the specified conditions for a gravity effect”. Their primary focus was to reproduce Podkletnov’s ceramic disc. In the nomenclature of the source-field-effect schema, they focused on the source component, and had not reached the field-effect components of this schema. Therefore, their results were inconclusive.
Solomon [7] using the field-effect schema, proposed that two vital components of Podkletnov’s experiments were missing from the Woods, Cooke, Helme & Caldwell [8] investigation. First, the bilayer disc, top-side superconducting and bottom-side non-superconducting, may not have been built correctly. Second, the electric field was missing from Woods, Cooke, Helme & Caldwell experimental investigation. The field-effect schema, therefore, advocates a need for a new theory on gravity that will facilitate the investigation into gravity modification. The photo in the Woods, Cooke, Helme & Caldwell paper shows a sample disc with the crack in the middle. The disc was not able to withstand the rotational forces that Podkletnov’s disc could.
Hathaway, Cleveland & Bao [9] paper suggests that they too had similar difficulties. They [9] report a rotational speed of between 400 - 800 rpm, very substantially less than Podkletnov’s 5000 rpm. This suggests that there were other problems in their disc not reported in their paper. With 400 - 800 rpm, if they were to observe a significant weight change it would have been less than the repeatable experimental sensitivity of 0.5 mg.
Quoting Hathaway, Cleveland & Bao’s original paper “As a result of these tests it was decided that either the coil designs were inefficient at producing …”, “the rapid induction heating at room temperature cracked the nonsuperconducting disk into two pieces within 3 s”, “Further tests are needed to determine the proper test set-up required to detect the reverse Josephson junction effect in multi-grain bulk YBCO superconductors”.
It is obvious that neither teams were able to faithfully reproduce Podkletnov’s work. It is no wonder that at least Woods et al. team stated “the tests have not fulfilled the specified conditions for a gravity effect”. This statement definitely applies to Hathaway, Cleveland & Bao’s research.
2. Insights from Empirical Inconsistencies in Contemporary Theories
Physics is always changing, improving, and getting closer to the true description of Nature, all the time. This is achieved by exploring all avenues, even if some of those avenues initially sound ridiculous. By a process of back tracking the physics community eliminates those branches of the tree of empirical & theoretical exploration, that turn out to be dead ends. Sometimes this may take a single journal paper and sometimes many decades.
So is there a method to speeding up this branch and bound exploration process? Operations research search procedures known as mathematical programming techniques would suggest a judicial use of boundary conditions that one would not want to cross. This reduces the scope of mathematical programming search by reducing the size of the feasible region to search, thereby arriving at a solution sooner rather than later.
Is there an equivalent to mathematical programming boundary conditions in physics? This author proposes that inconsistencies with the empirical data are the equivalent of boundary conditions. These boundary condition inconsistencies, raise a flag signaling to the community of physicists that something is not quite right here and that there is a very high probability that Nature does not operate in this manner. Many times new solutions will lead to new boundary condition inconsistencies. Like physics, boundary condition inconsistencies are always changing, improving, and getting us closer to the true description of Nature, all the time.
In this section, 12 inconsistencies between the empirical evidence and accepted theories are documented and explored. There are as follows:
2.1. Exotic Matter Cannot Exist in Nature
Bondi [10] proposed that negative mass was consistent within General Relativity and negative mass or exotic matter would gravitationally repel while positive mass or normal matter would gravitationally attract and if the “... motion is confined to the line of centers, then one would expect the pair to move off with uniform acceleration ...”
There are two problems with this. The first is perpetual motion physics. Attach two thin capsules to two radial spokes. The other end of these spokes are attached to the axis of an electric generator. The spokes are fixed a small angle apart so that the capsules are close to each other. The capsules are very, very thin so as to remove any significant complications with the normal matter of the thin capsule material. In one capsule insert exotic matter, and in the other insert normal matter. Release the spokes. What does one observe? Per Bondi’s “one would expect the pair to move off with uniform acceleration” one observers that the attraction-repulsion caused by the exotic-normal matter interaction would turn the electric generator to produce electrical energy. One concludes that exotic matter results in perpetual motion, a sacrilege in physics. Therefore, since Nature abhors perpetual motion, one infers that exotic matter cannot exist in Nature.
The second problem, however, is more subtle. The esteemed Bondi [10] was able to authenticate exotic matter using General Relativity or rephrasing, General Relativity was able to endorse perpetual motion physics. Therefore, any physical theory that uses exotic matter is now doubtful. The lesson here is that one has to be careful not to modify or develop a theory that leads to perpetual motion physics.
2.2. The Baking Bread Model Is Incorrect
The baking bread model has problems. To quote from the NASA2 page“The expanding raisin bread model at left illustrates why this proportion law is important. If every portion of the bread expands by the same amount in a given interval of time, then the raisins would recede from each other with exactly a Hubble type expansion law. In a given time interval, a nearby raisin would move relatively little, but a distant raisin would move relatively farther—and the same behavior would be seen from any raisin in the loaf. In other words, the Hubble law is just what one would expect for a homogeneous expanding universe, as predicted by the Big Bang theory. Moreover no raisin, or galaxy, occupies a special place in this universe—unless you get too close to the edge of the loaf where the analogy breaks down.”
Notice the two qualifications. The obvious one is “unless you get too close to the edge of the loaf where the analogy breaks down”. The other is that this description is only correct from the perspective of velocity. But there is a problem with this.
On some nights one can see the band of stars called the Milky Way3. Notice that the Earth is not at the edge of the Milky Way. The Earth is half way inside the Milky Way. So since we are halfway inside, “unless you get too close to the edge of the loaf where the analogy breaks down” should not happen. Right?
Wrong. The Earth is only half way in and one observes the Milky Way severely constrained to a narrow band of stars. That is, if the baking bread model is to be correct one has to be far from the center of the Milky Way to observe this narrow band. Halfway definitely cannot be considered “too close to the edge”.
The Universe is on the order of 103 to 106 times larger. Using our Milky Way as an example the Universe should look like a large smudge on one side and a small smudge on the other side if the Earth is even half way out from the ‘center’ of this baking bread model. One should be surrounded by an even distribution of galaxies, in any direction, if the Earth is at the center of the Universe. And if the Earth was off center, the center-facing side of the Universe should have more galaxies than the edgefacing side of the Universe. More importantly by the distribution of the galaxies on each side one could calculate our position with respect to the center of the Universe. But the Hubble pictures show that this is not the case. One does not see directional nonrandom distribution of galaxies, but a random and even distribution of galaxies across the sky in any direction one looks.
Another problem with the baking bread model is that the early Universe should only be visible at a specific region in the sky where the “center” was/is supposed to be. Hubble shows that this is not the case. Therefore the baking bread model is an incorrect model of the Universe and necessarily any theoretical model that is dependent on the baking bread structure of the Universe is incorrect. One “knows” that the Earth is not at the center of the Universe. The Universe is not geocentric. Neither is it heliocentric. The Universe is such that anywhere, where one is in the Universe the distribution of galaxies across the sky must be the same.
Einstein4 once described an infinite Universe being the surface of a finite sphere. If the Universe was a 4-dimensional surface of a 4-dimensional sphere, then from any perspective or from any position on this surface, all the galaxies would be moving away from each other due to the expansion of this 4-dimensional Universe sphere. More importantly, unlike the baking bread model one could not have a “center” reference point on this surface. That is the Universe would be (to coin a term) “isoacentric” and both the velocity property and the center property would hold simultaneously.
This raises another question. Given that the Universe is most likely to be the surface of a 4-dimensional sphere, how would contemporary physical theories define a flat and non-flat Universe? Therefore, it is advisable that one should develop cosmological models of the Universe in the context of a well-defined physical shape of the Universe. One could add that the baking bread model is symptomatic of the lack of research into the shape of the Universe. Such research could eliminate some of the theoretical cosmological models.
2.3. Only Compressive Particles Exist in Nature
For the sake of discussion, when particles increase in energy they can elongate (are tensile), contract (are compressive) or experience no change (are inelastic). Therefore, from the perspective of energy increase there are three types of particles, tensile, compressive and inelastic.
To arrive at Equation (7), Solomon [2,4] model compressive particles that deformed under the space, time and mass deformations Γ(a) in a gravitational field.
 (8)
(8)
where and x, t & m are space, time and mass at infinity (with subscript 0) and at gravitational acceleration a (with subscript a) at a distance r from the gravitational source of mass M. The gravitational acceleration on any elementary particle is the internal effect of the deformation of the shape of the particle due to non-inertia transformations Γ(a) present in the local region of the gravitational field such that the spacetime transformations Γs(x,y,z,t) are concurrently reflected as particle transformations Γp(x,y,z,t) or,
 (9)
(9)
String theories require particles be tensile because in string theories “particles” elongate when their energy is increased. The empirical evidence suggests the opposite. Consider a photon’s wavelength. It decreases with increases in energy. Consider Lorentz-FitzGerald transformations Γ(v) for space x, time t and mass m, at velocity v, Equation (10). Length contracts with increased velocity or energy. Therefore, Lorentz-FitzGerald transformations require particles be compressive.
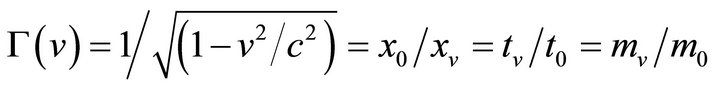 (10)
(10)
One could presume that tidal gravity was the main influence in string theories’ axiom that particles elongate with increased energy. Macro bodies elongate5 as the body falls into a gravitational field, and one presumes that this elongation is the paradigm for this axiom. However, let’s reexamine this tidal behavior with the additional requirement that this tidal gravity property be consistent with Lorentz-FitzGerald transformations or Special Theory of Relativity.
To be consistent with Lorentz-FitzGerald transformations, the atoms and elementary particles would contract in the direction of the fall. However, to be consistent with tidal gravity’s elongation, the distances between atoms in the macro body has to increase at a rate consistent with the acceleration and velocities experienced by the various parts of the macro body. That is, as the atoms get flatter, the distances apart get longer. One suspects that this axiom’s inconsistency with the empirical evidence has led to an explosion of string theories, each trying to explain Nature with no joy.
Nature favors compressive properties. Therefore tensile particles cannot exist is Nature. And by similar deduction inelastic particles per theories in quantum gravity cannot exist in Nature, too. If one is to pursue a particle-based theory of gravity, these particles need to have compressive properties. But the really important observation here is Equation (9), that whatever deformation is locally present in spacetime, must be also observed by a particle in that same local region of spacetime.
2.4. Spacetime Is More Sophisticated than a Continuum
Solomon [11] had proposed the 5-particle Box Paradox to show that spacetime could take on any length contraction and time dilation simultaneously, and concurrently. See Figure 1. The four particles, A, B, C and D form a square of length s under a specific set of conditions. A, B, C, and D, are at rest relative to each other. Their relative velocities are zero, and, therefore, no relativistic effects are present with respect to each other. From the perspec-

Figure 1. The 5-particle box paradox.
tive of particle D which has no relativistic effects, the distances of CD, SCD and AD, SAD are given by the respective Equation (11),
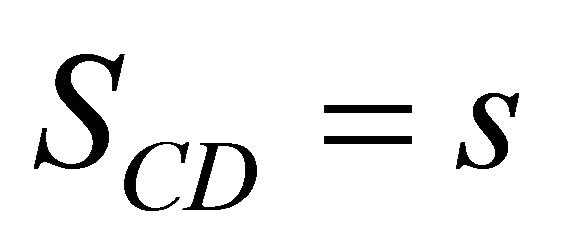 (11)
(11)
and by the hypotenuse of the right angled triangle, ACD, Equation (12),
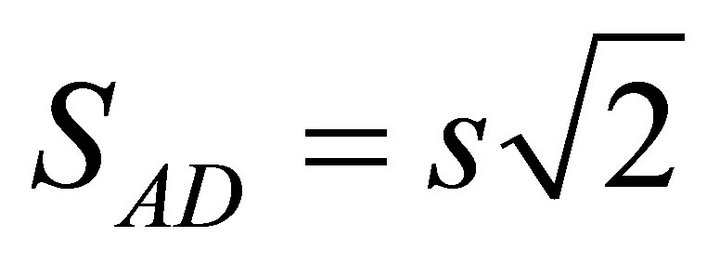 (12)
(12)
Add a fifth particle, particle E. Particle E is moving at a velocity v along CD on a collision course with D. To eliminate any possibility of relative simultaneity we require particle E to collide with D. At the moment of collision, the distance between D and E, SDE is zero.
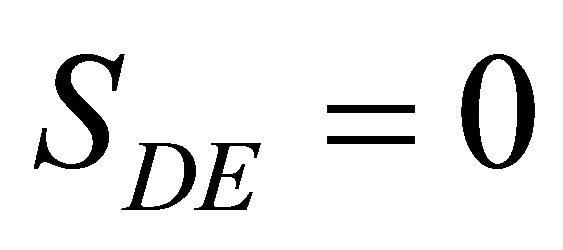 (13)
(13)
At this moment, E is aligned with D such that it, too, forms a four-sided shape with A, B and C, or ABCE. At this moment, since E is moving perpendicularly to B, the relative velocity between B and E, vBE is zero.
 (14)
(14)
However, from the perspective of particle E within the four-sided shape ABCE, E has relativistic effects along the x-axis CE and along the diagonal AE. The LorentzFitzGerald contraction dictates that particle E’s measurement of CE, SCE and AE, SAE are determined by the respective relative velocities vCE and vAE,
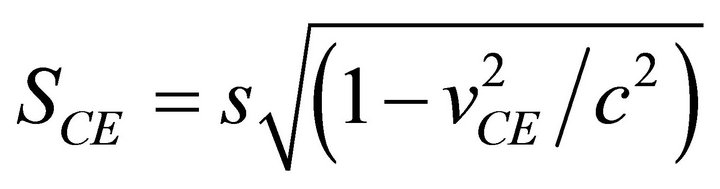 (15)
(15)
and
 (16)
(16)
Note that particles A and C are one and the same for both particles D and E; and D and E are both at the same location. Therefore, the space between particles in this particle arrangement is the same.
The only logical resolution to the differences in distances is that the measurement of distance with respect to particles D and E are different due to their different relative velocities. That is, different relative velocities transform measurement of distances differently, per LorentzFitzGerald transformations.
The necessary inferences are that many different measurements, and therefore rulers, can co-exist in the same spacetime region. Further, spacetime as a continuum is a simplification of its true nature, and obviously spacetime is more sophisticated a structure than General Relativity requires.
Therefore, new theories on gravitational fields need to be able to account for different measurements in space for the same “amount” of space.
2.5. Mass Is a Proxy for Matter
As discussed in the §1. Introduction, mass is a measure of the quantity of matter. However, digging deeper the question still remains, which part of matter causes the gravitational field?
One could divide matter into several components, electron shell, nuclei and quarks. Mass as a measure of quantity cannot distinguish between any of these three when matter is in its atomic state.
Therefore for discussion’s sake, one could propose three possibilities. First, that gravity is caused by the electron-proton interaction between the electron shell and the nuclei. Second, the proton-neutron interaction within the nuclei is the cause of gravity. And third, that it is quark interaction within the protons and neutrons that cause the gravitational field.
Which is which? Contemporary theories on gravity generally focus of the field structure (of the source-fieldeffect schema). There isn’t a theory or hypothesis that attempts to investigate the gravitational source that is not dependent upon mass as a proxy for the quantity of matter.
If there were, one could attempt to device experimental tests to falsify such hypotheses.
2.6. The Wave Function Is Inconsistent
All particles, with and without mass, have wave functions that spread out into the region of space surrounding the particle. As a result, single and double slit experiments exhibit wave interference irrespective of whether particles are mass-based or not.
This would suggest that both photons and mass-based particles have similar, if not identical mechanisms for the wave function that is not originated from the mass of the particle.
However, photons travel at the velocity of light (vp = c) and mass-based particles travel at less than that (vp < c). To be consistent with Lorentz-FitzGerald and Special Theory of Relativity, anything traveling at the velocity of light must have zero thickness and cannot spread out like the wave function does in the direction of propagation.
The logical resolution is that the wave function has zero velocity vwf = 0, that it does not travel. The wave function is not moving. It is independent of vp. A zero velocity vwf = 0 wave function is consistent with both types of particle velocities vp < c and vp = c. How could Nature implement such a property?
Here is an analogy. Take a garden rake, turn it upside down and place it under a carpet. Move it. What does one observe?
The carpet exhibits a wave function like envelope bulge that appears to be moving in the direction the garden rake is moving.
But the bulge is not moving. It shows up wherever the garden rake is. The rake is moving but not the bulge. The bulge is simply a displacement of the carpet caused by the rake.
The wave function, like the carpet bulge is a displacement disturbance in spacetime caused by the presence of the particle. Therefore, the wave function is not moving and therefore it spreads across the spacetime where the photon or particle is.
This zero-velocity bulge-like wave function is consistent with Einstein’s Special Theory of Relativity and with the empirical Lorentz-FitzGerald transformations.
The Standard Model is successful because, just as the shape of the carpet bulge is unique to the shape of the garden rake, so are the wave function displacement disturbances of spacetime unique to the properties of the respective particles.
That is, the Standard Model correctly describes a particle’s signature displacement disturbance in spacetime, but not the particle itself.
Therefore, any new theory on gravitational fields or particles, will have to account for particle displacement disturbance of spacetime.
2.7. Particle Probability Is Not Gaussian
Extensive numerical analysis of the Airy disc, involving comparing the intensity dispersion with known and new statistical distributions confirms that photon localization on the Airy disc at some distance from the pin hole, is governed by a single probability field described as the “spatial probability field”. This probability field is described by a variable Gamma distribution along the radius, orthogonal to photon propagation. It is thus named the Var-Gamma distribution.
The Gamma distribution is determined by the shape and scale parameters α > 0 and β > 0, respectively in Equation (17),
 (17)
(17)
In the Var-Gamma distribution, the shape and scale parameters are not constants, but functions of the orthogonal radius r, as follows,
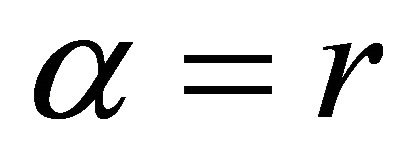 (18)
(18)
 (19)
(19)
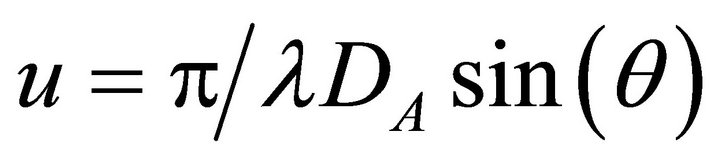 (20)
(20)
where the intensity of the photons passing through a pinhole, and hitting the visual plane screen is described by I the transmitted intensity of light on the visual plane as a function of the angle θ, the angle between the perpendicular from pinhole and screen, to the hypotenuse from the pinhole, λ is wavelength of light photon, DA is aperture diameter of the pinhole and r is radius of the Airy pattern concentric circle on the visual plane screen.
That is, if the standard hypothesis is that the photon probability is Gaussian, there now is an alternative hypothesis, it is not. It is a Var-Gamma distribution. The power of the Var-Gamma distribution is that it lends itself to the unification of shielding, transmission, and invisibility as a single phenomenon, with the further clarification that cloaking and resolution are variations of the transmission phenomenon. See Figures 2(a)-(c).
And squeezing the Var-Gamma distribution leads to a new definition of invisibility that is similar to neutrino behavior; that squeezing the spatial probability field results in a smaller spatial probability field and lowers the probability that the photon will interact with its surrounding environment.
The observation here is that there exists a single volume spatial probability field in spacetime that governs photon localization in space. Therefore, a new theory on gravitational fields will need to account for spatial probability fields as a consistent property of spacetime.
2.8. Spectrum Independent Photon Analytics
Radio antennas [12] exhibit a skin effect that the electromagnetic energy inside the antenna goes to zero. Where else in the nanowire [13] no skin effect is present. Using the new Var-Gamma distribution, Solomon [14] & [15] showed that it is possible to get similar nanowire behavior as Oulton, Sorger, Genov, Pile, & Zhang [13] if the nanowire is treated as a radio antenna. That the light photon in a nanowire behaves in the same manner as a radio wave in a radio antenna.
This suggests that photon interaction with matter is related to the ratio λ/d of the photon wavelength λ to orthogonal distance d to the surrounding region. Therefore, radio wave properties can be translated to microwave, optical and higher frequencies, by taking into account this λ/d ratio. Further, research is necessary, but it is quite clear [11] that a spectrum independent photon analytics will soon be a reality.
The inconsistency here is that unlike our physical theories, the photon does not “know” it is a radio wave, microwave, infrared, light, ultraviolet, x-ray or gamma ray. The photon as a single type of particle is responding to the physical structure of its environment in a manner that is consistent across the electromagnetic spectrum. Therefore, our physical theories need to comprehend photon analytics in an all-encompassing manner, too.
2.9. Consistency between Γ(v) and Γ(a)
A body falling in a gravitational field from infinity (where t∞ is time dilation at infinity) has both acceleration a and velocity v. Solomon [2,4] showed that the gravitational time dilation derived from the non-inertia transformation Γ(a) produces the correct instantaneous free fall velocity when plugged into the inertia transformation Γ(v). That these transformations are consistent in some manner or that the time dilations as a function of acceleration t(a) and time dilation as a function of velocity t(v) are equal or t(a) = t(v). To state it differently, the Lorentz-FitzGerald transformations of flat spacetime is observable in non-flat gravitational fields and this could be considered evidence that local space is Lorentzian.
However, Misner, Thorne, & Wheeler [4] point to elementary particle experiments that demonstrate time measured by atomic clocks depend only on velocity and not on acceleration; but by the principle of equivalence that all effects of a uniform gravitational field are identical to the effects of a uniform acceleration of the coordinate system, one could propose that the time dilation t(a) derived from Γ(a) and the time dilation t(v) derived by Γ(v) should not be correlated or t(a) ≠ t(v) should in general be true. This is contrary to the empirical evidence [2,4].
Therefore, the derivation of time dilation from the non-inertia Γ(a) demonstrates that in addition to the principle of equivalence, in free fall Nature requires inertia Γ(v) relationships to be consistent with non-inertia Γ(a) relationships; that these two transformations are not separate from or independent of each other. This consistency holds even when inertia motion is not a degenerated special case of non-inertia motion because it is verifiable for any acceleration a and velocity v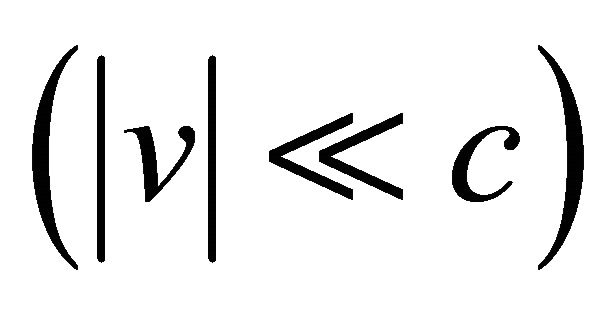 .
.
One infers firstly, that the nature of transformations govern time dilation, length contraction, mass increase, velocity, and acceleration. Second, that Γ(v) and Γ(a) co-exist in a manner that is consistent with each other and possibly imply that other (as yet unknown) transfor-
 (a)
(a)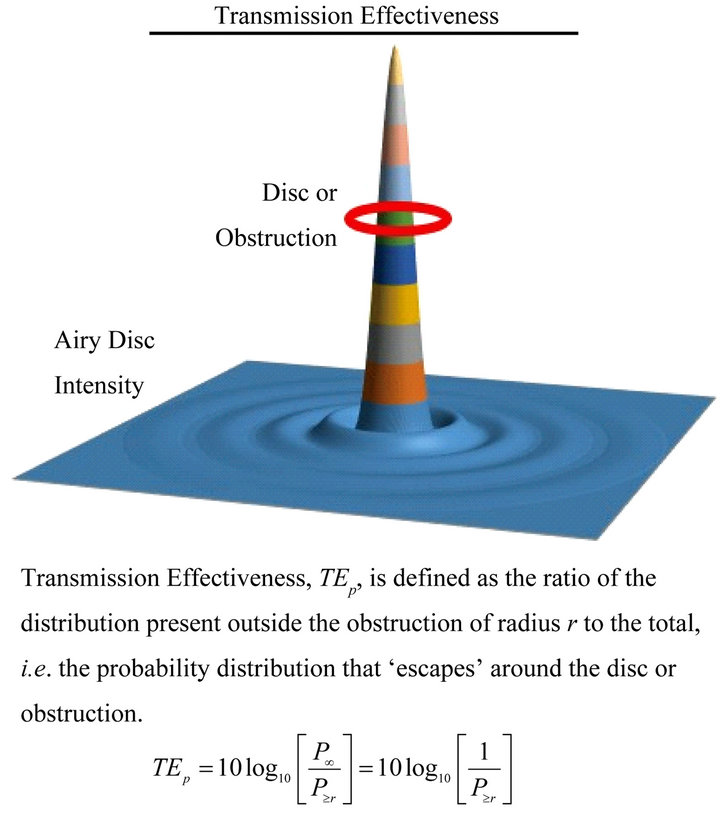 (b)
(b) (c)
(c)
Figure 2. (a) Photon shielding; (b) Photon transmission; (c) Photon invisibility.
mations may exist consistently with these two. Third, for there to be consistency, the inertia Γ(v) and non-inertia Γ(a) transformations are specific properties of something more general, the Non-Inertia Ni field, a spatial gradient of time dilations and thus a spatial gradient of velocities. And therefore fourth, that Γ(v) and Γ(a) are different representations of this Ni field. Therefore, this Γ(a) & Γ(v) consistency could be used to test for real versus theoretical gravitational fields. Therefore, any new theory of gravitational fields must account for these Ni field consistencies.
2.10. Forces Are Not Transmitted by Virtual Particles
Solomon [2,4] constructed extensive numerical models of an elementary particle in gravitational field that obeyed the gravitational transformation Γ(a) Equation (8). Equation (8) necessarily requires that particles are compressive and this extensive numerical modeling led to the discovery of Equation (7) g = τc2.
Briefly, τ the change in time dilation divided by the height across this change is described as a Non-Inertia Ni field, a spatial gradient of time dilations and thus a spatial gradient of velocities. Solomon [2,4] showed that Equation (7) correctly evaluated gravitational, electromagnetic and mechanical accelerations, which neither quantum or string theories have been able to achieve to date. This shows that macro forces are not transmitted by exchange of particles, but are present where Ni fields are. Therefore, any new theory of gravitational fields will be similar to General Relativity but will evolve from Ni field considerations.
2.11. Photon Structure Should Be Consistent with Special Theory
In §2.6 above, an alternative wave function concept was proposed that would be consistent with Special Theory of Relativity. One can apply the same logic [11] to the electromagnetic transverse wave. Since the transverse wave is travelling at the velocity of light c by Lorentz-FitzGerald transformation, its thickness must be zero in the direction of propagation but this is not the case with the transverse wave.
Both the electric and magnetic field components are zero thickness vectors whose magnitudes oscillates sinusoidally between −100% and +100% of field strength in phase with each other. The Lorentz-FitzGerald zero thickness requirement combined with the in phase property necessarily implies that the total energy oscillates between 0% and 100% of the transverse wave energy. But total energy cannot be created or destroyed. Therefore, logic requires that this energy is transformed in such a manner that it is conserved but not observable with our contemporary theories.
To solve this apparent destruction/creation problem Solomon [11] proposed that the Universe consists of at least two kenos (Greek for vacuous), or overlapping layers or regions. The first kenos is the familiar spacetime continuum K(x, y, z, t), the second is subspace K′(x, y, z) a type of spacetime that does not have the time dimension.
Spacetime and subspace, under specific conditions (see §2.12), are joined at the common (x, y, z) coordinates. That is, the intersection of spacetime and subspace is not an empty set, and both (x, y, z) positions map one-to-one. The subspace kenos concept then allows for the conservation of energy by requiring the electric and magnetic vectors to rotate from spacetime through subspace, and back into spacetime per rotation. Necessarily these vectors are 90˚ out of phase between spacetime and subspace. The projection of this rotation in spacetime is then observed as electromagnetic transverse waves.
This model of the photon is now consistent with both Lorentz-FitzGerald transformations and conservation of mass-energy, right down to the minute vector components. Therefore, contemporary electromagnetic transverse wave photon models are inconsistent with Special Theory of Relativity and the Lorentz FitzGerald transformations. Addressing this inconsistency has led to the proposal of two new properties of the Universe that of kenos and of subspace. Therefore, any new theory of gravitational fields will need to incorporate the concept of kenos.
2.12. How Are Probabilities Implemented in Nature?
Neither quantum theory nor string theories have addressed this question. The basic approach in contemporary theories has been, that there is this Gaussian formula that dictates how probabilities behave. This is not the same as asking the question, how are probabilities implemented in Nature? This paper proposes that the photon’s spatial probability field exists as a joined spacetime and subspace structure. That spacetime by itself is not probabilistic, and probabilities are only observable in that region where subspace is joined to spacetime.
From the perspective of the photon’s structure, one possible inference is that photons can modify spacetime. The numerical modeling [14] suggests that the photon’s spatial probability field is of a large volume, 32 m in radius and approximately 100,000 km long. This probability field changes direction with the direction of the photon propagation and suggests that the photon is able to modify spacetime around itself to maintain this probability field. That is, just as mass is able to modify spacetime to deformed it gravitationally, photons and other particles are able to modify spacetime by joining subspace to spacetime, in the region of the spatial probability field.
Since, in the plane orthogonal to motion, the probability of photon localization P(L) along any orthogonal radius is governed by the Var-Gamma probability distribution, one can propose that in this orthogonal plane, localization is necessarily independent of time. That is, the photon does not move to that point where it localizes. It can localize anywhere simultaneously & instantaneously within the spatial probability field.
Therefore, one infers that the probability field is absent of the time dimension, and that the large volume spatial probability field comes about by the photon modifying that specific volume of space such as to remove any effects of time to itself within this volume. Equation (21) illustrates this probability of localization P(L) as a function ρ of spatial coordinates x, y, & z.
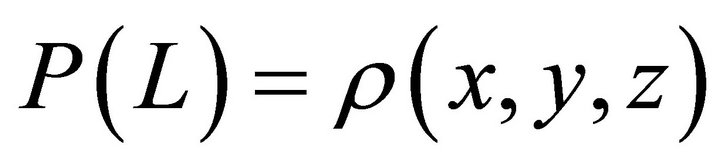 (21)
(21)
That is, the probability of localization is the property of the subspace kenos K'(x, y, z) as the time dimension is missing. Given that localization is simultaneously & instantaneously realizable, would suggest two more properties for this probability field. First, that any information Ι (Greek letter iota) within this probability field is simultaneously & instantaneously present everywhere in this field. That is, given any two random points within this large volume probability field, the information Ι(xA, yA, zA) at Point A must be identical to the information Ι(xB, yB, zB) at Point B.
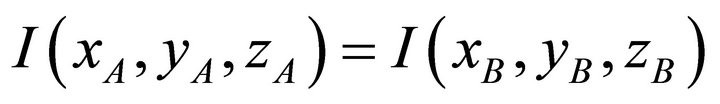 (22)
(22)
The photon is able to modify or apply a transformation Φ to spacetime S(x, y, z, t) such that spacetime is converted into a large volume spatial probability field ρ(x, y, z).
 (23)
(23)
In effect making the subspace kenos accessible from the spacetime kenos. But Equation (21) is not a sufficient condition for the probability field because by the VarGamma distribution, probability of localization 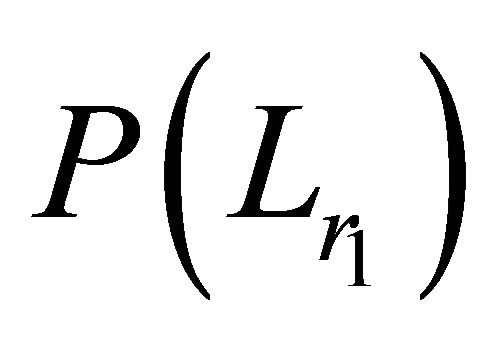 is less, at a radial distance r1 further away from the axis of motion than the probability of localization
is less, at a radial distance r1 further away from the axis of motion than the probability of localization  where it is nearer r2 such that,
where it is nearer r2 such that,
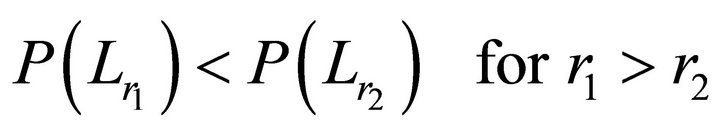 (24)
(24)
That there is a deformation present in subspace that alters the probabilistic behavior but not the x, y & z dimensions or the information content Ι(x,y,z). Suggesting that space has more properties than just spatial x, y & z. Without time t, subspace has the ability to deform in such a manner as to exhibit a probability field. And without time it also has the ability to exhibit information Ι(x,y,z) simultaneously & instantaneously across a region that has been transformed into a probability field.
That is, spacetime is a very much more sophisticated structure than just a 4-dimensional continuum, and is capable of multiple measurements, multiple kenoses, and probability fields. There is also, a much closer relationship between spacetime and particle structure, and any new theory on gravity needs to account for these.
3. New Instruments & New Experiments
Any new hypothesis needs to be falsifiable. Therefore, one method of testing a new hypothesis is to propose new experiments or instruments. This paper proposes three tests, the near field gravity probe, the gravity wave telescope, and the non-locality test.
3.1. The Near Field Gravity Probe
Recent attempts to measure [16-20], the gravitational constant G has not led to a single value. Unlike direct measurements of force using torsion balance, laser interferometer, pendulums, torsion pendulums, this paper proposes a new method using time dilations. This is possible as Equation (7) provides for measuring gravitational acceleration directly by measuring the change in time dilation. See Figure 3.
The experimental set up consists of two clocks, near and far, to measure the effect of time dilation in the presence of the test mass. In the absence of test mass both clocks should have the same time dilations. Approximately, the total noise NT in the time dilations can be attributed to three parts, equipment noise NE, local environmental noise NL and stellar & galactic noise NG, per Equation (25)
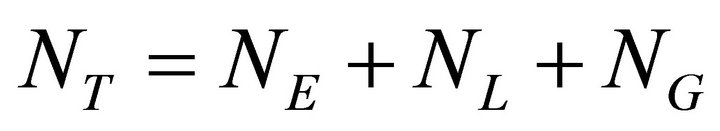 (25)
(25)
If the clocks are identical and close together the equipment noise NE and local environmental noise NL are essentially identical, and can be reduced to a combine noise NC. The galactic noise measured by the near and far clocks can be denoted as NGn and NGf. The local time dilation without the test mass is denoted by τ0. Or the measurements of near τn and far τf time dilations are
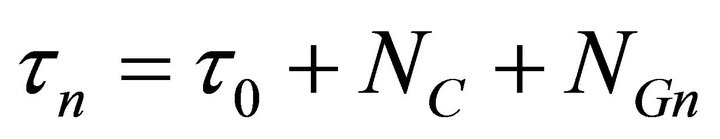 (26)
(26)
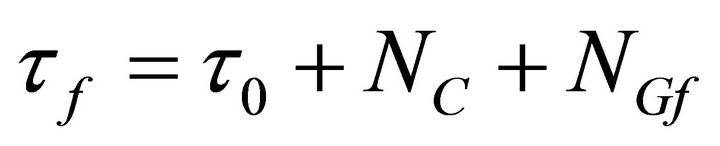 (27)
(27)
Therefore, the Equation (7) requires the difference in time dilations τn – τf divided by the separation d of the two clocks, giving,
 (28)
(28)
That is, the error attributed to this measurement is due to galactic noise. When the test mass is present and alters the near and far time dilations by δn and δf gives
 (29)
(29)

Figure 3. Near field gravity probe.
This method eliminates the equipment and local noise while recognizing that galactic noise can alter measurement results. G can then be calculated since one knows the new horizontal acceleration g. By observing NGn – NGf over a period of a year, one can determine the minimum mass required of the test mass to arrive at a stable repeatable G.
3.2. Gravity Wave Telescope
The proposed gravity wave telescope, Figure 4, inverts the proposed near field gravity probe into a telescope as one needs to measure the galactic noise, NG or τG.
Assuming that the clocks are fairly close, the signal τG one is interested is the galactic noise, NG. Since the clocks are some distance d apart, the far clock receives the same signal τGf delayed by d/c. To process the signal of interest requires a 2-pass method. First minus out the equipment and local noise from both signals. These signals will have no delays. Second, match far signal τGf to the near signal τGn by introducing the d/c delay into the near signal. This gives an amplified signal τGa,
 (30)
(30)
This method allows for directional searches as the separation between the two clocks provides a means to filtering out all other galactic signals. If the clocks are much further apart such that the local environmental noise NL is no longer the same, one can eliminate this noise by removing any signals that don’t appear on the other clock, or remove any signals having delays that are greater than d/c.
3.3. Non-Locality Test
The Airy disc is proof that the spatial probability field exists. What is of interest to test is the spatial behavior, Equation (24) to the information hypothesis, Equation (22). Locality [21] demands the conservation of causality, meaning that information cannot be exchanged between
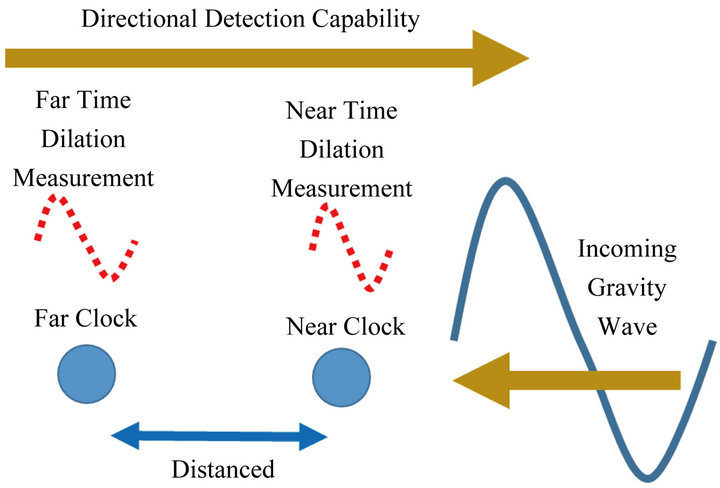
Figure 4. Gravity wave telescope.
two space-like separated parties or actions. Quantum entanglement [22] can be described as non-local interactions or the idea that distant particles do interact without the hidden variables. The information hypothesis, Equation (22) suggest that non-locality is a property of the subspace kenos, just as causality is a property of the spacetime kenos.
By Equation (24), the strength of the spatial probability field decreases with the radius that is orthogonal to propagation. Then the ability to maintain information (22) should reduce with the orthogonal radius as the strength of the spatial probability field reduces (24). If non-locality is due to the information hypothesis (22) one could use quantum entanglement to test for this information hypothesis. That is, information between Point A and Point B is preserved when localization occurs or,
 (31)
(31)
And information is not preserved when localization cannot occur, as the strength of the spatial probability field has been significantly reduced or,
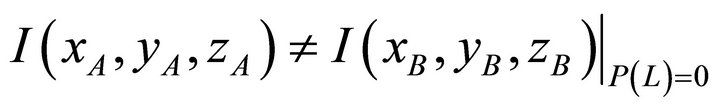 (32)
(32)
Therefore, if quantum entanglement is due to the spatial probability field, one should be able to observe a degradation in observable quantum entanglement as the orthogonal distance between two entangled photons are increased.
Assuming that entangle photons have a joint probability distribution, using extensive numerical modeling Solomon [14] showed that this joint distribution reduces as the two entangled photons are separated orthogonally. See Figures 5(a)-(c). The average joint probability within the orthogonal cross section areas (16 m2, 16 m2 & 64 m2) shown is 8.3%, 8.2% & 1.6% for 0.1 m, 0.4 m & 2.6 m separations, respectively. The joint probabilities approximately 0.0% when the separations is greater than 12m for red light wavelength λ = 700 nm per the Airy disc parameters λ/DA = 2, DP = 100 mm.
The work of other experimenters, [22-26] were reviewed for physical layout. Except for Howell [22] very little information of the physical layout of these experiments are provided. Howell’s experimental set up was ≤0.5 m across and one infers that Aspect’s [23] and Yao’s [24] experiments were on the order of 6 m and 1 m, respectively. The exception to these experiments is Tittel et al. [27] 10 km experiment in Geneva, which appears to confirm quantum entanglement at 10 km except that in this experiment returning photons are required and therefore overlapping probability fields were present. To exclude the effects of the spatial probability field, some restrictions on physical layout of entanglement experiments, are necessary. 1) Entangled photons travelling in
 (a)
(a) (b)
(b)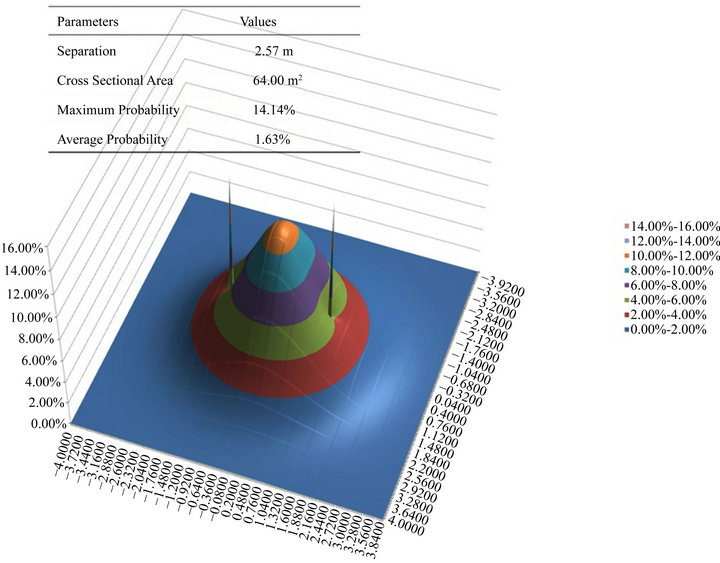 (c)
(c)
Figure 5. (a) Joint probability at 0.1 m separation; (b) Joint probability at 0.4 m separation; (c) Joint probability at 2.6 m separation.
parallel must be >32 m apart; 2) Entanglement testing cannot be done when photons are coming together head on as their probability fields overlap; 3) Photons are only allowed to be reflected away from each other as reflection of the probability field is not fully understood at this time; 4) There can be no other reflections other than returning the photons to parallel paths; and, 5) No returning photons as their probability fields would interfere with the test.
A weak confirmation requires, entanglement substantially ceases to exist when two entangled photons are orthogonally separated by a distance of 32 m, this would prove that the spatial probability field and the subspace kenos are the mechanisms for non-locality. A stronger confirmation requires that the degradation in observable entanglement should be governed by the joint distribution per Figures 5(a)-(c), and would prove the existence of the joint distribution.
4. Conclusion
12 inconsistencies have been documented and where possible alternative solutions have been proposed. As a result it is possible to propose two new instruments, and a test for non-locality. The first instrument, the near field gravity probe, provides a means of measuring G, without moving parts, stress, tension or torsion and a means to define the minimum mass required of the test mass to determine repeatable measurements of G. The second instrument, the gravity wave telescope, has the ability to directionally seek gravity waves as two clocks are used in a sequential manner. Finally, this paper has proposed a non-locality test that could substantiate the existence of the subspace kenos, and the mechanism for particle probabilities.
REFERENCES
- R. Nemiroff, “Bounds on Spectral Dispersion from Fermi-Detected Gamma Ray Bursts,” Physical Review Letters, Vol. 108, No. 23, 2012, Article ID: 231103. doi:10.1103/PhysRevLett.108.231103
- B. T. Solomon, “Gravitational Acceleration without Mass and Noninertia Fields,” Physics Essays, Vol. 24, No. 3, 2011, pp. 327-337. doi:10.4006/1.3595113
- C. W. Misner, K. S. Thorne and J. A. Wheeler, “Gravitation,” W. H. Freeman and Company, New York, 1973.
- B. T. Solomon, “An Approach to Gravity Modification as a Propulsion Technology,” The Proceedings of the Space, Propulsion & Energy Sciences International Forum (SPESIF-09), AIP Conference Proceedings 1103, Melville, 2009, pp. 317-325. http://scitation.aip.org/proceedings/confproceed/1103.jsp
- E. Podkletnov, “Weak Gravitational Shielding Properties of Composite Bulk YBa2Cu3O7−x Superconductor below 70 K under e.m. Field,” 1997. arXiv:cond-mat/9701074
- E. Podkletnov and R. Nieminen, “A Possibility of Gravitational Force Shielding by Bulk YBa2Cu3O7-x Superconductor,” Physica C, Vol. 203, No. 3-4, 1992, pp. 441- 444. doi:10.1016/0921-4534(92)90055-H
- B. T. Solomon, “Reverse Engineering Podkletnov’s Experiments,” The Proceedings of the Space, Propulsion & Energy Sciences International Forum (SPESIF-11), College Park, 15-17 March 2011. http://www.sciencedirect.com/science/journal/18753892/20
- R. C. Woods, S. G. Cooke, J. Helme and C. H. Caldwell, “Gravity Modification by High-Temperature Supercondoctors,” The Proceedings of the 37th AIAA/ASME/SAE/ ASSEE Joint Propulsion Conference & Exhibit, Salt Lake City, 8-11 July 2001, pp. 1-10.
- G. Hathaway, B. Cleveland and Y. Bao, “Gravity Modification Experiments Using a Rotating Superconducting Disk and Radio Frequency Fields,” Physica C, Vol. 385, No. 4, 2003, pp. 488-500.
- H. Bondi, “Negative Mass in General Relativity,” Reviews of Modern Physics, Vol. 29, No. 3, 1957, pp. 423- 428. doi:10.1103/RevModPhys.29.423
- B. T. Solomon, “An Introduction to Gravity Modification: A Guide to Using Laithwaite’s and Podkletnov’s Experiments and the Physics of Forces for Empirical Results,” Universal Publishers, Boca Raton, 2012. http://www.universal-publishers.com/book.php?method=ISBN&book=1612330894
- W. C. Elmore and M. A. Heald, “Physics of Waves,” Dover Publications, New York, 1985.
- R. F. Oulton, V. J. Sorger, D. A. Genov, D. F. P. Pile and X. Zhang, “A Hybrid Plasmonic Waveguide for Subwavelength Confinement and Long-Range Propogation,” Nature Photonics, Vol. 2, 2008, No. 8, pp. 496- 500.
- B. T. Solomon, “Non-Gaussian Photon Probability Distributions,” The Proceedings of the Space, Propulsion & Energy Sciences International Forum (SPESIF-10), AIP Conference Proceedings 1208, Melville, 2010, pp. 317- 325. http://scitation.aip.org/proceedings/confproceed/1208.jsp
- B. T. Solomon, “Non-Gaussian Radiation Shielding,” The Proceedings of the 100 Year Starship Study Public Symposium (100YSS), Orlando, 30 September-2 October, 2011.
- E. S. Reich, “G-Whizzes Disagree over Gravity,” Nature, Vol. 466, 2010, p. 1030. doi:10.1038/4661030a
- J. H. Gundlach and S. M. Merkowitz, “Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Feedback,” Physical Review Letters, Vol. 85, No. 14, 2000, pp. 2869-2872. doi:10.1103/PhysRevLett.85.2869
- H. V. Parks and J. E. Faller, “A Simple Pendulum Determination of the Gravitational Constant,” Physical Review Letters, Vol. 105, 2010, Article ID: 110801.
- J. Luo, Q. Liu, L.-C. Tu, C.-G. Shao, L.-X. Liu, S.-Q. Yang, Q. Li and Y.-T. Zhang, “Determination of the Newtonian Gravitational Constant G with Time-of-Swing Method,” Physical Review Letters, Vol. 102, No. 24, 2009, Article ID: 240801. doi:10.1103/PhysRevLett.102.240801
- St. Schlamminger, E. Holzschuh, W. Kündig, F. Nolting, R. E. Pixley, J. Schurr and U. Straumann, “Measurement of Newton’s Gravitational Constant,” Physical Review D, Vol. 74, No. 8, 2006, Article ID: 082001. doi:10.1103/PhysRevD.74.082001
- M. D. Eisaman, E. A. Goldschmidt, J. Chen, J. Fan and A. Migdall, “Experimental Test of Nonlocal Realism Using a Fiber-Based Source of Polarization-Entangled Photon Pairs,” Physical Review A, Vol. 77, No. 3, 2008, Article ID: 032339. doi:10.1103/PhysRevA.77.032339
- J. C. Howell, R. S. Bennink, S. J. Bentley and R. W. Boyd, “Realization of the Einstein-Podolsky-Rosen Paradox Using Momentum and Position-Entangled Photons from Spontaneous Parametric Down Conversion,” Physical Review Letters, Vol. 92, No. 21, 2004, Article ID: 210403. doi:10.1103/PhysRevLett.92.210403
- A. Aspect, J. Dalibard and G. Roger, “Experimental Test of Bell’s Inequalities Using Time-Varying Analyzer,” Physical Review Letters, Vol. 49, No. 25, 1982, pp. 1804-1807. doi:10.1103/PhysRevLett.49.1804
- E. Yao, S. Franke-Arnold, J. Courtial and M. J. Padgett, “Observation of Quantum Entanglement Using Spatial Light Modulators,” Optics Express, Vol. 14, No. 26, 2006, p. 13089. doi:10.1364/OE.14.013089
- T. Yarnall, A. F. Abouraddy, B. E. A. Saleh and M. C. Teich, “Experimental Violation of Bell’s Inequality in Spatial-Parity Space,” Physical Review Letters, Vol. 99, No. 17, 2007, Article ID: 170408. doi:10.1103/PhysRevLett.99.170408
- J. Leach, B. Jack, J. Romero, M. Rirsch-Marte, R. W. Boyd, A. K. Jha, S. M. Barnett, S. Franke-Arnold and M. J. Padgett, “Violation of a Bell inequality in Two-Dimensional Orbital Angular Momentum Stat-Spaces,” Optics Express, Vol. 17, No. 10, 2009, pp. 8287-8293. doi:10.1364/OE.17.008287
- W. Tittel, J. Brendel, B. Gisin, T. Herzog, H. Zbinden and N. Gisin, “Experimental Demonstration of QuantumCorrelations over More than 10 Kilometers,” Physical Review A, Vol. 57, No. 5, 1998, pp. 3229-3232. doi:10.1103/PhysRevA.57.3229
NOTES
1Three teams set out to investigate Podkletnov’s claims. The first was led by RC Woods. The second led by Hathaway. These are discussed in this paper. Ning Li led the third team comprised of members from NASA and University of Huntsville, AL. It was revealed in conversations with a former team member that Ning Li’s team was disbanded before they could build the superconducting discs required to investigate Podkletnov’s claims.
2http://map.gsfc.nasa.gov/universe/bb_tests_exp.html
3Google, Dan Duriscoe’s Milky Way from Death Valley, California, to see an excellent picture of our Milky Way.
4TV series Cosmic Journey, Episode 11, Is the Universe Infinite?
5This was attributed to Roger Penrose who, in the 1950s, proved this, however, this author could not find the reference in time for this paper.

