Journal of Modern Physics
Vol.2 No.9(2011), Article ID:7148,5 pages DOI:10.4236/jmp.2011.29127
A Search on Two-Electron Atoms
Department of Engineering Physics, University of Gaziantep, Gaziantep, Turkey
E-mail: gonul@gantep.edu.tr
Received December 6, 2010; revised April 7, 2011; accepted May 4, 2011
Keywords: Hydrogen Like Atoms, Screening Parameter
ABSTRACT
Using the basic ingredient of two-body problem, we propose accurate algebraic solutions in a closed form for the ground state of helium and helium-like atoms. These simple but explicit expressions involve exact screening parameters for each system considered and provide an insight into their physical structure. The energy eigenvalues have been exactly calculated for atoms with nuclear charge Z in the range 1 ≤ Z ≤ 12, clarifying the relation between the screening parameteter and Z.
1. Introduction
One of the challenging problems in non-relativistic quantum mechanics is to find exact solutions to the Schrödinger equation for potentials that can be used in different fields of physics. In connection with this, two-electron atoms have been subjected to intensive investigations during the last decades. The determination of accurate wavefunctions for few-body Coulombic systems can be achieved in many ways, and could be considered nowadays to be resolved problem if one overlooks the necessity of simple and compact wavefunctions for further calculations. The last point is of importance in the theoretical study of inelastic process involving two electrons. In order to calculate the cross section of such processes one needs a convenient form of the ground state wavefunction to describe the initial state of target, and to perform subsequent calculations. More generally, the search for simpler but more accurate wavefunctions should result in more insight and understanding of the collision dynamics. We believe that this goal remains up to date and the recent theoretical contributions [1-6], together with all the related references therein, indicate that this is true.
Within this context, we propose a novel treatment revealing that an exact solution can be clearly produced with the introduction of accurate screening parameters in the calculations carried out. These solutions naturally remove the need for involving the correlation wavefunction for the consideration of the interaction betwen two electrons, the effects of which have been a subject of interest from the early days of quantum mechanics. This leads to more explicit and accurate analytical expressions for the spectra of helium and isoelectronic atoms when compared to the calculations reported previously by several workers. Moreover, the long-standing dichotomy of choosing distinct parameters and correlation function descriptions in providing an appropriate prescription for the analysis of quantum mechanical three-body problem of interest is greatly clarified by the present discussion.
So far, the ground state energies of helium and helium-like atoms have been calculated by the use of wavefunctions constructed from the conventional orbital product, times a correlation function depending on the interelectronic distance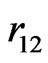 . These wavefunctions involve, in general, a number of adjustable parameters which are constrained to satisfy some kind of variational principle to give an improved value for the ground state energy. Although one achieves the desired accuracy in energy eigenvalue by introducing a large number variational parameters in the trial wavefunction as done in the earlier calculations based on variational procedure, one quickly loses the physical meaning of the parameters, and also is required to perform tedious and cumbersome calculations in the theoretical study of the atomic properties using such functions. In particular, it is well known that integration of the functions of
. These wavefunctions involve, in general, a number of adjustable parameters which are constrained to satisfy some kind of variational principle to give an improved value for the ground state energy. Although one achieves the desired accuracy in energy eigenvalue by introducing a large number variational parameters in the trial wavefunction as done in the earlier calculations based on variational procedure, one quickly loses the physical meaning of the parameters, and also is required to perform tedious and cumbersome calculations in the theoretical study of the atomic properties using such functions. In particular, it is well known that integration of the functions of 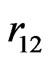 is quite difficult, so the topic of electron correlation is often studied by using numerical routines only. Hence, there is a need to obtain a simple, yet physically meaningful, wavefunction by choosing fewer parameters.
is quite difficult, so the topic of electron correlation is often studied by using numerical routines only. Hence, there is a need to obtain a simple, yet physically meaningful, wavefunction by choosing fewer parameters.
In this article, using the spirit of the work in [2], we report that an exact analytical expression for the total wavefunction underlined, having only one parameter due to screening of the nucleus, is able to define the physics behind the whole interaction mechanism, providing a deeper understanding, and yields accurate energies for the systems under consideration. This reveals the existence of a link between the screening parameter and the charge of the nucleus, which is one of the main motivetions behind this work. It is however emphasized that this unique parameter in the present work is introduced in the Hamiltonian of the system rather than in the trial wavefunction, unlike the earlier calculation techniques. Although, the literature covered similar problems, to our knowledge an investigation such as the one we have discussed here was nonexistined. Further, the whole development is very elegant, appealing, and yet rather simple, even any student of quantum mechanics may easily understand and appreaciate it. Hence, we kept this article at a pedagogical level and made it self-contained.
The paper is set out as follows. In Section 2, we discuss the present procedure and its application to distinct sytems, together with the analysis of the results obtained. Section 3 summarizes the conclusions of the present investigation.
2. Theoretical Consideration
The motivation for adopting the alternative approach stems from the consideration of the one-parameter exact wavefunction for the two-electron atom amounting to screening of the nucleus. For the case of nondegenerate S-states, the idea of screening the nucleus can be reflected in the Hamiltonian of the systems by writing it (in atomic units) as
 (1)
(1)
where
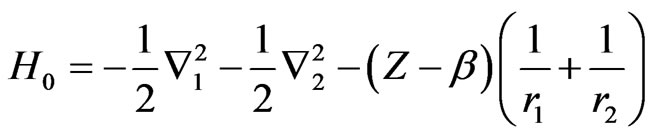 (2)
(2)
and
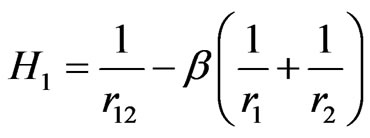 (3)
(3)
which was first discussed by Tripathy et al. [2] in a different manner. In the above equations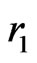 ,
, 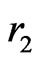 are the positions of electrons with respect to the nucleus having a charge of
are the positions of electrons with respect to the nucleus having a charge of 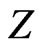 with infinite mass, and
with infinite mass, and  is the distance between electrons. For those electronic configuretions of the system in which two electrons are at unequal distances from the nucleus, the outer electron should experience a smaller effective charge than the inner one. In other words, each electron is partially screened from screening the full charge of the nucleus due to the presence of the other electron. This would suggest introduceing an appropriate parameter,
is the distance between electrons. For those electronic configuretions of the system in which two electrons are at unequal distances from the nucleus, the outer electron should experience a smaller effective charge than the inner one. In other words, each electron is partially screened from screening the full charge of the nucleus due to the presence of the other electron. This would suggest introduceing an appropriate parameter,  , in the calculations.
, in the calculations.
The unperturbed Hamiltonian, 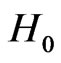 , is separable and hence the corresponding Schrödinger equation is solved analytically. Each of these independent electron picture is the same as the Schrödinger equation for the Hydrogen atom, leading to the full unperturbed solutions
, is separable and hence the corresponding Schrödinger equation is solved analytically. Each of these independent electron picture is the same as the Schrödinger equation for the Hydrogen atom, leading to the full unperturbed solutions

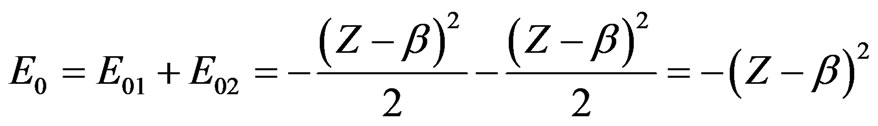 (4)
(4)
The reader is referred to [7] for a comprehensive discussion of exactly solvable potentials within the framework of supersymmetric quantum mechanics, the advent of which has had a significant impact on the theoretical physics in a number of distinct disciplines.
Assuming that
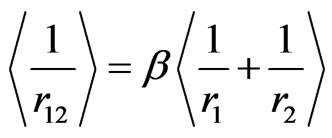 (5)
(5)
the Hamiltonian,  , incorporating a perturbation due to the correlation term vanishes. In this case, Equation (2) gains a physical importance, the solution of which reflects also the correlation effects indirectly. This is in agreement with the well known fact from the literature that the inclusion of electron correlation in the Hamiltonian accounts for the screening precisely.
, incorporating a perturbation due to the correlation term vanishes. In this case, Equation (2) gains a physical importance, the solution of which reflects also the correlation effects indirectly. This is in agreement with the well known fact from the literature that the inclusion of electron correlation in the Hamiltonian accounts for the screening precisely.
Physically, the parameter introduced above screens the nuclear charge and produces a change in the wavefunctions corresponding to the interaction of the each electron with the nucleus. Bearing in mind that the interelectronic interaction is repulsive, one may think of this repulsion resulting in some kind of positional displacement for the electronic wavefunctions such that the correlated atomic state might not be associated only with pure S-orbitals. This justifies the claim put forward with Equations (2) and (5) that correlation can also be accounted for by introducing a correct screening parameter.
To proceed, in both cases we consider the form of the exact energy
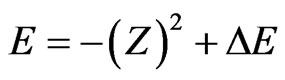 (6)
(6)
where 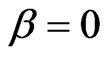 and
and 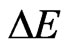 is the correction term to the energy value within the consideration of electron correlation, and
is the correction term to the energy value within the consideration of electron correlation, and
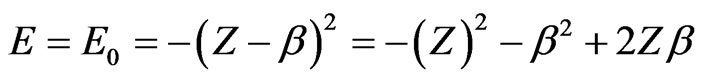 (7)
(7)
in case of screening, leading to a connection between energy expressions
 (8)
(8)
of different physical considerations.
In order to provide an insight into the physical nature of the screening parameter, we obtain
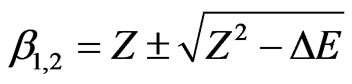 (9)
(9)
using Equation (8). Though mathematically we have arrived at two roots for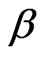 , the substitution of Equation (8) into (9) and a careful study of Equation (4) direct us to choose the physically reasonable lower root due to the physical fact that
, the substitution of Equation (8) into (9) and a careful study of Equation (4) direct us to choose the physically reasonable lower root due to the physical fact that  The dependence of
The dependence of 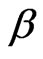 on nuclear charge
on nuclear charge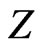 , in Equation (9), is in quite striking contrast with the previous calculations used trial functions where, in general,
, in Equation (9), is in quite striking contrast with the previous calculations used trial functions where, in general, 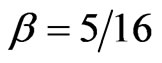 irrespective of
irrespective of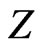 . Equation (9) thus justifies the discussion in [2]. As far as we know, this feature has not been perceived in an explicit way until now.
. Equation (9) thus justifies the discussion in [2]. As far as we know, this feature has not been perceived in an explicit way until now.
The accurate values of screening parameter for different atoms having two electrons are shown in Table 1. In calculating these parameters, exact energy values which are taken from the works in [8,9] are employed within the frame of Equations (6), (8) and (9).
Clearly,  slightly increases with increasing
slightly increases with increasing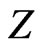 . In addition, we observe that there is a universal relation between the reduced energy
. In addition, we observe that there is a universal relation between the reduced energy 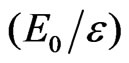 and the reduced screening parameter
and the reduced screening parameter 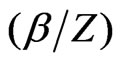 such that
such that
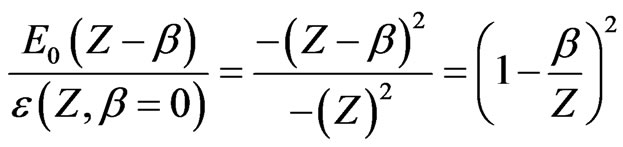 (10)
(10)
for 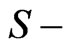 states. The present result indicates another interesting point. Here,
states. The present result indicates another interesting point. Here, 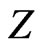 behaves as a critical screening parameter for which the binding energy of the level, Equations (4), (7) and subsequently (10), in question becomes zero. It is of interest however to examine whether such a relationship is also valid for
behaves as a critical screening parameter for which the binding energy of the level, Equations (4), (7) and subsequently (10), in question becomes zero. It is of interest however to examine whether such a relationship is also valid for 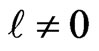 states.
states.
Afterall, we wish to generalize the framework of our discussion by focusing on Equation (5), in which there are two unknowns: the positions of electrons with respect to the nucleus  and the distance between interacting electrons
and the distance between interacting electrons . It is therefore obvious that there is a need for a second equation to be able to estimate these two unknown observables. By the use of Heisenberg’s uncertainty relation, we propose a similar idea to that of Yukawa for the correlation between the electrons,
. It is therefore obvious that there is a need for a second equation to be able to estimate these two unknown observables. By the use of Heisenberg’s uncertainty relation, we propose a similar idea to that of Yukawa for the correlation between the electrons,
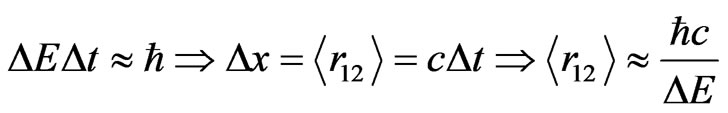 (11)
(11)
Throughout the work presented here we work in atomic units, Equation (11) is thus formed as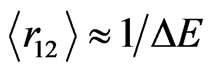 . During the electron-electron interaction, we can expect a considerable change in total energy
. During the electron-electron interaction, we can expect a considerable change in total energy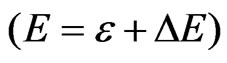 , on average, due to the correlation
, on average, due to the correlation 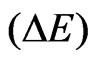 visualized as in Equation (11), keeping in mind that the time required a
visualized as in Equation (11), keeping in mind that the time required a

Table 1. Exact screening parameters.
photon exchange between these charged particles is quite short due to the photon moving with the speed of light.
Therefore, in the light of Equations (5), (8) and (11) one gets
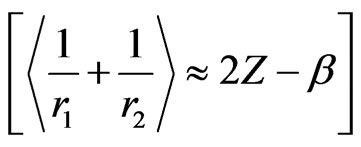 (12)
(12)
and with the use of either Equation (7) or Equation (10), the energy expression in a closed algebraic form is given as
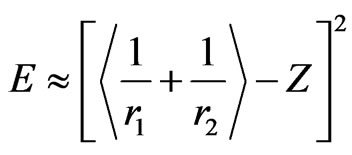 (13)
(13)
It is useful at this stage to remind ourselves that these results are in a very good agreement with a significant but ongoing discussion in the literature. In brief, Equation (13) clarifies explicitly that for low Z values, when one of the electrons coalesces with the nucleus the radial distribution of the second electron extends over several atomic units. As the charge increases, the second electron moves nearer to the nucleus. The equations above, also agree with the Bohr’s suggestion that the radius of hydrogen-like atoms is inversely proportional with the charge of the nucleus if electron-nucleus problem is treated independently without considering the correlation effect.
Additionally, Equations (12) and (13) also reveals that one needs either a reasonable parameter reletad to the screening effect or the accurate positions of electrons to obtain exact binding energies for the cases of interest. To end up this discussion, we provide  values in Table 2 for the atoms appeared in Table 1 considering
values in Table 2 for the atoms appeared in Table 1 considering
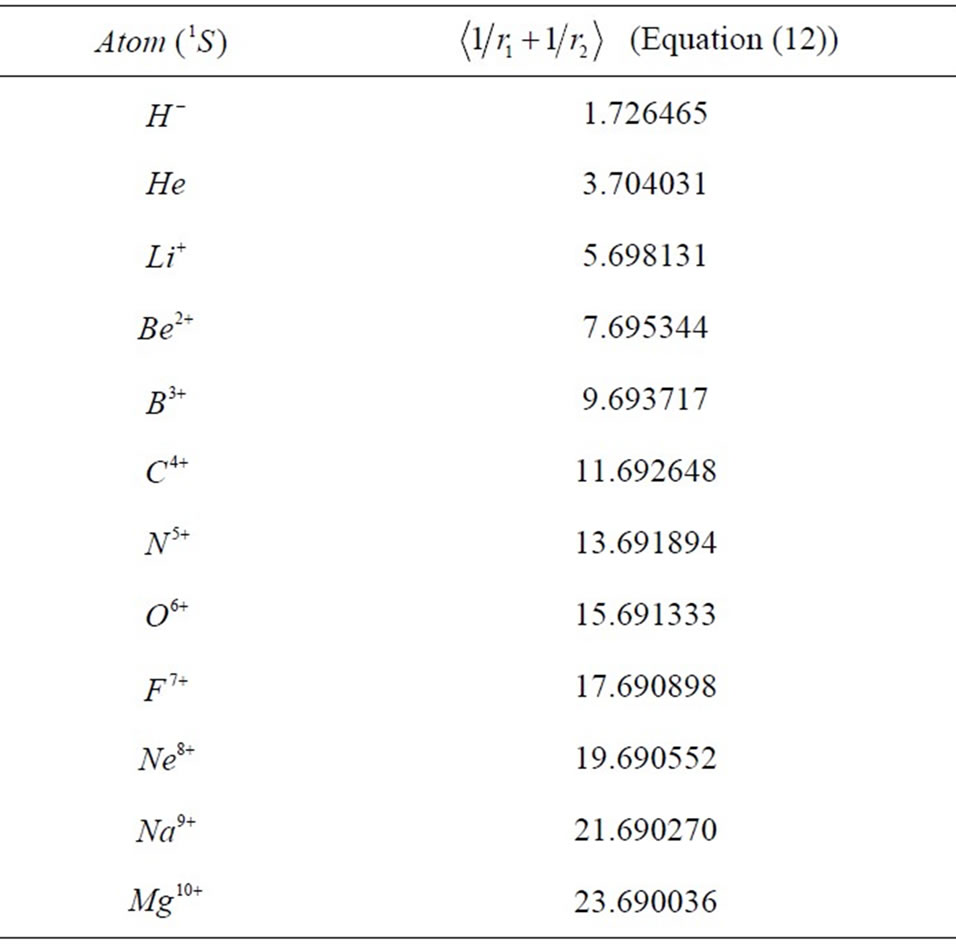
Table 2. Locations of electrons with respect to the nucleus.
the corresponding exact  values.
values.
The use of these numerical results in Equation (13) reproduces exact energy values in Table 1, indicating that our suggestion in Equation (11) within the frame of HUP is physically resonable, leading to reliability of the tabulated results. Moreover, the comparison of the present results, 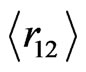 and
and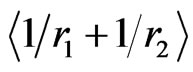 , with those of [5,10,11] confirms the physics behind the idea proposed in Equation (11). We believe that these equations, in their present form, would hence raise many interesting conceptual problems of a fundamental nature.
, with those of [5,10,11] confirms the physics behind the idea proposed in Equation (11). We believe that these equations, in their present form, would hence raise many interesting conceptual problems of a fundamental nature.
3. Concluding Remarks
The helium atom and isoelectronic ions are universal examples which illustrate the properties of few-electron atoms and ions, and the complications introduced by many-particle systems. By the consideration of this essential point, we have been principally concerned in this work with finding correct secreening parameters for the systems considered. We have observed that for helium and its isoelectronic series the size of  scales with the nuclear charge. It has been also demonstrated that physically reasonable parameters can be included in the hamiltonian rather than in the trial functions.
scales with the nuclear charge. It has been also demonstrated that physically reasonable parameters can be included in the hamiltonian rather than in the trial functions.
The screening factor is a refinement taking the screening of the nuclear charges by the electrons into account. Since a screening factor complicates in general the calculation of off-diagonal matrix elements, many theoretical techniques do not include this parameter in the wavefunction due to the structure of their framework. Therefore, one can expect that the results will be less accurate in cases where screening becomes important; i.e. at smaller internuclear distances of two-electron molecules, or for dissociation limits involving negative atomic ions, see [1]. However, the present approach would be helpful in removing such deficiencies. In addition, the relatively simple and compact form of the present wavefunction would be of interest for the calculation of electronic transition moments needed in dynamical studies, where intermediate and large internuclear distances are involved.
Clearly, considerable additional work is still needed to extend the present scenario to the excited states of helium and its isoelectronic ions with the consideration of electrons’ spins. Further, since the same 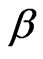 value has been chosen for both electrons, our method can be easily extended to doubly-excited configurations in which both the electrons occupy the same orbital. With this considerations, the authors hope to stimulate further examples of applications of the present procedure in important problems in physics. Along this line the works are in progress.
value has been chosen for both electrons, our method can be easily extended to doubly-excited configurations in which both the electrons occupy the same orbital. With this considerations, the authors hope to stimulate further examples of applications of the present procedure in important problems in physics. Along this line the works are in progress.
As a final remark, with the wide application of the screened Coulomb potential families in different areas of physics, we believe that our discussion presented in this letter would also provide new insights to the research communities of atomic physics.
REFERENCES
- L. D. A. Siebbeles and C. Le Sech, “ A Simple Method to Calculate Potential Curves of Two-Electron Molecules at Intermediate Nuclear Distance,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 27, No. 19, 1994, pp. 4443-4452. doi:10.1088/0953-4075/27/19/007
- D. N. Tripathy, B. Padhy and D. K. Rai, “ Two-Parameter Wavefunction for the Ground State of the Helium Isoelectronic Sequence,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 28, No. 3, 1995, pp. L41-L46. doi:10.1088/0953-4075/28/3/001
- S. Bhattacharyya, A. Bhattacharyya, B. Talukdar and N. C. Deb, “Analytical Approach to the Helium-Atom Ground State Using Correlated Wavefunctions,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 29, No. 5, 1996, pp. L147-L150. doi:10.1088/0953-4075/29/5/003
- C. Le Sech, “Accurate Analytic Wavefunctions for Two-Electron Atoms,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 30, No. 2, 1997, pp. L47-L50. doi:10.1088/0953-4075/30/2/003
- S. H. Patil, “Electron Correlation in He and Isoelectronic Ions,” European Journal of Physics, Vol. 25, No. 1, 2004, pp. 91-100. doi:10.1088/0143-0807/25/1/012
- V. A. Yerokhin and K. Pachucki, “Theoretical Energies of Low-Lying States of Light Helium-Like Ions,” Physical Review A, Vol. 81, No. 2, 2010, Article ID: 022507.
- F. Cooper, A. Khare and U. Sukhatme, “Supersymmetric Quantum Mechanics,” Physics Reports, Vol. 251. No. 5, 1995, pp. 267-385. doi:10.1016/0370-1573(94)00080-M
- D. E. Freund, B. D. Huxtabler and J. D. Morgan, “Variational Calculations on the Helium Isoelectronic Sequence,” Physical Review A, Vol. 29, No. 2, 1984, pp. 980-982. doi:10.1103/PhysRevA.29.980
- J. Thakkar and V. H. Jr. Smith, “Compact and Accurate Integral-Transform Wavefunctions,” Physical Review A, Vol. 15, No. 1, 1977, pp. 1-15. doi:10.1103/PhysRevA.15.1
- A. Moumeni, O. Dulieu and C. Le Sech, “Correlated Wavefunctions for Two-Electron Systems Using New Screened Hydrogen-Like Orbitals,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 23, No. 22, 1990, pp. L739-L745. doi:10.1088/0953-4075/23/22/002
- K. V. Rodriguez and G. Gasaneo, “Accurate Hylleraaslike Functions for the He Atom for the Correct Cusp Conditions,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 38, No. 16, 2005, pp. L259- L267. doi:10.1088/0953-4075/38/16/L01

