Applied Mathematics
Vol.5 No.4(2014), Article ID:43842,12 pages DOI:10.4236/am.2014.54072
Chebyshev Polynomials for Solving a Class of Singular Integral Equations
Samah M. Dardery1, Mohamed M. Allan2
1Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
2Department of Mathematics, Faculty of Science and Arts Al-Mithnab, Qassim University, Qassim, KSA
Email: sd.1974@hotmail.com, allanmm1999@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 18 November 2013; revised 18 December 2013; accepted 26 December 2013
ABSTRACT
This paper is devoted to study the approximate solution of singular integral equations by means of Chebyshev polynomials. Some examples are presented to illustrate the method.
Keywords:Singular Integral Equations; Cauchy Kernel; Chebyshev Polynomials; Weight Functions

1. Introduction
During the last three decades, the singular integral equation methods with applications to several basic fields of engineering mechanics, like elasticity, plasticity, aerodynamics and fracture mechanics have been studied and improved by several scientists (see [1] -[6] ). Hence, it is interest to solve numerically this type of integral equations (see [7] [8] ). Chebyshev polynomials are of great importance in many areas of mathematics particularly approximation theory (see [9] [10] ).
In this paper we analyze the numerical solution of singular integral equations by using Chebyshev polynomials of first, second, third and fourth kind to obtain systems of linear algebraic equations, these systems are solved numerically. The methodology of the present work expected to be useful for solving singular integral equations of the first kind, involving partly singular and partly regular kernels. The singularity is assumed to be of the Cauchy type. The method is illustrated by considering some examples.
Singular integral equation of first kind, with a Cauchy type singular kernel, over a finite interval can be represented by
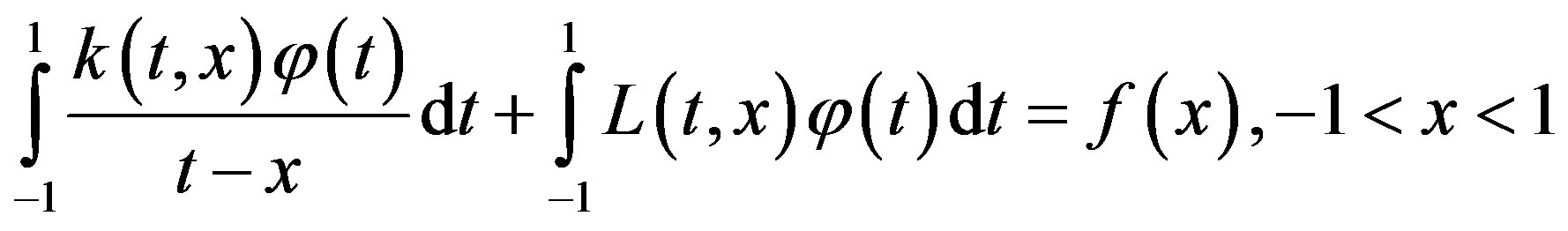 (1.1)
(1.1)
where 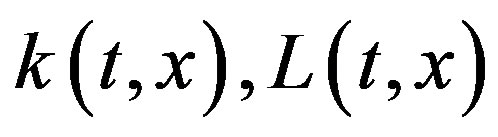 and
and  are given real-valued continuous functions belonging to the class Holder of continues functions and
are given real-valued continuous functions belonging to the class Holder of continues functions and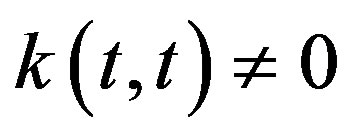 . In Equation (1.1) the singular kernel is interpreted as Cauchy principle value. Integral equation of form (1.1) and other different forms have many applications (see [1] [2] [6] [11] [12] ). The theory of this equation is well known and it is presented in [13] [14] . An approximate method for solving (1.1) using a polynomial approximation of degree
. In Equation (1.1) the singular kernel is interpreted as Cauchy principle value. Integral equation of form (1.1) and other different forms have many applications (see [1] [2] [6] [11] [12] ). The theory of this equation is well known and it is presented in [13] [14] . An approximate method for solving (1.1) using a polynomial approximation of degree  has been proposed in [7] .
has been proposed in [7] .
It is well known that the analytical solutions of the simple singular integral equation
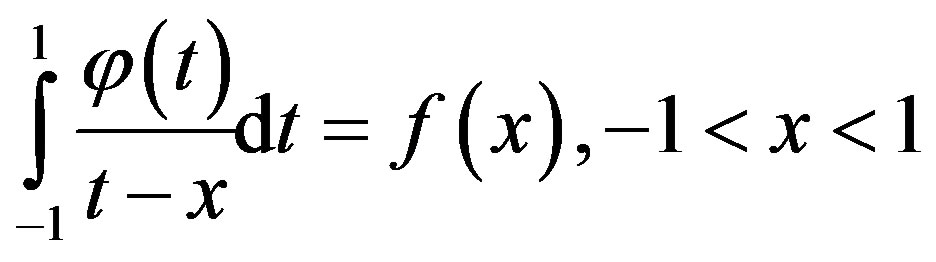 (1.2)
(1.2)
at  and
and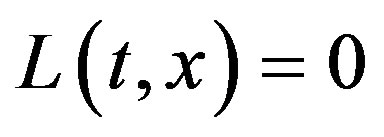 , for the following four cases:
, for the following four cases:
1) The solution is unbounded at both end-points 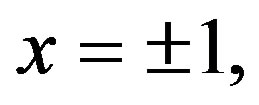
2) The solution is bounded at both end-points 
3) The solution is bounded at end  but unbounded at end
but unbounded at end 4) The solution is unbounded at end
4) The solution is unbounded at end 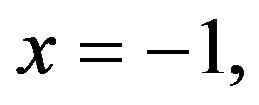 but bounded at end
but bounded at end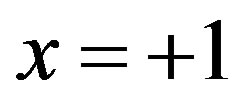 are given by [15] . In this paper the used approximate method for solving Equation (1.1) stems from recent work [10] wherein an approximate method has been developed to solve the simple Equation (1.2). The approximate method developed below appears to be quite appropriate for solving the most general type Equation (1.1). Some examples are presented to illustrate the method.
are given by [15] . In this paper the used approximate method for solving Equation (1.1) stems from recent work [10] wherein an approximate method has been developed to solve the simple Equation (1.2). The approximate method developed below appears to be quite appropriate for solving the most general type Equation (1.1). Some examples are presented to illustrate the method.
2. The Approximate Solution
In this section we present the method of the approximate solution of Equation (1.1) in four cases.
Let the unknown function  in Equation (1.1) be approximated by the polynomial function
in Equation (1.1) be approximated by the polynomial function
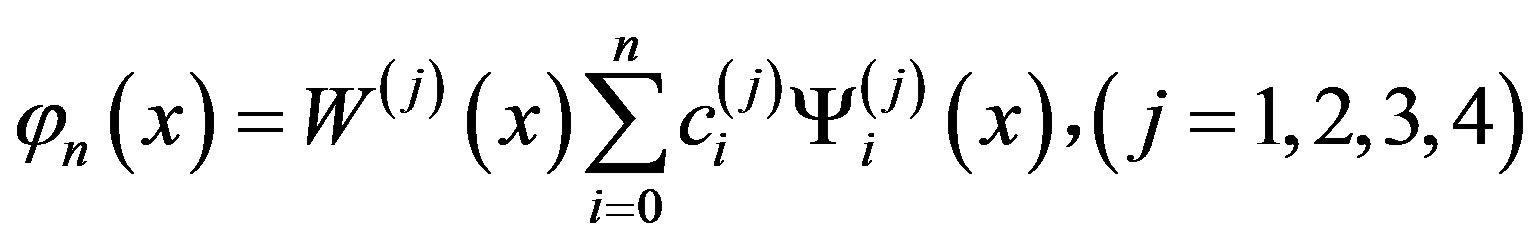 (2.1)
(2.1)
where  are unknown coefficients, to be determined, and in case (I):
are unknown coefficients, to be determined, and in case (I):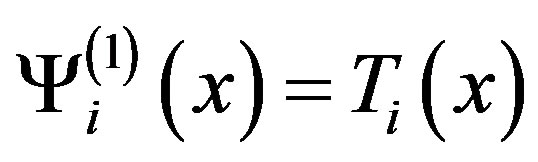 , in case (II):
, in case (II):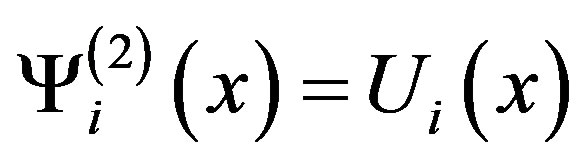 , in case (III):
, in case (III): 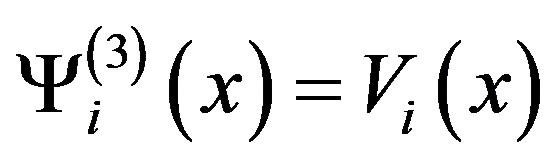 and in case (VI):
and in case (VI):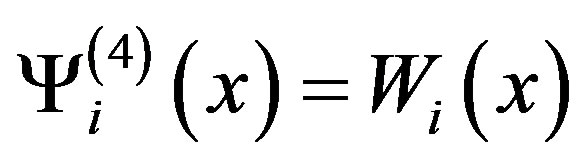 , where
, where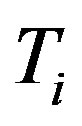 ,
, 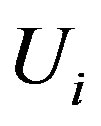 ,
, 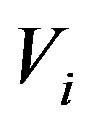 and
and  are The Chebyshev polynomials of the first, second, third and fourth kinds respectively can be defined by the recurrence relations [9] [16] .
are The Chebyshev polynomials of the first, second, third and fourth kinds respectively can be defined by the recurrence relations [9] [16] .
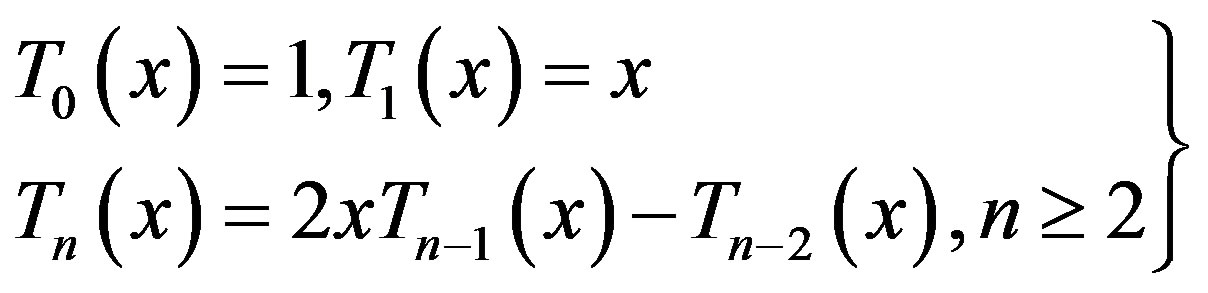 (2.2)
(2.2)
 (2.3)
(2.3)
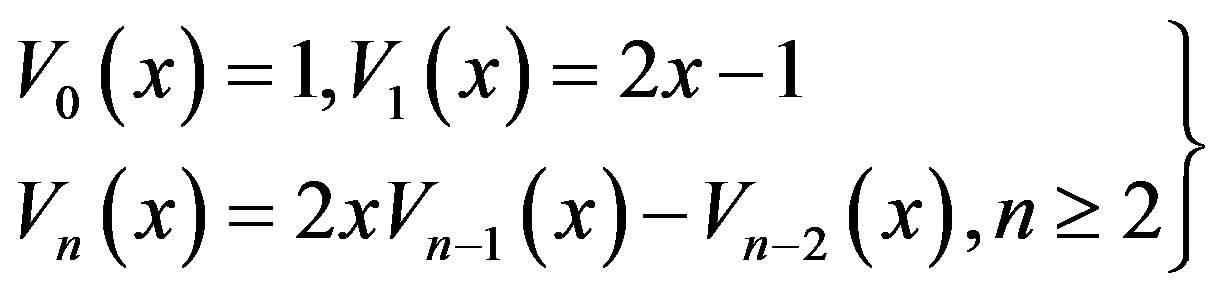 (2.4)
(2.4)
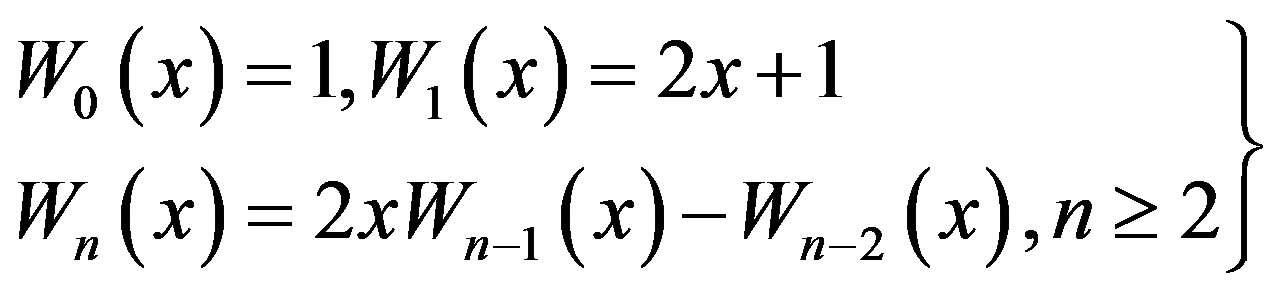 (2.5)
(2.5)
and 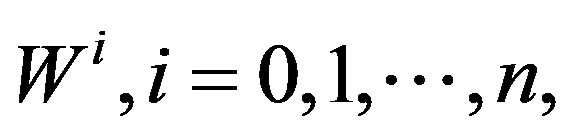 are the corresponding weight functions.
are the corresponding weight functions.
Substituting the approximate solution (2.1) for the unknown function into (1.1) yields
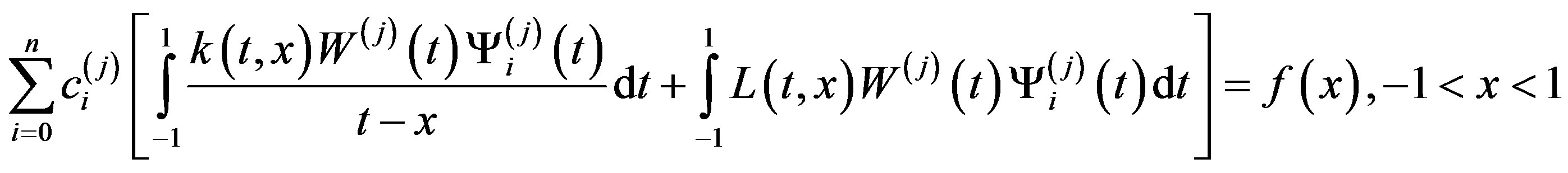 (2.6)
(2.6)
In above Equation (2.6), we next use the following Chebyshev approximation to the kernels 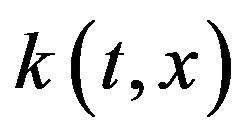 and
and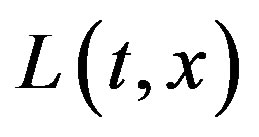 , given by (for fixed
, given by (for fixed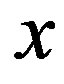 , cf. [7] )
, cf. [7] )
 (2.7)
(2.7)
with known expressions for  and
and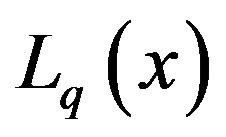 . Then (2.6) gives
. Then (2.6) gives
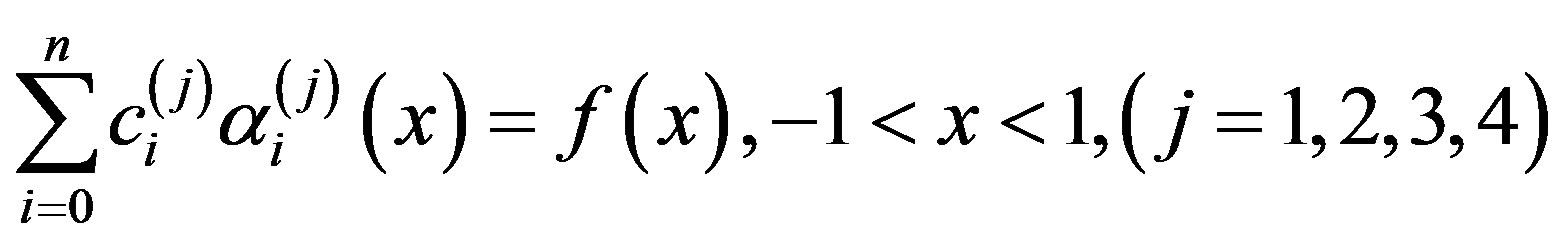 (2.8)
(2.8)
where
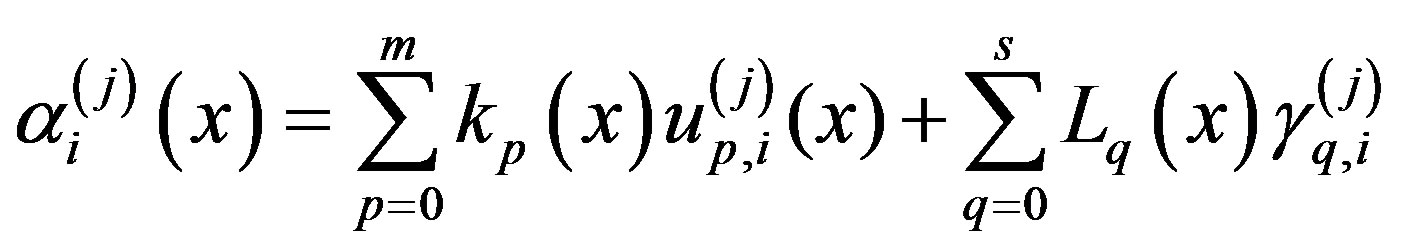 (2.9)
(2.9)
with
 (2.10)
(2.10)
and
 (2.11)
(2.11)
Let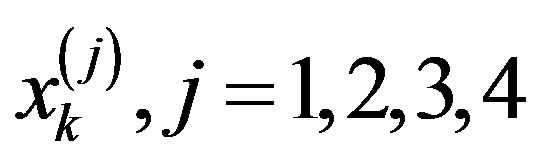 , be the zeros of
, be the zeros of  and
and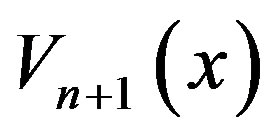 , respectively. Substituting the collocation points
, respectively. Substituting the collocation points 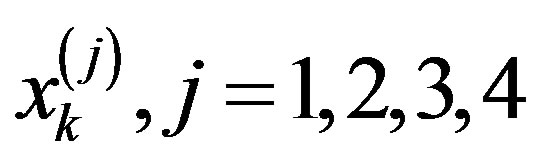 into (2.8) we obtain the following systems of linear equations:
into (2.8) we obtain the following systems of linear equations:
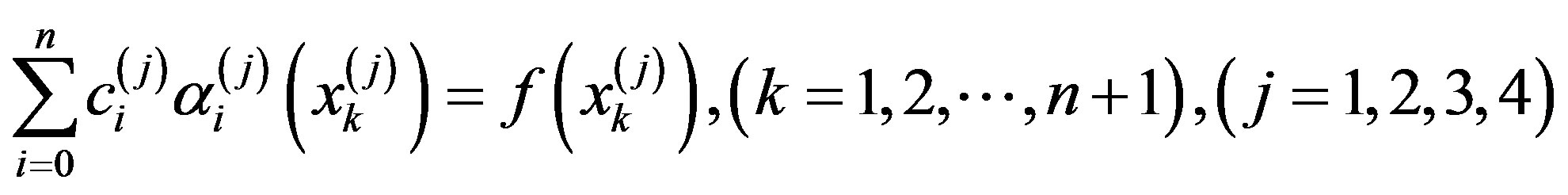 (2.12)
(2.12)
where
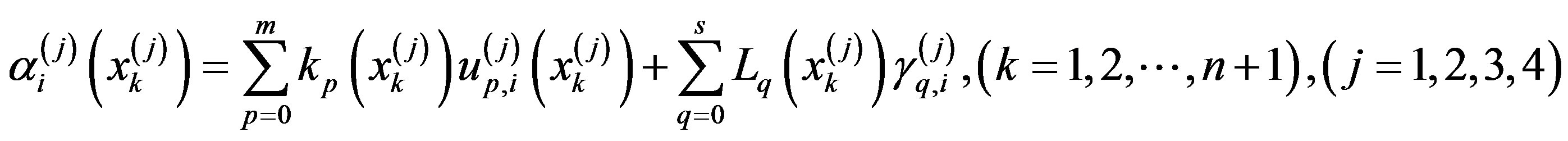 (2.13)
(2.13)
Solving the system of Equation (2.12) for the unknown coefficients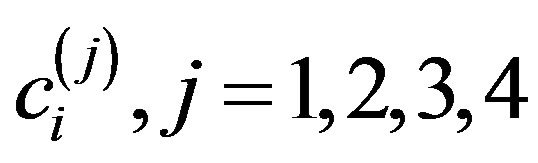 , and substituting the values of
, and substituting the values of 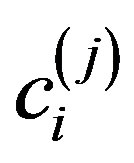 into (2.1) we obtain the approximate solutions of Equation (1.1).
into (2.1) we obtain the approximate solutions of Equation (1.1).
3. Numerical Examples
In this section, we consider some problems to illustrate the above method. All results were computed using FORTRAN code.
Example 1 Consider the following singular integral equation
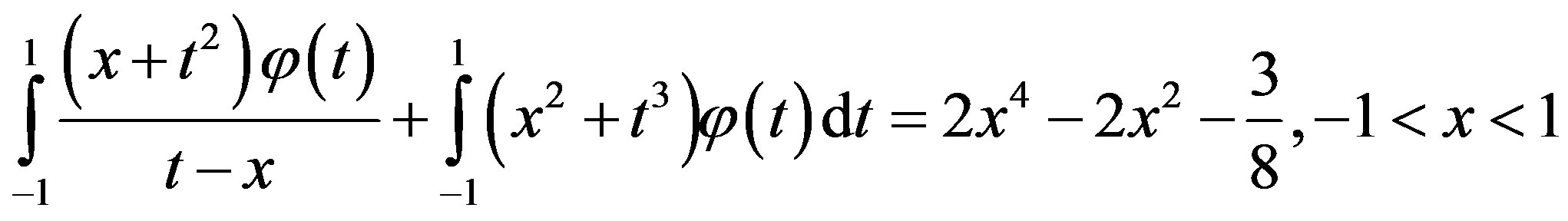 (3.1.1)
(3.1.1)
where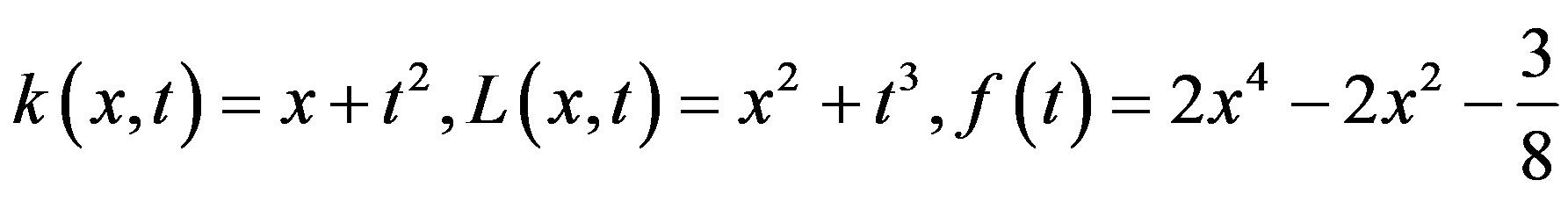 . So, one gets
. So, one gets
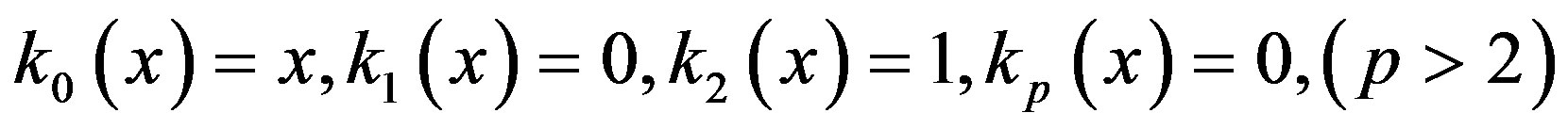

Hence we find that relation (2.8) produces
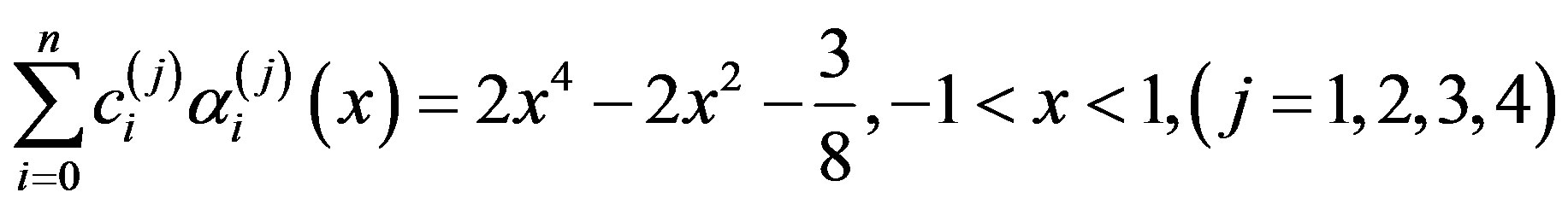
Thus (2.9) gives

Firstly, let us consider in detail the case (I), 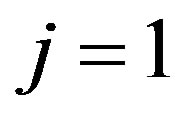 , for
, for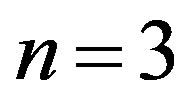 . This results in
. This results in
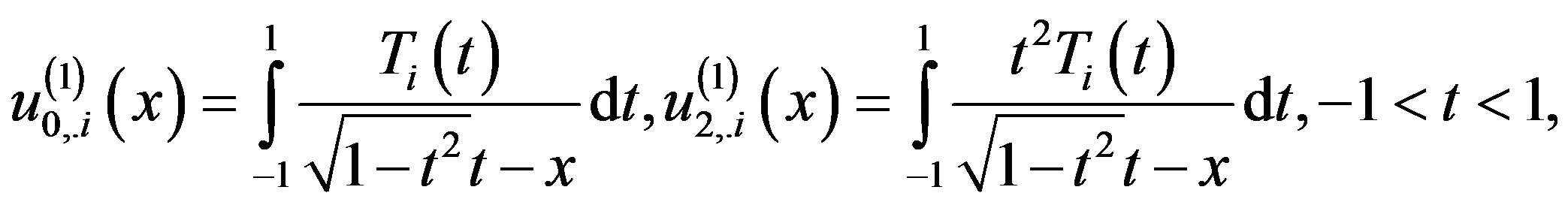 (3.1.2)
(3.1.2)
 (3.1.3)
(3.1.3)
By applying the following relations
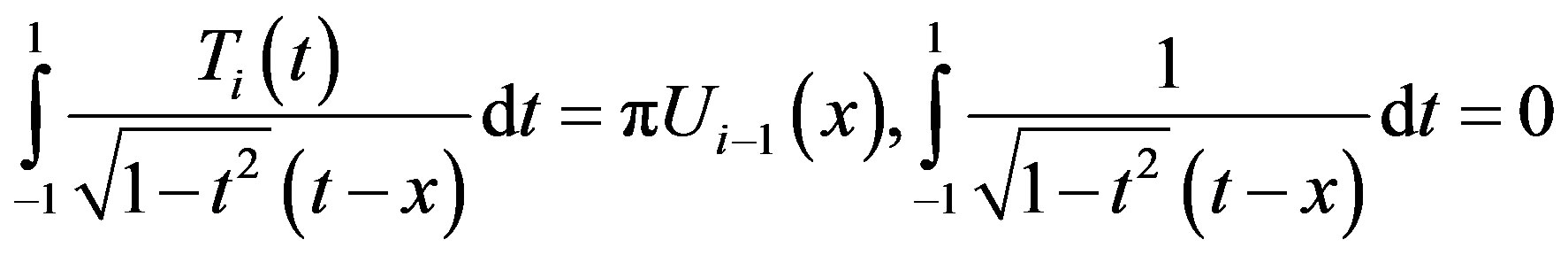 (3.1.4)
(3.1.4)
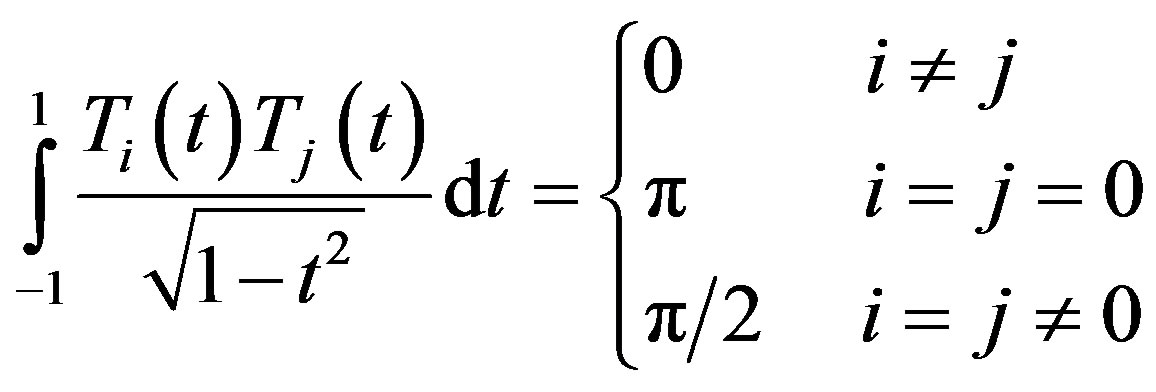 (3.1.5)
(3.1.5)
It is easy to estimate the values 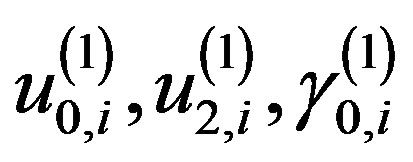 and
and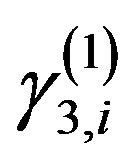 .
.
From (2.2) and (3.1.2)-(3.1.5) we get
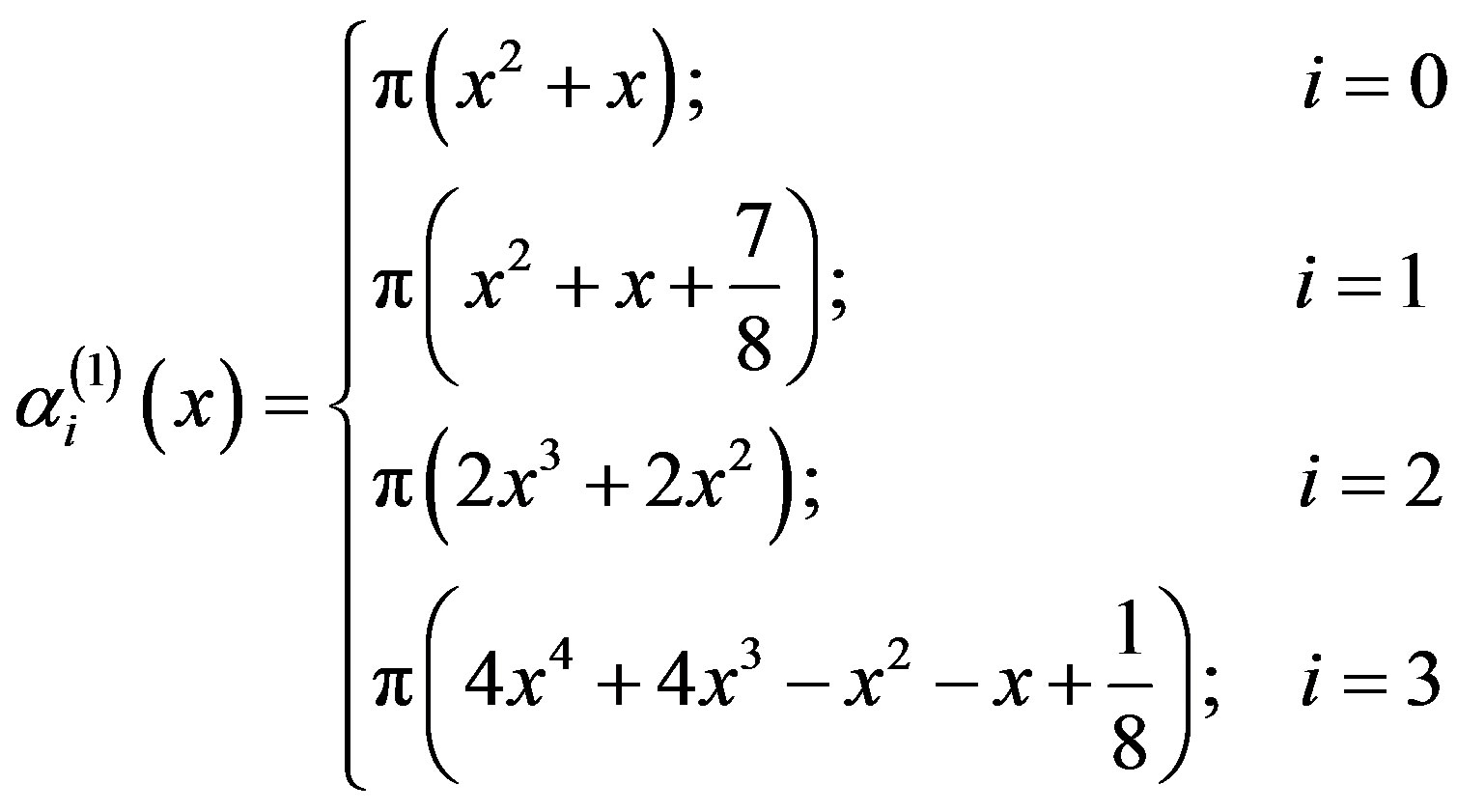 (3.1.6)
(3.1.6)
By choosing the collocation points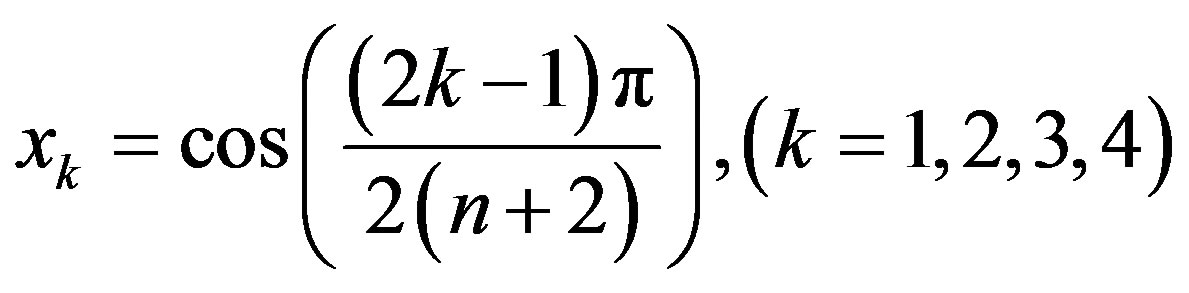 , for
, for 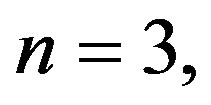 we obtain the following system of linear equations:
we obtain the following system of linear equations:

By solving this system for the unknown coefficients  that produces
that produces
 (3.1.7)
(3.1.7)
From (3.1.7) we obtain the approximate solution of Equation (3.1.1) in the form
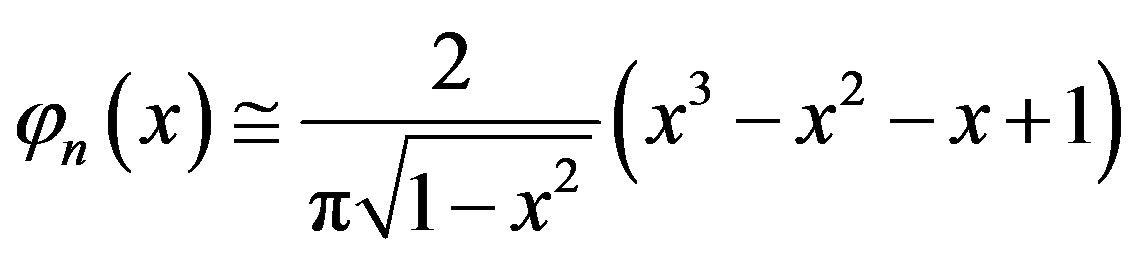 (3.1.8)
(3.1.8)
Which coincides with the exact solution. The error of approximate solution (3.1.8) of Equation (3.1.1) at 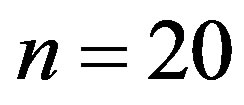 is given by Table 1.
is given by Table 1.
Secondly, let us consider in detail the case (II), 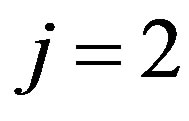 , for
, for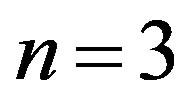 . This results in
. This results in
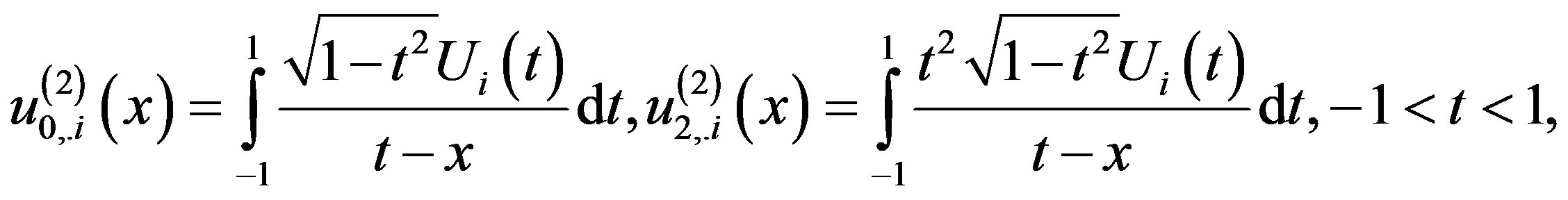 (3.1.9)
(3.1.9)
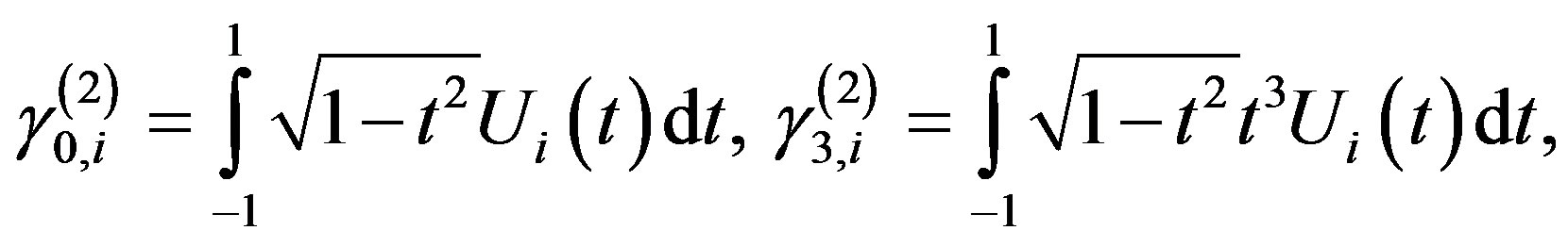 (3.1.10)
(3.1.10)
By applying the following relations
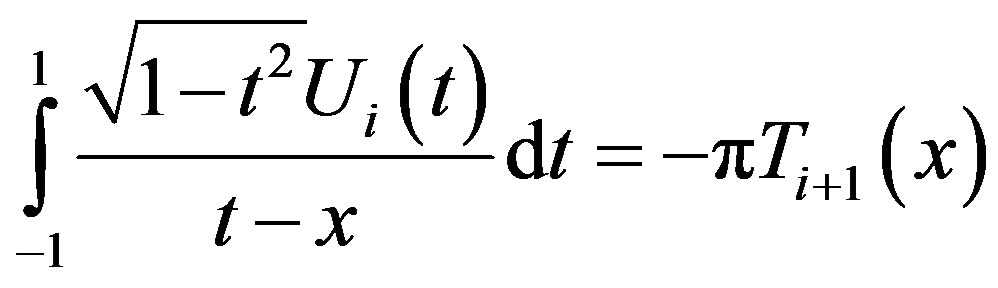 (3.1.11)
(3.1.11)
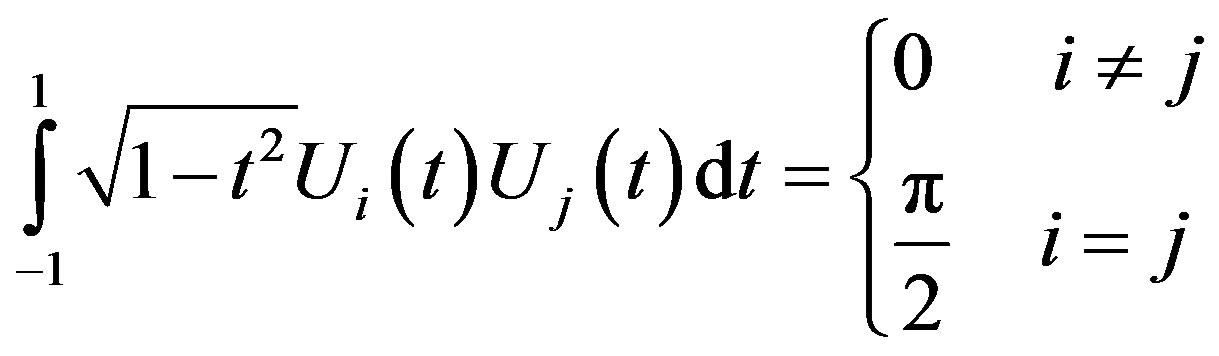 (3.1.12)
(3.1.12)
It is easy to estimate the values  and
and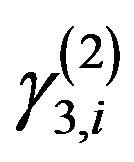 .
.
From the relations (2.3) and (3.1.9)-(3.1.12) we get
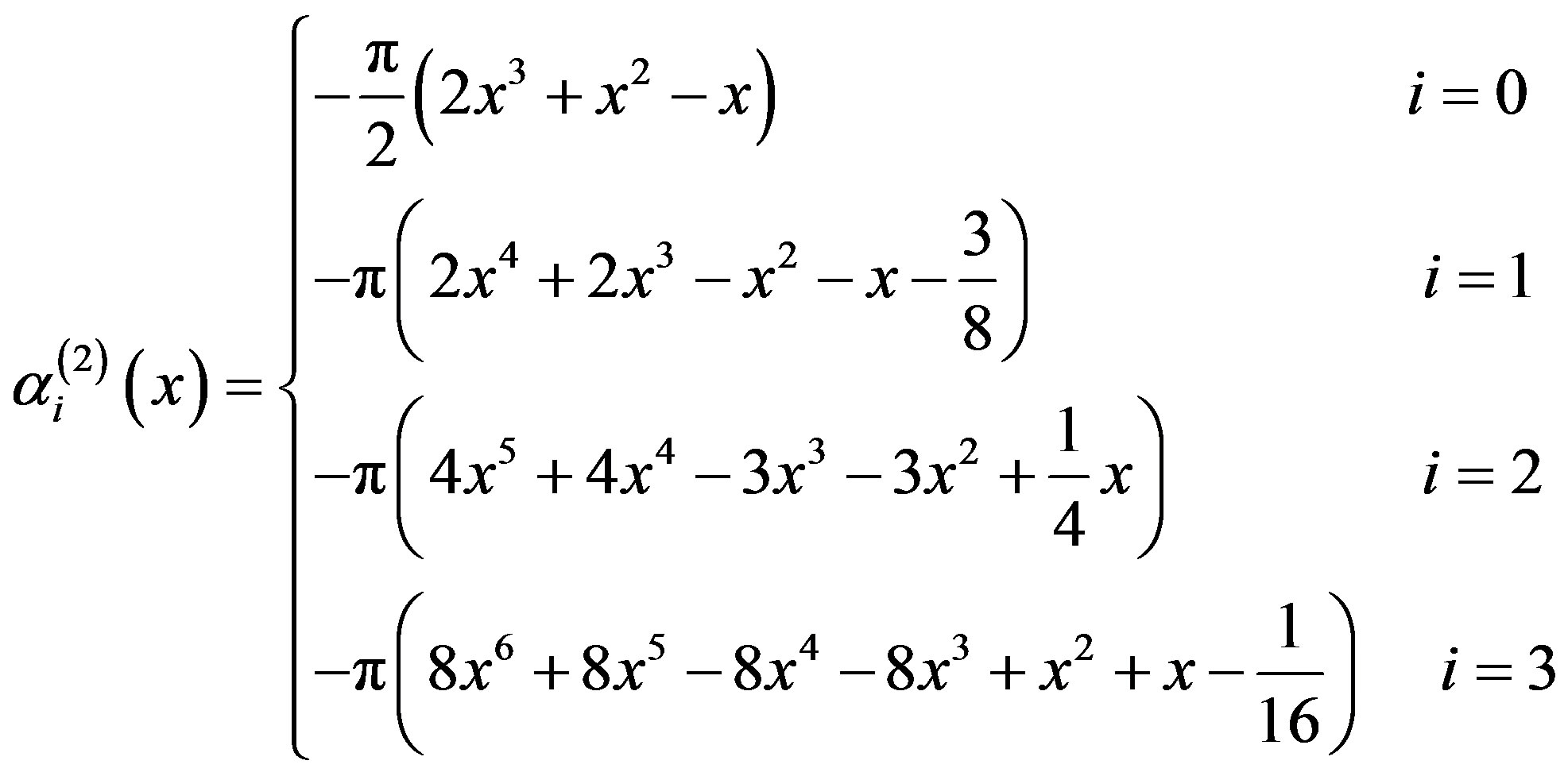 (3.1.13)
(3.1.13)
By choosing the collocation points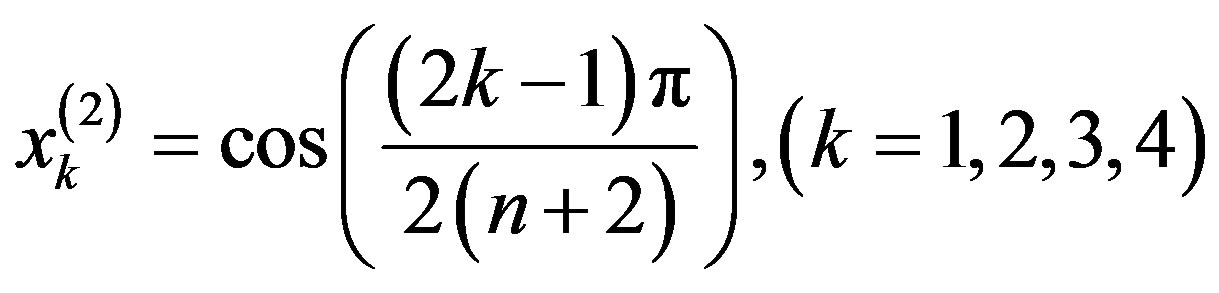 , for
, for 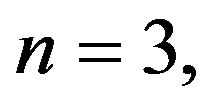 we obtain the following system of linear equations :
we obtain the following system of linear equations :
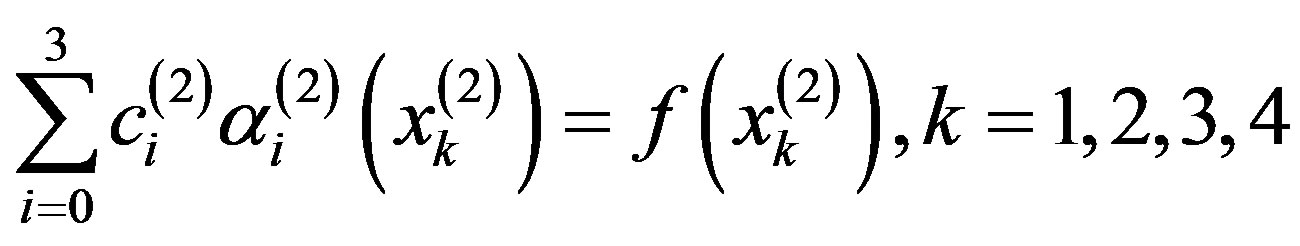
By solving this system for the unknown coefficients 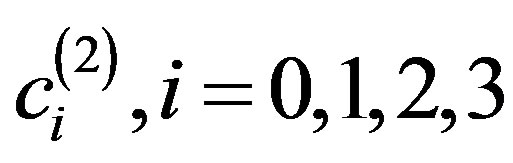 that produces
that produces
 (3.1.14)
(3.1.14)
From (3.1.14) we obtain the approximate solution of Equation (3.1.1) in the form
 (3.1.15)
(3.1.15)
Which coincides with the exact solution. The error of approximate solution (3.1.15) of Equation (3.1.1) at  is given by Table 1.
is given by Table 1.
Thirdly, let us consider in detail the case (III), 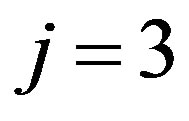 , for
, for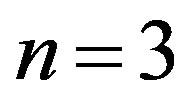 . This results in
. This results in
 (3.1.16)
(3.1.16)
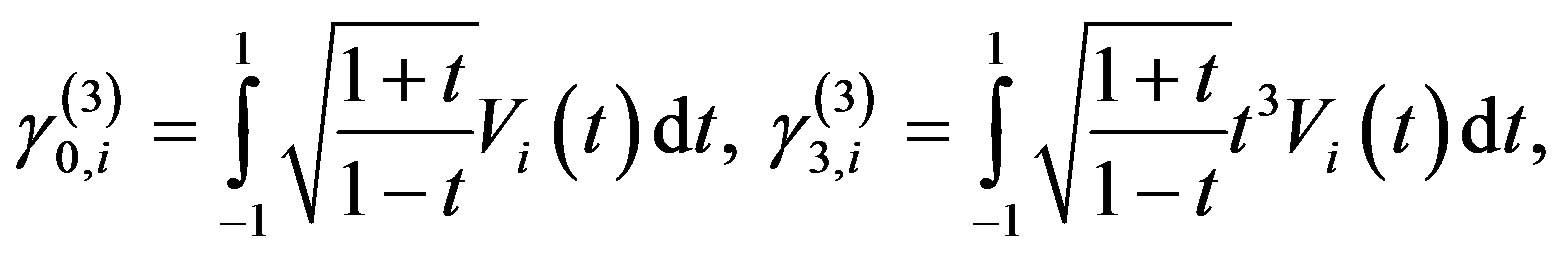 (3.1.17)
(3.1.17)
By applying the following relations
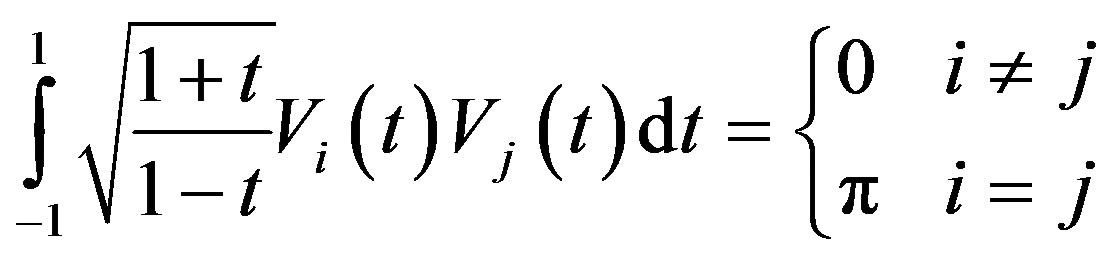 (3.1.18)
(3.1.18)
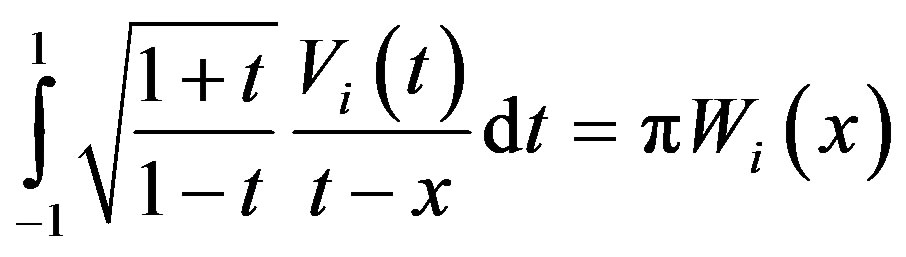 (3.1.19)
(3.1.19)
It is easy to estimate the values 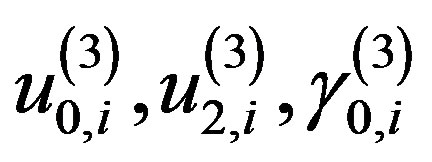 and
and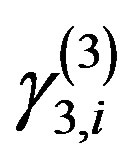 .
.
Table 1. Illustrates errors of approximate solutions of Equation (3.1.1) in Cases (I)-(IV) at n = 20.
From the relations (2.4) and (3.1.16)-(3.1.19) we get
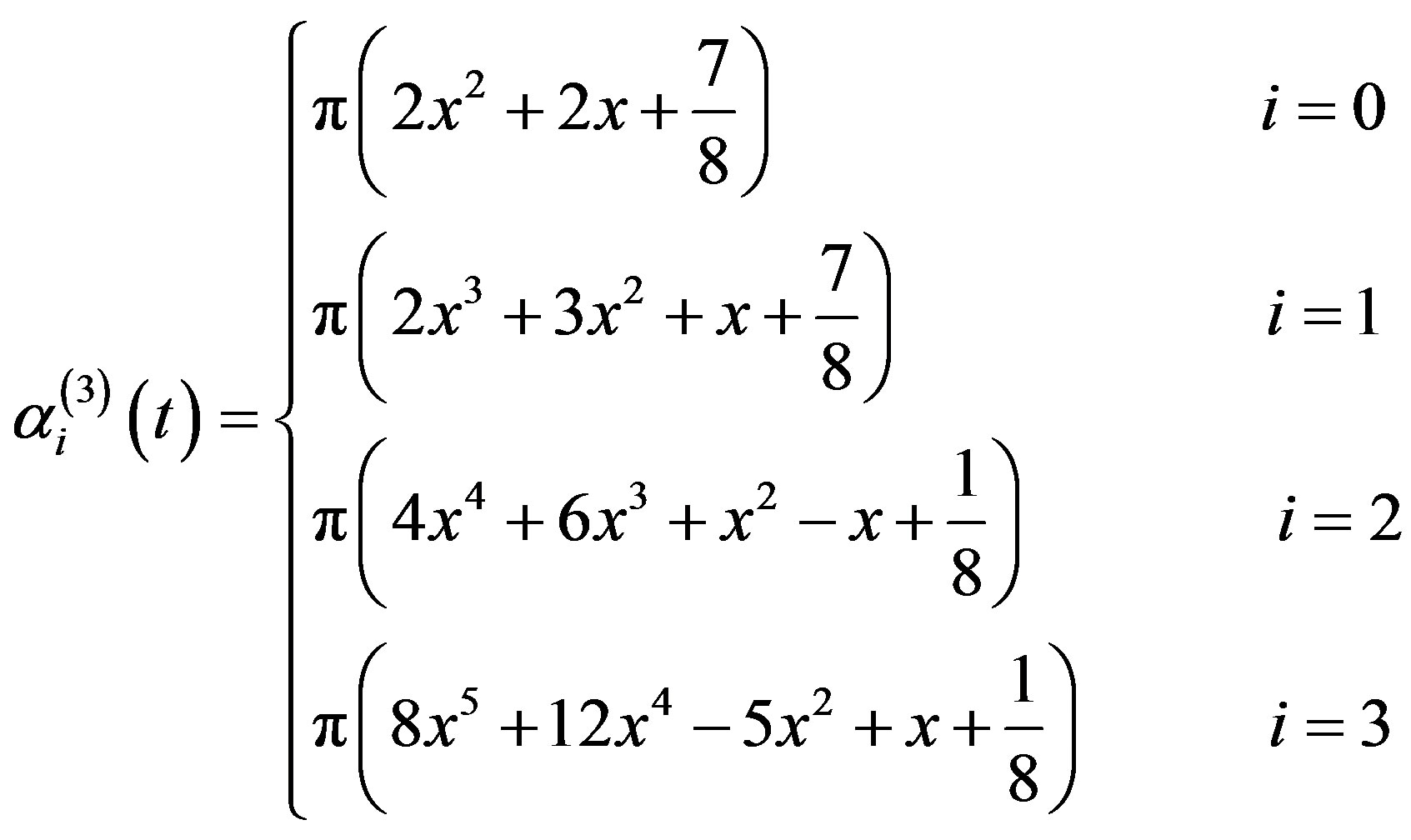 (3.1.20)
(3.1.20)
By choosing the collocation points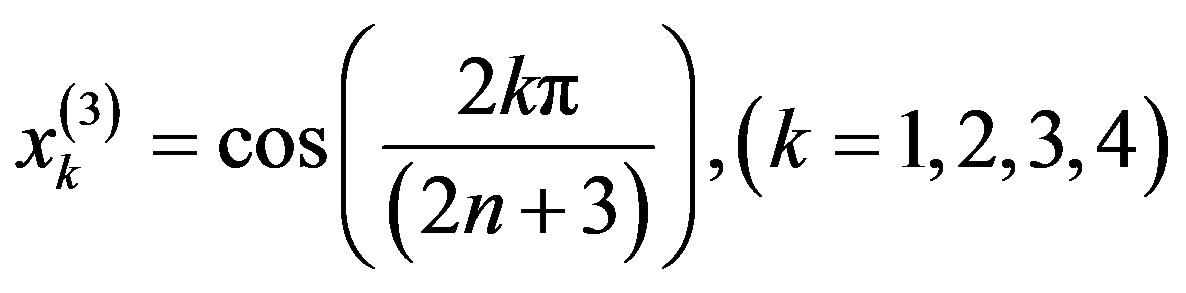 , for
, for 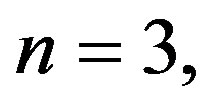 we obtain the following system of linear equations :
we obtain the following system of linear equations :

By solving this system for the unknown coefficients 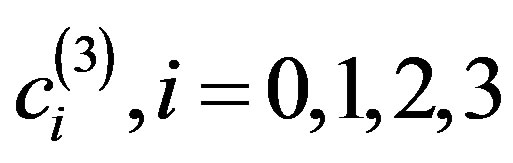 that produces
that produces
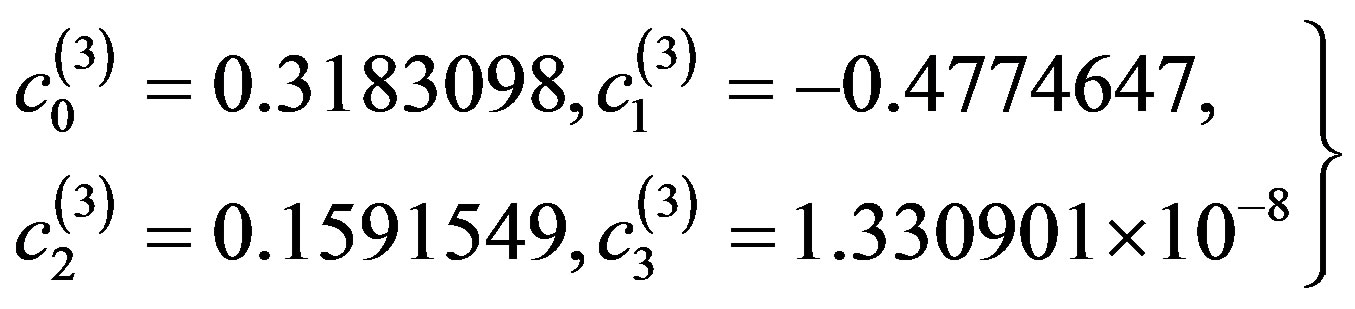 (3.1.21)
(3.1.21)
From (3.1.21) we obtain the approximate solution of Equation (3.1.1) in the form of
 (3.1.22)
(3.1.22)
Which coincides with the exact solution. The error of approximate solution (3.1.22) of Equation (3.1.1) at 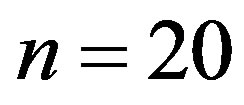 is given by Table 1.
is given by Table 1.
Fourthly, In case (IV),  , for
, for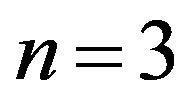 . This results in
. This results in
 (3.1.23)
(3.1.23)
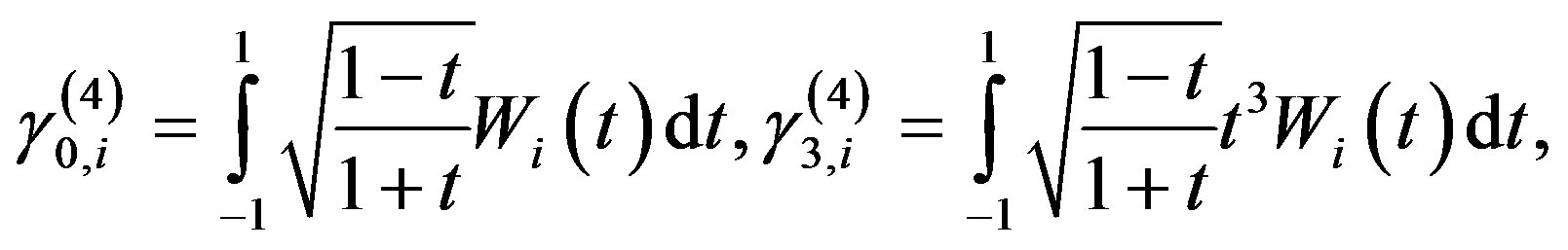 (3.1.24)
(3.1.24)
By applying the relations
 (3.1.25)
(3.1.25)
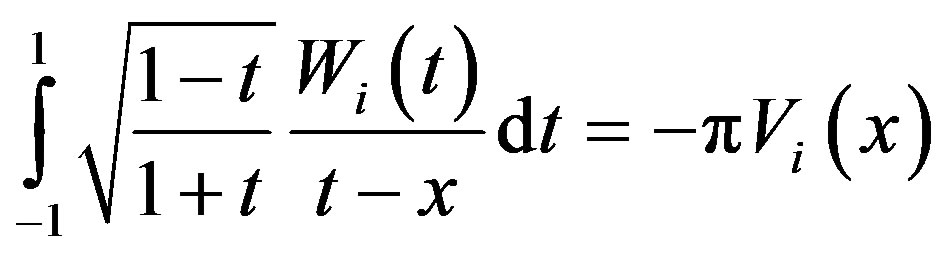 (3.1.26)
(3.1.26)
It is easy to estimate the values  and
and .
.
From the relations (2.5) and (3.1.23)-(3.1.26) we get
 (3.1.27)
(3.1.27)
By choosing the collocation points , for
, for 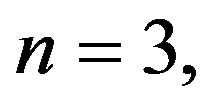 we obtain the following system of linear equations :
we obtain the following system of linear equations :
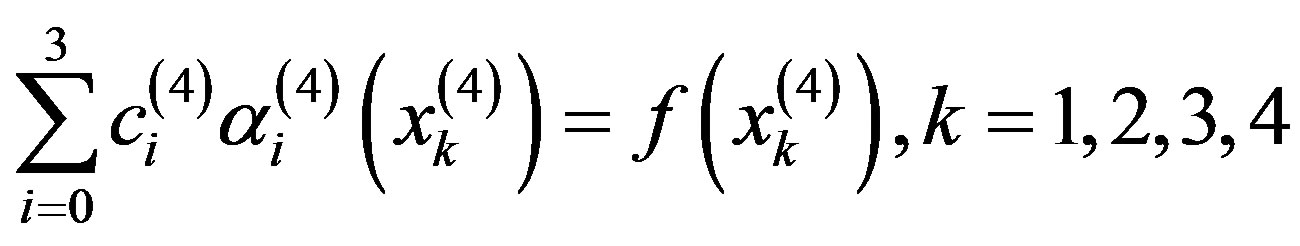
By solving this system for the unknown coefficients 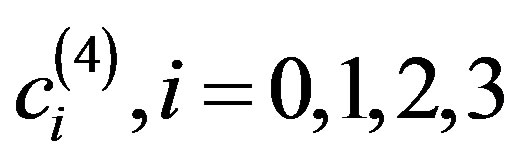 that produces
that produces
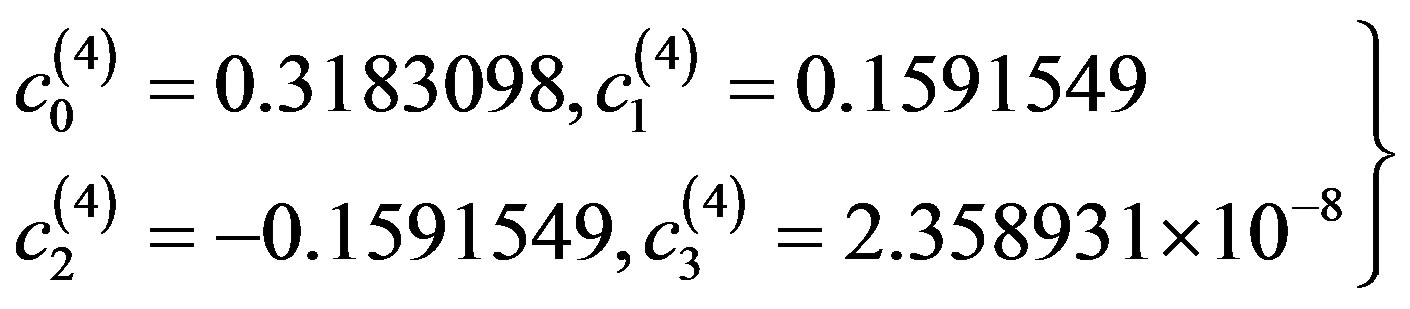 (3.1.28)
(3.1.28)
From (3.1.28) we obtain the approximate solution of Equation (3.1.1) in the form of
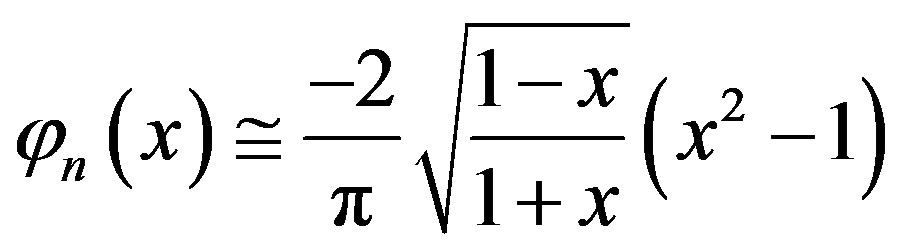 (3.1.29)
(3.1.29)
which coincides with the exact solution. The error of approximate solution (3.2.29) of Equation (3.2.1) at 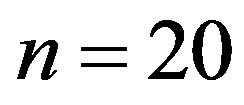 is given by Table 1.
is given by Table 1.
Example 2. Consider the following singular integral equation
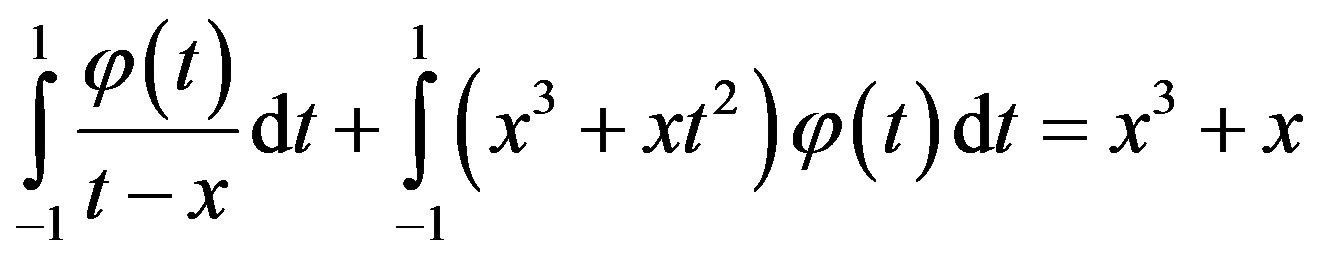 (3.2.1)
(3.2.1)
which corresponds with 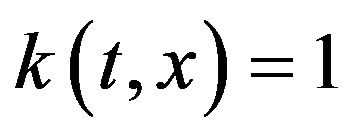 and
and . So one gets
. So one gets
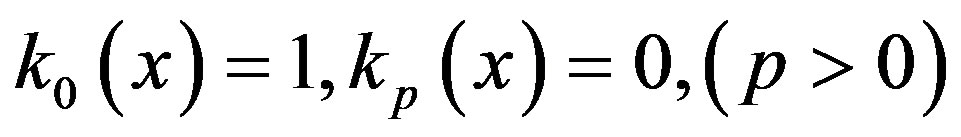
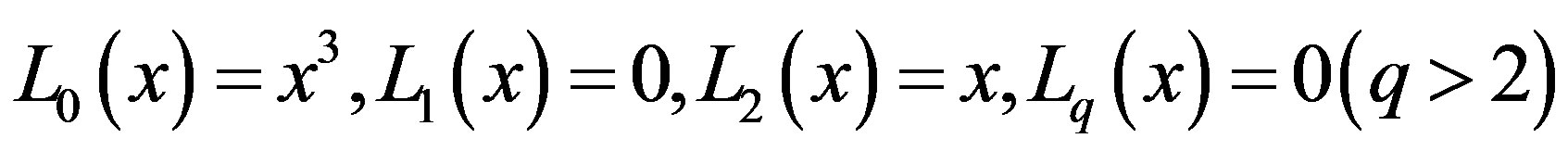
Hence we find that relation (2.8) produces
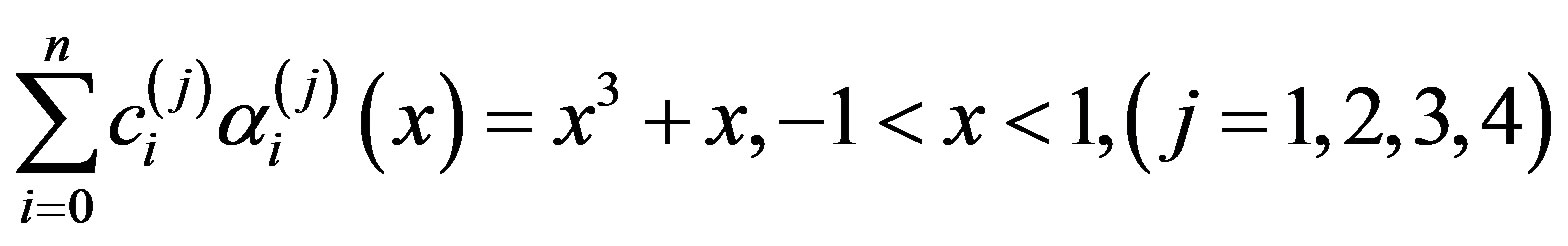
Thus (2.9) gives

Firstly, let us consider in detail the case (I), 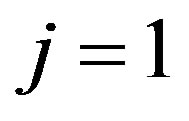 , for
, for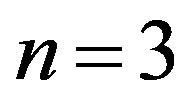 . This results in
. This results in
 (3.2.2)
(3.2.2)
From the relations (3.1.2)-(3.1.5) and (3.2.2) we obtain
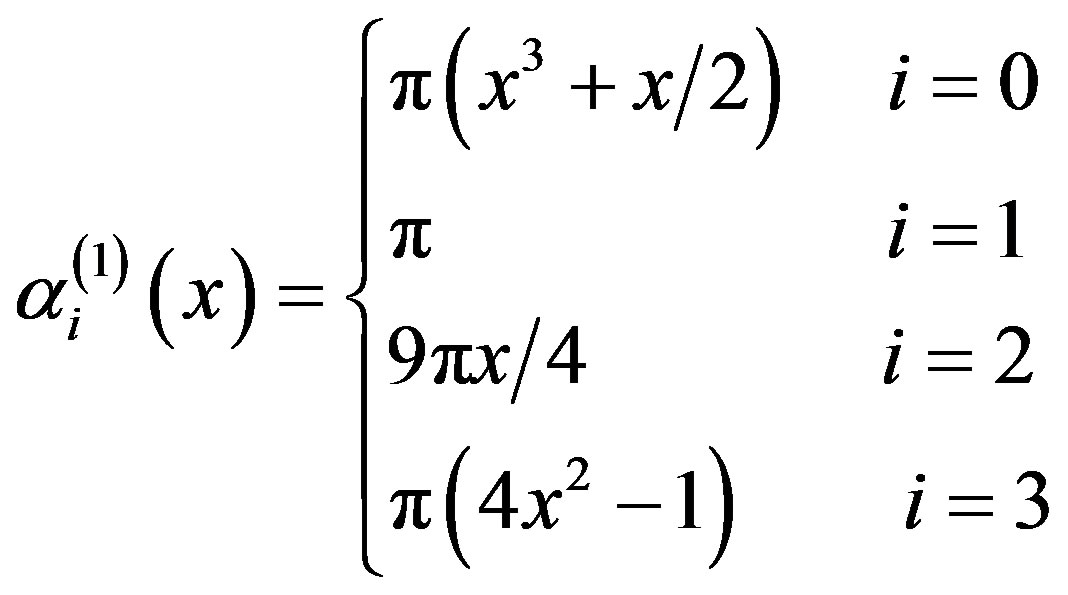 (3.2.3)
(3.2.3)
By choosing the collocation points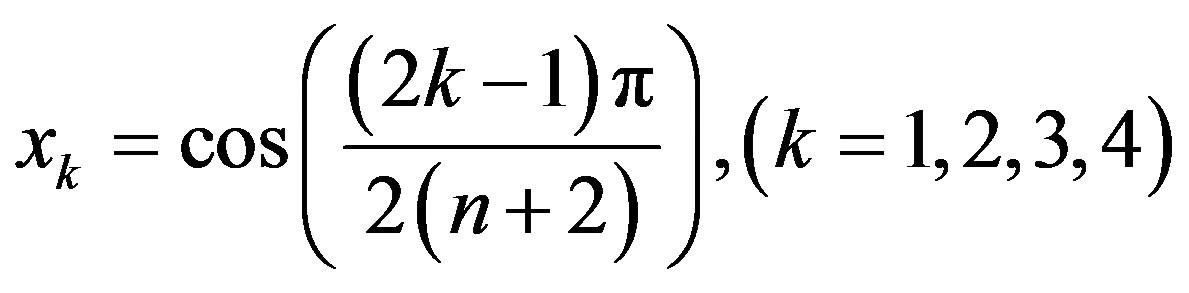 , for
, for 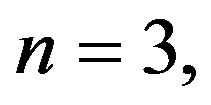 we obtain the following system of linear equations :
we obtain the following system of linear equations :

By solving this system for the unknown coefficients 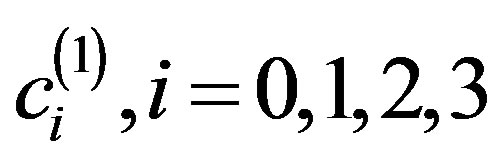 that produces
that produces
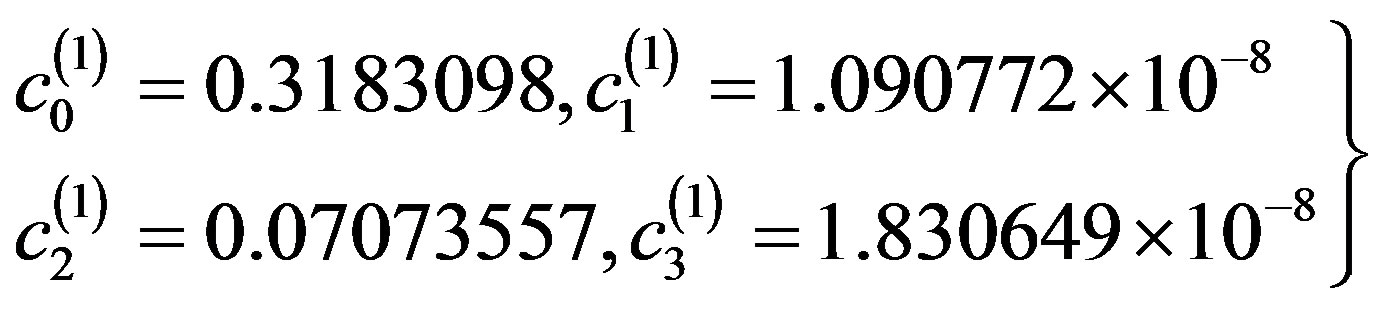 (3.2.4)
(3.2.4)
From (3.2.4) we obtain the approximate solution of Equation (3.2.1) in the form of
 (3.2.5)
(3.2.5)
which coincides with the exact solution. The error of approximate solution (3.2.5) of equation (3.2.1) at  is given by Table 2.
is given by Table 2.
Secondly, let us consider in detail the case (II), 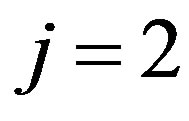 , for
, for . This results in
. This results in
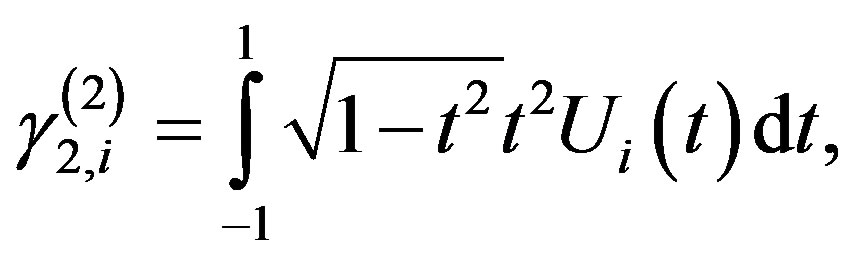 (3.2.6)
(3.2.6)
By applying the relations (3.1.9)-(3.1.12) and (3.2.6) we get
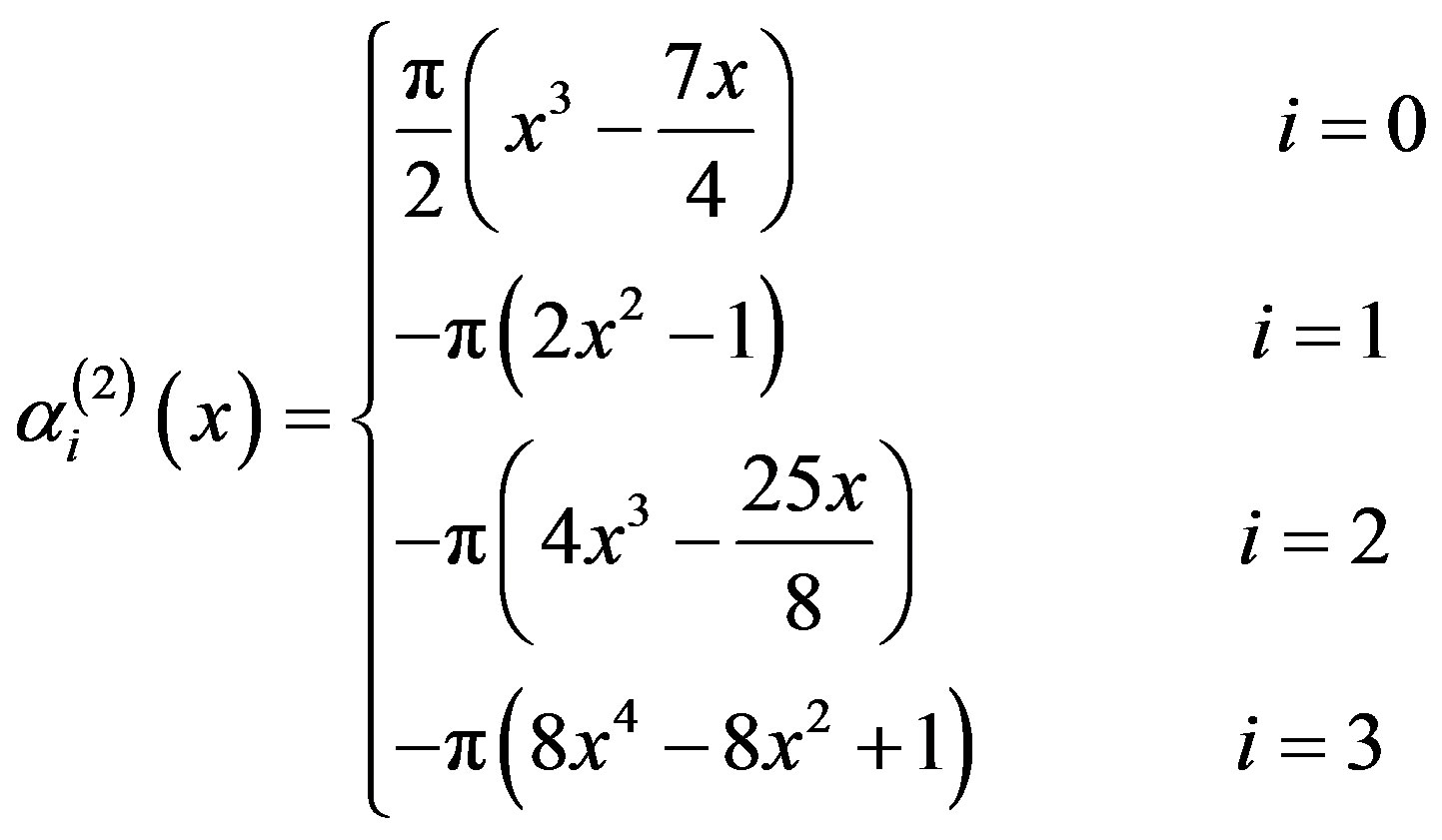 (3.2.7)
(3.2.7)
By choosing the collocation points , for
, for 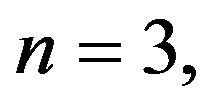 we obtain the following
we obtain the following
Table 2. Illustrates errors of approximate solutions of Equation (3.2.1) in Case (I), Case (II) and Case (IV) respectively at n = 20.
system of linear equations:
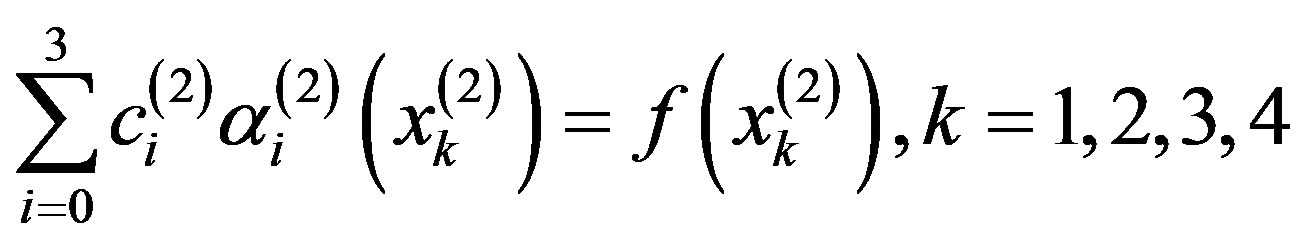
By solving this system for the unknown coefficients 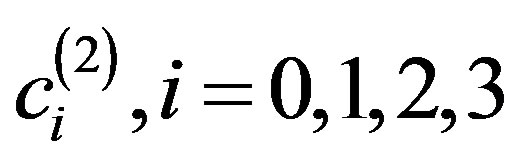 that produces
that produces
 (3.2.8)
(3.2.8)
From (3.2.8) we obtain the approximate solution of Equation (3.2.1) in the form of
 (3.2.9)
(3.2.9)
which coincides with the exact solution. The error of approximate solution (3.2.9) of Equation (3.2.1) at 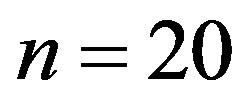 is given by Table 2.
is given by Table 2.
Thirdly, In case (IV), 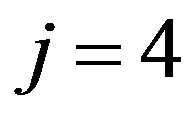 , for
, for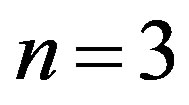 . This results in
. This results in
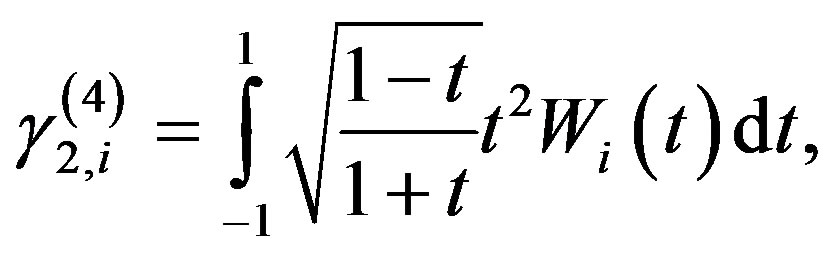 (3.2.10)
(3.2.10)
By applying the relations (3.1.23)-(3.1.26) and (3.2.10) we get
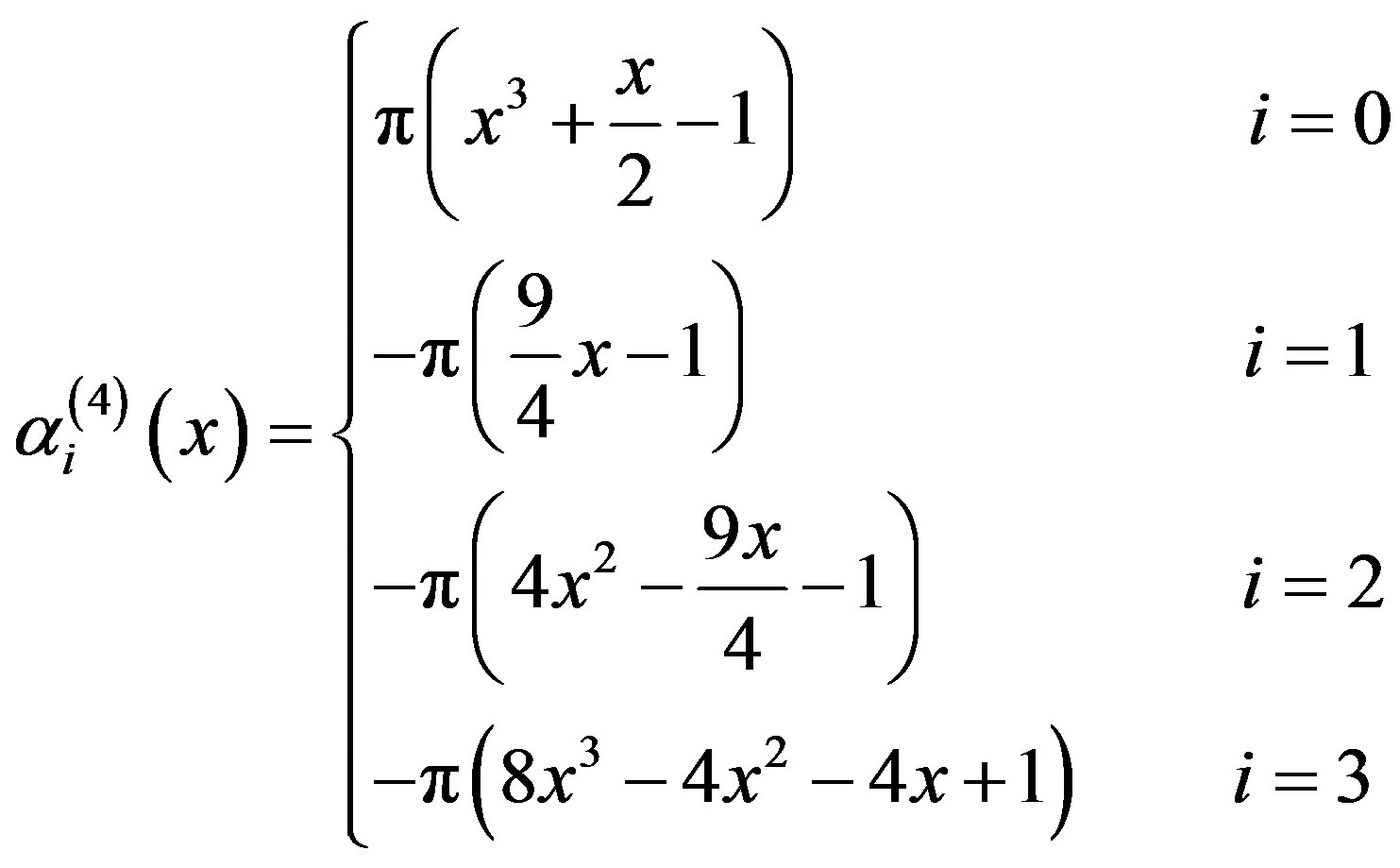 (3.2.11)
(3.2.11)
By choosing the collocation points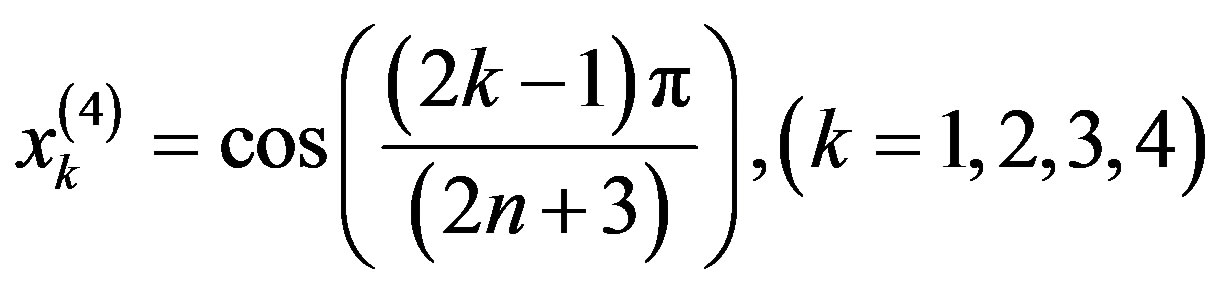 , for
, for  we obtain the following system of linear equations:
we obtain the following system of linear equations:

By solving this system for the unknown coefficients 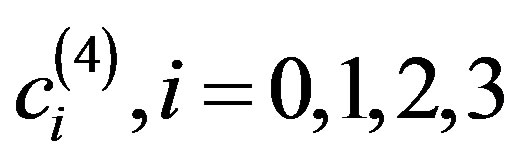 that produces
that produces
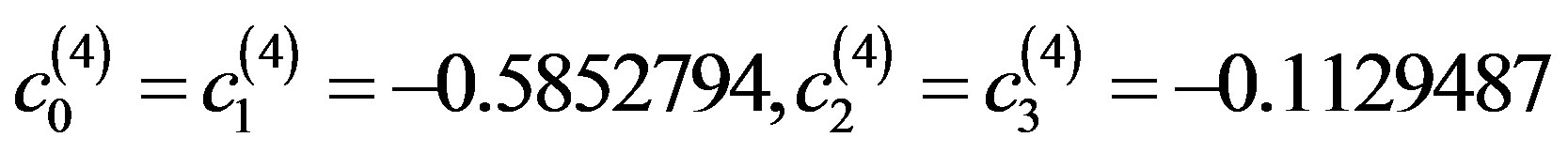 (3.2.12)
(3.2.12)
From (3.2.12) we obtain the approximate solution of Equation (3.2.1) in the form of
 (3.2.13)
(3.2.13)
which coincides with the exact solution. The error of approximate solution (3.2.13) of Equation (3.2.1) at 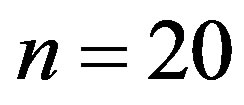 is given by Table 2.
is given by Table 2.
Similarly, doing the same operations as we did for Case (I), Case (II) and Case (IV), one can solve for Case (III) .
Example 3. Consider the following singular integral equation
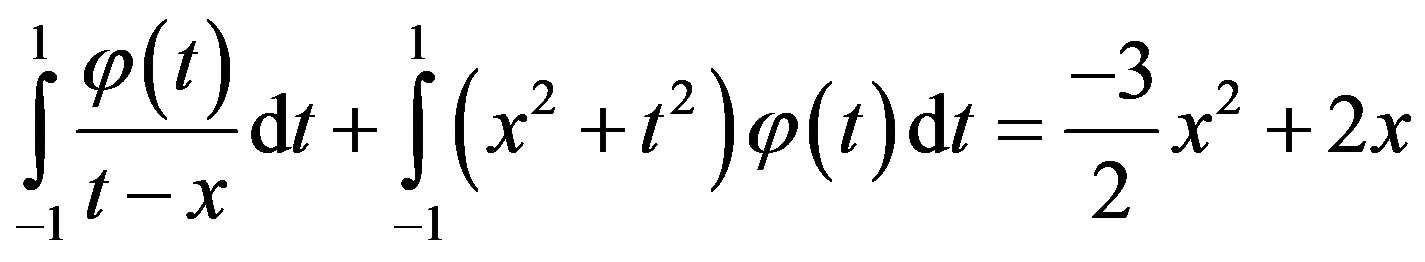 , (3.3.1)
, (3.3.1)
which corresponds with 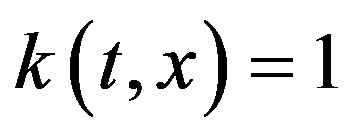 and
and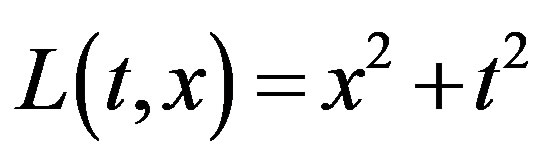 . So, one gets
. So, one gets
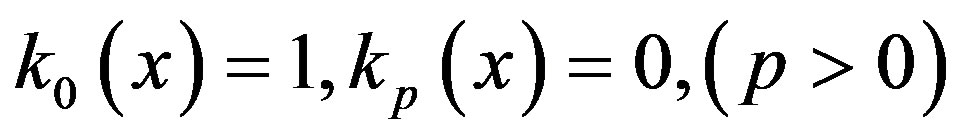
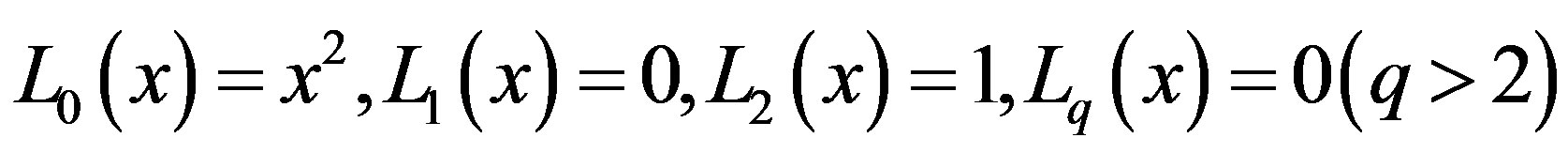
Hence the relation (2.8) produces
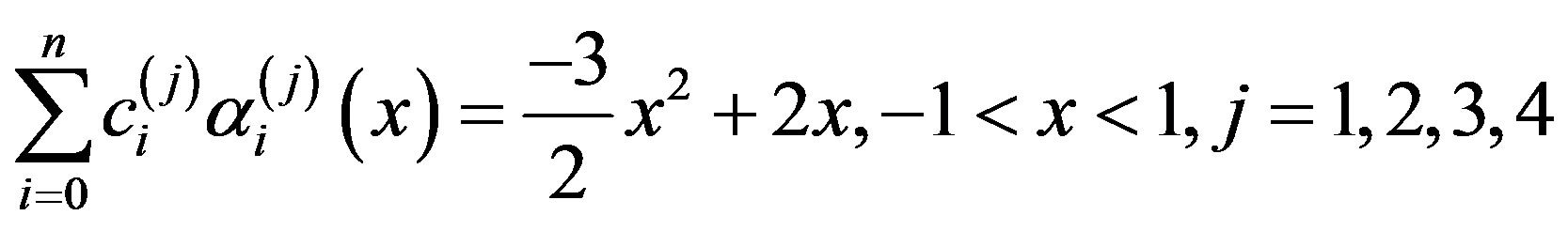 (3.3.2)
(3.3.2)
where (2.9) gives

Firstly, let us consider in detail the case (II), 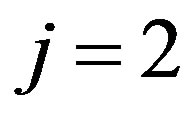 , for
, for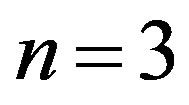 . From (3.1.9)-(3.1.12) and (3.2.6) we get
. From (3.1.9)-(3.1.12) and (3.2.6) we get
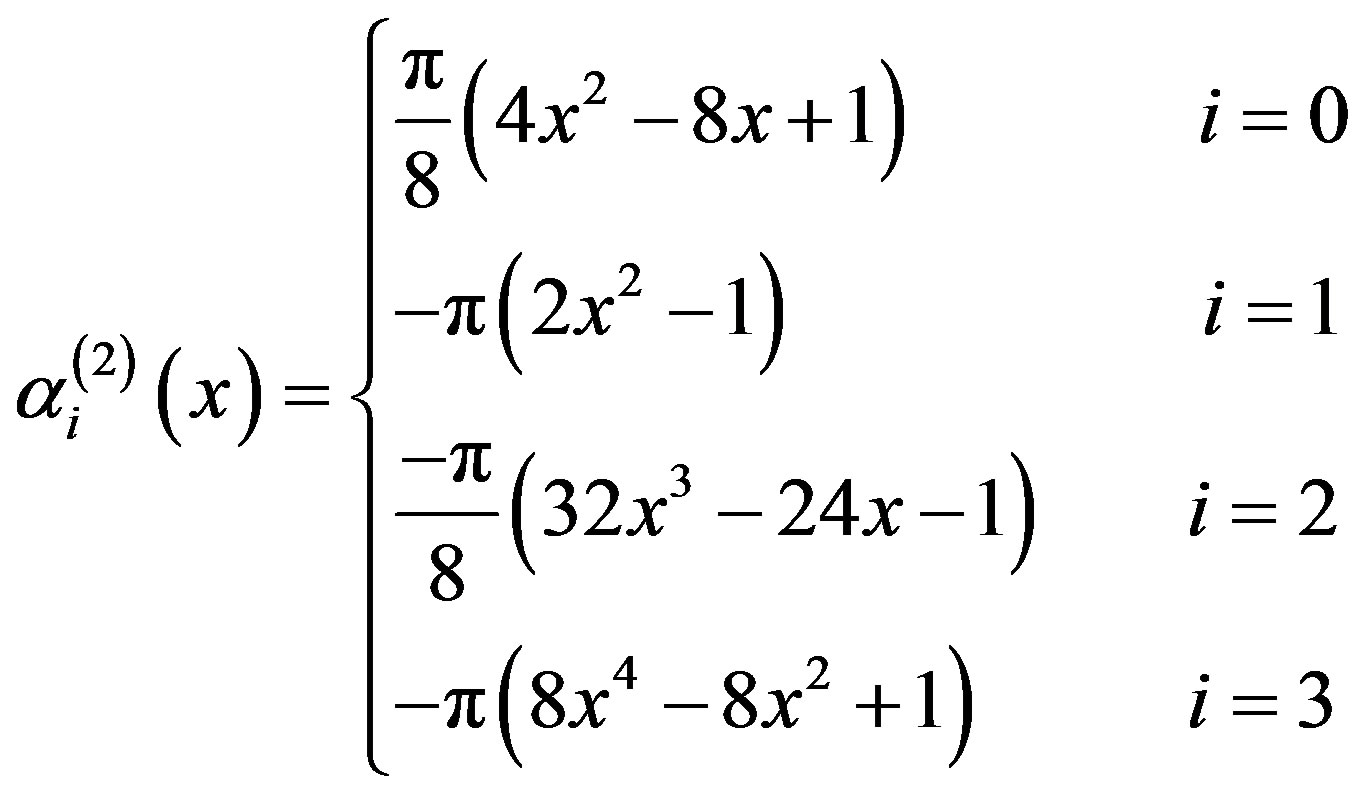 (3.3.3)
(3.3.3)
By solving the system (3.3.2), at the collocation points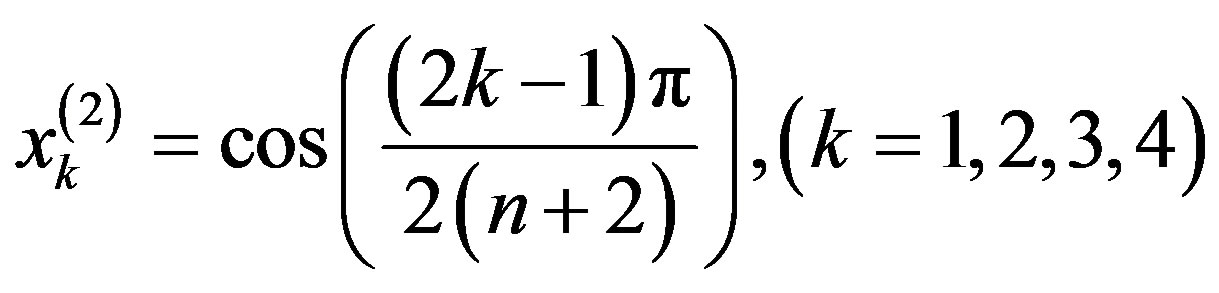 , for the unknown coefficients
, for the unknown coefficients 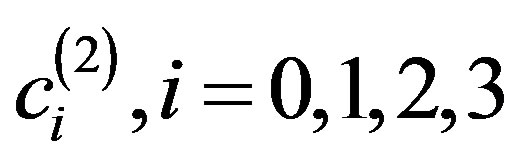 we obtain
we obtain
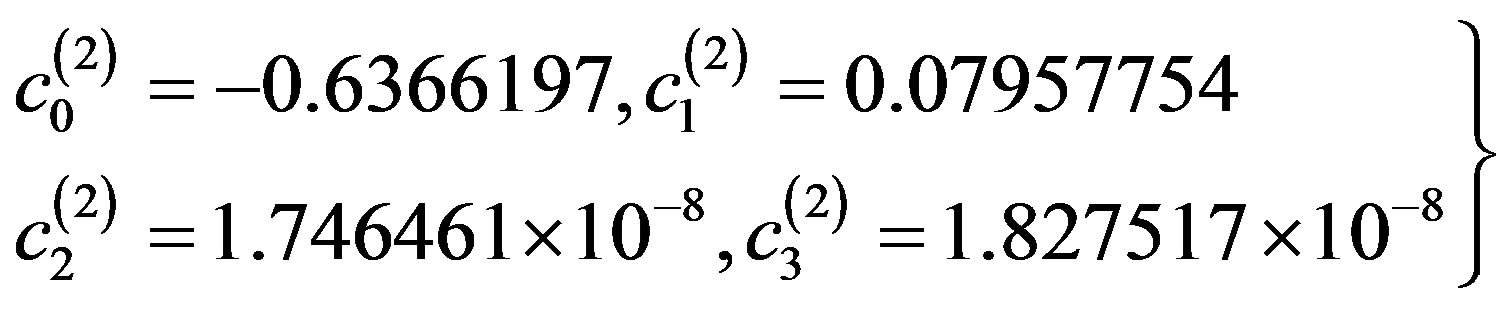 (3.3.4)
(3.3.4)
So the approximate solution of Equation (3.3.1) is given by
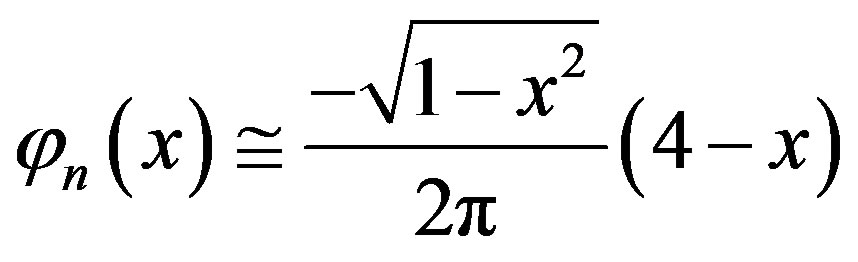 , (3.3.5)
, (3.3.5)
which coincides with the exact solution, the error of the approximate solution (3.3.5) of Equation (3.3.1) at  is given by Table 3.
is given by Table 3.
Secondly, in case (III),  , for
, for . This results in
. This results in
 (3.3.6)
(3.3.6)
From (3.1.16)-(3.1.19) and (3.3.6) we get
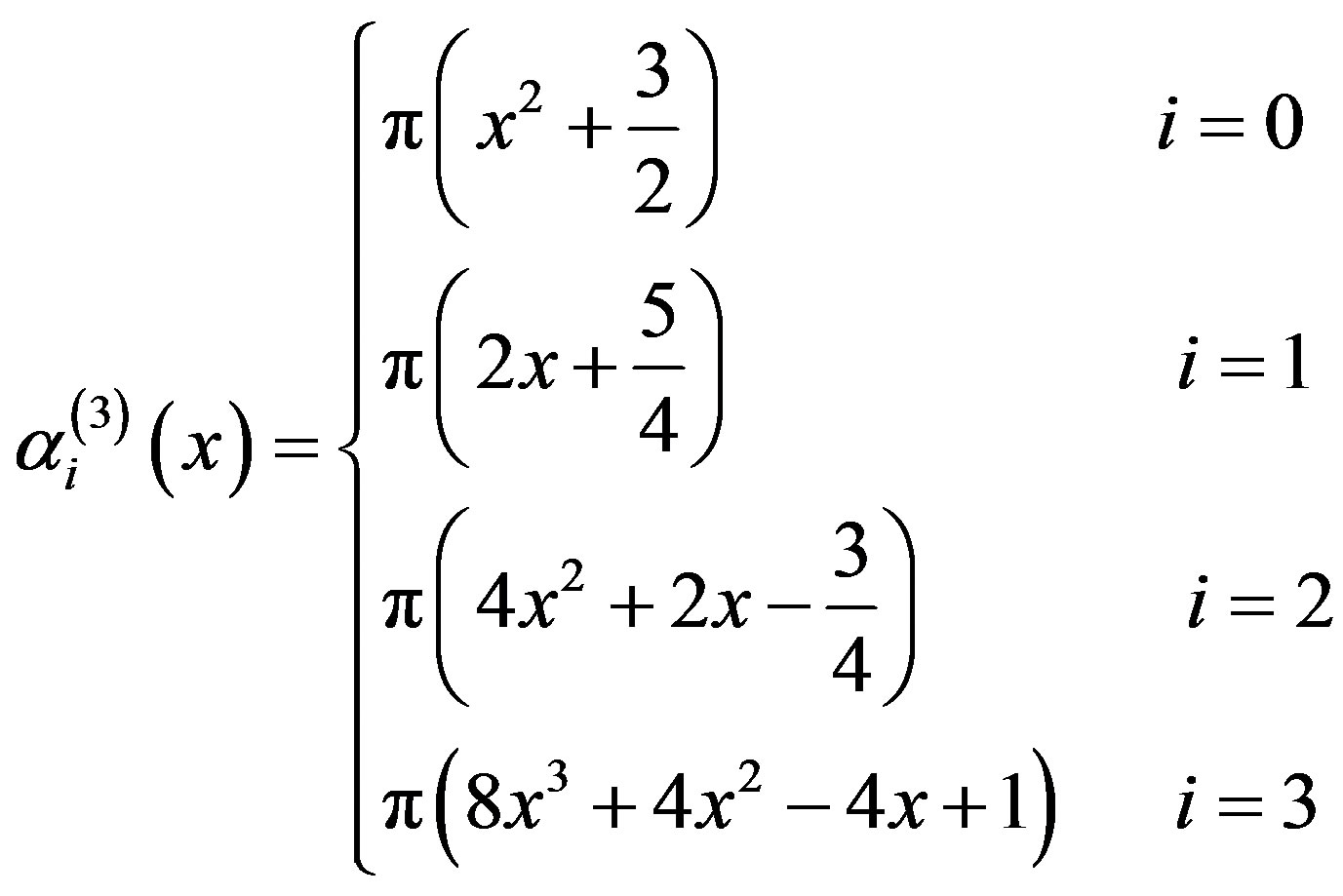 (3.3.7)
(3.3.7)
By solving the system (3.3.2), at the collocation points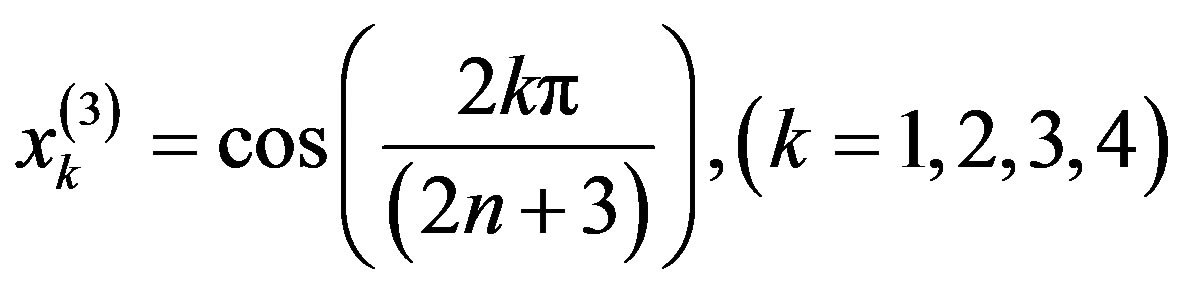 , for the unknown coefficients
, for the unknown coefficients  we obtain
we obtain
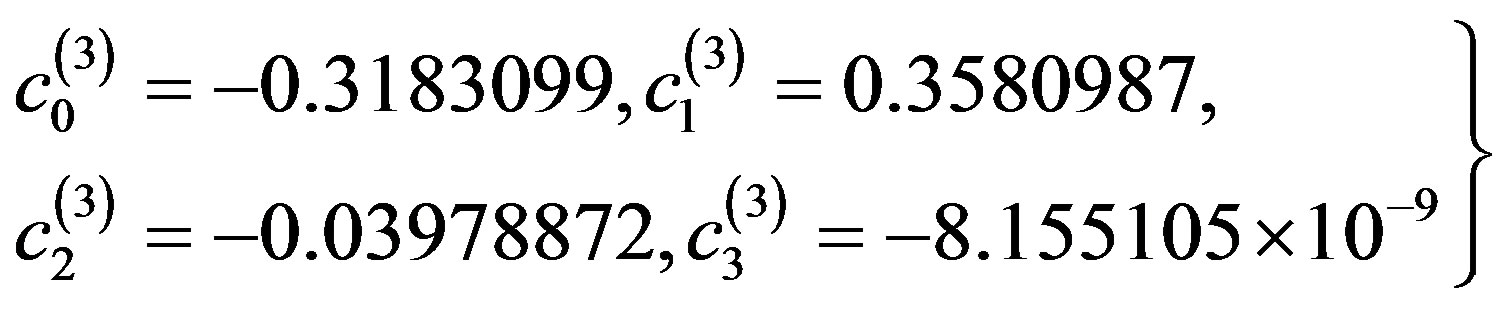 (3.3.8)
(3.3.8)
Hence, the approximate solution of Equation (3.3.1) is given by
 (3.3.9)
(3.3.9)
which coincides with the exact solution, the error of the approximate solution (3.3.9) of Equation (3.3.1) at 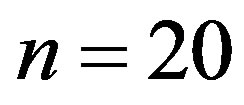 is given by Table 3.
is given by Table 3.
Table 3. Illustrates errors of approximate solutions of Equation (3.3.1) in Case (II) and Case (III) at n = 20.
Similarly, doing the same operations as we did for Case (II) and Case (III), one can solve for Case (I) and Case (IV).
4. Conclusion
Numerical results (Tables 1-3) show that the errors of approximate solutions of Examples 1-3 in different Cases with small value of n are very small. These show that the methods developed are very accurate and in fact for a linear function give the exact solution.
References
- Chakrabarti, A. (1989) Solution of Two Singular Integral Equations Arising in Water Wave Problems. ZAMM, 69, 457-459. http://dx.doi.org/10.1002/zamm.19890691209
- Ladopoulous, E.G. (2000) Singular Integral Equations Linear and Non-Linear Theory and Its Applications in Science and Engineering. Springer, Berlin.
- Ladopoulous, E.G. (1987) On the Solution of the Two-Dimensional Problem of a Plane Crack of Arbitrary Shape in an Anisotropic Material. Engineering Fracture Mechanics, 28, 187-195. http://dx.doi.org/10.1016/0013-7944(87)90212-8
- Zabreyko, P.P. (1975) Integral Equations—A Reference Text. Noordhoff, Leyden. http://dx.doi.org/10.1007/978-94-010-1909-5
- Prossdorf, S. (1977) On Approximate Methods for the Solution of One-Dimensional Singular Integral Equations. Applicable Analysis, 7, 259-270.
- Zisis, V.A. and Ladopoulos, E.G. (1989) Singular Integral Approximations in Hilbert Spaces for Elastic Stress Analysis in a Circular Ring with Curvilinear Cracks. Indus. Math., 39, 113-134.
- Chakrabarti, A. and Berghe, V.G. (2004) Approximate Solution of Singular Integral Equations. Applied Mathematics Letters, 17, 553-559. http://dx.doi.org/10.1016/S0893-9659(04)90125-5
- Abdou, M.A. and Naser, A.A. (2003) On the Numerical Treatment of the Singular Integral Equation of the Second Kind. Applied Mathematics and Computation, 146, 373-380. http://dx.doi.org/10.1016/S0096-3003(02)00587-8
- Abdulkawi, M., Eshkuvatov, Z.K. and Nik Long, N.M.A. (2009) A Note on the Numerical Solution of Singular Integral Equations of Cauchy Type. International Journal of Applied Mathematics and Computer Science, 5, 90-93.
- Eshkuvatov, Z.K., Nik Long, N.M.A. and Abdulkawi, M. (2009) Approximate Solution of Singular Integral Equations of the First Kind with Cauchy Kernel. Applied Mathematics Letters, 22, 651-657. http://dx.doi.org/10.1016/j.aml.2008.08.001
- Gakhov, F.D. (1966) Boundary Value Problems. Addison-Wesley, Boston.
- Martin, P.A. and Rizzo, F.J. (1989) On Boundary Integral Equations for Crack Problems. Proceedings of the Royal Society A, 421, 341-345. http://dx.doi.org/10.1098/rspa.1989.0014
- Sheshko, M. (2003) Singular Integral Equations with Cauchy and Hilbert Kernels and Their Approximated Solutions. The Learned Society of the Catholic University of Lublin, Lublin. (in Russian)
- Muskhelishvili, N.I. (1977) Singular Integral Equations. Noordhoff International Publishing, Leyden. http://dx.doi.org/10.1007/978-94-009-9994-7
- Lifanov, I.K. (1996) Singular Integral Equation and Discrete Vortices. VSP, Leiden.
- Kyth, K.P. and Schaferkotter, R.M. (2005) Handbook of Computational Methods for Integration. Chapman & Hall/ CRC Press, London.


