ABSTRACT

This paper presents new implicit algorithms for solving the variational inequality and shows that the proposed methods converge under certain conditions. Some special cases are also discussed.

1. Introduction

Variational inequality theory, introduced by Stampaccia [1], provides simple and unified framework to study a large number of problems arising in finance, economics, transportation, network and structural analysis, elasticity and optimization. Variational inequality theory, was emerged as an interesting and fascinating branch of applicable mathematics with a wide range of applications in unrelated linear and nonlinear problems.

The projection method provides important tools for finding the approximate solution of variational inequalities. This method is due to Lions and Stampacchia [2]. The main idea in this technique is to establish the equivalence between the variational inequalities and the fixed-point problem by using the concept of projection. This alternative formulation has played a significant part in developing various projection-type methods, the implicit iterative method, and the extra-gradient method which is due to Korpelevich [3], for solving the variational inequalities.

In this paper, we use the equivalent fixed point formulation to suggest and analyze some new implicit iterative methods for solving the variational inequalities. We have shown that these new implicit methods include the unified implicit, the proximal point and the modified extra gradient methods of Noor et al. [4,5], Noor [6] and the extra gradient method of Korpelevich [3] as special cases. We consider the convergence analysis of these methods under certain conditions.

2. Preliminaries

Let H be a real Hilbert space whose inner product and norm are denoted by and respectively. Let K be a nonempty closed convex subset in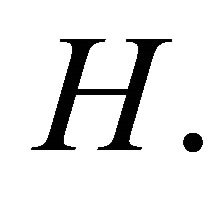

For a given nonlinear operator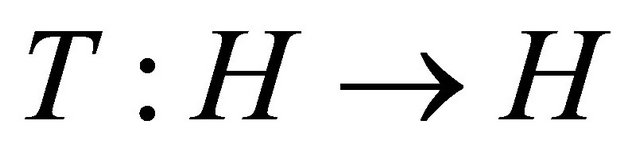, we consider the problem of finding 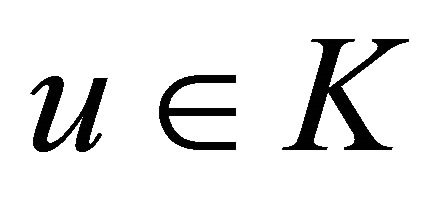such that

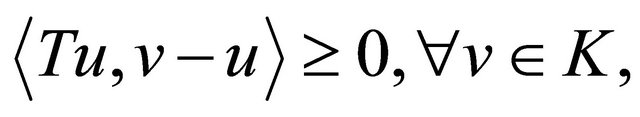(1)

Problem (1) is called the variational inequality, introduced and studied by Stampacchia [1]. For more information about applications,numerical methods and other aspects of variational inequalities, one may refer to [1- 12].

First we recall the following well-known results and concepts.

Lemma 1. Let K be a nonempty, closed, and convex set in. Then, for a given in, 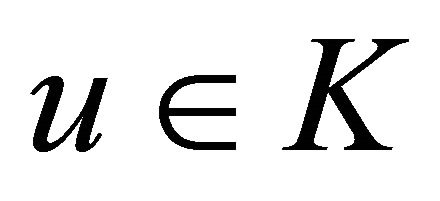satisfies the inequality

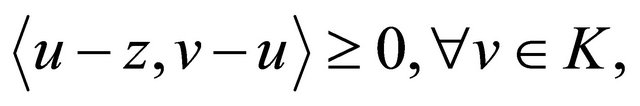
if and only if

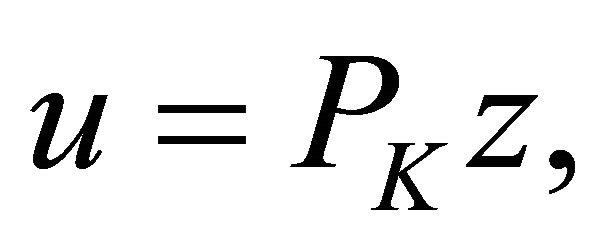
where 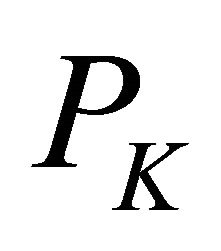is the projection of onto the closed and convex set.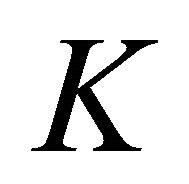

It is well known that the projection operator 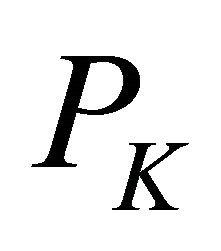is nonexpansive, that is

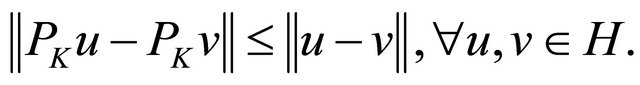
Now if 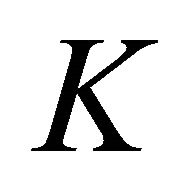is a nonempty, closed and convex subset in, then Problem (1) is equivalent to the existence of 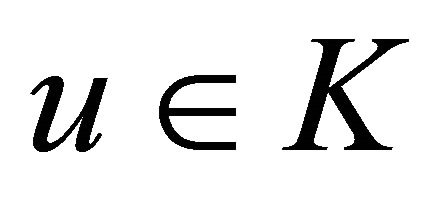such that

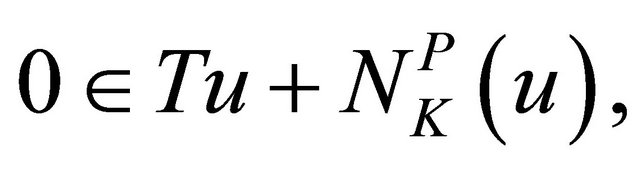(2)

where 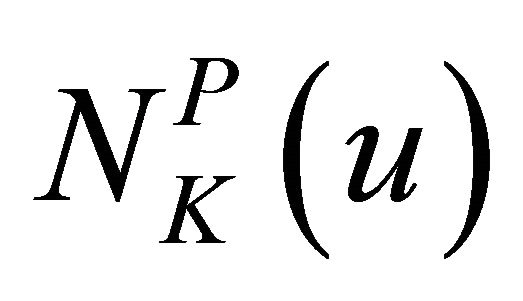denotes the normal cone of 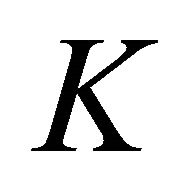at. Problem (2) is called the variational inclusion problem associated with the variational inequality (1).

Definition 1. An operator 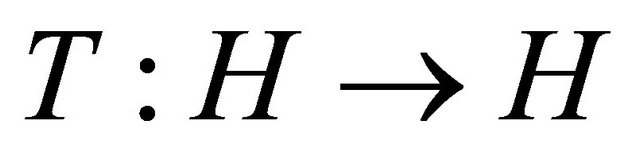is said to be strongly monotone if and only if there exists a constant 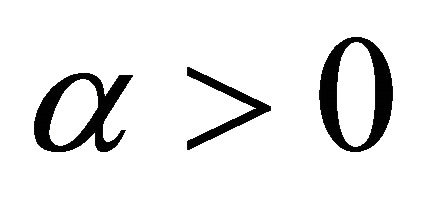such that

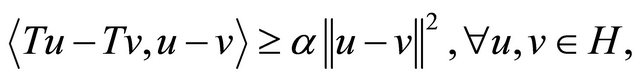
and Lipschitz continuous if there exists a constant 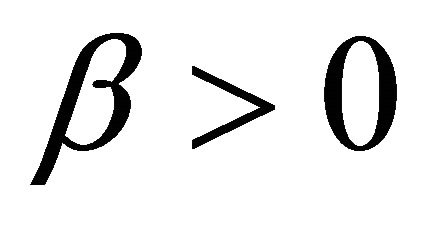such that

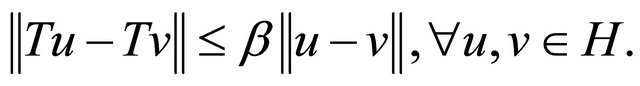
3. Main Results

In this section, using Lemma 1, one can easily show that the variational inequality (1) is equivalent to the existence of 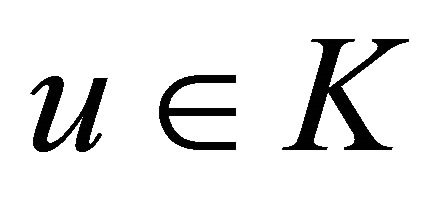such that

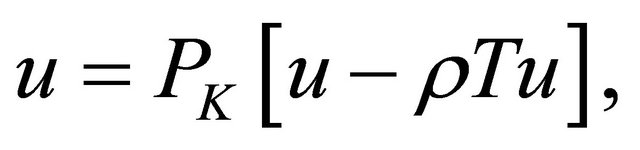(3)

where 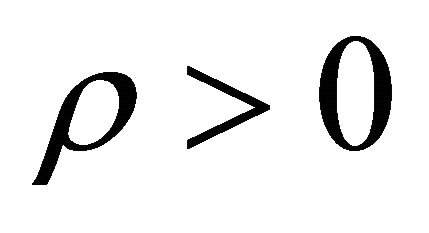is constant.

Equation (3) is a fixed point problem and will be used in suggesting some new implicit methods for solving the variational inequality (1), and this is the main motivation of this paper.

Now, using the equivalent fixed point formulation (3), one can suggest the following iterative method for solving the variational inequality (1).

Algorithm 1. For a given 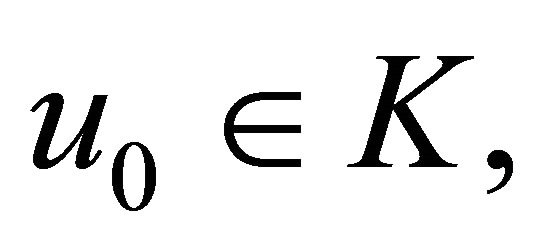find the approximate solution 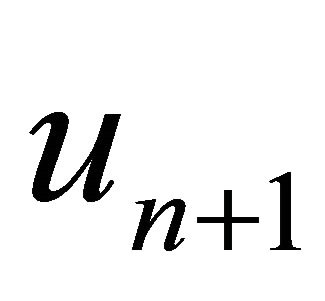by the iterative scheme

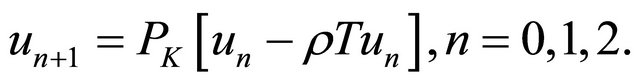
Algorithm 1 is known as the projection iterative method.

For a given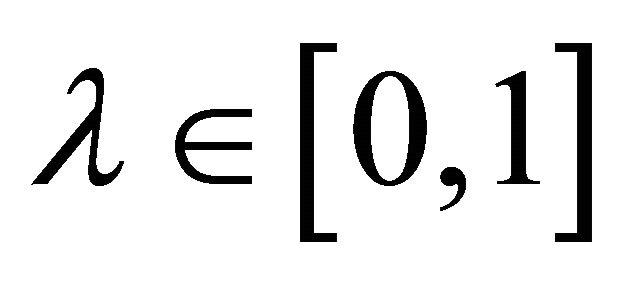, we can rewrite (3) as

(4)

This fixed point formulation is used to suggest the following iterative method for solving variational inequality (1).

Algorithm 2. For a given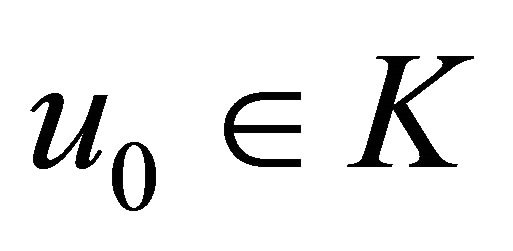, find the approximate solution 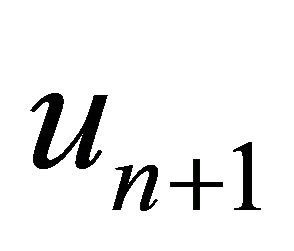by the iterative scheme

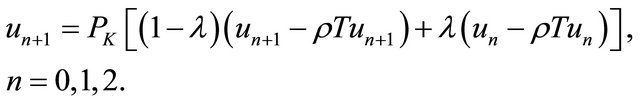
Note that Algorithm 2 is an implicit type iterative method and includes the implicit method of Noor [6] and the classical projection method as special cases.

In order to implement this method, we use the predictor-corrector technique. We use Algorithm 1 as the predictor and Algorithm 2 as the corrector. Consequently, we obtain the following two-step iterative method for solving the variational inequality (1).

Algorithm 3. For a given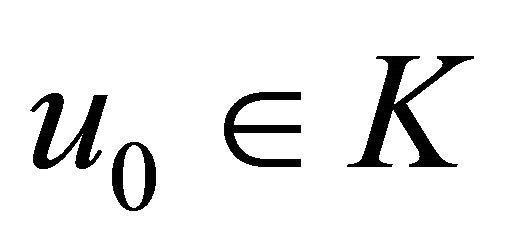, find the approximate solution 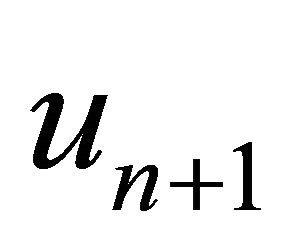by the iterative schemes

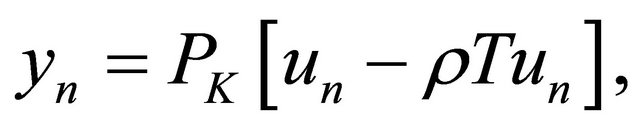(5)

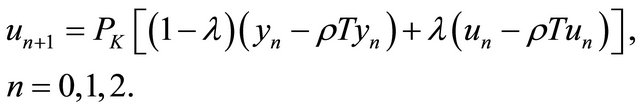(6)

Algorithm 3 is a new two-step implicit iterative method for solving the variational inequality (1). For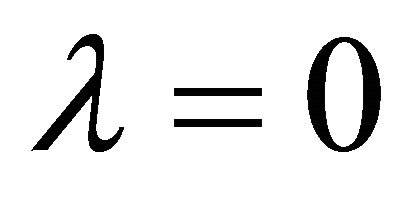, Algorithm 3 reduces to the following iterative method for solving variational inequality (1).

Algorithm 4. For a given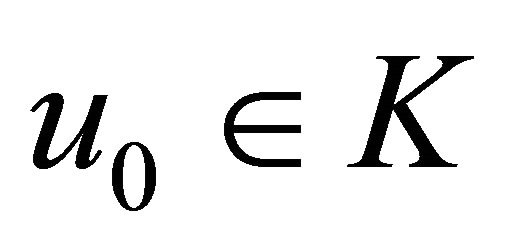, find the approximate solution 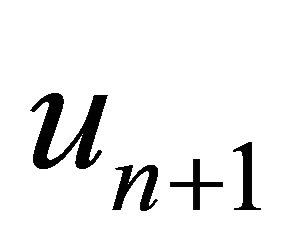by the iterative schemes

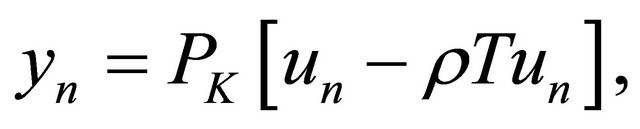
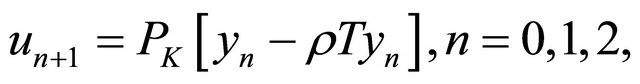
which is known as the modified double projection method, Noor [6].

For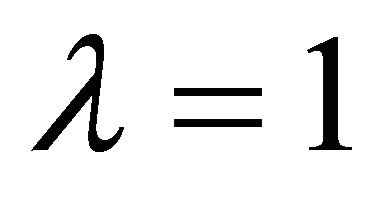, Algorithm 3 reduces to algorithm 1 for solving variational inequality (1).

This shows that Algorithm 3 is a unified implicit method and includes the previously known implicit and predictor-corrector methods as special cases.

Now for a given 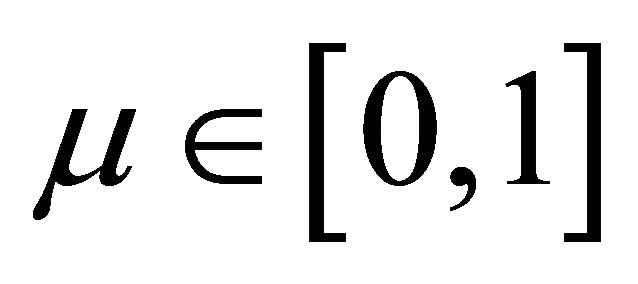and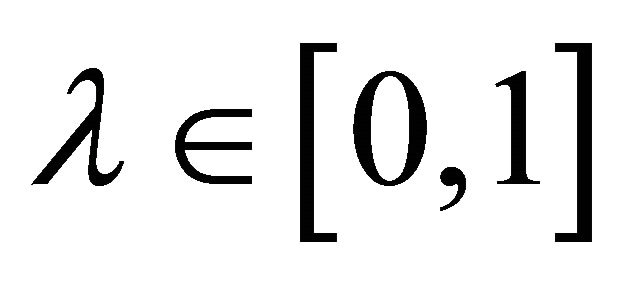, we can rewrite (3) as

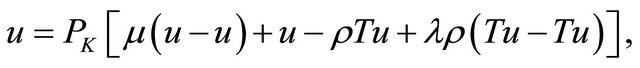(7)

For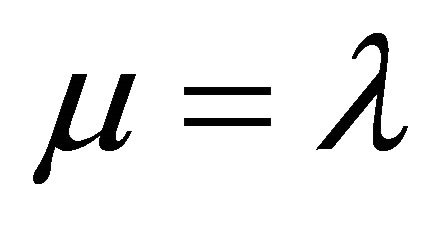, the fixed point formulation (7) reduces to the fixed point formulation (4).

Now we use (7) to suggest the following iterative methods for solving variational inequality (1).

Algorithm 5. For a given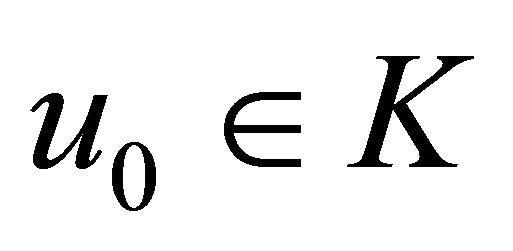, find the approximate solution 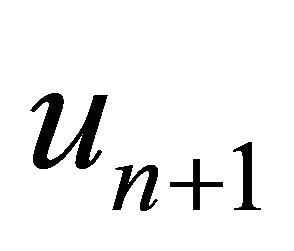by the iterative scheme

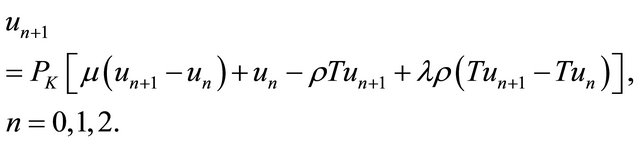
Note that Algorithm 5 is an implicit type iterative method and includes the implicit method of Noor et al. [7], and the classical implicit method of Korpelevich [3] as special cases.

In order to implement this method, we use the predictor-corrector technique. We use Algorithm 1 as the predictor and Algorithm 5 as the corrector. Consequently, we obtain the following iterative method for solving the variational inequality (1).

Algorithm 6. For a given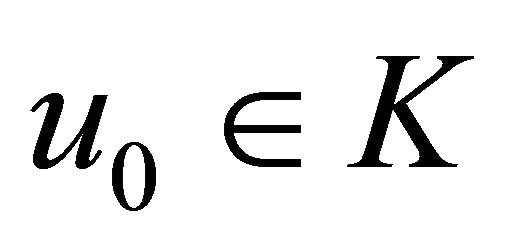, find the approximate solution 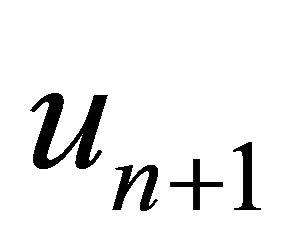by the iterative schemes

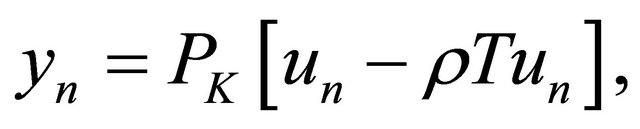
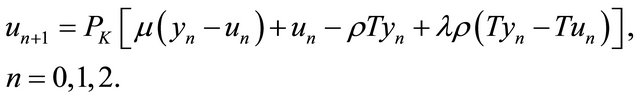(8)

Algorithm 6 is a new two-step implicit iterative method for solving the variational inequality (1). For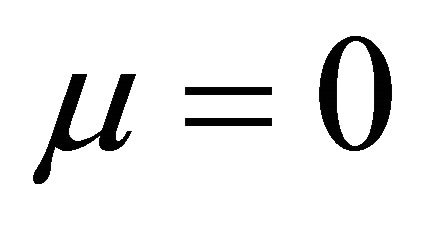, Algorithm 6 reduces to the following iterative method for solving variational inequality (1).

Algorithm 7. For a given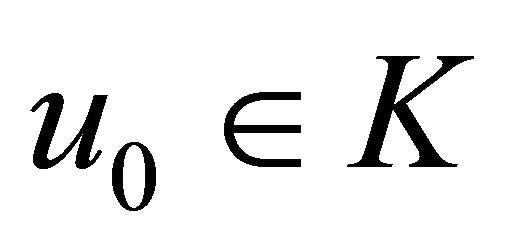, find the approximate solution 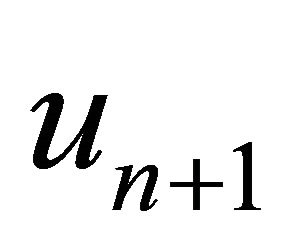by the iterative schemes

Algorithm 7 was studied by Noor et al. [4]. Note that for, Algorithm 7 reduces to Algorithm 1, and for , Algorithm 7 reduces to Korpelevich [3].

For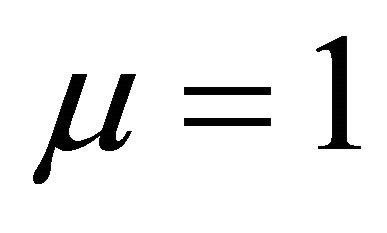, Algorithm 6 reduces to the following iterative method for solving variational inequality (1), and appears to be new.

Algorithm 8. For a given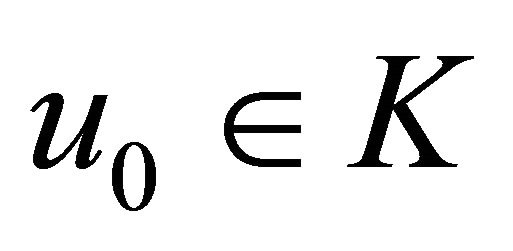, find the approximate solution 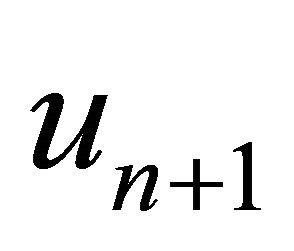by the iterative schemes

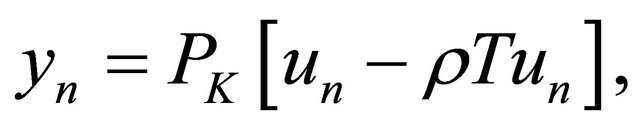
For, Algorithm 6 reduces to the following iterative method for solving variational inequality (1), and appears to be new.

Algorithm 9. For a given, find the approximate solution by the iterative schemes

For Algorithm 9 reduces to Noor [6] and for Algorithm 9 reduces to Korpelevich [3].

Now one can obtains the following iterative method for solving variational inequality (1), by using the fixed point formulation (7).

Algorithm 10. For a given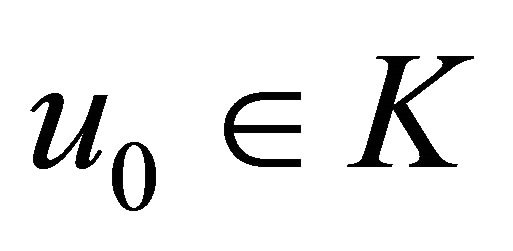, find the approximate solution 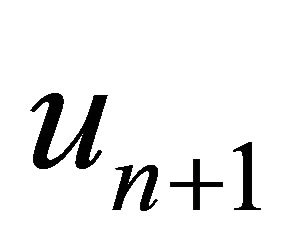by the iterative scheme

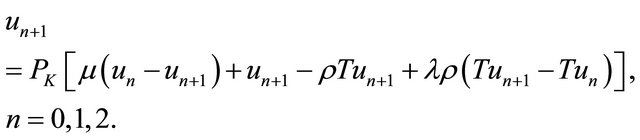
In order to implement this method, we use the predictor-corrector technique. We use Algorithm 1 as the predictor and Algorithm 10 as the corrector. Consequently, we obtain the following two-step iterative method for solving the variational inequality (1).

Algorithm 11. For a given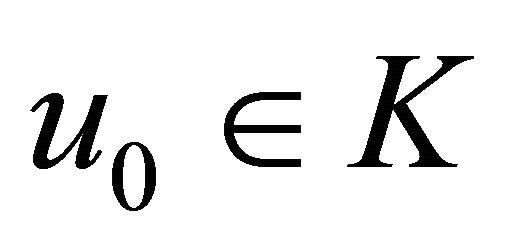, find the approximate solution 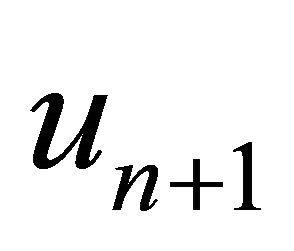by the iterative scheme

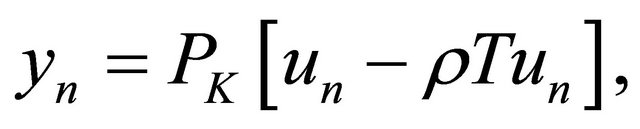
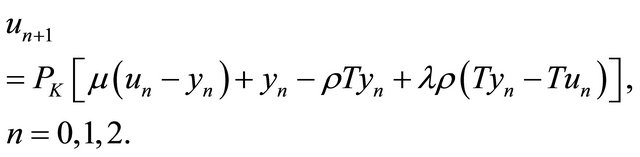(9)

Algorithm 11 is a new two-step implicit iterative method for solving the variational inequality (1). For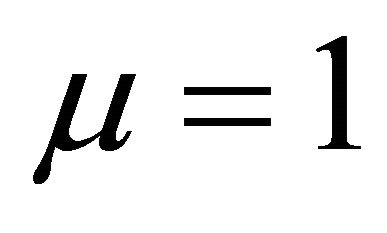, Algorithm 11 reduces to Algorithm 7 [4], and for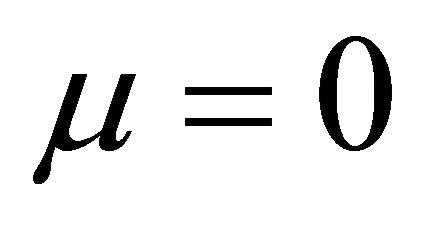, Algorithm 11 reduces to Algorithm 8 which is a new one, as we mentioned above.

4. Convergence

We now consider the convergence analysis of Algorithm 3, 6 and 11, and this is the motivation of next results.

Theorem 1. Let the operator be strongly monotone with constant 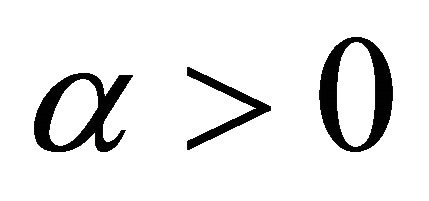and Lipschitz continuous with constant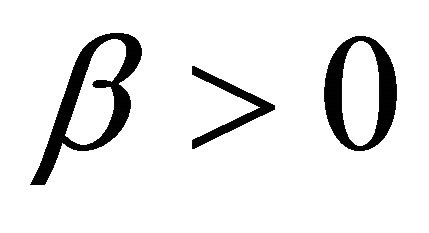. If there exists a constant 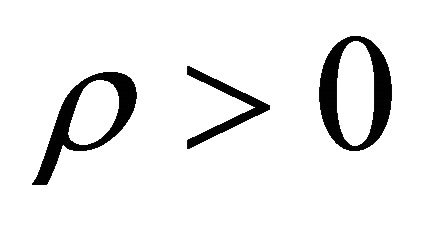such that

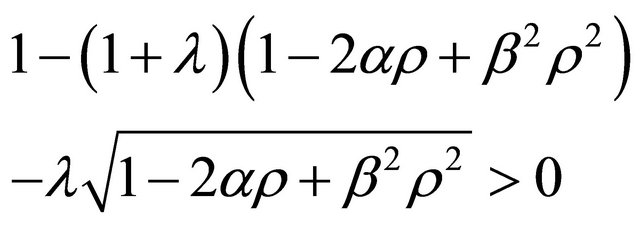(10)

then, the approximate solution 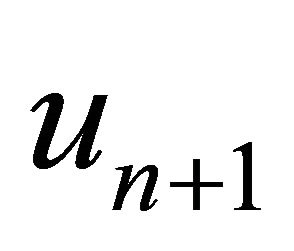obtained from Algorithm 3 converges strongly to the exact solution satisfying the variational inequality (1).

Proof. Let be a solution of (1) and 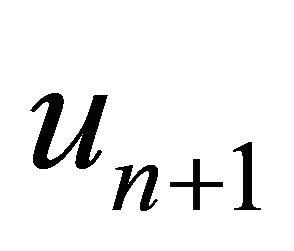be the approximate solution obtained from Algorithm 3. Then, from (3) and (5), we have

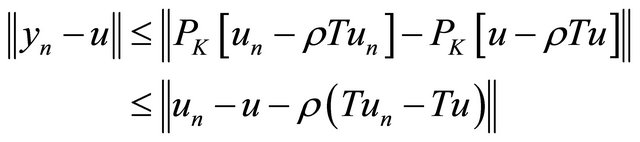(11)

From the strongly monotonicity and Lipschitz continuity of the operator, one obtains

(12)

From (11) and (12), one obtains

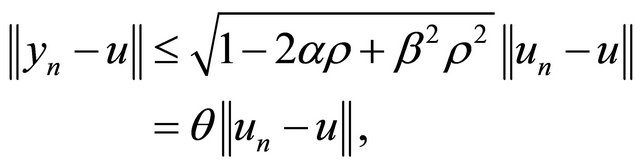(13)

where

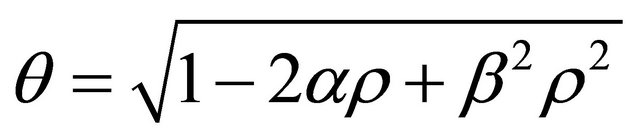
Now from (3), (6) and (13), we have

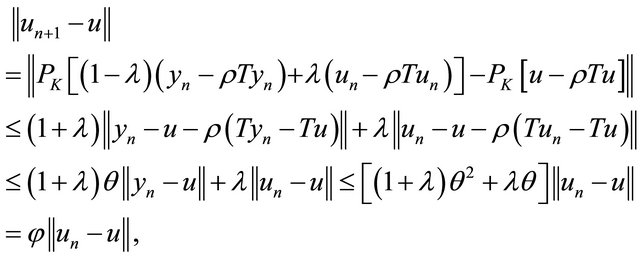
where

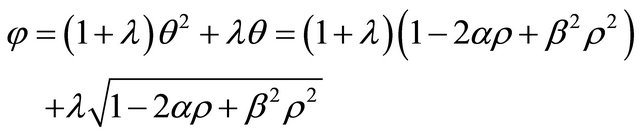
From (10), it follows that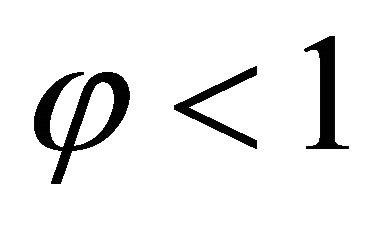. Hence, the fixed point Problem (3) has a unique solution and consequently the iterative solution 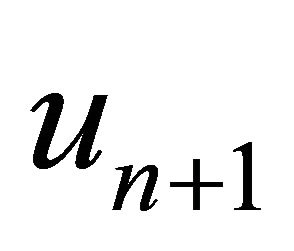obtained from Algorithm 3 converges to the exact solution and satisfying the variational inequality (1). □

Theorem 2. Let the operator T be strongly monotone with constant 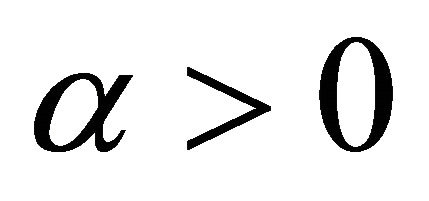and Lipschitz continuous with constant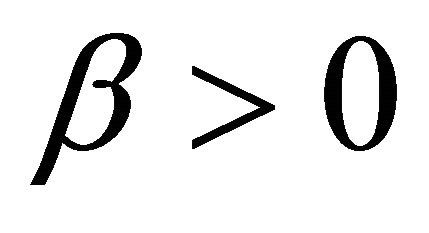. If there exists a constant 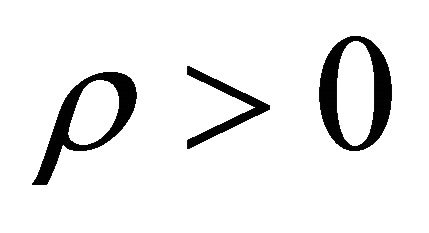such that

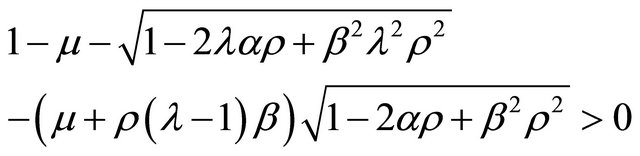(14)

then, the approximate solution 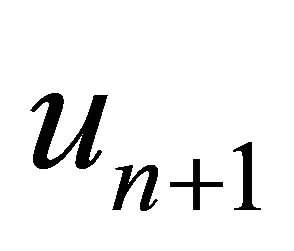obtained from Algorithm 6 converges strongly to the exact solution 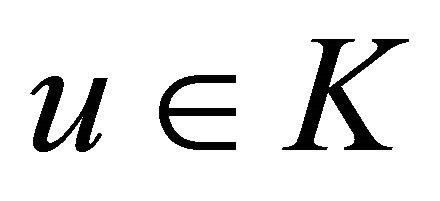satisfying the variational inequality (1).

Proof. Let 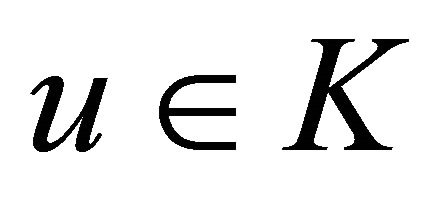be a solution of (1) and 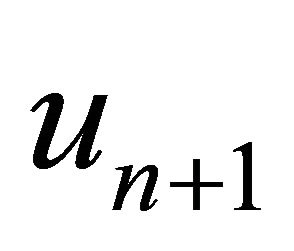be the approximate solution obtained from Algorithm 6. Then, from (3), (8) and (13), we have

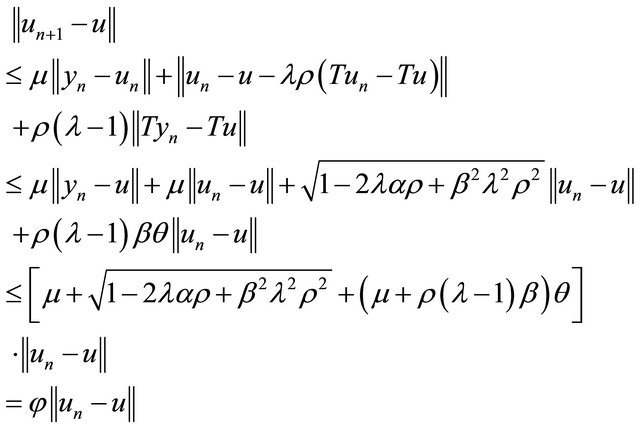
where

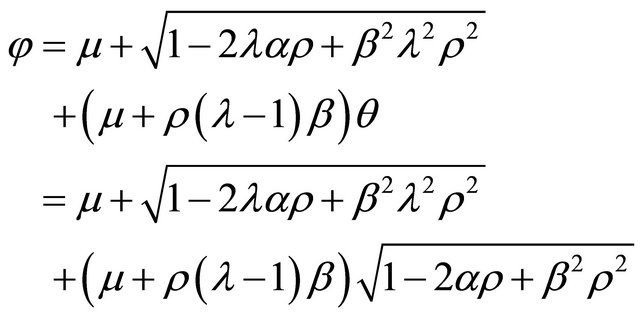
From (14), it follows that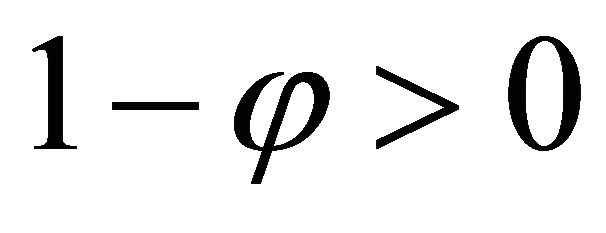. Hence, the fixed point Problem (3) has a unique solution and consequently the iterative solution obtained from algorithm 6 converges to the exact solution of (1). □

Theorem 3. Let the operator T be strongly monotone with constant 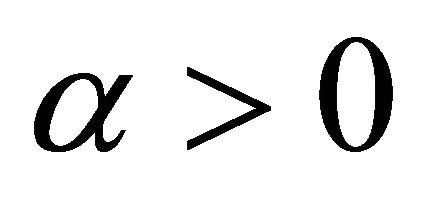and Lipschitz continuous with constant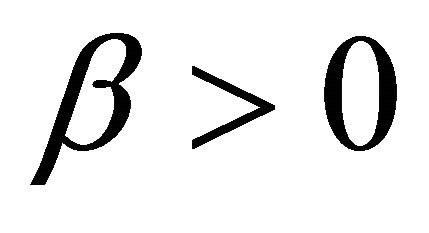. If there exists a constant 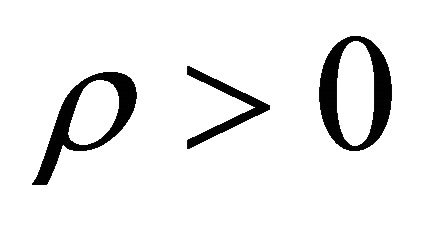such that

(15)

then, the approximate solution 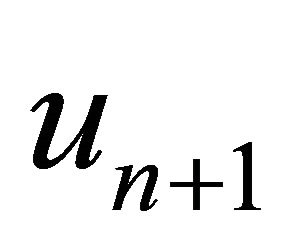obtained from Algorithm 11 converges strongly to the exact solution 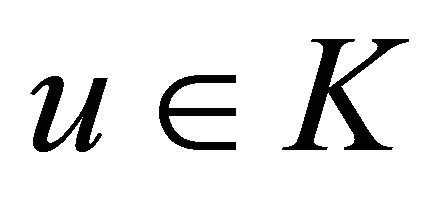and satisfying the variational inequality (1).

Proof. Let 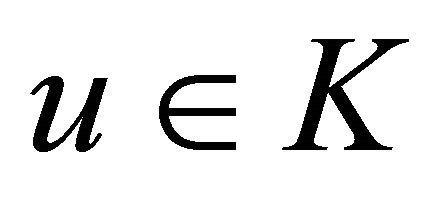be a solution of (1) and 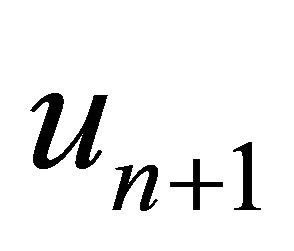be the approximate solution obtained from Algorithm 11. Then, from (3), (9) and (13), we have

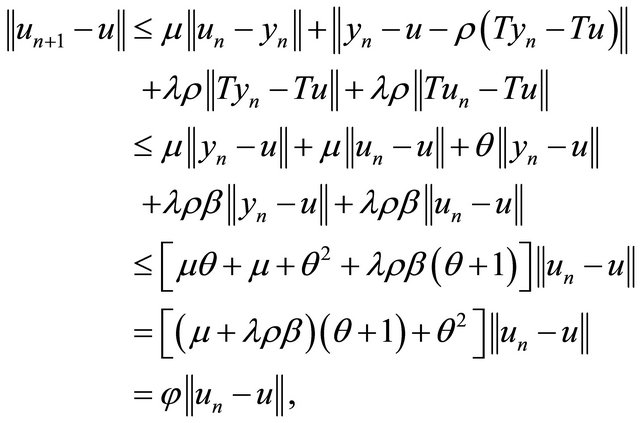
where

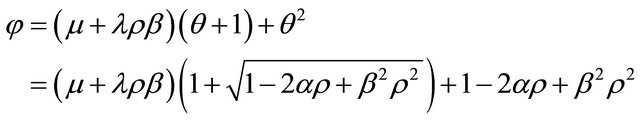
From (15), it follows that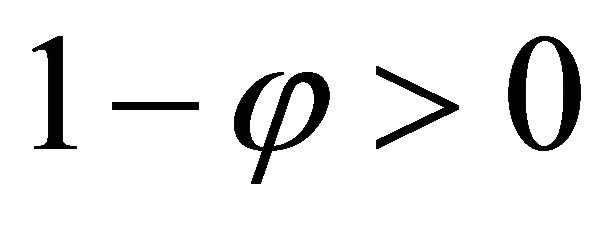. Hence, the fixed point Problem (3) has a unique solution and consequently the iterative solution 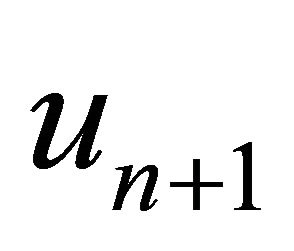obtained from algorithm 11 converges to the exact solution of (1). □

5. Conclusion

In this paper, we have used the equivalence between the variational inequality and the fixed point problem to suggest and analyze some new implicit iterative methods for solving the variational inequality. We also show that the new implicit methods includes the extra gradient method of Korpelevich [3], the modified extra gradient method of Noor [6], the proximal point methods of Noor et al. [4], and the unified implicit methods of Noor et al. [5] as special cases. We also have discussed the convergence analysis of the proposed new iterative methods under some suitable conditions. One may modify again this algorithmic schemes by different choices and rearrangement of the values of and.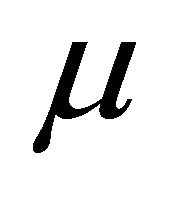

6. Acknowledgements

The author would like to express her thanks to the anonymous referee for his valuable comments to improve the final version of this paper.

REFERENCES