Applied Mathematics
Vol.3 No.12A(2012), Article ID:26075,15 pages DOI:10.4236/am.2012.312A294
Estimation for Nonnegative First-Order Autoregressive Processes with an Unknown Location Parameter
University of Georgia, Athens, USA
Email: wpmcc@uga.edu
Received September 10, 2012; revised October 10, 2012; accepted October 17, 2012
Keywords: Nonnegative Time Series; Autoregressive Processes; Extreme Value Estimator; Regular Variation; Point Processes
ABSTRACT
Consider a first-order autoregressive processes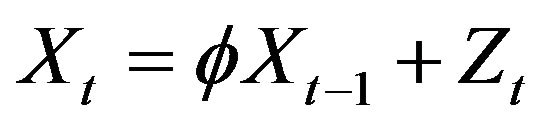 , where the innovations are nonnegative random variables with regular variation at both the right endpoint infinity and the unknown left endpoint θ. We propose estimates for the autocorrelation parameter f and the unknown location parameter θ by taking the ratio of two sample values chosen with respect to an extreme value criteria for f and by taking the minimum of
, where the innovations are nonnegative random variables with regular variation at both the right endpoint infinity and the unknown left endpoint θ. We propose estimates for the autocorrelation parameter f and the unknown location parameter θ by taking the ratio of two sample values chosen with respect to an extreme value criteria for f and by taking the minimum of 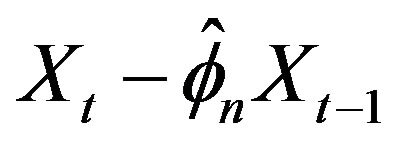 over the observed series, where
over the observed series, where 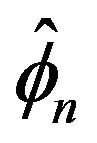 represents our estimate for f. The joint limit distribution of the proposed estimators is derived using point process techniques. A simulation study is provided to examine the small sample size behavior of these estimates.
represents our estimate for f. The joint limit distribution of the proposed estimators is derived using point process techniques. A simulation study is provided to examine the small sample size behavior of these estimates.
1. Introduction
In many applications, the desire to model the phenomena under study by non-negative dependent processes has increased. An excellent presentation of the classical theory concerning these models can be found, for example, in Brockwell and Davis [1]. Recently, advancements in such models have shifted focus to some specialized features of the model, e.g. heavy tail innovations or nonnegativity of the model. In this paper we examine the behavior of traditional estimates under conditions leading to non-Gaussian limits. For example, the standard approach to parameter estimation within the AR(1) process is through the Yule-Walker estimator;
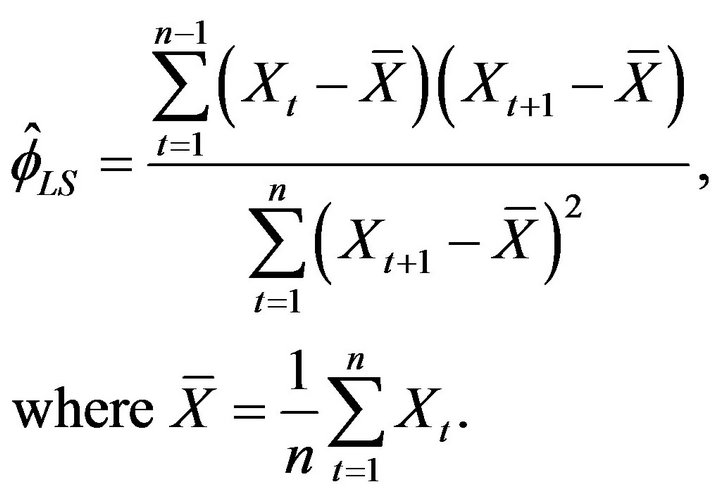 (1.1)
(1.1)
A slightly different approach presented in Mathew and McCormick [2] used linear programming to obtain estimates for 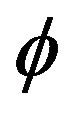 and
and  under certain optimization constraints. While there are many established methods to estimate the autocorrelation coefficient in an AR(1) model, there are just a few approaches on estimating the unknown location parameter in an AR(1) model. Onewas mentioned in McCormick and Mathew [2] where they considered
under certain optimization constraints. While there are many established methods to estimate the autocorrelation coefficient in an AR(1) model, there are just a few approaches on estimating the unknown location parameter in an AR(1) model. Onewas mentioned in McCormick and Mathew [2] where they considered
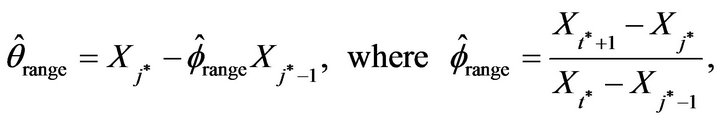
![]() and
and  provides the index of the maximal and minimal
provides the index of the maximal and minimal 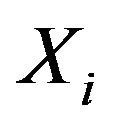 respectively for
respectively for .
.
In this paper we examine estimation questions and asymptotic properties of alternative estimates for 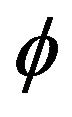 and
and  respectively, relating to the model
respectively, relating to the model

where 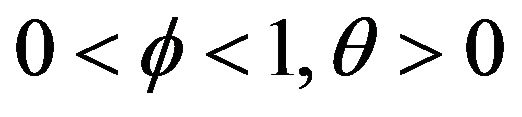 and
and  is an i.i.d. sequence of nonnegative random variables whose innovation distribution F is assumed to be regularly varying at infinity with index
is an i.i.d. sequence of nonnegative random variables whose innovation distribution F is assumed to be regularly varying at infinity with index 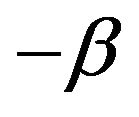 and regularly varying at
and regularly varying at  with index
with index![]() , where
, where , denotes the unknown but positive left endpoint. As a result of not restricting the innovations
, denotes the unknown but positive left endpoint. As a result of not restricting the innovations 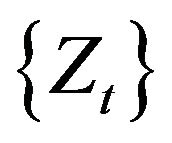 to be bounded on a finite range, we can first estimate the autoregressive parameter
to be bounded on a finite range, we can first estimate the autoregressive parameter  through regular variation at infinity and then estimate the positive but unknown location parameter through regular variation at
through regular variation at infinity and then estimate the positive but unknown location parameter through regular variation at , the left endpoint.
, the left endpoint.
While we have mentioned a few established estimation procedures, one notable exception was that of maximum likelihood. Although typically intractable and intricate in the time series setting, when the innovations in the AR(1) model are exponential, the maximum likelihood procedure had a major contribution on the estimation of positive heavy tailed time series. With these considerations in mind, Raftery [3] determined the limiting distribution of the maximum likelihood estimate for the autocorrelation coefficient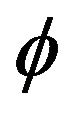 . As a result, the estimator
. As a result, the estimator
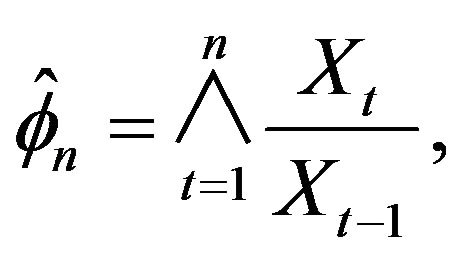 (1.2)
(1.2)
was considered. The realization of this estimator was the stepping stone for the work done in this paper along with Davis and McCormick [4] which first considered this alternative estimator and used a point process approach to obtain the asymptotic distribution of the natural estimator . This was done in the context that the innovations distribution
. This was done in the context that the innovations distribution  varies regularly at 0, the left endpoint, and satisfy some moment condition.
varies regularly at 0, the left endpoint, and satisfy some moment condition.
The work presented in this paper is an extension of the work done in Davis and McCormick [4] including the following contributions to dependent time series with heavy-tail innovations. The first contribution involves the development of estimates for the autocorrelation coefficient and unknown location parameter under regular variation at both endpoints, with a rate of convergence , where
, where  is slowly varying function. The second contribution involves using an extreme value method, e.g. point processes to establish the asymptotic distribution of the proposed estimators and weak convergence for the asymptotically independent joint distribution. An initial observation is that our estimation procedure is especially easy to implement for both
is slowly varying function. The second contribution involves using an extreme value method, e.g. point processes to establish the asymptotic distribution of the proposed estimators and weak convergence for the asymptotically independent joint distribution. An initial observation is that our estimation procedure is especially easy to implement for both 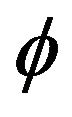 and
and . That is, the autoregressive coefficient
. That is, the autoregressive coefficient 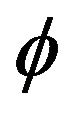 in the causal AR(1) process is estimated by taking the minimum of the ratio of two sample values while estimation for the unknown location parameter
in the causal AR(1) process is estimated by taking the minimum of the ratio of two sample values while estimation for the unknown location parameter  was achieved through minimizing
was achieved through minimizing  over the observed series.
over the observed series.
This naturally motivates a comparison between the estimation procedure presented in this paper and the standard linear programming estimates mentioned above, since within a nonnegative AR(1) model the linear programming estimate reduces to the estimate proposed, namely,  , where
, where  denotes the AR(1) process. This comparison along with the comparison between Mathew and McCormick’s [2] optimization method and Bartlett and McCormick [5] extreme value method was performed through simulation and is presented in Section 3. The results found appear to demonstrate a favorable performance for our extreme value method over the 3 alternative estimators.
denotes the AR(1) process. This comparison along with the comparison between Mathew and McCormick’s [2] optimization method and Bartlett and McCormick [5] extreme value method was performed through simulation and is presented in Section 3. The results found appear to demonstrate a favorable performance for our extreme value method over the 3 alternative estimators.
The main proofs in this paper rely heavily on point process methods from extreme value theory. The essential idea is to first establish the convergence of a sequence of point processes based on simple quantities and then apply the continuous mapping theorem to obtain convergence of the desired statistics. More background information on point processes, regular variation, and weak convergence can be found in Resnick [6]. Also, a nice survey on linear programming estimation procedures and nonnegative time series can be found in Anděl [7], Anděl [8], and Datta and McCormick [9], whereas more applications on modeling the phenomena with heavy tailed distributions and ensuing estimation issues can be found in Resnick [10].
The rest of the paper is organized as follows: asymptotic limit results for the autocorrelation parameter , unknown location parameter
, unknown location parameter , and joint distribution of
, and joint distribution of  are presented in Section 2, while Section 3 is concerned with the small sample size behavior of these estimates through simulation.
are presented in Section 2, while Section 3 is concerned with the small sample size behavior of these estimates through simulation.
2. Asymptotics
The following point process limit result is fundamental. Since the result makes no use of an ARMA structure, we present it for more general linear models subject to usual summability conditions on the coefficients. In that regard for this result, we assume that 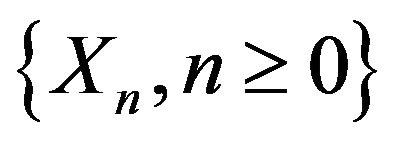 is the stationary linear process given by
is the stationary linear process given by
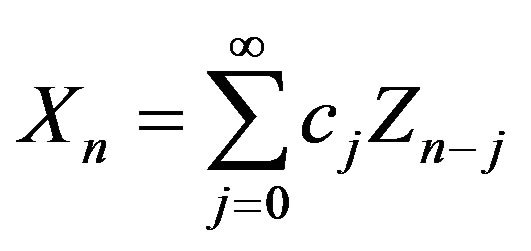
with  for some
for some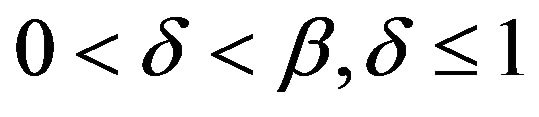 . Furthermore for this result we may relax our assumptions on the innovation distribution and we require that
. Furthermore for this result we may relax our assumptions on the innovation distribution and we require that 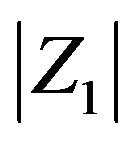 has a regularly varying tail distribution, i.e.,
has a regularly varying tail distribution, i.e.,
 for a slowly varying function
for a slowly varying function  and the innovation distribution is tail balanced
and the innovation distribution is tail balanced

Define point processes
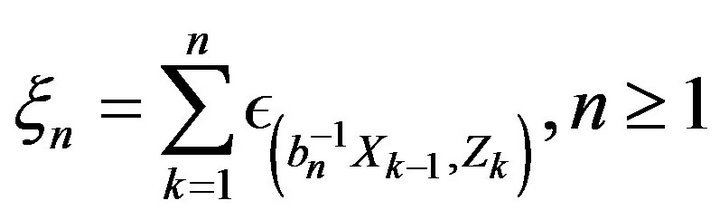
and let 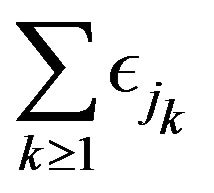 denote PRM
denote PRM on
on  where
where
![]() has Radon-Nikodym derivative with respect to Lebesgue measure
has Radon-Nikodym derivative with respect to Lebesgue measure
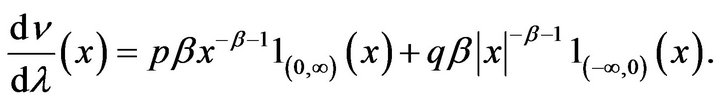
Let  be an iid array with
be an iid array with 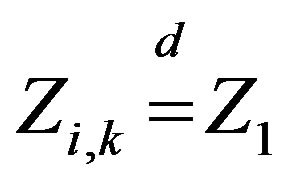 and independent of
and independent of . Define
. Define
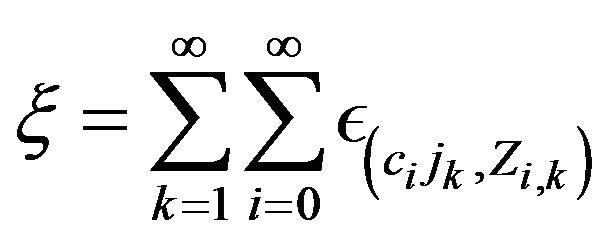
Our basic result is to show that 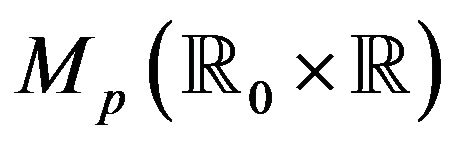 equipped with the topology of vague convergence
equipped with the topology of vague convergence
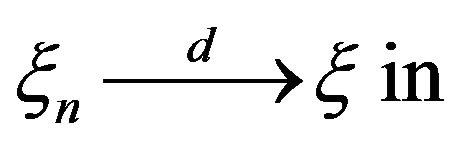
which is close in statement and spirit to Theorem 2.4 in Davis and Resnick [11]. In view of the commonality of the two results, we present only the needed changes to the Davis and Resnick proof to accommodate the current setting. Aside from keeping track of the time when points occur, i.e. large jumps, the difference in the point processes considered here with those in Davis and Resnick [11] is the inclusion of marks, i.e. the second component of the point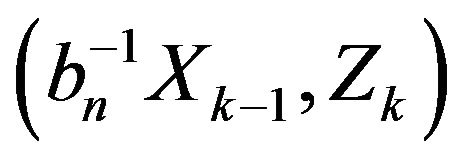 . This complication induces an additional weak dependence in the points which is addressed in Lemma 2.2 through a straight forward blocking argument. First, we establish weak convergence of marked point processes of a normalized vector of innovations. For a positive integer m define
. This complication induces an additional weak dependence in the points which is addressed in Lemma 2.2 through a straight forward blocking argument. First, we establish weak convergence of marked point processes of a normalized vector of innovations. For a positive integer m define
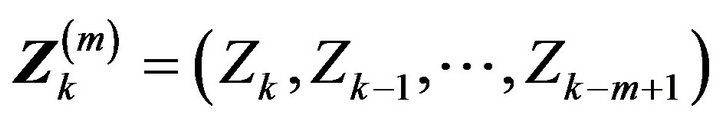
and point process
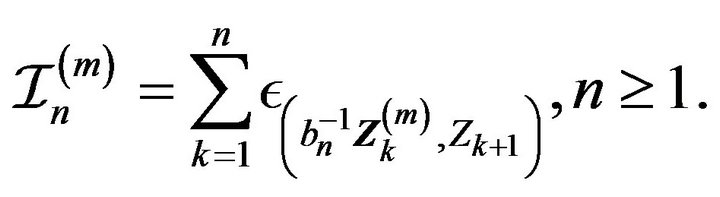
Let 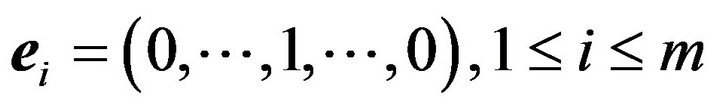 denote the standard basis vectors for
denote the standard basis vectors for . Define an associated marked point process with the first component placed on an axis by
. Define an associated marked point process with the first component placed on an axis by

In the following Lemma, we show that ![]() and
and ![]() are asymptotically indistinguishable in the following sense. Let
are asymptotically indistinguishable in the following sense. Let  and
and . Consider the class of rectangles
. Consider the class of rectangles

Lemma 2.1. As ![]() tends to infinity
tends to infinity
 .
.
Proof. Following the proof presented in Proposition 2.1 of Davis and Resnick [11], suppose that  is such that for some
is such that for some  As noted in Davis and Resnick [11] for all
As noted in Davis and Resnick [11] for all , one has
, one has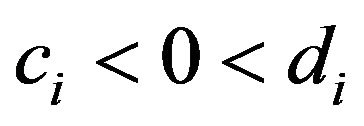 . Observe that
. Observe that

(2.1)
Similarly let 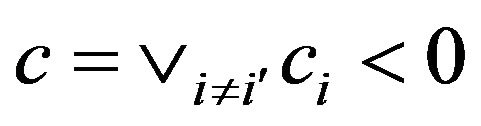 and
and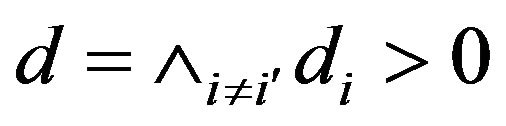 . Then
. Then
 (2.2)
(2.2)
where 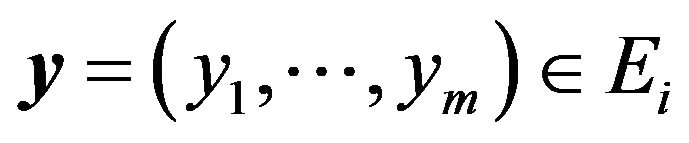 according to
according to 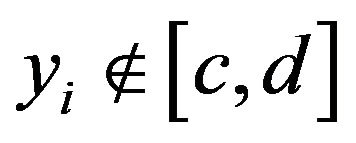 and
and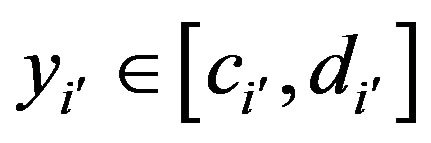 . Note that
. Note that
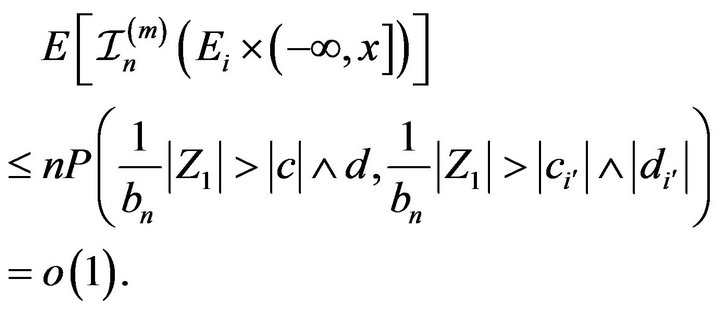 (2.3)
(2.3)
Thus from (2.1)-(2.3) we obtain
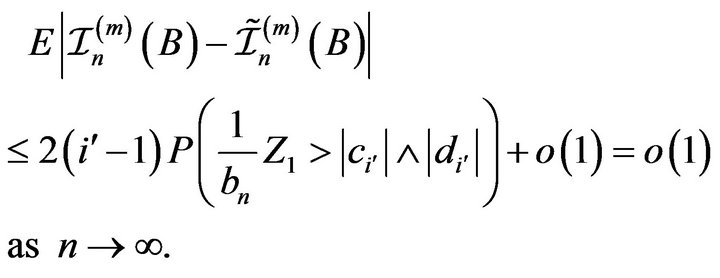 (2.4)
(2.4)
Then the result follows as in Davis and Resnick [11], Proposition 2.1, completing the proof. □
Lemma 2.2. Let ![]() and
and ![]() be the point processes on the space
be the point processes on the space  defined by
defined by

where  is an iid sequence with
is an iid sequence with
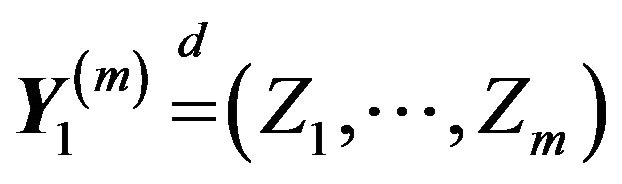 and is independent of
and is independent of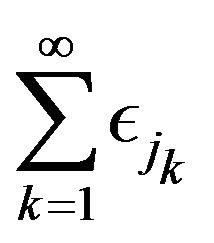 . Then in
. Then in ,
,

Proof. We employ a blocking argument to establish this result. Let ![]() be a sequence of integers such that
be a sequence of integers such that 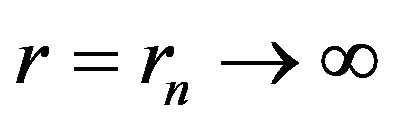 as
as ![]() and
and . Let
. Let 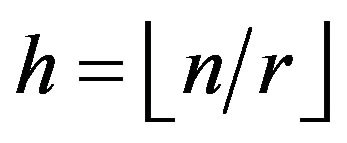 and
and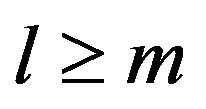 . Define blocks
. Define blocks

Then it is clear that for 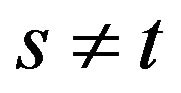
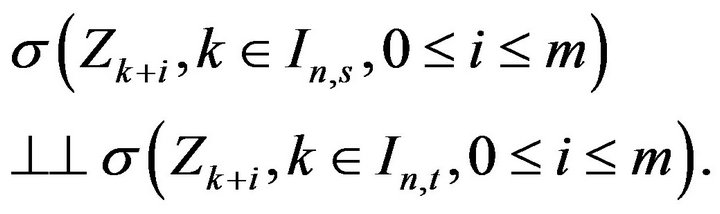
Write
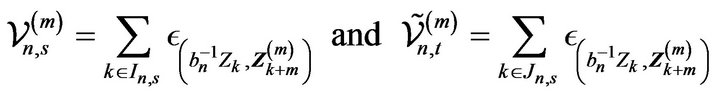
Then
 (2.5)
(2.5)
Let 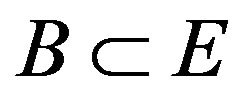 be a disjoint union of rectangles
be a disjoint union of rectangles
![]() (2.6)
(2.6)
where  with
with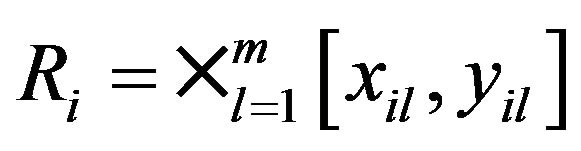 . Let
. Let  denote the mean measure of
denote the mean measure of ![]() which is PRM
which is PRM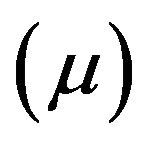 on
on . To complete the proof we first show that for all sets
. To complete the proof we first show that for all sets 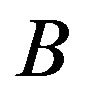 of the form given in (2.6) that
of the form given in (2.6) that
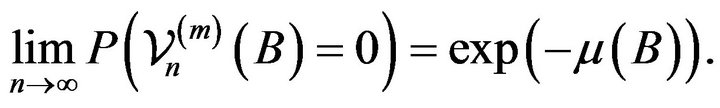 (2.7)
(2.7)
The above limit result follows from the easily verifiable relations:
 (2.8)
(2.8)
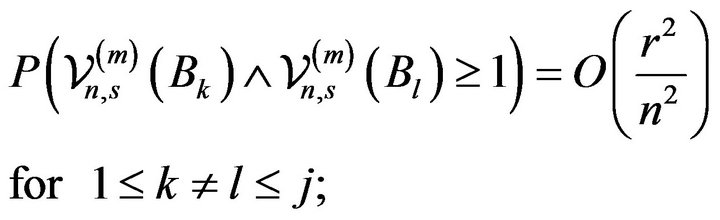 (2.9)
(2.9)
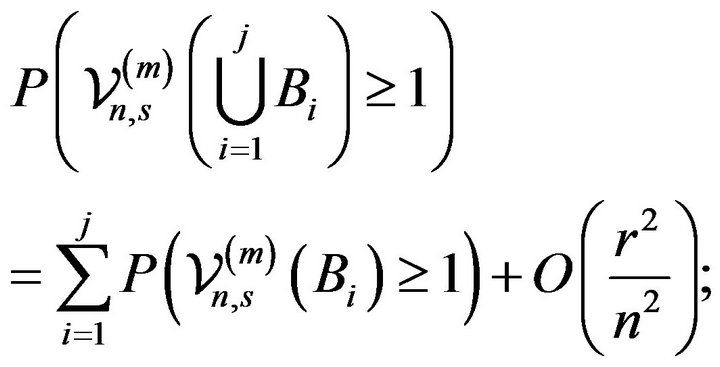 (2.10)
(2.10)
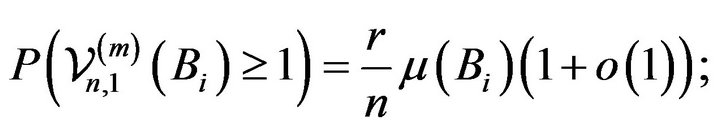 (2.11)
(2.11)
and
 (2.12)
(2.12)
Indeed, in view of (2.5) and (2.12), (2.7) is equivalent to showing
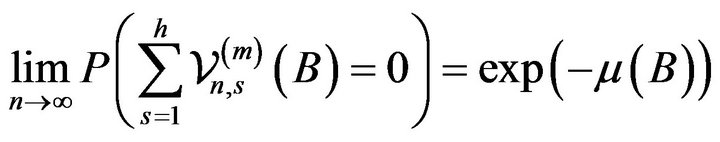 (2.13)
(2.13)
and the above relation holds by (2.8), (2.10), and (2.11), viz.
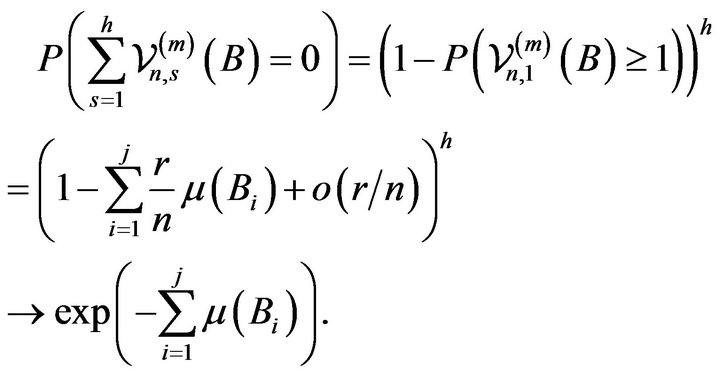
It is immediate that for a rectangle
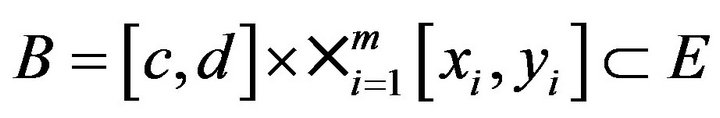 we have
we have
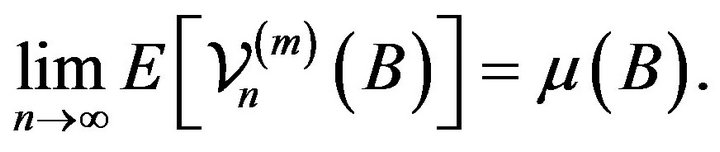 (2.14)
(2.14)
Therefore the result is seen to hold by (2.7) and (2.14) by application of Theorem 4.7 in Kallenberg [12]. □
Lemma 2.3. Let ![]() and
and ![]() be point processes on the space
be point processes on the space 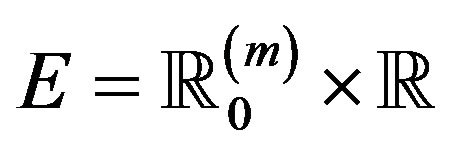

Then in ,
,

Proof. We begin by applying the argument used in Theorem 2.2 of Davis and Resnick [11] with the modification that the relevant composition of maps of point processes is given by

Each map being continuous, the composition is a continuous map from 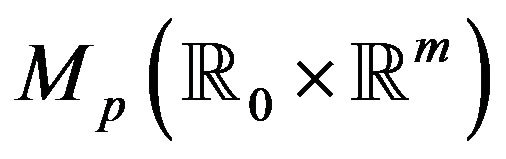 to
to  with each space being equipped with the topology of vague convergence. Therefore by the continuous mapping theorem and Lemma 2.2 we obtain
with each space being equipped with the topology of vague convergence. Therefore by the continuous mapping theorem and Lemma 2.2 we obtain
 (2.15)
(2.15)
Finally we complete the proof by Lemma 2.1 and (2.15) arguing as in Davis and Resnick [11].
We are now ready to present our fundamental result.
Theorem 2.1. Let  and
and  be the point processes on the space
be the point processes on the space  defined by
defined by

where 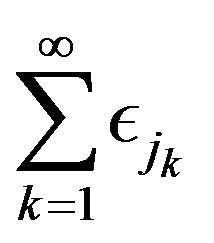 is
is 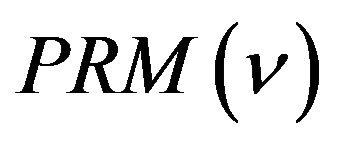 and
and  is an iid array with
is an iid array with 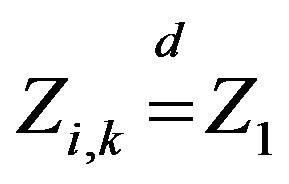 and independent of
and independent of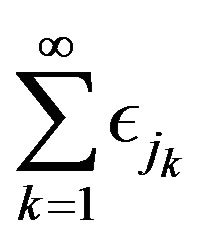 .
.
Then in 
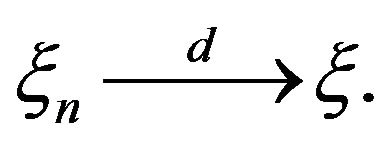
Remark. Apart from considering a time coordinate and restricting the process to an AR(1) process, the above Theorem 2.1 and Theorem 3.1 in Mathew and McCormick [2] consider essentially the same point process limit result. However, their result gave a wrong limit point process. This error is corrected in the current paper.
Proof. Observe that the map

induces a continuous map on point processes given by
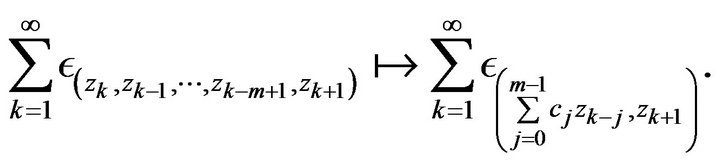
Thus we obtain from Lemma 2.3 that
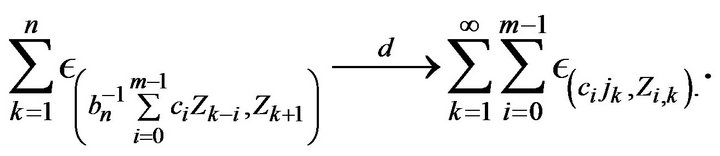 (2.16)
(2.16)
The result now follows from (2.16) by the same argument in Davis and Resnick [11] to finish their Theorem 2.4.
Returning to the AR(1) model under discussion in this paper and the estimate  given in (1.2), we obtain the following asymptotic limit result.
given in (1.2), we obtain the following asymptotic limit result.
Theorem 2.2. Let 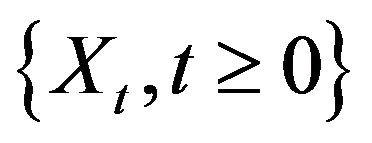 be the stationary solution to the AR(1) recursion
be the stationary solution to the AR(1) recursion 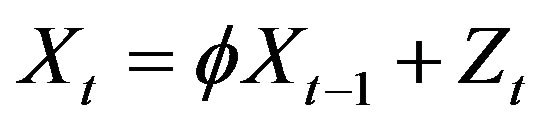 and
and
 . Under the assumptions that
. Under the assumptions that 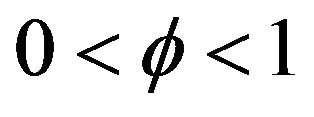
and the innovation distribution F has regularly varying right tail with index 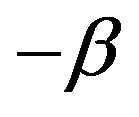 and finite positive left endpoint
and finite positive left endpoint ,
,
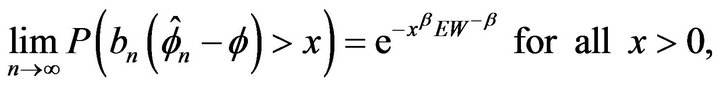
where  and
and .
.
Proof. For 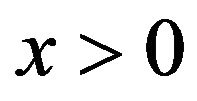 define a subset
define a subset

Then note that for the point processes
 , we have
, we have
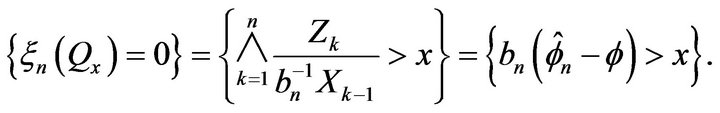
Applying Theorem 2.1 in the case of an AR(1) process so that , we have
, we have

Note that as a subset of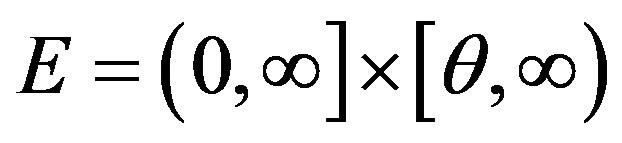 , the set
, the set 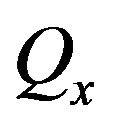 is a bounded continuity set with respect to the limit point process
is a bounded continuity set with respect to the limit point process  so that
so that
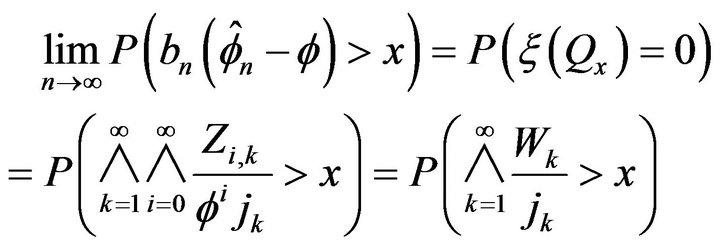
where 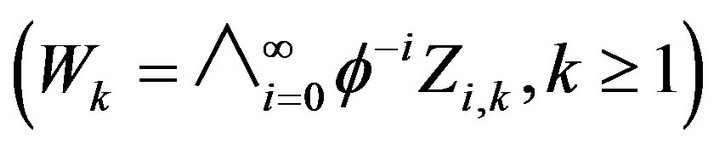 is an i.i.d. sequence independent of
is an i.i.d. sequence independent of . Let
. Let
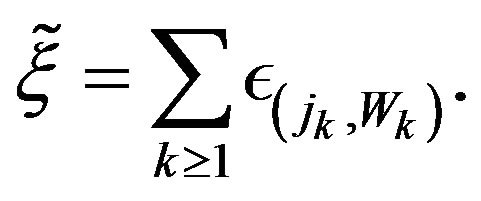 (2.17)
(2.17)
Then by Proposition 5.6 in Resnick [10], we have that if 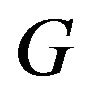 denotes the distribution of
denotes the distribution of , then
, then ![]() is a Poisson random measure on E with mean measure
is a Poisson random measure on E with mean measure , where
, where![]() . Using (2.17) we can write
. Using (2.17) we can write

Since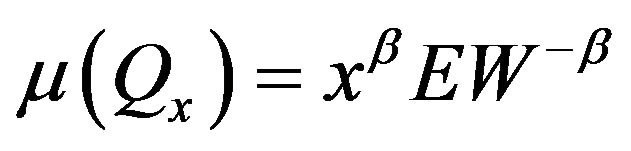 , the result follows.
, the result follows.
Corollary 2.1. Under conditions given in Theorem 2.2,

Proof. Since 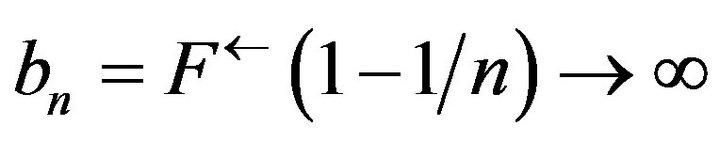 we have
we have
 . But this implies
. But this implies 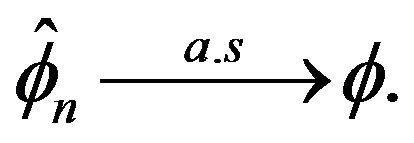 since
since 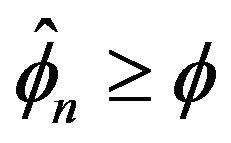
and is non-increasing.
Let us now define our estimate of :
:

where we define the index set
 where
where 
is a fixed value.
Lemma 2.4. Under the assumptions that F is regularly varying with index ![]() at its positive left endpoint
at its positive left endpoint  and
and  is regularly varying with index
is regularly varying with index  at infinity, its right endpoint, and
at infinity, its right endpoint, and , then
, then
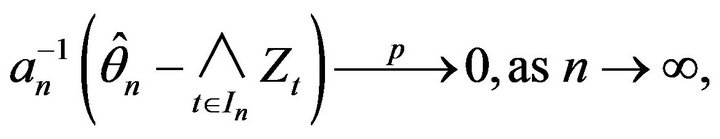
where . Furthermore, for any
. Furthermore, for any 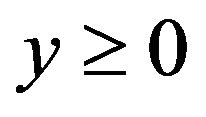
Proof. Since , we have
, we have .
.
Therefore since  is a tight sequence by Theorem 2.2 and since
is a tight sequence by Theorem 2.2 and since ![]() with
with
 , we have
, we have
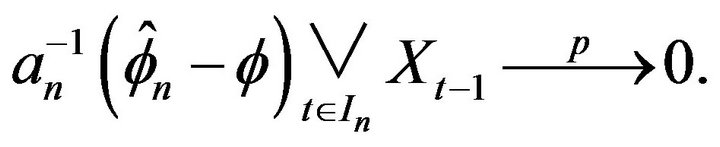
The first statement now follows since
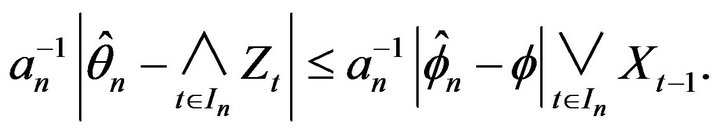
For the second statement observe

(2.18)
The result for the second statement now follows from (2.18) and the first part of the lemma. Finally, the identification of the limit distribution is well known. □
A useful observation follows from this lemma which we state as a corollary.
Corollary 2.2. Under the assumptions of Lemma 2.4 for any 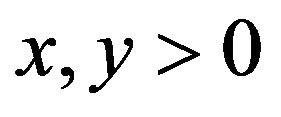

Proof. By Lemma 2.4 we have
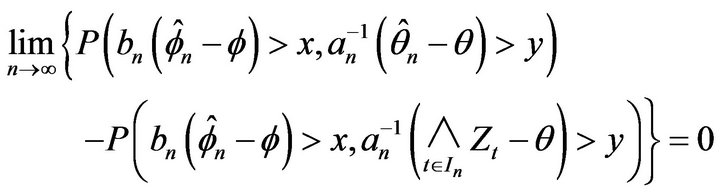
The result then follows from
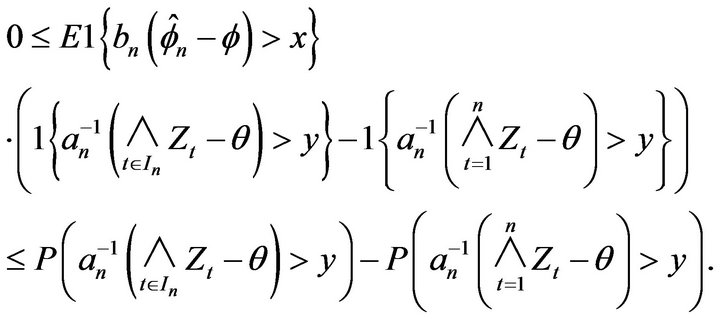
□
Corollary 2.2 allows a simplification in determining the joint asymptotic behavior of 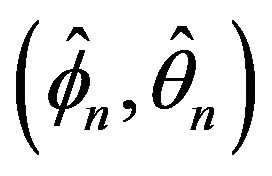 by allowing us to replace
by allowing us to replace  with
with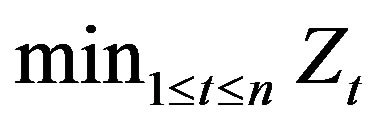 . The next lemma will provide another useful simplification—this time on
. The next lemma will provide another useful simplification—this time on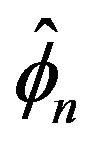 .
.
For a positive integer ![]() define
define
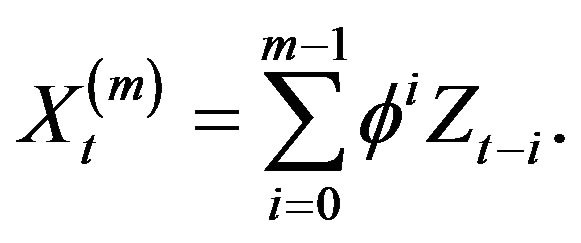
Lemma 2.5. Let  and
and 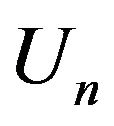 be defined as
be defined as
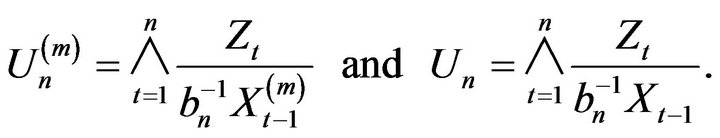
Then for any 
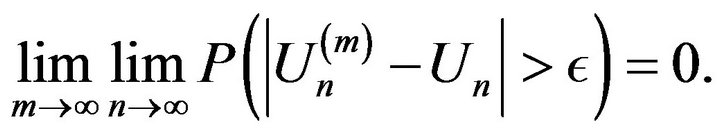
Proof. We first note for any positive  that
that
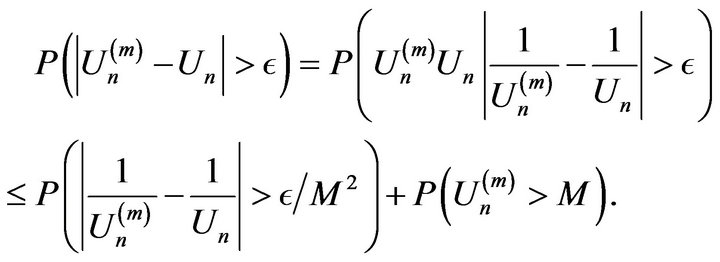
In order to calculate  we partition
we partition
 . That is, we write
. That is, we write

where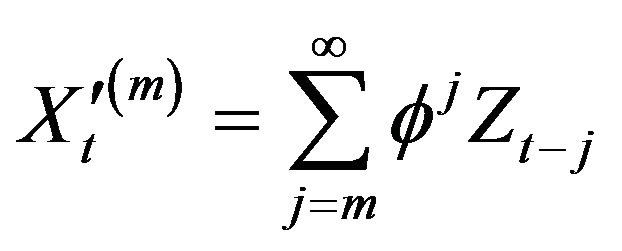 , so that
, so that

Define point processes

where 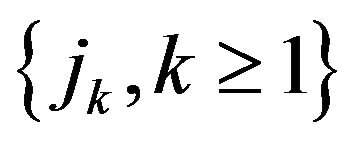 and
and  have the distributional properties given in Theorem 2.2. Applying Theorem 2.2 with
have the distributional properties given in Theorem 2.2. Applying Theorem 2.2 with 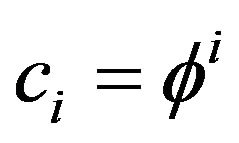 for
for  and
and ![]() equal to 0 otherwise, we obtain
equal to 0 otherwise, we obtain
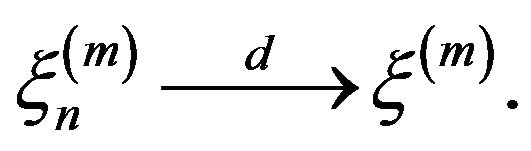
Then letting for 
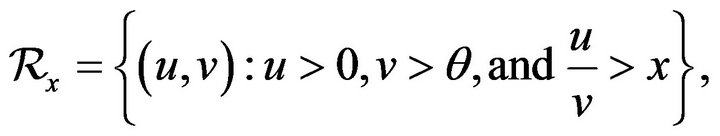
we have
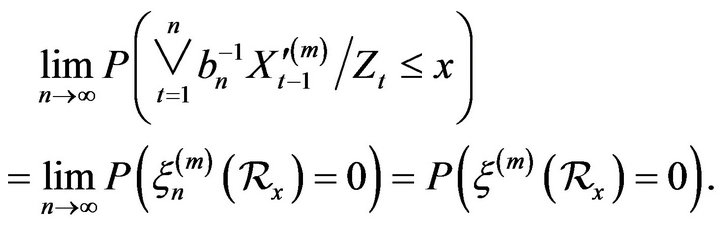
Setting
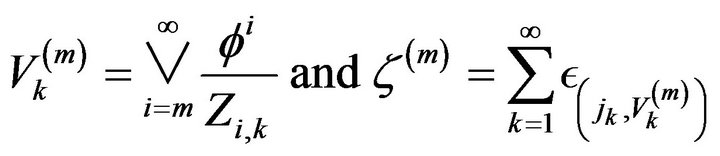
we have
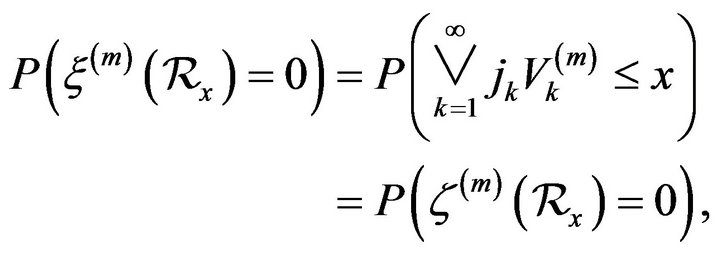
where
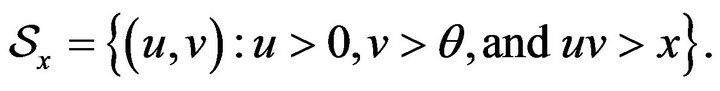
Since ![]() is Poisson random measure with mean measure
is Poisson random measure with mean measure 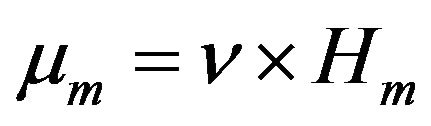 where
where  and
and

we obtain

Next since

we have for large n that

Therefore, since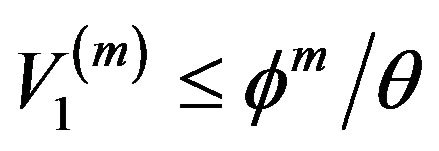 ,
,

Next, note that from the limit law for the maximum obtained above, by replacing  with
with  and by taking reciprocals, we derive the limit law for minimum,
and by taking reciprocals, we derive the limit law for minimum,
 (2.19)
(2.19)
where 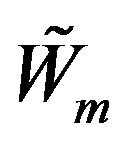 has the distribution of
has the distribution of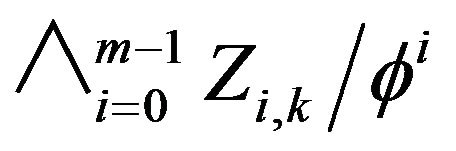 . Thus, for any integer
. Thus, for any integer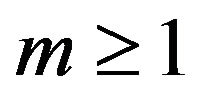 ,
,
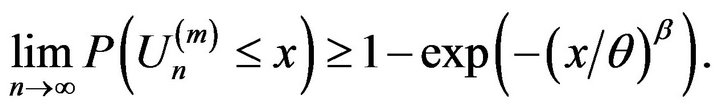
Thus for any , we have for
, we have for  large enough that
large enough that
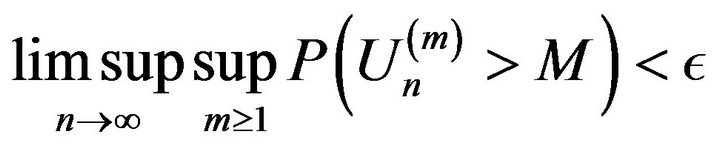
completing the proof. □
With Lemma 2.5 in hand we can now focus our attention to the limiting joint distribution of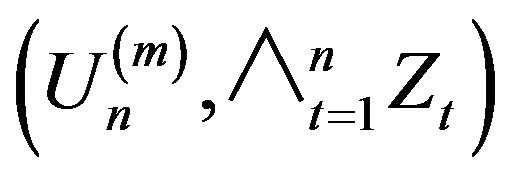 .
.
This will be accomplished by a blocking argument. To that end for a fixed positive integer , let
, let  and define blocks for
and define blocks for 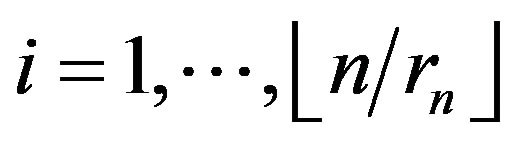 by
by
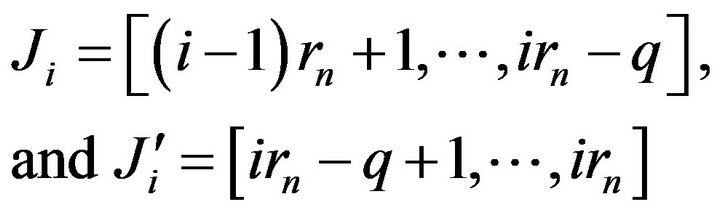
where 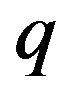 is a positive integer greater than
is a positive integer greater than![]() . Furthermore, let
. Furthermore, let

Now we define the events

and
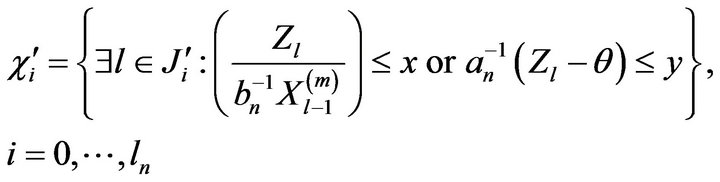
where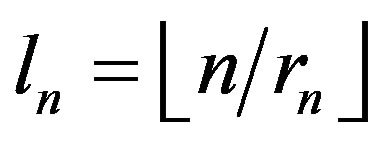 . We begin by showing that the events
. We begin by showing that the events  are negligible.
are negligible.
Lemma 2.6. For any
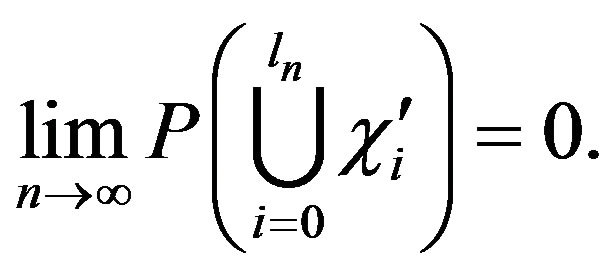
Proof. Observe that
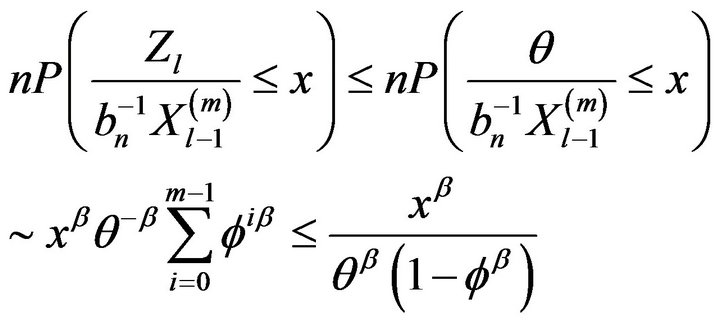 (2.20)
(2.20)
and
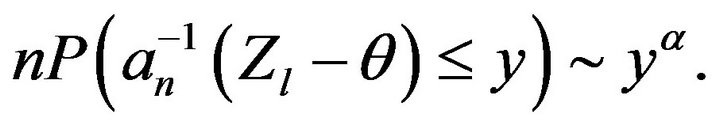 (2.21)
(2.21)
Thus for some constant ![]() and any
and any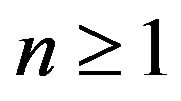 ,
,
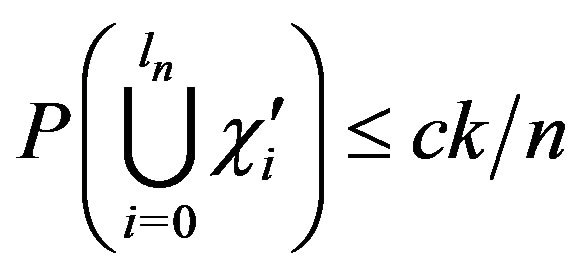
establishing the lemma.
Define events  and
and 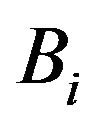 by
by

The following result provides the asymptotic behavior of the probability of these events.
Lemma 2.7. For any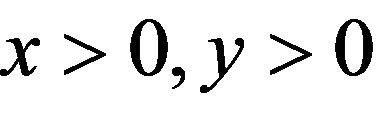 , we have as
, we have as 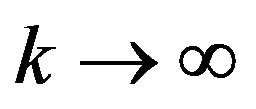
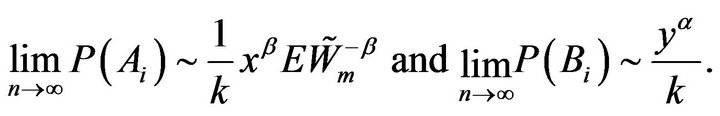
Proof. Since the events 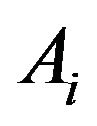 are independent, we have
are independent, we have

Using Lemma 2.6 we have that
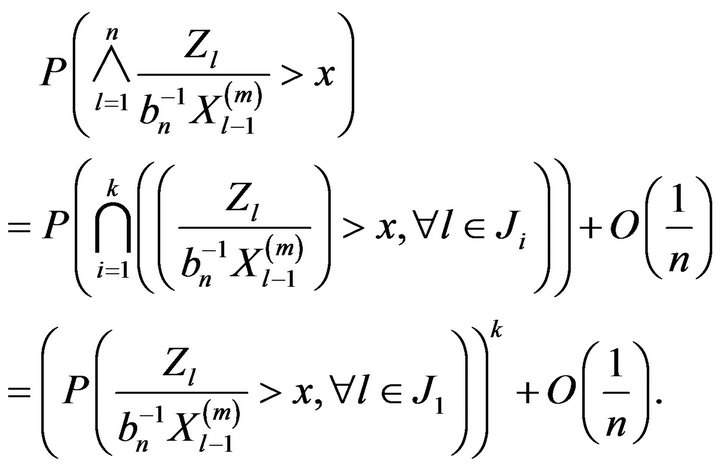
From (2.19) we showed that
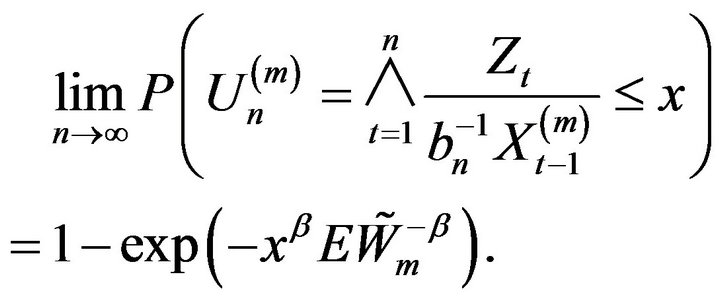
Hence using this limit law on , we obtain
, we obtain

Thus,
 (2.22)
(2.22)
Similarly using the result of Lemma 2.4, we obtain
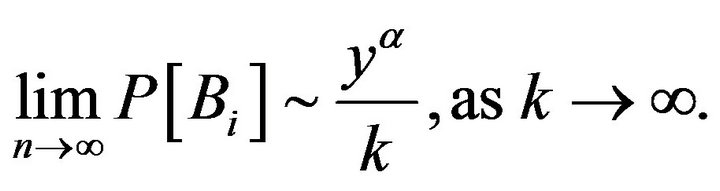 (2.23)
(2.23)
Hence the lemma holds. □
Lemma 2.8. For some constant ![]()
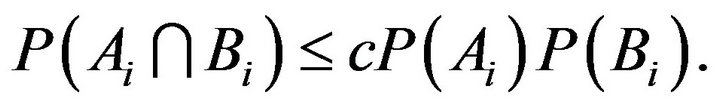
Remark. Since the cardinality of  depends on
depends on ![]() which depends on
which depends on  and the events
and the events 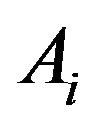 and
and 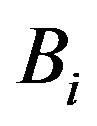 depend on
depend on![]() ,
,  and
and  depend on k and n. The conclusion of this lemma provides that for all
depend on k and n. The conclusion of this lemma provides that for all  and
and![]() , there is a constant dependent on no parameters for which the inequality stated there holds.
, there is a constant dependent on no parameters for which the inequality stated there holds.
Proof. To calculate the intersection we define the following sets
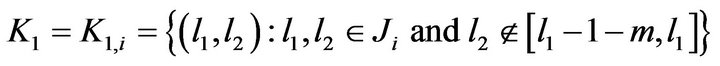
and
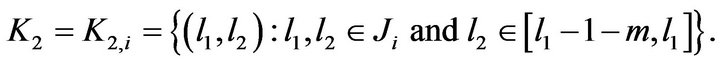
Now for 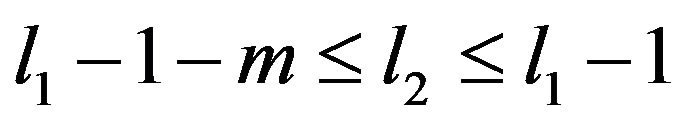 and n sufficiently large,
and n sufficiently large,
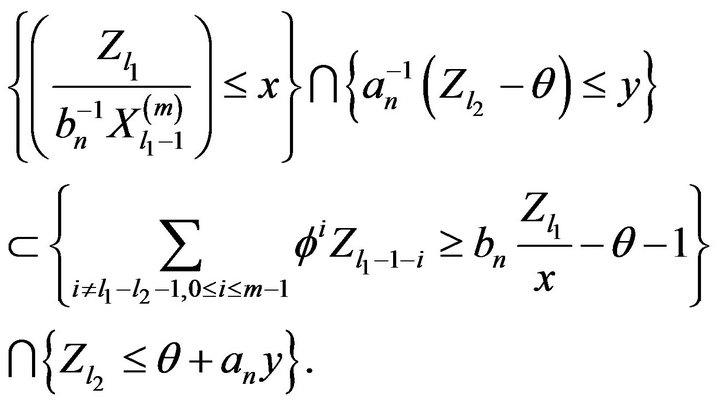
It then follows from (2.20), (2.21), and independence that
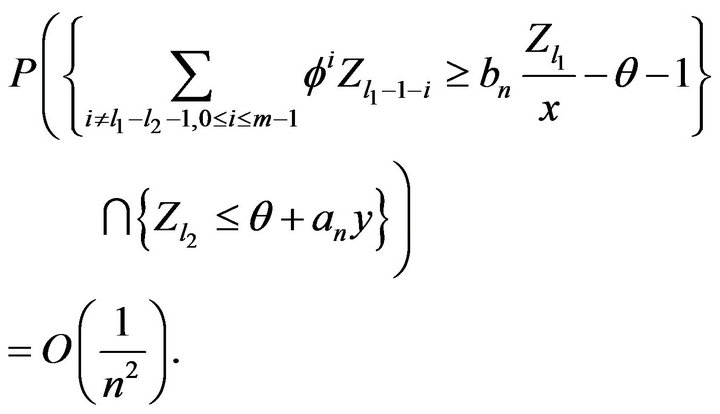
If , we have
, we have
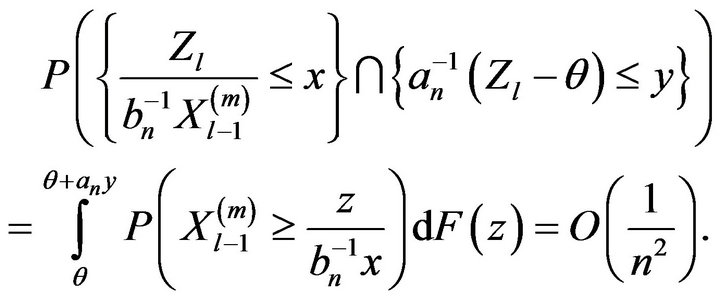
Therefore, for some constant ![]()
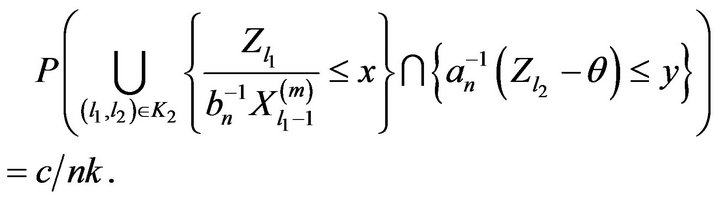
In order to handle set , observe from construction of the blocks
, observe from construction of the blocks 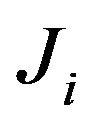 and set
and set 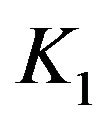 that if
that if  then the events
then the events

are independent. Thus, if we define 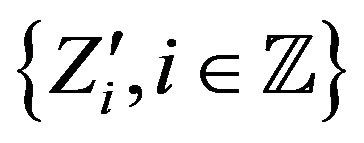 as an independent copy of
as an independent copy of , then
, then
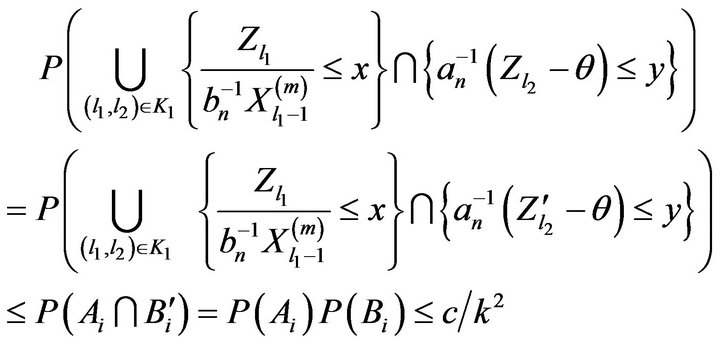
where 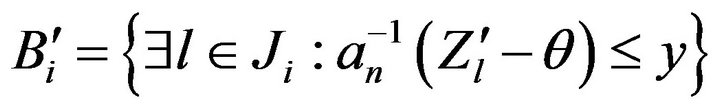 and where we used Lemma 2.7 in the last step. Thus, we have that for some constant
and where we used Lemma 2.7 in the last step. Thus, we have that for some constant ![]()
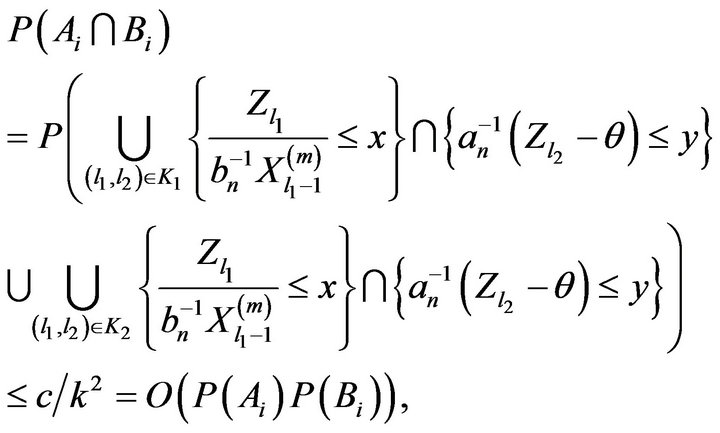
which completes the proof in view of Lemma 2.7. □
Lemma 2.9. For any ,
,
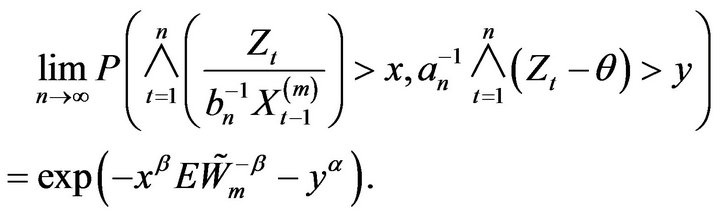
Proof. First from Lemma 2.6, we have as ![]() that
that
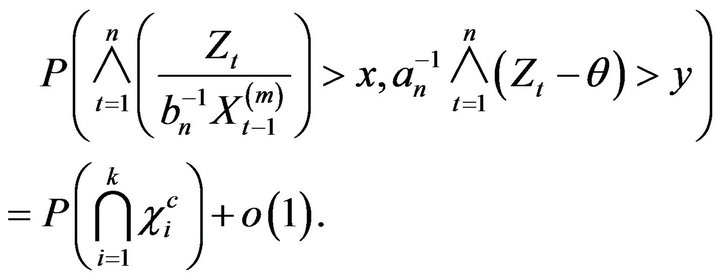
Next by (2.22), (2.23), and Lemma 2.8 we obtain that as 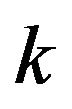 tends to infinity
tends to infinity
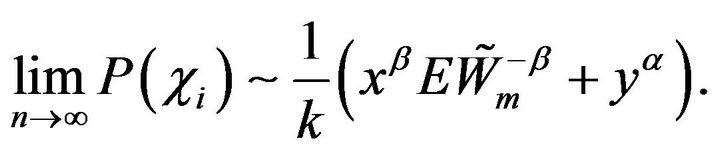
Therefore, we obtain

Hence

□
Theorem 2.3. Let  denote the stationary AR(1) process such that the innovation distribution
denote the stationary AR(1) process such that the innovation distribution 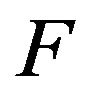 satisfies
satisfies 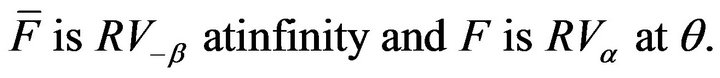
If  then for any
then for any  we have
we have

where .
.
Proof. Let us first observe that for 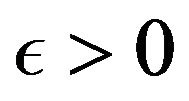

Thus by Lemma 2.9 we obtain

Letting ![]() tend to infinity in the above and then
tend to infinity in the above and then  tend to 0, we obtain from Lemma 2.5 and
tend to 0, we obtain from Lemma 2.5 and 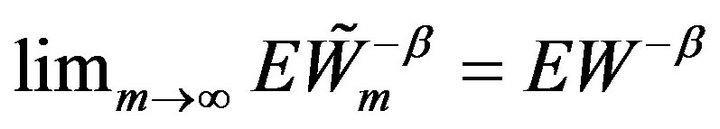 that
that

The theorem now follows from this and Corollary 2.2.
3. Simulation Study
In this section we assess the reliability of our extreme value estimation method through a simulation study. This included a comparison between our estimation procedure and that of three alternative estimation procedures for both the autocorrelation coefficient  and the unknown location parameter
and the unknown location parameter  under two different innovation distributions. Additionally, the degree of approximation for the empirical probabilities of
under two different innovation distributions. Additionally, the degree of approximation for the empirical probabilities of  and
and 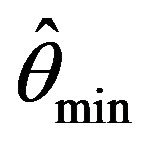 to its respective limiting distribution was reported.
to its respective limiting distribution was reported.
To study the performance of the estimators
 and
and  respectively, we generated 5000 replications for the nonnegative time series
respectively, we generated 5000 replications for the nonnegative time series 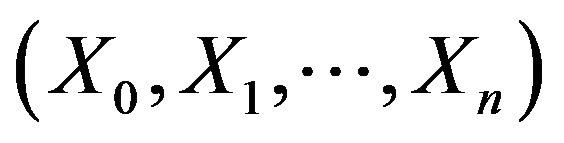 for two different sample sizes (500,1000), where
for two different sample sizes (500,1000), where  is an AR(1) process satisfying the difference equation
is an AR(1) process satisfying the difference equation

The autoregressive parameter  is taken to be in the range from 0 to 1 guaranteeing a nonnegative time series and the unknown location parameter
is taken to be in the range from 0 to 1 guaranteeing a nonnegative time series and the unknown location parameter  is positive when the innovations
is positive when the innovations 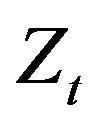 are taken to be
are taken to be

For this innovation distribution let ![]() and
and ![]() be nonnegative constants such that
be nonnegative constants such that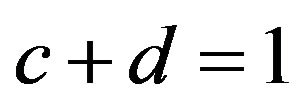 , then this distribution is regularly varying at both endpoints with index of regular variation
, then this distribution is regularly varying at both endpoints with index of regular variation  at infinity and index of regular variation
at infinity and index of regular variation ![]() at
at . For this simulation study two distributions were considered:
. For this simulation study two distributions were considered: 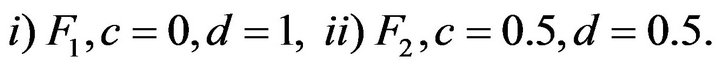
Now observe in case i) the innovation distribution  is a Pareto distribution with a regular varying tail distribution at
is a Pareto distribution with a regular varying tail distribution at  with index of regular variation
with index of regular variation 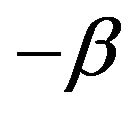 and regular varying at
and regular varying at 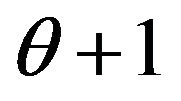 with a fixed index
with a fixed index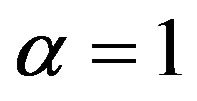 , whereas in case ii) the innovation distribution
, whereas in case ii) the innovation distribution  is regular varying at
is regular varying at  and
and  with no restriction on
with no restriction on ![]() or
or .
.
First we examine the simulation results for 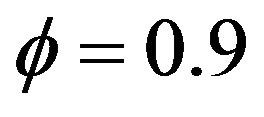 under
under  for each of the six different
for each of the six different  values considered by computing 5000 estimates using
values considered by computing 5000 estimates using
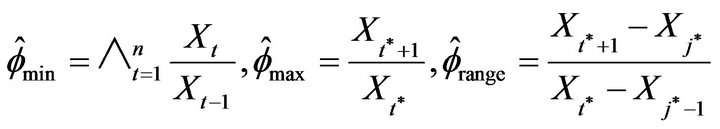 where
where ![]() and
and  provides the index of the maximal and minimal
provides the index of the maximal and minimal 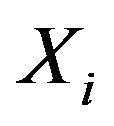 respectively for
respectively for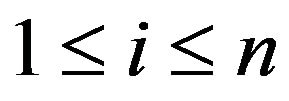 , and
, and

where . The means and standard deviations (written below in parentheses), of these estimates are reported in Table 1 along with the average
. The means and standard deviations (written below in parentheses), of these estimates are reported in Table 1 along with the average

Table 1. Comparison of estimators for f = 0.9 under F1.
length for a  percent empirical confidence intervals with exact coverage. Since the main purpose of this section is to compare our estimator
percent empirical confidence intervals with exact coverage. Since the main purpose of this section is to compare our estimator  to Bartlett and McCormick [5] estimator
to Bartlett and McCormick [5] estimator , McCormick and Mathew [2] estimator
, McCormick and Mathew [2] estimator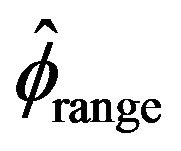 , and Davis and Resnick’s [13] estimator
, and Davis and Resnick’s [13] estimator , the confidence intervals were directly constructed from the empirical distributions of
, the confidence intervals were directly constructed from the empirical distributions of
 respectively.
respectively.
To evaluate and compare the performance of four location estimators, six different scenarios for ![]() and
and  are presented in Table 2 under
are presented in Table 2 under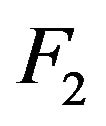 . When
. When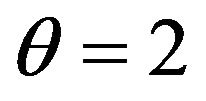 , 5000 estimates for each estimator;
, 5000 estimates for each estimator;
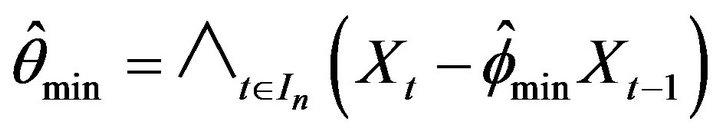 ,
, ![]() ,
, 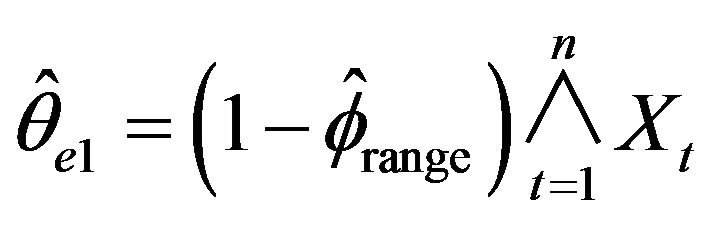 , and
, and 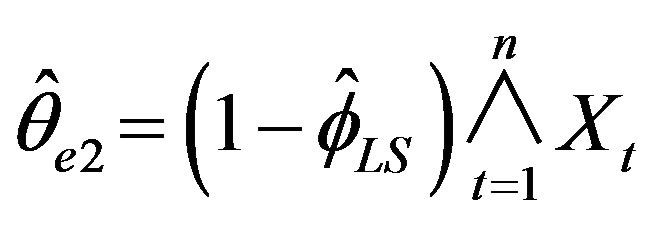 were obtained. The exponent
were obtained. The exponent  inside the index set
inside the index set
 , was set to 0.9.
, was set to 0.9.
The means and standard deviations (written below in parentheses), of these estimates are reported in Table 2 along with the average length for a 95 percent empirical confidence intervals. For convenience, the empirical distributions of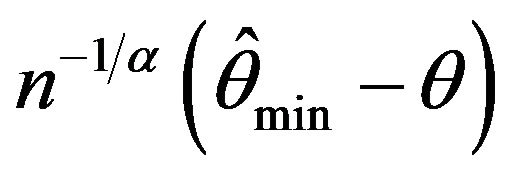 ,
, 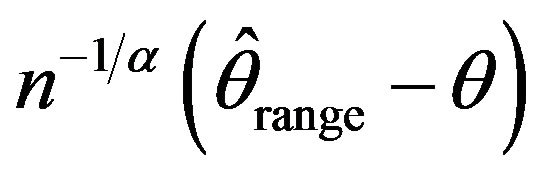 ,
,
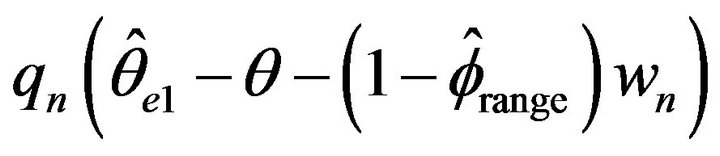 , and
, and
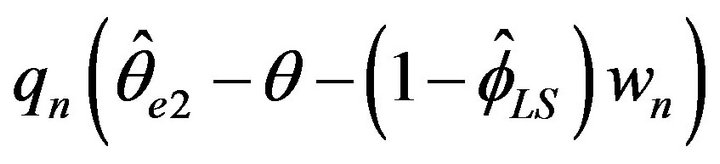 were respectively used, where the normalizing constants
were respectively used, where the normalizing constants  and
and  are obtained through Equations (3.12)-(3.16) of McCormick and Mathew [2].
are obtained through Equations (3.12)-(3.16) of McCormick and Mathew [2].
Remark. In the case that ,
, 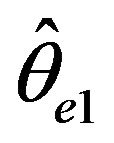 converge at
converge at

Table 2. Comparison of estimators for f = 2 under F2.
a faster rate than 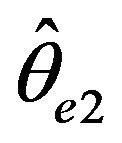 and in the case that
and in the case that ,
,  converges at a faster rate than
converges at a faster rate than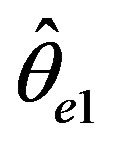 . Lastly, since the McCormick and Mathew [2] paper has the restriction that
. Lastly, since the McCormick and Mathew [2] paper has the restriction that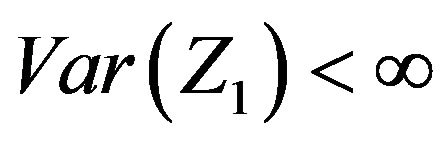 , only when
, only when 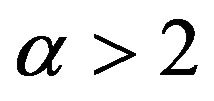 can the estimators
can the estimators  and
and  be fairly compared, whereas only when
be fairly compared, whereas only when 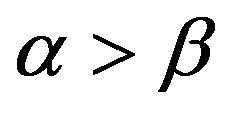 is our estimator applicable.
is our estimator applicable.
Now observe for the selected  values being considered, Table 1 shows that our estimator performs at least as well as the three other alternative estimators. This is particularly true under the heavier tail models, i.e. when
values being considered, Table 1 shows that our estimator performs at least as well as the three other alternative estimators. This is particularly true under the heavier tail models, i.e. when . In this regime our estimate shows little bias and the average lengths of the confidence intervals are smaller than the other three estimates, sometimes by a wide margin. In particular, when
. In this regime our estimate shows little bias and the average lengths of the confidence intervals are smaller than the other three estimates, sometimes by a wide margin. In particular, when 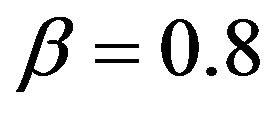 and n = 1000 the
and n = 1000 the 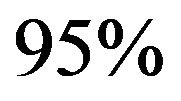 confidence interval average length for our method is 3.13, 5.78 and
confidence interval average length for our method is 3.13, 5.78 and  times smaller than the three alternative estimators respectively. This is in part due to the use of one-sided confidence intervals since
times smaller than the three alternative estimators respectively. This is in part due to the use of one-sided confidence intervals since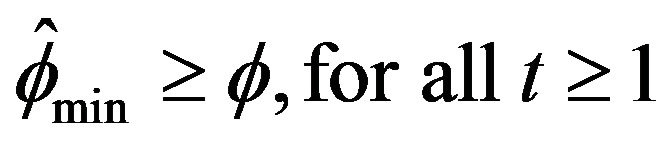 . Naturally, when
. Naturally, when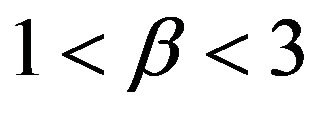 , Davis and Resnick least square estimator is more efficient than all three extreme value estimators. While our estimator
, Davis and Resnick least square estimator is more efficient than all three extreme value estimators. While our estimator  will always perform slightly better than the
will always perform slightly better than the 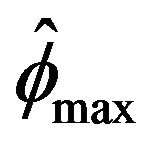
estimator, Bartlett’s and McCormick [5] estimator 
main advantage lies with its versatility to perform well for various nonnegative time series, including but not restricted to higher order autoregressive models, along with ARMA models.
Table 2 reveals that our estimator for  generally performs better than the three alternative estimators for
generally performs better than the three alternative estimators for 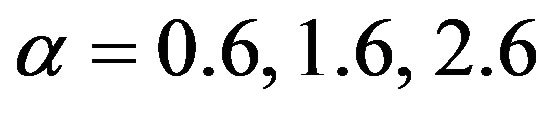 when
when . This is particularly true when comparing average confidence interval lengths. Although all three estimators
. This is particularly true when comparing average confidence interval lengths. Although all three estimators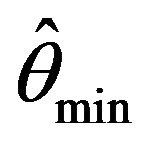 ,
, 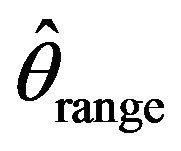 , and
, and  converge to the true value of the parameter
converge to the true value of the parameter  as
as ![]() tends to infinity respectively, in this setting they may not compete asymptotically with, say, a conditional least square estimator
tends to infinity respectively, in this setting they may not compete asymptotically with, say, a conditional least square estimator 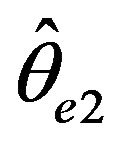 when
when . Nonetheless for small sample sizes our simulation study favors
. Nonetheless for small sample sizes our simulation study favors 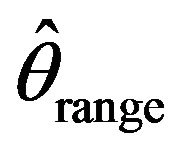 over the other three estimators. The difficulty for a least square estimate is that a small negative bias for the estimate of the autocorrelation parameter
over the other three estimators. The difficulty for a least square estimate is that a small negative bias for the estimate of the autocorrelation parameter 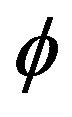 gives rise to a much larger positive bias in the estimate of
gives rise to a much larger positive bias in the estimate of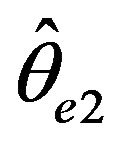 . While the affect is not as great, the positive bias found in our estimator
. While the affect is not as great, the positive bias found in our estimator  and the others for
and the others for  has a significant effect on the estimate for
has a significant effect on the estimate for .
.
Figures 1-4 show a comparison be tween the probability that estimators ,
, 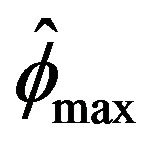 ,
, 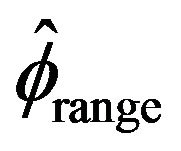 , and
, and 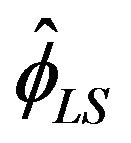 are within 0.01 of the true autocorrelation parameter value, respectively. With a sample size of 500, these figures plotted the sample fraction of estimates which fell within a bound of
are within 0.01 of the true autocorrelation parameter value, respectively. With a sample size of 500, these figures plotted the sample fraction of estimates which fell within a bound of 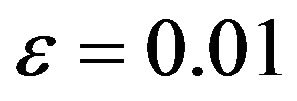 of the true value. Good performance with respect to this measure is reflected in curves near to 1.0 with diminishing good behavior as curves approach 0.0. When
of the true value. Good performance with respect to this measure is reflected in curves near to 1.0 with diminishing good behavior as curves approach 0.0. When , the figures seem to show that our estimator compared to the other three
, the figures seem to show that our estimator compared to the other three
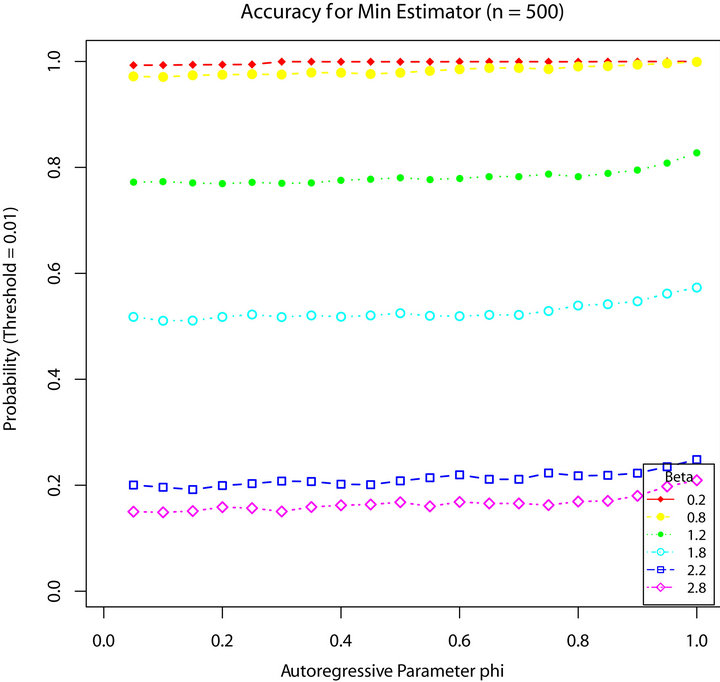
Figure 1.  for
for .
.

Figure 2.  for
for .
.
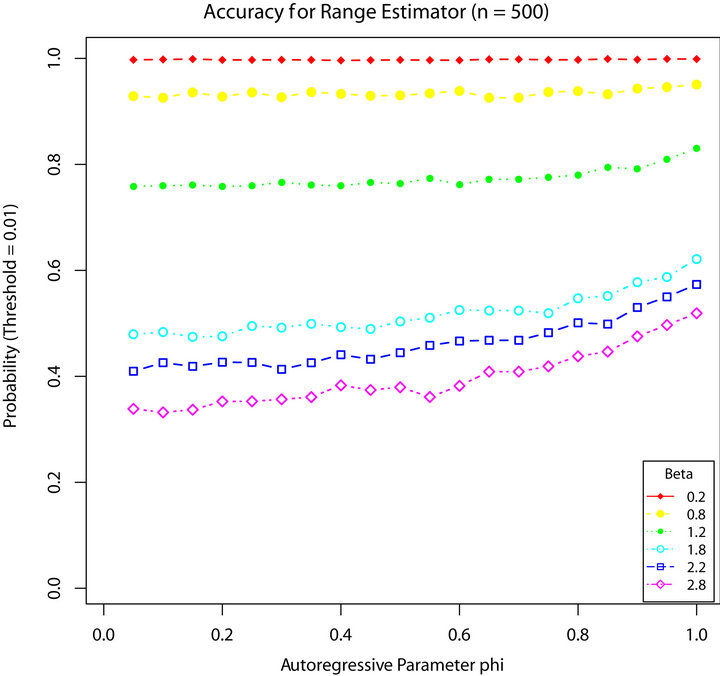
Figure 3.  for
for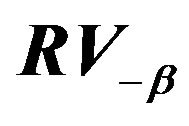 .
.

Figure 4. 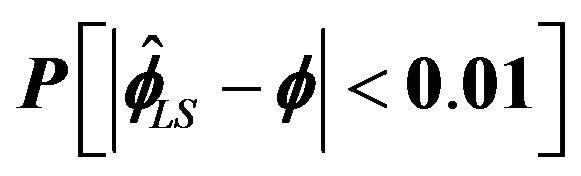 for
for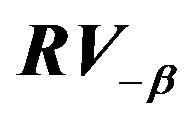 .
.

Figure 5. Empirical vs. theoretical probability.
produced a higher fraction of precise estimates, especially compared to Davis and Resnick estimator. When the regular variation index value is closer to 2, we see a higher fraction of the Davis-Resnick estimates showing better accuracy by this measure. The figures also indicate that McCormick and Mathew’s range estimator produced a consistent high fraction of precise estimates when .
.
Lastly, we performed a Monte Carlo simulation to study the degree of approximation for the empirical probability ,
, 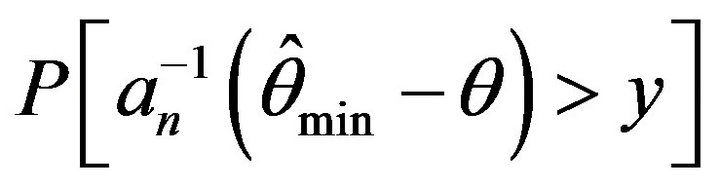 , and
, and  to its limiting values
to its limiting values ,
, ![]() , and
, and  respectively. The empirical distributions were calculated from 5000 replications of the nonnegative time series
respectively. The empirical distributions were calculated from 5000 replications of the nonnegative time series  for a sample size of 5000, where
for a sample size of 5000, where
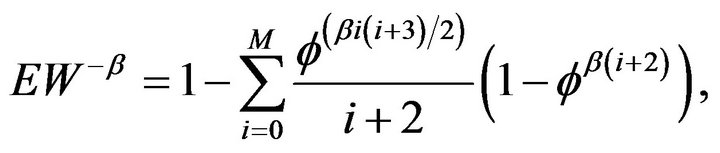 and M was set to 500. Additionally, we restricted
and M was set to 500. Additionally, we restricted . The top two plots in Figure 5 below shows the performance when
. The top two plots in Figure 5 below shows the performance when 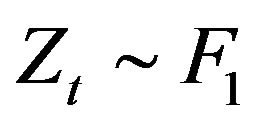 and the autocorrelation coefficient
and the autocorrelation coefficient 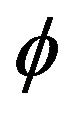 is
is  for
for 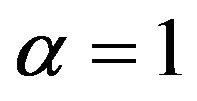 and
and  equal to 0.8, 1.5 respectively. Observe for
equal to 0.8, 1.5 respectively. Observe for  that the empirical tail probability
that the empirical tail probability
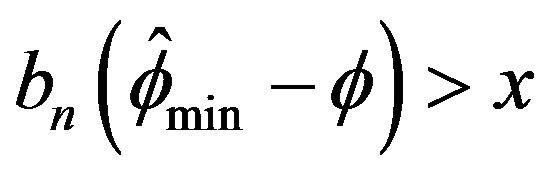 mirrors the theoretical probability quite nicely. The lower left plot in Figure 5 displays the asymptotic performance when
mirrors the theoretical probability quite nicely. The lower left plot in Figure 5 displays the asymptotic performance when 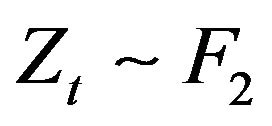 and the location parameter
and the location parameter  is
is  for
for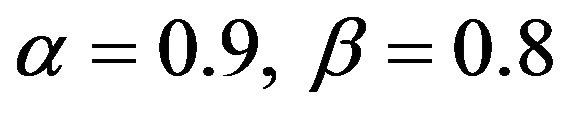 . Notice that the convergence rate of the empirical probability to the theoretical probability is extremely slow. This is not surprising since on average our estimate falls more than 0.1 from the true value when
. Notice that the convergence rate of the empirical probability to the theoretical probability is extremely slow. This is not surprising since on average our estimate falls more than 0.1 from the true value when . The lower right plot in Figure 5 displays the asymptotic performance when
. The lower right plot in Figure 5 displays the asymptotic performance when
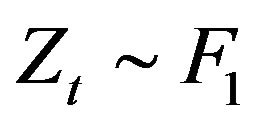 for the joint distribution of
for the joint distribution of . Observe that this plot solidifies the asymptotic independence between
. Observe that this plot solidifies the asymptotic independence between 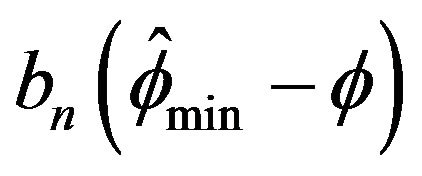 and
and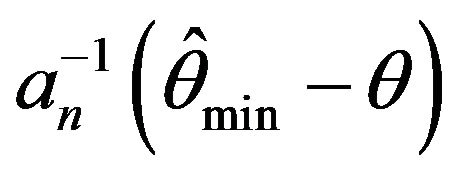 .
.
REFERENCES
- P. J. Brockwell and R. A Davis, “Time Series: Theory and Methods,” 2nd Edition, Springer, New York, 1987.
- W. P. McCormick and G. Mathew, “Estimation for Nonnegative Autoregressive Processes with an Unknown Location Parameter,” Journal of Time Series Analysis, Vol. 14, No. 1, 1993, pp. 71-92. doi:10.1111/j.1467-9892.1993.tb00130.x
- A. E. Raftery, “Estimation Eficace Pour un Processus Autoregressif Exponentiel a Densite Discontinue,” Publications de l’Institut de Statistique de l’Université de Paris, Vol. 25, No. 1, 1980, pp. 65-91.
- R. A. Davis and W. P. McCormick, “Estimation for FirstOrder Autoregressive Processes with Positive or Bounded Innovations,” Stochastic Processes and Their Applications, Vol. 31, No. 1, 1989, pp. 237-250. doi:10.1016/0304-4149(89)90090-2
- A. Bartlett and W. P. McCormick, “Estimation for NonNegative Time Series with Heavy-Tail Innovations,” Journal of Time Series Analysis, 2012. http://onlinelibrary.wiley.com/journal/10.1111/%28ISSN%291467-9892/earlyview
- S. I. Resnick, “Point Processes, Regular Variation and Weak Convergence,” Advances in Applied Probability, Vol. 18, No. 1, 1986, pp. 66-138. doi:10.2307/1427239
- Jiří Anděl, “Non-Negative Autoregressive Processes,” Journal of Time Series Analysis, Vol. 10, No. 1, 1989, pp. 1-11. doi:10.1111/j.1467-9892.1989.tb00011.x
- Jiří Anděl, “Non-Negative Linear Processes,” Applications of Mathematics, Vol. 36, No. 1, 1991, pp. 277-283.
- S. Datta and W. P. McCormick, “Bootstrap Inference for a First-Order Autoregression with Positive Innovations,” Journal of American Statistical Association, Vol. 90, No. 1, 1995, pp. 1289-1300. doi:10.1080/01621459.1995.10476633
- S. I. Resnick, “Heavy-Tail Phenomena: Probabilistic and Statistical Modeling,” Springer, New York, 2007.
- R. A. Davis and S. Resnick, “Limit Theory for Moving Averages of Random Variables with Regularly Varying Tail Probabilities,” Annals of Probability, Vol. 13, No. 1, 1985, pp. 179-195. doi:10.1214/aop/1176993074
- O. Kallenberg, “Random Measures,” Akademie-Verlag, Berlin, 1976.
- R. A. Davis and S. Resnick, “Limit Theory for the Sample Covariance and Correlation Functions of Moving Averages,” Annals of Statistics, Vol. 14, No. 1, 1986, pp. 533-558. doi:10.1214/aos/1176349937

