ABSTRACT

A game swaption, newly proposed in this paper, is a game version of usual interest- rate swaptions. It provides the both parties, fixed-rate payer and variable rate payer, with the right that they can choose an exercise time to enter a swap from a set of prespecified multiple exercise opportunities. We evaluate two types of game swaptions: game spot-start swaption and game forward-start swaption, under the generalized Ho-Lee model. The generalized Ho-Lee model is an arbitrage-free binomial- lattice interest-rate model. Using the generalized Ho-Lee model as a term structure model of interest rates, we propose an evaluation method of the arbitrage-free price for the game swaptions via a stochastic game formulation, and illustrate its effectiveness by some numerical results.

Keywords:

Generalized Ho-Lee Model, Game Spot-Start Swaption, Game Forward-Start Swaption, Stochastic Game Formulation, Dynamic Programming Approach

1. Introduction

A game swaption, newly proposed in this paper, is a kind of exotic interest-rate derivatives whose payoff depends on interest rates or bond prices. After the early 1980’s, many financial institutions have served such exotic derivatives to respond various needs of clients. In general, it is commonly known that there is not any analytical solution to the pricing problems of many exotic derivatives due to their structural complexity, and the valuation of these derivatives has to rely on a method of a numerical computation. In order to evaluate such derivatives, tree methods and finite difference methods are widely used in many financial institutions.

In this paper, we propose an evaluation method of exotic interest-rate derivatives via a tree method based on the generalized Ho-Lee model [1] , which is a discrete-time and arbitrage-free term-structure model of interest rates. Since Ho and Lee [2] firstly proposed an arbitrage-free binomial term-structure model of interest rates (Ho-Lee model), several authors have been proposed new discrete-time term-structure models of interest rates in order to extend and/or sophisticate the Ho-Lee model (see e.g. Chapter 13 of van der Hoek and Elliott [3] ). Among them, in the generalized Ho-Lee model recently proposed by Ho and Lee themselves, the stochastic movements of term structure of interest rates are also expressed on a binomial lattice. It seems very promising in the sense that since the volatilities of interest rates on the lattice are dependent on time and states it gives us a very flexible framework of interest-rate processes to express various real term-structure movements. In particular, there is a strong point that the model includes the term structure of interest rates (discount function, yield curve, and/or forward curve) in all nodes on the binomial lattice so that it enables us straightforward valuation of fundamental interest-rate instruments and variables such as prices of fixed and variable coupon bonds, and swap rates, etc.

In this paper, we consider valuation problems of swaptions with game features. Several papers have addressed such valuation problems of interest-rate derivatives with some game structures. Among them, Ben et al. [4] discussed the pricing problem of an option-embedded bond with game characteristics, where they approximately calculated the value of that derivative based on a continuous-time interest-rate model by applying a dynamic programming approach. In contrast, Ochiai and Ohnishi [5] dealt with a similar problem in a discrete-time binomial lattice and applied directly a dynamic programming approach based on the generalized Ho-Lee model. The theory on which we base in this paper is in the spirit of them [5] for valuating exotic interest-rate derivatives via a discrete-time and arbitrage-free term-structure model of interest rates.

A game swaption, newly proposed in this paper, is a game version of usual interest- rate swaptions. A usual swaption provides only one side of the two parties (fixed- rate payer and variable rate payer) with the right to enter a swap at a predetermined future time. In contrast, a game swaption provides the both parties with the right of choosing an exercise time to enter a swap from a set of prespecified multiple exercise opportunities. We evaluate two types of game swaptions: game spot-start swaption and game forward-start swaption. A game spot-start swaption allows us to enter the swap at the next setting time just after the exercise time, while a game forward-start swaption entitles us to enter the swap at a predetermined fixed calendar time regardless of the exercise time. In order to formulate the valuation problem of these two game swaptions, we apply a stochastic game formulation. The theory of stochastic games was originated by the seminal paper of Shapley [6] . Players in a stochastic game play a series of stage games that depend on a time and a state. Using the generalized Ho-Lee model, we can apply the stochastic game theory to formulate our problem as a finite time-horizon and two-person zero-sum stochastic game on a binomial lattice under the risk-neutral probability. Then, the no-arbitrage price of the game swaption is evaluated as the value of the whole game by using a backward induction algorithm based on a dynamic programming principle. Owing to the above mentioned nice feature of the generalized Ho-Lee model, all nodes on the binomial lattice involve fundamental informations about the term structure of interest rates, and accordingly we can execute the backward induction algorithm very effectively.

This paper is organized as follows. We introduce and explain the generalized Ho-Lee model in the next Section 2. In Section 3, we first illustrate the game spot-start swaption and derive the optimality equation to evaluate the no-arbitrage values of the game spot-start swaption. Then, Section 4 provides the valuation for the game forward-start swaption as in the previous Section 3. Some numerical examples for these two game swaptions are shown in Section 5. Finally, we conclude the main contributions in this paper.

2. The Generalized Ho-Lee Model

The generalized Ho-Lee model is an arbitrage-free binomial-lattice interest-rate model, where time is discrete. Let 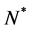be a finite time-horizon and 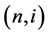be a node on the binomial lattice where n (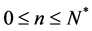) denotes a time and i (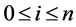) a state. 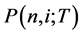represents the zero-coupon bond price at node 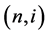with a remaining maturity of T (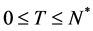) period, which pays 1 at the end of the T-th period. We have 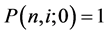for any n and i according to the definition of default-free discount bond. Moreover, the zero-coupon bond prices for any remaining maturity T at the initial time, 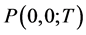, can be observed in the initial market, and the set of these prices determines the discount function, yield curve, and/or forward curve at the initial time 0.

In order to represent the degree of uncertainty of interest rates on the binomial lattice, we introduce the binomial volatilities 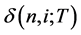(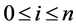).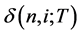is the proportional decrease in the one-period bond value from i to i + 1 at time n, and 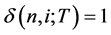implies that there is no risk. The binomial volatility 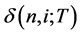is defined by

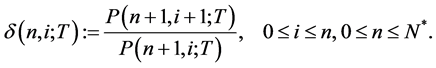(1)

As the binomial volatilities become bigger, the uncertainty of interest rates also increases more. Let 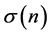be the term structure of volatilities of interest rates. Ho and Lee [1] assumed that the function 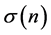is given by

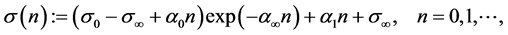(2)

where is the short-rate volatility over the first period, is approximately the short-rate forward volatility at sufficiently large time n, and and are the short-term and long-term slopes of the term structure of volatilities, respectively.

Then, the one-period binomial volatility is defined by

(3)

where denotes the one-period yield, R the threshold rate, and the time interval.

The generalized Ho-Lee model is an arbitrage-free term-structure model of interest rates. Therefore, the bond prices for all different maturities at each node are modeled to satisfy the risk-neutral valuation formula:

(4)

under the risk-neutral probability, where we assume for simplicity that the transition probabilities have the same for the up-state and down-state movements at the next period. Then, the arbitrage-free condition for the generalized Ho-Lee model is given by

(5)

By using straightforwardly Equations (1) and (4), we can confirm Equation (5) to be an arbitrage-free condition. Thereby, as long as the T-period binomial volatility is defined by Equation (5), the generalized Ho-Lee model is no-arbitrage. Then, the one- period bond prices at node for the generalized Ho-Lee model are given by

(6)

Similarly, the T-period bond prices at node are given by

(7)

Next, we explain the algorithm to derive the one-period bond prices based on the above arguments. The constructions of the generalized Ho-Lee model are decomposed into the following five steps:

Step 1. Derive one-period bond price at node:

(8)

Step 2. Derive one-period bond price at node:

(9)

Step 3. Derive one-period yields by one-period bond price:

(10)

Step 4. Derive one-period binomial volatilities:

(11)

Step 5. Derive T-period binomial volatilities:

(12)

3. Valuation of Game Spot-Start Swaption

Game swaptions can be classified into two types with respect to the timing of entering into the underlying swap. A game spot-start swaption allows us to enter the swap at the next setting time just after an exercise, while a game forward-start swaption allows us to enter the swap at a predetermined calender time regardless of the exercise time. First, in this section, we consider the game spot-start swaption.

A (plain vanilla) swap is an agreement to exchange a fixed rate and a variable rate (or floating rate) for a common notional principal over a prespecified period (e.g., Hull [7] , Kolb [8] ). We usually refer LIBOR (London Interbank Offered Rate) as the variable interest rate. A usual swaption is an option on a swap. A payer swaption gives the holder the right to enter a particular swap agreement as the fixed-rate payer. On the other hand, a receiver swaption gives the holder the right to enter a particular swap agreement as the fixed rate receiver. The holder of a European swaption is allowed to enter the swap only on the expiration time. In contrast, the holder of an American swaption is allowed to enter the swap on any time that falls within a range of two time instants. A Bermudan swaption, which we refer in this paper, allows its holder to enter the swap on multiple prespecified times.

In this paper, we consider a game swaption which is an extension of Bermudan swaption. The game swaption entitles both of the fixed-rate side and variable-rate side to enter into the swap at multiple prespecified times. The sequence of setting/payment times is

(13)

where N is an agreement time of the swap, are the L setting/payment times, and is a finite time-horizon. Now, we suppose that for a game spot-start swaption. We assume that he time periods are equidistant, and, for some unit time,

(14)

For the following discussions, we further let.

Let be a spot-start swap rate at an agreement time N. The spot-start swap rate, , specifies the fixed rate that makes the value of the interest-rate swap equal zero at the agreement time N, and it is given by

(15)

Next, we define the exercise rate for a game swaption. If the fixed-rate side exercises at an exercisable time, he will pay the fixed rate over the future period of swap. If the variable-rate side exercises, the fixed-rate side has to pay the fixed rate over the future period. If the both sides simultaneously exercise, the fixed-rate side has to pay the fixed rate. Naturally, we suppose

(16)

Moreover, the sets, of multiple exercisable times for the fixed-rate side and the variable-rate side, and the prespecified exercisable time-intervals are given by

(17)

(18)

respectively. We let. When the game spot-start swaption is exercised at an admissible exercise node, the payoff value of the spot-start swap with a fixed rate at the node is considered to be given by

(19)

Now, we apply the theory of two-person and zero-sum stopping game to the valuation of the game swaption. The players of the game are the fixed-rate-payer side and the variable-rate-payer side. We shortly call them fixed-rate player and variable-rate player, respectively. At a jointly exercisable node (n, i) (), the fixed-rate player chooses a pure strategy x and the variable-rate player chooses a pure strategy y from the set of pure strategies. Suppose that a pure-strategy profile (pair) is selected at a node, and denote the payoff value of the spot-start swap at the node as.

Definition 3.1. When the game spot-start swaption is exercised at an exercisable node, the payoff value of the game spot-start swaption is given by

(20)

If the both players do not exercise at an admissible time, the stochastic game moves to the following node

(21)

at the next time, where is a random state of interest rates at time.

Then, the both players face a two-person and zero-sum stage game whose payoff is dependent on a state of interest rates and their strategies at every exercisable nodes (). In this stochastic game, the fixed- rate player chooses a strategy to maximize her payoff, while the variable-rate player chooses a strategy to minimize his payoff.

Given a two-person and zero-sum game specified by a payoff matrix , we define the value of the game as follows:

(22)

where is an m-dimensional probability vector representing a mixed strategy for the row player, is an n-dimensional probability vector representing a mixed strategy for the column player, and the second equality is due to the von Neumann Minimax Theorem.

Let be the value of the game spot-start swaption at node. Then, we can derive it by solving the following equations backwardly in time:

Step 0. (Terminal condition) for,

(23)

Step 1. (Recursion) from to 0,

Case 1-1. (When both players can exercise) for,

(24)

Case 1-2. (When only fixed-rate player can exercise) for,

(25)

Case 1-3. (When only variable-rate player can exercise) for,

(26)

Case 1-4. (When neither player can exercise) for

(27)

where is the one-period discount factor at node based on the generalized Ho-Lee model, is the risk-neutral probability measure, is the conditional expectation given node, is the random state of interest rate at, and we define a continuation value at node by

(28)

In the terminal condition, , we have according to the maturity of the game swaption.

At a node where both players can exercise, we need to solve the following two-person and zero-sum game:

(29)

where the fixed-rate side chooses the row as a maximizer and the variable-rate side chooses the column as a minimizer. In general, a saddle point equilibrium of two-person and zero-sum game is known to exist in mixed strategies including pure strategies. However, the following theorem shows that the above game has a saddle point in pure strategies.

Theorem 1. Suppose, that is, or. Then, at a jointly exercisable node (), the stage matrix-game played at the node has a saddle point in pure strategies:

(30)

where x and y are pure strategies of the fixed-rate player and the variable-rate player, respectively. Furthermore, if we denote E and N the pure strategies “Exercise” and “Not Exercise”, respectively, then the equilibrium-strategy profile is as follows:

(31)

Proof. We suppose the former case. The latter case can be dealt very similarly. Then, we have

(32)

1) If then pure strategy N of the variable-rate player is the weakly dominant strategy for him. Its best response strategy for the fixed-rate player is pure strategy E, therefore is a saddle point.

2) If then pure strategy N is the weakly dominant strategy for both players, and is a saddle point.

3) If then the fixed-rate player chooses a pure strategy N that is the strictly dominant strategy because she is the maximizer. Its best response strategy for the variable-rate player is pure strategy E, therefore is a saddle point.

4. Valuation of Game Forward-Start Swaption

A game forward-start swaption entitles the both parties to enter into the swap at a predetermined calender time regardless of the exercise time. It is more practical than the game spot-start swaptions. The solution method is similar to the game spot-start swaptions, thus we discuss only the different points.

In previous section, we suppose that the sequence of setting/payment times of the game spot-start swaption starts. For a game forward-start swaption, we define the distance between N and:

(33)

Then, a forward-start swap rate at an agreement time N is given by

(34)

Note that decreases with increasing N because the remaining maturity must decrease with postponing the exercise time. We assume that the fixed rates of the game forward-start swaption and the set of exercisable opportunities are the same as that shown in Section 3. The payoff value of the forward-start swap with a fixed rate is

(35)

As in the previous section, we apply a stochastic game formulation to the valuation of the game forward-start swaption. At a jointly exercisable node, the fixed-rate player chooses a strategy x and the variable-rate player chooses a strategy y from the pure strategy set.

Definition 4.1. When the game forward-start swaption is exercised at an exercisable node, the payoff value of the game forward-start swaption is given by

(36)

Let be the value of a game forward-start swaption at node. Then, as before, we can obtain it by solving the following equations backwardly in time:

Step 0. (Terminal condition) for,

(37)

Step 1. (Recursion) from to 0,

Case 1-1. (When both players can exercise) for,

(38)

Case 1-2. (When only fixed-rate player can exercise) for,

(39)

Case 1-3. (When only variable-rate player can exercise) for,

(40)

Case 1-4. (When neither player can exercise) for,

(41)

where we define a continuation value at node by

(42)

The following theorem shows that the above game for the forward-start swaption has a saddle point in pure strategies.

Theorem 2. Suppose, that is, or. Then, at a jointly exercisable node (), the stage matrix-game played at the node has a saddle point in pure strategies:

(43)

Furthermore, the equilibrium strategy profiles in the stage-matrix game are as follows:

(44)

Proof. Since the proof is almost the same as Theorem 1, it is omitted.

5. Numerical Examples

In this section, we show some numerical examples for a game spot-start swaption and a game forward-start swaption. Firstly, we consider a game spot-start swaption with the swaption maturity of 5 years, the protection period of 1 year, and the swap period of 5 years. The both players can choose to exercise at any time in prescribed exercisable time-intervals after the protection period. If either or both players exercise the option, they enter the 5-years swap at the next setting/payment time. We set, , and. The parameters in the generalized Ho-Lee model are set as follows: (3 months), , and a flat yield curve of 5%. Table 1 shows the (skewed) binomial tree for an American-type game spot-start swaption. The horizontal axis represents time n, the vertical axis state i, the leftmost node the initilal node, and the rightmost nodes the maturity node of the swaption. In Table 1, an up-state transition in a next time (on the binomial tree) corresponds to a move to the upper-right, while a down-state transition in a next time a move to the right. We assume that the both players can exercise the option at any time except the 1-year protection period, namely from time 4 to time 20.

The upper surrounded area stands for the exercise area of the fixed-rate player, while the lower surrounded area stands for the one of the variable-rate player. According to the numerical results, we can confirm that the spot-start swap rate is increased with an increase in state i for any time n. In exercisable nodes, the aim for the fixed-rate player is to maximize the payoff value of because she is a maximizer. Consequently, when the spot-swap rates are higher (state i is larger), she would exercise the right of the swaption. On the other hand, the aim for the variable-rate player is to minimize the payoff value of because of his minimizing objective, and thereby he would exercise the right of the swaption with a decrease in the spot-swap rate. A value in Table 1 stands for the value of the swaption for the fixed-rate player. Thus, a negative value in a node means that the spot-start swaption is favorable for the variable-rate player in that situation. Furthermore, if both players never exercise the option, the value of the spot-start swaption is equal to zero, because it signifies the value of exercising the right for the players.

Next, Table 2 shows a (skewed) binomial tree for a Bermudan-type game spot-start swaption. The Bermudan-type swaption permits the both players to exercise at a time every year, namely time. In addition, the only fixed-rate player can

also exercise at any time. As with Table 1, the upper surrounded area represents the exercise area for the fixed-rate player, while the lower surrounded area represents the exercise area for the variable-rate player.

Finally, we consider a game forward-start swaption. The game forward-start swap- tion is the agreement where the protection period is 1 year, the swap starts at the 5th year later, and the swap period is 5 years. The both players can exercise the option at any time after the protection period of 1 year to the maturity of the swaption, namely from time 4 to time 20. If either player exercises at a time, the corresponding swap starts from the 5th year regardless of the exercise time, namely from time 21. The numerical results are displayed in Table 3. In contrast to Table 1, the exercise areas in Table 3 are smaller in both the fixed-rate player and the variable-rate player than those in Table 1. The influence is probably caused by an increase in the discount factor of Equation (35) due to the forward-start swaption. Moreover, Table 1 shows that the exercise areas of both players for the forward-start swaption are closed in the following meaning: once the pair of time and state enters into one of the exercise areas it does never go out from that area no matter what would happen thereafter. Since this observation was obtained only from some numerical examples, further studies are needed in order to verify analytically whether this property is valid in general.

6. Concluding Remarks

This paper newly proposed game swaptions as game versions of a Bermudan swaption. These game swaptions are also considered as generalizations of the receiver swaption and payer swaption. Furthermore, in this paper, with respect to the time to start the underlying swap, we treated two types of game swaptions, that is, game spot-start swaption and game forward-start swaption.

In a plain vanilla interest-rate swap, although, at the agreement time of the contract (ex ante), by setting the fixed exercise rate as the swap rate at that time, the fair value of the contract can be almost zero, it will be possible to become largely positive for one of two parties and largely negative for the other party as time passes (ex post) because of a large change in variable interest rate.

On the other hand, concerning the usual swaptions, since the option (right) to enter the underlying swap is given only to one party, its value continues to be positive for that party regardless of realized changes in variable interest rate, and it will be possible to become largely positive for that party and largely negative for the other party.

In contrast, in the case of our newly proposed game swaptions, like a plain vanilla interest-rate swap, by appropriately setting the three exercise rates, , and, the fair value of the contract to the both parties at the agreement time (ex ante) can be made to be almost zero. In addition, after the possible large changes in variable interest rates as time passes (ex post), since the both parties have the option (right) to enter the underlying swap, the value of the contract will not become too unfavorable for the both of two parties, we can say that, with this excellent features, the game swaptions can be suitably designed to reduce possible contract risks for both parties.

In this paper, we proposed computational methods for no-arbitrage prices and exercise areas of these game spot-start swaptions under the generalized Ho-Lee model as the term-structure model of interest rate. Although we have confirmed the effectiveness of our proposed algorithms by some numerical examples, further mathematical analysis of the structure of the exercise areas of both players in both game swaptions is remained as our future research.

Acknowledgements

The authors would like to express sincere thanks to an anonymous reviewer for helpful comments on an earlier version of this paper, and they are also grateful to an author assistant of Scientific Research Publishing and an editorial assistant of Journal of Mathematical Finance.

Cite this paper

Ebina, A., Ochiai, N. and Ohnishi, M. (2016) Valuation of Game Swaptions under the Generalized Ho- Lee Model. Journal of Mathematical Fi- nance, 6, 1002-1016. http://dx.doi.org/10.4236/jmf.2016.65065

References