ABSTRACT

In this paper we suggest a simple mathematical procedure to derive the classical probability density of quantum systems via Bohr’s correspondence principle. Using Fourier expansions for the classical and quantum distributions, we assume that the Fourier coefficients coincide for the case of large quantum number. We illustrate the procedure by analyzing the classical limit for the quantum harmonic oscillator and the particle in a box, although the method is quite general. We find, in an analytical fashion, the classical distribution arising from the quantum one as the zeroth order term in an expansion in powers of Planck’s constant. We interpret the correction terms as residual quantum effects at the microscopic-macroscopic boundary.

1. Introduction

In physics, a new theory should not only describe phenomena unexplained by the old theory but must also be consistent with it in the appropriate limit [1]. In this sense, Newtonian mechanics can be recovered from relativistic mechanics in the domain of low velocities compared with the speed of light in the vacuum. Since its formulation, quantum mechanics has established itself as the most successful physical theory for the description of microscopic systems, such as atoms and elementary particles. Unlike special and general relativity, relations between classical and quantum mechanics are more subtle, given that the conceptual framework of these theories are fundamentally different. While in classical mechanics it is possible to know the exact position and momentum of a particle at any given time, quantum mechanics only specifies the probability of finding a particle at a certain position [2].

The first statement of a mathematical procedure to obtain the classical limit of quantum mechanics can be traced back to Max Planck [3]. He postulated that classical results can be recovered from quantum ones when Planck’s constant is taken to zero. Planck originally formulated this limit to show that his energy density for black body radiation approaches the classical RayleighJeans energy density when. A different approach is due to Niels Bohr [4]. He postulated that the classical behavior of periodic quantum systems can be determined when the principal quantum number is large. Bohr enunciated it in this way because in his model of the hydrogen atom the transition frequency between two neighboring energy levels tends to the classical orbital frequency of the electron when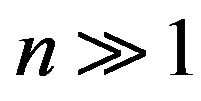. Some researchers, however, have argued that the two methods are not equivalent [5-7].

Textbooks and articles on quantum mechanics usually discuss a variety of ways to make the connection between classical and quantum physics. Most of them are based on either Planck’s limit or Bohr’s correspondence principle. For example, the WKB [8-10] and quantum potential [11] methods and the phase space formulation of quantum mechanics are discussed using Planck’s limit, while some authors [2,12] compare the classical and quantum probability densities for both position and momentum, showing that these distributions approach each other in a locally averaged sense (coarse-graining) for large quantum number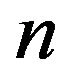. There are other proposals, like Ehrenfest’s theorem [13], based on semi-classical approximations to quantum mechanics. Another method is by means of coherent states. The standard coherent states of the one-dimensional harmonic oscillator [14-16] are localized wave packets which follow the classical equations of motion. However, for non-quadratic Hamiltonians this only holds approximately over short times.

Wigner’s phase-space formulation of quantum mechanics offers a comprehensive framework in which quantum phenomena can be described using classical language. The Wigner distribution function (WDF), however, does not satisfy the conventional properties of a probability distribution [17]; e.g., WDF is in general positive semi-definite. Therefore, in order to interpret it as a classical probability distribution, strictly one needs to restrict the analysis to situations where it is non-negative (this is the case for coherent and squeezed vacuum states only) [18,19]. W. B. Case has made a careful discussion of the classical limit and its difficulties via WDF [20].

According to Bohr’s correspondence principle, classical mechanics is expected to be valid in the regime in which dynamical variables are large compared to the relevant quantum units [21]. In addition, some authors [2, 12,22,23] suggest that we must compare the same physical quantities in both approaches, e.g. probability distributions and not trajectories or wave functions.

In 1924, Heisenberg made an attempt to give Bohr’s correspondence principle an exact mathematical form in order to apply to simple quantum systems. He suggested that for a classical quantity 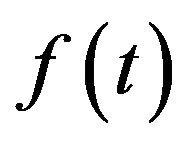in the case of large quantum numbers, the following approximate relation is valid:

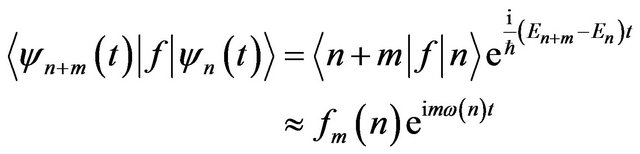(1)

where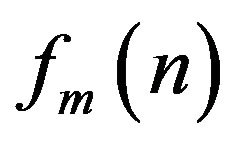 is the mth Fourier component of the classical variable 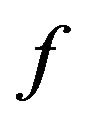and is the classical frequency [24,25]. The application of this procedure, however, was limited to the study of light polarization in atoms subject to resonant fluorescence [26,27].

In 1926, E. Schrödinger proposed a different application of the correspondence principle applied to the quantum harmonic oscillator. His approximation consists of adding all the wave function oscillation modes, generating a semiclassical wave packet [28], from which other interesting ideas have recently evolved [29,30]. On the other hand, discrepancies and discussion remains about the adequacy of Bohr’s correspondence principle [31-34]. Some authors suggest that the harmonic oscillator does not have a true classical limit when described by means of stationary states [35] and others argue that this system violates Bohr’s correspondence principle [36].

2. General Procedure

In this paper, we suggest a conceptually simple mathematical procedure to connect the classical and quantum probability densities using Bohr’s correspondence principle.

It is well know that for periodic systems, the quantum probability distribution (QPD) 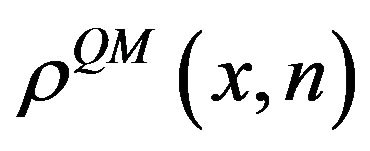is an oscillatory function, while the classical probability distribution (CPD) 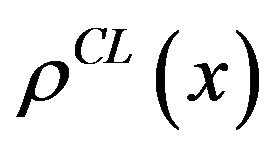does not have this behavior. However, both functions can be written as a Fourier expansion, i.e.

(2)

where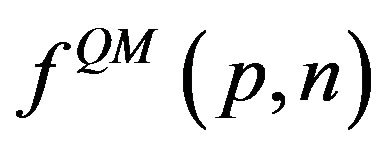 and are the quantum and classical Fourier coefficients, respectively. In addition, we know that for simple periodic systems these distributions approach each other in a locally averaged sense for large quantum numbers. This implies that the Fourier expansion coefficients should approach each other for: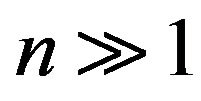

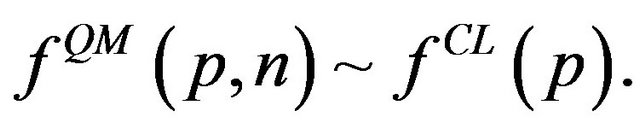(3)

In order to make this comparison we first substitute the value of the principal quantum number by equating the quantum and classical expressions [2,12,23]. Note that the Planck constant keeps a finite value, so 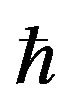-dependent corrections may arise in Equation (3).

Our proposal can be summarized as follows. First we calculate the coefficients of the expansion 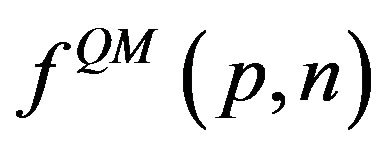by using the Fourier transform of QPD, and then obtain its asymptotic behavior for large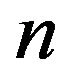. We then equate the classical and quantum expressions for the energy, to define the value of the principal quantum number. Finally calculating the inverse Fourier transform we obtain, at least in a first approximation, the CPD. The procedure can be also applied to probability distributions in momentum space.

3. Examples

The quantum mechanical systems we consider are the harmonic oscillator and the particle in a box. We find, in an analytical fashion, the classical distribution arising from the quantum one.

3.1. Harmonic Oscillator

The QPD for a one-dimensional harmonic oscillator is given by

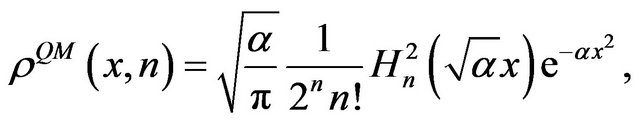(4)

where 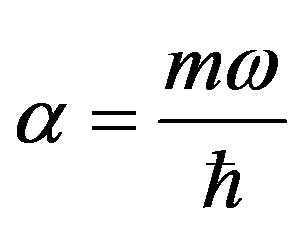[21,22]. One of the main differences between the classical and quantum descriptions of the harmonic oscillator is that the QPD is distributed completely throughout the x-axis, while the CPD is bounded by the classical amplitude. However, when increase the value of the principal quantum number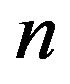, the QPD exhibits a confinement effect, akin to the classical behavior.

We now calculate the Fourier coefficients. The corresponding integral can be found in many handbooks of mathematical functions [37,38]:

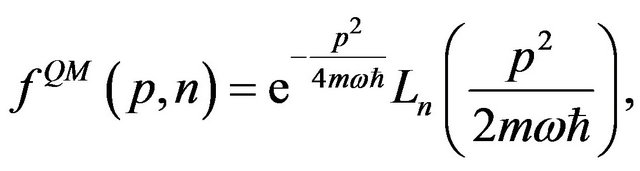(5)

where is a Laguerre polynomial of degree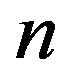. We remark that the mathematical structure of the coefficients 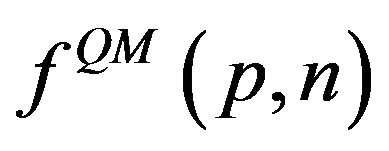is similar to the Wigner function for the harmonic oscillator [39], but formally different, due to the dependence of the wave functions on parity [40]. Technically, the WDF is a member of the Cohen class of phase-space distributions which is related to the fractional Fourier transform [41], and not with the usual Fourier transform as is the case for the expansion coefficients.

The asymptotic behavior of Fourier coefficients for n large is also well known. Szegӧ [42] finds the following iterative relation:

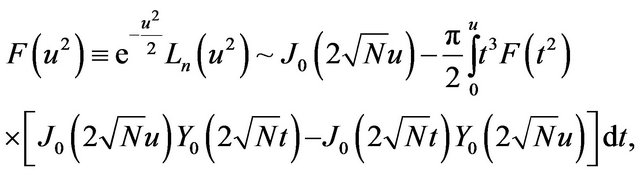(6)

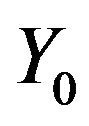where and are the usual Bessel functions of the first and second kind respectively, and.

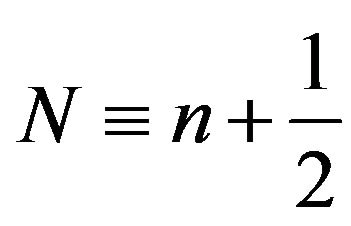Szegӧ shows that in 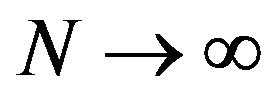limit the iteration terms are strongly suppressed compared to 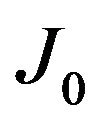Bessel function.

Using the above relation and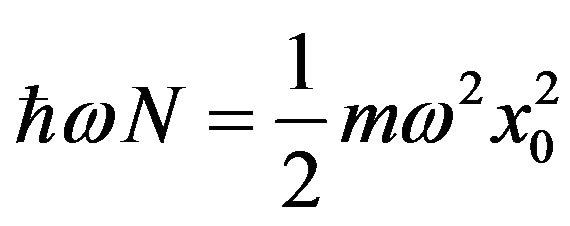, we can write the asymptotic expression for the Fourier coefficients as follows

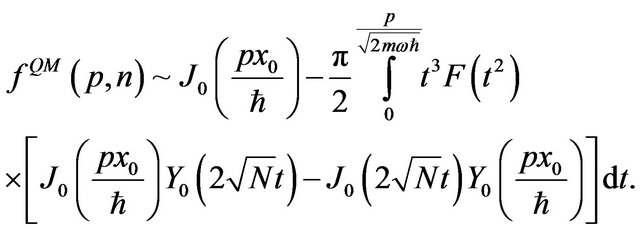(7)

Finally, we compute the inverse Fourier transform. The first term can be obtained directly, while the iterated terms can be written as dimensionless integrals

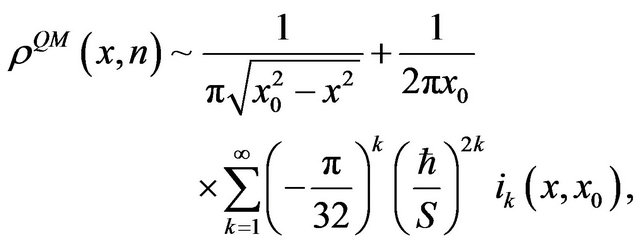(8)

where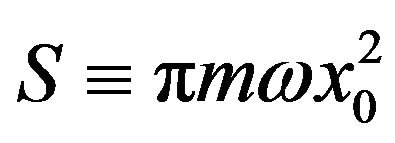 is the classical action and the 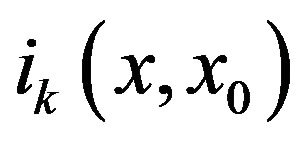is the dimensionless integral. In particular:

(9)

We can also evaluate higher order iterations in a simple fashion [42].

Note that the first term in equation (8) is 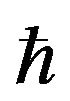-independient and corresponds exactly with the CPD [2,12]. The remaining terms are proportional to increasing powers of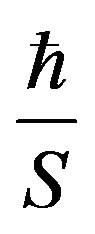, which are very small for classical systemsso these terms are strongly suppressed compared with the CPD. A residual oscillatory behavior, as observed in the QPD is preserved through the harmonic behavior of the iterated integrals. If we now consider Planck’s limit, the classical result is exactly recovered. This, however, is not necessary, as the correction terms are very small and seem to reflect a residual quantum behavior at the classical level. In this particular system, a physical quantity that exhibits this residual behavior and can be experimentally tested is the period of oscillation. From Equation (8), we find that at lowest order, the deviation from the classical period T is:

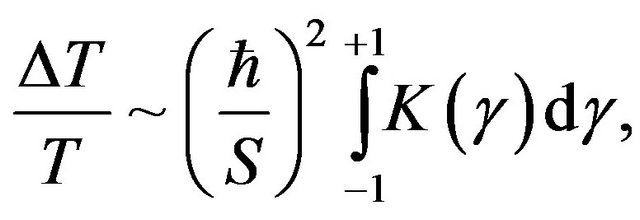(10)

where 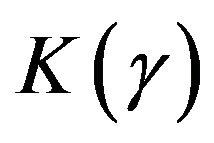is given by

(11)

Therefore, although the deviation is too small to be measured with modern experimental methods, is not zero.

A complete agreement of both the position and momentum distribution functions at the classical limit is necessary for the theory to recover the classical results in the appropriate energy limit [43]. In this case, due to the symmetry of the harmonic oscillator, the QPD in momentum space can be obtained easily, so the asymptotic behavior of the QPD for large quantum numbers is given by:

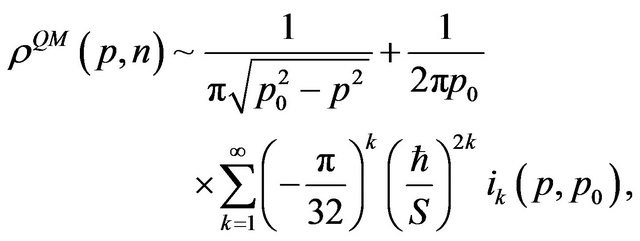(12)

where p₀ is its maximum momentum, 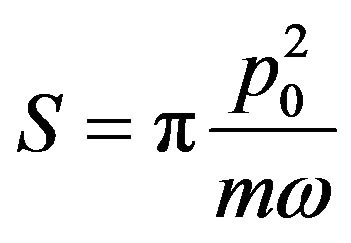is the classical action and 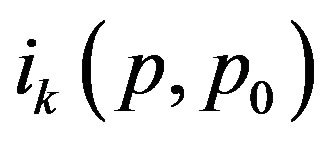is the same dimensionless integral defined by Equation (9).

Expectation values of physical quantities can be calculated using our previous results and the classical values are then recovered, i.e.

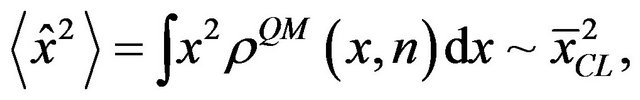(13)

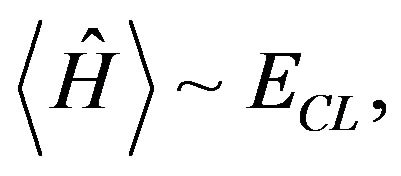
where we have not included the correction terms. These results do not ensure that the time dependence of position and momentum operators defined by the Heisenberg equation reduces to the classical equations of motion, due to the fact that the classical limit is not a single trajectory, but an ensemble of trajectories.

3.2. Particle in a Box

The infinite square well potential is one of the simplest examples discussed in an introductory course on quantum mechanics. This system is instructive for students because it shows the fundamental differences between quantum and classical mechanics; but likewise, should illustrate the quantum-classical transition. We briefly discuss this issue.

The QPD in this case have a simple form [21,22]:

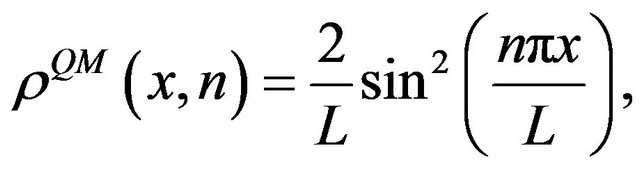(14)

where 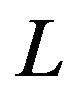is the length of the box. A simple calculation shows that the asymptotic behavior of Fourier coefficients is

(15)

and finally the inverse Fourier transform gives

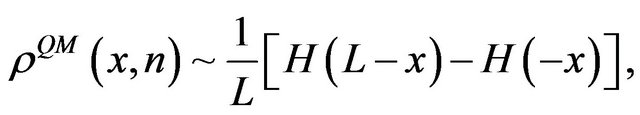(16)

where is the Heaviside step function [37,38]. The above equation coincides with the expected classical result, which is constant CPD inside the well. Thus, the classical expectation values of physical quantities are then recovered.

4. Summary

To summarize, the classical limit problem has been debated since the birth of quantum theory and is still a subject of research. In this paper, we present a simple mathematical formulation of Bohr’s correspondence principle. We consider the simplest quantum system, the harmonic oscillator, and obtain exact classical results. We think that this approach illustrates in a clear fashion the difference between Planck’s limit and Bohr’s correspondence principle.

Finally, using this simple procedure we find corrections to the exact classical result as a series in the ratio

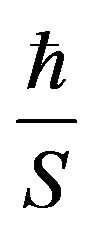, which is very small for classical energies but not zero. It would be interesting to test whether this energy dependence could be observed for the case of real quantum systems approaching the microscopic-macroscopic boundary. We are currently analyzing other simple quantum mechanical systems in order to assess this possibility.

5. Acknowledgements

We thank Alejandro Frank Hoeflich and José Adrián Carabajal Domínguez for their valuable contribution to the fulfillment of this work.

REFERENCES

[44]    NOTES

[45]     

[46]    ^*Corresponding author.

[47]