World Journal of Condensed Matter Physics
Vol. 2 No. 4 (2012) , Article ID: 25064 , 7 pages DOI:10.4236/wjcmp.2012.24044
First-Principles Study on Stability and Magnetism of MAln (M = Ni, Cu) (n = 1 - 9) Clusters
![]()
Department of Physics, Microfluidic Chip Institute, Key Laboratory of Organosilicon Chemistry and Material Technology of Ministry of Education, Hangzhou Normal University, Hangzhou, China.
Email: *phybxli@yahoo.com.cn
Received April 28th, 2012; revised May 30th, 2012; accepted June 13th, 2012
Keywords: NiAl Cluster; CuAl Cluster; Stable Structure; Magnetism
ABSTRACT
We have investigated the structures, stabilities and magnetism of NiAln and CuAln (n = 1 - 9) clusters systematically by using first-principles density functional theory. Our calculated results indicate that most of the ground state structures for the Al clusters doped with one nickel or copper atom are different from those of the corresponding pure Al clusters. NiAln and CuAln (n = 1 - 9) cluster ions have similar geometrical configurations to the corresponding neutral clusters, except for positive NiAl9 ion. The magnetic moments of NiAln (n = odd number) and CuAln (n = even number) cluster anions, neutrals and cations are 0, 1 μB, and 2 μB, respectively. The magnetic moments of NiAl4 and NiAl6 cluster anions, neutrals and cations are associated with 1 μB, 2 μB, and 3 μB, respectively. NiAl2, NiAl8 and CuAln (n = odd number) clusters do not have any net magnetic moment. But, NiAl2 and NiAl8 cluster ions have the net magnetic moment of 1 μB.
1. Introduction
Transition-metal aluminides [1] and nickel-aluminum alloys [2] have attracted much attention due to their wide applications in advanced material technology. Both Albased compounds of transition-metals (TM) [3] and nickel-based superalloys [4-6] are among the most promising candidates for high-performance structural materials. In the nanoscale regime, the nickel-aluminum bimetallic nanocluster has martensitic transformation as temperature alternation, which aroused many studies [7-10]. Their chemical and physical properties may vary with the composition, atomic ordering and the cluster size.
Wen et al. investigated NinAl (n = 2 8) neutral clusters using the density functional theory based on generalized gradient approximation (GGA) with the exchangecorrelation potential (BPW91) [7]. They found that atomization energies per atom for NinAl (n = 2 - 8) clusters has the same trend as the binding energies per atom for Nin (n = 3 - 9) clusters. Ni5Al is the relatively most stable structure in the series. Ni average magnetic moment decreases when alloyed with Al atoms than that in pure Ni clusters. Wang et al. [8] calculated the magnetic properties of MAln (M = Cr, Mn, Fe, Co, Ni; n =1 - 7, 12)
clusters using density-functional theory based on generalized gradient approximation. They found that the MAln clusters have similar geometries as that of Aln+1 clusters. The computed total magnetic moments of the lowest-energy structures oscillate with the cluster size. Deshpande et al. reported the magnetic properties of small Ni13–nAln clusters with n = 0 - 13 calculated in the framework of density functional theory [9]. The overall magnetic moment of the Ni13–nAln cluster decreases as Al atoms increases. Bailey et al. presented their research results about nickel and aluminum clusters and nickelaluminum nanoalloy clusters with up to 55 atoms. They investigated the effect of doping Al atoms into pure Ni clusters and vice versa [10].
In this paper, we will report our result about investigation on the NiAln and CuAln (n = 1 - 9) clusters by using first-principles calculations. Our calculations were performed with the generalized gradient approximation (GGA) by means of the Becke-Perdew functional, which uses Becke’s [11] gradient correction to the local expression for the exchange energy and Perdew’s [6] gradient correction to the local expression of the correlation energy, as implemented in the Amsterdam Density Functional (ADF) codes [12,13]. The self-consistent field was converged to a value of 10-6.
Frequencies were computed using numerical differenttiation of gradients computed in slightly displaced geometries. The binding energy (BE) for the NiAln cluster is calculated according to the following atomization reaction: NiA1n ® Ni + nA1. It is defined by the following: BE = ENi + nEA1 -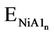 , where E is the total energy of the system. For the CuAln cluster, similar calculation is made.
, where E is the total energy of the system. For the CuAln cluster, similar calculation is made.
2. Results and Discussions
In order to reach the global minimum at energy surface, we chose a random way to produce initial geometrical configurations, and then used the Amsterdam Density Functional (ADF) package for geometrical optimizations. In this way, about one hundred thousand initial geometrical configurations are produced automatically within a three-dimensional box, or a cage, or a ball in real space. The separations of Al-Al, Ni-Al and Ni-Ni atoms are properly chosen to avoid overlapping or loosely packing. After the structural optimization on the initial configuretions is performed, some of them are stable, but some structures are not convergent. In many cases, several different starting configurations are found to give the same structure upon optimization. A frequencies calculation has been performed to ensure that all the imaginary frequencies vanish and the structures are stable. Only the most stable structures for the Aln (n = 3 - 10), NiAln, CuAln (n = 2 - 9) clusters and their ions are presented in Figures 1 and 2. The similar structures for the cluster ions to their neutrals’ are not plotted in the figures. But a different structure for 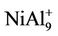 cluster from NiAl9 cluster’s is also presented in Figure 1.
cluster from NiAl9 cluster’s is also presented in Figure 1.
NiAl cluster is a dimer with different atoms. NiAl2 cluster and its ions have an isosceles triangle with C2v symmetry as their ground state structures. NiAl3 cluster, its positive and negative ions have one three-dimensional tetrahedral structure with C3v symmetry as their lowest energy structures, which are different from that of Al4 cluster. Similarly, the ground state structure for NiAl4, 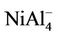 and
and 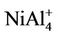 clusters is one pentahedral structure with C4v symmetry, differing from the planar structure of Al5 cluster. The most stable structures for NiAl5 cluster neutral, anion and cation have the same geometric configurations with Cs symmetry, which are obtained from the pentahedral structure of NiAl4 by putting a surface Al atom. The lowest energy structures of NiAl6 and NiAl8 clusters cannot be obtained from Al7 and Al9 clusters by substituting one aluminum atom with nickel atom. Both of them have Cs symmetry. Al7 cluster is an anti-trigonal prism with a capping atom (C3v symmetry), while NiAl6 cluster is a trigonal prism with a capping atom. The ground state structure for Al9 cluster is regarded as a bicapped hexagonal bipyramids with a capping atom. But NiAl8 cluster possesses another different structure. For
clusters is one pentahedral structure with C4v symmetry, differing from the planar structure of Al5 cluster. The most stable structures for NiAl5 cluster neutral, anion and cation have the same geometric configurations with Cs symmetry, which are obtained from the pentahedral structure of NiAl4 by putting a surface Al atom. The lowest energy structures of NiAl6 and NiAl8 clusters cannot be obtained from Al7 and Al9 clusters by substituting one aluminum atom with nickel atom. Both of them have Cs symmetry. Al7 cluster is an anti-trigonal prism with a capping atom (C3v symmetry), while NiAl6 cluster is a trigonal prism with a capping atom. The ground state structure for Al9 cluster is regarded as a bicapped hexagonal bipyramids with a capping atom. But NiAl8 cluster possesses another different structure. For
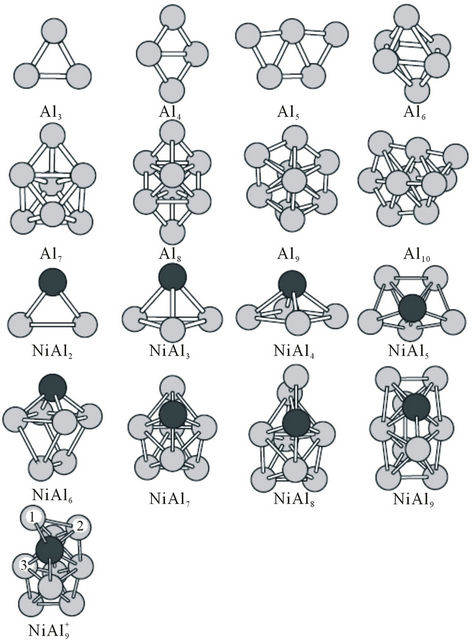
Figure 1. The ground state structures of Aln (n = 3 - 10), NiAln (n = 2 - 9) and 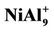 ion clusters. Larger black spheres and smaller gray sphere refer to Ni atom and Al atom, respectively.
ion clusters. Larger black spheres and smaller gray sphere refer to Ni atom and Al atom, respectively.
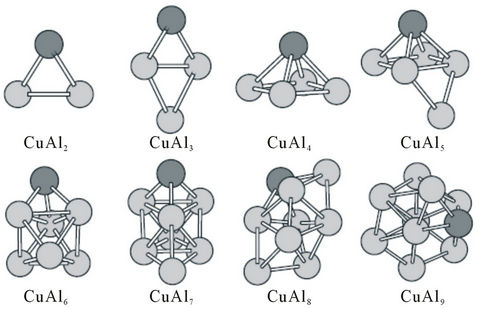
Figure 2. The ground state structures of CuAln (n = 2 - 9) clusters. Larger black spheres and smaller gray sphere refer to Cu atom and Al atom, respectively.
NiAl7 and NiAl9 clusters, the lowest structures are different from those of pure Al8 and Al10 clusters. It is worthy mentioning that positive NiAl9 cluster ion has a severe distorted ground state structure compared with its neutral and anion (see  structure in Figure 1). Mulliken population analysis shows that the Al atoms labeled 1, 2 and 3 letters lose 37%, 28%, and 20% electron in the
structure in Figure 1). Mulliken population analysis shows that the Al atoms labeled 1, 2 and 3 letters lose 37%, 28%, and 20% electron in the 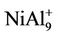 structure, respectively. This makes the bond energies among them decrease. The severe structure distortion is mainly resulted from the non-uniform charge lose.
structure, respectively. This makes the bond energies among them decrease. The severe structure distortion is mainly resulted from the non-uniform charge lose.
NiAl cluster has a single electron besides the paired electrons. If we add an electron into NiAl cluster, the electron would pair up with the original single electron, producing zero magnetic moment in NiAl- cluster. But, the electron removed is from paired electrons in NiAl cluster. Thus, NiAl+ cluster have two unpaired electrons, showing magnetic moment of 2 μB. Loss of an electron weakens the NiAl bond, which makes NiAl+ cluster unstable due to positive binding energy. All the orbitals in neutral NiAl2 cluster are doubly occupied. But the ionic clusters have the magnetic moment of 1 μB because there is one single-occupied orbital. Interestingly, 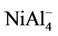 , NiAl4, and
, NiAl4, and 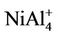 clusters have magnetic moments of 1 μB, 2 μB and 3 μB, respectively. It is found from observing Table 1 that NiAl3, NiAl5, NiAl7, NiAl9 clusters and their ions with odd-aluminum atoms have the same magnetic moments as NiAl cluster and their ions. That is to say, their anions have no magnetic moments, but the cations show the magnetic moment of 2 μB.
clusters have magnetic moments of 1 μB, 2 μB and 3 μB, respectively. It is found from observing Table 1 that NiAl3, NiAl5, NiAl7, NiAl9 clusters and their ions with odd-aluminum atoms have the same magnetic moments as NiAl cluster and their ions. That is to say, their anions have no magnetic moments, but the cations show the magnetic moment of 2 μB.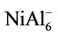 , NiAl6, and
, NiAl6, and 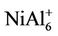 clusters have the same magnetic moments of 1 μB, 2 μB and 3 μB as
clusters have the same magnetic moments of 1 μB, 2 μB and 3 μB as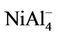 , NiAl4, and
, NiAl4, and 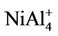 clusters, respectively. But, the magnetic properties of
clusters, respectively. But, the magnetic properties of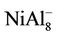 , NiAl8, and
, NiAl8, and 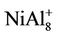 clusters are the same as those of
clusters are the same as those of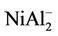 , NiAl2, and
, NiAl2, and 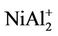 clusters, respecttively.
clusters, respecttively.
Figure 3 presents the calculated total density of states (DOS) for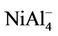 , NiAl4,
, NiAl4,  , and NiAl6 clusters. DOS further provides an explanation of the magnetic behavior of these clusters. The majority spin is contributed by the Ni-d orbitals in the clusters. DOS for spin up and spin down are asymmetric in the clusters suggesting the systems to be magnetic. Similar situations can be found in other clusters.
, and NiAl6 clusters. DOS further provides an explanation of the magnetic behavior of these clusters. The majority spin is contributed by the Ni-d orbitals in the clusters. DOS for spin up and spin down are asymmetric in the clusters suggesting the systems to be magnetic. Similar situations can be found in other clusters.
The magnetic moments of the Ni-Al clusters are considered to be from the strong sp-d hybridization. The electronic configurations of Ni atom and Al atom are 3d84s2 and 3s23p1, respectively. The Ni 3d orbitals are open shells. For the Ni-Al clusters, we note that the Ni atom obtain charge of about 0.4e from the Al atoms according to Mulliken populations. At the same time, some charge transfers into the 4p and 3d orbitals from the Ni 4s orbitals. For example,  cluster has magnetic moment of 2 μB, in which 0.494 μB and 0.502 μB are from the Ni atom and each Al atom, respectively. A part of the Ni 4s, Al 3s and 3p charge goes to the Ni 4p and 3d orbitals to form sp-d hybridization.
cluster has magnetic moment of 2 μB, in which 0.494 μB and 0.502 μB are from the Ni atom and each Al atom, respectively. A part of the Ni 4s, Al 3s and 3p charge goes to the Ni 4p and 3d orbitals to form sp-d hybridization.
In order to better understand the role of the impurity Ni atom in the Al host clusters, we have also investigated the structural and magnetic properties of the copper-doped aluminum clusters by comparative study. The ground state structures for CuAln (n = 2 - 9) clusters are presented in Figure 2. Their magnetic moments, binding energies, energy gaps, electron affinities and ionization potentials are presented in Table 2. Although most of the structures can not be obtained from those of Aln (n = 3 - 10) clusters either by replacing one Al atom with a Cu atom, more structures are similar to the lowest energy structures of Aln (n = 3 - 10) clusters compared with NiAln (n = 2 - 9) clusters. It is found from observing the structures in Figure 1 that some of the aluminum cluster structures get a cardinal change after doping one impurity nickel atom. But, one substitutional zinc atom only causes some local structural distortion without changing the basic geometrical configurations of the original Aln
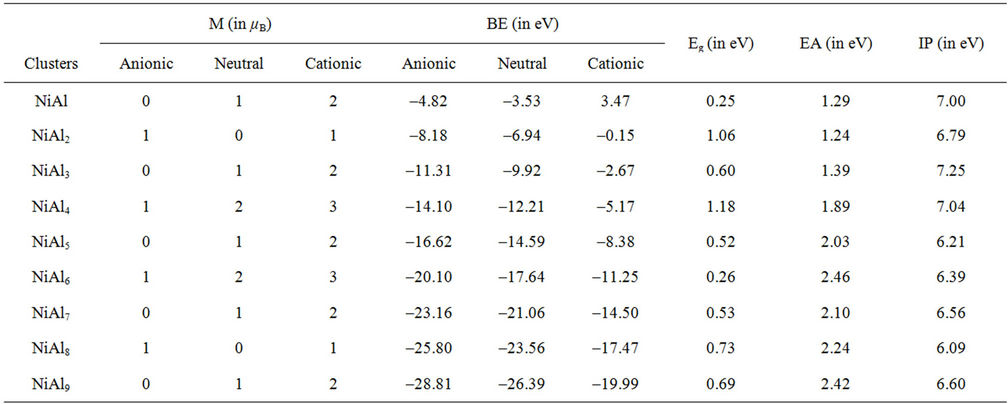
Table 1. The total magnetic moments (M, in μB) and the binding energies (BE, in eV) for NiAln (n = 2 - 9) clusters and their ions. The energy gaps (Eg, in eV), the electron affinities (EA, in eV) and ionization potentials (IP, in eV) of neutral NiAln (n = 2 - 9) clusters.
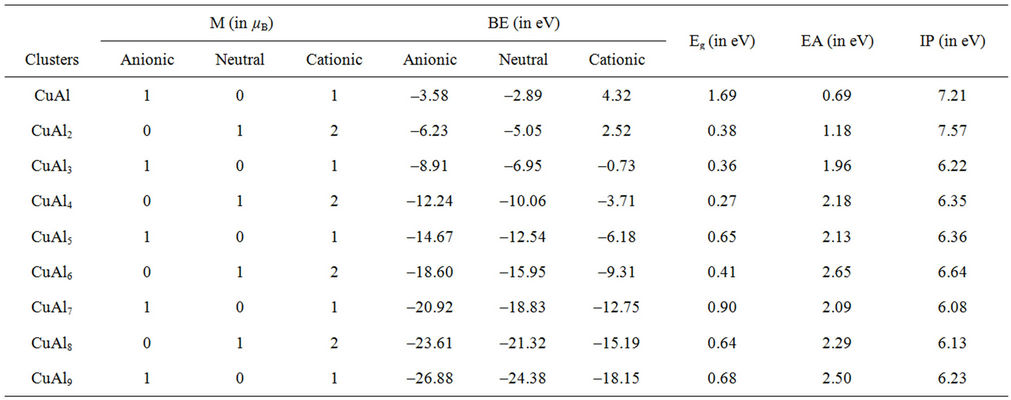
Table 2. The total magnetic moments (M, in μB) and the binding energies (BE, in eV) for CuAln (n = 2 - 9) clusters and their ions. The energy gaps (Eg, in eV), the electron affinities (EA, in eV) and ionization potentials (IP, in eV) of neutral CuAln (n = 2 - 9) clusters.
(n = 3 - 10) clusters [14]. This is considered to be related to the electronic configurations of the impurity atoms. As the number of electrons from Cr atom to Zn atom increases, the 3d orbital’s hybridization intensity of metal atom with the orbital of Al reduces gradually. In addition, the cohesive energies of Ni, Cu, and Zn are 4.44, 3.49, and 1.35 eV, respectively [15]. Therefore, the influence of the impurity Cu atoms on the structures of the host Al clusters is less than that of the Ni atom. The influence caused by Zn atoms is even less.
Some of the ground state structures of CuAln (n = 2 - 9) clusters are different from those of NiAln (n = 2 - 9) clusters. They also present different magnetic properties. Note that the magnetic moments of all the anionic, neutral and cationic CuAl clusters with odd Al atoms are of 1 μB, 0, and 1 μB, respectively. But, the corresponding Cu-Al system containing even Al atoms are associated with the magnetic moments of 0, 1 μB, and 2 μB, respecttively. The cations have two unpaired electrons, showing the magnetic moment of 2 μB.
Wang et al. [8] investigated the properties of MAln (M = Cr, Mn, Fe, Co, Ni; n = 1 - 7, 12) clusters. They found that the MAln clusters have similar structures to Aln+1 clusters. Our calculated ground state structures for Aln (n = 2 - 10) clusters are in excellent agreement with the results reported in the Ref. [16], but differing from the structures obtained by Wang [8]. For NiAln (n = 5 - 7) clusters, ours structures are also different from Wang’s. We performed further structural optimization calculations on their structures. As a result, the structures are unstable. Some of them transfer into our structures. The differences are probably caused by the different choice of the functional and the basis set for the problem under investigation. But, for the magnetic moments from NiAl cluster to NiAl7 cluster, our calculated results fully consistent with their results.
Figure 4 shows the second difference of cluster energies, D2E(n) = E(NiAln-1) + E(NiAln+1) – 2E(NiAln), which is a sensitive quantities that reflects the stabilities of clusters. The maxima can be found at n = 2, 3, 7 for NiAln (n = 1 - 9) clusters, implying that the clusters are more stable than their neighboring clusters. But, for CuAln (n = 1 - 9) clusters, the maxima can be found at n = 2, 4, 6, 7. Obviously, different impurity atoms would change their relative stabilities.
The electron affinities (EA) and ionization potentials (IP) of the mixed clusters as the function of the clusters size (shown as Figure 4) are also important quantities that reflect the stability of the clusters. The positive EAs imply that the clusters have a tendency to gain an electron under normal conditions. In the mixed NiAln and CuAln (n = 1 - 9) clusters, all the EAs are positive. Their trend is basically the same. The smaller clusters have a small electron affinity. However, for the ionization potentials, an opposite situation is observed. Generally speaking, the highly stable structure has small electron affinity and large ionization potential. For example, NiAl3 and NiAl7 clusters are comparatively highly stable. They have smaller EAs and larger IPs relative to their neighbors. Figure 4 also presents the energy gaps (Eg) between the highest-occupied molecular orbital (HOMO) and the lowest-unoccupied molecular orbital (LUMO). Most of them are less than 1.0 eV.
3. Summary
We optimized the geometric structures of the mixed NiAln and CuAln (n = 1 - 9) clusters by using first-principles density functional theory. The ground state structures are obtained, and their relative stabilities are discussed. Most of the Al clusters doped one Ni or Cu atom are different from those of the host Al clusters. NiAln and CuAln (n = 1 - 9) cluster ions present the similar structures to their neutral clusters. In addition, their magnetic properties are investigated. The magnetic moments of
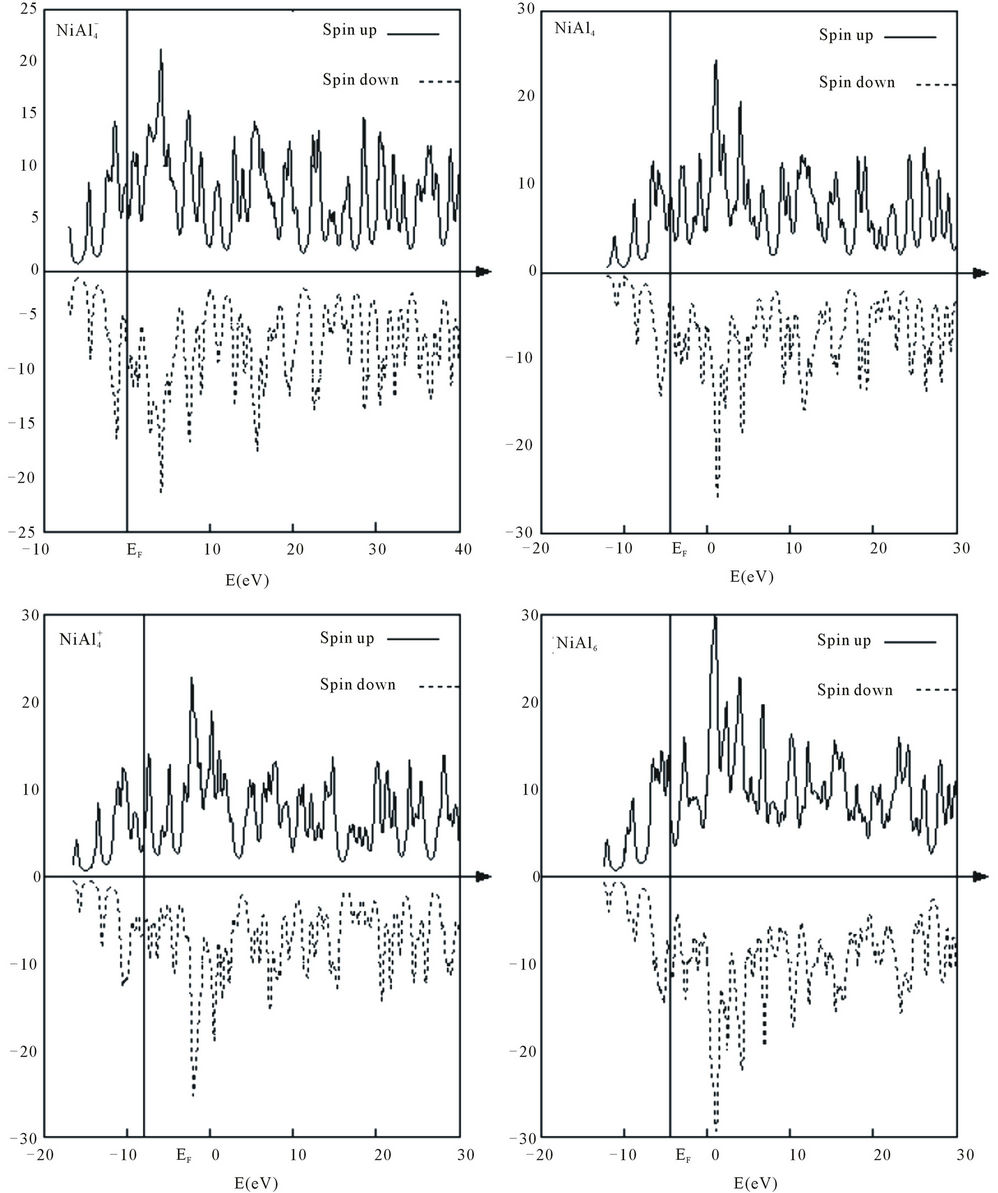
Figure 3. Total density of states (DOS) for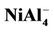 , NiAl4,
, NiAl4,  , and NiAl6 clusters. The Fermi level is given by a vertical line.
, and NiAl6 clusters. The Fermi level is given by a vertical line.
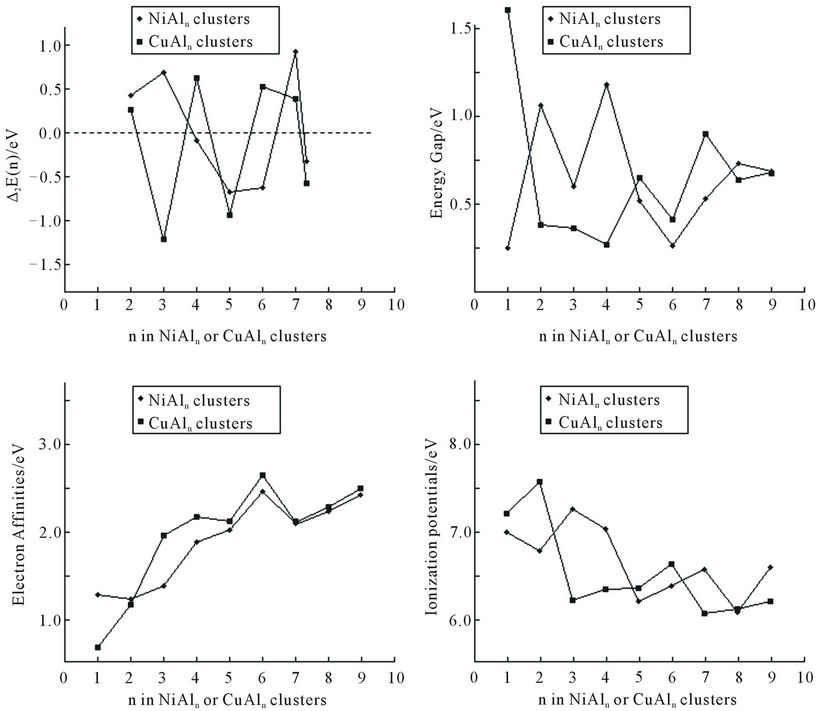
Figure 4. The second difference of cluster energies, the electron affinities, the ionization potentials, and the energy gaps Eg between the highest-occupied molecular orbital (HOMO) and the lowest-unoccupied molecular orbital (LUMO) of NiAln and CuAln (n = 2 - 9) clusters.
NiAln (n=odd number) and CuAln (n = even number) cluster anions, neutrals and cations are 0, 1 μB, and 2 μB, respectively. Negative, neutral and positive NiAl4 and NiAl6 clusters show the magnetic moments of 1 μB, 2 μB, and 3 μB, respectively. NiAl2, NiAl8 and CuAln (n = odd number) clusters do not have any magnetic moments, while NiAl2 and NiAl8 cluster ions have the magnetic moment of 1 μB. The magnetic moments of the Ni-Al clusters are from the strong sp-d hybridization.
4. Acknowledgements
A Foundation for the Author of National Excellent Doctoral Dissertation of PR China (Grant No. 200320), the Natural Science Foundation of Zhejiang Province (Grant No. Y6100098) supported this work.
REFERENCES
- R. L. Fleischer, D. M. Dimidick and H. A. Lipsitt, “Intermetallic Compounds for Strong High-Temperature Materials: Status and Potential,” Annual Review of Materials Science, Vol. 19, 1989, pp. 231-263. Hdoi:10.1146/annurev.ms.19.080189.001311
- A. N. Mansour, A. Dmitrienko and A. V. Soldatov, “Electronic Structure of Ni3Al and NiAl3 Alloys: mX-Ray-Absorption Fine-Structure Analysis,” Physical Review B, Vol. 55, No. 23, 1997, pp. 15531-15536. Hdoi:10.1103/PhysRevB.55.15531
- B. Grushko and T. Ya. Velikanova, “Stable and Metastable Quasicrystals in Al-Based Alloy Systems with Transition Metals,” Journal of Alloys and Compounds, Vol. 367, No. 1-2, 2004, pp. 58-63. Hdoi:10.1016/j.jallcom.2003.08.012
- H. S. Park, “Stress-Induced Martensitic Phase Transformation in Intermetallic Nickel Aluminum Nanowires,” Nano Letters, Vol. 6, No. 5, 2006, pp. 958-962.
- S. M. Shpiro, B. X. Yang, G. Shirane, Y. Noda and L. E. Tanner, “Neutron Scattering Study of the Martensitic Transformation in a Ni-Al β-Phase Alloy,” Physical Review Letters, Vol. 62, No. 11, 1989, pp. 1298-1301. Hdoi:10.1103/PhysRevLett.62.1298
- S. Rubini and P. Ballone, “Phonon Localization and Martensitic Transformation in NixAl1−x Alloys,” Physical Review B, Vol. 50, No. 2, 1994, pp. 1297-1300. Hdoi:10.1103/PhysRevB.50.1297
- J. Q. Wen, Z. Y. Jiang, J. Q. Li, L. K. Cao and S. Y. Chu, “Geometrical Structures, Electronic States, and Stability of NinAl Clusters,” International Journal of Quantum Chemistry, Vol. 110, No. 7, pp. 1368-1375.
- M. Wang, X. W. Huang, Z. L. Du and Y. C. Li, “Structural, Electronic, and Magnetic Properties of a Series of Aluminum Clusters Doped with Various Transition Metals,” Chemical Physics Letters, Vol. 480, No. 4-6, 2009, pp. 258-264. Hdoi:10.1016/j.cplett.2009.09.027
- M. D. Deshpande, R. Pandey, M. A. Blanco and A. Khalkar, “Magnetic Properties of Ni13−nAlnNi13−nAln Clusters with n = 0 - 13,” Journal of Nanoparticle Research, Vol. 12, No. 4, 2010, pp. 1129-1136. Hdoi:10.1007/s11051-009-9654-6
- M. S. Bailey, N. T. Wilson, C. Roberts and R. L. Johnston, “Structures, Stabilities and Ordering in Ni-Al Nanoalloy Clusters,” The European Physical Journal D, Vol. 25, No. 1, 2003, pp. 41-55. Hdoi:10.1140/epjd/e2003-00218-2
- A. D. Becke, “Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior,” Physical Review A, Vol. 38, No. 6, 1988, pp. 3098-3100. Hdoi:10.1103/PhysRevA.38.3098
- J. P. Perdew, “Density-Functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas,” Physical Review B, Vol. 33, No. 12, 1986, pp. 8822-8824. Hdoi:10.1103/PhysRevB.33.8822
- ADF, “SCM, Theoretical Chemistry,” Vrije Universiteit, Amsterdam, 2007. http://www.scm.com
- X. J. Ren and B. X. Li, “First-Principles Study on Stability and Magnetism of AlnZn (n = 1 - 9) Clusters,” Physica B, Vol. 405, No. 9, 2010, pp. 2344-2349. Hdoi:10.1016/j.physb.2010.02.045
- P. H. T. Philipsen and E. J. Baerends, “Cohesive Energy of 3d Transition Metals: Density Functional Theory Atomic and Bulk Calculations,” Physical Review B, Vol. 54, No. 8, 1996, pp. 5326-5333. Hdoi:10.1103/PhysRevB.54.5326
- F.-C. Chuang, C. Z. Wang and K. H. Ho, “Structure of Neutral Aluminum Clusters Aln (2 £ n £ 23): Genetic Algorithm Tight-Binding Calculations,” Physical Review B, Vol. 73, No. 12, 2006, pp. 1-7.
NOTES
*Corresponding author.

