ABSTRACT

We have derived exact axisymmetric solutions of the two-dimensional Lane-Emden equations with rotation. These solutions are intrinsically favored by the differential equations regardless of any adopted boundary conditions and the physical solutions of the Cauchy problem are bound to oscillate about and remain close to these intrinsic solutions. The isothermal solutions are described by power-law density profiles in the radial direction, whereas the polytropic solutions are described by radial density profiles that are powers of the zeroth-order Bessel function of the first kind. Both families of solutions decay exponentially in the vertical direction and both result in increasing or nearly flat radial rotation curves. The results are applicable to gaseous spiral-galaxy disks that exhibit flat rotation curves and to the early stages of protoplanetary disk formation before the central star is formed.

Keywords:

Dark Matter, Gravitation, Galaxies, Protoplanetary Disks

1. Introduction

We use a new method to solve analytically the axisymmetric Lane-Emden equations [1] [2] with rotation in two dimensions. The method is an extension of the one-dimensional algorithm that we applied to ordinary second-order differential equations of mathematical physics [3] [4] [5] and produces separable equations in two dimensions [6] . The solutions are intrinsically favored by the differential equations themselves and dictate that the physical solutions of the Cauchy problem should oscillate about and remain close to these preferred solutions [4] [5] .

The two-dimensional analytic solutions show that both the densities and the rotation speeds decay exponentially with height from the symmetry plane 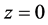while the radial rotation curves are increasing or nearly flat at all heights. Thus, the Newtonian rotation profiles so derived are similar to the “flat” rotation curves observed in gaseous spiral galaxies [7] without the need of invoking dark matter [8] - [22] or the various modifications of the Newtonian dynamics [23] - [30] .

In what follows, we derive the exact solutions of the 2-D Lane-Emden equations with rotation in the isothermal case (Section 2) and in the general polytropic case (Section 3), and we discuss the astrophysical implications of our results (Section 4).

2. Isothermal Self-Gravitating Newtonian Gaseous Disks

We use the scaling constants 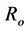and 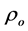to normalize the cylindrical coordinates (R, Z) and the density profiles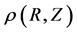, respectively. We thus define the dimensionless radius, height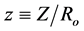, and density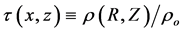. Velocities 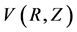are also normalized consistently by the constant, where G is the Newtonian gravitational constant, in which case we define the dimensionless rotation velocity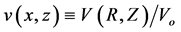. The same scaling also applies to the sound speed 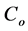of the gas which in this section is a constant, i.e., the dimensionless sound speed is.

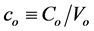The 2-D axisymmetric isothermal Lane-Emden equation with rotation [1] [2] [5] can then be written in dimensionless form as

(1)

where and v are functions of x and z, and

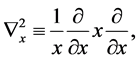(2)

and

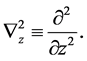(3)

This equation describes the axisymmetric equilibrium of a rotating, self-gravitating, gaseous disk in which the gas obeys the isothermal equation of state 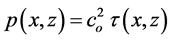, where p is the dimensionless pressure of the gas.

If we equate the last two terms of Equation (1), viz.

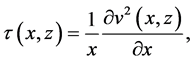(4)

then this is an intrinsic solution [4] [5] provided that the rest of the equation also vanishes:

(5)

Equations ((4) and (5)) form a system in which is determined from which, in turn, is determined by solving the Laplace Equation (5).

We now introduce the following scaling relations in the z-direction:

(6)

where the three new functions, , and are to be determined self- consistently from Equations (4) and (5). Combining Equations (4) and (6), we find that at every height z, the radial variation of the rotation velocity is determined from an integral of the radial density function using the equation

(7)

This is precisely the equation that was solved by [5] on the symmetry plane of the disk. We proceed now to solve for the z-dependence in Equations ((1) to (6)). Substituting the first of Equations (6) into Equation (5), we find that

(8)

The two terms are independent, thus they must be constant and the constants should combine to produce zero. We can then write

(9)

where the separation constant is taken to be positive (or zero) to ensure that is a decreasing function of. Integrating these two equations separately, we find for that

(10)

where the integration constant c is taken to be negative to guarantee monotonically decreasing density profiles away from the symmetry plane; and that

(11)

where are the integration constants. Because of the exponential term, the function is asymptotically increasing with x, and this leads to radially increasing density profiles. These solutions are unphysical and we are forced to choose

(12)

in which case the solutions become

(13)

and

(14)

Equation (14) was derived by [5] for, whereas in this treatment, equation (13) describes the solutions for heights away from the equatorial plane. The solutions in the entire () plane take the form

(15)

where is determined from Equations ((7) and (14)) as was done in [5] , where it was shown that all rotation curves are slowly increasing or flat with radius x. This feature of the rotation profiles remains valid away from despite the exponential decay of the density with.

Figure 1 shows the density profile of the isothermal Lane-Emden equation for and (Equation (15)). The choice causes a rapid decline of the densities with height and gives the model the appearance of a disk-like structure that is centrally condensed because of the steep radial dependence of the density. The rotation curve of this solution was shown in [5] where increases logarithmically with radius for.

3. Polytropic Self-Gravitating Newtonian Gaseous Disks

The 2-D axisymmetric polytropic Lane-Emden equation with rotation [1] [2] [5] can be written in dimensionless form as

(16)

where is the polytropic index and the dimensionless constant sound speed was defined for. (In general, the square of the sound speed varies as across the medium, where, again, is the dimensionless pressure of the gas.) This equation describes the axisymmetric equilibrium of a rotating, self- gravitating, gaseous disk in which the gas obeys a polytropic equation of state of the form.

We repeat the procedure outlined in Section 2 in order to obtain the intrinsic solution of Equation (16): If we equate the last two terms of Equation (16), viz.

(17)

then this is an intrinsic solution [4] [5] provided that the rest of the equation also vanishes:

(18)

Equations (17) and (18) form a system in which is determined from which, in turn, is determined by solving the Laplace Equation (18).

We now introduce the scaling relations (6) in the z-direction, where the three functions, , and are to be determined self-consistently from Equations ((17) and (18)). Combining Equations ((17) and (6)), we find that at every height z, the radial variation of the rotation velocity is determined from an integral of the radial density function using the equation

(19)

as was also found in the isothermal case of Section 2.

Substituting the first of Equations (6) into Equation (18) and diving all terms by, we find that

(20)

The two terms are independent, thus they must be constant and the constants should combine to produce zero. We can then write

(21)

where the separation constant is taken to be negative to ensure that is not a monotonically increasing function of x and is not singular at. Such solutions (the zeroth-order modified Bessel functions of the first kind described in [31] ) are obtained for positive separation constants, whereas the case produces the singular solutions found in [5] . Integrating the two Equations (21) separately, we find for that

(22)

where the particular solution with the minus sign was chosen so that decreases with; and that

(23)

where A is the integration constant and the Bessel function of the first kind was chosen because it does not diverge at. These solutions are monotonically decreasing with x and terminate at the first zero of the Bessel function, viz. [12]

(24)

except in cases of even polytropic indices n in which they produce rings touching one another at consecutive zeroes of.

The solutions in the entire () plane take the form

(25)

where is determined from Equations (19) and (23), viz.

(26)

where. The integral in Equation (26) can be written analytically in terms of the Bessel functions of the first kind and for some integer values of n as follows [31] [32] :

(27)

where is given by Equation (24).

Figure 2 and Figure 3 show the density and rotation profiles, respectively, of the Lane-Emden equation for (Equation (25)). These profiles are representative of other solutions as well with, whereas for even values of n, larger

values of produce differentially rotating ring-like structures in which the rings touch one another at the zeroes of the Bessel function. An example of such a ring solution with and and its rotation profile are shown in Figure 4 and Figure 5.

In the inner region of the rotation profile of Figure 3, the contours are nearly vertical as expected from measurements of the rotation profile of the Milky Way [33] . In the outer region where the rotation speeds are larger, the contours are however tilted and the tilt becomes more pronounced for larger values of. In this region, nearly vertical contours can, however, be produced for smaller values of, so it does not appear to be difficult to produce a Newtonian rotation profile such as that observed in our Galaxy for heights pc [33] . An example of such a rotation profile with nearly vertical contours at all radii is shown in Figure 6 for and.

Figure 7 shows the radial rotation curve for and, and for the cases and 3 (Equations ((26) and (27))). The and curves terminate at the first zero of the Bessel function (Equation (24)). These curves rise in the inner region and then they become asymptotically flat. The flat segments can be extended farther out in radius if values of are used. In contrast, the curve

continues to increase with radius as it passes through a sequence of inflection points. Each jump in the profile represents the rotation curve inside the next outward ring.

4. Discussion

In this work, we derived exact axisymmetric solutions of the 2-D Lane-Emden equations with rotation. In the isothermal case, the solutions show a power-law dependence on the radius x and an exponential decline with height. In the general polytropic case with index, the radial solutions depend on powers of the zeroth-order Bessel function of the first kind and they also decline with. Both families of solutions are intrinsic to the differential equations themselves; any solutions that obey physical boundary conditions will have to remain close to these solutions and they will be forced to oscillate about them if the boundary conditions will be different than the conditions that produced the intrinsic solutions [4] [5] .

The gaseous disk equilibria produced in Sections 2 and 3 are Newtonian in nature and they all have rising or asymptotically flat radial rotation curves. Such rotation profiles are demanded by the analytic solutions for self-consistency. The resulting Newtonian models argue against the need to assume the existence of dark matter in spiral galaxies in order to produce the observed flat rotation curves and against the need to modify the Newtonian dynamics to achieve the same effect (references were given in Section 1). The same models may also prove useful in studies of the rotation curves in protoplanetary disks [34] [35] [36] at their very early stages of evolution and before the central star is formed.

It is important to note that the flat and rising rotation profiles were not prescribed as input to the Lane-Emden equations; instead, they were the result of the intrinsic equilibrium solutions. Similar types of rotation profiles have been previously found in models of Newtonian gaseous disks [37] [38] [39] [40] but they were dismissed because they were thought to be peculiar in nature. We now find that these models were giving us clues as to the true behavior of the gas in self-gravitating astrophysical disks.

The main obstacle in understanding the dynamical behavior of gas in spiral galaxies is an old argument [7] that relies solely on particle dynamics―that an orbiting particle at radius r enclosing mass must experience a rotation speed of in equilibrium, thus only a mass can produce a flat rotation curve. This argument is invalid for gaseous disks where the enthalpy of the gas controls the dynamics absolutely [5] . The intrinsic solutions derived here and in [5] show that the specific enthaply of the gas arranges the local density profile in equilibrium and, subsequently, it is this density that sources and manipulates both the self-gravitational potential (via Poisson’s equation) and the rotational potential (via Equation (17)). Thus, naive arguments that rely on massless particles reacting to a prescribed gravitational potential simply do not describe the dynamics of the gas which is entirely determined by the local distribution of the thermodynamical potential.

Acknowledgements

We thank Joel Tohline for feedback and guidance over many years.

Cite this paper

Christodoulou, D.M. and Kazanas, D. (2016) Exact Axisymmetric Solutions of the 2-D Lane-Emden Equations with Rotation. Journal of Modern Physics, 7, 2177-2187. http://dx.doi.org/10.4236/jmp.2016.715189

References