Received 1 February 2015; accepted 24 March 2015; published 27 March 2015

ABSTRACT

In a recently published paper Metal-Like Gravity (MLG) and Its Cosmological Applications [1] , it was determined that a new modification of Newtonian gravity could explain many of the cosmological mysteries such as the nature of dark matter and dark energy. The theory provided a gravitational physical system and explained the flatness of the galactic rotational curves (RC). A RC fit that was identical to MOND’s RC fit for spiral galaxies was generated with α as a fitting parameter determined as equal to 1.345. In this paper I am elaborating more on the theory’s cosmological extrapolation of MOND’s critical acceleration a₀. This is done by further assessing the gravitational interaction between the galactic baryonic mass and the halo-DM mass in the star-galaxy overlapping volume estimated in MLG framework interpreting a₀ as only a factor induced from the reduction of the galactic luminous mass. It is asserted that MOND and MLG dynamic equations are equivalent with MOND’s form, only expressing the equation with an intermediate solution by equating the magnitudes of δ (a parameter that defines a scaled surface galactic DM-density perpendicular to the galactic radial direction in the galaxy-star halo overlapping volume) and G.

Keywords:

MLG, MOND, Antigravity, Flat Rotation Curves

1. Introduction

Metal-like gravity (MLG) is a recently published theory that modifies Newtonian gravity by introducing new physics characterized by gravitational interaction between baryonic mass and dark matter mass (DM) as like mass repel and unlike mass attract. It describes DM particles as universal particles that mainly act as the binding agent to baryonic objects in the universe. The theory introduces baryonic objects as mass neutral because they attract much lighter DM particles and form DM-halos. According to MLG, baryonic objects should repel each other. Two baryonic objects can attract each other only when their DM-halos overlap. The theory simply attributes the centripetal force between an edge star and the galactic core to the Newtonian gravitational attractive force between the galactic DM-mass in the galaxy-edge star overlapping volume of their halos and the star’s baryonic mass (see Figure 1). Since the galactic DM density in the galaxy-star overlapping volume is proportional to the galactic luminous mass, the edge-star’s dynamics is seen proportional to the galactic luminous mass (see [1] ).

Modified Newtonian Dynamic theory (MOND) is a theory that modifies Newton’s gravitational law by introducing an empirical formula that describes well flat galactic rotation curves (RC) in spiral galaxies by introducing a critical acceleration a₀ at which galactic rotation curves are flat. MOND’s empirical formula is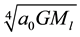, where 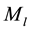is the galactic luminous mass [2] . MOND by far solved the mystery of fine-tuning problem of ΛCDM cosmological model on galaxy scales and pointed to new physics for the nature of DM particles and/or to modification of gravity, but among others failed to account for the dynamics and lensing of galaxy clusters [3] . MLG is believed to add faith to MOND’s success by projecting a physical meaning to its abstract formulation. In the original paper [1] , the author compared MLG cosmological dynamics with that of MOND and found out that they were identical, thereby introducing a physical system that explained the success of MOND and probably presented a system that played a fundamental role in a new quantum gravity theory, i.e. the self-repulsive DM- particles’ bonding medium in MLG could introduce the required conditions for the plasma needed for superfluid vacuum theory. For example, an analogy to a superconductor would be, the cosmological self-repulsive DM- vacuum representing the condensed self-repulsive “electron-sea” and the self-repulsive baryons representing the cations in the superconducting metal. Here, I argue that MOND’s critical acceleration parameter a₀ arises from the fact that the bonding agent “DM mass” in the galactic halo interacts with much smaller magnitude of galactic baryonic mass than that of the galactic luminous mass. In particular, I further describe galactic dynamics under the eyes of MLG theory and extrapolate that MOND’s critical acceleration a₀ arises from the process of shielding of the galactic luminous mass by the body of the enclosed galactic DM-halo at the location of the edge-star.

2. Edge-Star’s Dynamics

In the original paper, MLG edge-star’s dynamics yields flat rotation curves, with galactic luminous mass as the sole determining factor of the rotational velocity, characterized by the formula,

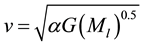(1)

where 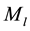is the galactic luminous mass, α is a fitting parameter.

MLG describes the edge-star dynamics as governed by Equation (1) where a fitting parameter α is determined with magnitude 1.345. In the original paper, a first order approximation is considered when evaluating the gravitational force between a galactic DM-halo particle and the galactic luminous mass [1] . To better estimate the parameter α and describe a physical interpretation to it, the approximation can be removed and the galactic luminous mass is suggested to be reduced by a numerical factor of that of the magnitude of MOND’s a₀ of the order of 10⁻¹⁰.

3. MLG Extrapolation of MOND’s Critical Acceleration a₀

MLG describes a DM-halo density for any baryonic object as inversely proportional to the radial distance from its center due to the self-repelling nature of DM particles. This configurational analysis of galactic DM halos allows the derivation of the fitting constant α as a function of DM halo’s density in Equation (2). The sequence of derivation is as follows,

We assume that the galaxy-star overlapping volume for an edge-star is invariable and dominated by the star’s potential since the edge star is far away from the galactic core while the galactic component of the DM-mass in the overlapping volume is variable with its density increasing the closer the edge star to the galactic core as Figure 2 shows (see reference [1] ).

The halo’s DM particle dynamics is obtained by balancing the repulsive force between a DM particle in an arbitrary location in the halo and the one preceding it from the galactic core (as described in the original paper to first order approximation) and the attractive force between that DM particle and the galactic baryonic (luminous) mass as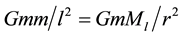, which yields,

(2)

where m is the DM particles’ mass, 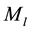is the galactic luminous baryonic mass, r is the star’s radial distance to the center of the galactic core, and l is the spacing between DM particles (Figure 1).

MOND introduces critical acceleration a₀ at which cosmological dynamics is described by MOND’s regime that departs from Newtonian one and produces flat rotation curves mainly for spiral galaxies. Unlike MOND, MLG asserts that the transition acceleration at which galactic centripetal acceleration of edge-stars deviates to produce constant galactic rotational velocity is due to configurational transition from galactic core dynamics to halo dynamics. This is interpreted as that the dynamics transition occurs when the star is located far away from the galactic coreas MLG describes the dynamics of the star in the galactic core as governed by a star-star interaction and not a star-galactic-core interaction as in the galactic halo. Under MLG, MOND’s critical acceleration must have gravitational origin. In this regard, it is very tempting to assume that the magnitude of a₀ 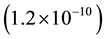can safely be associated with the gravitational source, that is to say the galactic luminous mass, if we want to assume the form of Newton’s law assuming its integrity at all times as MLG demands (proportional to the product of the two masses and the inverse square of the distance). In MLG, the magnitude of the fitting parameter α can safely be treated as unity for the sake of comparison with MOND. But when MLG dynamic equation was fitted in the original paper it considered the source of gravity in the galactic core as the total luminous mass (as MOND did).

This is not the case though as only first approximation for balancing the gravitational forces at the location of the edge-star was considered.

To describe an effective “net” galactic luminous mass at the location of the edge-star as ordained by MLG, we need to describe the repulsive gravitational force between two halo-DM particles as balanced by the attractive force with the “net” luminous mass as shown in Figure 3 where the DM-mass enclosed by the Gaussian surface (Region I) can be deducted from the total galactic luminous mass to produce the “net” galactic luminous mass. Region I contains most of the halo’s DM-mass since it contains the core. The DM-mass enclosed in Region II should equal the net galactic luminous mass since the whole galaxy is mass-neutral.

MOND’s cosmological dynamic equation can be rewritten in the following form,

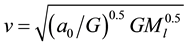(3)

Notice that this is exactly the MLG dynamic equation with the fitting parameter as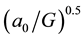. The dimensions are satisfied when the dimension of the parameter α is considered since we are only associating the magnitude of a₀ to the luminous mass.

Here I estimate that the reduction factor of the luminous mass in MLG dynamic equation as in the order of the magnitude of that of a₀ but may not be conclusively estimated unless we identify the mass of the DM particle. This may be justified as the following line of reasoning;

It happens that MOND considers the reduction factor of 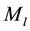is in the same order as that of the gravitational constant G (or a₀) of about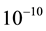. If we insert this factor to 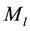in MLG dynamic Equation (1), the fitting parameter α should be adjusted by an inverse of that factor of the square root of 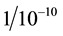to maintain its unity magnitude as determined by the process of galactic fitting. Note that to maintain the unity magnitude of α, the numerator (luminous mass reduction factor) as well as the denominator δ (a parameter that defines a scaled surface galactic DM-density perpendicular to the galactic radial direction [4] in the overlapping volume should be of the same magnitude. The magnitude of the denominator as only suits MOND’s form. It is not surprising now that a₀ and G both have about the same magnitude.

Inserting the reduction factor to and adjusting for the fitting parameter α, Equation (1) becomes,

(4)

Equation (4) describes a gravitationally effective “net” luminous mass of the order of and fitting parameter of units of in the order of 10⁵ with actual dimensions of a parameter, where l is the spacing distance between DM particles perpendicular to the galactic radial direction in the overlapping volume and represents the invariable galactic halo’s DM surface density, R is the volume’s radius (where the volume is taken as spherical for simplification), and is the DM-particle’s mass (see original paper). It is worth noting that unless a DM particle is identified, R and l-spacing cannot be estimated.

To further illustrate the close relationship between MLG and MOND, we configurationally can see that the parameter α remains “~unity” if the effective luminous mass is taken as the total luminous mass (representing one solution to the equation, as taken by MOND) because the magnitude of the parameter δ is proportional to the magnitude of the reduction factor of the galactic luminous mass at all times. The author believes that the luminous mass reduction factor as the magnitude of a₀ appears when galactic stars are located just beyond the galactic core announcing the beginning of the MONDian regime where the magnitudes of δ and G are equal. The reduction factor assumes a smaller magnitude and continues with this trend to the galactic border but is also accompanied by similar reduction of the parameter δ since the galactic DM radial density decreases proportional to the radial distance; see Equation (2), maintaining a constant ～α Qualitatively, this is because as we approach the galactic core the reduction factor gets larger but so does R since the galaxy-star overlapping volume inflates when the star is closer to the galactic core due to higher galactic halo DM-density, see original paper and Figure 1.

4. The Significance of the Parameter α

The parameter can be treated as nearly a constant in the MONDian regimeas it describes the square root of the ratio of luminous mass reduction factor to the term δ. It represents a scaled DM surface density of magnitude of in MOND’s regime when the baryonic mass is considered the sole source of galactic gravity without reduction as MOND asserts. It is also clear that from Equation (3) the parameter can be associated with the luminous mass M_l to become. The parameter can be interpreted as the transition (critical) surface baryonic density at which the DM dominates the dynamics of galaxies [5] . Here, this is interpreted as the transition from core-dynamics to halo dynamics. Milgrom (MOND’s creator) also attempted to attribute the assumed missing mass in MOND’s regime as a “phantom” nonrelativistic negative mass [6] . The parameter α can be treated as nearly a constant that equals in the MONDian regime as it describes the square root of the ratio of luminous mass reduction factor to the term δ. The choice of a₀ in MOND’s dynamic formula as a critical acceleration of its regime limits the power of the dynamical aspect of the parameter α in MLG dynamic formula where only the ratio of the luminous mass reduction factor to the parameter δ is significant. It is clear that MOND and MLG dynamic equations are equivalent with MOND’s form only expressing the equation with an intermediate solution by equating the magnitudes of δ and G. The significance of the parameter α in MLG is that it provides a physical meaning to the MOND’s critical acceleration a₀.

5. Conclusion

I have compared the critical acceleration calculated in the framework of MOND with a possible reduction factor of “net” galactic baryonic mass in the frame work of MLG and have predicted that MOND’s critical acceleration only arises as a consequence of that mass reduction. I conclude that the appearance of a₀ in MOND’s dynamic equation is only a coincidence and results in ignoring a dynamical process of a true physical system. MLG theory describes well this physical system and attributes a configurational parameter α whose magnitude remains equal to the magnitude of ~ at all times if the total galactic luminous mass is used in MLG/MOND dynamic equation. Analysis of MLG fitting parameter α also reveals that MOND’s critical acceleration a₀ must have the same magnitude as the gravitational constant G since it only describes an intermediate solution of MLG dynamic equation.

References