Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.02(2017), Article ID:75808,20 pages
10.4236/jhepgc.2017.32031
On the Cohomological Derivation of Yang-Mills Theory in the Antifield Formalism
Ashkbiz Danehkar1,2
1Faculty of Physics, University of Craiova, Craiova, Romania
2Present Address: Center for Astrophysics, Cambridge, MA, USA

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 17, 2017; Accepted: April 27, 2017; Published: April 30, 2017
ABSTRACT
We present a brief review of the cohomological solutions of self-coupling interactions of the fields in the free Yang-Mills theory. All consistent interactions among the fields have been obtained using the antifield formalism through several order BRST deformations of the master equation. It is found that the coupling deformations halt exclusively at the second order, whereas higher order deformations are obstructed due to non-local interactions. The results demonstrate the BRST cohomological derivation of the interacting Yang-Mills theory.
Keywords:
Yang-Mills Theory, BRST Symmetry, BRST Cohomology, Antifield Formalism

1. Introduction
Dirac’s pioneering approach [1] [2] [3] has been used for constrained systems in quantum field theory [4] [5] [6] . This approach allowed us to construct the action in either Lagrangian or Hamiltonian forms [7] [8] , while both of them are equivalent [9] . In this way, the Hamiltonian quantization is derived using canonical variables (coordinate and momentum) involving constrained dynamics [10] - [15] . Physical variables of a constrained system possess gauge invariance and locally independent symmetry. The gauge symmetry introduces some arbitrary time independent functions to the Hamilton’s equations of motion. We notice that all canonical variables are not independent. Therefore, some conditions for canonical variables are required to be imposed, i.e., the first- and second-class constraints. Furthermore, the framework should be generalized to include both commutative (bosonic) and anticommutative (fermionic) variables in constrained systems.
To generalize constrained systems for canonical conditions and (anti-)com- mutative variables, Becchi, Rouet, Stora [16] [17] [18] , and Tyutin [19] developed the BRST formalism to extend the gauge symmetry in terms of the BRST differential and co-/homological classes. The aim was to replace the original gauge symmetry with the BRST symmetry. Noting that the gauge symmetry can be constructed from a nilpotent derivation, so the gauge action is invariant under a nilpotent symmetry, called the BRST symmetry. By replacing the original gauge symmetry with the BRST symmetry, antifield, ghosts, and antighosts are introduced for each gauge variable [20] [21] . It yields a generalized framework for solutions of the equations of motion [22] [23] . Moreover, BRST cohomology extended by the antifield formalism [23] - [30] allowed us to construct all consistent interactions among the fields using coupling deformations of the master equation [31] [32] . The BRST-antifield formalism appears as efficient mathematical tool to analyze the consistent interactions, and has been applied to many gauge models, e.g., Yang-Mills model [33] , topological Yang-Mills model [34] , 5-D topological BF model [35] , and 5-D dual linearized gravity coupled to topological BF model [36] .
In this paper, we briefly review the construction of all consistent interactions of the free Yang-Mills theory determined from all coupling deformations of the master equation. We see that the resulting action presents deformed structures of the gauge transformation and yields a commutator for it. In Section 2, the BRST differential and the antifield formalism are introduced. Section 3 introduces the consistent interactions among the fields. We consider the BRST coupling deformations of the master equations in the antifield formalism in Section 4. In Section 5, we demonstrate its application to the massless Yang-Mills theory by calculating all several order deformation of the master equation. Section 6 presents a conclusion.
2. BRST Differential
The gauge invariant in a phase space implies that the smooth phase space 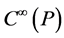 is substituted by the smooth manifold of the constraint surface
is substituted by the smooth manifold of the constraint surface 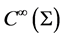 while the elements of
while the elements of  vanish due to the longitudinal exterior derivative on manifold
vanish due to the longitudinal exterior derivative on manifold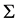 . The manifold
. The manifold , which is embedded in a phase space and a set of vectors tangent to
, which is embedded in a phase space and a set of vectors tangent to , and is closed on it, presents the definition of the gauge orbits. It manifests the presentation of a nilpotent derivation
, and is closed on it, presents the definition of the gauge orbits. It manifests the presentation of a nilpotent derivation , the so-called BRST differential, that includes an algebra involving
, the so-called BRST differential, that includes an algebra involving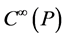 , where the cohomology of
, where the cohomology of 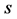 indicates that the gauge transformations of the constraint surface
indicates that the gauge transformations of the constraint surface  are constant along the gauge orbits (denoted by
are constant along the gauge orbits (denoted by ).
).
The reduced space, by taking 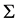 over gauge orbits, denote by algebra
over gauge orbits, denote by algebra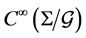 , includes all variables of the gauge invariant. However, it is not possible to construct
, includes all variables of the gauge invariant. However, it is not possible to construct  from physical observables, as one cannot solve equations defining
from physical observables, as one cannot solve equations defining  and trace the gauge orbits
and trace the gauge orbits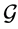 . Hence, the BRST symmetry should be used to reformulate the physical observables in a convenient approach. To construct the BRST differential
. Hence, the BRST symmetry should be used to reformulate the physical observables in a convenient approach. To construct the BRST differential , two auxiliary derivations
, two auxiliary derivations 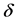 and
and 







whose cohomology is equal to the cohomology of the longitudinal differential








where 

Any nilpotent derivation has a degree in a 

The positive degree of the differential 






with the following property
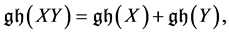
where the operators 




such




The cohomology algebra of the differential 




while the elements of its image subspace, 

The cohomology algebra of




If the co-/homology 


The zeroth cohomology group of the BRST differential 



and also their anticommutation:

It means that the Koszul-Tate differential 

The generator of the Koszul-Tate complex may be chosen in an equal number of freedom as the generator of the longitudinal exterior complex. It follows that they are canonically conjugate in the extended space of original and new generators of 



which is called the Poisson bracket and defined as follows:

where 

Equation (13) represents the BRST symmetry in the Hamiltonian formalism. The choice of 


which is the master equation of the BRST generator in the Hamiltonian formalism.
3. Consistent Interactions
To understand the consistent interactions among fields with a gauge freedom, we begin our study with a Lagrangian action:

where the action 

The equations of motion then read 



The equations of motion is then determined from the action principle:
Let consider the deformations of the action in such a way

that implies the deformation of gauge symmetries as

This provides the deformed gauge transformations:

Equation (18) and Equation (19) lead to the following expression:

Hence, the deformations by their orders are as follows:

which define the deformed gauge transformations that close on-shell for the interacting action, the so-called consistent interactions, while the original gauge transformations are reducible [28] .
Assume that the gauge fields of consistent interactions are trivially defined to be the following sum:

we then obtain

which does not manifest an exact interacting theory. A theory is strict if the consistent deformations are merely proportional to its free theory action 
where charges 



It represents the unperturbed action by charges of the coupling constants.
4. BRST Deformations of the Master Equation
Let us consider the gauge transformation defined by the Equation (17). The classical fields 



which have the following ghost numbers, 


It also implies antifields 





The presentation of the gauge variables is therefore provided by

where a set of fields 

The BRST symmetry is a canonical transformation, and defined by an antibracket structure:

where 



The Grassmann parity and ghost number of the antibracket are, respectively:


The antifields are now considered as mathematical tool to construct the BRST formalism. The solution can be interpreted as source coefficient for BRST transformation, i.e., an effective action in the theory.
The fields and antifields establish the solution 

Section 2 presented the master Equation (15) of the BRST generator in the Hamiltonian formalism. The gauge structure is now constructed through the solution 

This shows the consistency of the gauge transformations. The master Equation (36) includes the closure of the gauge transformations, the higher-order gauge identities, and the Noether identities. The master equation maintains the consistent specifications on 

Substituting the definition (35) into the master Equation (36) yields

We then derive

which are simplified as follows [31] [36] [37] [38]






the so-called deformations of the master equation [31] [32] .
The Equation (40) implies that 















The free gauge invariant action 

by setting

It provides the solution 

The BRST differential 


Using the definitions (48), the deformations of the master equation are rewritten as follows:

which are the deformations of the master equation in terms of the BRST differential
5. BRST Cohomology of the Free Yang-Mills Theory
Let us consider a set of 


where 




in such a way

where 




The gauge transformation with the free equation of motion,

manifests an irreducible transformation by

while

The differential operator 

The implementation of the BRST transformation in the minimal sector provides the field




which can schematically be illustrated:
We calculate the BRST-differential 




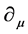




The classical master Equation (47) of the action (50) holds the minimal solution (45) in such a way

5.1. First-Order Deformation
We now consider the deformed solution of the master equation for the action (50) smoothly in the coupling constant 




Let us assume

where 



where 



To evaluate Equation (60), we assume


where 

obviously

They can be decomposed on the several orders of the antighost number:

The positive antighost number are strictly given as replacement for the first expression [35] :

To proof it, let us consider 


while

The objects 





Moreover, 


corresponding to a trivial definition, which states




Hence, the non-triviality of the first-order deformation 








where

For an irreducible linear situation, where gauge generators are field independent, we assume that

where 




The first-order deformation up to antighost number two are:

The 




where 


We now consider the Koszul-Tate differential 

The local cohomology of the exterior longitudinal derivative 





From (79), we then solve
by

where 


The expression 


We simply notice that

This indicates

To obtain




The last term in above relation vanishes, i.e.
since
while
Therefore, we derive

It shows

The results for the first-order deformation are summarized as follows:

Finally, we derive

The first-order deformations of the solution (
5.2. Higher-Order Deformations
We now consider the higher-order deformations of the master equation for the action (50). The second-order deformation (


that takes the local form

Using the Equation (88) from Section 5.1, we calculate
while employing the following relations


and the definitions


They lead to the following expression
that is reduced to
We then decompose 

namely,



We also define

From (91), it follows a set of equations



Equations (99) and (101) imply

and

The later expression is called the Jacobi identity. Similarly, we obtain

So, the Equation (103) remains to be solved:

We solve it by substituting the exterior longitudinal differential 


Accordingly, we derive
Hence, the second-order deformations becomes

The Jacobi identity (105) obviously implies
Similarly, all deformations with orders higher than the second-order completely vanish:
As a result, the solution to the deformations becomes

We have determined the Yang-Mills theory from the first- and second-order deformations of the master equation. The solutions of the master equation, which entirely include the gauge structures, are decomposed into terms with the antighost numbers from zero to two. In other words, the part with the antighost number equal to zero represents the Lagrangian action, while the antighost number one is proportional to the gauge generators. The terms with higher antighost numbers provide the reducibility functions, where the on-shell relations become linear components in the ghosts for ghosts. It is shown that all functions with order higher than second vanish in this model.
5.3. Interacting Theory
Let us consider the Equation (109) and identify the entire gauge structure of the Lagrangian model that describes all consistent interactions in the 
The antighost number zero of (109) shall provide the Lagrangian action of the interacting theory:

Accordingly, the Yang-Mills theory is characterized by the following non- abelian action:

where the non-abelian field strengths 
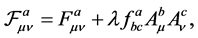
and 

So, the commutator among the deformed gauge transformations becomes:

The gauge symmetry remains abelian to order

The invariance of the action under the gauge transformations (113) is also obtained by the Noether identities

The antighost number one of the deformation of the master equation allows to identify the gauge transformations (113) of the action (110) by substituting the ghost 

6. Conclusion
In this paper, we reviewed deformed gauge transformations in the framework of the BRST-antifield formalism characterized by the antibracket that acts similar to the Poisson bracket in the Hamiltonian formalism. We provided the BRST cohomology of the consistent interactions through several order deformations of the master equation. The BRST-antifield formalism in the cohomological space provides the generalized framework of consistent interactions among fields with a gauge freedom by any types of invariant action. We see that higher order deformations could be neglected due to non local interactions and their obstruction of consistent local couplings, which are associated with the anomalous gauge quantization. We demonstrated its functions by applying the BRST-antifield formalism to the 




Acknowledgements
The author thanks the editor and the referee for their comments. Research of A. Danehkar is funded by the EU contract MRTN-CT-2004-005104. This support is greatly appreciated.
Cite this paper
Danehkar, A. (2017) On the Cohomological Derivation of Yang-Mills Theory in the Antifield Formalism. Journal of High Energy Physics, Gravitation and Cosmology, 3, 368-387. https://doi.org/10.4236/jhepgc.2017.32031
References
- 1. Dirac, P.A.M. (1950) Generalized Hamiltonian Dynamics. Canadian Journal of Mathematics, 2, 129-148. https://doi.org/10.4153/CJM-1950-012-1
- 2. Dirac, P.A.M. (1958) The Theory of Gravitation in Hamiltonian Form. Proceedings of the Royal Society A Mathematical, Physical and Engineering Sciences, London, 246, 333-343. https://doi.org/10.1098/rspa.1958.0142
- 3. Dirac, P. (1964) Lectures on Quantum Mechanics. Yeshiva University, New York.
- 4. Anderson, J.L. and Bergmann, P.G. (1951) Constraints in Covariant Field Theories. Physical Review, 83, 1018-1025. https://doi.org/10.1103/PhysRev.83.1018
- 5. Bergmann, P.G. and Goldberg, I. (1955) Dirac Bracket Transformations in Phase Space. Physical Review, 98, 531-538. https://doi.org/10.1103/PhysRev.98.531
- 6. Weinberg, S. (1995) The Quantum Theory of Fields. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781139644167
- 7. Gotay, M.J. and Nester, J.M. (1979) Presymplectic Lagrangian Systems. I: The Constraint Algorithm and the Equivalence Theorem. Annales de l’Institut Henri Poincaré, 30, 129-142.
- 8. Gotay, M.J. and Nester, J.M. (1980) Presymplectic Lagrangian Systems. II: The Second-Order Equation Problem. Annales de l’Institut Henri Poincaré, 32, 1-13.
- 9. Batlle, C., Gomis, J., Pons, J.M. and Roman-Roy, N. (1986) Equivalence between the Lagrangian and Hamiltonian Formalism for Constrained Systems. Journal of Mathematical Physics, 27, 2953-2962. https://doi.org/10.1063/1.527274
- 10. Gitman, D.M. and Tyutin, I.V. (1990) Quantization of Fields with Constraints. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-83938-2
- 11. Govaerts, J. (1991) Hamiltonian Quantisation and Constrained Dynamics. Leuven University Press, Leuven.
- 12. Hanson, A., Regge, T. and Teitelboim, C. (1976) Constrained Hamiltonian Systems. Accademia Nazionale dei Lincei, Rome.
- 13. Landau, L.D. and Lifshitz, E.M. (1976) Mechanics. Sykes, J.B. and Bell, J.S., Trans., Cambridge University Press, Cambridge.
- 14. Sudarshan, E.C.G. and Mukunda, N. (1974) Classical Dynamics. Wiley, New York.
- 15. Sundermeyer, K. (1982) Constrained Dynamics. Lecture Notes in Physics, Springer, Berlin.
- 16. Becchi, C., Rouet, A. and Stora, R. (1974) The Abelian Higgs Kibble Model, Unitarity of the S-Operator. Physics Letters B, 52, 344-346. https://doi.org/10.1016/0370-2693(74)90058-6
- 17. Becchi, C., Rouet, A. and Stora, R. (1975) Renormalization of the Abelian Higgs-Kibble Model. Communications in Mathematical Physics, 42, 127-162. https://doi.org/10.1007/BF01614158
- 18. Becchi, C., Rouet, A. and Stora, R. (1976) Renormalization of Gauge Theories. Annals of Physics, 98, 287-321. https://doi.org/10.1016/0003-4916(76)90156-1
- 19. Tyutin, I.V. (1975) Gauge Invariance in Field Theory and Statistical Physics in Operator Formalism. LEBEDEV-75-39. arXiv:0812.0580 [hep-th]
- 20. Brandt, F., Dragon, N. and Kreuzer, M. (1989) All Consistent Yang-Mills Anomalies. Physics Letters B, 231, 263-270. https://doi.org/10.1016/0370-2693(89)90211-6
- 21. Brandt, F., Dragon, N. and Kreuzer, M. (1989) All Solutions of the Consistency Equations. DESY 89-076, ITP-UH 2/89.
- 22. Fisch, J., Henneaux, M., Stasheff, J. and Teitelboim, C. (1989) Existence, Uniqueness and Cohomology of the Classical BRST Charge with Ghosts of Ghosts. Communications in Mathematical Physics, 120, 379-407. https://doi.org/10.1007/BF01225504
- 23. Henneaux, M. (1990) Lectures on the Antifield-BRST Formalism for Gauge Theories. Nuclear Physics B—Proceedings Supplements, 18, 47-105. https://doi.org/10.1016/0920-5632(90)90647-D
- 24. Batalin, I.A. and Vilkovisky, G.A. (1981) Gauge Algebra and Quantization. Physics Letters B, 102, 27-31. https://doi.org/10.1016/0370-2693(81)90205-7
- 25. Batalin, I.A. and Vilkovisky, G.A. (1983) Quantization of Gauge Theories with Linearly Dependent Generators. Physical Review D, 28, 2567-2582. https://doi.org/10.1103/PhysRevD.28.2567
- 26. Batalin, I.A. and Vilkovisky, G.A. (1984) Erratum: Quantization of Gauge Theories with Linearly Dependent Generators. Physical Review D, 30, 508. https://doi.org/10.1103/PhysRevD.30.508
- 27. Fisch, J.M.L. and Henneaux, M. (1990) Homological Perturbation Theory and the Algebraic Structure of the Antifield-Antibracket Formalism for Gauge Theories. Communications in Mathematical Physics, 128, 627-640. https://doi.org/10.1007/BF02096877
- 28. Henneaux, M. and Teitelboim, C. (1991) Quantization of Gauge Systems. Princeton University Press, Princeton.
- 29. Gomis, J. and Paris, J. (1993) Field-Antifield Formalism for Anomalous Gauge Theories. Nuclear Physics B, 395, 288-324. hep-th/9204065 https://doi.org/10.1016/0550-3213(93)90218-E
- 30. Gomis, J., Pars, J. and Samuel, S. (1995) Antibracket, Antifields and Gauge-Theory Quantization. Physics Reports, 259, 1-145. hep-th/9412228 https://doi.org/10.1016/0370-1573(94)00112-G
- 31. Barnich, G. and Henneaux, M. (1993) Consistent Couplings between Fields with a Gauge Freedom and Deformations of the Master Equation. Physics Letters B, 311, 123-129. hep-th/9304057 https://doi.org/10.1016/0370-2693(93)90544-R
- 32. Henneaux, M. (1998) Consistent Interactions between Gauge Fields: The Cohomological Approach. Contemporary Mathematics, 219, 93-109. hep-th/9712226 https://doi.org/10.1090/conm/219/03070
- 33. Barnich, G., Brandt, F. and Henneaux, M. (1995) Local BRST Cohomology in the Antifield Formalism: II. Application to Yang-Mills theory. Communications in Mathematical Physics, 174, 93-116. hep-th/9405194 https://doi.org/10.1007/BF02099465
- 34. Bizdadea, C. (2000) On the Cohomological Derivation of Topological Yang-Mills Theory. Europhysics Letters, 52, 123-129. hep-th/0006218 https://doi.org/10.1209/epl/i2000-00413-7
- 35. Cioroianu, E.M. and Sararu, S.C. (2005) Self-Interactions in a Topological BF-Type Model in D=5. Journal of High Energy Physics, 2005, JHEP07. hep-th/0508035 https://doi.org/10.1088/1126-6708/2005/07/056
- 36. Bizdadea, C., Cioroianu, E.M., Danehkar, A., Iordache, M., Saliu, S.O. and Sararu, S.C. (2009) Consistent Interactions of Dual Linearized Gravity in D=5: Couplings with a Topological BF Model. European Physical Journal C, 63, 491-519. arXiv:hep-th/0908.2169 https://doi.org/10.1140/epjc/s10052-009-1105-0
- 37. Barnich, G., Henneaux, M. and Tatar, R. (1994) Consistent Interactions between Gauge Fields and Local BRST Cohomology: The Example of Yang-Mills Models. International Journal of Modern Physics D, 3, 139-144. hep-th/9307155 https://doi.org/10.1142/S0218271894000149
- 38. Bizdadea, C., Ciobirca, C.C., Cioroianu, E.M., Saliu, S.O. and Sararu, S.C. (2003) Hamiltonian BRST Deformation of a Class of N-Dimensional BF-Type Theories. Journal of High Energy Physics, 2003, JHEP01. hep-th/0302037 https://doi.org/10.1088/1126-6708/2003/01/049
- 39. Barnich, G., Brandt, F. and Henneaux, M. (2000) Local BRST Cohomology in Gauge Theories. Physics Reports, 338, 439-569. hep-th/0002245 https://doi.org/10.1016/S0370-1573(00)00049-1
Appendix
Antibracket Structure
For a function 

The left derivative 

For any 

Considering Equation (32) and Equation (118), it follows that
Assuming

For bosonic (commutative) and fermionic (anticommutative) variables, we have

For any

Furthermore, the antibracket has the following properties:






















