Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:58997,12 pages
10.4236/tel.2015.54067
Characterizing the Volatility Transmission across International Stock Markets
Amarnath Mitra1, Vishwanathan Iyer2, Anto Joseph1*
1Department of Finance, IBS-Hyderabad, ICFAI Foundation for Higher Education (IFHE), Hyderabad, India
2Department of Finance, T. A. Pai Management Institute, Manipal, India
Email: amarnath.mitra@gmail.com, viyer@tapmi.edu.in, *ajoseph@ibsindia.org
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 July 2015; accepted 21 August 2015; published 24 August 2015
ABSTRACT
The present study attempts to track the transmission of volatility across major international stock markets over a span of 20 years, which includes both crisis (contagion form) and non-crisis periods. It also investigates whether global transmission of volatility follows a pattern. The study uses bi-variate EGARCH model in order to capture spillover between a pair of stock markets and the estimation window is one year with a sliding frequency of one quarter. The results show that, there is a spillover of volatility between international stock markets at all times. Results also indicate that in almost all cases, the pattern of spillover is non-random. Finally, the study characterizes the spillover pattern between international stock markets using suitable theoretical distributions.
Keywords:
Volatility Spillover, Financial Contagion, Volatility Pattern

1. Introduction
The liberalization of capital markets has improved economic ties among countries through policy coordination and has promoted economic integration by means of trade and investments. On the other hand, globalization of capital markets has led to their dependence on one-another, as a result stock markets in one country react to the information from other stock markets of the world. King and Wadhwani [1] and Dungey and Martin [2] have found that increasing integration and openness between international capital markets has led to more exposure in the economic and financial turbulence and thereby leading to higher volatility in the markets. Hence, the greater the integration among international capital markets, the greater the chances of financial contagions i.e. spillover of volatility due to a financial crisis.
A traditional approach to evaluate the level of integration among international stock markets has been to study the correlation among them over time [3] [4] . The degree of correlation of stock markets prices is generally taken as evidence of the degree of market integration. However, such an approach has been found to be flawed, since there exist time-varying properties in data, such as short term noises and long term fundamental relationships, which are not captured by simple correlation technique. Subsequent studies have measured the interdependencies between stock markets through examining the spillover of volatilities between them [5] .
The concept of spillover of volatility of asset returns can be drawn from the seminal work of Engle et al. [6] . Borrowing from meteorological lexicon, the authors lay down the theoretical foundations for “own” and “cross” type spillovers. The “heat wave” hypothesis, representing own-spillover, states that present volatility of a market is a function of past volatility of the same market (also sometimes referred to as volatility clustering). On the other hand, the “meteor shower” hypothesis, representing cross-spillover, states that the present volatility of a market is a function of both past volatility of the same market and past volatility from other markets (also termed as volatility transmission)1. Thus, the “meteor shower” definition of spillover encompasses both “own” and “cross” aspects.
The literature on volatility spillover across stock markets can be categorized into two broad strands i.e. crisis specific studies, and country or region specific studies. The crisis specific studies mainly focus on the examination of volatility spillover during financial crises, especially, during four major financial crises: the Black Monday stock market crisis of October, 1987; the Asian Crisis of 1997; the Subprime Crisis of 2007-2008 and the very recent Euro-zone Crisis of 2009-2012. Several authors2 examined the transmission of volatility across different stock markets during the 1987 crisis in detail. The Asian crisis of 1997 and the recent Subprime crisis of 2007-2008 were also thoroughly examined by authors like Shamiri and Isa, 2009 [9] ; Islam et al. 2013; Abbas et al. 2013 and Achraf et al. 2013 among several others [10] .
The country or region specific studies observe the volatility transmission between selected countries or regions. Most of the country related studies concentrate on the developed economies (such as the US, Japan and the UK). Gradually studies started to focus on the developing markets, especially after the Asian crisis of 1997. The region based studies mainly focus on economic zones such as the European Union, the ASEAN countries and the Asia-Pacific region. These studies, in general, are characterized by having large sample, both in terms of number of countries and the span of study. Eun and Shim [3] and others3 study volatility transmissions across few major stock markets4. Emerging markets are studied by Bekaert and Harvey [11] ; De Santis and Imrohoroglu [12] among others. European region is analyzed by Baele [13] ; Islam et al. [10] and Tiwari et al. [14] . Bhar and Nikolova [15] investigate the level of volatility transmission involving the BRIC nations. Engle and Susmel [5] study the volatility process of 18 major international stock markets across four major continents.
The basic findings common to all the above mentioned studies can be summed up into the following points. The volatilities of stock-prices are time varying. The returns and volatilities of stock markets of different countries show significant correlation in general. Lagged spillovers5 are found to exist between international stock markets. Correlations in stock returns and their volatilities appear to be causal from one country to another. US was found to be the source of volatility spillover in most of the cases. However, the reverse condition (i.e. spillover from other countries to US) was found to be rare. There has been a gradual shift i.e. from the developed nations to the developing countries in the choice of sample set in spillover related studies. However, large parts of Asia, Africa and South America have yet to be explored in this regard.
The motivation for the present study originates from the meteor shower hypothesis and its implications. Meteor shower hypothesis proposes that present volatility of a stock market is a function of past volatility from other market(s). It implies that shocks generated in one market, travel to other market(s). In this context, we empirically examine the nature and pattern of volatility transmissions across international stock markets over a span of last 20 years. Moreover, the study empirically tests whether the volatility transmissions across international stock markets consistent over spatial and temporal dimensions especially in the wake of a financial crisis. The period of study covers both crisis and tranquil periods. The crises period includes 3 major financial crises since 1987: the Asian Crisis (1997), the Subprime Crisis (2007-2008), and the European Debt Crisis (2009-2012). And finally, we observe the behavior of individual stock markets in propagation of volatility.
The results of the study indicate that volatility spillover between all international stock markets under the study happens at all time6 and there is conclusive evidence that spillover of volatility between international stock markets is non-random (95% cases). Further, leverage effect plays a dominant role in spillover between international stock markets. Also, the results show that in roughly 8% cases, the contagion form of spillover is significantly distinct from the normal (or tranquil) form in terms of magnitude. Moreover, about 18% of cases show that changes in the direction of spillover between international stock markets are brought about by financial crisis. In addition, the results imply that, the transmission of volatility between stock markets are predictable as they follow a definite pattern and hence have been modeled using suitable theoretical distributions. The study of volatility spillover is essential for two reasons. Firstly, volatility spillover across international stock markets shows the extent of market integration. Secondly, it indicates the level of information efficiency of a market in factoring international news and shocks. A clear understanding of the mechanism of volatility transmission across international stock markets is important for its implication on risk hedging, resource allocation, asset valuation, and monetary policies. The rest of the paper is organized as follows. Section 2 describes the data and methodology used. Section 3 describes the empirical results and finally we summarize and conclude the study in Section 4.
2. Data and Methodology
The daily data of stock indices values from 10 countries7 across the world for a period 20 years, from Jan. 1995 to Dec. 2014 has been considered. The data has been obtained from Bloomberg Database. Since in some countries, there are multiple stock exchanges so that we have included the most prominent ones, such as BSE from India and NYSE from US, in our study. The data set contains equal representation from both developed and emerging economies8 (five each). Moreover, care has been taken to represent each continent. Choice of stock markets in the data set is based upon their market capitalization and the GDP of their respective countries9. Recognizing the fact that national stock exchanges of different countries may have overlapping trading hours, we take the close to close criteria which encompass both overnight as well as day time segments and also take care of short term corrections due to noise. Table 1 briefly describes the research design of the study.
We start our main empirical analysis by testing the meteor shower hypothesis. We use time-varying correlation measures, obtained from bi-variate VAR-EGARCH model, to define the links between a pair of stock indices. Due to non-synchronicity of trading days between stock markets of different countries, care was taken to include only the common dates of business between a pair of international stock markets. A brief description of the bivariate EGARCH model with time varying correlations between any two stock indices is given below.
We denote the index return from one country by r1t and r2t represents returns from second index.
Table 1. Summary of the research design.
The mean equation of the VAR model is given below,
 (1)
(1)
here,
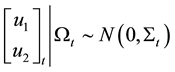 (2)
(2)
Here, the diagonal elements (c11 and c22) represent auto-regression and off-diagonal elements (c12 and c21) represent spillover-in-mean. Ωt indicate all relevant information known at time t, and St is the time varying covariance matrix. The diagonal elements of the (2 × 2) covariance matrix are modeled as:
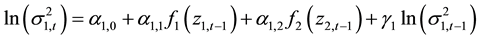 (3)
(3)
and
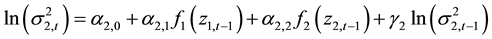 (4)
(4)
where,
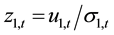 and
and
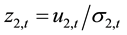
The second term of Equation (3) and third term of Equation (4) represents ARCH effects. Fourth terms of Equation (3) and Equation (4) captures the GARCH effect; and the third term in Equation (3) and second term in (4) captures cross-market spillover. f1and f2 are functions of standardized innovations which capture the effect of sign and the size of the lagged innovations as:
 (5)
(5)
 (6)
(6)
The functions f1 and f2 generate sequences of zero mean, iid11 random variables by construction and allow past standardized innovations to affect asymmetrically. The first two terms in Equations (5) and (6) capture the size effect and the third term measures the sign effect. When δ is negative it will increase the volatility by more than a positive realization of equal magnitude. Similarly, if the past absolute value of zt is greater than its expected value, the current volatility will rise. This effect is known as leverage effect and is documented by Black [16] and Nelson [17] among others [18] . The parameter γ determines the influence of the past conditional volatility on the current conditional volatility. For the conditional volatility process to be stationary it is required that, |γi| < 1; (i = 1, 2). The cross-market volatility linkage i.e. volatility spillover effects are controlled by the parameters, α12 and α21. Thus, if α12 is positive and δ2 is negative then a negative innovation in market “2” will be followed by higher volatility in market “1” than in the case of an advance positive innovation in market “1”. The asymmetric effect of standardized innovations on volatility may be measured as derivatives from Equations (5) and (6),
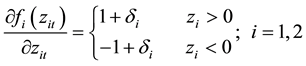 (7)
(7)
The relative asymmetry is defined as,
 (8)
(8)
The off-diagonal elements of the covariance matrix St are defined in a manner similar to that in Darbar and Deb [19] . The key is to define a time varying conditional correlation which when combined with the conditional variances given in the Equations (3) and (4) generate the required conditional covariance. The conditional correlation is allowed to depend on the lagged standardized innovations and is transformed using the following function so that it lies between (−1, 1).
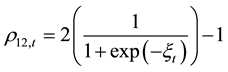
where,
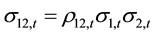 ; and (9)
; and (9)
Although the function ξt may be unbounded, the sine function transformation will restrict it to the desired range for correlation. For a given pair of return series a set of 19 parameters {Θ} are to be estimated. The estimation of these parameters is achieved by numerical maximization of the joint likelihood function under the distributional assumption of this model. If the sample size is T, then the log likelihood function to be maximized with respect to the parameter set {Θ} is:
 (10)
(10)
The parameters of the above bi-variate EGARCH model are estimated by numerically maximizing the likelihood function discussed above using the algorithm developed by Berndt et al. [20] (BHHH12) without imposing any parameter restriction. As a note, we would like to mention here that each stock market has different regulations, trading system and transaction costs, which as an assumption, has not been considered in this study. Using the above bivariate EGARCH model, we obtain the spillover parameters which are used for further analyze in the study. There are 45 pairs from 10 stock market data series and approximately 77 estimation windows, each of length one year and rolling over at an interval of a quarter. The rationale for using rolling analysis for our study is for two reasons i.e. to assess a model’s stability over time and to evaluate predictive accuracy.
3. Empirical Results
Table 1 gives a brief summary of the descriptive statistics for the unconditional daily returns of the stock markets of 10 countries for a period of 20 years from 1995-2014. The reported statistics include the mean logarithmic returns along with their respective minimum, maximum and median values. The distributional properties of mean returns are given by standard deviation, skewness and kurtosis. Jarque-Bera statistic, testing normality of return distribution, have also been reported.
As evident from the above Table 2 the unconditional mean daily returns of all the markets are close to zero, however, their dispersion is high as apparent from the standard deviation values. Barring Brazil, the return
Table 2. Descriptive statistics.
distribution of all other stock markets show negative skewness, implying that impact of negative news is more than positive news. The kurtosis measure show that the return distributions of all the markets are leptokurtic in nature, indicating that probability of rare events, such as crisis, is higher than normal. The Jarque-Bera statistics confirm that the return distribution of all the above stock markets are non-normal, hence all the assumptions of normal distribution needs to be modified. The results of Ljung-Box Q-test indicate high persistence of linear dependence in the returns. Linear dependence in returns has been attributed to several factors such as non-syn- chronous trading (French et al. 1987), market imperfections such as infrequent trading of the component securities in the respective markets, or due to some fundamental forces, such as predictable changes in responsiveness to world risk factors (Lo and Mackinley, 1988; Harvey, 1995; Koutmos and Booth, 1995; Bekaert and Harvey [11] ).
The preliminary analysis of the data indicates that every stock market manifests all the typical attributes of financial data, such as leptokurtosis, non-normality, asymmetry and auto-correlation. Both lepto-kurtosis and non-normality characteristics of stock market data (as given by JB statistics) points towards presence of fat tails in return distribution which indicates that extreme event such as crashes and booms are likely to occur with a higher probability than normal [21] . These issues that were raised by the descriptive statistics, prompted us to employ a comprehensive and robust analytical framework of bi-variate EGARCH that models all the above mentioned aberrations. The following are the rationale for the use of such a framework: 1) the high persistence of linear dependencies in the series justifies the use of autoregressive models; 2) due to the leptokurtic nature found in the return series coupled with the strong presence of non-linear dependencies in the daily returns for all the markets validates our choice of autoregressive conditional heteroskedasticity (ARCH) models to analyze the linkages among these markets; 3) the asymmetric property of return distribution is captured through exponential-GARCH which distinctively models the extreme negative returns from the positive ones; and 4) as the data manifests strong evidence against normality, care was taken to address the assumptions made about the distributional properties of the residual terms from the models by using student’s t-distribution, in order to avoid mis- specification (Table 3).
Table 3. Snapshot of raw result13 (matrix size 3465 * 13).
Note: 1. Column 0-Total number of estimations (3465); 2. Column 1 and 2―First and second stock markets respectively (market i ≠ market j); 3. Column 3 and 4―Spillover coefficients from market 2 to 1 (Col. 3) and from market 1 to 2 (Col. 4) respectively; 4. Column 5 and 6―Half life values, corresponding to the spillover coefficients, from market 2 to 1 (Col. 5) and from market 1 to 2 (Col. 6) respectively; 5. Column 7 and 8-Leverage coefficient from market 1 to 2 (Col. 7) and from market 2 to 1 (Col. 8) respectively; 6. Column 9―Estimation variable indicating whether estimation for a particular window was achieved14. est = 1 means estimation achieved, est = 0 means otherwise. We have achieved 2772 out of 3465 = 80% successful estimation15; 7. Column 10―Crisis variable signifying whether the given estimation window falls in a crisis period16. Crisis = 0 means tranquil period, Crisis = 1 means crisis period (22 crisis and 47 tranquil out of total 77 periods); 8. Column 11―Denotes nth estimation window, n = 1 to 77 (Jan. 1995-Dec. 2014); 9. Column 12―Shows direction of spillover. dir = 1 => no spillover, dir = 2 => spillover from market 1 to 2, dir = 3 => spillover from market 2 to 1, and dir = 4 => both way spillover; 10. Out of all the terms mentioned above, further analysis of only the volatility spillover terms have been reported here.
The spillover data is used to test the meteor shower hypothesis. A t-test is conducted on the cross-market spillover coefficients (α1,2 and α2,1) obtained from the bi-variate EGARCH model. The coefficients are tested at 5% level of significance. The results confirm the presence of meteor shower, i.e. cross market spillovers, across dimensions of space (all stock markets included in the sample) and time (over a period of 20 years). The results are provided in Table A1 and Table A2 in Appendix 2. Further, to check whether, for a pair of stock markets, the magnitude of spillovers is different with respect to direction of spillover (i.e. whether spillovers from market i to j is different from spillovers from market j to i), z-test has been carried out. Table 4 shows the z-statistic along with the relevant level of significance between all pairs of markets.
The results show that, in general, the magnitudes of spillover for all pair of stock markets are different with respect to the direction of spillover (in 80% of cases)17. However, it may be kept in mind that the z-tests were carried out on an aggregate level data (average over 20 years). Hence, in the cases where the difference in magnitude over direction is not statistically significant, the results are likely to change in the inter-temporal periods. Further, we test the pattern hypothesis. A run test, using WW-test statistic18, is conducted to test whether for a given pair of markets the spillover coefficients follow a random pattern across 77 period windows (i.e. over a period of 20 years). Table 5 shows the results obtained from WW-tests along with their significance.
Table 4. Results of test of spillover hypothesis.
Table 5. Result of test of pattern hypothesis.
Results of test of pattern hypothesis show that for the last 20 years’, barring a few cases19 the spillover of volatility between international stock markets, in general, follow a definite pattern. Out of total 10 stock markets, Egypt and Japan display maximum inclination towards randomness (3 cases each), both as a source and as a sink; while markets like Australia, China, India, Israel and the UK show definite pattern in spillover with respect to all other markets both as a source and as a sink. In the case of developed markets, US, while acting as a source of spillover to other markets, display non-random characteristics with all the markets; same is the case as a sink of spillover except with markets like Brazil. Japan in general display definite pattern in spillover. Notable exceptions are there for markets like Egypt and France, when Japan is the source of spillover and with the market of Egypt, when Japan acts as sink. In case of developing markets, India and China assertively display non-ran- domness in volatility spillover with all markets. Brazil too displays similar characteristics. In case of Brazil, the exception is the market of Egypt, when Brazil plays the role of source. In the pacific region, Australia display non-random property for cross-market spillover with all the other markets. From Africa and Middle East, both Egypt and Israel in general show non-random property for stock market spillovers. In case of Egypt, the exception is the markets of Japan, when Egypt is the source of spillover; and the markets of Brazil, and Japan, when Egypt acts the sink. For Israel, there are no exceptions. Overall, the results indicate that there is conclusive evidence (95%) of spillover of volatility between international stock markets follow a definite pattern. The results also imply that, in most cases, the transmission of volatility between stock markets is predictable. Unlike Li and Giles [22] , we find significant bidirectional spillover of stock market volatility between the US market, the Japanese and the Asian emerging markets. However, our observations coincide with Li and Giles [22] as we also find stronger and bidirectional spillovers between the US and the Asian stock markets during the Asian financial crisis.
Table 6 shows the average spillover of each stock market with respect to world stock markets in last 20 years (1995-2014). It depicts the role of each stock market in the propagation of spillover and contagion.
Although the above data show aggregate of aggregate statistics, it can be seen that 8 out of 10 world markets (almost 80%) distinctively behave as source and sink with respect to spillover of volatility. Notably, in case of developed markets, the US predictably acts more of a source than as sink of stock market spillover. Similar is the case with European markets (expect for UK). The pacific market, denoted by Australia, also shows general inclination towards being sink. In case of developing markets, China and India participate as more as sink than as source of spillover; while markets like Brazil act more as source than as sink of spillover.
After establishing pattern in volatility transmission across international stock markets, we modeled the spillover patterns using suitable theoretical distributions. A number of distributions were fitted against the spillover data pertaining to each pair of stock markets. The fitting of these distributions were tested using Kolmogrov- Smirnov (K-S) test statistic. The distribution which gave the least error was chosen as the best fit. Table 7 presents the type of spillover distribution between various stock markets. The results obtained on spillover
Table 6. The average spillover of each stock market with respect to world stock markets.
Table 7. Characterization of Volatility spillover between international stock markets.
patterns that are prevailing for last 20 years (1995-2014). Appendix 3 gives a detail account of the spillover distribution types along with the K-S test statistics and their respective p-values, for a give pair of stock markets.
4. Conclusion
In this study, we empirically examine the nature and pattern of volatility transmissions across international stock markets over a span of last 20 years. Moreover, the study empirically tests whether the volatility transmissions across international stock markets are consistent over spatial and temporal dimensions especially in the wake of a financial crisis. The period of study covers both crisis and tranquil periods. The results of the study indicate that volatility spillover between all international stock markets is under the study happens at all time20 and there is a conclusive evidence that spillover of volatility between international stock markets is non-random (95% cases). Further, leverage effect plays a dominant role in spillover between international stock markets. Also, the results show that in roughly 8% cases, the contagion form of spillover is significantly distinct from the normal (or tranquil) form in terms of magnitude. Moreover, about 18% of cases show that changes in the direction of spillover between international stock markets are brought about by financial crisis. In addition, the results imply that the transmission of volatility between stock markets is predictable as they follow a definite pattern and hence is modeled using suitable theoretical distributions. The implication of this is immense. Characterizing the cross-market volatility pattern between various stock markets give us the opportunity to create international volatility index (I-VIX). In addition, one may look into the possibility of creating synthetic assets with characteristics similar to those of exchange traded funds (ETFs) but of international nature (I-ETFs).
Cite this paper
AmarnathMitra,VishwanathanIyer,AntoJoseph, (2015) Characterizing the Volatility Transmission across International Stock Markets. Theoretical Economics Letters,05,571-583. doi: 10.4236/tel.2015.54067
References
- 1. King, M.A. and Wadhwani, S. (1990) Transmission of Volatility between Stock Markets. Review of Financial studies, 3, 5-33. http://dx.doi.org/10.1093/rfs/3.1.5
- 2. Dungey, M. and Martin, V.L. (2007) Unravelling Financial Market Linkages during Crises. Journal of Applied Econometrics, 22, 89-119. http://dx.doi.org/10.1002/jae.936
- 3. Eun, C.S. and Shim, S. (1989) International Transmission of Stock Market Movements. Journal of financial and Quantitative Analysis, 24, 241-256. http://dx.doi.org/10.2307/2330774
- 4. Goetzmann, W.N., Li, L.F. and Rouwenhorst, G.K. (2005) Long-Term Global Market Correlations. Journal of Business, 78, 1-38. http://dx.doi.org/10.1086/426518
- 5. Engle, R.F. and Susmel, R. (1993) Common Volatility in International Equity Markets. Journal of Business & Economic Statistics, 11, 167-176.
- 6. Engle, R.F., Ito, T. and Lin, W.L. (1990) Meteor Showers or Heat Waves? Heteroskedastic Intra-Daily Volatility in the Foreign Exchange Market. Econometrica, 58, 525-542. http://dx.doi.org/10.2307/2938189
- 7. Hamao, Y., Masulis, R.W. and Ng, V. (1990) Correlations in Price Changes and Volatility across International Stock Markets. Review of Financial studies, 3, 281-307. http://dx.doi.org/10.1093/rfs/3.2.281
- 8. Lin, W.L., Engle, R.F. and Ito, T. (1994) Do Bulls and Bears Move across Borders? International Transmission of Stock Returns and Volatility. Review of Financial Studies, 7, 507-538. http://dx.doi.org/10.1093/rfs/7.3.507
- 9. Shamiri, A. and Isa, Z. (2009) The US Crisis and the Volatility Spillover across South East Asia Stock Markets. International Research Journal of Finance and Economics, 34, 7-17.
- 10. Issam, C., Achraf, G. and Boujelbene, Y. (2013) Volatility Spillover and Channels Transmission during Subprime Crisis: Empirical Study of USA Stock Market and Other Developed Stock Markets. Journal of Applied Economic Sciences (JAES), 1, 7-21.
- 11. Bekaert, G. and Harvey, C.R. (1997) Emerging Equity Market Volatility. Journal of Financial Economics, 43, 29-77. http://dx.doi.org/10.1016/S0304-405X(96)00889-6
- 12. De Santis, G. (1997) Stock Returns and Volatility in Emerging Financial Markets. Journal of International Money and Finance, 16, 561-579. http://dx.doi.org/10.1016/S0261-5606(97)00020-X
- 13. Baele, L. (2005) Volatility Spillover Effects in European Equity Markets. Journal of Financial and Quantitative Analysis, 40, 373-401. http://dx.doi.org/10.1017/S0022109000002350
- 14. Tiwari, A., Bhanja, N. and Dar, A. (2015) Uncertainty Co-Movement in Major European Countries. Theoretical Economics Letters, 5, 256-261. http://dx.doi.org/10.4236/tel.2015.52030
- 15. Bhar, R. and Nikolova, B. (2009) Return, Volatility Spillovers and Dynamic Correlation in the BRIC Equity Markets: An Analysis Using a Bivariate EGARCH Framework. Global Finance Journal, 19, 203-218. http://dx.doi.org/10.1016/j.gfj.2008.09.005
- 16. Black, F. (1976) Studies of Stock Market Volatility Changes. Proceedings of the 1976 Meetings of the American Statistical Association, Business and Economic Statistics Section, 177-181.
- 17. Nelson, D.B. (1991) Conditional Heteroscedasticity in Asset Returns: A New Approach. Econometrica, 59, 347-370. http://dx.doi.org/10.2307/2938260
- 18. Bhar, R. (2001) Return and Volatility Dynamics in the Spot and Futures Markets in Australia: An Intervention Analysis in a Bivariate EGARCH-X Framework. Journal of Futures Markets, 21, 833-850. http://dx.doi.org/10.1002/fut.1903
- 19. Darbar, S.M. and Deb, P. (2002) Cross-Market Correlations and Transmission of Information. Journal of Futures Markets, 22, 1059-1082. http://dx.doi.org/10.1002/fut.10045
- 20. Berndt, E.K., Hall, H.B., Hall, R.E. and Hausman, J.A. (1974) Estimation and Inference in Non-Linear Structural Model. Analysis of Economic and Social Measurement, 4, 653-666.
- 21. Cont, R. (2001) Empirical Properties of Asset Returns: Stylized Facts and Statistical Issues. Quantitative Finance, 1, 223-236. http://dx.doi.org/10.1080/713665670
- 22. Li, Y. and Giles, D.E. (2015) Modelling Volatility Spillover Effects between Developed Stock Markets and Asian Emerging Stock Markets. International Journal of Finance & Economics, 20, 155-177. http://dx.doi.org/10.1002/ijfe.1506
Appendix 1
The developed and developing categorization of countries is based on World Bank Classification (2013). GDP per capita values are at current prices in USD21. Domestic market capitalization and Value of shares traded are in annual figures in USD (billions) updated till Dec. 201322.
Appendix 2
Table A1. Result of test of pattern hypothesis.
Notes: 1. Each of the spillover matrixes is a non-symmetric matrix. Mi, j ≠ Mj, i; where, first subscript denotes row and second subscript denotes column; 2. Each cell C{i, j} represents spillover from country i to j. Here, i = row, j = column; 3. Each cell represents four statistics: minimum, maximum, count and count (%) respectively, each separated by a semi-colon; 4. Each of these statistics is a measure aggregated over 77 period windows from year 1995-2014; 5. Each period window is a length one calendar year which slides after every quarter (i.e. three months calendar period); 6. All the statistics are an aggregate measure of spillover coefficient significant at 5% level; 7. The count estimate indicates the percentage of significant spillover values out of 77 periods; 8. All the values are approximated to two decimal places. The count values are approximated to nearest integer.
Table A2. Result of test of pattern hypothesis.
Notes: 1. Each of the spillover matrixes is a non-symmetric matrix. Mi, j ≠ Mj, i; where, first subscript denotes row and second subscript denotes column; 2. Each cell C{i, j} represents spillover from country i to j. Here, i = row, j = column; 3. Each cell represents two statistics: average spillover and standard deviation (in parenthesis), respectively; 4. Each of these statistics is a measure aggregated over 77 period windows from year 1995-2014; 5. Each period window is a length one calendar year which slides after every quarter (i.e. three months calendar period); 6. All the statistics are an aggregate measure of spillover coefficient significant at 5% level; 7. All the values are approximated to two/three decimal places.
Appendix 3
Table B1. Result of test of pattern hypothesis.
Table B2. Result of test of pattern hypothesis.
Notes: 1. Each of the tables is a non-symmetric matrix. Mi, j ≠ Mj, i; where, first subscript denotes row and second subscript denotes column; 2. Each cell C{i, j} represents spillover from country i to j. Here, i = row, j = column; 3. Each cell represents three items: distribution type, Kolmogrov-Smirnov test statistic and p-value (in parenthesis), respectively; 4. Each of these statistics is a measure aggregated over 77 period windows from year 1995-2014; 5. Each period window is a length one calendar year which slides after every quarter (i.e. three months calendar period); 6. All the statistics are measured at 5% level of significance; 7. All the values are approximated to three decimal places.
NOTES
*Corresponding author.
1Although in literature, the terms: volatility spillover and volatility transmission are synonymous, the term “transmission” generally indicates the “cross” (i.e. cross market or cross country) aspect of spillover only. In this study, wherever the term volatility transmission appears, it is to be understood that the reference is towards cross-country spillover.
2King and Wadhwani, 1990 [1] ; Hamao and Ng, 1990 [7] ; Lin et al. 1994 [8] ; Liu and Pan, 1997 among others.
3They include King and Wadhwani, 1990 [1] ; Hamao and Ng, 1990 [7] ; Lin et al. 1994 [8] ; Achraf et al. 2013 [10] .
4Mainly US, UK and Japan.
5Correlations between foreign market’s previous day return or its volatility with today’s return or its volatility in the domestic market.
6It must be noted that in last 20 years (1995-2014) tranquil phase occupies over 70% of the total period.
7Australia, Brazil, China, Egypt, France, India, Israel, Japan, UK and US.
8As per World Bank classification (2014).
9Refer to Appendix 1.
10Only those observations for dates that are common across 26 markets have been included in the study.
11Identically and independently distributed.
12Berndt Hall Hall Hausman algorithm.
13Obtained from bivariate EGARCH model. All the non-zero values for the variables: spillover (Col. 3 - 4), half life (Col. 5 - 6) and leverage (Col. 7 - 8) are significant at 5%.
14Based on convergence of the iterative estimation procedure.
15The rest could not be achieved due to insufficiency of data.
16Predetermined based on literature.
17Only in some 9 out of 45 cases (i.e. less than 20%) the difference in magnitude with respect to direction is found to be statistically not significant.
18Null hypothesis for WW test: spillover coefficients follow a random sequence.
19Only 5 out of total 90 pairwise cases (i.e. 5%) show that volatility spillover follow random distribution.
20It must be noted that in last 20 years (1995-2014) tranquil phase occupies over 70% of the total period.
21Source: http://data.worldbank.org/indicator/NY.GDP.PCAP.CD
22Source: www.world-exchanges.org












