Received 22 October 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT

The Harmonic Neutron Hypothesis, HNH, has demonstrated that many of the fundamental physical constants are associated with quantum integers, n, within a classic integer and partial harmonic fraction system, and follow a known two-dimensional, 2D, power law geometry. These are exponents of a fundamental frequency, 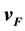, the basis of which is the annhilation frequency of the neutron,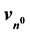. 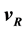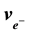Our goal to a first approximation is to derive the frequency equivalents of the Rydberg constant, , the Bohr radius, , the electron, , and the reciprocal fine structure constant, 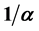all from, π, and a small set of prime integers only. The primes used in the derivations are respectively 2, 3, 5, 7, and 11. This is possible since it is known that the number 3 is associated with R, 5 with, 7 with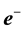, and 11 with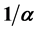. In addition, the inter-relationships of the frequency ratio equivalents of these natural units with 2 and π are known, thus allowing for the derivation of any one from the others. Also the integer and partial fractions of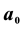, , and define Planck time squared,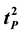. An accurate estimate of 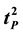from alone is also related to the integer 2 since gravity is a kinetic force. Planck time squared, scales the Y-axis, and scales the X-axis. In conclusion the quantum properties of hydrogen are derived from only the natural unit physical data of the neutron, to a relative precision ranging from 2.6 × 10⁻³ to 6.7 × 10⁻⁴. This supports the hypothesis that many of the fundamental constants are related to.

Keywords:

Neutron, Fundamental Physical Constants, Unification Models, Hydrogen, Fine Structure Constant, Bohr Radius, Rydberg Constant, Electron, Quantum Harmonic Oscillators

1. Introduction

1.1. Unresolved Unification of the Fundamental Physical Constants

The primary method organizing and conceptualizing the fundamental physical constants is the Standard Model SM [1] -[5] . The SM has had excellent success in many areas, but fails in defining a global system that spans the classic, quantum, and cosmic physical domains. String Theory, ST, has attempted to solve these issues for multiple decades as well, but has not succeeded either [6] [7] . A logical, computational model, explaining a global unified organization and the relative scaling of the physical constants is not yet accepted [8] -[14] .

The directly observable properties of hydrogen, H, include the proton, p⁺, electron, e⁻; the Bohr radius, a₀; and the ionization energy, developed with Rydberg’s constant, R. These represent some of the most fundamental constants of mass, distance, and electromagnetic bosonic energy scaling factors in physics. As frequency equivalents these are inter-related with the fine structure constant, α, by the ubiquitous factors 2, and π [15] . These are also related to the reduced Planck’s constant, ħ. This factor converts a frequency into a radius and an angular frequency. Excluding the p⁺, if any two of hydrogen’s physical constants are known then the other two can be derived. They are not truly independent, but they represent a unique integrated quantum linear domain ratio system that is linked through classic Euclidean geometric scaling factors, 2 and π. Consequently these constants correlate with different physical values, for mass; distance; frequency; and for electromagnetic energy which when normalized to a single Hertzian unit are unified. These same four constants are related to Coulomb’s law; the free space constants of permittivity and permeability; Planck’s constant, h, and the speed of light, c through computational definitions of a₀. These entities also define the classic kinetic energy relationship of mass times velocity squared divided by two. The fine structure constant α is the ratio of a specific velocity and the speed of light, c. In Special Relativity this is called a β ratio. If the mass is that of the electron, the velocity is; then the kinetic energy is equivalent to the ionization energy of hydrogen, in terms of R.

If the fundamental constants represent a truly integrated unified system, all of them should be derivable from a single natural unit value in the ideal situation, or at least just a few fundamental values. This paper explores the possibility that all of the fundamental constants are inter-related in a similar fashion as these four hydrogen constants. In classic simple harmonic systems it is possible to derive any harmonic frequency provided one frequency and its single harmonic number are known. This is also a property of quantum spectra such as that developed in the Rydberg series. This type of integration of multiple physical constants into a unified system, while commonplace; though it is not typical to imagine that the whole structure of the fundamental constants represents such a system.

1.2. Goal

The goal is to logically derive to a first approximation the frequency equivalents of the electron,; the Bohr radius,; the Rydberg constant,; and the reciprocal fine structure constant, from a single fundamental natural physical constant, the annihilation frequency of the neutron, , and a small finite set of prime integers. This is done solely in utilizing methods of the Harmonic Neutron Hypothesis, HNH [16] - [21] . The HNH is an innovative method which assumes that the annihilation frequency of the neutron represents the fundamental frequency, , of a classic harmonic system that unifies physical constants. The fundamental constants are hypothesized to represent individual harmonic values within a global harmonic integer-based system. Many of the fundamental constants are associated with the smallest prime numbers [16] . It has been demonstrated that it is possible to derive many of the fundamental constants starting with only four natural unit values:, , , and. These constants include the quarks; the Higgs boson,; the Hubble constant,; Planck time, , and the lost mass in negative beta decay to hydrogen.This paper focuses on accurately deriving other fundamental constants from only and the first five prime integers. This would be a significant theoretical and computational advancement demonstrating that the fundamental constants actually represent a classic unified harmonic prime number system, within the Standard Model.

2. Methods

2.1. An Overview of the Harmonic Neutron Hypothesis

The following is a limited review and explanation of the HNH. The details have been described in multiple previous publications, and will not be repeated [16] - [21] . Our model is a purely computational, finite-integer system, based on pure number properties of integers, and natural physical units. An example of a natural unit is Planck time. The primary hypothesis is that the fundamental constants are inter-related by a simple, ubiquitous mathematical and integral-geometric pattern and its associated properties. The HNH is a natural unit harmonic system spanning different physical domains based on a single fundamental frequency, , which logically is the annihilation frequency of the neutron. Here equals where is the mass of the neutron, c is the speed of light, and h is Planck’s constant. Other physical constants and states such as frequency, energy, and distance are associated with an integer described as a quantum number, n. These can be linear states or fundamental constant states. The smallest integers {0, 1, 2, 3, …} are assumed to be associated with the most basic fundamental constants, such as the properties of hydrogen. The smallest primes {2, 3, 5, 7, 11} have shown particular importance [16] . This is similar to the concept of the second law of thermodynamics where a macroscopic system equilibrates to the highest probability of its microstates, with least variability. In our case the physical state equilibrates to the smallest possible integer values and smallest number of integers.

The primes used in our model define a global organization of inter-relationships among the fundamental constants in a resonant harmonic system. And we postulate that higher prime numbers, higher composites of those primes, and larger partial fractions are possibly associated with higher order physical entities. The HNH model has accurately explained the global organization of the fundamental constants based purely on integer properties including why black body radiation and the elements form a consecutive integer series, why the fundamental constants cluster around the neutron in a partial fraction pattern, and why the SM constants are grouped in pairs of three entities each [16] .

We define a collection of different integer n values. They are referred to as a consecutive integer series, , integer exponents, , as in, and harmonic and partial harmonic integer fraction exponents, , as in

. Note, our HNH model makes explicit use of just these exponentiations of the fundamental frequen-

cy. Each physical state in the linear domain, for example, distance; time or frequency; and mass is defined by an integer from a consecutive series, , scaled by the fundamental frequency,. Each force is scaled by an integer exponent, , of from the consecutive series {−1, 0, 1, 2}. These exponents represent respectively the elemental graviton, twice the gravitational binding energy of the electron in hydrogen; Planck’s constant, h; the neutron; and the hyper-dense boson elements of a black hole. The Compton wavelength of this hyper dense boson is smaller than its Schwarzschild radius, and therefore within a Black Hole. Other observable fundamental

constants are defined by integer partial fraction exponents of, such as the electron; the Bohr radius; Rydberg’s constant, R; and Higgs boson.

For the fundamental particles and bosons their integer-n values are logically and computationally derived based upon the relative scale between the individual constant and the neutron, similar in concept to the chemical periodic chart. We also find that the physical constants must follow power law properties within a harmonic system with the four natural unit frequency equivalent values that scale the whole harmonic system, namely the neutron,; the electron,; the Bohr radius,; and the Rydberg constant, R [22] .

The harmonic fractions and partial harmonic fractions not only define the possible harmonic frequency ratios, but also define the X, and Y coordinates of a unit circle. When n is associated with the harmonic fraction, X equals. Conversely Y equals the partial harmonic fraction, which is defined by the square root of 1 mi-

nus the square of the harmonic fraction, , or. For example when,

and. Similarly when Y is first determined from the square of the harmonic fraction, then X fol-

lows the second computation. Therefore, harmonic and partial fractions are defined by the scaling of a unit circle on a Cartesian plane, and are logically closely related to all sinusoidal periodic relationships.

The model has predictive power beyond standard methods by analyzing the whole system as an integrated harmonic spectrum rather than individual, isolated and independent physical values. The methods of prediction are similar to standard methods seen in atomic spectra. We use dimensional analysis methods similar to that of Rayleigh and Buckingham’s Pi Theorem, where the exponential base is the dimensionless neutron annihilation

frequency, , which equals. Here, equals the rest mass of the neutron

in kg, s equals one second, c equals the speed of light, and h equals Planck’s constant. The Buckingham Pi Theorem states that physical laws are independent of the form of the physical units. Therefore, acceptable laws of physics are homogeneous in all dimensions.

All of the physical phenomena are evaluated as frequency equivalents, and secondarily as dimensionless coupling constant ratios. The actual physical units can be stripped away then logically re-installed, after the dimensionless calculations. The system is standard physical unit-independent. Arbitrary physical units such as kilogram, kg; second, s; electron volt, eV; Joule, J; meter, m; electron charge, e; and the speed of light, c, are transformed to frequency equivalents, and purged from the calculations. In the linear domain all fundamental constants are defined solely by ratios. In the exponential domain they are uniquely associated with harmonic or

integer fraction exponents of.

This fundamental ratio, is an invariant, independent of the initial physical units utilized since it is a natural unit, and most of the other units are driven to unity. The unit system of the HNH is simplified with the physical units for Planck’s constant; unit electric charge; time; the distance light travels in one unit of time; and the speed of light all set to equaling 1. Energy, mass, frequency, temperature are all scaled equally. Distance is

scaled as divided by its associated frequency. Hence the speed of light equals times the distance. In these rationalized units defines the Compton wavelength of the neutron.

In this type of single-variable physical system, the units are all dimensionless coupling constants and completely defined by exponents or integer values of.

Previous HNH predictions and derivations have been made from two (2) finite integer sets. The first set includes four natural units based on known atomic quantities as frequency equivalents. Included in this set is the neutron, , and comprises the ratio of the system. A partition of this set includes the frequency equivalents of the electron, , the Bohr radius, , and the ionization energy of hydrogen, derived from the Rydberg constant,. For this paper only will be utilized in the derivations. The second set is related to the integer fraction denominators and numerators of the partial fractions which include: {1, 2, 3, 4, 5, 6, 7, 11, 35, 128}. These are all (and the only) integers that define the constants evaluated in this paper.

2.2. Conversion of Physical Constants to Frequency Equivalents, Exponents, δ, and Partial Fractions

All of the data for the fundamental constants were obtained from the websites: http://physics.nist.gov/cuu/Constants/ and www.wikipedia.org. The NIST site http://physics.nist.gov/cuu/Constants/energy.html has an online physical unit converter that can be used for these types of calculations so the values used in the model are all standard unit conversions.

The floating point accuracy is based upon known experimental atomic data for hydrogen and the neutron, of approximately 5 × 10⁻⁸. Subscript “k” denotes a known experimental value, and subscript “d” represents a derived value. All of the known fundamental constants are converted to frequency equivalents,. Equation (1) demonstrates the frequency equivalent conversion of the neutron as an example. Table 2 lists the standard unit; frequency equivalent;;; partial harmonic fraction, δ; and known exponents,; of the constants evaluated in this paper. Conversion of other constants has been previously published. Masses are converted by multiplying by c² (speed of light squared) then dividing by h (Planck’s constant). Distances are converted by dividing the wavelength into c. Energies in Joules are converted to Hz by dividing by h. The eV value for the neutron is 939.565378 (21) × 10⁶. Its frequency in Hz is converted to eV by multiplying by the constant, 4.13566750 (21) × 10⁻¹⁵ eV/Hz. The eV was converted to frequency by multiplying by the constant 2.41798930 (13) × 10¹⁴ Hz/eV. N_A equals Avogadro’s number, and amu equal atomic mass unit.

or

(1)

Our model has two parallel domains both describing identical physical values. One domain is the frequency equivalent of any physical value. This is the linear domain of possible physical states. The other domain is a set

of exponents applied to the base, which when exponentiated equals the frequency equivalent of that

specific value, Equation (2). This is the domain of the fundamental constants. The known exponent, exp_k, of a

fundamental constant is the ratio of the log_e of its frequency equivalent, , divided by the, Equation (2). Here, equals 53.780055612 (22).

(2)

The known or derived exponent minus the quantum fraction, , or partial harmonic fraction equals the known or derived, Equation (3). A quantum fraction, qf, is a possible integer-fractional exponent, not solely a harmonic partial fraction in some settings. In this case Planck time squared, , represents such a composite

constant. The known or derived frequency equivalent of a constant, v, is calculated by raising to the

exponent. In a classic simple harmonic system there are no δ values since all of the possible harmonic frequencies are defined by the and simple harmonic fractions. There are also no restrictions of which qf is associated with any specific number. In the HNH model there is a mathematical imperative that some qf exponents are associated with specific numbers. For example, 10/1155 is related to the number 2. This relationship is

equals 2. The fraction 29/1155 is associated with π. This relationship is equals π. The quantum fraction 39/1155 is associated with 2π. This relationship is equals 2π.

This is associated with equals. equals. equals. There is no common that can fulfill those restrictions. The mathematical solution to add small δ values to the quantum fractions that “shim” the system to a single resonant harmonic frequency.

(3)

Equation (4) demonstrates that raised to the known or derived exponent equals the known or derived frequency equivalent, v.

(4)

2.3. 2D Power Law Universal Harmonic Plane

Table 1 lists the values of, and the known and respectively the derived slope and Y-intercept of the

wk δ-line, bwk, awk; and both the slope and Y-intercept of the EM δ-line [17] [19] . Also, wk refers to the weak kinetic entities. EM refers to electromagnetic entities. The known values have been used for the derivations of multiple fundamental constants. These are the only natural values used for all of the derivations in the past. For

this paper only is utilized.

Each individual fundamental constant is plotted on a 2D power law universal harmonic plane, Figure 1.

The X-axis is scaled by equaling 1. The X-axis is related to the partial or quantum fractions

minus 1. This centers the neutron at the origin (0, 0). All of these ratio values and all points on the X-axis are rational numbers. These define discrete integer-based locations. This axis location is defined by the individual partial harmonic fractions or the sum of multiple partial harmonic fractions defining a composite constant such as Planck time squared, , for example, the summation: equals [18] . This is equivalent to a constant defined as the product or division of multiple other constants such as the Newtonian gravitational constant, G.

The Y-axis, δ, is related to the difference between the known subscript k, or derived subscript d, the exponents and the harmonic or quantum fraction, Equation (3). The Y-axis is scaled by the, , and R. If one knows the harmonic fraction and the δ-value is derived, then the frequency equivalent and exponent can be derived, Equation (4). Associated constants follow power law relationships and fall on a common line. For example, the top, charm, and bottom quarks fall on a common δ-line [21] . There are two points that scale the X-axis

to the, and; h, at (−1, 0), and at (0, 0). These define the degenerate qf exponents of any con-

stant. The degenerate exponent value is the partial fraction or with an un-split δ of 0.

There are two fundamental lines defined by four points that scale the global δ Y-axis 2D power law plane.

These are referred to as δ-lines, Table 1. The Y-axis also represents exponents of. The known or de-

rived exponent equals the sum of the partial fraction or and the, Equation (3). These lines define a series of possible discrete points that only exist at values so they are discrete. These are not continuous lines in a classic mathematical sense since these relationships are point discrete, but fall on a line. Each -line is composed of a series of discrete points that fall on a line. When the division between the different values exceeds the precision of the experimental measurements this integer pattern appears as a continuous line as in black body radiation [19] [20] .

The first line of the 2D plane is defined by the points of the Bohr radius, and the electron. This is logically defined as the weak kinetic, (wk), line since it scales weak force constants, such as the mass lost in negative beta neutron decay, which are kinetic phenomena. The Y-intercept is defined as bwk, and the slope as awk. Their derivations are shown in references [19] [20] .

The second δ-line is defined by the points of Planck’s constant, , and the ionization energy of hydrogen, R,. This is logically defined as the electromagnetic, (EM), line since it scales electromagnetic force constants such as the quarks [21] . The Y intercept is defined as bem, and the slope as aem. In this case bem and aem are equal and referred to as bem only. These two lines are symmetrically reflected around the X and Y axes forming a diamond pattern [17] .

3. Results

3.1. The Relationship of bwk, bem, and Planck Time Squared,

Table 2 lists the physical constants, quantum numbers, standard values, frequency equivalents, , , known and derived exponents, , and the integer or partial harmonic fractions. The derived values closely predict known values.

Planck time, , is a unique fundamental constant in physics since it is the only one that unifies the electromagnetic with the speed of light, c; quantum phenomena through Planck’s constant, h; and the cosmologic, via the Newtonian gravitational constant, G, into a single composite scale. Planck time therefore spans across the forces. Planck time squared, though not commonly held to represent a computational unit is equivalent to G within a system where c, and h equal 1. The product of and the frequency equivalents of one mass, another mass, and their separation distance equals the frequency equivalent of their gravitational binding energy.

In prior publications, the HNH has accurately derived the square of Planck time, from these same four natural quantum units, bem, bwk, and awk, and integer fractions [18] -[21] . The previously derived, h (not the reduced Planck’s constant, ħ) value is. The known value is

. This is equivalent to a reduced ħ t_P value of. The known t_P value is. Our derived Newtonian gravitational constant is. The known experimental value is. Our previously derived exponent when

applied to is, which is a significant improvement over the known exponent,

. Our previously derived delta is, the known delta is .

We define the degeneracy of any physical constant to be related to the frequency of the neutron raised to a simple integer ratio exponent; all values of which fall on the X-axis and therefore have no δ value. An estimated degenerate value of can be derived from and the number 2 only. This is possible since the exponents of the gravitational binding energy of the electron in hydrogen are known. These include 1 for the proton, 6/7 for the, 4/5 for, and −1 for the gravitational binding energy of the electron. The degenerate value for is

raised to the exponent divided by 2, Equation (5). The number 2 is related to the fact that

gravity is a kinetic-inducing force. Since 2 is a known constant the slope of this point to the h-point scales the

entire Y-axis, independent of force. This is referred to as the point,.

The value equals. The equals. The

ħ degenerate value is. The experimental ħ value equals.

The exponent is plus,. The equals

,.

(5)

The slope and Y-intercept of the line from the point through the h, point (−1, 0) is

, Equation (6). This slope should logically scale the lines and intercepts in the 2D harmonic plane including bwk, awk, and bem. This slope is referred to as since the is based on 1/2. Y-intercept is referred to as. Here and are equal, and bwk equals. The bem value equals. This is near to the inverse of bwk and.

(6)

The, line is defined as. For the derivations of hydrogen constants value is assumed to be a surrogate of bwk and bem. The actual error is 2.2270 × 10⁻³ for bwk, and 2.1013 × 10⁻², for bem.

3.2. The Transformation of the Ionization R-Point from the EM Line to the Weak Kinetic Line by the 8p² Factor

Ref. [15] has demonstrated that the hydrogen constants as frequency equivalents and α, are all inter-related by factors of 2 and π in a dimensionless system. For example, the ratio of the product of 2π and divided by equals. It is possible to transpose the R-point which is defined on the EM line to the wk line using a product of 2 and π, in this case, Figure 1, Equation (7). The ratio of divided by equals. The ratio of divided by equals. The ratio of these two ratios, equals, since the αs cancel out. The product of and is related to, which in a physical sense scales the electromagnetic force to the weak force through a classical geometry employing a set of physical constants. This result appears to be a classical unification of electromagnetism with the weak force. This ratio is only related to wk entities, and therefore transforms v_R to the wk line. The X-axis value of this wk entity product must equals the sum of the partial fractions, , , or. This ratio, , equals. This is referred to as the point. The known ex- ponent equals. The equals. The -value on the line point at the X-axis value of or also equals confirming that transforms an electromagnetic property to a weak kinetic line. This point and the point define the slope, awk. This geometric relationship will be used in the later derivations to calculate an approximate awk_d.

(7)

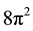
3.3. Derivation of from, and

It is assumed that the equals −1/3 on the X-axis on the δ-line:. The value equals, , and equals. The known is. The derived exponent_d equals. The known R exponent_k is. The derived is. The known is. The relative error of the frequency equivalents is. We submit that our derivations within the HNH model account for non-coinci- dental accuracy.

3.4. Derivation of awk from

Multiplying times equals. The known value is. The derived exponent for the point equals. The known exponent value is. The derived δ for the point equals. The known δ equals. The derived awk_d equals minus divided by , or. The known awk_k equals. The relative error is.

3.5. Derivation of, from

The derived exponent for equals, or. The known electron ex-

ponent is. The derive equals. The known equals . The derived equals. This equals . The known equals. The known eV value equals. The relative error is.

The derived exponent for equals, or. The known exponent is. The derive equals. The known equals . The derived equals. The known equals . The relative error is.

3.6. Derivation of from

There are multiple possible ratios of, , and that could be used to derive [17] . The relation-

ship arbitrarily chosen for the derived is the product of times divided by,. The known value of equals. The relative error of the ratio of the values is. The derived exponent for equals. The known exponent of is. The derived for equals. The known is.

4. Discussion

4.1. Alternate Models Other than the Standard Model and String Theory Should Be Considered Valid

A robust model that accurately scales from classic, to quantum, to cosmic physical constants does not exist [6] . The SM and ST have both failed in this regard. Despite these failures any other model, including the HNH, is almost universally met with derision, denial, and skepticism. An important aspect of the Harmonic Neutron Hypothesis is that it does resolve some of these limitations by analyzing the scaling relationships between the physical constants as a unified harmonic resonance, finite integer, and prime number-dominated power law system. Derivation of accurate quark masses, Planck time, the Hubble constant, and the Higgs boson from only sub-atomic natural physical units supports the validity of the model [16] - [21] .

4.2. The Fundamental Constants as an Integrated Unified Harmonic System Based on Prime Numbers

There have been a few publications demonstrating indirect dominance of prime numbers manifest in physical systems. One of our previous papers demonstrated that the global organization of the fundamental constants including the particles and bosons can be represented within a purely mathematical system [16] . It is based on a consecutive integer series, partial harmonic fractions, and the dominant influence of prime number factors. These specific integer patterns explain the organization of the elements, black body radiation, the scaling of the constants clustering around the neutron, and the actual scale of the quarks. There is no other unification model, or theory of everything that encompasses these important characteristics of the known physical systems within the actual mathematical definition of the model [22] - [31] .

Previous publications have demonstrated that starting with the four natural units of frequency equivalents of the n₀, e⁻, a₀, and R it is possible to derive many other fundamental constants to within or beyond their known experimental ranges including the quarks, the proton, , , G, and. Knowledge of these four subatomic fundamental constants accurately scales the 2D harmonic space. This paper demonstrates that it is possible to start with a single natural physical unit, and to a first approximation derive other fundamental constants. This is possible since the constants follow classic harmonic properties related to known partial fractions and quantum numbers. This is analogous to predicting masses of unmeasured isotope elements based on the mass of the neutron. The, , R, and are quantum values, but they are linked within a classic Euclidean geometric system allowing for transformation of one to the other based on factors of 2 and π. These hydrogen quantum values are respectively associated with the prime numbers, 3, 5, 7, and 11. These represent the first four odd prime numbers. The sole even prime number 2, is associated with the kinetic energy lost in the negative neutron beta decay process and cosmic background microwave radiation.

4.3. Planck Time as a Global Time-Space-Matter Fundamental Constant

The geometry of the 2D harmonic plane is scaled in the X-axis dimension solely by. The Y-axis is

scaled by, , R, and defined by two fundamental lines, wk, and the EM δ-lines. Planck time squared, , represents a unique physical constant that is a composite of constants encompassing quantum, electromagnetic, and cosmologic domains. In standard physical units is defined by h, c, and G. In our model, represents the identical constant as G in the frequency domain since c and h equal 1 in this natural unit setting.

Also can be derived to a first approximation utilizing, the degenerate exponents as the integers

and partial fractions, and the factor 2, Equation (5). Thus, is a composite constant that scales the complete 2D harmonic plane and is closely related to bwk and bem.

In the physical domain scales all of time-space-matter. Lastly, is computationally defined in the HNH by all of the natural units and represents a unique single synthesis of the complete harmonic system. encompasses Special Relativity and cosmology in c, quantum phenomena in h, and kinetic energy in G. Most physical models do not consider to have any special computational or conceptual significance. In some models is believed to be a critical physical unit scaling the limits of its organization. In the frequency domain the actual unit is does have important conceptual and computation significance to all areas of physics. Planck time squared represents the minimum gravitational binding energy in the frequency domain. It also represents an “area”, one half the reciprocal of which represents the frequency equivalent of the mass of a Black Hole with a Schwarzschild radius equal to the speed of light times one second. Planck time squared is also equivalent to the binding energy of two masses with a frequency equivalent of one separated by the distance light travels in one unit of time.

The quote of Gilles Cohen-Tannoudji paraphrases the significance of Planck time within the global context of physical systems [32] :

“The new interpretation of the gravitational constant, when it is associated with h and c, opens up amazing prospects: thus the Planck time and length suggest a quantum structure of space-time itself. Imagine the fascinating implication of a limit to the divisibility of space and especially the divisibility of time!”

These derivations are based on the concept that does represent the penultimate fusion/division of time, space, and matter to its smallest possible units. And to which subsequent derivations within the Harmonic Neutron Hypothesis attests.

5. Conclusion

It is possible to a first approximation derive the frequency equivalents of the electron, Bohr radius, Rydberg constant, and the reciprocal of the fine structure constant starting with the single natural physical unit of the frequency equivalent of the neutron and a few integers. These derivations support the hypothesis that the fundamental constants represent a classic unified harmonic power law integer based system.

6. Figures

Figure 1 is a 2D harmonic plane plot. The X-axis equals the harmonic fraction or value. The Y-axis, the δ value, is the difference of the known or derived exponent and the partial harmonic fraction, or. The previously published points related to h, , , R, are plotted. These points define two lines. The electron and a₀ define the wk-line with slope of awk and Y-intercept, bwk (dashed green solid line). The EM line is defined by h and R (solid green line). The points defined by (0, bwk) and (0, bem) are plotted. The known values are plotted as points the derived values are plotted as open circles demonstrating their relative error. The dot dash red arrow represents the, , plus factor for 2. The dashed red arrow represents the qf, , plus factor for. The solid short red arrows represent the, , plus factor for. The equals and used as a surrogate derived values for bwk_d and. This is related to the slope of the degenerate. The point is transformed from the EM line to the wk line by a factor of. The product of times equals, which is solely defined by wk entities. On the 2D plane this ratio represents one 2 vector and two vectors. The point at X-axis and were utilized to derive the awk_d slope. From those derived slopes and Y-intercepts the values for derived, , , and were calculated.

7. Tables

Table 1 lists the values of, and the slope and Y-intercept of the wk δ-line, bwk, awk; and slope and

Y-intercept of the EM δ-line, bem, aem used for the derivations of e⁻, a₀, R, and 1/α. The derived values closely approximate the known values.

Table 2 lists the physical constants, quantum numbers, standard unit values, frequency equivalents, , , exponents, , and the integer or partial harmonic fractions. The derived values closely predict the known values.

Acknowledgements

I would like to thank Richard White MD, Vola Andrianarijaona Ph.D. for their support and help.

Cite this paper

Donald WilliamChakeres,RichardVento, (2015) The Association of the Neutron, and the Quantum Properties of Hydrogen, with the Prime Numbers 2, 3, 5, 7, 11. Journal of Modern Physics,06,2145-2157. doi: 10.4236/jmp.2015.614218

References