Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60696,12 pages
10.4236/jmp.2015.613192
Theory of a Mach Effect Thruster II
Heidi Fearn1, Nolan van Rossum2, Keith Wanser1, James F. Woodward1
1Department of Physics, California State University Fullerton, Fullerton, CA, USA
2Department of Aerospace Engineering, Iowa State University, Ames, IA, USA
Email: hfearn@fullerton.edu, jwoodward@fullerton.edu, kwanser@fullerton.edu, nolanv@iastate.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 August 2015; accepted 24 October 2015; published 29 October 2015
ABSTRACT
According to Einstein, General Relativity contains the essence of Mach’s ideas. Mach’s principle can be summarized by stating that the inertia of a body is determined by the rest of the mass-energy content of the universe. Inertia here arises from mass-energy there. The latter, was a statement made by John Wheeler in his 1995 book, Gravitation and Inertia, coauthored by Ciufolini. Einstein believed that to be fully Machian, gravity would need a radiative component, an action-at-a-dis- tance character, so that gravitational influences on a body from far away could be felt immediately. In 1960’s, Hoyle and Narlikar (HN) developed such a theory which was a gravitational version of the Absorber theory derived by Wheeler-Feynman for classical electrodynamics and later expanded upon by Davies and Narlikar for quantum electrodynamics. The HN-field equation has the same type of mass fluctuation terms as in the Woodward Mach effect thruster theory. The force equation, used to predict the thrust in our device, can be derived from the mass fluctuation. We outline a new method for deriving the force equation. We present new experimental tests of the thruster to show that the thrust seen in our device is not due to either heating or Dean Drive effects. Successful replications have been performed by groups in Austria and Canada, but their work is still pending in the peer review literature.
Keywords:
Mach Effect Drive, Transient Mass Fluctuations, Mach’s Principle, Action at a Distance, Advanced Waves, Event Horizon

1. Introduction: Einstein & Mach’s Principle
Mach’s principle was the name Einstein gave, in 1918, to the proposition that the inertia of a body is the result of the gravitational interaction between the body and the rest of the mass-energy in the universe. In 1912, Einstein considered the gravitational interaction of a spherical shell of material and a point mass located at the center of the shell [1] . What he found was that the mass shell increased the inertial mass of the particle inside the shell. According to Einstein, this suggested that the entire inertial mass of the material particle was an effect of the presence of all other masses in the universe, based on a gravitational interaction with the latter. The Einstein shell paper was for a weak (linear approximation of) gravitational theory, but later Lynden-Bell et al. carried out a similar particle shell scheme for a strong gravitational field and found a similar result [2] . At this time, Ein- stein understood his ideas on gravity and inertia were just speculations, as he did not then possess a “serviceable dynamical theory of the gravitational field”. A few years after his development of the general theory of relativity, Einstein published his 1921 Princeton lectures in a small book, The Meaning of Relativity [3] . This book contains his most extensive comments on Mach’s ideas and his interpretation of them.
Moreover, Einstein had come to appreciate that as inertial forces are acceleration dependent forces, they had at least one of the signatures of radiative interactions. This had led him to draw a distinction between, as he called it, “the relativity of inertia” and “Mach’s principle”. Einstein took Mach’s principle to encompass the radiative nature of the presumed interaction between test particles and the rest of the “matter” in the universe. For this interaction matter, Einstein claimed it was based on “action-at-a-distance”, as inertial forces were experienced instantly on the application of “external” forces. The relativity of inertia merely required that inertia and inertial forces be dependent on the presence of a field to act on accelerating objects, and thus could be encompassed by his theory of gravity, general relativity. The type of action-at-a-distance that Einstein was talking about was the Newtonian type: instantaneous communication of effects over finite distances. The modern concept of action-at-a-distance is one that is consistent with the principle of relativity.
This paper is a follow on to paper I [4] where we develop the theory of the Mach effect thruster and derive the mass fluctuation which accounts for the thrust in our device. Our device is a space drive, it is a propellentless thruster which uses electricity only and no fuel is ejected out of a tailpipe. The Mach effect thruster (MET) consists of 3 parts. A brass reaction mass, a stack of lead zirconium titanate (PZT) discs and an aluminum end cap, all bolted together. The PZT has both piezoelectric and electrostrictive properties and will deform when electric current is applied. In this second paper we document a little more of the history behind the theory of the device and outline the experimental results and report on replication papers already in the literature.
1.1. Absorber Theory
The modern version of action-at-a-distance was first introduced in the 1920s by Hugo Tetrode [5] and Adriaan Fokker [6] . It was Fokker’s action that Dirac invoked when he wrote his classic paper on the self-energy and radiation reaction issues for classical electrons in 1938 [7] . All relativistic wave equations have advanced solutions. This makes seemingly instantaneous action possible as advanced waves, travel backward in time, and can be used to communicate the influence of future events to the present. Dirac’s radiation field could be though of as constructed from half retarded minus half advanced Lienard Wiechert potential fields. Dirac showed that this radia- tion field gave exactly the well known relativistic result for radiation reaction which can be found in standard text books on electromagnetism. John Wheeler and Richard Feynman [8] showed that what made the theory work was complete absorption of all retarded waves propagating into the future, and the generation of advanced waves as the absorber was acted upon. These combine with the retarded waves to produce what appears to be a purely retarded interaction. Paul Davies and Hoyle-Narlikar had originally extended the classical electrodynamics absorber theory for relativistic QED. Later Cramer [9] introduced his transactional interpre- tation of quantum mechanics, also using absorber theory, which is fully consistent with the Copenhagen inter- pretation but eliminates the instantaneous collapsing wave function. See the new book by Cramer [10] and the book by Kastner [11] .
Absorber theory, which is a direct particle interaction theory, is never caught on. Wheeler never abandoned it and was still writing about direct particle interactions in his 1995 book, Gravitation and Inertia, 1995. Feynman recounted that when he presented the theory to a Princeton Physics Department colloquium [12] :
Wolfgang Pauli who was sitting next to Einstein, said: “I do not think this theory can be right because of this, that and the other thing” …At the end of this criticism, Pauli said to Einstein, “Don’t you agree, Professor Einstein? I don’t believe this is right, don’t you agree, Professor Einstein?” Einstein said, “No,” in a soft German voice that sounded very pleasant to me, very polite. “I find only that it would be very difficult to make a corresponding theory [i.e., an action at a distance theory] for gravitational interactions.”
Einstein didn’t need to try to construct such a theory, for he was certain that inertia was already accounted for as a gravitational phenomenon in general relativity. General relativity does not encompass the version of Mach’s principle that includes inertial actions as radiative in nature.
1.2. Hoyle-Narlikar Theory
Fred Hoyle and Jayant Narlikar [13] -[15] tried to generalize general relativity to correct this perceived defect in the mid-1960s by constructing an action-at-a-distance theory of gravity along the lines of the Wheeler-Feynman absorber theory of electrodynamics. The theory did not find much favor at the time, no doubt in part due to Hoyle’s ardent support for steady state cosmology. But there was a more fundamental problem, quickly spotted by the then graduate student Stephen Hawking [16] . The analogy between electrodynamics and gravity is not exact. Electromagnetic fields can be “screened” by matter. So, they will be absorbed if there is sufficient matter along the future light cone. This is not true for the gravitational interaction as it is normally understood. While energy can be extracted (absorbed) from gravitational waves, the underlying gravitational field is not absorbed. That is, gravity cannot be “screened” by any known substance or process. Not yet anyway.
Hawking [16] was quick to see that this meant that all gravitational influences, propagating at speed c, did so into the infinitely distant future and if the retarded influences can get there, the advanced influences can get back to the present. This means that the integral of all of the advanced contributions from those propagating influ- ences will diverge. Unless one’s theory of gravity allows for an “absorption” or “screening” mechanism, it would seem that this objection to action at a distance gravity is insurmountable. What is needed is a way to cut the gravitational interaction off at a finite distance. Accelerating expansion of the universe can do the trick. Since we have covered this material elsewhere [17] [18] , we will not repeat the derivation here and only state that when the acceleration of the universe is properly taken into account, there exists a Rindler horizon which acts as a cut off and the advanced wave integral no longer diverges [17] .
1.3. Hoyle-Narlikar Results Relating to the Mach Effect Thruster
In the conformal theory of Hoyle and Narlikar [19] , the smooth fluid approximation alone leads to the field equation;
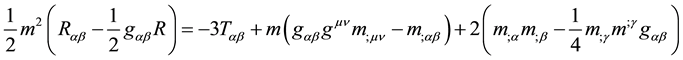 (1)
(1)
a further conformal transformation is needed to convert this equation into the Einstein field equation, see below.
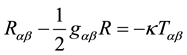 (2)
(2)
where 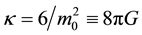 and
and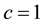 . The Einstein field equation takes a simpler form, which is analogous to solving in the rest frame in special relativity. The stress-energy tensor normally used in General Relativity is that for a “perfect fluid” (or ideal gas) in the rest frame of the fluid, see p. 140 MTW [20] .
. The Einstein field equation takes a simpler form, which is analogous to solving in the rest frame in special relativity. The stress-energy tensor normally used in General Relativity is that for a “perfect fluid” (or ideal gas) in the rest frame of the fluid, see p. 140 MTW [20] .
To connect with the Woodward’s mass change equations, which were originally derived from Einstein’s and Maxwell’s results, we consider the extra terms in Equation (1) alone. The extra terms are on the right side of the equation along with the energy stress tensor. The 4-momentum density can be written,
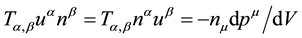 (3)
(3)
as measured by an observer in a Lorentz frame with 4-velocity  along the
along the 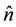 direction [20] (p. 131). If we write in the minus sign and a factor of 1/3, we can envelope the mass parts as belonging to the energy stress tensor, then the extra terms become [21]
direction [20] (p. 131). If we write in the minus sign and a factor of 1/3, we can envelope the mass parts as belonging to the energy stress tensor, then the extra terms become [21]
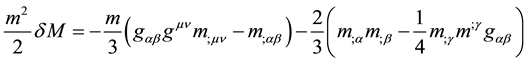 (4)
(4)
where the , see below. Consider the time component only in a flat space-time using
, see below. Consider the time component only in a flat space-time using 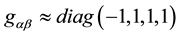 . The time component is taken as the zeroth component in a 4 vector with labels 0-3. Taking the Christoffel symbols (of the covariant derivatives) to be zero, and using
. The time component is taken as the zeroth component in a 4 vector with labels 0-3. Taking the Christoffel symbols (of the covariant derivatives) to be zero, and using 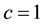 for consistency,
for consistency,
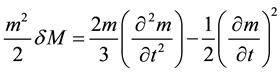 (5)
(5)
when we divide by 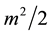 (which is multiplied throughout in Equation (1)) we get mass fluctuation terms as follows,
(which is multiplied throughout in Equation (1)) we get mass fluctuation terms as follows,
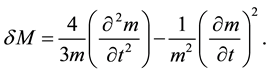 (6)
(6)
Apart from a 4/3 numerical factor, these are the mass fluctuation terms, originally derived by one of us JFW [21] . The first bracketed term with the  in it, has a possibly question mark. We have taken this term to be overall negative to add to the
in it, has a possibly question mark. We have taken this term to be overall negative to add to the 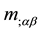 term to give an overall positive term of twice the magnitude. In principle, this term also has derivatives with respect to spatial coordinates. For instance,
term to give an overall positive term of twice the magnitude. In principle, this term also has derivatives with respect to spatial coordinates. For instance, 






These results were reported in the last Joint Propulsion Conference Ohio 2014 [18] , but at that time we had not shown that the Hoyle Narlikar (HN) theory could yield a non-divergent advanced mass integral [17] . Using the advanced waves built into HN-theory, it is possible to explain momentum conservation of the Mach effect thruster device.
1.4. Derivation of Force from Mass Fluctuation Equation
Our standard derivation for the force is not ideal by any means. It should be considered an estimate only, and appears to give predictions within an order of magnitude of the actual result. For example see Woodward’s book [22] and papers [23] [24] . Here, we give a brief discussion for convenience and explain how we intend to improve the force derivation in the near future. The Mach effect mass fluctuation, with correct factors in front, is given by the first term in Equation (6).

where energy 










After some simple trignometric manipulation we get,

where we have used expansions for 


where 


On resonance when 

where we have substituted back for 

The 




Figure 1. Single resonance circuit used in mason model: LCR circuit.
tional to



In previous work, we always took the second line interpretation, and proceeded in terms of bulk acceleration. The previous assumption was that if no bulk acceleration of the object takes place, there would be no Mach type mass fluctuation. We previously took a sum over all the masses that make up the device. Using


The resulting mass fluctuation is caused only by the center of mass (COM) motion of the device,

where (1/m) 


parts. The simplest Mach effect depends on the square of the acceleration of the COM of the body in which it is produced. [22] -[24] . The thrust comes about by applying a periodic force at the frequency of the mass fluctua- tions. The force and the mass fluctuations need to be in phase to deliver maximum thrust. If these terms are out of phase we would expect zero thrust, and that indeed is what we see in practice.
The chief response of the PZT stack is piezoelectric. The stack responds to a periodic voltage,

The PZT stack has both a piezo electric and an electrostrictive response. The easiest way to include the piezo and electrostrictive constants is via the displacements in the material. The electrostrictive response corresponds to 

where N is the number of discs in the stack, 









we have neglected smaller terms here for convenience only. Using only electrostriction for the external applied force, we get,

here we have left in the arbitrary phase

If the phase difference between the piezoelectric and the electrostriction is zero, then we get for the magnitude of the thrust/force;

The trigonometric terms time average to zero, but the unity term does not and leads to the constant thrust seen in our device to first approximation. However, when there is a phase difference 


which oscillates and time averages to zero. Clearly, we require the mass fluctuation (caused primarily by the piezoelectric effect) and the applied force (caused by electrosctriction) to be in phase, to see thrust.
In summary, the force equation prediction for the Mach effect is given by Woodward in his book [22] and in previous works [23] . Usually 

where 











A quick look at the online literature shows that the usual model used by the engineering community for piezoelectric materials is the Mason Model [27] or Butterworth-van Dyke equivalent circuit. This is a very basic description, we will need to add more detail and diagrams later. We have drawn the basic circuit in Figure 1. This has the convenient feature that the equivalent LCR circuit is similar to a damped driven harmonic oscillator equation of the form,

The system mass is equivalent to inductance l, a large value drags the resonant frequency down. The system stiffness k (like a spring constant) is equal to the inverse capacitance C. A high value increases the resonance of the device. The system damping 



This can easily be solved by assuming that 


which when differentiated with respect to time gives,

Off resonance, if 






However, if 





2. New Experimental Results for the MET
Here we describe the work, in the last 6 months, in the Woodward laboratory at California State University Fullerton, Physics Department. Figure 2 shows a photo of one of our latest devices, in an open Faraday cage. The device is shown vertically but when the box is closed the device would be horizontal. You can see the end of the balance beam inside the plastic vacuum chamber. The device is made from a stack of lead zirconium titanate (PZT) discs, glued as a stack of capacitors with positive plates facing positive and negative facing negative. The objective is propellantless propulsion, where the rest mass of some object, a stack of PZT crystals in fact, is caused to fluctuate periodically with a varying applied voltage. A second periodic force is applied to the stack, acting in one direction when the stack is less massive, and the opposite direction when it is more massive, to produce a steady thrust in one direction. If the piezoelectric effect were the only electro- mechanical effect present in the crystals, a mass fluctuation would be produced, but no thrust would be generated. To generate thrust you have to apply a voltage to the stack comprised of two frequencies, one to produce the mass fluctuation, and the second to produce the mechanical oscillation at the frequency of the mass fluctuation to generate a periodic force. The frequency of the second force turns out to be twice the frequency of the voltage that produces the mass fluctuation. If the material (say PZT) possesses the property of electrostriction, since electrostriction depends quadratically on the applied voltage, the second, double frequency voltage signal can be dispensed with, for the signal that produces the mass fluctuation will also produce the mechanical oscillation at the second harmonic needed to convert the mass fluctuation into a periodic force that acts only in one direction producing propellant-less propulsion.
We have thermistors embedded in the aluminum end cap and the brass reaction mass. Thrust forces in the devices are very small, on the order of a few micro-Newtons. A very sensitive torsional thrust balance was constructed to measure the predicted forces. It consists of a beam supported by “c-flex” flexural bearings that provide a small restoring torque when the beam is displaced from its rest position.
Details of the device and experimental set up can be found in previous works [18] [22] -[25] . Our standard operating proceedure is that the device is run in say the forward direction and data taken, then we reverse the direction and take more data. To get the thrust we subtract the averaged reverse data from the forward data, thus removing any non reversing signals in the process. This signal processing gives us much cleaner thrust data, but it should be pointed out that thrusts are measurable with a clear signature of several micro-Newtons, well above the noise level (5 to 10 standard deviations) on each individual run.
Figure 2. The mach effect thruster on a balance.
2.1. Thermal Results and Dean Drive Effects
As one might guess, there is a linear dependence on voltage for the heating of the device, see [21] . It occurred by accident that we found ourselves with a device that had been partially depoled. This could be due to overuse and heating effects most likely. This device, called device 4, showed no thrust at all, see Figure 3. We compare the device 4 with a similar device 1 which was still showing thrust. One should note that the maximum voltage going into device 4 actually exceeds the voltage going into device 1. We also took data of the temperature of the devices while the voltage was applied.
Two thermal effects are important: First, heating or cooling of the device during operation will cause the expansion/contraction of parts of the device, causing the center of mass of the device to move, resulting in rezeroing of the position of the balance beam. Second, motion induced by heating/cooling will produce forces on the balance when the velocity induced by heating/cooling changes. That is, thermally induced accelerations of parts of the device are present. Qualitatively, these are expected when the heating rate changes. In Figure 4, you can see that both devices get hot (green curve) but only device 1 shows any thrust (red curve). Clearly heating is not the cause of the thrust.
Dean drive effects depend on the coefficient of friction in relatively moving parts differing as the relative speed of the parts changes-allowing a displacement in one direction to accumulate more rapidly than average, as the vibration continues. Asymmetry effects, rather than being accumulated displacements, depend on the expansion/contraction of the device being prolonged/shortened in one part of each cycle, leading to a displace- ment of the time-averaged center of mass of the device. This displacement of the center of mass produces a shift in the zero position of the balance beam when the device is powered that masquerades as thrust. In Figure 4, if vibration was the cause and directional frictional effects in the balance beam, we should see that in either case and not just in device 1.
The obvious question is: why do we get thrust with device 1 and not with a very similar constructed device 4?
The answer is simply that the first and second harmonics need to be in phase for the Mach effect to work and to get thrust. In device 1 both first and second harmonics are in phase as you can see in Figure 5. For device 4, the 1st and 2nd harmonics are out of phase by 90 degrees. This is the condition that kills the thrust of device 4. The harmonic phase difference would have no effect on heating or on a Dean drive type effects due to ratcheting in one direction, caused by vibration and friction effects in the balance beam. The only way to understand the lack of thrust is by application of the Mach Effect equations for the force. The first and second harmonics need to be in phase and on resonance with the device to obtain thrust.
Figure 3. Graph showing the thrust (in red) for device 4 and 1. Device 4 actually has a higher voltage applied (in blue) and yet shows no thrust. During these averaged data runs, there was an on resonance pulse for 3 seconds, followed by a 30 KHz frequency sweep centered on the resonant frequency of the device, followed by another 3 second on resonant pulse and then quiesent data to show the noise level. The runs lasted 32 seconds each.
Figure 4. Graph showing the thrust (in red) for device 4 and 1. The temperature of each device is shown in green. The full scale temperature for device 4 is about 10 degrees Celcius, for device 1 it is less than half that. Since both devices show a temperature rise, clearly temperature is not resoponsible for the majority of the thrust seen.
Figure 5. The blue traces represent the device voltages. The yellow traces are the accelerometer reading for the devices. What changes is the relative phases of the mechanical response to the applied voltage. The blue curve goes as the first harmonic, the accelerometer varies as the second harmonic. In device 1these harmonics are in phase, in device 4 they are 90 degree out of phase.
2.2. MET-Thrust Dependance on Voltage
The force equation prediction for the Mach effect is given by Woodward in his book [22] and in previous works [23] , see Equation (18) above. Here, we show data taken over a range of voltages to show consistency with the 
The mathematica fit to the data gave a cubic and a quartic of the form,

for V in volts and F in Newtons. Using the following constants, ω =228 Krad/s, corresponding to 36.3 KHz frequency, m0 = 0.025 Kg, 


Figure 6. Thrust dependence on voltage showing linear and quadratic fits. We assume zero volts gives zero thrust as a real point and that there are no unique features at low voltage. Note that given only 4 data points we cannot assume a definite result and show all fits for comparison with available data.
Figure 7. Thrust dependence on voltage showing quartic fit. This assumes we can take (0,0) as a realalistic point and that there are no unique features at low voltage. Note that given only 4 data points we cannot assume a definite result and show all fits for comparison with available data. There is also a reasonable fit for a cubic voltage dependance, only that goes negative at low voltages. It cannot yet be ruled out with only 4 data points.
observation of power loss of -13 dB from first to second harmonics, 



which agrees quite well with the Mathematica curve fit for the quartic. The resonant frequency 






3. Conclusions
Einstein understood Mach’s principle, as a gravitational interaction between a test particle and the rest of the mass-energy of the universe, to be of a radiative nature and to act instantaneously. This is made possible if the gravitational interaction is carried by advanced waves as in the HN-theory. It has been shown that the Wood- ward result [22] for mass fluctuations can be derived from first principles from HN-theory [17] [18] . This is a generalization of Einstein’s General Relativity to include radiative effects and advanced waves. The advanced waves explain how momentum can be conserved in our devices. Experimentally we have shown that the thrust produced by these devices is not due to heating and it is not a Dean Drive type effect. The thrust is only seen in devices that have the first and second harmonic frequencies in phase. Finally the thrust appears to be consistent with a quartic power law for voltage, which is a signature of Mach effects.
We are currently modeling the device with COMSOL and ANSYS software. There have been two successful replications seeing the thrust from devices supplied by JFW. One result is still pending publication, the other was by Nembo Baldrini in Austria [28] . Nembo’s most recent results are still pending publication.
Acknowledgements
JFW thanks N. Herbert for suggesting the voltage scaling test because of its unusual quartic signature in these devices. We thank A. Zachar for helpful discussion during the writing of this paper. One of us, NvR, thanks the Space Studies Institute (ssi.org, Mojave, California), for a research stipend which is paid for accommodation and expenses for a summer trip to CSU Fullerton to work on this project 2015.
Cite this paper
HeidiFearn,Nolan vanRossum,KeithWanser,James F.Woodward, (2015) Theory of a Mach Effect Thruster II. Journal of Modern Physics,06,1868-1880. doi: 10.4236/jmp.2015.613192
References
- 1. Einstein A. (1912) Is There a Gravitational Effect which Is Analogous to Electrodynamic Induction? Vierteljahrsschrift fur gerichtliche Medizin und offentliches Sanitatswesen, 44, 37-40. Translated in English and Reprinted in the Collected Papers of Albert Einstein (CPAE), 4, 126.
- 2. Lynden-Bell, D., Bicak, J. and Katz, J. (1999) On Accelerated Inertial Frames in Gravity and Electromagnetism.
http://arxiv.org/abs/gr-qc/9812033 - 3. Einstein, A. (1955) The Meaning of Relativity. Princeton, New York.
- 4. Fearn, H., Zachar, A., Wanser, K. and Woodward, J. (2015) Theory of a Mach Effect Thruster I. Journal of Modern Physics, 6, 1510-1525.
http://dx.doi.org/10.4236/jmp.2015.611155 - 5. Tetrode, H. (1922) über den Wirkungszusammenhang der Welt. Eine Erweiterung der klassischen Dynamik. Zeitschrift für Physik, 10, 317-328.
http://dx.doi.org/10.1007/BF01332574 - 6. Fokker, A.D. (1928) Ein invarianter Variationssatz für die Bewegung mehrerer elektrischer Massenteilchen. Zeitschrift für Physik, 58, 386-393.
http://dx.doi.org/10.1007/BF01340389 - 7. Dirac, P.A.M. (1938) Classical Theory of Radiating Electrons. Proceedings of the Royal Society of London A, 167, 148.
- 8. Wheeler, J.A. and Feynman, R.P. (1945) Interaction with the Absorber as a Mechanism of Radiation. Reviews of Modern Physics, 17, 157.
http://dx.doi.org/10.1103/RevModPhys.17.157 - 9. Cramer, J.G. (1986) The Transactional Interpretation of Quantum Mechanics. Reviews of Modern Physics, 58, 647.
http://dx.doi.org/10.1103/RevModPhys.58.647 - 10. Cramer, J.G. (2015) The Quantum Handshake, Entanglement, Nonlocality and Transactions. Springer Verlag.
- 11. Kastner, R.E. (2013) The Transactional Interpretation of Quantum Mechanics. Cambridge University Press, Cambridge.
- 12. Mehra, J. (1994) The Beat of a Different Drum. The life and science of Richard Feynman. Clarendon Press, Oxford, 96.
- 13. Hoyle, F. and Narlikar, J.V. (1964) A New Theory of Gravitation. Proceedings of the Royal Society of London A, 282, 191.
http://dx.doi.org/10.1098/rspa.1964.0227 - 14. Hoyle, F. and Narlikar, J.V. (1964) On the Gravitational Influence of Direct Particle Fields. Proceedings of the Royal Society of London A, 282, 184-190.
- 15. Hoyle, F. and Narlikar, J.V. (1974) Action at a Distance in Physics and Cosmology. W. H. Freeman and Company, San Francisco.
- 16. Hawking, S.W. (1965) On the Hoyl-Narlikar Theory of Gravitation. Proceedings of the Royal Society of London A, 286 313.
http://dx.doi.org/10.1098/rspa.1965.0146 - 17. Fearn, H. (2015) Mach’s Principle, Action at a Distance and Cosmology. Journal of Modern Physics, 6, 260-272.
http://dx.doi.org/10.4236/jmp.2015.63031. http://arxiv.org/abs/1412.5426 - 18. Fearn, H., Zachar, A., Woodward, J.F. and Wanser, K. (2014) Theory of a Mach Effect Thruster. Proceedings of the 50th AIAA Joint Propulsion Conference, Nuclear and Future Flight Session, Cleveland, 28-30th July 2014.
- 19. Misner, C.W., Thorne K.S. and Wheeler, J.A. (1973) Gravitation. W. H. Freeman and Co., New York, See Section 18.1, pp. 445-459, 470 for Definition of Energy-Stress Tensor in Terms of Density, Pressure and Proper-Velocity.
- 20. Fearn, H., Woodward, J.F. and van Rossum, N. (2015) New Theoretical Results for the Mach Effect Thruster. 51st AIAA Joint Propulsion Conference, Orlando, 26-29 July 2015.
http://dx.doi.org/10.2514/6.2015-4082 - 21. Woodward, J.F. (2012) Making Starships and Stargates. Springer Press, Berlin, 70, 73, 82-86, 134-142, 175-176.
- 22. Fearn, H. and Woodward, J.F. (2012) Recent Investigation of Mach Effect Thrusters? Proceedings of the 48th AIAA Joint Propulsion Conference, Atlanta, 29th July-1st August 2012.
- 23. Fearn, H. and Woodward, J.F. (2013) Experimental Null Test of a Mach Effect Thruster. Journal of Space Exploration, 2, 98-105.
http://arxiv.org/abs/1301.6178 - 24. Fearn, H. and Wanser, K. (2014) Experimental Tests of the Mach Effect Thruster. Journal of Space Exploration, 3, 197-205.
- 25. Wanser, K.H. (2014) Center of Mass Acceleration of an Isolates System. Journal of Space Exploration, 2, 121-130.
- 26. Mason, W.P. (1943) Quartz Crystal Applicayions. Bell System Technical Journal, 22, 178-223.
- 27. Buldrini, N., Tajmar, M., Marigold, K. and Seifert, B. (2006) Experimental Study of the Machine Mass Fluctuation Effect Using a μN Thrust balance. AIP Conference Proceedings, Space Technology and Applications Forum STAIFF, Albuquerque, 1313-1320. Chapter 11, Frontiers of Propulsion Science, Edited by Millis, M.G. and Davis, E.W., Vol. 227, Progress in Astronautics and Aeronautics, 2009.
- 28. Baldrini, N. (2015) Private Communication.









