Journal of Modern Physics
Vol.4 No.1(2013), Article ID:27236,5 pages DOI:10.4236/jmp.2013.41015
Oscillator Subject to Periodic and Random Forces
Department of Physics, Bar Ilan University, Ramat Gan, Israel
Email: gittem2001@yahoo.com
Received September 29, 2012; revised October 30, 2012; accepted November 8, 2012
Keywords: Stochastic Oscillator; Periodic Force; Stochastic and Vibrational Resonances; Birth-Death Process
ABSTRACT
We illustrate the influence of an external periodic force and noise on a physical system by the example of an oscillator. These two forces seem to be the reverse of each other, since the latter leads to disorder while the former works in an orderly fashion. Nevertheless, it is shown that they may influence a system in a similar way, sometime even substituting for one another. These examples serve to illustrate one of the main achievements of twentieth-century physics, which has established that deterministic and random phenomena complement rather than contradict each other.
1. Introduction
Physical intuition suggests that the action of periodic (for instance, sinusoidal) and random (for instance, white noise) forces on a physical system act in the reverse manner, namely, the latter leads to disorder while the former works in an orderly fashion. The best known example against this conclusion is the phenomenon of fluctuation driven transport and the stochastic resonance [1], where the noise helps to increase a weak input signal. In addition to the stochastic resonance, there are different phenomena showing that noise may be a source of order rather than disorder. Let us mention noise-induced transitions [2], noise-induce transport [3], noise-induced pattern formation [4], noise-induced resonances [5], noiseenhanced stability [6], noise-induced hypersensitivity [7], resonance activation [8], stochastic transport in ratches [9], stochastic localization [10], self-organization and dissipative structures [11], coherent stochastic resonance [12], fluctuation barrier kinetics [13] and amplification of weak signals via on-off intermittency [14].
However, according to the second law of thermodynamics, a system naturally progresses from order to disorder and not in the opposite direction. The explanation of this apparent paradox is that noise does not transfer energy to a system, playing the role of a tuner (like emitter in a transistor), helping the system absorb more energy from the external force [15]. In this note, using the simple example of an oscillator, we give other examples of such “unnatural” behavior of noise and a periodic signal. This example is complementary to that of a classical rotor, where it was shown [16] that “order and chaos are complementary rather than contradictory”.
2. Overdamped Harmonic Oscillator
The simple equation
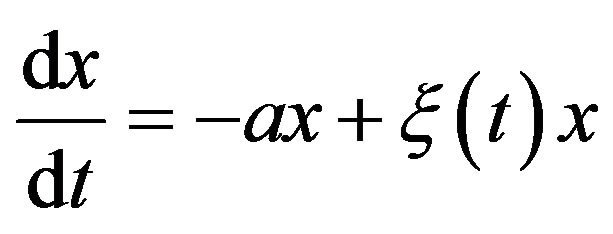 (1)
(1)
can be solved both in the absence and in the presence of white noise 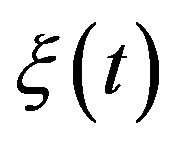 of strength
of strength  In the former case, the solution is
In the former case, the solution is 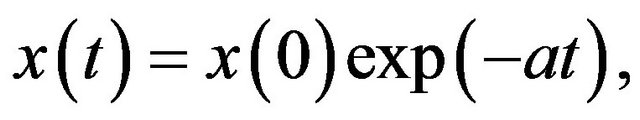 which vanishes at
which vanishes at  In the presence of noise, the average moment
In the presence of noise, the average moment
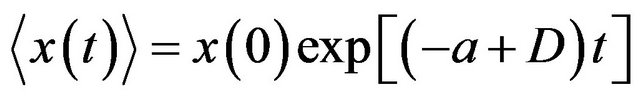 (2)
(2)
diverges as  for
for 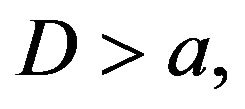 i.e., noise plays its usual “destructive” role.
i.e., noise plays its usual “destructive” role.
With an additional periodic force,
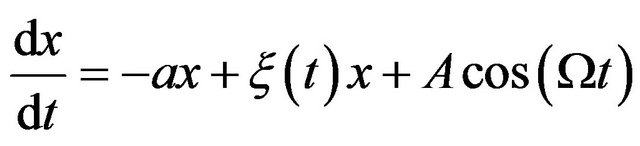 (3)
(3)
the solution of Equation (3) performs oscillations with the frequency  for
for 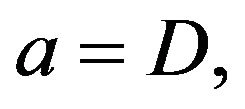 as expected for a periodic external force. However, as we will show, the situation is not so simple for nonlinear equations.
as expected for a periodic external force. However, as we will show, the situation is not so simple for nonlinear equations.
One can illustrate the appearance of stochastic resonance by Equation (3) with dichotomous noise of strength  and rate
and rate  for transitions
for transitions  and
and 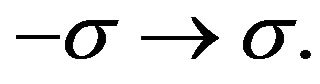 For the limiting case
For the limiting case 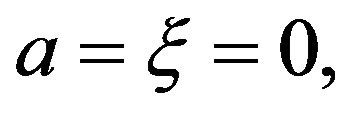 the particle executes periodic motion with an amplitude
the particle executes periodic motion with an amplitude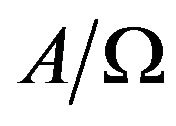 . If there is no random force,
. If there is no random force, 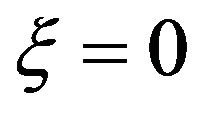 , for
, for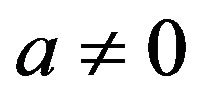 , the particle moves along the parabola
, the particle moves along the parabola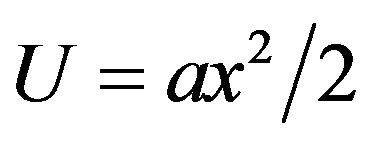 . For dichotomous noise
. For dichotomous noise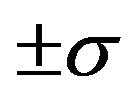 , the particle moves along the parabola
, the particle moves along the parabola
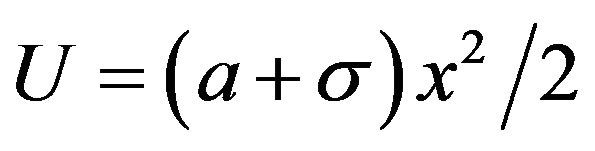
then jumps at rate 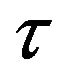 to the parabola
to the parabola
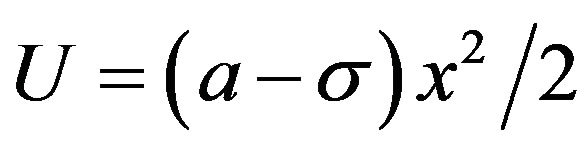 etc.
etc.
For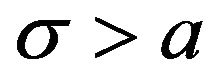 , but
, but
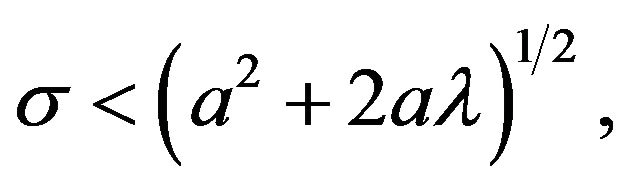
these two parabolas have curvatures of opposite sign, and thus they act in opposite directions tending to increase (decrease) the displacement 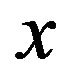 of the particle. Their mutual influence is defined by noise which causes jumps between the parabolas and by a periodic force which determines the amplitude of oscillations along the parabolas. Accordingly, the amplitude of the stationary output signal has a maximum as a function of noise strength (stochastic resonance).
of the particle. Their mutual influence is defined by noise which causes jumps between the parabolas and by a periodic force which determines the amplitude of oscillations along the parabolas. Accordingly, the amplitude of the stationary output signal has a maximum as a function of noise strength (stochastic resonance).
3. Birth-Death Process
The birth-death differential equation for positive 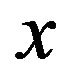
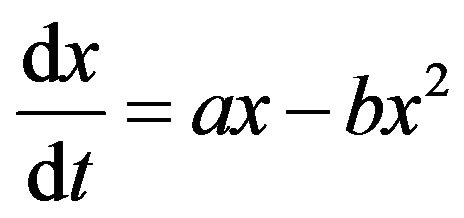 (4)
(4)
has an exact solution. The associated potential energy
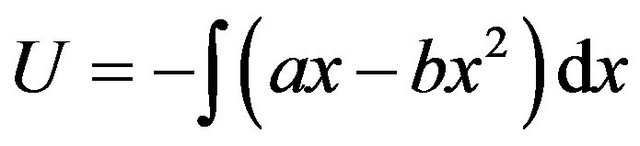 is shown in Figure 1. There are two two fixed points
is shown in Figure 1. There are two two fixed points 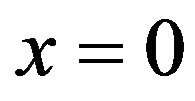 and
and  which are stable for
which are stable for 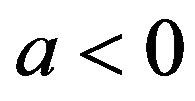 and
and 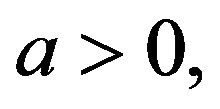 respectively. If the parameter
respectively. If the parameter  fluctuates,
fluctuates, 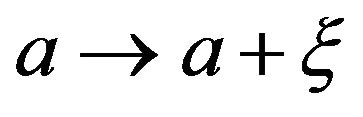 , with white noise
, with white noise 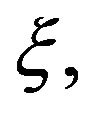
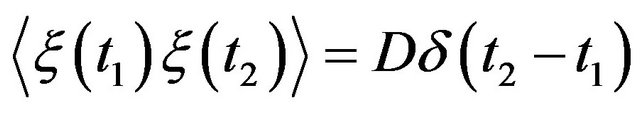 , Equation (4) has two control parameters,
, Equation (4) has two control parameters,  and
and 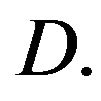 For
For 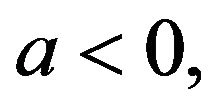 the fixed point
the fixed point 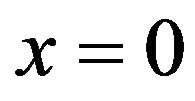 is stable. For
is stable. For 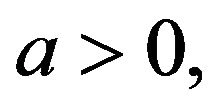 the point
the point  becomes unstable but most probable for
becomes unstable but most probable for 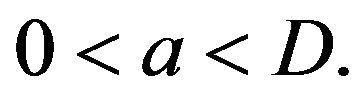 Finally, for
Finally, for 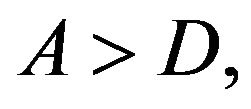 the point
the point 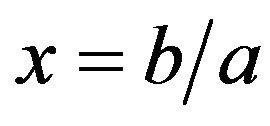 becomes stable.
becomes stable.
Let us now add a periodic force to Equation (4),
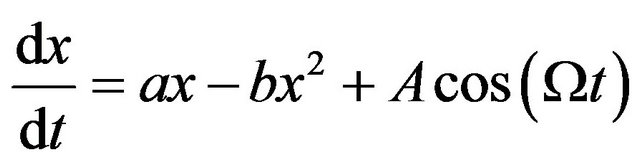 (5)
(5)
If the amplitude of the external field  is smaller than the barrier height,
is smaller than the barrier height, 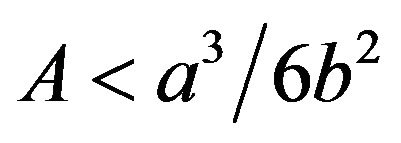 the particle will never leave the well provided that the initial position
the particle will never leave the well provided that the initial position 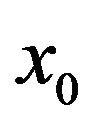 satisfies the condition
satisfies the condition
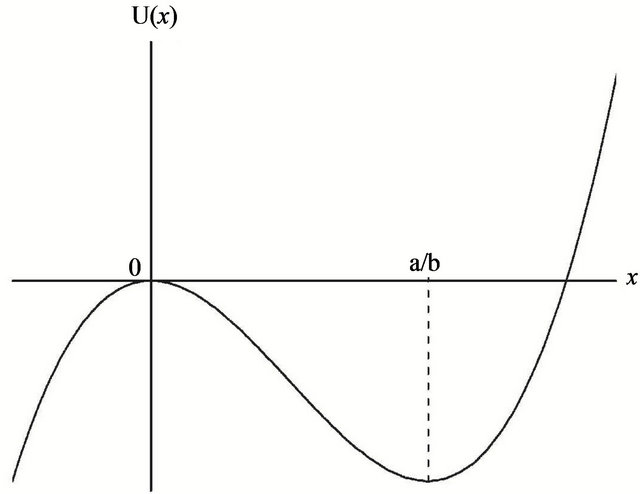
Figure 1. A single-well potential.
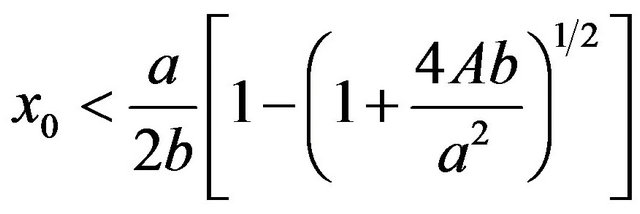 (6)
(6)
This follows from the fact that for  obeying Equation (6), the right-hand side of Equation (5) has two real roots,
obeying Equation (6), the right-hand side of Equation (5) has two real roots, 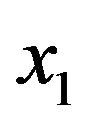 and
and 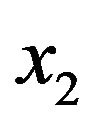 implying that
implying that 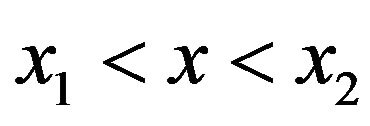 and the particle is trapped. Although the dependence of the solution of Equation (5) on
and the particle is trapped. Although the dependence of the solution of Equation (5) on  is physically obvious, the dependence on the field frequency
is physically obvious, the dependence on the field frequency  is not so obvious. It turns out that even a change of only
is not so obvious. It turns out that even a change of only 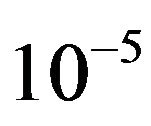 in the frequency changes the time at which the particle escapes from the potential well.
in the frequency changes the time at which the particle escapes from the potential well.
Consider now the common action of both random and periodic forces,
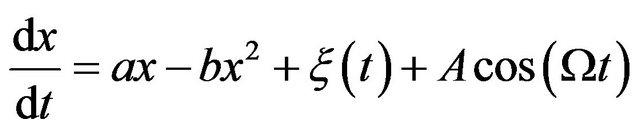 (7)
(7)
The numerical solution of Equation (7) shows that for  not too small, both the periodic force and the noise increase the escape time, i.e., these two factors act in the same direction. However, adding noise to a periodically driven system will increase the escape time for some noise strengths. This effect is known as noise-enhanced stability [17].
not too small, both the periodic force and the noise increase the escape time, i.e., these two factors act in the same direction. However, adding noise to a periodically driven system will increase the escape time for some noise strengths. This effect is known as noise-enhanced stability [17].
4. Piece-Wise Potential
Since the behavior of a system is probably not too sensitive to the exact form of the nonlinear potential, we consider the simplest form of the piece-wise potential, shown in Figure 2,
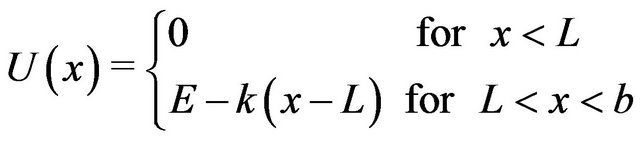 (8)
(8)
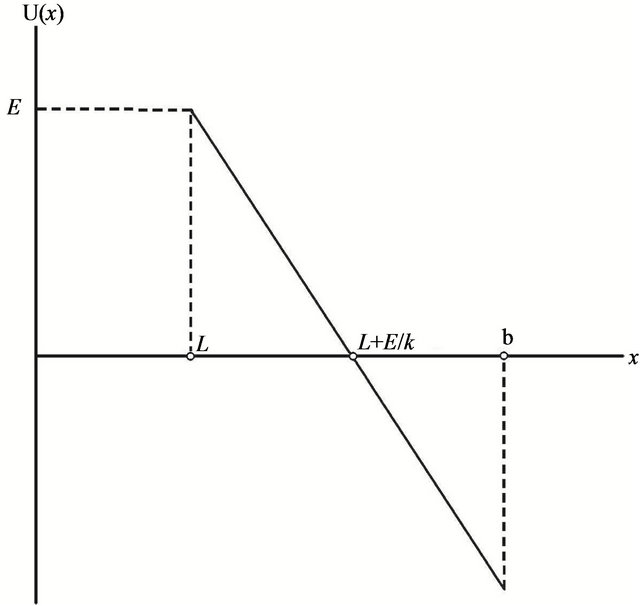
Figure 2. The triangle piece-wise potential described by Equation (8).
where 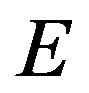 is the height of the potential barrier, and
is the height of the potential barrier, and 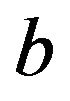 is the absorbing boundary. The states for
is the absorbing boundary. The states for 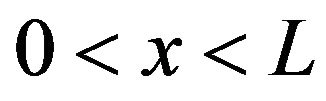 are metastable, and those for
are metastable, and those for 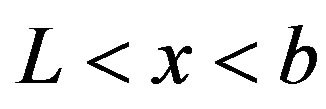 are unstable. The overdamped periodically driven motion of a particle in the potential (8) is described by the following equation
are unstable. The overdamped periodically driven motion of a particle in the potential (8) is described by the following equation
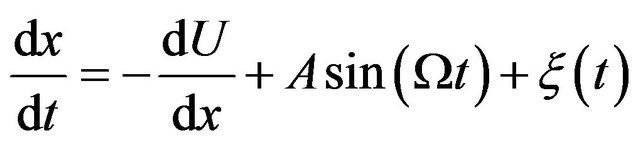 (9)
(9)
with white noise 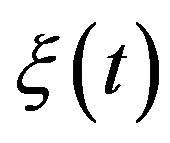 of strength
of strength 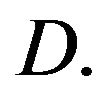
Consider first the time-independent potential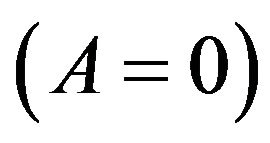 . If the initial position of a particle is unstable,
. If the initial position of a particle is unstable, 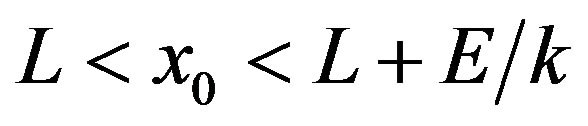 , the average escape time grows in the presence of noise since the particle may jump into the potential well. For very weak noise, the probability of such jumps is very low. If only these jumps are operating, the particle will be trapped in the well for a long time (noise enhanced stability).
, the average escape time grows in the presence of noise since the particle may jump into the potential well. For very weak noise, the probability of such jumps is very low. If only these jumps are operating, the particle will be trapped in the well for a long time (noise enhanced stability).
Consider now 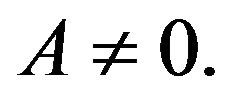 For
For 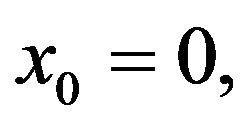 the particle at
the particle at 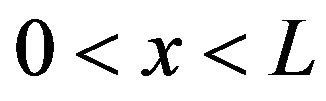 will move according to the equation
will move according to the equation
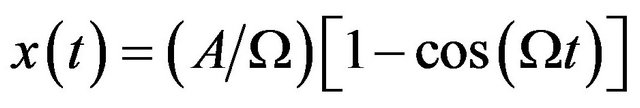 .
.
If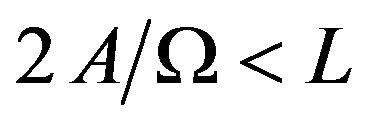 , the particle will always remain inside the region
, the particle will always remain inside the region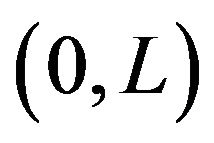 . However, if
. However, if 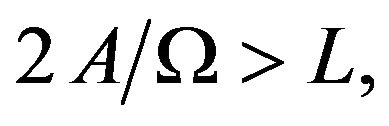 the particle surmounts the region
the particle surmounts the region 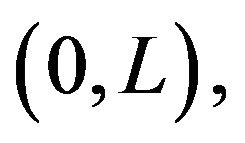 and its position will change with time as
and its position will change with time as
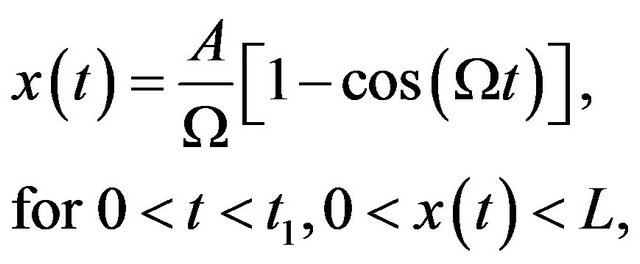 (10)
(10)
and
 (11)
(11)
where 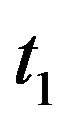 is the time at which the particle crosses the point
is the time at which the particle crosses the point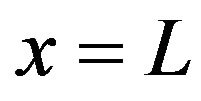 ,
,
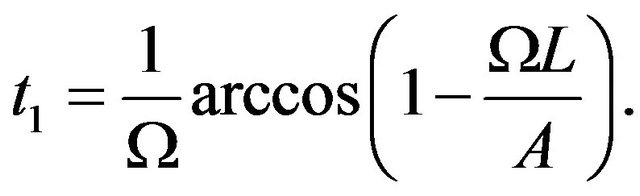 (12)
(12)
Noise enhanced stability occurs at time 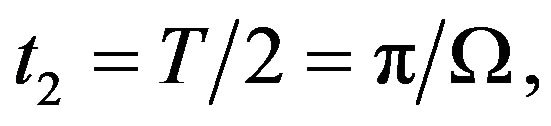 (when the periodic force changes it sign), tending to return the particle to the region
(when the periodic force changes it sign), tending to return the particle to the region 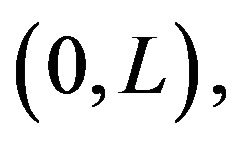 and the particle is still located inside the interval
and the particle is still located inside the interval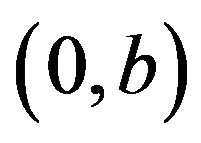 ,
,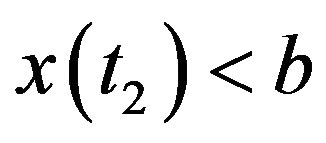 . Using (12) and (11), the latter inequality can be rewritten as
. Using (12) and (11), the latter inequality can be rewritten as
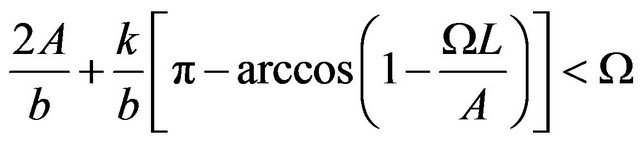 (13)
(13)
In addition to the inequality 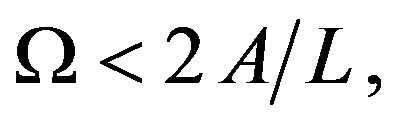 Equation (13) defines the conditions for the appearance of the noise enhanced stability. Therefore, both noise and a periodic force influence the escape time of a particle in a metastable state, thereby increasing the stability of the system. Another form of potential barrier is the rectangular bistable potential shown in Figure 3. The barriers heights
Equation (13) defines the conditions for the appearance of the noise enhanced stability. Therefore, both noise and a periodic force influence the escape time of a particle in a metastable state, thereby increasing the stability of the system. Another form of potential barrier is the rectangular bistable potential shown in Figure 3. The barriers heights 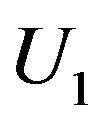 and
and 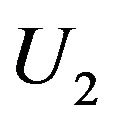 are different for the right (stable) and the left (metastable) states. For such a form of the potential, there is no force in the equation of motion, which has the following form
are different for the right (stable) and the left (metastable) states. For such a form of the potential, there is no force in the equation of motion, which has the following form
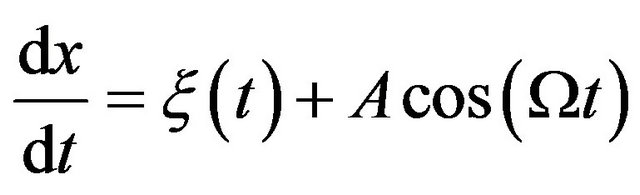 (14)
(14)
For the case 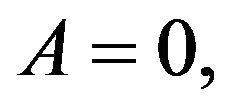 one can easily solve the Fokker-Planck equation associated with the Langevin equation (14) in each of the three regions in Figure 3 and find the integration constants from the matching conditions on two boundaries between different regions complemented by reflection boundary conditions at the walls,
one can easily solve the Fokker-Planck equation associated with the Langevin equation (14) in each of the three regions in Figure 3 and find the integration constants from the matching conditions on two boundaries between different regions complemented by reflection boundary conditions at the walls, 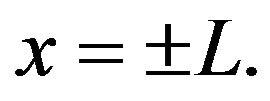 Finally, one can find the time-independent number of particles
Finally, one can find the time-independent number of particles 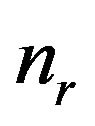 and
and 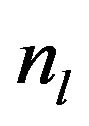 in the right (stable) and in the left (metastable) wells, respectively. Therefore, the population of a metastable state can be increased by adding an external periodic field or by fluctuations of the barrier height. The analogous situation exists with a simple pendulum which is stable (metastable) in the vertically downward (upward) position. One can, however, stabilize a metastable position by high-frequency harmonic vibrations of its suspension parametric oscillations of a pendulum (“Kapitza pendulum” [18]).
in the right (stable) and in the left (metastable) wells, respectively. Therefore, the population of a metastable state can be increased by adding an external periodic field or by fluctuations of the barrier height. The analogous situation exists with a simple pendulum which is stable (metastable) in the vertically downward (upward) position. One can, however, stabilize a metastable position by high-frequency harmonic vibrations of its suspension parametric oscillations of a pendulum (“Kapitza pendulum” [18]).
An external force 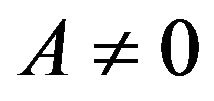 in Equation (14) can be chosen as a periodic force acting on the left well or as a random force acting on the barrier. It turns out that for both cases, an external force tends to equalize the populations as
in Equation (14) can be chosen as a periodic force acting on the left well or as a random force acting on the barrier. It turns out that for both cases, an external force tends to equalize the populations as  (stabilizing the metastable state), and even reversing the populations of these states. Our choice of the periodic signal does not introduce an additional force into the equation of motion, and the periodic signal enters only in the matching conditions. It turns out that with the help of an external periodic field, one can increase the population of the left (metastable) state, or even reverse the populations [19].
(stabilizing the metastable state), and even reversing the populations of these states. Our choice of the periodic signal does not introduce an additional force into the equation of motion, and the periodic signal enters only in the matching conditions. It turns out that with the help of an external periodic field, one can increase the population of the left (metastable) state, or even reverse the populations [19].
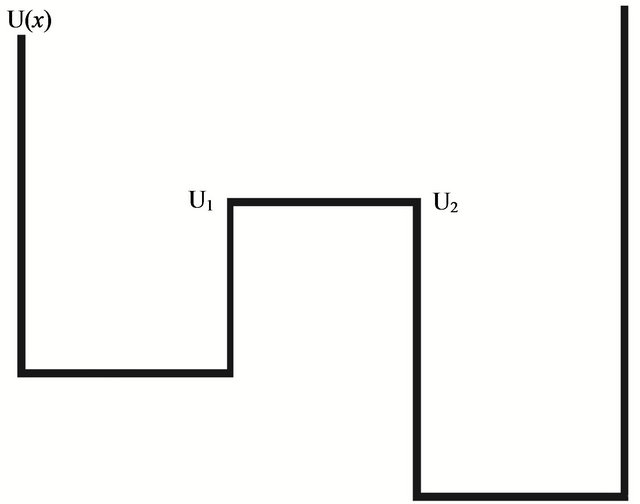
Figure 3. The rectangular piece-wise bistable potential.
5. Harmonic Oscillator with Random Mass
Recently we considered a harmonic oscillator subject to the periodic force 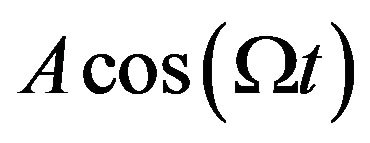 and white noise
and white noise 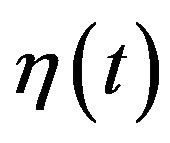 of strength
of strength  with asymmetric (
with asymmetric ( and
and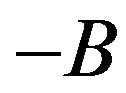 ) dichotomous random mass, which is described by the following equation
) dichotomous random mass, which is described by the following equation
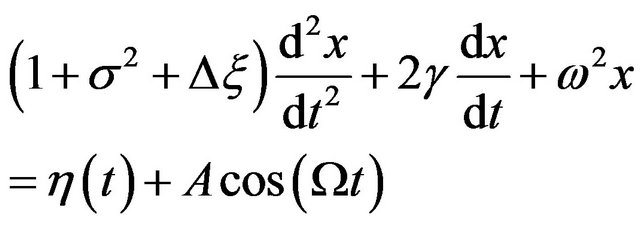 (15)
(15)
where  and
and 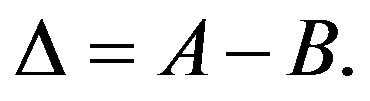 The asymptotic values of the first two moments
The asymptotic values of the first two moments 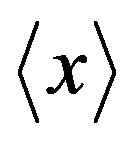 and
and 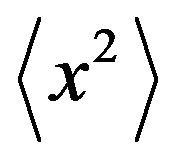 have been found in [20].
have been found in [20].
For 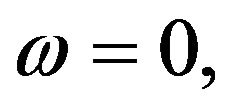 Equation (15) describes Brownian motion with adhesion, when the surrounding molecules not only collide with the Brownian particle, inducing zigzag motion, but also adhere to it for a random time. For this case, the stationary
Equation (15) describes Brownian motion with adhesion, when the surrounding molecules not only collide with the Brownian particle, inducing zigzag motion, but also adhere to it for a random time. For this case, the stationary 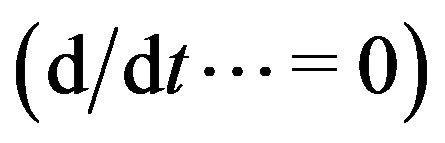 second moment
second moment 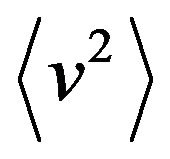 of the velocity
of the velocity 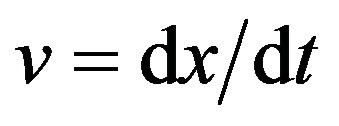 of the Brownian particle has the following form [20]
of the Brownian particle has the following form [20]
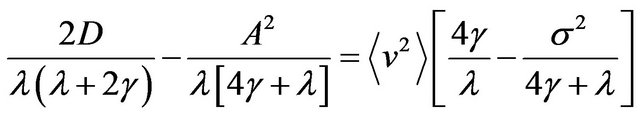 (16)
(16)
Let us consider the different limiting cases of Equation (16).
1) In the absence of an external field, 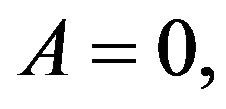 the second moment
the second moment 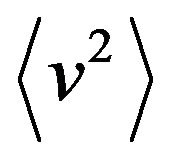 is given by
is given by
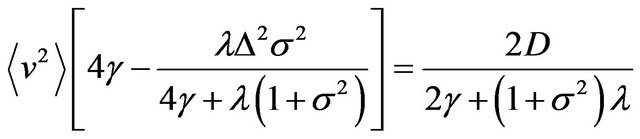 (17)
(17)
i.e., 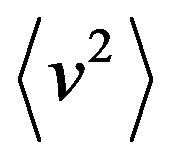 becomes negative for large strength
becomes negative for large strength 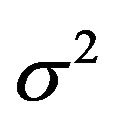 of the mass fluctuations, showing an instability of the system, i.e., a system cannot reach a stationary state.
of the mass fluctuations, showing an instability of the system, i.e., a system cannot reach a stationary state.
2) In the absence of the mass fluctuation, 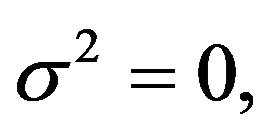 the system becomes unstable for large amplitude
the system becomes unstable for large amplitude  of the external periodic field.
of the external periodic field.
In both cases, the instability occurs due to the violation of the energetic balance (fluctuation-dissipation theorem) for the Brownian motion, namely, the energy gained by a system due to the external field or due to fluctuations is not balanced by the friction. However, Equation (16) shows that including a strong external field in the former case or large fluctuations in the latter case, one can restore the energetic balance and the stability of a system. Therefore, both the external periodic force and fluctuations are able to be “ordering” factors.
6. Vibrational Resonance
As we have already seen, a shift of the stable points occurs either through multiplicative noise or through a parametric periodic force, although the physical mechanism is quite different. Indeed, this effect occurs because of the low frequencies of the correlator of noise and the high frequencies of an external field. It turns out that the analogous effect occurs for two additive periodic fields. A bistable underdamped oscillator subject to two periodic fields is described by the following equation
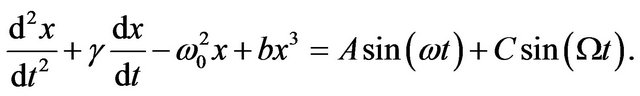 (18)
(18)
Analogous to Equation (7), the stochastic resonance occurs also in a bistable underdamped oscillator described by the following Equations [21,22]
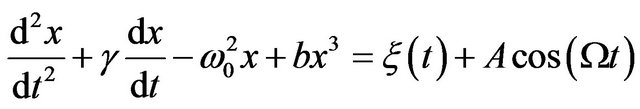 (19)
(19)
One can link the last two equations. The phenomenon of the stochastic resonance, described by Equation (19), was considered previously. We now turn to the analysis of Equation (18). Suppose that one of the fields has a large amplitude (larger than the barrier height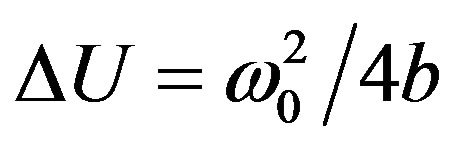 ),
), 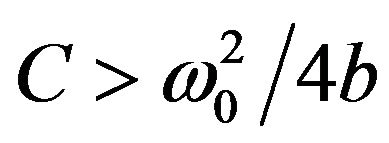 and high frequency,
and high frequency,  . The former means that during each half-period, this field transfers the particle from one potential well to the other. A similar situation holds in a random system where the large amplitude field in (18) is replaced by an additive random force, which plays the same role of switching the particle between the two minima. Therefore, by choosing the appropriate relation between the input signal
. The former means that during each half-period, this field transfers the particle from one potential well to the other. A similar situation holds in a random system where the large amplitude field in (18) is replaced by an additive random force, which plays the same role of switching the particle between the two minima. Therefore, by choosing the appropriate relation between the input signal 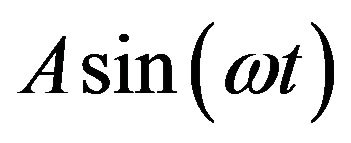 and the amplitude
and the amplitude  of the large signal (or the strength of noise), one can obtain a non-monotonic dependence of the output signal on the noise strength (stochastic resonance as considered before) or on the amplitude
of the large signal (or the strength of noise), one can obtain a non-monotonic dependence of the output signal on the noise strength (stochastic resonance as considered before) or on the amplitude  (vibrational resonance [21]). Therefore, paradoxically the “ordered” periodic signal and “disordering” noise play analogous roles in stochastic and vibrational resonances.
(vibrational resonance [21]). Therefore, paradoxically the “ordered” periodic signal and “disordering” noise play analogous roles in stochastic and vibrational resonances.
7. Conclusion
As it follows from all the examples considered, periodic and random signals do not unnecessarily act in opposite directions. They may play the same role, sometimes even substituting for one another in both above considered linear (overdamped harmonic oscillator, harmonic oscillator with random mass, harmonic oscillator with piecewise potentials) and nonlinear (birth-death process, vibrational resonance) systems.
REFERENCES
- R. Dean Astumian and F. Moss, “Overview: The Constructive Role of Noise in Fluctuations of Driven Transport and Stochastic Resonance,” Chaos, Vol. 8, No. 5, 1998, pp. 533-539. doi:10.1063/1.166334
- W. Horsthemke and R. Lefever, “Noise-Induced Transitions,” Springer, Berlin, 1084.
- P. Hanggi and R. Bartussek, “Lecture Notes in Physics,” Springer, Berlin, 1996.
- J. M. R. Parrondo, C. Van den Broeck and F. de la Rubia, “Noise-Induced Spatial Patterns,” Physica A, Vol. 224, No. 1-2, 1996, pp. 153-161. doi:10.1016/0378-4371(95)00350-9
- P. Yung and P. Talkner, “Suppression of Higher Harmonics at Noise Induced Resonances,” Physical Review E, Vol. 51, No. 3, 1995, pp. 2640-2643. doi:10.1103/PhysRevE.51.2640
- I. Dayan, M. Gitterman and G. H. Weiss, “Stochastic Resonance in Transient Dynamics,” Physical Review A, Vol. 46, No. 2, 1992, pp. 757-761. doi:10.1103/PhysRevA.46.757
- S. L. Ginzburg and M. A. Pustovoit, “Noise-Induced Hypersensitivity to Small Time-Dependent Signals,” Physical Review Letters, Vol. 80, No. 22, pp. 4840-4842. doi:10.1103/PhysRevLett.80.4840
- C. R. Doering and J. C. Gadoua, “Resonant Activation over a Fluctuating Barrier,” Physical Review Letters, Vol. 69, No. 16, 1992, pp. 2318-2321. doi:10.1103/PhysRevLett.69.2318
- F. Marchesoni, “Conceptual Design of a Molecular Shuttle,” Physical Letters A, Vol. 237, No. 3, 1998, pp. 126- 130.
- D. W. Brown, L. J. Bernstein and K. Lindenberg, “Resonant Activation over a Fluctuating Barrier,” Physical Review E, Vol. 54, No. 4, 1996, pp. 3352-3360. doi:10.1103/PhysRevE.54.3352
- G. Nicolis and I. Prigogine, “Self-Organization in NonEquilibrium Systems,” Wiley, New York, 1977.
- J. E. Fletcher, S. Havlin and G. H. Weiss, “First Passage Time Problems in Time-Dependent Fields,” Journal of Statistical Physics, Vol. 51, No. 1-2, 1988, pp. 215-232. doi:10.1007/BF01015328
- P. Reimann and P. Hanggi, “Lecture Notes in Physics,” Springer, Berlin, 1997.
- C. Zhou and C.-H. Lai, “Robustness of Supersensitivity to Small Signals in Nonlinear Dynamical Systems,” Physical Review E, Vol. 59, No. 6, 1999, pp. R6243-R6246. doi:10.1103/PhysRevE.59.R6243
- P. Yung and E. Marchesoni, “Energetics of Stochastic Resonance,” Chaos, Vol. 21, No. 4, 2011, Article ID: 046516.
- M. Gitterman, “Order and Chaos: Are They Contradicting or Complimentary?” European Journal of Physics, Vol. 23, No. 2, 2002, pp. 119-122. doi:10.1088/0143-0807/23/2/304
- R. N. Mantegna and R. Spagnolo, “Noise Enhanced Stability in an Unstable System,” Physical Review Letters, Vol. 76, No. 4, 1996, pp. 563-566. doi:10.1103/PhysRevLett.76.563
- L. Landau and E. Lifshitz, “Mechanics,” Mechanics, Pergamon, 1976.
- M. Gitterman, “Stabilization of Metastable States,” Physical Review E, Vol. 65, No. 3, 2002, Article ID: 031103. doi:10.1103/PhysRevE.65.031103
- M. Gitterman, “Mean-Square Displacement of a Stochastic Oscillator: Linear vs. Quadratic Noise,” Physica A, Vol. 391, No. 11, 2012, pp. 3033-3048. doi:10.1016/j.physa.2012.01.021
- P. S. Landa and P. V. E. McClintock, “Vibrational Resonance,” Journal of Physics A, Vol. 33, No. 45, 2000, pp. L433-L438.
- Y. M. Kang, J.-X. Xu and Y. Xie, “Observing Stochastic Resonance in an Underdamped Bistable Duffing Oscillator by the Method of Moments,” Physical Review E, Vol. 68, No. 3, 2003, Article ID: 036123. doi:10.1103/PhysRevE.68.036123

