Applied Mathematics
Vol.05 No.16(2014), Article ID:49484,17 pages
10.4236/am.2014.516247
A Geometric Approach to the Design of Serial and Parallel Manipulators with Passive Joints
Cong Dung Pham1, Pål Johan From1, Jan Tommy Gravdahl2
1Department of Mathematical Sciences and Technology, Norwegian University of Life Sciences, Ås, Norway
2Department of Engineering Cybernetics, Norwegian University of Science and Technology, Trondheim, Norway
Email: cong.dung.pham@nmbu.no
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 June 2014; revised 28 July 2014; accepted 7 August 2014
ABSTRACT
The use of robotic manipulators in remote and sensitive areas calls for more robust solutions when handling joint failure, and the industry demands mathematically robust approaches to handle even the worst case scenarios. For both serial and parallel manipulators torque failure is indeed a worst case scenario. Thus, a systematic analysis of the effects of external forces on manipulators with passive joints is presented. For serial manipulators we find under what conditions the robot is conditionally equilibrated, that is, equilibrated with respect to a specific external force. These conditions are, as expected, very restrictive. The serial, or subchain, case serves as a good platform for analyzing parallel manipulators. In parallel manipulators passive joints can appear as a design choice or as a result of torque failure. In both cases a good understanding of the effects that passive joints have on the mobility and motion of the parallel manipulator is crucial. We first look at the effects that passive joints have on the mobility of the mechanism. Then, if the mobility considering passive joints only is not zero we find a condition similar to the serial case for which the parallel manipulator is conditionally equilibrated with respect to a specific external force.
Keywords:
Robot Kinematics, Fault Tolerance, Parallel Manipulators

1. Introduction
Serial and parallel robots are widely used in remote and harsh environments where humans cannot or do not want to operate. The need for a rigorous theory on what happens when joint failure occurs is thus important to be able to cope with unforeseen events such as actuation failure. This paper endeavors to convey a complete theory of the effects that passive joints have on serial and parallel manipulators when external forces are present. We start by looking at how joint failure affects the mobility of closed chain manipulators. We are interested in the undesired motion generated by the passive joints that cannot be compensated for by the active joints. For parallel manipulators, joint failure may or may not allow a motion generated by the passive joints. If the mani- pulator does not allow such a passive motion, we will denote it equilibrated. In this case it can resist a wrench in an arbitrary direction either through kinematic constraints or through actuator torques. We obtain this if the manipulator, considering the passive joints only, has mobility equal to zero, i.e. we do not want the passive joints to allow any motion when the active joints are locked. If this property is satisfied the manipulator does not have an unstable singularity, following the classification in Matone and Roth [1] . On the other hand, for serial manipulators joint failure will always result in an undesired motion if an arbitrary external force is present. In this case we investigate under what conditions, i.e. for what external forces and for what configurations, the external forces do not affect the motion of the passive joints. We will say that the manipulator is conditionally equilibrated with respect to an external force at all configurations for which the passive joints are not affected by the given force.
Many papers discussing the mobility of parallel manipulators and the relation between the active and passive joints can be found in literature. The Jacobian of the parallel manipulator is investigated in Liu et al. [2] and Bicchi and Prattichizzo [3] where the passive joint accelerations are found from the active joint accelerations by dividing the Jacobian into an active and a passive part. For non-overconstrained mechanisms, i.e. when there are no redundant constraints, we can find the mobility by the well known Grübler formula [4] . For overconstrained mechanisms there are many approaches to determine the mobility. In Dai et al. [5] the mobility of the mecha- nism is found from the constraint space. The constraints of the system are found systematically and the redun- dant constraints are identified. The mobility is then found by adding the degrees of freedom represented by these redundant constraints to the Grübler formula for non-overconstrained mechanisms. This approach illustrates well the effect of redundant constraints in the mechanism.
The mobility can also be found by the motion space as in Rico et al. [6] [7] . The degree of freedom of the motion of the end effector is first found. Then the degree of freedom of the self-motion manifold of each chain is added. By this approach the redundant constraints are not found directly, but this approach gives valuable in- sight into where to place redundant actuators in the mechanism.
Even though the mobility of closed chain manipulators is given a lot of attention in literature, there does not seem to be a thorough treatment of mobility in the light of joint failure. In this paper we are mainly concerned with the effects of torque failure [1] , also known as free-swinging joint faults (FSJF), see English and Macie- jewski [8] and Tinós et al. [9] [10] . This occurs when an active joint suddenly loses its actuation and starts behaving like a passive joint. For a comprehensive treatment on how to identify joint failures see Tinós et al. [10] . Once these are identified the appropriate control actions should be applied to minimise damage to the surroundings.
Passive joints will in general not be an intrinsic property of an open chain manipulator as this would make the manipulator collapse due to gravity or other external forces. In the case of free-swinging joint faults, however, the study of passive joints is important also for serial manipulators in order to prevent damage from the free- swinging joint. FSJF may occur for any joint and for any configuration of the manipulator. A systematic and rigorous description is thus essential in order to find a good and fast solution and to prevent damage to the surroundings. For serial manipulators the strongest property we can obtain is that the robot is conditionally equilibrated, i.e. a set of configurations for which the manipulator is equilibrated with respect to a given external force. Passive joints in serial manipulators are treated only briefly in literature, see for example Oriolo and Nakamura [11] and Arai and Tachi [12] , and case studies such as the Acrobot [13] .
Parallel manipulators can be designed such that all the degrees of freedom of the motion remain controllable when joint failure occurs for an arbitrary joint. This will, however, require more active joints than necessary to control the degrees of freedom of the manipulator. This actuator redundancy is in many cases undesirable due to manufacturing and maintenance costs, weight, performance, and so on. If the fault tolerance problem is not addressed in the design process it must be handled in the control of the manipulator in the case of such an occurrence. In this case the serial and parallel manipulators are treated in a similar manner and we search the configuration space of the manipulator for a set of joint positions for which the manipulator remains equilibrated for a given external force.
The approach presented in this paper is in itself very simple. First, we use Grübler’s formula or a generic method based on the results in Rico et al. [6] [7] to verify whether the manipulator, considering the passive joints only, generates a non-trivial motion. This is based on the results found in From and Gravdahl [14] . Then, if the passive joints of the manipulator allow a motion, we investigate what kind of motion it implements. From this we can conclude the two main results of this paper: 1) given a mechanism, with respect to what kind of external forces is the manipulator equilibrated; and 2) given an external force, what kind of mechanism and for what configurations is the mechanism equilibrated with respect to the external force.
In Meng et al. [15] , a precise geometric theory for analysis and synthesis of sub-6 DOF manipulators was presented. The low dimensional subgroups or submanifolds of
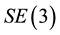 were used to represent the lower pairs, or primitive generators, while the high dimensional subgroups were used to represent the desired end-effector motion types. Given a desired end-effector motion type as a Lie subgroup or a submanifold, the synthesis problem was solved for serial and parallel manipulators. Then, from a pre-specified list of primitive generators, all possible serial and parallel arrangements of the primitive generators so that the resulting manipulator has the desired end-effector motion type were found. Using the formalism of [15] , we find that a mechanism is con- ditionally equilibrated with respect to an external force if the mechanism considering the passive joints only, is a motion generator of a motion for which the reciprocal product with the external force vanishes. Thus, while [15] uses the general concept of motion type (reference frame not specified) in their definition of motion generator, we will use a motion defined in a specific coordinate frame in our definitions. This allows us to verify resistance with respect to a specific external force, as opposed to a type or class of forces.
were used to represent the lower pairs, or primitive generators, while the high dimensional subgroups were used to represent the desired end-effector motion types. Given a desired end-effector motion type as a Lie subgroup or a submanifold, the synthesis problem was solved for serial and parallel manipulators. Then, from a pre-specified list of primitive generators, all possible serial and parallel arrangements of the primitive generators so that the resulting manipulator has the desired end-effector motion type were found. Using the formalism of [15] , we find that a mechanism is con- ditionally equilibrated with respect to an external force if the mechanism considering the passive joints only, is a motion generator of a motion for which the reciprocal product with the external force vanishes. Thus, while [15] uses the general concept of motion type (reference frame not specified) in their definition of motion generator, we will use a motion defined in a specific coordinate frame in our definitions. This allows us to verify resistance with respect to a specific external force, as opposed to a type or class of forces.
2. Preliminaries
This section presents a brief overview of mathematical modelling of rigid body motion and the definition of motion type. For a detailed treatment of the topic, the reader is referred to Murray et al. [4] , Meng et al. [15] , and From et al. [16] .
2.1. Rigid Body Motion
The special Euclidean group
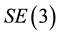 represents the configuration space of a rigid body. In addition to its group structure,
represents the configuration space of a rigid body. In addition to its group structure,
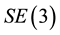 is a differentiable manifold, and is what is known as a Lie group.
is a differentiable manifold, and is what is known as a Lie group.
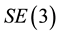 as a matrix Lie group can be written by homogeneous coordinates
as a matrix Lie group can be written by homogeneous coordinates
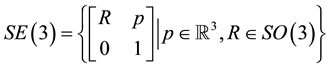 (1)
(1)
where
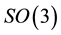 is the 3-dimensional special orthogonal group. An element
is the 3-dimensional special orthogonal group. An element
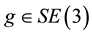 represents a rotation and a displacement of a rigid body relative to a reference configuration. Associated with every Lie group
represents a rotation and a displacement of a rigid body relative to a reference configuration. Associated with every Lie group
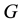 is its Lie algebra
is its Lie algebra
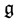 which is defined as the tangent space of
which is defined as the tangent space of
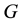 at the identity
at the identity
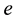 and is written as
and is written as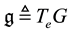 . The Lie algebra
. The Lie algebra
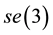 of
of
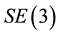 consists of all
consists of all
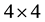 matrices
matrices
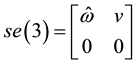 (2)
(2)
where




An element of


tified with the twist

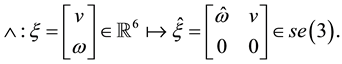
Let Q be the configuration space of the constrained system. In our case

can be represented by
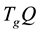

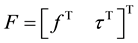
at



where
Denote by Lg and Rg the left and right translation maps, respectively. The differential






while the spatial velocity is given by

where
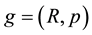

For a robotic mechanism with several sub-chains



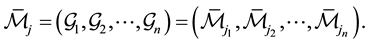
where we use the second notation


Let the parallel manipulator

consist of


where
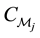


We are interested in the passive motion, i.e. the motion due to the passive joints when the active joints are fixed. We denote this by

where


Although only the passive joints are considered, the twists of the passive joints depend on the configuration of the active joints. The twist of joint

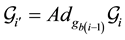
where


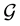



2.2. Motion Type
We now define motion type as in Meng et al. [15] . Motion type describes a class of motions, that is the con- jugacy class of a normal form subgroup or submanifold of

Definition 2.1. The group of similarity transformations of


Under the group of similarity transformations, helical motion with distinct pitches belong to the same conjugacy class. This is desirable in the definition of motion type as defined in [15] . We will need the following definition from Meng et al. [15] .
Definition 2.2. Let






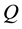
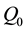


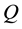





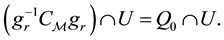
Equivalently we can write
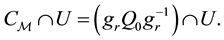
We are now ready to give the conditions for which serial and parallel manipulators have the motion type of Q.
Definition 2.3. We will denote a serial manipulator

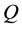

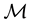
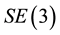



For parallel manipulators the corresponding definition of a Parallel Motion (PM) generator is given by
Definition 2.4. A parallel manipulator





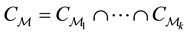
The conditions for which


Theorem 2.1. Given a motion type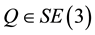
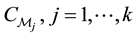



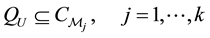
and consequently
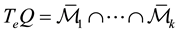
or the dual condition

holds, where

denotes the set of constraint forces for


Proof. The proof is given in [15] . □
In the setting of this paper the following is also important. If for every
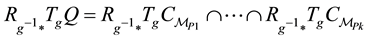
or its dual holds, then there exists a connected open subset







Thus, alternatively we can write (19) in the transformed form as

3. Equilibrated and Conditionally Equilibrated Serial and Parallel Manipulators
A parallel manipulator for which the mobility of

Definition 3.1. A parallel manipulator


straints or through actuator torques, can resist an arbitrary external wrench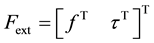
that an arbitrary wrench can be accommodated by the kinematic constraints, we will say that the manipulator is passively sustained. When an arbitrary wrench can be produced by the actuation torque, we will denote it actively equilibrated.
A parallel manipulator is equilibrated with respect to an arbitrary wrench if and only if the mobility is equal to zero. To guarantee fault tolerance the mobility needs to remain zero when torque failure occurs for an arbitrary joint. This will require redundant actuators to be implemented. We note that a serial manipulator with passive joints can never be equilibrated.
When the mobility is not zero, the best result we can obtain is that the mechanism is conditionally equili- brated with respect to a given external wrench. This applies both to serial and parallel manipulators.
Definition 3.2. A manipulator

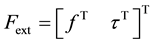



Note that in this case we do not require that the manipulator can resist any external wrench, only that it can produce a wrench of a given type and direction. This can for example be used to verify if a mechanism can resist forces in the direction of the gavitational forces, but not necessarily gravitational forces of an arbitrary magnitude.
We see that we will need a different definition of motion than the one given in Section 2. While Definition 2.2 requires the existence of some



Definition 3.3. Let
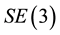
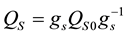
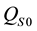


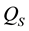
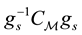


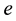

or equivalently

Note that


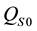

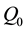
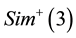



Definition 3.4. A manipulator
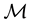



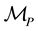


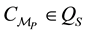
Thus we want the mechanism
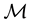



To get the desired properties for a parallel manipulator, we choose

・


・


When joint failure occurs in a parallel mechanism we want the second property to remain true. We note that



For parallel manipulators we start the analysis by finding the mobility



4. Fault Tolerance
In this section, we look into the effect of free-swinging joint failure (FSJF), or torque failure, in parallel mani- pulators and in particular how the results found in From and Gravdahl [14] can be used to prevent that the mechanism turns unequilibrated when this occurs. For a general treatment and an approach on how to identify joint failure see [10] In this case, as the number of passive joints in the manipulator increases by one, the mobility of
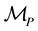




and the mechanism remains equilibrated with respect to all external forces. When


the mechanism is not fault tolerant. In this case the mechanism can at best be conditionally equilibrated, this is discussed in the remainder of the paper.
5. Robustness to External Forces for Serial Manipulators
The results presented in Section 2 let us quickly verify if a given serial or parallel manipulator has the desired type of end-effector motion. We will now use the same approach to analyse if a manipulator allows an undesired motion due to passive joints. We will start with a motivating example for the serial case.
Example 5.1. Consider a serial manipulator with one passive revolute joint at the end of the manipulator chain in Figure 1.
Attach a coordinate frame at the base of the manipulator and choose the reference configuration so that the revolute axis of the last joint and the



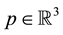



Assume further two external (linear) forces
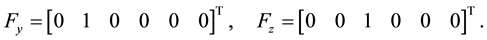
Figure 1. A serial manipulator with one passive re- volute joint at the end of the manipulator chain.
For the chosen reference configuration the set of constraint forces for the twist
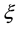



Thus, for the twist describing a joint that revolutes about the




From the simple example presented above, we see that the end-effector configuration is equilibrated with respect to one “type” or group of external forces, but not to others. We will denote the mechanism conditionally equilibrated when it is equilibrated with respect to a specific type of external force, e.g. gravity. In the following we will generalise this using the formalism presented in Meng et al. [15] .
We will restrict ourselves to

Example 5 is special in the sense that the axis of the passive joint is constant. This is obviously not always the case, for example when the passive joint is at the end of a manipulator chain. Thus, we will divide the problem into two parts: 1) when the mechanism is locally equilibrated (at reference configuration); and 2) when the mechanism is globally equilibrated (for any position of the active joints). A mechanism can be equilibrated with respect to an external disturbance for one configuration but not for another. We will start by looking at the local case and look at how external disturbances affect the mechanism at the reference configuration. In Section 5.2 we will extend this to the entire workspace of the manipulator.
5.1. A Local Solution
To analyse the manipulator when it is in the reference configuration is very much related to the work presented in [15] , and their results can be applied with a few simple modifications. From Example 5 we see that another definition of motion than the one given in Definition 2.2 is needed. We need to define the motion with respect to a given reference frame.
Thus, for a given external wrench, the equilibrated motion represents all the “directions” in which we can allow the manipulator to move, i.e. the directions that are not affected by the external force. This is formalised in the following.
Definition 5.1. For a given nominal external wrench



We see that




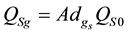
Assume now a manipulator with
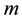

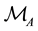

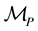


For a mechanism to be resistant to an external force it can only allow motions in
Definition 5.2. Given



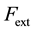
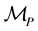

This becomes clearer with the following proposition:
Proposition 5.1. Let





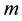



This proposition states that the external force must lie in the constraint motion of each joint and that each joint can be looked at independently. We will write this on a more compact form as

We will say that when Equation (34) is satisfied,

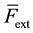
5.2. A Global Solution
The results presented in the previous section give a simple condition for the mechanism to be equilibrated with respect to an external force around the reference configuration. We now expand this to the entire workspace, i.e. for what positions of the active joints is the mechanism conditionally equilibrated. We start with a simple example.
Example 5.2. Assume we want to check if a mechanism is equilibrated with respect to the gravitational forces, i.e.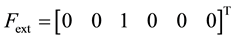

We have
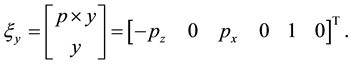
Then the problem amounts to finding all configurations

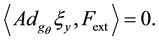
where

where
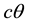



The solution is obtained by a rotation


with respect to forces working in the same direction as the axis of the revolute joint only. Note in addition to these there are certain positions of the passive joint for which the external forces do not affect the configuration,
Figure 2. A serial manipulator with one passive re- volute joint at the end of the manipulator chain.
such as the stable and unstable equilibrium of a pendulum, but we require that the mechanism can resist external forces for all positions in order to denote it conditionally equilibrated and isolated points in the configuration space are thus not included in the solution.
For serial manipulators the formulation described can give us a restriction on the configuration of the last “active link” for the manipulator to be conditionally equilibrated. By last active link we mean the link after the last active joint. This is formalized in the following.
A transformation from the reference configuration to a joint can be given as a rigid transformation



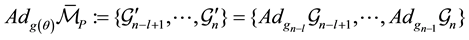
where




5.3. Free Swinging Joint Faults in Serial Manipulators
For a serial manipulator free-swinging joint fault is extremely serious and will in general cause the manipulator to collapse, or at least lose its controllability. This can cause damage both to humans and the surroundings. In this case we will need an additional requirement on the active joint positions so that the manipulator is condi- tionally equilibrated.
Definition 5.3. A serial manipulator


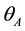
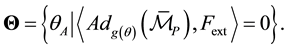
When joint failure occurs for any of the joints close to the base, this requirement is practically impossible to satisfy. Due to the kinematics of many commonly used manipulators such as the Motoman DIA or ABB IRB, this condition is, on the other side, quite easy to satisfy when the joint error occurs for one of the last joints. Examples of this are given below.
Example 5.3. Assume a manipulator with one active and one passive revolute joint and where the passive joint is parallel to the disturbance (gravity)


We are to verify under what condition, i.e. for what configurations of
・ when the active joint rotates about the

・ when the active joint rotates about the

In both cases, the twist of the passive joint is written as

Figure 3. A serial manipulator with one active and one passive revolute joint.
Figure 4. A serial manipulator with one active and one passive revolute joint.
The rotational and translational displacements due to the active joint in the two cases are given by
where




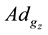
and we get that

As (39) is always satisfied, the mechanism is equilibrated for all configurations and no further action is required.
For the second case, we have
and we get that
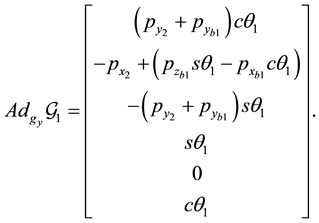
We see that in the second case, the manipulator is conditionally equilibrated with respect to Fext if and only if

This is the case when


in order to minimise damage to the surroundings.
Example 5.4. Assume a manipulator with two active (


In this case the set of equilibrated configurations

Figure 5. A serial manipulator with two active (z- and y-axes in reference configuration) and one passive (z- axis) joint.
We see that the stability depends on the position of


6. Robustness to External Forces for Parallel Manipulators
From From and Gravdahl [14] and Section 4, we learned that when



an additional requirement needs to be satisfied for the mechanism to be equilibrated. In this case the mechanism cannot be equilibrated with respect to an arbitrary external force, as there will always exist a force that results in the free motion. Thus, the strongest result we can obtain in this case is to guarantee that the mechanism is passively sustained with respect to a given external force.
As for the serial case, we get that this is true when the allowed motion lies in the annihilating space of the external forces. Finally we look at the global case and find for what configurations, i.e. positions of the active joints, this is true.
6.1. A Local Solution
Again we start by choosing a reference configuration and identify the joint positions with zero. In this section we apply the same modifications to the results presented in [15] as for serial manipulators. Recall that our definition of motion differs from the definition of motion type in [15] in that
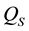






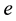

and consequently,

Recall that


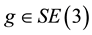
Proposition 6.1. Let
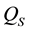




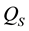

Alternatively we can verify that



holds, which means that every component of

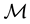
This guarantees that the end-effector motion is not affected by the external forces. Note that we also have to check for the internal motion of each chain. Hence, if joint failure occurs in chain

6.2. A Global Solution
In this section we generalise the results from the previous section to find all configurations for which the mecha- nism is conditionally equilibrated with respect to a given external force. We will first assume that all the passive joints are at the end of the sub-chains

Again we need to verify if the mechanism, considering the passive joints only, is equilibrated with respect to an external force

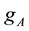

where

is the attainable spatial velocities of

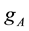


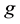
The main observation here is that the infinitesimal motions attainable by

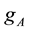
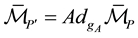
and we can use


We will divide the motion of the mechanism into two motions. First,



We will write

where




We need to verify if

where
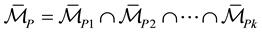


which is found by

which is the set of all equilibrated configurations for
6.3. Free Swinging Joint Faults in Parallel Manipulators
Free swinging joint faults affect parallel manipulators differently than serial manipulators. For serial manipula- tors joint faults is extremely serious while this is not always the case for closed chain manipulators due to the kinematic constraints. In this section we present several examples illustrating the effects of torque failure in pa- rallel mechanisms.
Consider the parallel manipulator in Figure 6. We consider two cases when joint failure occurs in
・ the actuated joints are chosen as in Figure 6,
・ the actuated joints are chosen as in Figure 6 but with
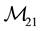

Example 6.1. Assume that the actuated joints are chosen as in Figure 6 and joint failure occurs in

Figure 6. Trivial Linkage of Type I. Bad choice of active joints. If joint failure occurs in joint




and we get

Thus for the chosen reference configuration,

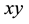
We now look into for what configurations this is true. This is straight forward due to the observation
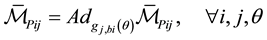
and thus the twists of the passive joints are independent of positions of the active joints. The set of joint posi- tions for which the manipulator is conditionally equilibrated with respect to


Similarly, the set of joint positions for which the manipulator is conditionally equilibrated with respect to
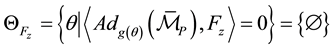
Example 6.2. Again we assume that the actuated joints are chosen as in Figure 6 and joint failure occurs in



and we get
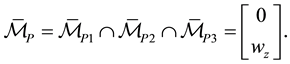
Thus for the chosen reference configuration,

We now look into for what configurations this is true. Again we have that Equation (62) is true and that the twists of the passive joints are independent of positions of the active joints. The set of joint positions for which the manipulator is conditionally equilibrated with respect to


Similarly, the set of joint positions for which the manipulator is conditionally equilibrated with respect to


This example illustrates the difference between the effects of joint failure in serial and parallel manipulators. For serial manipulators we can often take the manipulator to a certain configuration for which it is conditionally equilibrated. For parallel manipulators, however, we find that this requirement is either satisfied for all con- figurations, as in (67), or it is not satisfied at all, as in (68). Thus, if the parallel mechanism is conditionally equilibrated, this is an intrinsic property of the mechanical design and only in very special cases can it be taken care of in the control. For serial manipulators, however, the design of the manipulator does affect the condition to a certain extent, but we have more freedom to deal with external disturbances in the control when joint failure occurs.
7. Conclusions
A mathematically rigorous framework for analysing the effects of joint failure in serial and parallel manipulators is presented. For serial manipulators we find that for certain configurations the manipulator remains con- ditionally equilibrated with respect to a specific external force, such as gravity, even after joint failure occurs. This must thus be handled in the control algorithms as there is no way to guarantee fault tolerance through a fault tolerant design of the mechanism.
For parallel manipulators, however, we can find a set of active joints for which the design itself is fault tolerant. In this sense, the parallel manipulators are more robust than their serial counterparts. On the other hand, when actuator failure occurs and this allows for a motion in the passive joints, we have less flexibility to deal with this in the control algorithms than for serial manipulators. In general we find that the parallel manipulator is either conditionally equilibrated for all configurations, or it is never conditionally equilibrated. Fault tolerance of parallel manipulators should thus be addressed in the design of the mechanism.
Cite this paper
Cong DungPham,Pål JohanFrom,Jan TommyGravdahl, (2014) A Geometric Approach to the Design of Serial and Parallel Manipulators with Passive Joints. Applied Mathematics,05,2585-2601. doi: 10.4236/am.2014.516247
References
- 1. Matone, R. and Roth, B. (1999) In-Parallel Manipulators: A Framework on How to Model Actuation Schemes and a Study of Their Effects on Singular Postures. Transaction of ASME, 121, 2-8.
- 2. Liu, Y.H., Xu, Y. and Bergerman, M. (1999) Cooperation Control of Multiple Manipulators with Passive Joints. IEEE Transactions on Robotics and Automation, 15, 258-267. http://dx.doi.org/10.1109/70.760347
- 3. Bicchi, A. and Prattichizzo, D. (2000) Manipulability of Cooperating Robots with Unactuated Joints and Closed-Chain Mechanisms. IEEE Transaction of Robotics and Automation, 16, 336-345. http://dx.doi.org/10.1109/70.864226
- 4. Murray, R.M., Li, Z. and Sastry, S.S. (1994) A Mathematical Introduction to Robotic Manipulation. CRC Press, Boca Raton.
- 5. Dai, J.S., Huang, Z. and Lipkin, H. (2006) Mobility of Overconstrained Parallel Mechanisms. Transactions of ASME, 128, 220-229.
- 6. Rico, J.M., Gallardo, J. and Ravani, B. (2003) Lie Algebra and the Mobility of Kinematic Chains. Journal of Robotic Systems, 20, 477-499. http://dx.doi.org/10.1002/rob.10099
- 7. Rico, J.M., Aguilera, L.D., Gallardo, J., Rodriguez, R., Orozco, H. and Barrera, J.M. (2006) A More General Mobility Criterion for Parallel Mechanisms. Journal of Mechanical Design, 128, 207-219. http://dx.doi.org/10.1115/1.2118687
- 8. English, J.D. and Maciejewski, A.A. (1998) Fault Tolerance for Kinematically Redundant Manipulators: Anticipating Free-Swinging Joint Failures. IEEE Transactions of Robotics and Automation, 14, 566-575. http://dx.doi.org/10.1109/70.704223
- 9. Tinos, R. and Terra, M.H. (2002) Control of Cooperative Manipulators with Passive Joints. American Control Conference, Anchorage, 1129-1134.
- 10. Tinós, R., Terra, M.H. and Bergerman, M. (2007) A Fault Tolerance Framework for Cooperative Robotic Manipulators. Control Engineering Practice, 15, 615-625. http://dx.doi.org/10.1016/j.conengprac.2006.10.018
- 11. Oriolo, G. and Nakamura, Y. (1991) Free-Joint Manipulators: Motion Control under Second-Order Nonholonomic Constraints. Proceedings of IEEE International Workshop on Intelligent Robots and Systems, Osaka, 3-5 November 1991, 1248-1253. http://dx.doi.org/10.1109/IROS.1991.174671
- 12. Arai, H. and Tachi, S. (1990) Dynamic Control of a Manipulator with Passive Joints-Position Control Experiments by a Prototype Manipulator. IEEE/RSJ International Conference on Intelligent Robots and Systems, Ibaraki, 3-6 July 1990, 935-940.
- 13. Hauser, J. and Murray, R.M. (1990) Nonlinear Controllers for Non-Integrable Systems: The Acrobat Example. American Control Conference, San Diego, 23-25 May 1990, 669-671.
- 14. From, P.J. and Gravdahl, J.T. (2008) On the Mobility and Fault Tolerance of Closed Chain Manipulators with Passive Joints. Modeling, Identification and Control, 29, 151-165. http://dx.doi.org/10.4173/mic.2008.4.3
- 15. Meng, J., Liu, G. and Li, Z. (2007) A Geometric Theory for Analysis and Synthesis of Sub-6 DoF Parallel Manipulators. IEEE Transactions on Robotics, 23, 625-649. http://dx.doi.org/10.1109/TRO.2007.898995
- 16. From, P.J., Pettersen, K.Y. and Gravdahl, J.T. (2014) Vehicle-Manipulator Systems: Modeling for Simulation, Analysis, and Control. Springer Verlag, London. http://dx.doi.org/10.1007/978-1-4471-5463-1
- 17. From, P.J., Gravdahl, J.T. and Abbeel, P. (2010) On the Influence of Ship Motion Prediction Accuracy on Motion Planning and Control of Robotic Manipulators on Seaborne Platforms. Proceedings of International Conference of Robotics and Automation, Anchorage, 3-7 May 2010, 5281-5288.
NOTES
1For simplicity we will write twist for both twist coordinates and twists.
2In this context, spatial means that the velocity is given with respect to a globally defined coordinate system. We will also use spatial for the 3-dimensional space, as opposed to the 2-dimensional space.
3The case when