Applied Mathematics
Vol.5 No.13(2014), Article ID:47832,15 pages
DOI:10.4236/am.2014.513192
Local Search-Inspired Rough Sets for Improving Multiobjective Evolutionary Algorithm
Ahmed A. EL-Sawy1,2, Mohamed A. Hussein1*, El-Sayed Mohamed Zaki1, Abd Allah A. Mousa1,3
1Department of Basic Engineering Sciences, Faculty of Engineering, Menoufia University, Shibin El-Kom, Egypt
2Department of Mathematics, Faculty of Science, Qassim University, Buraydah, Saudi Arabia
3Department of Mathematics, Faculty of sciences, Taif University, Taif, Saudi Arabia
Email: *moh_abdelsameea_h@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 22 May 2014; accepted 5 June 2014
ABSTRACT
In this paper we present a new optimization algorithm, and the proposed algorithm operates in two phases. In the first one, multiobjective version of genetic algorithm is used as search engine in order to generate approximate true Pareto front. This algorithm is based on concept of co-evolution and repair algorithm for handling nonlinear constraints. Also it maintains a finite-sized archive of non-dominated solutions which gets iteratively updated in the presence of new solutions based on the concept of (-dominance. Then, in the second stage, rough set theory is adopted as local search engine in order to improve the spread of the solutions found so far. The results, provided by the proposed algorithm for benchmark problems, are promising when compared with exiting well-known algorithms. Also, our results suggest that our algorithm is better applicable for solving real-world application problems.
Keywords:Multiobjective Optimization, Genetic Algorithms, Rough Sets Theory

1. Introduction
Many real optimization problems require optimizing multiple conflicting objectives with each other. These problems with more than one objective are called Multiobjective Optimization Problems (MOPs). There is no single optimal solution, but a set of alternative solutions; these solutions are optimal in the wider sense that no other solutions in the search space dominate them when all objectives are considered. They are known as Pareto optimal solutions [1] [2] . MOPs naturally arise in many area of knowledge such as economics [3] -[5] , machine learning [6] -[8] and electrical power system [9] -[12] .
Deb [13] classified optimization methods as classical (traditional) methods and evolutionary methods (evolutionary algorithms). Traditional multiobjective methods attempt to find the set of nondominated solutions using mathematical programming. In traditional methods such as weighted method and ε-constraint method which are most commonly used [1] , the MOPs are transformed into a single objective problem which can be solved using nonlinear optimization techniques.
On the other hand, evolutionary methods (evolutionary algorithms EAs) for MOPs optimize all objectives simultaneously and generate a set of alternative solutions. The simultaneous optimization can fit with population based approaches, such as EAs, because they generate multiple solutions in a single run. These populationbased approaches are more successful when solving MOPs. There are many algorithms for solving unconstrained MOPs. A representative collection of these algorithms includes the vector evaluated genetic algorithm by Schaffer [14] , the niched Pareto genetic algorithm (NPGA) [15] and the nondominated sorting genetic algorithm by Srinivas and Deb [16] , the nondominated sorting genetic algorithm II (NSGA-II) by Deb et al. [17] , the strength Pareto evolutionary algorithm by Zitzler and Thiele [18] , the strength Pareto evolutionary algorithm II (SPEA-II) by Zitzler et al. [19] , the Pareto archived evolution strategy by Knowles and Corne [20] and the memetic PAES by Knowles and Corne [21] . These MOEAs differ from each other in both exploitation and exploration; they share the common purpose, searching for a near-optimal, well-extended and uniformly diversified Pareto optimal front for a given MOP [22] -[25] .
In case of constrained multiobjective optimization problems, there are a few evolutionary algorithms developed. Despite the developments for solving constrained optimization problems, there seem to be not enough studies concerning procedure for handling constraints. For example, Fonseca [26] suggested treating constraints as high-priority objectives, and Harade [27] proposed a few efficient constraint-handling guidelines and designed a Pareto descent repair method. For MOPs, a properly designed fitness assignment method is always required to guide the population to evolve to the Pareto front, as the objective vector cannot be used as the fitness function value directly. Most of the existing MOEAs assign the fitness function values based on the Pareto dominance relationship.
In this paper we present a new optimization algorithm, and the proposed algorithm operates in two phases: in the first one, multiobjective version of genetic algorithm is used as search engine in order to generate approximate true Pareto front. Then in the second phase, rough set theory is adopted as local search engine in order to improve the spread of the solutions found so far. The remainder of the paper is organized as follows. In section 2, we describe some basic concepts and definitions of MOPs. Section 3 presents constraint multiobjective optimization via genetic algorithm. Experimental results are given and discussed in section 4. Section 5 indicates our conclusion and notes for future work
2. Basic Concepts and Definitions
2.1. Problem Formulation
General multiobjective optimization problem is expressed by MOP:
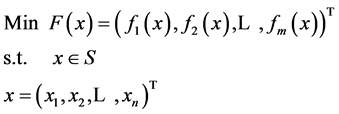
where
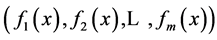 are the m objectives functions,
are the m objectives functions,
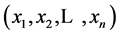 are the n decision variables, and
are the n decision variables, and
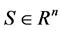 is the solution (parameter) space.
is the solution (parameter) space.
Definition 1. (Pareto optimal solution):
![]() is said to be a Pareto optimal solution of MOP if there exists
no other feasible
is said to be a Pareto optimal solution of MOP if there exists
no other feasible
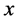 (i.e.,
(i.e.,![]() ) such that,
) such that,
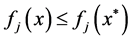 for all
for all
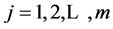 and
and
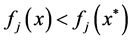 for at least one objective function
for at least one objective function![]() .
.
Definition 2. [28] (ε-dominance) Let
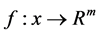 and
and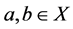 . Then a is said to ε-dominate b for some ε > 0, denoted as
. Then a is said to ε-dominate b for some ε > 0, denoted as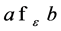 , if and only if for
, if and only if for
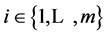
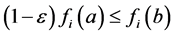
Definition 3. (ε-approximate Pareto set) Let X be a set of decision alternatives
and![]() . Then a set
. Then a set
![]() is called an ε-approximate Pareto set of X, if any vector
is called an ε-approximate Pareto set of X, if any vector
 is ε-dominated by at least one vector
is ε-dominated by at least one vector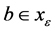 , i.e.
, i.e.
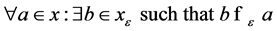
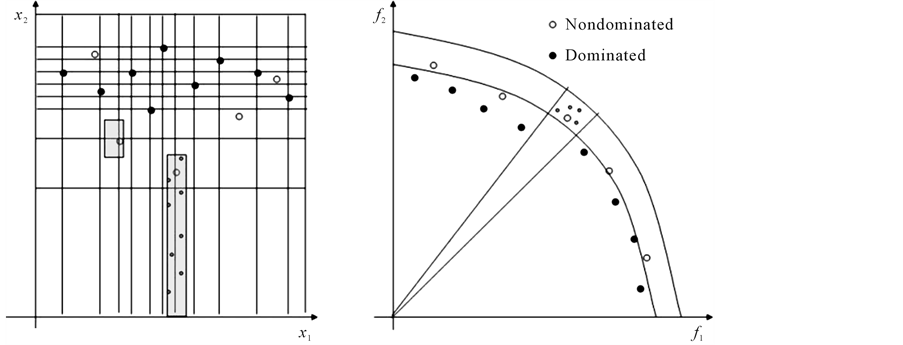
According to definition 2, the ε value stands for a relative allowed for the objective values as declared in Figure 1. This is especially important in higher dimensional objective spaces, where the concept of ε-dominance can reduce the required number of solutions considerably. Also, makes the algorithms practical by allowing a decision maker to control the resolution of the Pareto set approximation by choosing an appropriate ε-value
2.2. Use of Rough Sets in Multiobjective Optimization
For our proposed approach we will try to investigate the Pareto front using a Rough sets grid. To do this, we will use an initial approximate of the Pareto front (provided by any evolutionary algorithm) and will implement a grid in order to get more information about the front that will let to improve this initial approximation [29] .
To create this grid, as an input we will have N feasible points divided in two sets: the nondominated points (NS) and the dominated ones (DS). Using these two sets we want to create a grid to describe the set NS in order to intensify the search on it. This is, we want to describe the Pareto front in the decision variable space because then we could easily use this information to generate more efficient points and then improve this initial Pareto approximation. Figure 2 shows how information in objective function space can be translated into information in decision variable space through the use of a grid. We must note the importance of the DS sets as in a rough sets method, where the information comes from the description of the boundary of the two sets NS, DS. Then the more efficient points provided the better. However, it is also required to provide dominated points, since we need to estimate the boundary between being dominated and being nondominated. Once the information is computed we can simply generate more points in the “efficient side”.
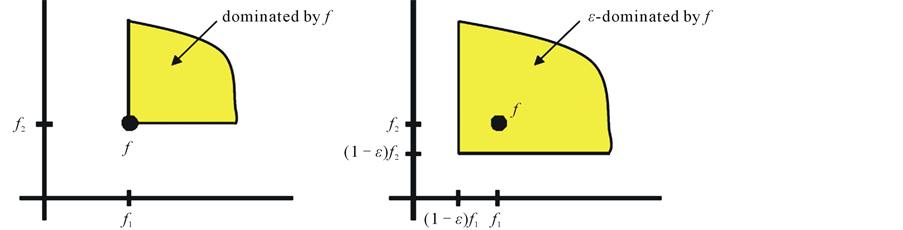
Figure 1. Graphs visualizing the concepts of dominance (left) and ε-dominance (right).
2.3. Structure of an Iterative Multiobjective Search Algorithm
The purpose of this section is to informally describe the problem we are dealing with. To this end, let us first give a template for a large class of iterative search procedures which are characterized by the generation of a sequence of search points and a finite memory.
An abstract description of a generic iterative search algorithm is given in Algorithm 1 [30] . The
integer t denotes the iteration count, the n-dimensional vector
![]() is the sample generated at iteration t and the set
is the sample generated at iteration t and the set
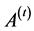 will be called the archive at iteration t and should contain a representative subset
of the samples in the objective space
will be called the archive at iteration t and should contain a representative subset
of the samples in the objective space
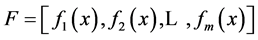 generated so far. To simplify the notation, we represent samples by ndimensional
real vectors f where each coordinate represents one of the objective values as shown
in Figure 3.
generated so far. To simplify the notation, we represent samples by ndimensional
real vectors f where each coordinate represents one of the objective values as shown
in Figure 3.
The purpose of the function
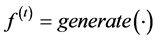 is to generate a new solutions in each iteration t, possibly using the contents
of the old archive set
is to generate a new solutions in each iteration t, possibly using the contents
of the old archive set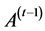 . The function
. The function
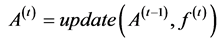 gets the new solutions
gets the new solutions
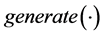 and the old archive set
and the old archive set
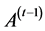 and determines the updated one, namely
and determines the updated one, namely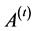 . In general, the purpose of this sample storage
is to gather “useful” information about the underlying search problem during the
run. Its use is usually two-fold: On the one hand it is used to store the “best”
solutions found so far, on the other hand the search operator exploits this information
to steer the search to promising regions. This procedure could easily be viewed
as an evolutionary algorithm when the generate operator is associated with variation
(recombination and mutation). However, we would like to point out that all following
investigations are equally valid for any kind of iterative process which can be
described as Algorithm 1 and used for approximating
the Pareto set of multiobjective optimization problems.
. In general, the purpose of this sample storage
is to gather “useful” information about the underlying search problem during the
run. Its use is usually two-fold: On the one hand it is used to store the “best”
solutions found so far, on the other hand the search operator exploits this information
to steer the search to promising regions. This procedure could easily be viewed
as an evolutionary algorithm when the generate operator is associated with variation
(recombination and mutation). However, we would like to point out that all following
investigations are equally valid for any kind of iterative process which can be
described as Algorithm 1 and used for approximating
the Pareto set of multiobjective optimization problems.
3. Constraint Multiobjective Optimization via Genetic Algorithm
In any interesting multiobjective optimization problem, there exist a number of such solutions which are of interest to designers and practitioners. Since no one solution is better than any other solution in the Pareto-optimal set, it is also a goal in a multiobjective optimization to find as many such Pareto-optimal solutions as possible. Unlike most classical search and optimization problems, GAs works with a population of solutions and thus are
Algorithm 1 . Iterative search algorithm.
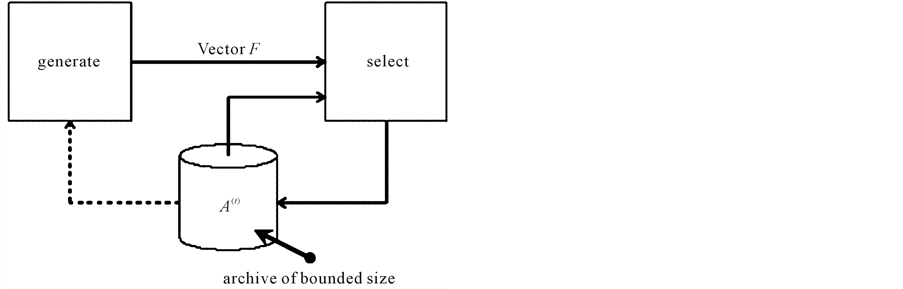
Figure 3. Block diagram of Archive/selection strategy.
likely (and unique) candidates for finding multiple Pareto-optimal solutions simultaneously. There are two tasks that are achieved in a multiobjective GA. 1) Convergence to the Pareto-optimal set; and 2) Maintenance of diversity among solutions of the Pareto-optimal set. Here we present a new optimization system, which is based on concept of co-evolution and repair algorithms. Also it is based on the ε-dominance concept. The use of ε- dominance also makes the algorithms practical by allowing a decision maker to control the resolution of the Pareto set approximation by choosing an appropriate ε value.
3.1. Initialization Stage
The algorithm uses two separate population, the first population
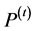 consists of the individuals which initialized randomly satisfying the search space
(the lower and upper bounds), while the second population
consists of the individuals which initialized randomly satisfying the search space
(the lower and upper bounds), while the second population
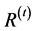 consists of reference points which satisfying all constraints (feasible points),
However, in order to ensure convergence to the true Pareto-optimal solutions, we
concentrated on how elitism could be introduced. So, we propose an “archiving/selection”
strategy that guarantees at the same time progress towards the Pareto-optimal set
and a covering of the whole range of the non-dominated solutions. The algorithm
maintains an externally finitesized archive
consists of reference points which satisfying all constraints (feasible points),
However, in order to ensure convergence to the true Pareto-optimal solutions, we
concentrated on how elitism could be introduced. So, we propose an “archiving/selection”
strategy that guarantees at the same time progress towards the Pareto-optimal set
and a covering of the whole range of the non-dominated solutions. The algorithm
maintains an externally finitesized archive
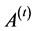 of non-dominated solutions which gets iteratively updated in the presence of new
solutions based on the concept of ε-dominance.
of non-dominated solutions which gets iteratively updated in the presence of new
solutions based on the concept of ε-dominance.
3.2. Repair Algorithm
The idea of this technique is to separate any feasible individuals in a population from those that are infeasible by repairing infeasible individuals.
This approach co-evolves the population of infeasible individuals until they become
feasible. Repair process works as follows. Assume, there is a search point
![]() (where S is the feasible space). In such a case the algorithm selects one of the
reference points (Better reference point has better chances to be selected), say
(where S is the feasible space). In such a case the algorithm selects one of the
reference points (Better reference point has better chances to be selected), say
![]() and creates random points
and creates random points
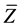 from the segment defined between
from the segment defined between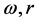 , but the segment may be extended equally [8] [23] on both sides
determined by a user specified parameter
, but the segment may be extended equally [8] [23] on both sides
determined by a user specified parameter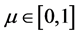 . Thus, a new feasible individual is expressed
as:
. Thus, a new feasible individual is expressed
as:
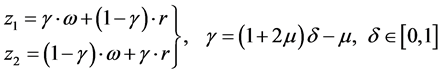
3.3. Evolutionary Algorithm: Phase 1
In the first phase, the proposed algorithm uses two separate population, the first
population
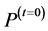 (where t is the iteration counter) consists of the individuals which initialized
randomly satisfying the search space (The lower and upper bounds), while the second
population
(where t is the iteration counter) consists of the individuals which initialized
randomly satisfying the search space (The lower and upper bounds), while the second
population
![]() consists of reference points which satisfying all constraints (feasible points).
Also, it stores initially the Pareto-optimal solutions externally in a finite sized
archive of non-dominated solutions
consists of reference points which satisfying all constraints (feasible points).
Also, it stores initially the Pareto-optimal solutions externally in a finite sized
archive of non-dominated solutions![]() . We use cluster algorithm to create the next population
. We use cluster algorithm to create the next population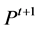 , if
, if
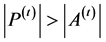 then new population
then new population
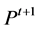 consists of all individual from
consists of all individual from
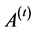 and the population
and the population
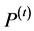 are considered for the clustering procedure to complete
are considered for the clustering procedure to complete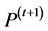 , if
, if
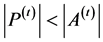 then
then
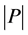 solutions are picked up at random from
solutions are picked up at random from
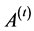 and directly copied to the new population
and directly copied to the new population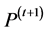 .
.
Since our goal is to find new nondominated solutions, one simple way to combine multiple objective functions into a scalar fitness function [31] [32] is the following weighted sum approach
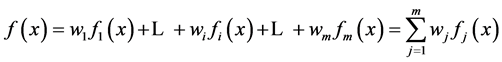
where x is a string (i.e., individual),
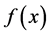 is a combined fitness function,
is a combined fitness function,
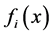 is the ith objective function When a pair of strings are selected
for a crossover operation, we assign a random number to each weight as follows:
is the ith objective function When a pair of strings are selected
for a crossover operation, we assign a random number to each weight as follows:
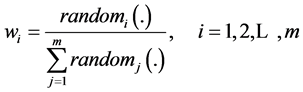
Calculate the fitness value of each string using the random weights![]() . Select a pair of strings from the current population
according to the following selection probability
. Select a pair of strings from the current population
according to the following selection probability
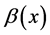 of a string x in the population
of a string x in the population
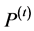
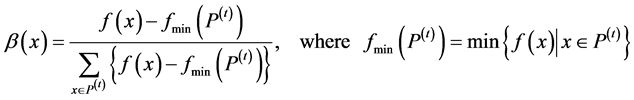
This step is repeated for selecting
 Paris of strings from the current populations. For each selected pair apply crossover
operation to generate two new strings, for each strings generated by crossover operation,
apply a mutation operator with a prespecified mutation probability. The system also
includes the survival of some of good individuals without crossover or mutation.
The algorithm maintains a finite-sized archive
Paris of strings from the current populations. For each selected pair apply crossover
operation to generate two new strings, for each strings generated by crossover operation,
apply a mutation operator with a prespecified mutation probability. The system also
includes the survival of some of good individuals without crossover or mutation.
The algorithm maintains a finite-sized archive
 of nondominated solutions which gets iteratively updated in the presence of a new
solutions based on the concept of ε-dominance, such that new solutions are only
accepted in the archive if they are not ε-dominated by any other element in the
current archive, the use of ε-dominance also makes the algorithms practical by allowing
a decision maker to control the resolution of the Pareto set approximation by choosing
an appropriate ε value.
of nondominated solutions which gets iteratively updated in the presence of a new
solutions based on the concept of ε-dominance, such that new solutions are only
accepted in the archive if they are not ε-dominated by any other element in the
current archive, the use of ε-dominance also makes the algorithms practical by allowing
a decision maker to control the resolution of the Pareto set approximation by choosing
an appropriate ε value.
3.4. Local Search Mechanism Inspired on Rough Sets Theory: Phase 2
Upon termination of phase 1, we start phase 2, with initial approximate of the Pareto front (provided by the proposed algorithm in phase 1) which noted as NS. Also all dominated solutions are marked as DS. It is worth remarking that NS can simply be a list of solutions.
From the set NS we choose NNS points previously unselected. If we do not have enough unselected points, we choose the rest randomly from the set DS. Next, we choose from the set DS, NDS points previously unselected (and in the same way if we do not have enough unselected points, we complete them in a random fashion) these points will be used to approximate the boundary between the Pareto front and the rest of the feasible set in decision variable space. We store theses points in the set Items and perform rough sets iterations:
1) Range Initialization: for each decision variable i, we compute and sort (from
smallest and highest) the different values it takes in the set Items. Then, for
each decision variable, we have a set of
![]() values and combining all these sets we have a non-uniform grid in decision variable
space.
values and combining all these sets we have a non-uniform grid in decision variable
space.
2) Compute Atoms: we compute “NNS rectangular atoms” centered in the NNS efficient
points selected. To build a rectangular atom associated to a nondominated point
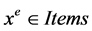 we compute the following upper and lower bounds for each decision variable i:
we compute the following upper and lower bounds for each decision variable i:
• Lower Bound i: Middle point between
![]() and the previous value in the set
and the previous value in the set

• Upper Bound i: Middle point between
![]() and the following value in the set
and the following value in the set
• If there are no pervious or subsequent values in , we consider the absolute lower or upper bound
of variable i. This setting lets the method to explore close to the feasible set
boundaries.
, we consider the absolute lower or upper bound
of variable i. This setting lets the method to explore close to the feasible set
boundaries.
3) Generate Offspring: inside each atom we randomly generate offspring new points. Each of these points is sent to the set NS as follows. The idea is that “new solutions are only accepted in the archive if they are not ε-dominated by any other element of the current archive”. If a solution is accepted, all dominated solutions are removed. Algorithm 2 shows the operator for ε-approximate Pareto set.
The pseudo code of the proposed algorithm is declared in Algorithm 3.
4. Experimental Results
In order to validate the proposed approach and quantitatively compare its performance with other MOEAs, we present in this section comparison study for some benchmark test functions with distinct Pareto-optimal front, which was used in [28] [33] -[35] . The degree of difficulty of these problems varies from simple to difficult. Graphical presentation, of the experimental results and associated observations are presented in this section. Table 1 lists the parameter setting used in our algorithm for all runs and Table 2 lists the variable bounds, objective functions and constraints for all these problems.
The problem BNH was used by Binh and Korn [33] , SRN was used by Srinivas, Deb [16] , TNK was proposed by Tanaka [35] and OSY was used by Osyczka, Kundu [34] . All these problems are constrained multiobjective problems.
Algorithm 2 .Operator for ε-approximate Pareto set.
Algorithm 3 . The proposed algorithm (pseudo code of the proposed algorithm).
Table 1. The parameter setting.
Table 2. Test benchmark problems used in our study.
The BNH and the SRN problems are fairly simple in that the constraints may not introduce additional difficulty in finding the Pareto-optimal solutions as shown in Figure 4 and Figure 5. It was observed that all MOEAs methods performed equally well, and gave a dense sampling of solutions along the true Pareto-optimal curve.
The TNK (Figure 6) and the OSY (Figure 7) are relatively difficult. The constraints in the TNK problem make the Pareto-optimal set discontinuous. The constraints in the TNK problem divide the Pareto-optimal set into five regions that can demand a proposed algorithm to maintain its sub-population at different intersections of the constraint boundaries. We compare our method with a reliable and efficient multiobjective genetic algorithm NSGA II. The results show that our method can be used efficiently for constrained MOP than NSGA-II. For the OSY problem, it can be seen that our approach gave a good sampling of points at the midsection of the curve and also found a lot of points at extreme ends of the curve. In the other hand NSGA-II did not give a good sampling of points at the extreme ends of Pareto curve.
Also, the proposed approach is applied to the problem was chosen from the engineering application, A welded beam design by Deb [36] and Two-Bar Truss [37] [38] .
Welded Beam: A welded beam design is used by Deb [36] , where a beam needs to be welded on another beam and must carry a certain load F as shown in Figure 8.
It is desired to find four design parameters (thickness b, width t, length of weld l, and weld thickness h) for which the cost function of the beam and the deflection function at the open end are minimum. The overhang portion of the beam has a length of “14 inch” and “F = 6000 Ib” force is applied at the end of the beam. A little thought will reveal that a design for minimum deflection at the end (or maximum rigidity of the above beam) will make all four design dimensions to take large dimensions. Thus, the design solutions for minimum cost and
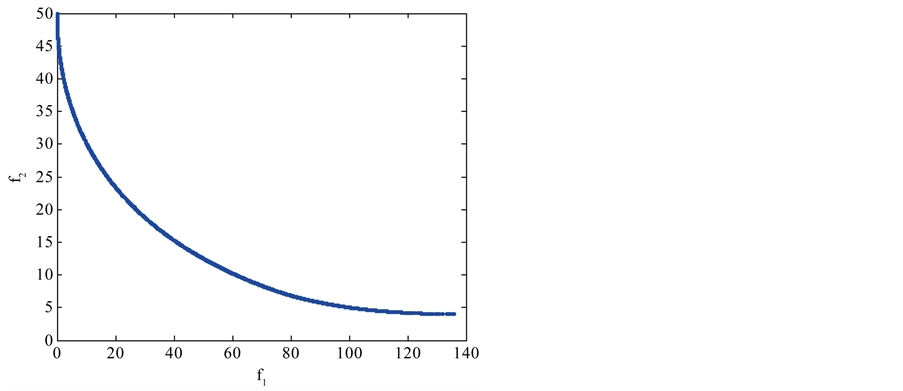
Figure 4. Pareto optimal front of BNH problem using our approach.
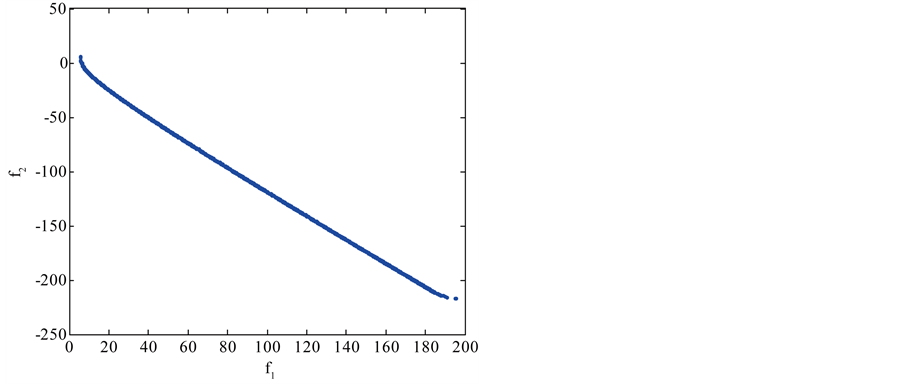
Figure 5. Pareto optimal front of SRN problem using our approach.
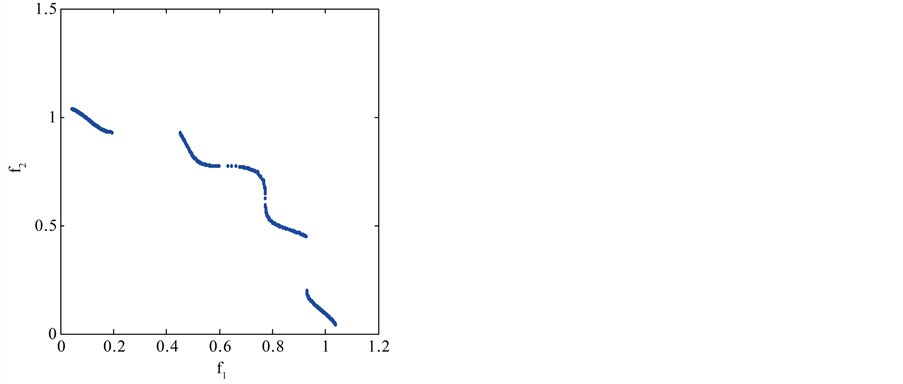
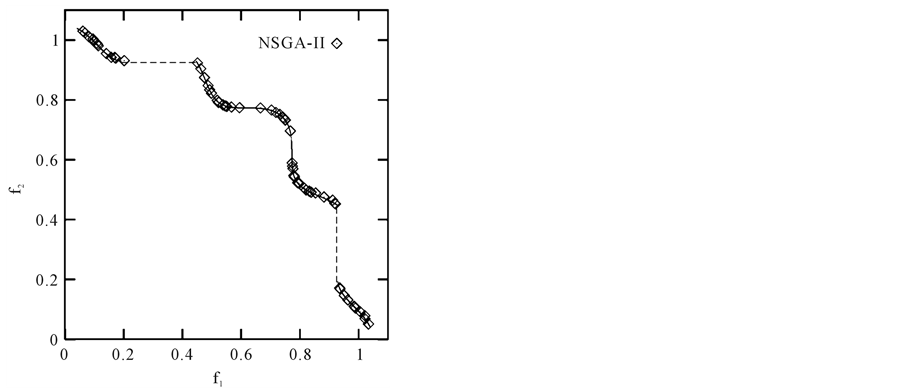
Figure 6. Pareto optimal front of TNK problem using our approach and NSGA-II.
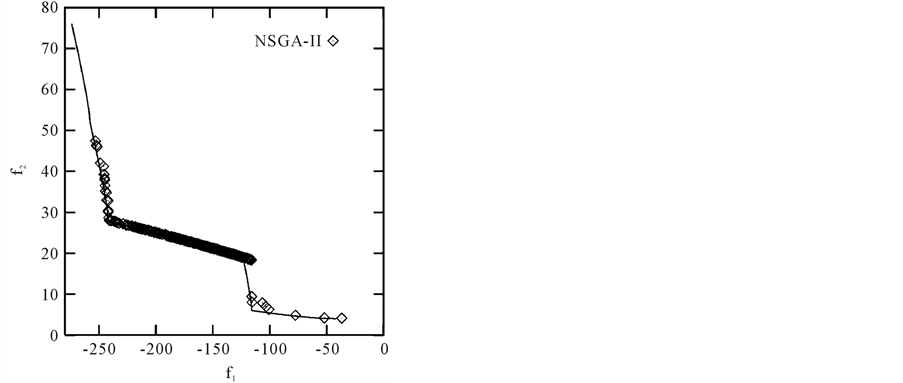
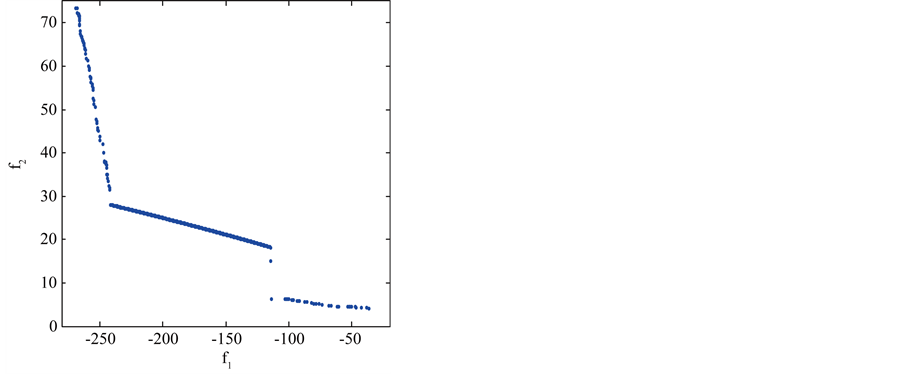
Figure 7. Pareto optimal front of OSY problem using our approach and NSGA-II.
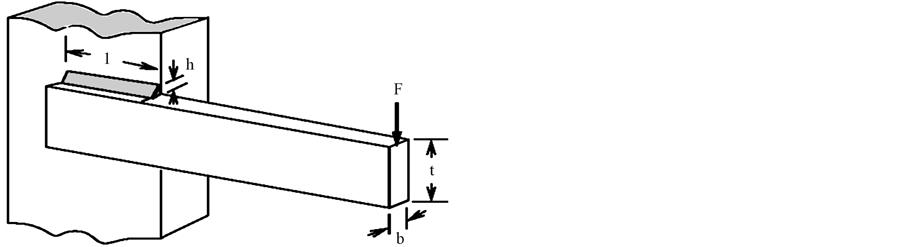
Figure 8. Welded Beam design problem.
maximum rigidity (or minimum-end-deflection) are conflicting to each other, which leads to Pareto-optimal solutions. In the following, the mathematical formulations of the two-objective optimization problem of minimizing cost and the end deflection are presented:
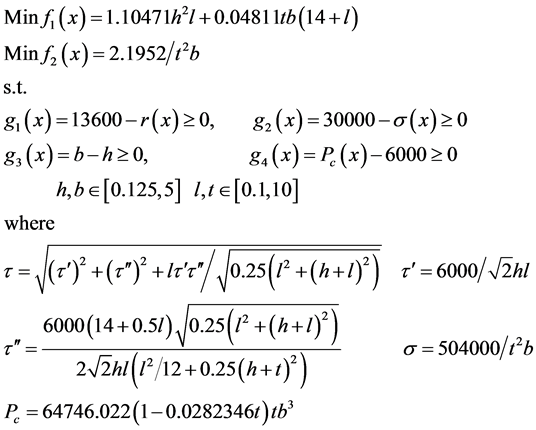
In the Welded Beam design problem, the non-linear constraints can cause difficulties in finding the Pareto front. As shown in Figure 9 and Figure 10 our proposed approach outperformed NSGA and NSGA-II in both
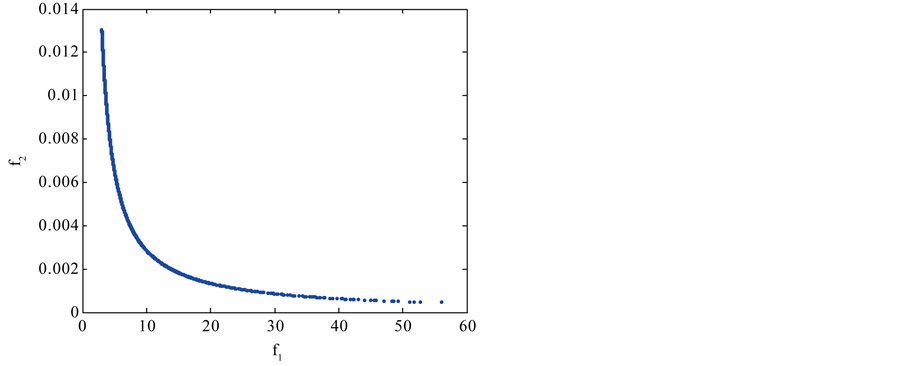
Figure 9. Pareto optimal front of welded beam using our approach.
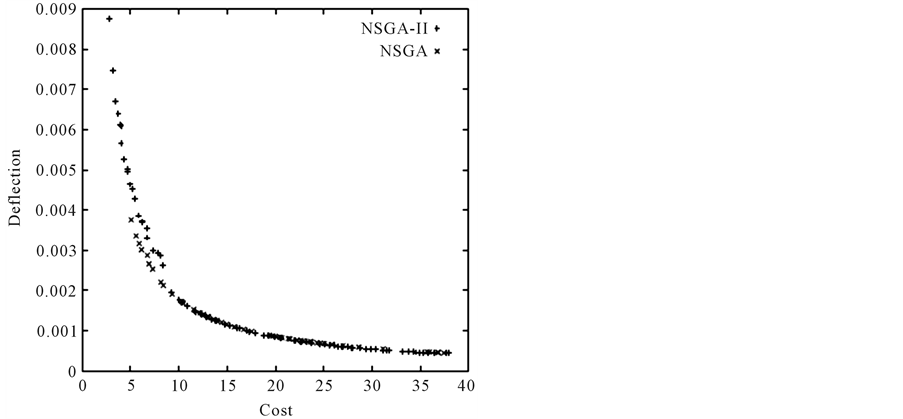
Figure 10. Pareto optimal front of welded beam using NSGA, NSGA-II.
distribution and spread.
Two-Bar Truss: Figure 11 illustrates the two-bar truss that is to be optimized [37] . This problem was adapted from Kirsch [38] . It is comprised of two stationary pinned joints, A and B, where each one is connected to one of the two bars in the truss. The two bars are pinned where the join one another at joint C, and a 100 kN force acts directly downward at that point. The cross-sectional areas of the two bars are represented as x1 and x2, the cross-sectional areas of trusses AC and BC respectively. Finally, y represents the perpendicular distance from the line AB that contains the two-pinned base joints to the connection of the bars where the force acts (joint C).
The problem has been modified into a two-objective problem in order to show the
non-inferior Pareto set clearly in two dimensions. The stresses in AC and BC should
not exceed “100,000 kPa” and the total volume of material should not exceed 0.1
m3. The reason the objective constraints have been imposed is that the
Pareto set is asymptotic and extends from −∞ to ∞. As x1 and x2
go to zero,
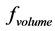 goes to zero and
goes to zero and
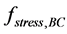 go to infinity. As x1 and x2 go to infinity,
go to infinity. As x1 and x2 go to infinity,
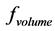 goes to infinity and
goes to infinity and
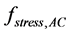 and
and
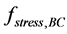 go to zero. Hence, in order to generate Pareto optimal solutions in a reasonable
range, objective constraints are imposed. The problem formulation is shown below.
go to zero. Hence, in order to generate Pareto optimal solutions in a reasonable
range, objective constraints are imposed. The problem formulation is shown below.
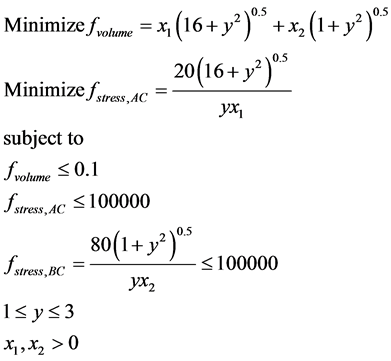
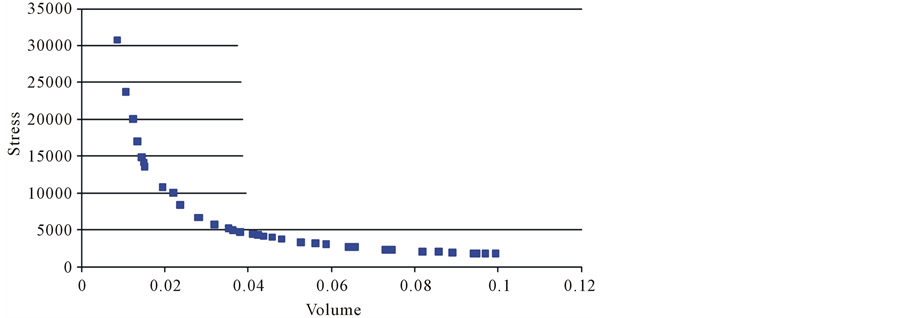
Figure 12 declares the Pareto optimal solution of the Two-Bar Truss. Obviously from the results, the proposed algorithm is able to maintain an almost uniform set of non-dominated solution points along the true Pareto-optimal front. Figure 13 shows Pareto optimal front of Two-Bar Truss (MOGA Solution) [37] [38] . It is clear that the proposed algorithm outperformed the algorithm in [37] [38] .
5. Conclusions
Finding a good distribution of solutions near the Pareto optimal front in small computational time is a dream of multiobjective EAs researchers and practitioner. In this paper a new optimization algorithm was presented, and
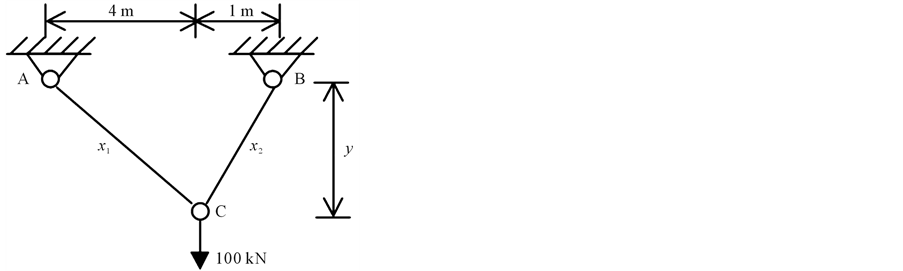
Figure 11. Two-bar truss problem.
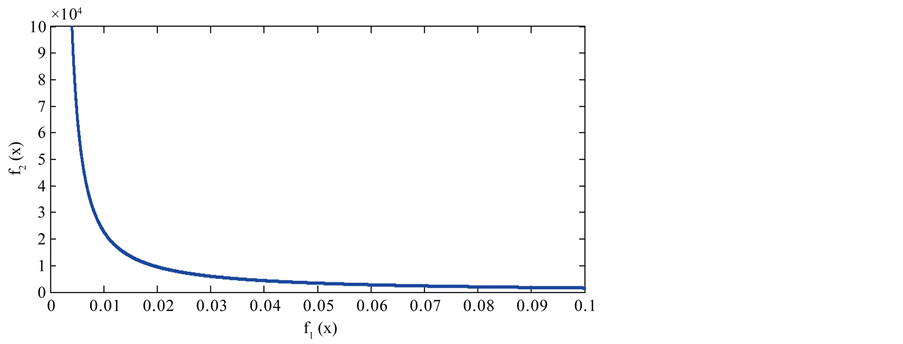
Figure 12. Pareto optimal front of two-truss using our approach.
the proposed algorithm operates in two Phases. In the first one, multiobjective version of genetic algorithm is used as search engine in order to generate approximate true Pareto front. This algorithm is based on concept of co-evolution and repair algorithm. Also it maintains a finite-sized archive of nondominated solutions which gets iteratively updated in the presence of new solutions based on the concept of ε-dominance. Then in the second phase, rough set theory is adopted as local search engine in order to improve the spread of the solutions found so far. Our proposed approach keeps track of all the feasible solutions found during the optimization. The results, provided by the proposed algorithm for benchmark problems and engineering applications, are promising when compared with exiting well-known algorithms. Also, our results suggest that our algorithm is better applicable for solving real-world application problems.
For future work, we would like to apply our proposed algorithm for more complex real world application.
References
- Miettinen, K. (2002) Non-Linear Multiobjective Optimization. Kluwer Academic Publisher, Dordrecht.
- Mousa, A.A. (2013) A New Stopping and Evaluation Criteria for Linear Multiobjective Heuristic Algorithms. Journal of Global Research in Mathematical Archives, 1, 1-11.
- Cai, Q.S., Zhang, D.F., Wu, B. and Leung, S.C.H. (2013) A Novel Stock Fore-Casting Model Based on Fuzzy Time Series and Genetic Algorithm. Procedia Computer Science, 18, 1155-1162. http://dx.doi.org/10.1016/j.procs.2013.05.281
- Ni, H. and Wang, Y.Q. (2013) Stock Index Tracking by Pareto Efficient Genetic Algorithm. Applied Soft Computing, 13, 4519-4535. http://dx.doi.org/10.1016/j.asoc.2013.08.012
- Straßburg, J., Gonzàlez-Martel, C. and Alexandrov, V. (2012) Parallel Genetic Algorithms for Stock Market Trading Rules. Procedia Computer Science, 9, 1306-1313.
- Xue, X.-W., Yao, M., Wu, Z.H. and Yang, J.H. (2013) Genetic Ensemble of Extreme Learning Machine. Neurocomputing, Accepted Manuscript. (In Press)
- Yang, J.D., Xu, H. and Jia, P.F. (2013) Effective Search for Genetic-Based Machine Learning Systems via Estimation of Distribution Algorithms and Embedded Feature Reduction Techniques. Neurocomputing, 113, 105-121. http://dx.doi.org/10.1016/j.neucom.2013.01.014
- Yang, H.M., Yi, J., Zhao, J.H. and Dong, Z.Y. (2013) Extreme Learning Machine Based Genetic Algorithm and Its Application in Power System Economic Dispatch. Neurocomputing, 102, 154-162. http://dx.doi.org/10.1016/j.neucom.2011.12.054
- Osman, M.S., Abo-Sinna, M.A. and Mousa, A.A. (2005) A Solution to the Optimal Power Flow Using Genetic Algorithm. Journal of Applied Mathematics & Computation (AMC), 155, 391-405.
- Osman, M.S., Abo-Sinna, M.A. and Mousa, A.A. (2009) Epsilon-Dominance Based Multiobjective Genetic Algorithm for Economic Emission Load Dispatch Optimization Problem. Electric Power Systems Research, 79, 1561-1567. http://dx.doi.org/10.1016/j.epsr.2009.06.003
- AL-Matrafi, B.N. and Mousa, A.A. (2013) Optimization Methodology Based on Quantum Computing Applied to Fuzzy Practical Unit Commitment Problem. International Journal of Scientific & Engineering Research, 4, 1138.
- Galal, A.A., Mousa, A.A. and Al-Matrafi, B.N. (2013) Hybrid Ant Optimization System for Multiobjective Optimal Power Flow Problem Under Fuzziness. Journal of Natural Sciences and Mathematics, 6, 179-199.
- Deb, K. (2001) Multiobjective Optimization Using Evolutionary Algorithms. Wiley, Chichester.
- Schaffer, J.D. (1985) Multiple Objective Optimization with Vector Evaluated Genetic Algorithms. In: Grefenstette, J.J., et al., Eds., Genetic Algorithms and Their Applications, Proceedings of the 1st International Conference on Genetic Algorithms, Lawrence Erlbaum, Mahwah, 93-100.
- Horn, J., Nafpliotis, N. and Goldberg, D.E. (1994) A Niched Pareto Genetic Algorithm for Multiobjective Optimization. In: Grefenstette, J.J., et al., Eds., IEEE World Congress on Computational Intelligence, Proceedings of the 1st IEEE Conference on Evolutionary Computation, IEEE Press, Piscataway, 82-87. http://dx.doi.org/10.1109/ICEC.1994.350037
- Srinivas, N. and Deb, K. (1999) Multiobjective Optimization Using Nondominated Sorting in Genetic Algorithms. Evolutionary Computation, 2, 221-248. http://dx.doi.org/10.1162/evco.1994.2.3.221
- Deb, K., Agrawal, S., Pratab, A. and Meyarivan, T. (2000) A Fast Elitist Non-Dominated Sorting Genetic Algorithms for Multiobjective Optimization: NSGA II, KanGAL Report 200001. Indian Institute of Technology, Kanpur.
- Zitzler, E. and Thiele, L. (1998) Multiobjective Optimization Using Evolutionary Algorithms—A Comparative Case Study. In: Eiben, A.E., Back, T., Schoenauer, M. and Schwefel, H.P., Eds., 5th International Conference on Parallel Problem Solving from Nature (PPSN-V), Springer, Berlin, 292-301. http://dx.doi.org/10.1007/BFb0056872
- Zitzler, E., Laumanns, M. and Thiele, L. (2001) SPEA2: Improving the Strength Pareto Evolutionary Algorithm for Multiobjective Optimization. Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems, EUROGEN 2001, Athens, 19-21 September 2001, 1-21.
- Knowles, J.D. and Corne, D.W. (1999) The Pareto Archived Evolution Strategy: A New Baseline Algorithm for Multiobjective Optimization. In: Proceedings of the 1999 Congress on Evolutionary Computation, IEEE Press, Piscataway, 98-105.
- Knowles, J.D. and Corne, D.W. (2000) M-PAES: A Memetic Algorithm for Multiobjective Optimization. In: Proceedings of the 2000 Congress on Evolutionary Computation, IEEE Press, Piscataway, 325-332.
- Jimenez, F. and Verdegay, J.L. (1998) Constrained Multiobjective Optimization by Evolutionary Algorithm. Proceeding of the International ICSC Symposition on Engineering of Intelligent Systems (EIS’98), 266-271.
- Michalewiz, Z. (1996) Genetic Algorithms + Data Structures = Evolution Programs. 3rd Edition, Springer-Verlag, Berlin.
- Michalewicz, Z. and Schoenauer, M. (1996) Evolutionary Algorithms for Constrained Parameter Optimization Problems. Evolutionary Computation, 4, 1-32.
- EL-Sawy, A.A., Hussein, M.A., Zaki, E.S.M. and Mousa, A.A. (2014) An Introduction to Genetic Algorithms: A Survey A Practical Issues. International Journal of Scientific & Engineering Research, 5, 252-262.
- Fonseca, C.M. and Fleming, P.J. (1998) Multiobjective Optimization and Multiple Constraint Handling with Evolutionary Algorithms: Part I: A Unified Formulation. IEEE Transactions on Systems and Cybernetics. Part A: Systems and Humans, 28, 26-37. http://dx.doi.org/10.1109/3468.650319
- Harada, K., Sakuma, J., Isao, O. and Kobayashi, S. (2007) Constraint-Handling Method for Multi-Objective Function Optimization: Pareto Descent Repair Operator. Proceedings of the 4th International Conference on Evolutionary Multicriterion Optimization, Matsushima, 5-8 March 2007, 156-170.
- Osman, M.S., Abo-Sinna, M.A. and Mousa, A.A. (2006) IT-CEMOP: An Iterative Co-Evolutionary Algorithm for Multiobjective Optimization Problem with Nonlinear Constraints. Journal of Applied Mathematics & Computation, 183, 373-389. http://dx.doi.org/10.1016/j.amc.2006.05.095
- Hernández-Díaz, A.G., Santana-Quintero, L.V., Coello Coello, C.A., Caballero, R. and Molina, J. (2008) Improving Multi-Objective Evolutionary Algorithms by Using Rough Sets. In: Ligeza, A., Reich, S., Schaefer, R. and Cotta, C., Eds., Knowledge-Driven Computing: Knowledge Engineering and Intelligent Computations, Studies in Computational Intelligence, Vol. 102, Springer-Verlag, Berlin, 81-98.
- Laumanns, M., Thiele, L., Deb, K. and Zitzler, E. (2002) Archiving with Guaranteed Convergence and Diversity in Multi-Objective Optimization. GECCO 2002: Proceedings of the Genetic and Evolutionary Computation Conference, Morgan Kaufmann Publishers, New York, 439-447.
- Osman, M.S., Abo-Sinna, M.A. and Mousa, A.A. (2005) An Effective Genetic Algorithm Approach to Multiobjective Resource Allocation Problems (MORAPs). Journal of Applied Mathematics & Computation, 163, 755-768. http://dx.doi.org/10.1016/j.amc.2003.10.057
- Murata, T., Ishibuchi, H. and Tanaka, H. (1996) Multiobjective Genetic Algorithm and Its Application to Flowshop Scheduling. Computers and Industrial Engineering, 30, 957-968. http://dx.doi.org/10.1016/0360-8352(96)00045-9
- Binh, T.T. and Korn, U. (1997) MOBES: A Multi-Objective Evolution Strategy for Constrained Optimization Problems. Proceeding of the 3rd International Conference on Genetic Algorithm MENDEL, Brno, 176-182.
- Osyczka, A. and Kundu, S. (1995) A New Method to Solve Generalized Multicriteria Optimization Problems Using the Simple Genetic Algorithm. Structural Optimization, 10, 94-99.
- Tanaka, M., Watanabe, H., Furukawa, Y. and Tanino, T. (1995) GA-Based Decision Support System for Multi-Criteria Optimization. Proceeding of the International Conference on Systems, Man and Cybernetics, 2, 1556-1561.
- Deb, K., Pratap, A. and Moitra, S. (2000) Mechanical Component Design for Multiple Objectives Using Elitist Non-Dominated Sorting GA. Kangal Report No. 200002.
- Sarker, R., Abbass, H.A. and Karim, S. (2001) An Evolutionary Algorithm for Constrained Multiobjective Optimization Problems. 5th Australasia-Japan Joint Workshop, University of Otago, Dunedin, 19-21 November 2001, 1-10.
- Kirsch, U. (1981) Optimal Structural Design. McGraw-Hill Co., New York.
NOTES

*Corresponding author.