Simulation for chaos game representation of
genomes by recurrent iterated function systems
Simulation for chaos game representation of
genomes by recurrent iterated function systems
1,2,*11 2
Zu-Guo Yu , Long Shi , Qian-Jun Xiao & Vo Anh
12
School of Mathematics and Computational Science, Xiangtan University, Hunan 411105, China. School of Mathematical Sciences, Queensland
University of Technology, GPO Box 2434, Brisbane, Q 4001, Australia.* Correspondence should be addressed to Zu-Guo Yu
bases, the CGR would be a uniformly filled square,
ABSTRACT conversely, any patterns visible in the CGR represent
some pattern (information) in the DNA sequence
Chaos game representation (CGR) of DNA (Goldman 1993). Goldman (1993) interpreted the
sequences and linked protein sequences CGRs in a biologically meaningful way. All points
from genomes was proposed by Jeffrey (1990) plotted within a quadrant must corresponding to sub-
and Yu et al. (2004), respectively. In this sequences of the DNA sequence that end with the
paper, we consider the CGR of three kinds of base labelling the corner of that quadrant. He also pro-
sequences from complete genomes: whole posed a discrete time Markov Chain model to simu-
genome DNA sequences, linked coding DNA late the CGR of DNA sequences and use the
sequences and linked protein sequences. sequence's dinucleotide and trinucleotide frequen-
Some fractal patterns are found in these cies to calculate the probabilities in these models.
CGRs. A recurrent iterated function systems Goldman's Markov model can be calculated directly
(RIFS) model is proposed to simulate the and easily from the raw DNA sequences, without ref-
CGRs of these sequences from genomes and erence to the CGR.
their induced measures. Numerical results Deschavanne et al. (1999) used CGR of genomes
on 50 genomes show that the RIFS model can to discuss the classification of species. Almeida et al.
simulate very well the CGRs and their (2001) showed the distribution of positions in the
induced measures. The parameters esti-CGR plane is a generalization of Markov Chain prob-
mated in the RIFS model reflect information ability tables that accommodates non-integer orders.
on species classification.Joseph and Sasikumar (2006) proposed a fast algo-
rithm for identifying all local alignments between
two genome sequences using the sequence informa-
tion contained in their CGR.
Twenty different kinds of amino acids are found in
1. INTRODUCTIONproteins. The idea of CGR of DNA sequences pro-
The hereditary information of organisms (except for posed by Jeffrey (1990) was generalized and applied
RNA-viruses) is encoded in their DNA sequences for visualizing and analyzing protein databases by
which are one-dimensional unbranched polymers Fiser et al. (1994). Generalization of CGR of DNA
made up from four different kinds of monomers (nu-may take place in several ways. In the simplest case,
cleotides): adenine (a), cytosine (c), guanine (g), and the square in CGR of DNA is replaced by an n-sided
thymine (t). Based on a technique from chaotic regular polygon (n-gon), where n is the number of dif-
dynamics, Jeffrey (1990) proposed a chaos game rep-ferent elements in the sequence to be represented. As
resentation (CGR) of DNA sequences by using the proteins consist of 20 kinds of amino acids, a 20-
four vertices of a square in the plane to represent sided regular polygon (regular 20-gon) is the most
a,c,g and t. The method produces a plot of a DNA adequate for protein sequence representation. A few
sequence which displays both local and global pat-thousand points result in an 'attractor' which gives a
terns. Self-similarity or fractal structures were found visualization of the rare or frequent residues and
in these plots. Some open questions from the biologi-sequence motifs. Fiser et al. (1994) pointed out that
cal point of view based on the CGR were proposed the chaos game representation can also be used to
(Jeffrey 1990). study 3D structures of proteins.
If the DNA sequences were a random collection of
Keywords: Genomes; Chaos game representa-
tion; Recurrent iterated function systems
J. Biomedical Science and Engineering, 2008, 1, 44-51Scientific
Research
Publishing
JBiSE
Published Online May 2008 in SciRes. http://www.srpublishing.org/journal/jbise
SciRes Copyright © 2008

Basu et al. (1998) proposed a new method for the sequences and linked sequences of all protein
chaos game representation of different families of sequences from complete genomes.
proteins. Using concatenated amino acid sequences For DNA sequences, the CGR is obtained by using
of proteins belonging to a particular family and a 12-the four vertices of a square in the plane to represent
sided regular polygon, each vertex of which repre-a,c,g and t (Jeffrey 1990). The first point of the plot is
sents a group of amino acid residues leading to con-placed half way between the center of the square and
servative substitutions, the method generates the the vertex corresponding to the first letter, the ith
CGR of the family and allows pictorial representa-point of the plot is placed half way between the (i-
tion of the pattern characterizing the family. Basu et 1)th point and the vertex corresponding to the ith let-
al. (1998) found that the CGRs of different protein ter in the DNA sequence.
families exhibit distinct visually identifiable patterns. For linked protein sequences, we outline here the
This implies that different functional classes of pro-way to get the CGR from Yu et al. (2004b). The pro-
teins produce specific statistical biases in the distri-tein sequence is formed by twenty different kinds of
bution of different mono-, di-, tri-, or higher order amino acids, namely Alanine (A), Arginine (R),
peptides along their primary sequences.Asparagine (N), Aspartic acid (D), Cysteine (C),
A well-known model of protein sequence analysis Glutamic acid (E), Glutamine (Q), Glycine (G),
is the HP model proposed by Dill et al. (1985). In this Histidine (H), Isoleucine (I), Leucine (L), Lysine (K),
model 20 kinds of amino acids are divided into two Methionine (M), Phenylalanine (F), Proline (P),
types, hydrophobic (H) (or non-polar) and polar (P) Serine (S), Threonine (T), Tryptophan (W), Tyrosine
(or hydrophilic). But the HP model may be too simple (Y) and Valine (V) (Brown 1998, page 109). In the
and lacks sufficient information on the heterogeneity detailed HP model, they can be divided into four
and the complexity of the natural set of residues classes: non-polar, negative polar, uncharged polar
(Wang and Wang 2000). According to Brown (1998), and positive polar. The eight residues A, I, L, M, F, P,
one can divide the polar class in the HP model into W, V designate the non-polar class; the two residues
three classes: positive polar, uncharged polar and neg-D, E designate the negative polar class; the seven resi-
ative polar. So 20 different kinds of amino acids can dues N, C, Q, G, S, T, Y designate the uncharged polar
be divided into four classes: non-polar, negative class; and the remaining three residues R, H, K desig-
polar, uncharged polar and positive polar. In this nate the positive polar class.
model, one considers more details than in the HP For a given protein sequence s=ss with length l,
1l
model. We call this model a detailed HP model (Yu et where s is one of the twenty kinds of amino acids for
i
al.2004a). Based on the detailed HP model, we pro-i=1,,l ,we define
posed a CGR for the linked protein sequences from
the genomes (Yu et al. 2004b).
The recurrent iterated function system in fractal
theory (Barnsley and Demko, 1985; Falconer, 1997)
has been applied successfully to fractal image con-
struction (Barnsley and Demko, 1985; Vrscay, 1991),
one dimensional measure representation of genomes
(Anh et al. 2002; Yu et al. 2001, 2003) and magnetic
We then obtain a sequence X(s)=aa , where a is
field data (Wanliss et al. 2005; Anh et al. 2005) for 1l i
example. Yu et al. (2007) proposed a CGR for the a letter of the alphabet {0,1,2,3}. We next define the
magnetic field data and used the RIFS model to simu-CRG for a sequence X(s) in a square [0,1][ 0,1],
late the CGR.where the four vertices correspond to the four letters
Although we proposed the CGR for linked protein 0,1,2,3. The first point of the plot is placed half way
sequences from genomes (Yu et al. 2004b), we did between the center of the square and the vertex corre-
not consider how to simulate the CGRs. In this paper, sponding to the first letter of the sequence X(s); the
we extend the CGR to the study of whole-genome ith point of the plot is then placed half way between
DNA sequences and linked coding DNA sequences the (i-1)th point and the vertex corresponding to the
from genomes. Then we use the RIFS model to simu-ith letter. We then call the obtained plot the CGR of
late the CGR of these 3 kinds of data from genomes the protein sequence s based on the detailed HP
and their induced measures. The probability matrix in model.
our RIFS model is similar to the one in Markov model Usually whole-genome DNA sequences and linked
used by Goldman (1993), but the way to estimate this coding DNA sequences are relatively long, hence the
matrix is different. resulting CGRs are too dense to visualize any pattern
directly. The linked protein sequences are 3 times
shorter than the linked coding DNA sequences, and
2. CHAOS GAME REPRESENTATION OF
their CGRs produce clearer self-similar patterns. For
GENOMES example, we show the CGR of the linked protein
Three kinds of sequences from complete genomes are sequence of the bacterium Mycobacterium tuberculo-
considered, namely, whole-genome DNA sequences sis CDC1551 (MtubC) in .
(including protein-coding and non-coding regions), Considering the points in a CGR of an organism,
linked sequences of all protein-coding DNA
Figure 1
(1)
SciRes JBiSE Copyright © 2008
Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51 45

we define a measureby(B)=#(B)/N , where #(B) is The coefficients in the contractive maps and the
l
the number of points lying in a subset B of the CGR and probabilities in the RIFS are the parameters to be esti-
N is the length of the sequence. We divide the square mated for the measure that we want to simulate. We
lnow describe the method of moments to perform this
[0,1][0,1] into meshes of sizes 6464, 128128, task. In the two-dimensional case of our CGRs, we
512512 or 10241024. This results in a measure for consider a system of N contractive maps
each mesh. We then obtain a 6464, 128128,
512512 or 10241024 matrixA=() , where
kl JJ
J=64,128,512 or 1024, each elementis the measure
kl
value on the corresponding mesh. We call A the mea-
sure matrix of the organism. The measure based on Ifis the invariant measure and A the attractor of
2
a 128128 mesh on the CGRs are considered in this the RIFS in R, the moments ofare
paper. For example, the measurebased on a
128128 mesh of the CGR in is shown in
.
Using the properties of the Markov operator
3. RECURRENT ITERATED FUNCTION defined by (S, P) (Vrscay, 1991), we get
SYSTEM FOR A MEASURE
Consider a system of contractive maps S={S,S,
12
S} and the associated matrix of probabilities P=(p)
Nij
such that p=1,i=1,2, ,N. We consider a random
jij
sequence generated by a dynamical system
where x is any starting point andis chosen
0n
among the set {1,2,,N}with a probability that
depends on the previous index : P(=i)=p .
n-1ni-1,i
Then (S, P) is called a recurrent iterated function sys-When n=0, m=0, from we have
tem. Then there exist compact setsA,A,i=1,2, N
i
such that
for i=1,2, ,N.
where set A is called the attractor of the RIFS (S, P). j
Then we can get the values for g,j12,,Nby ,
00
A major result for RIFS is that there exists a unique solving the above linear equations.
invariant measureof the random walk (Eq. 2)
When m=0, n1 whose support is A (Barnsley et al., 1989).
Figure 1
Figure 2
Figure 1. Chaos game representation of the linked protein
sequence from genome of Mycobacterium tuberculosis
CDC1551(MtubC) (with 1325681 amino acids).
Figure 2. The measurebased on a 128128 mesh of the
CGR in Figure 1.
(2)
(3)
(4)
SciRes JBiSE Copyright © 2008
46Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51

If we denote by G the moments obtained directly
mn
from a given measure, and g the formal expression
mn
of moments obtained from the above formulae, then
solving the optimization problem
hence the moments are given by the solution of the
linear equations
will provide the estimates of the parameters of the
RIFS.
Once the RIFS (S(x),p,i,j=1,2, ,N ) has been esti-
iij
mated, its invariant measure can be simulated in the
following way: Generate the attractor of the RIFS via
the random walk (Eq. 2). Letbe the indicator func-
B
When n=0,m1 tion of a subset B of the attractor A. From the ergodic
theorem for RIFS (Barnsley et al., 1989), the invari-
ant measure is then given by
hence the moments are given by the solution of the
linear equations
By definition, an RIFS describes the scale
invariance of a measure. Hence a comparison of the
given measure with the invariant measure simulated
from the RIFS will confirm whether the given mea-
sure has this scaling behaviour. This comparison can
be undertaken by computing the cumulative walk of a
measure visualized as intensity values on a JJ
mesh; here J=128 in this paper.
When m,n1If we convert the two-dimensional matrix
A=()to an one dimensional vector by concate-
kl JJ
nate every row in A at the end of previous row. We
denote the one-dimensional vector as f=(f,f,,f).
12 JJ
The cumulative walk is defined as
Where f is the average value of all element in vec-
tor f.
Returning to the CGR, an RIFS with 4 contractive
hence the moments are given by the solution of the
maps {S,S,S,S} is fitted to the measure obtained
linear equations1234
from the CGR using the method of moments. Here we
can fix
Hence the parameters needed to be estimated are the
probabilities in the matrix P. Once we have estimated
the probability matrix in the RIFS, we can start from
the point (0.5, 0.5) and use the chaos game algorithm
Eq. (2) to generate a random point sequence{x} with
i
the same length N of the whole- genome DNA
l
for i=1,2, ,N.sequence, linked coding DNA sequence or the linked
(6)
(7)
SciRes JBiSE Copyright © 2008
47
Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51
(5)

protein sequence. Then the plot of the random point
sequences is the RIFS simulation of the original CGR
of the data. For example the RIFS simulated CGR of
the CGR in is shown in . Compar-
ing the RIFS simulation in with the original and
CGR in , it is apparent that they are quite sim-
ilar. We then obtain the 128128 mesh measure
based on the simulated CGR. The measure can be
regarded as a simulation of the measure induced
MM from the original CGR. For example, we show the Here M=128128, (F)and (F)are the walks
jj=1 jj=1
128128 mesh measure based on the simulated of the original measure and the RIFS simulated mea-
CGR of in . The cumulative walks M
sure respectively, Fis the mean value of(F).
of these two measures can then be obtained to show avej j=1
the performance of the simulation.The goodness e1.0 indicates the simulation is
We determine the goodness of fit of the measure very well (Anh et al. 2002). For example, the cumula-
simulated from the RIFS model relative to the origi-tive walks for the measure induced by the CGR in
nal measure based on the following relative standard and its RIFS simulation in are given in
error (RSE) (Anh et al. 2002):. It is seen that the two walks are almost iden-
tical. This indicates that RIFS fits very well the mea-
sure induced by the original CGR. The RSE e=0.0300
is very small, which also indicates excellent fitting.
Where 4. DATA, DISCUSSION AND CONCLUSION
We downloaded whole-genome DNA sequences,
coding DNA sequences and protein sequences from
50 complete genomes of Archaea and Eubacteria
from the public database Genbank at the web site
http://www.ncbi.nlm.nih.gov/Genbank/. We list the
name of the 50 bacteria in Appendix.
We then produce the CGRs of the data from the 50
genomes as described in . For more exam-
ples, we plot the chaos game representation of the
linked coding sequence from genome of Mycoplasma
pulmonis UAB CTIP (Mpul) in .Fractal
(self-similarity) patterns can be seen in these CGRs.
We only use the moments of 128128 mesh
measurebased on the CGRs to estimate the param-
eters (probability matrix) in the RIFS model. Then
the RIFS simulation of the original CGRs is per-
formed using the chaos game algorithm. We then get
Figure 1Figure 3
Figure 3
Figure 1
Figure 3Figure 4
Fig-
ure 1 Figure 4
Figure 5
Section 2
Figure 6
Figure 3. The RIFS simulated CGR for the CGR in Figure 1.Figure 4. The measure based on a 128128 mesh of the
RIFS simulated CGR in Figure 3.
Figure 5. The walk representation of measures induced by
the CGR in Figure 1 and its RIFS simulation in Figure 4.
SciRes JBiSE Copyright © 2008
48Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51
Pixel position
Walk representation

the 128128 mesh measurebased on the simulated
CGR. To show the performance of the simulation, we
compare the cumulative walks of the original mea-
sure and its simulation. For example, the RIFS sim-
ulated CGR of the linked coding sequence from
genome of Mycoplasma pulmonis UAB CTIP (Mpul)
based on the 128128 mesh measurefrom
is shown in , while the walk representation
of measures induced by the CGR in and its
RIFS simulation in are shown in .
Goldman (1993) interpreted the patterns in CGRs
of DNA sequences by the dinucleotide and
trinucleotide frequencies in the original sequence.
The probability matrix in our RIFS model character-
izes the dinucleotide or di-amino acid frequencies (in-
formation) which is similar to the one in Markov
model used by Goldman (1993), but the way to esti-
mate this matrix is different.
The values of the RSE of the simulation for 50
Figure
6Figure 7
Figure 6
Figure 7Figure 8
Figure 6. Chaos game representation of the linked coding
sequence from genome of Mycoplasma pulmonis UAB CTIP
(Mpul) (with 873,651 bps).
Figure 7. The RIFS simulated CGR for the CGR in Figure 6.
Figure 8. The walk representation of measures induced by
the CGR in Figure 6 and its RIFS simulation in Figure 7.
Table 1. The goodness of fit for the walk representations of
three kinds of data from 50 genomes.
Species
(abbrev.)
Aful
Paby
Pyro
Mjan
haloNRC
Taci
Tvol
Mthe
Aero
Ssol
MtubH
MtubC
p
Mle &
Mpneu
Mgen
Mpul
Uure
Bsub
Bhal
Llac
Spyo
Spne
SaurN
SaurM
CaceA
Aqua
Tmar
Ctra
Cpneu
CpneuA
p
CneuJ
Syne
Nost
Bbur
p
Tal
Atum
smel
Ccre
p
Rro
Nmen
NmenA
EcoliKM
EcoliOH
Hinf
Xfas
Paer
Pmul
Buch
Hpyl
Cjej
e f or
wholeDN A
0.5797
0.3502
0.4324
0.2136
0.3728
0.2707
0.3126
0.5188
0.6213
0.3798
1.3037
1.3010
0.4271
0.0484
0.0731
0.0639
0.0783
0.4051
0.1198
0.1032
0.1049
0.1125
0.1264
0.1229
0.1887
0.4825
0.4470
0.8986
0.7786
0.7593
0.7899
0.0521
0.1411
0.1466
0.3068
0.2614
0.1739
0.1171
0.3887
0.1973
0.2039
0.3225
0.3222
0.0677
0.1246
0.2149
0.1032
0.1954
0.2567
0.1540
e f o r
codingDN A
0.2669
0.3214
0.3411
0.2675
0.3569
0.2735
0.2716
0.5676
0.2222
0.3612
0.5862
0.5711
0.3332
0.0589
0.2305
0.1261
0.2064
0.8012
0.2652
0.1879
0.1759
0.1358
0.2728
0.2680
0.1693
0.3457
0.6674
0.4769
0.7170
0.7093
0.7352
0.0396
0.1439
0.1255
0.1212
0.2655
0.1957
0.1558
0.7126
0.1933
0.1993
0.3472
0.3810
0.2388
0.1460
0.1823
0.2087
0.2598
0.2615
0.1797
e for
linked
proteins
0.0366
0.0333
0.0361
0.0647
0.0297
0.1030
0.1308
0.0299
0.0452
0.1098
0.0333
0.0300
0.0404
0.1686
0.2617
0.2267
0.4058
0.0684
0.0489
0.0500
0.0678
0.0932
0.1020
0.1054
0.1859
0.0661
0.0597
0.1066
0.1312
0.1044
0.1290
0.0667
0.0931
0.2008
0.0908
0.0403
0.0380
0.0259
0.2132
0.0430
0.0559
0.0714
0.0868
0.0883
0.0324
0.0470
0.0911
0.3911
0.1161
0.0802
SciRes JBiSECopyright © 2008
49
Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51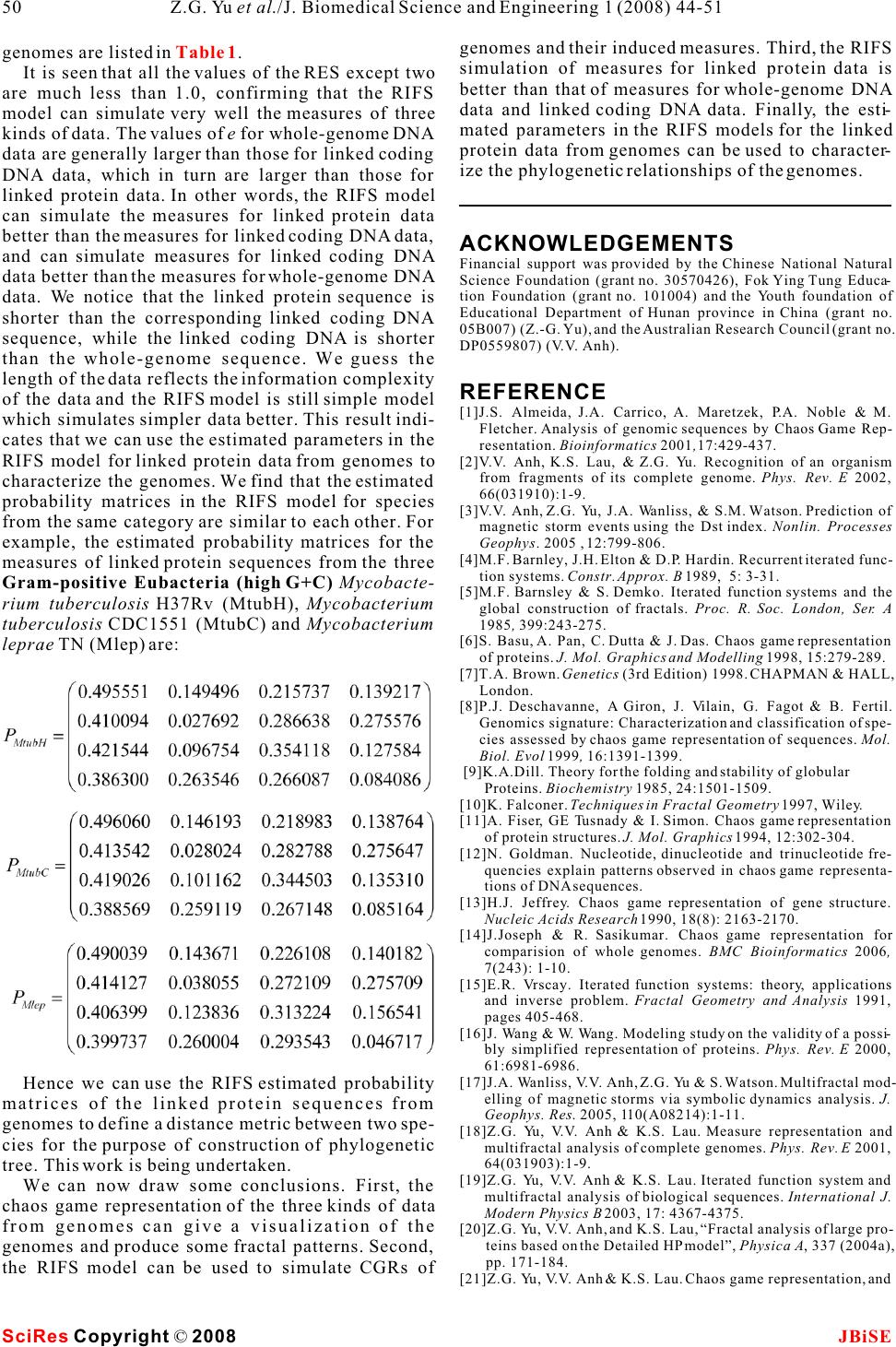

genomes and their induced measures. Third, the RIFS
genomes are listed in .simulation of measures for linked protein data is
It is seen that all the values of the RES except two better than that of measures for whole-genome DNA
are much less than 1.0, confirming that the RIFS data and linked coding DNA data. Finally, the esti-
model can simulate very well the measures of three mated parameters in the RIFS models for the linked
kinds of data. The values of e for whole-genome DNA protein data from genomes can be used to character-
data are generally larger than those for linked coding ize the phylogenetic relationships of the genomes.
DNA data, which in turn are larger than those for
linked protein data. In other words, the RIFS model
can simulate the measures for linked protein data
better than the measures for linked coding DNA data, ACKNOWLEDGEMENTS
and can simulate measures for linked coding DNA Financial support was provided by the Chinese National Natural
data better than the measures for whole-genome DNA Science Foundation (grant no. 30570426), Fok Ying Tung Educa-
tion Foundation (grant no. 101004) and the Youth foundation of
data. We notice that the linked protein sequence is
Educational Department of Hunan province in China (grant no.
shorter than the corresponding linked coding DNA 05B007) (Z.-G. Yu), and the Australian Research Council (grant no.
sequence, while the linked coding DNA is shorter DP0559807) (V.V. Anh).
than the whole-genome sequence. We guess the
length of the data reflects the information complexity REFERENCE
of the data and the RIFS model is still simple model [1]J.S. Almeida, J.A. Carrico, A. Maretzek, P.A. Noble & M.
which simulates simpler data better. This result indi-Fletcher. Analysis of genomic sequences by Chaos Game Rep-
cates that we can use the estimated parameters in the resentation. Bioinformatics 2001,17:429-437.
RIFS model for linked protein data from genomes to [2]V.V. Anh, K.S. Lau, & Z.G. Yu. Recognition of an organism
from fragments of its complete genome. Phys. Rev. E 2002,
characterize the genomes. We find that the estimated 66(031910):1-9.
probability matrices in the RIFS model for species [3]V.V. Anh, Z.G. Yu, J.A. Wanliss, & S.M. Watson. Prediction of
from the same category are similar to each other. For magnetic storm events using the Dst index. Nonlin. Processes
example, the estimated probability matrices for the Geophys. 2005 , 12:799-806.
[4]M.F. Barnley, J.H. Elton & D.P. Hardin. Recurrent iterated func-
measures of linked protein sequences from the three tion systems. Constr. Approx. B 1989, 5: 3-31.
Gram-positive Eubacteria (high G+C) Mycobacte- [5]M.F. Barnsley & S. Demko. Iterated function systems and the
rium tuberculosis H37Rv (MtubH), Mycobacterium global construction of fractals. Proc. R. Soc. London, Ser. A
tuberculosis CDC1551 (MtubC) and Mycobacterium 1985, 399:243-275.
[6]S. Basu, A. Pan, C. Dutta & J. Das. Chaos game representation
leprae TN (Mlep) are:of proteins. J. Mol. Graphics and Modelling 1998, 15:279-289.
[7]T.A. Brown. Genetics (3rd Edition) 1998. CHAPMAN & HALL,
London.
[8]P.J. Deschavanne, A Giron, J. Vilain, G. Fagot & B. Fertil.
Genomics signature: Characterization and classification of spe-
cies assessed by chaos game representation of sequences. Mol.
Biol. Evol 1999, 16:1391-1399.
[9]K.A.Dill. Theory for the folding and stability of globular
Proteins. Biochemistry 1985, 24:1501-1509.
[10]K. Falconer. Techniques in Fractal Geometry 1997, Wiley.
[11]A. Fiser, GE Tusnady & I. Simon. Chaos game representation
of protein structures. J. Mol. Graphics 1994, 12:302-304.
[12]N. Goldman. Nucleotide, dinucleotide and trinucleotide fre-
quencies explain patterns observed in chaos game representa-
tions of DNA sequences.
[13]H.J. Jeffrey. Chaos game representation of gene structure.
Nucleic Acids Research 1990, 18(8): 2163-2170.
[14]J.Joseph & R. Sasikumar. Chaos game representation for
comparision of whole genomes. BMC Bioinformatics 2006,
7(243): 1-10.
[15]E.R. Vrscay. Iterated function systems: theory, applications
and inverse problem. Fractal Geometry and Analysis 1991,
pages 405-468.
[16]J. Wang & W. Wang. Modeling study on the validity of a possi-
bly simplified representation of proteins. Phys. Rev. E 2000,
61:6981-6986.
[17]J.A. Wanliss, V.V. Anh, Z.G. Yu & S. Watson. Multifractal mod-
Hence we can use the RIFS estimated probability
elling of magnetic storms via symbolic dynamics analysis. J.
matrices of the linked protein sequences from Geophys. Res. 2005, 110(A08214):1-11.
genomes to define a distance metric between two spe-[18]Z.G. Yu, V.V. Anh & K.S. Lau. Measure representation and
cies for the purpose of construction of phylogenetic multifractal analysis of complete genomes. Phys. Rev. E 2001,
64(031903):1-9.
tree. This work is being undertaken.
[19]Z.G. Yu, V.V. Anh & K.S. Lau. Iterated function system and
We can now draw some conclusions. First, the multifractal analysis of biological sequences. International J.
chaos game representation of the three kinds of data Modern Physics B 2003, 17: 4367-4375.
from genomes can give a visualization of the [20]Z.G. Yu, V.V. Anh, and K.S. Lau, “Fractal analysis of large pro-
teins based on the Detailed HP model”, Physica A, 337 (2004a),
genomes and produce some fractal patterns. Second,
pp. 171-184.
the RIFS model can be used to simulate CGRs of [21]Z.G. Yu, V.V. Anh & K.S. Lau. Chaos game representation, and
Table 1
SciRes JBiSE Copyright © 2008
50Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51

multifractal and correlation analysis of protein sequences from
complete genome based on detailed HP model. J. Theor. Biol.
2004, 226(3): 341-348.
[22]Z.G. Yu, V.V. Anh, J.A. Wanliss & S.M. Watson. Chaos game
representation of the Dst index and prediction of geomagnetic
storm events. Chaos, Solitons & Fractals 2007, 31:736-746.
NC002745), Staphylococcus aureus subsp. aureus Mu50 (SaurM,
NC002758), and Clostridium acetobutylicum ATCC 824 (CaceA,
NC003030). The others are Gram-negative Eubacteria, which consist of two
hyperthermophilic bacteria: Aquifex aeolicus VF5 (Aqua, NC000918) and
Thermotoga maritima MSB8 (Tmar, NC000853); four Chlamydia:
Chlamydia trachomatis D/UW-3/CX (Ctra, NC000117), Chlamydia
pneumoniae CWL029 (Cpneu, NC000922), Chlamydia pneumoniae AR39
(CpneuA, NC002179) and Chlamydia pneumoniae J138 (CpneuJ,
APPENDIX NC002491); two Cyanobacterium: Synechocystis sp. PCC6803 (Syne,
These 50 bacteria include eight Archae Euryarchaeota: Archaeoglobus NC000911) and Nostoc sp. PCC 7120 (Nost, NC003272); two Spirochaete:
fulgidus DSM 4304 (Aful, NC000917), Pyrococcus abyssi GE5 (Paby, Borrelia burgdorferi B31 (Bbur, NC001318) and Treponema pallidum
NC000868), Pyrococcus horikoshii OT3 (Pyro, NC000961), Nichols (Tpal, NC000919); and fifteen Proteobacteria. The fifteen
Methanococcus jannaschii DSM 2661 (Mjan, NC000909), Halobacterium Proteobacteria are divided into four subdivisions, namely alpha subdivision:
sp. NRC-1 (haloNRC, NC002607), Thermoplasma acidophilum DSM 1728 Agrobacterium tumefaciens strain C58 (Atum, NC003062), Sinorhizobium
(Taci, NC002578), Thermoplasma volcanium GSS1 (Tvol,NC002689), and meliloti 1021 (smel, NC003047), Caulobacter crescentus CB15 (Ccre,
Methanobacterium thermoautotrophicum deltaH (Mthe, NC000916); two NC002696) and Rickettsia prowazekii Madrid (Rpro, NC000963); beta sub-
Archae Crenarchaeota: Aeropyrum pernix K1 (Aero, NC000854) and division: Neisseria meningitidis MC58 (Nmen, NC003112) and Neisseria
Sulfolobus solfataricus P2 (Ssol, NC002754); three Gram-positive meningitidis Z2491 (NmenA, NC003116); gamma subdivision: Esche-
Eubacteria (high G+C): Mycobacterium tuberculosis H37Rv (MtubH, richia coli K-12 MG1655 (EcoliKM, NC000913), Escherichia coli O157:H7
NC000962), Mycobacterium tuberculosis CDC1551 (MtubC, NC002755) EDL933 (EcoliOH, NC002695), Haemophilus influenzae Rd (Hinf,
and Mycobacterium leprae TN (Mlep, NC002677); twelve Gram-positive NC000907), Xylella fastidiosa 9a5c (Xfas, NC002488), Pseudomonas
Eubacteria (low G+C): Mycoplasma pneumoniae M129 (Mpneu, aeruginosa PA01 (Paer, NC002516), Pasteurella multocida subsp.
NC000912), Mycoplasma genitalium G37 (Mgen, NC000908), Mycoplasma multocida str. Pm70 (Pmul, NC002663) and Buchnera str. APS (Buch,
pulmonis UAB CTIP (Mpul, NC002771), Ureaplasma urealyticum serovar NC002528); and epsilon subdivision: Helicobacter pylori 26695 (Hpyl,
3 str. ATCC 700970 (Uure, NC002162), Bacillus subtilis subsp. subtilis str. NC000915) and Campylobacter jejuni subsp. jejuni NCTC 11168 (Cjej,
168 (Bsub, NC000964), Bacillus halodurans C-125 (Bhal, NC002570), NC002163). The abbreviations in the brackets stand for the names of these
Lactococcus lactis subsp. lactis Il1403 (Llac, NC002662), Streptococcus species and their NCBI accession numbers.
pyogenes M1 GAS (Spyo, NC002737), Streptococcus pneumoniae TIGR4
(Spne, NC003028), Staphylococcus aureus subsp. aureus N315 (SaurN,
SciRes JBiSECopyright © 2008
51
Z.G. Yu et al./J. Biomedical Science and Engineering 1 (2008) 44-51