Applied Mathematics
Vol.5 No.4(2014), Article ID:43583,16 pages DOI:10.4236/am.2014.54068
A General Model for Hepatitis B Disease with Age-Dependent Susceptibility and Transmission Probabilities
Danga Duplex Elvis Houpa, Tagne Eric Miamdjo, Tchaptchie Yannick Kouakep*
Department of Mathematics and Computer Science, Ngaoundéré University, Ngaoundere, Cameroon
Email: e_houpa@yahoo.com, ericmiamdjo5@gmail.com, *kouakep@aims-senegal.org
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 9 December 2013; revised 9 January 2014; accepted 17 January 2014
ABSTRACT
A SEI model for hepatitis B is constructed where the susceptibility and other crucial transmission probabilities depend on the chronological age and the basic reproduction rate 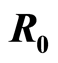 is derived. Under suitable (biological and mathematical) assumptions in a closed population, results of Houpa D. D. E. et al. [1] are extended from constant case of
is derived. Under suitable (biological and mathematical) assumptions in a closed population, results of Houpa D. D. E. et al. [1] are extended from constant case of 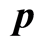 and
and 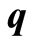 to age-dependent case: the disease-free equilibrium is globally asymptotically stable (GAS) if
to age-dependent case: the disease-free equilibrium is globally asymptotically stable (GAS) if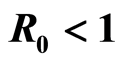 . On the other hand,
. On the other hand, 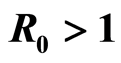 induces that endemic equilibrium is GAS and the system is uniformly persistent.
induces that endemic equilibrium is GAS and the system is uniformly persistent.
Keywords: Hepatitis B; PDE Model; Global Stability; Lyapunov-LaSalle Functionals

1. Introduction
This paper studies a system of equations modelling the dynamic of hepatitis B with age-dependent susceptibility in a closed population. Its manifestations in human body are shown by hepatitis B antigens (small spherical particles, tubular forms and a large shelled spherical particles) because of their association with a high risk of hepatitis [2] . Hepatitis B caused acute hepatitis and severe chronic liver disease. Hepatitis is endemic in Africa [3] [4] . According to Pasquini et al. [5] (with a computer model), Bonzi et al. [6] (with an EDOs model), Inaba et al. [7] (theoretically with a PDE) or D. J. Nokes et al. [8] (with statistics tools) and L. Zou et al. [9] (with PDE by fitting model to data), age factor is important in epidemiology of disease like hepatitis and reveals most of time useful informations on the dynamics of the epidemic.
A SEI model for hepatitis B is constructed where the susceptibility and other crucial transmission probabilities depend on the chronological age and the basic reproduction rate 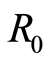 is derived. Under suitable (biological and mathematical) assumptions in a closed population, it is proved that the disease-free equilibrium is globally asymptotically stable (GAS) if
is derived. Under suitable (biological and mathematical) assumptions in a closed population, it is proved that the disease-free equilibrium is globally asymptotically stable (GAS) if 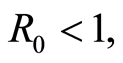 and
and 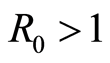 induces that endemic equilibrium is GAS and the system is uniformly persistent.
induces that endemic equilibrium is GAS and the system is uniformly persistent.
The work is organized as follows. After the presentation of the mathematical model with its main results, Section 2 studies the well posedness of the PDE and derives preliminary results useful to study the long-term behaviour of the model. Moreover, it deals with the wellposedness of the model and proves the global asymptotic stability of the disease-free equilibrium when the basic reproduction number 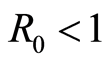 and stability of the endemic equilibrium (EE) with the carriers (E) transmission rate
and stability of the endemic equilibrium (EE) with the carriers (E) transmission rate 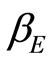 small enough to be considered as zero. These results are verified through numerical simulations extended by a discussion and conclusions in Section 3.
small enough to be considered as zero. These results are verified through numerical simulations extended by a discussion and conclusions in Section 3.
2. Mathematical Model
2.1. Presentation
In this study we will consider the following (chronological) age-dependent susceptibility model:
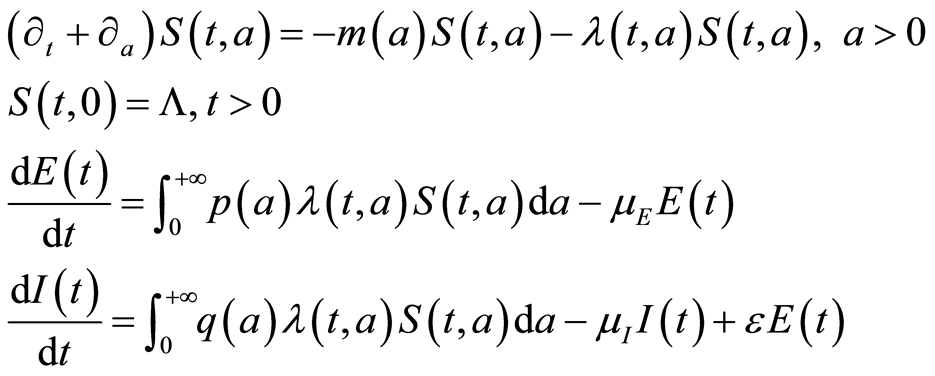 (1.1)
(1.1)
posed for 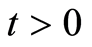 and
and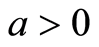 . Here
. Here  denotes the age-specific density of susceptible,
denotes the age-specific density of susceptible, 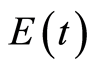 and
and  denotes respectively the age-specific densities of acute infected (that can be symptomatic or asymptomatic) and chronic carriers. In addition
denotes respectively the age-specific densities of acute infected (that can be symptomatic or asymptomatic) and chronic carriers. In addition 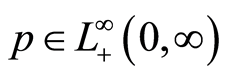 is a given function such that
is a given function such that 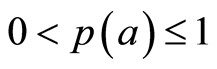
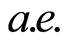 while
while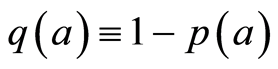 . Function
. Function 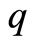 represents the age-specific probability to become a chronic carrier when becoming infected. Function
represents the age-specific probability to become a chronic carrier when becoming infected. Function 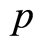 denotes the probability to develop an acute infection when getting the infection at age
denotes the probability to develop an acute infection when getting the infection at age 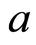 ([8] studied the age-dependence susceptibility to the infection). We conditionally extend in some sens results of Houpa D. D. E. et al. [1] who analyzed the case where
([8] studied the age-dependence susceptibility to the infection). We conditionally extend in some sens results of Houpa D. D. E. et al. [1] who analyzed the case where 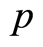 and
and  are constant. Parameter
are constant. Parameter  denotes the natural death rate at age
denotes the natural death rate at age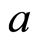 ,
,  and
and 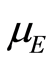 denotes the exit rates associated to each infected class. Clearly at each age
denotes the exit rates associated to each infected class. Clearly at each age ,
,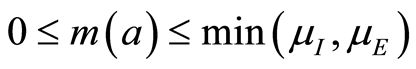 .
. 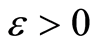 is the transition rate from
is the transition rate from  to
to . Obviously,
. Obviously,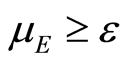 . In some studies (like Kouakep et al. [10] ) authors set
. In some studies (like Kouakep et al. [10] ) authors set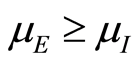 . The term
. The term 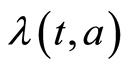 corresponds to the age-specific force of infection and follows the usual law of mass-action, that reads as
corresponds to the age-specific force of infection and follows the usual law of mass-action, that reads as
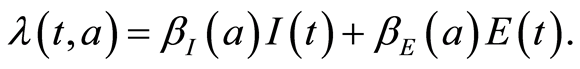
This problem (1.1) is supplemented together with the boundary conditions:
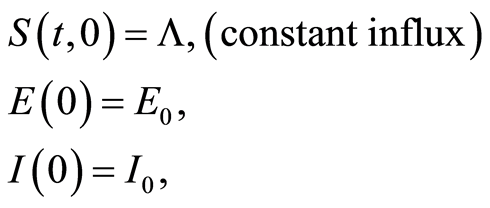 (1.2)
(1.2)
and initial data
 (1.3)
(1.3)
This model (1.1) is suggested by Melnik et al. [11] for the age-dependent susceptibility concept supplemented with Kouakep et al. [10] introducing  and
and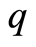 .
.
We recall that according to WHO [4] , Bonzi et al. [6] and Fall et al. [3] , asymptomatic carriers has a low infectious rate. As a consequence in most part of this work one will assume that
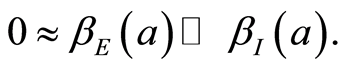 (1.4)
(1.4)
Then
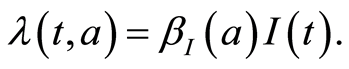 (1.5)
(1.5)
In the above model (1.1)-(1.5), we do not take into account possible vertical transmission and we do not consider any control strategy such as vaccination campaign. It seems to be relevant together the assumption of WHO [4] wich considers that vertical transmission of the disease exists in sub-Saharan Africa. But its influence on the dynamics of the disease is rather small because the proportion of chronic infections acquired perinatally is low [12] .
Using the data, Nokes et al. in [8] constructed the prototype (useful for us) in the simulations:
 (1.6)
(1.6)
We do not focus on chronological age in the infective classes.
2.2. Main Results and Simulations
The basic reproduction rate is defined by
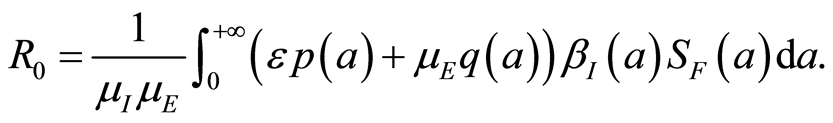 (1.7)
(1.7)
The DFE is defined by
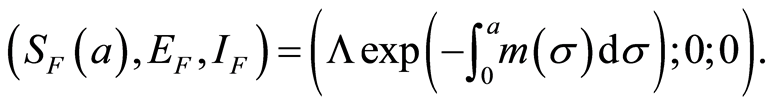 (1.8)
(1.8)
For endemic equilibrium, we obtain only in the case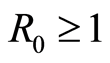 ,
,
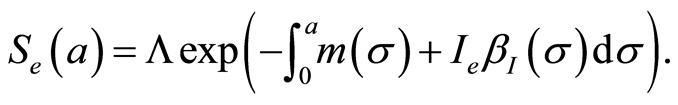 (1.9)
(1.9)
linked to
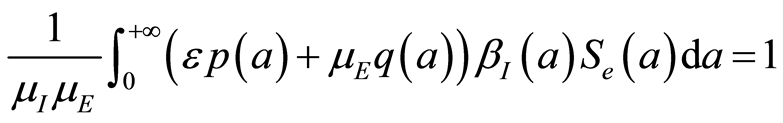
That means
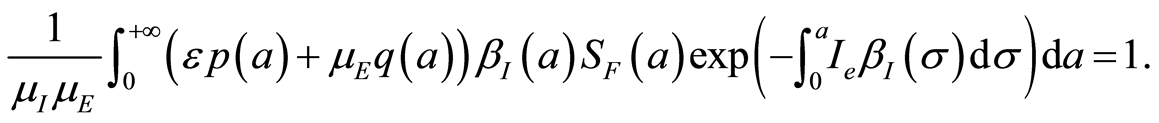
Assumption 1. Assume that the maps 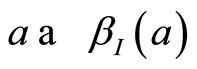 is bounded and uniformly continuous from
is bounded and uniformly continuous from 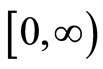 into itself.
into itself.
Let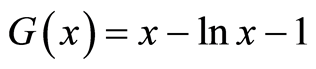 . The function
. The function 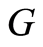 has only one extremum which is a global minimum 0 at 1, satisfying
has only one extremum which is a global minimum 0 at 1, satisfying 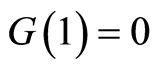 (see [13] ). We make these assumptions for the endemic equilibrium
(see [13] ). We make these assumptions for the endemic equilibrium 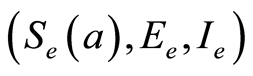 when
when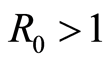 :
:
Assumption 2.
1. 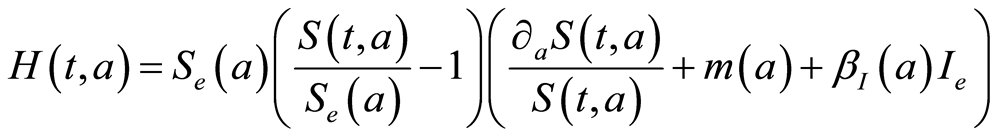 has a constant sign on
has a constant sign on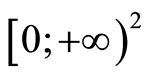 .
.
2. On the attractor 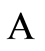 (an invariant compact attractor of all bounded sets following the Proposition 2 therein), the following inequality holds true:
(an invariant compact attractor of all bounded sets following the Proposition 2 therein), the following inequality holds true:
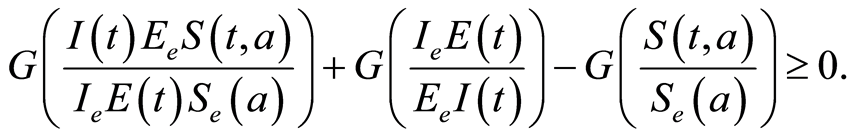
We make also this assumption for the disease free equilibrium 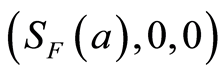 when
when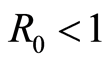 :
:
Assumption 3. 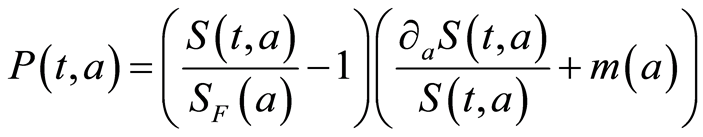 has a constant sign on
has a constant sign on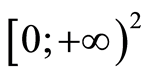 .
.
The global stability of the steady states is resumed in the following Theorem 1.
Theorem 1. Assume Assumptions 1, 2 and 3. Then:
Ÿ If , then the DFE, the disease free equilibrium, is globally asymptotically stable.
, then the DFE, the disease free equilibrium, is globally asymptotically stable.
Ÿ If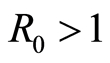 , then there exists an endemic equilibrium that is globally asymptotically stable for all
, then there exists an endemic equilibrium that is globally asymptotically stable for all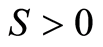 ,
, 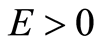 and
and . Moreover, in that case
. Moreover, in that case 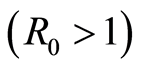 the system is uniformly persistent.
the system is uniformly persistent.
Remark 1. We will see that disease free equilibrium (DFE) exists whenever 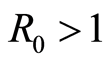 or
or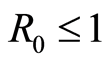 . But endemic equilibrium exists only when
. But endemic equilibrium exists only when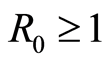 .
.
We denote in Tables 1 and 2: “p” for people(s), “yr” for year and “nbb” for “new born babies”. We made simulations with the values in Tables 1 and 2 and denoted by  the constant birth rate at any positive time (with year unit). We consider the following parameters for DFE case (
the constant birth rate at any positive time (with year unit). We consider the following parameters for DFE case ( related to Figures 1-3).
related to Figures 1-3).
For endemic case ( related to Figures 4-10), we consider the values in the Table 2.
related to Figures 4-10), we consider the values in the Table 2.
We have tested our Assumption 2-2 on the Figures 9 and 10 with  and
and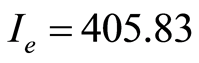 : it is verified in our simulations up to some time (considered as origin by time shifting or rescalling, wich is not very important in our case for long term dynamics in our simulations or calculations) with the global asymptotic stability of the endemic case
: it is verified in our simulations up to some time (considered as origin by time shifting or rescalling, wich is not very important in our case for long term dynamics in our simulations or calculations) with the global asymptotic stability of the endemic case . One could see that Assumption 2 and 3 could be relaxed by proving them for
. One could see that Assumption 2 and 3 could be relaxed by proving them for 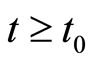 with
with  an arbitrary positive real constant (or number). In all the cases, we observe a period of stability after a severe outbreak of the disease.
an arbitrary positive real constant (or number). In all the cases, we observe a period of stability after a severe outbreak of the disease.
2.3. Technical Materials
Let us introduce the Banach space 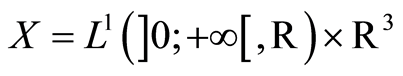 and
and  endowed with the usual product norm as well as its positive cone
endowed with the usual product norm as well as its positive cone 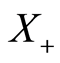 defined (with
defined (with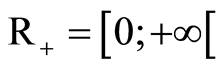 ) by:
) by:
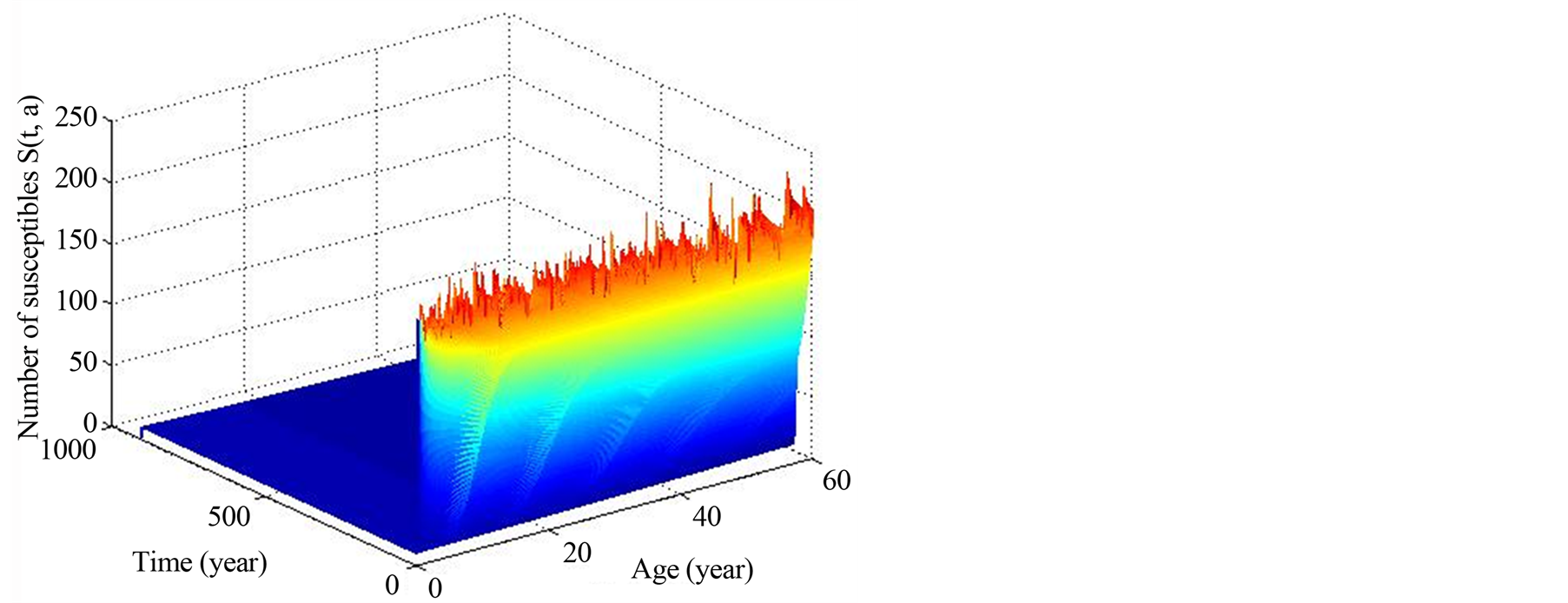
Figure 1. Function S(t, a) with R0 < 1.
Table 2. Values for R0 < 1.
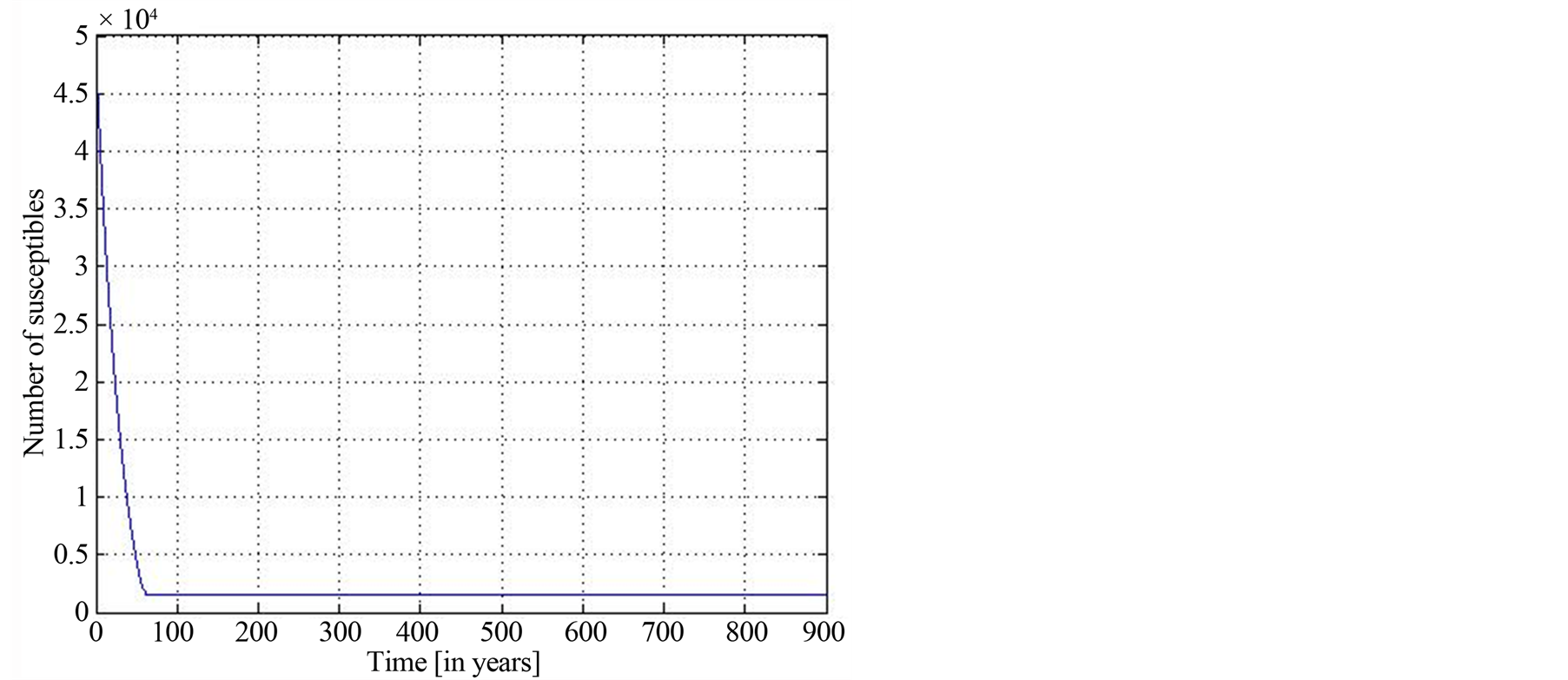
Figure 2. Function 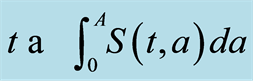 with
with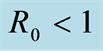 .
.
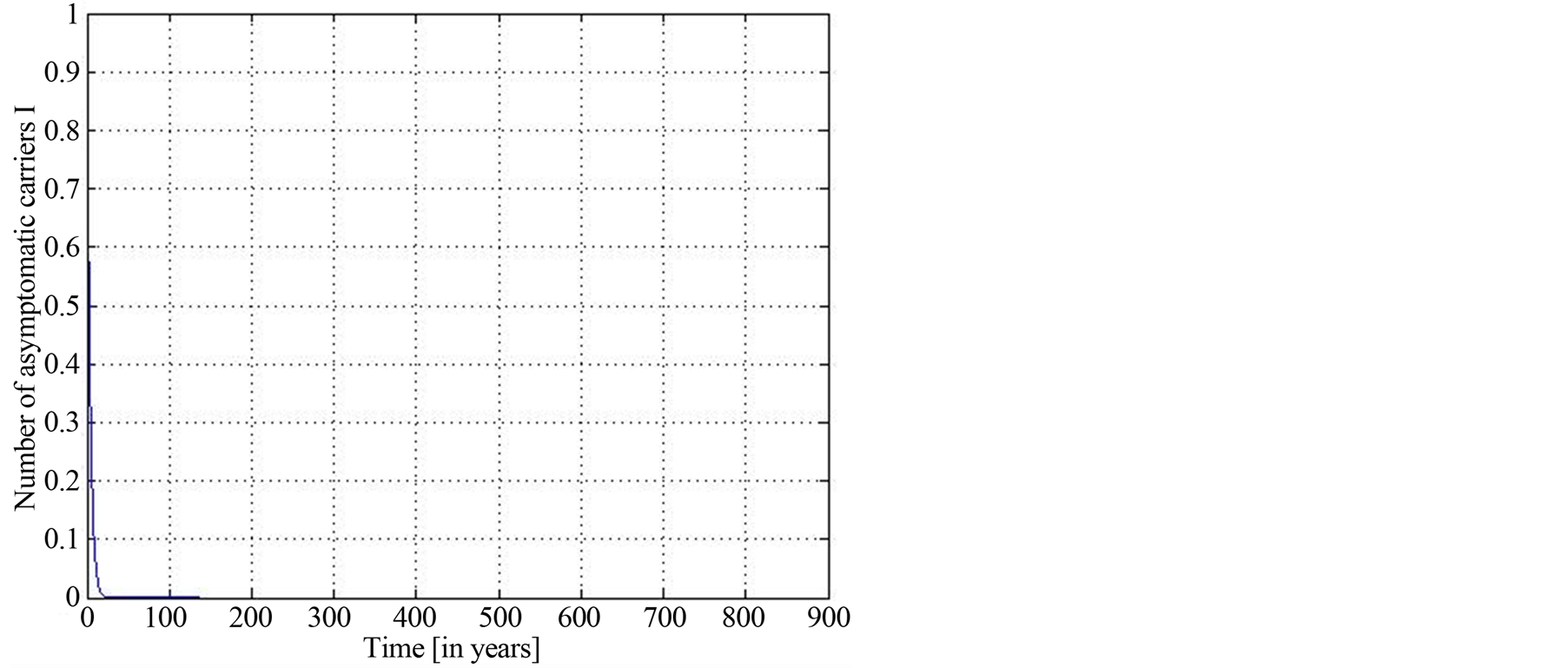
Figure 3. Function 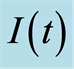 with
with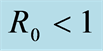 .
.

Figure 4. Function 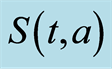 with
with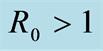 .
.
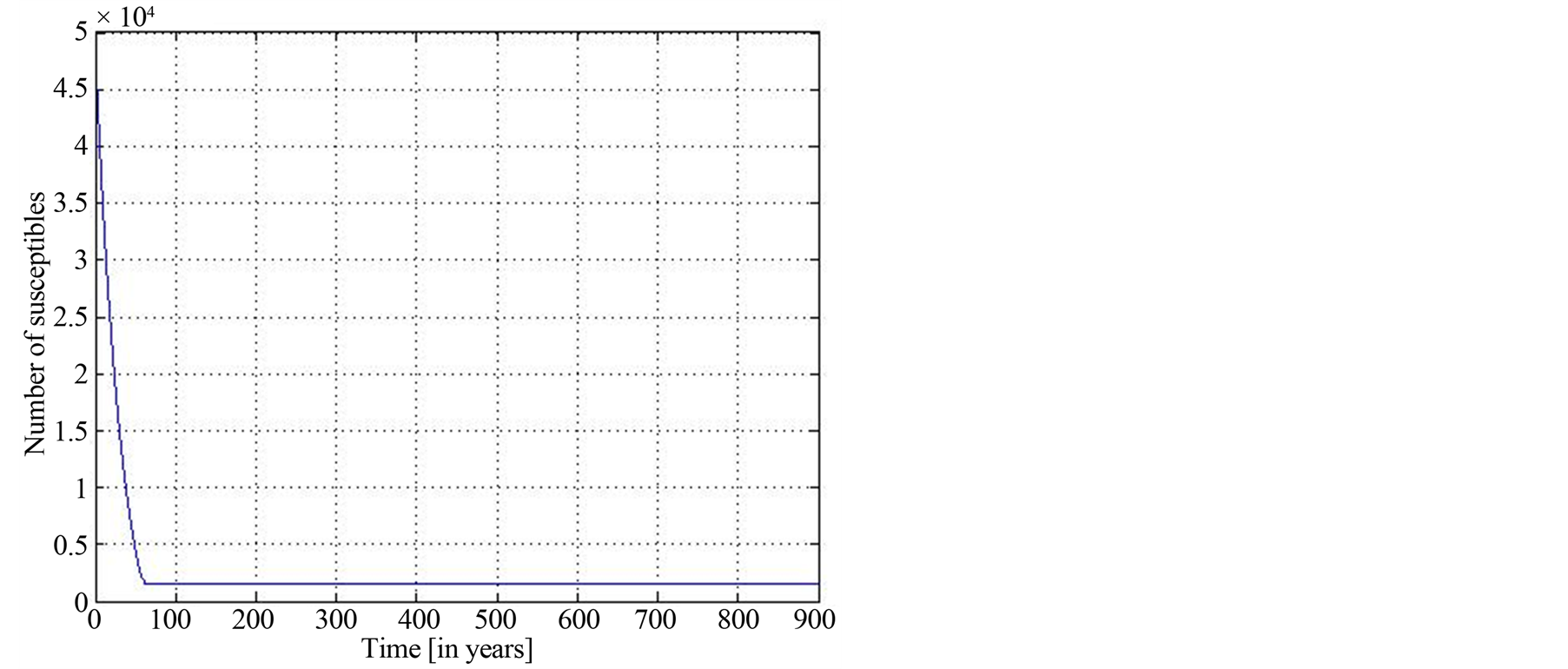
Figure 5. Function 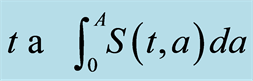 with
with .
.

Figure 6. Function 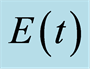 with
with .
.
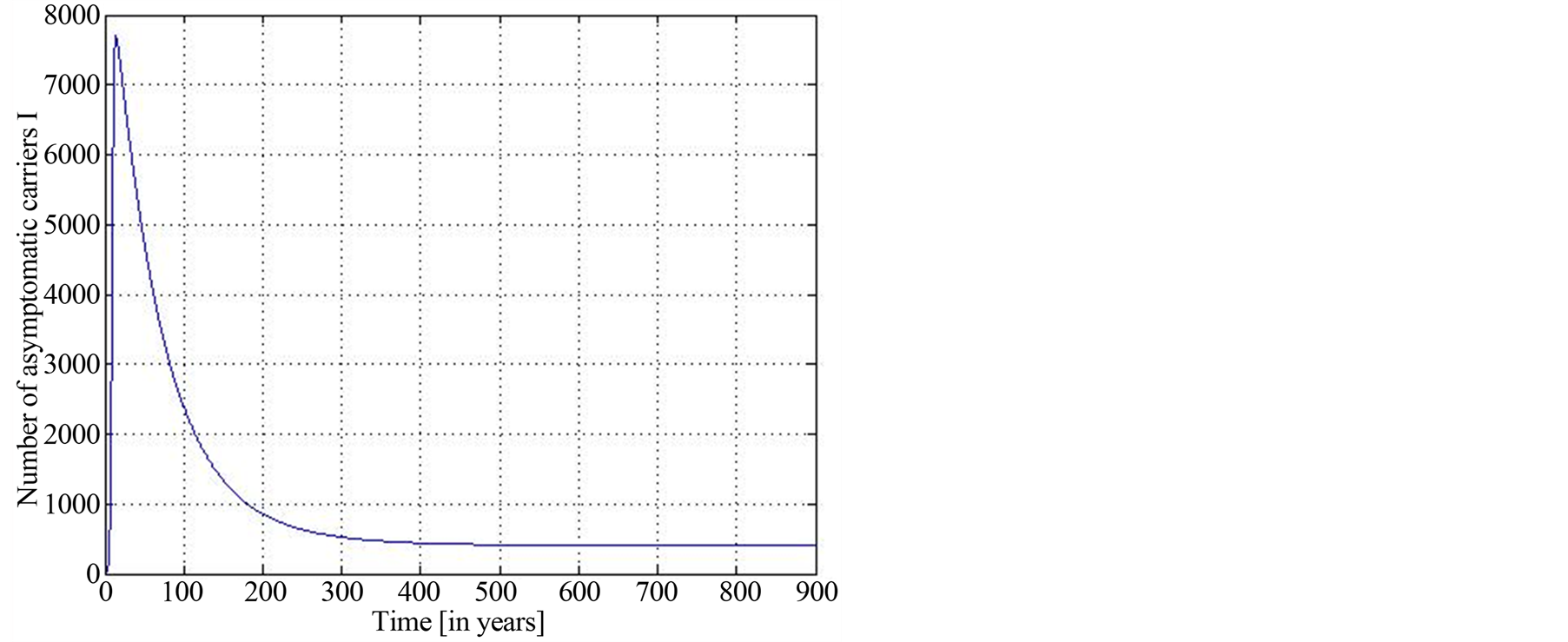
Figure 7. Function  with
with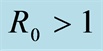 .
.

Figure 8. Function prevalence with .
.
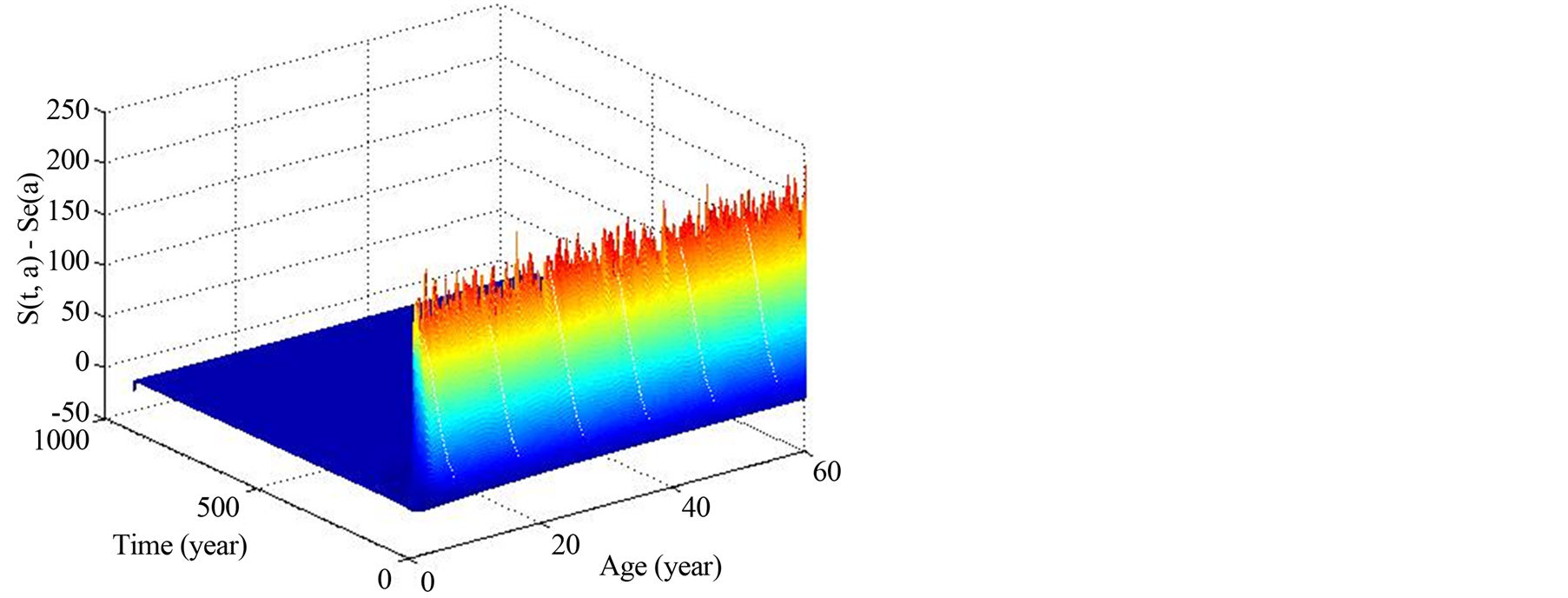
Figure 9. Positivity of 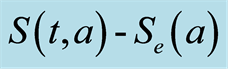 with
with .
.
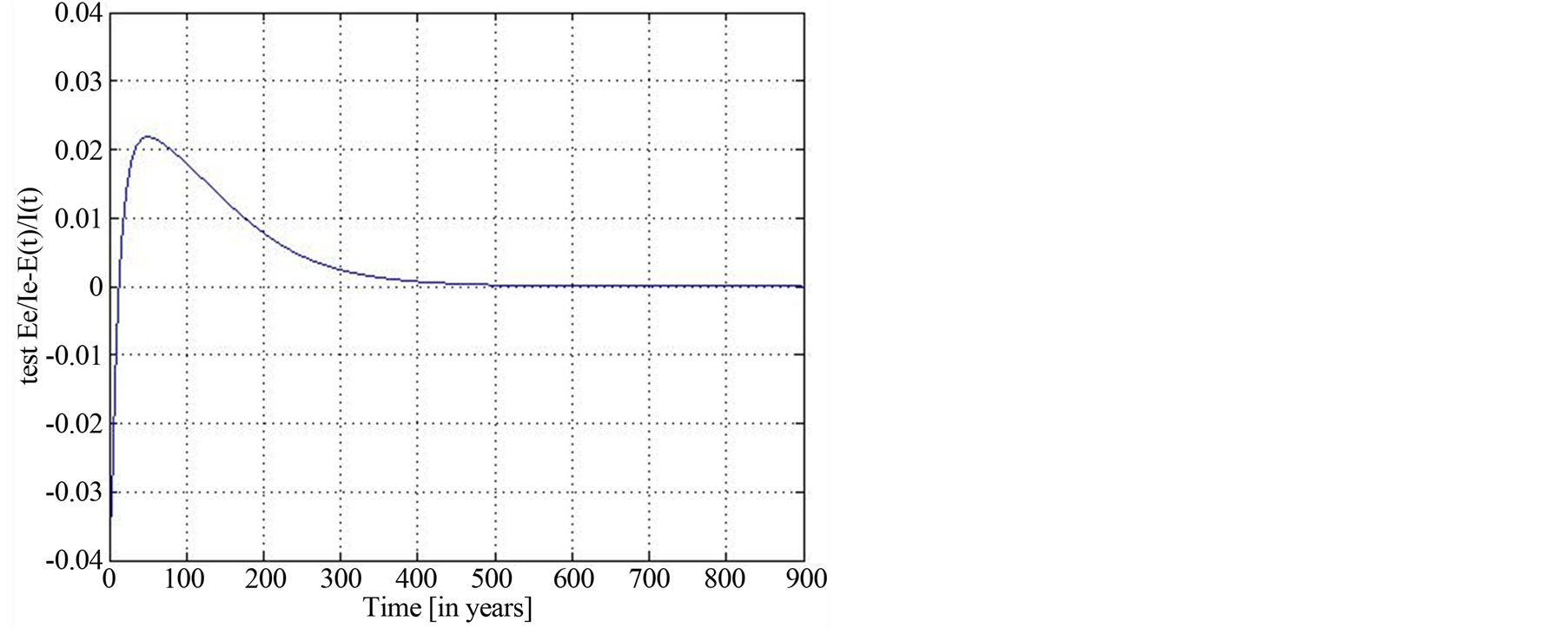
Figure 10. Positivity for long term dynamics of 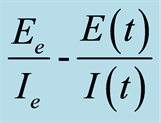 with
with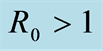 .
.
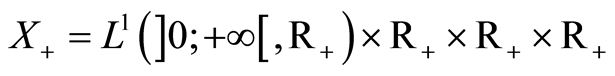
with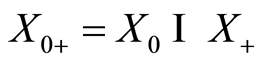 .
.
We consider also the linear operator 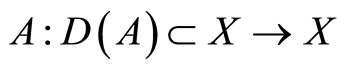 defined by
defined by

with the non densily domain 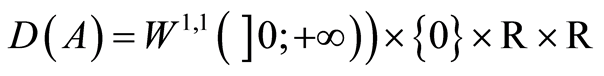 in
in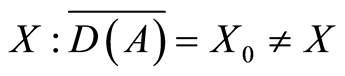 .
.
Finally let us introduce the nonlinear and Frechet differentiable map 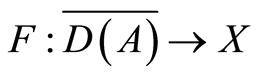 defined by:
defined by:

Identifying 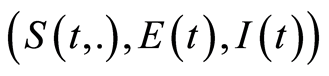 and
and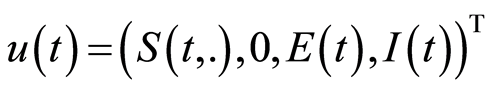 , one obtains that System (1.1)-(1.5) rewrites as the following non-densely defined Cauchy problem (1.10):
, one obtains that System (1.1)-(1.5) rewrites as the following non-densely defined Cauchy problem (1.10):
 (1.10)
(1.10)
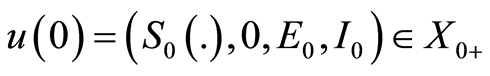
We first derive that the above abstract Cauchy problem (1.10)-(1.11) generates a unique globally defined and positive semiflow. Moreover 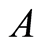 satisfies the Hille-Yosida property. Then standard methodologies apply to provide the existence and uniqueness of mild solution for system (1.10)-(1.11) (see for instance [10] [14] -[17] ):
satisfies the Hille-Yosida property. Then standard methodologies apply to provide the existence and uniqueness of mild solution for system (1.10)-(1.11) (see for instance [10] [14] -[17] ):
Proposition 1. Let Mathematical Assumption 1 be satisfied.
Then there exists a continuous semiflow that is bounded dissipative 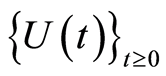 on
on 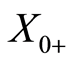 into itself such that for each
into itself such that for each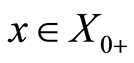 , the map
, the map 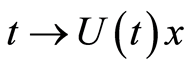 is the unique integrated solution of (1.10)-(1.11) with initial data
is the unique integrated solution of (1.10)-(1.11) with initial data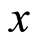 , namely
, namely 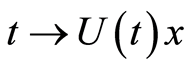 satisfies
satisfies
(i)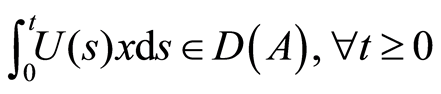 (ii)
(ii)  for each
for each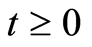 .
.
Remark 2. One can prove the proposition 1 by using ideas of corollaries 1 and 2 in Melnik et al. [11] .
By using results in Sell and You [18] , one can prove that  is asymptotically smooth. Then using results of Hale [19] [20] , Hale et al. [21] , one obtains the following proposition.
is asymptotically smooth. Then using results of Hale [19] [20] , Hale et al. [21] , one obtains the following proposition.
Proposition 2. Let Mathematical Assumption 1 be satisfied. Then there exists a compact set  such that
such that
(i) 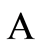 is invariant under the semiflow
is invariant under the semiflow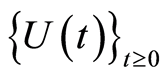 .
.
(ii) 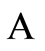 attracts the bounded sets of
attracts the bounded sets of  under
under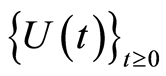 . This means that for each bounded set
. This means that for each bounded set 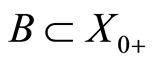 we have
we have

where 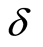 is defined as
is defined as
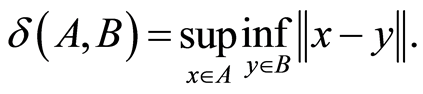
Moreover 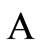 is locally asymptotically stable.
is locally asymptotically stable.
We will widely adapt ideas of Magal et al. [13] and Melnik et al. [11] here with Lyapunov functionals on 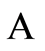 for the global stability of DFE and EE.
for the global stability of DFE and EE.
1) Stability of the DFE: 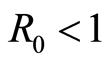
Let us introduce the positive map defined on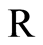 :
:
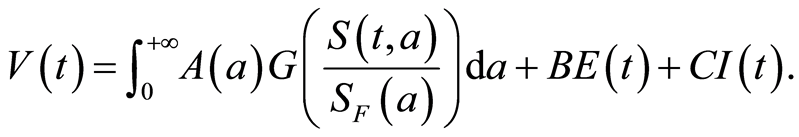
is positive defin ite at the DFE. We evaluate 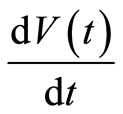 as
as
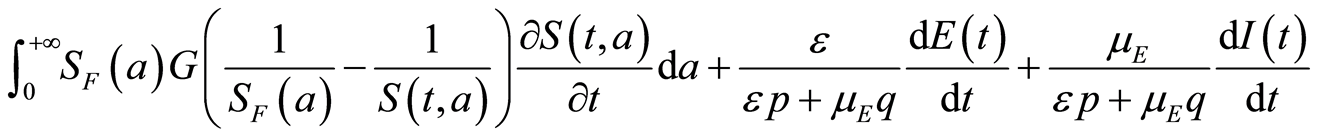
with ,
, 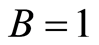 and
and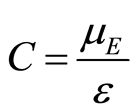 . The equations of the system 1.1 help us to get for
. The equations of the system 1.1 help us to get for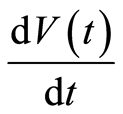 :
:
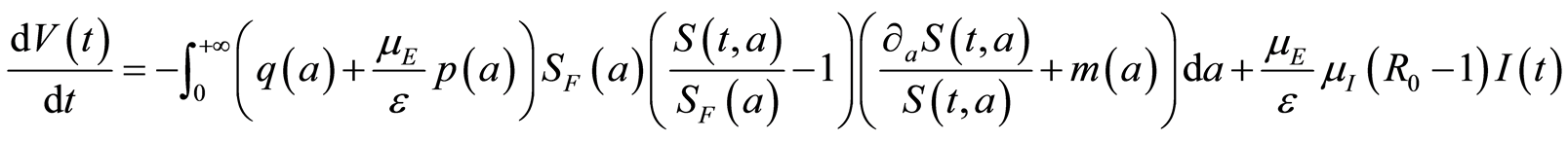
We would like to prove that

Three cases occur by Assumption 3:
1. If , one obtains:
, one obtains:

And by integrating from 0 to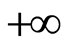 , one gets:
, one gets:
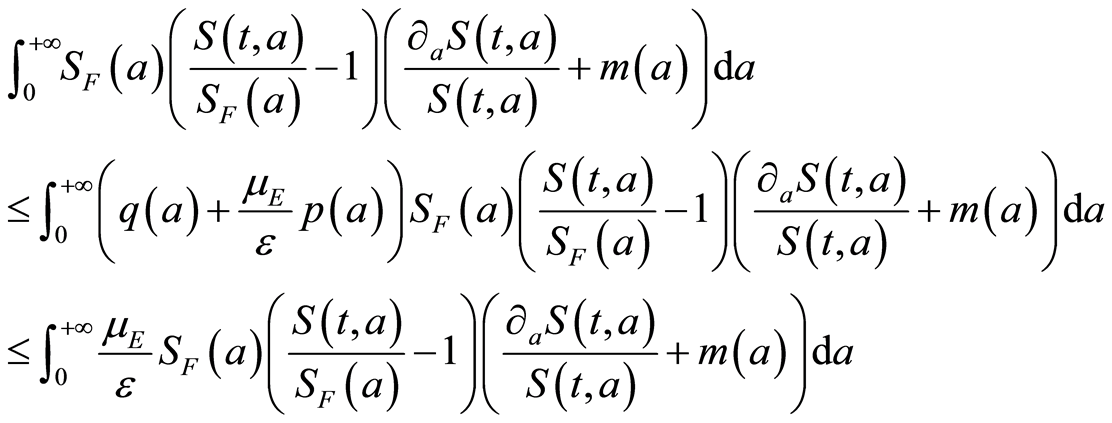
Then
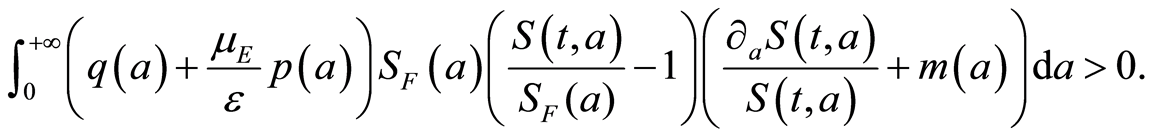
2. If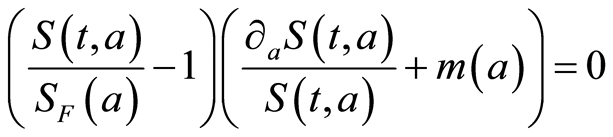 , one gets:
, one gets:

3. If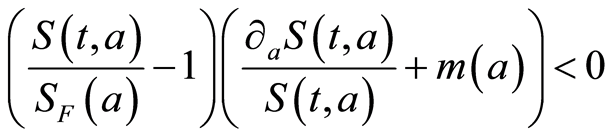 , one gets:
, one gets:
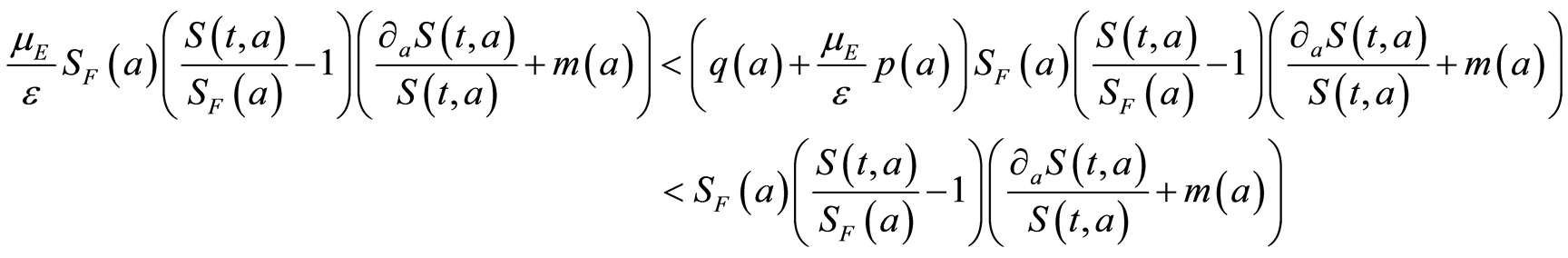
And by integrating from 0 to , one gets:
, one gets:
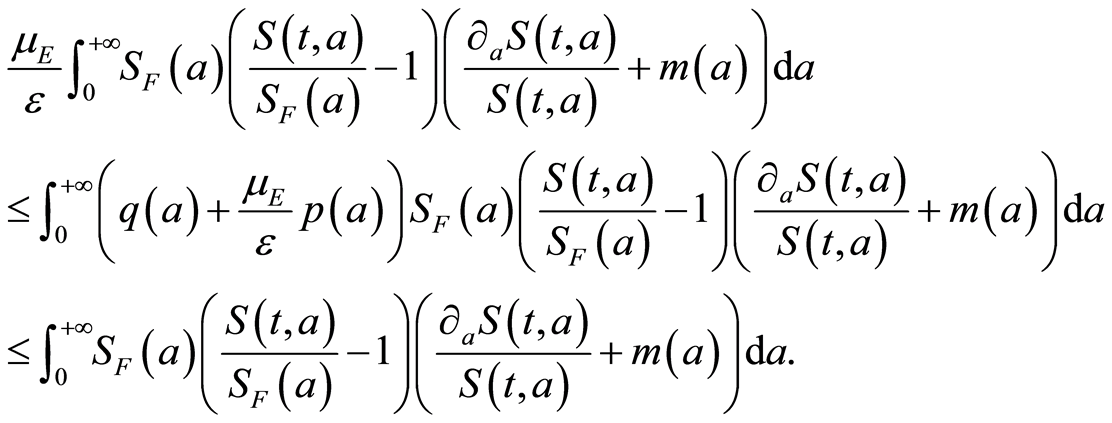
but 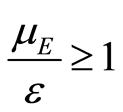 and,
and,
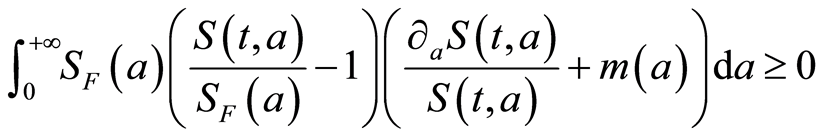
that implies
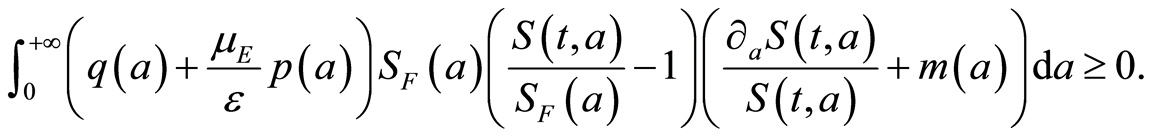
Hence

Finally

Hence by recalling that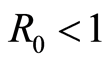 ,
,

Finally by global stability Lyapunov-LaSalle theorem [11] [13] [22] , the DFE =  is globally asymptotically stable because the largest invariant set of orbits
is globally asymptotically stable because the largest invariant set of orbits  verifying
verifying  is reduced for all positive
is reduced for all positive 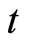 and
and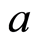 , to
, to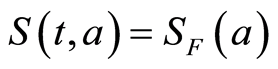 ,
, 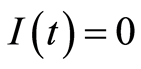 and
and 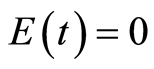 corresponding to the disease free steady state (DFE) seen as
corresponding to the disease free steady state (DFE) seen as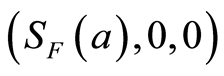 .
.
2) Stability of the endemic equilibrium: 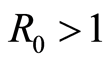
Any solution of system (1.1) with positive initial condition remains positive indefinitely: then the system (1.1) is uniformly persistent (the tools are similar to Melnik [11] ).
Let . The function
. The function  has only one extremum which is a global minimum 0 at 1, satisfying
has only one extremum which is a global minimum 0 at 1, satisfying  (see [13] ). Then, we will analyse the Lyapunov functional
(see [13] ). Then, we will analyse the Lyapunov functional
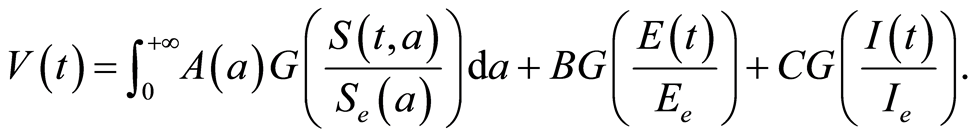
We notice that  and
and 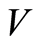 is positive definite at EE =
is positive definite at EE =  that provides the minimum of
that provides the minimum of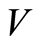 . Moreover
. Moreover 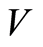 is defined for all
is defined for all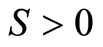 ,
,  ,
,  and
and
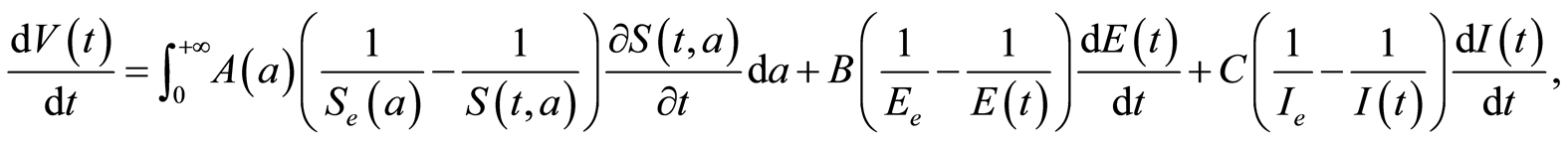
With

we obtain:

We set  By assumption,
By assumption,
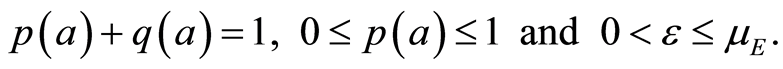
Then

Three cases appear by Assumption 2-1:
1. If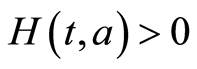 , then
, then
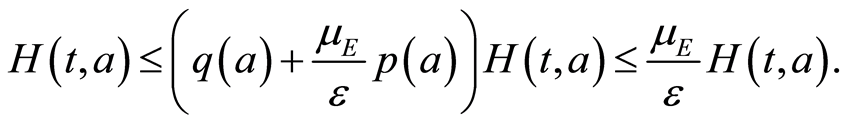
By integrating from 0 to , one gets:
, one gets:
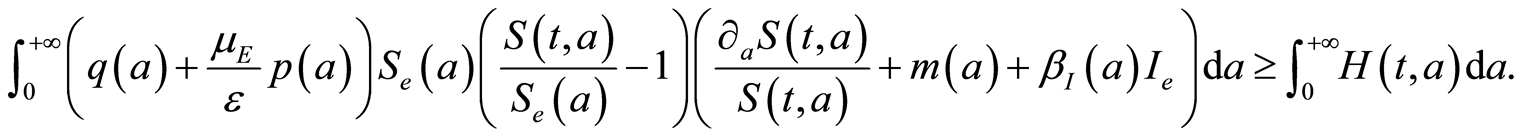
Then
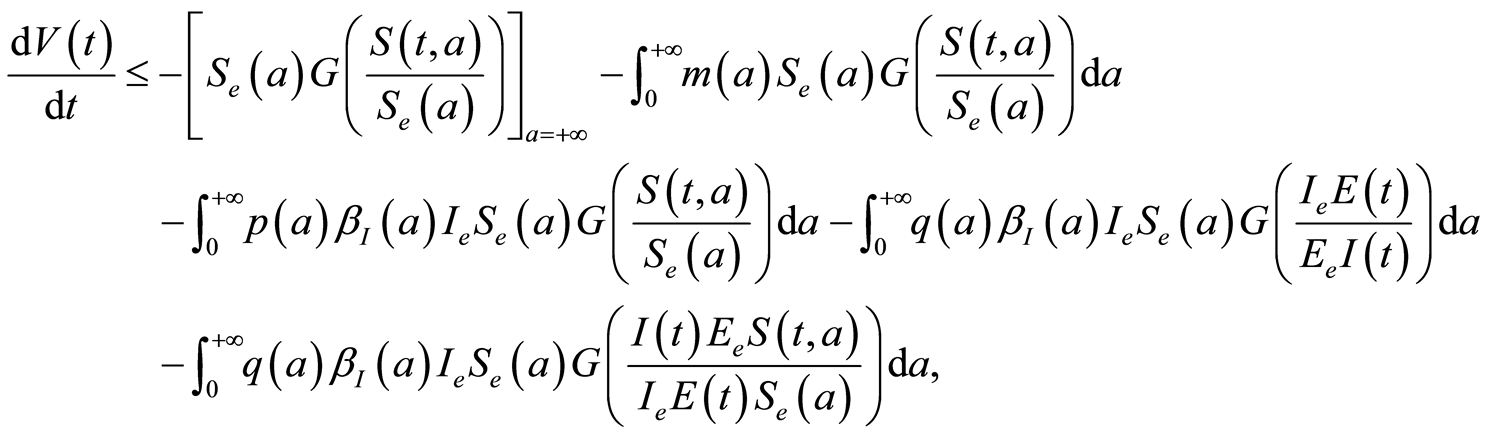
And finally 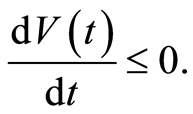
2. If 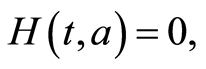 we get:
we get: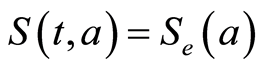 . But
. But 
1) For 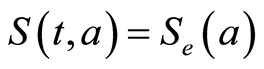 and
and , one has:
, one has:

then
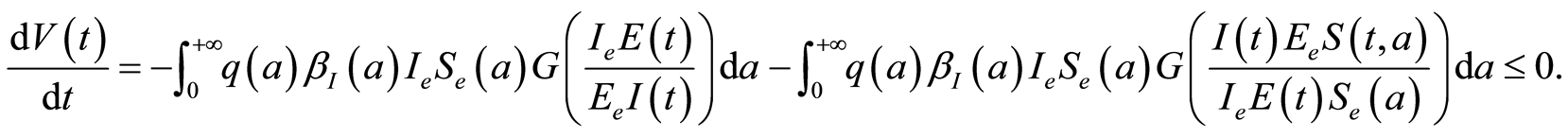
2) For 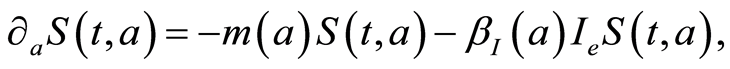 one obtains:
one obtains:
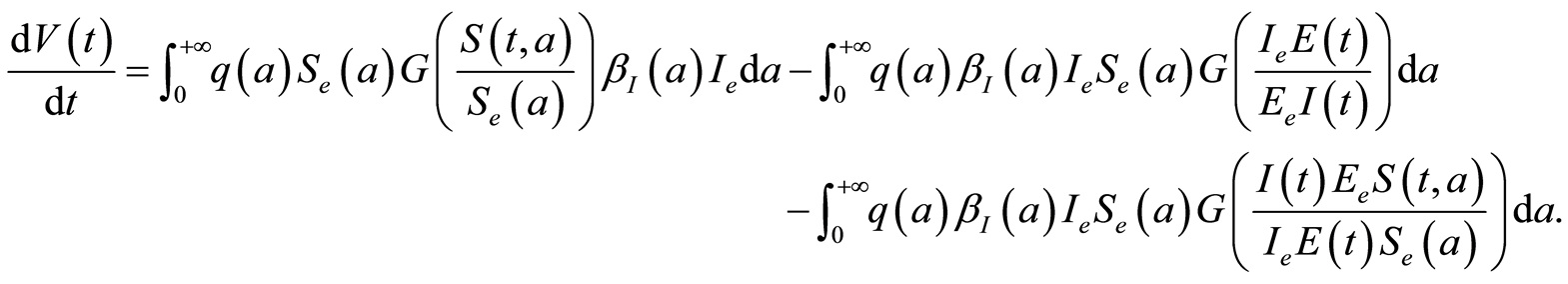
To get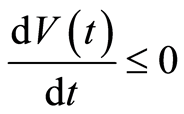 , it is enough to show that:
, it is enough to show that:
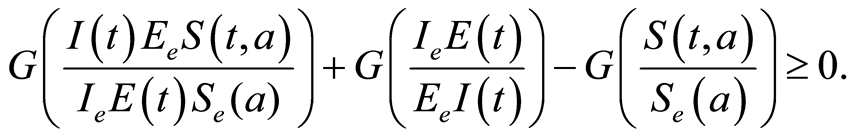
We set:
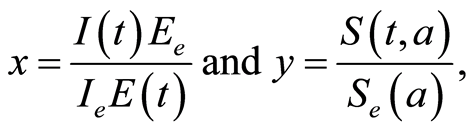
We want to prove that:
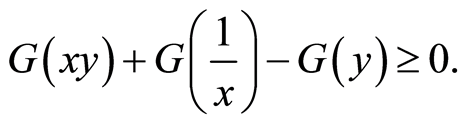
By definition of  we have
we have

then
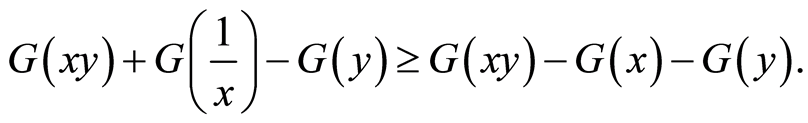
It enough to verify this sufficient condition
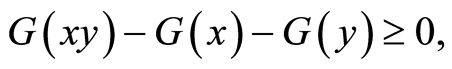
Recall that
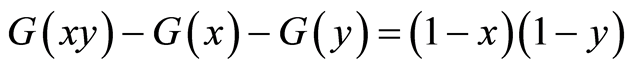
Then
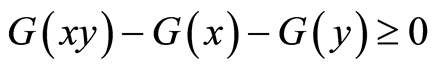
if and only if
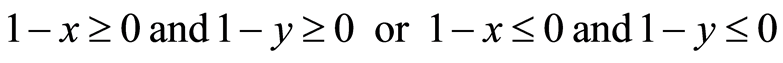
that means (see Figures 9 and 10 in the simulations of subsection 1.2.2)
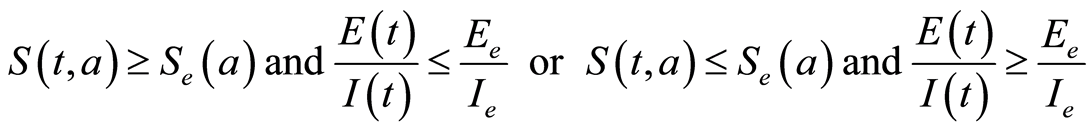
and,

By Assumption 2-2,
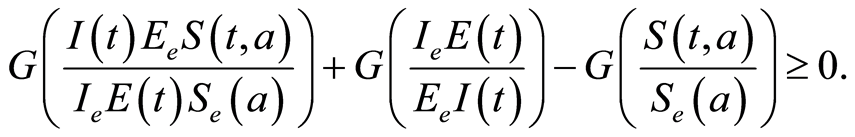
we obtain,
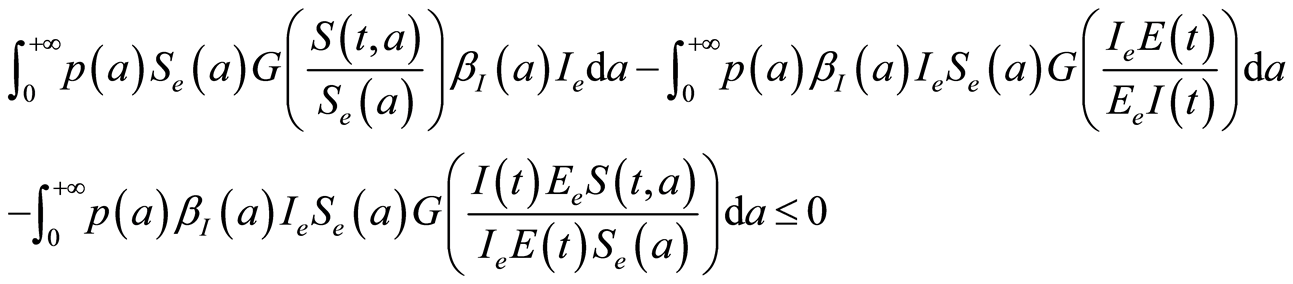
and

3. If 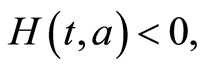 then:
then:

By integrating from 0 to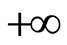 , one gets:
, one gets:
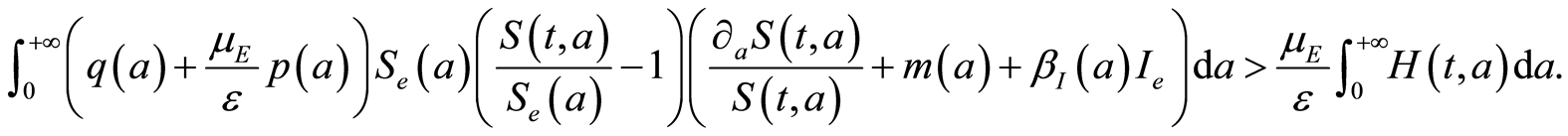
Then,

but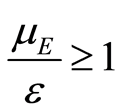 . So
. So
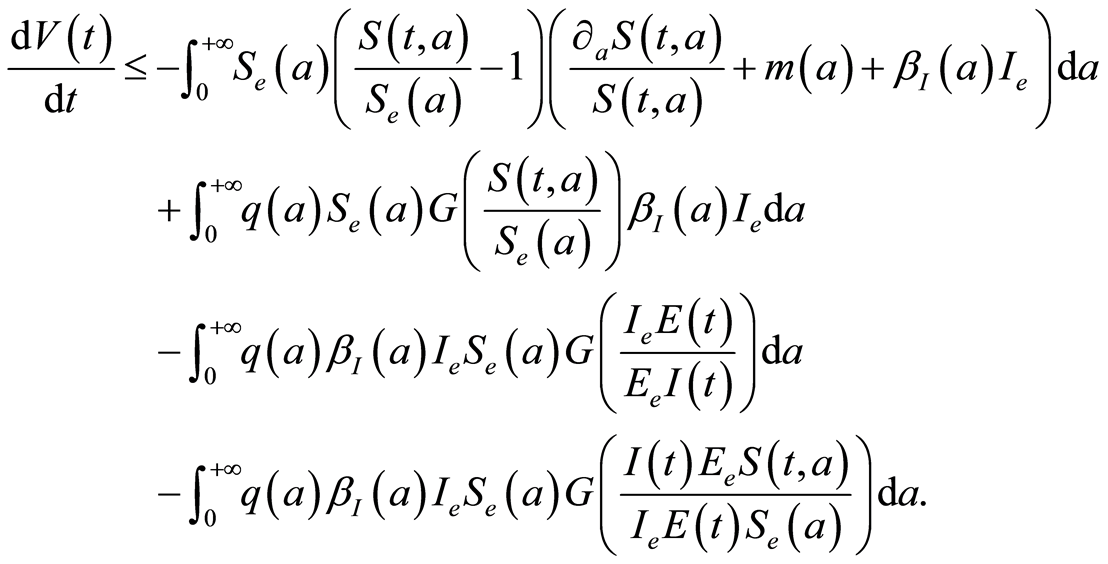
by using results in case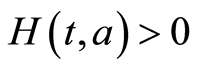 , one has:
, one has: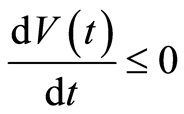 .
.
Then by global stability Lyapunov-LaSalle theorem [11] [13] [22] , the endemic equilibrium (EE) is globally asymptotically stable because the largest invariant set of orbits 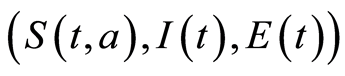 verifying
verifying  is reduced for all positive
is reduced for all positive  and
and , to
, to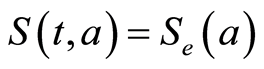 ,
,  and
and 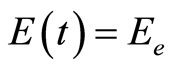 corresponding to the endemic steady state
corresponding to the endemic steady state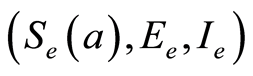 .
.
3. Conclusions
We observe that our computations for stability of DFE and EE are confirmed by simulations. It is also established that increasing the transmission coefficient , increases the basic reproduction rate. In a forthcoming work, we will introduce vertical transmission (because of the contreversal article Sall et al. [23] on WHOs [12] neglection of vertical transmission in sub-Saharan Africa), studies of (optimal) vaccination strategies and immigration by other ways than birth. The results of this work extend those of Melnik et al. [11] and Kouakep et al. [10] on a more realistic case applied to hepatitis B situation. One can study the stability of the endemic equilibrium (EE) with
, increases the basic reproduction rate. In a forthcoming work, we will introduce vertical transmission (because of the contreversal article Sall et al. [23] on WHOs [12] neglection of vertical transmission in sub-Saharan Africa), studies of (optimal) vaccination strategies and immigration by other ways than birth. The results of this work extend those of Melnik et al. [11] and Kouakep et al. [10] on a more realistic case applied to hepatitis B situation. One can study the stability of the endemic equilibrium (EE) with 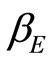 small enough (like Ducrot et al. [10] ) using perturbation arguments of Magal [24] . For the case (avoid here) where
small enough (like Ducrot et al. [10] ) using perturbation arguments of Magal [24] . For the case (avoid here) where  and the map
and the map 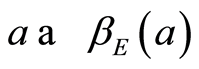 is bounded and uniformly continuous from
is bounded and uniformly continuous from 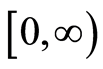 into itself, Ducrot et al. [25] deal with global stability of the disease free equilibrium with (constant) functions
into itself, Ducrot et al. [25] deal with global stability of the disease free equilibrium with (constant) functions 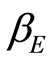 and
and 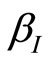 by considering a particular case of the Lyapunov functional (similar to Magal et al. [13] and Kouakep et al. [10] )
by considering a particular case of the Lyapunov functional (similar to Magal et al. [13] and Kouakep et al. [10] )  which is non-increasing along the complete orbits with
which is non-increasing along the complete orbits with  and
and 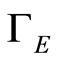 such that
such that
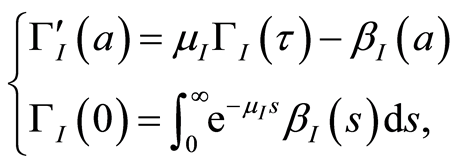
and
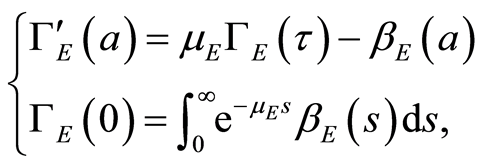
Note that for ,
,
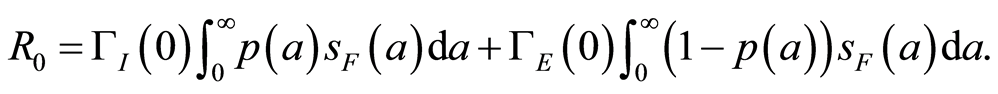
Ducrot et al. [25] used also arguments like those in (Demasse et al. [17] , proposition 4.1 and its proof). For global stability of endemic equilibrium in the case , Ducrot et al. [25] used the following Lyapunov functional (under special assumptions on
, Ducrot et al. [25] used the following Lyapunov functional (under special assumptions on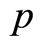 ) with a well-chosen positive constant
) with a well-chosen positive constant :
:
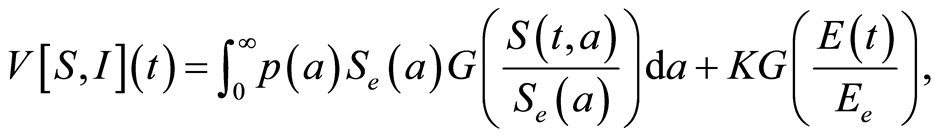 (1.11)
(1.11)
The model (1.1)-(1.5) is formally equivalent (with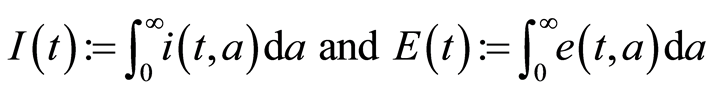 ) to the following model:
) to the following model:
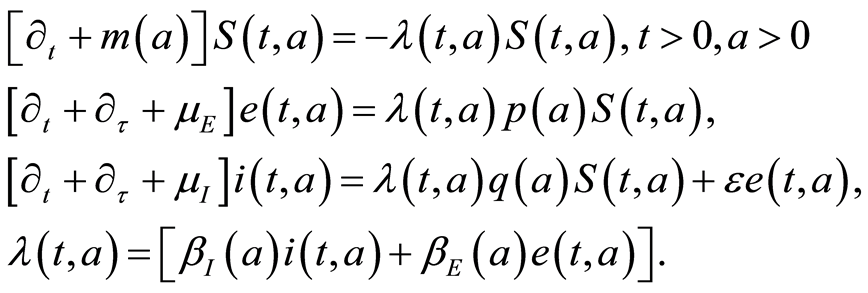 (1.12)
(1.12)
supplemented together with the boundary conditions:
 (1.13)
(1.13)
and initial data
 (1.14)
(1.14)
By replacing  (chronological age) by
(chronological age) by  (infection age) in the infectives classes
(infection age) in the infectives classes 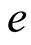 and
and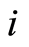 , the model (1.1)-(1.5) is equivalent (with
, the model (1.1)-(1.5) is equivalent (with ) to the following model (see Kouakep et al. [10] ):
) to the following model (see Kouakep et al. [10] ):
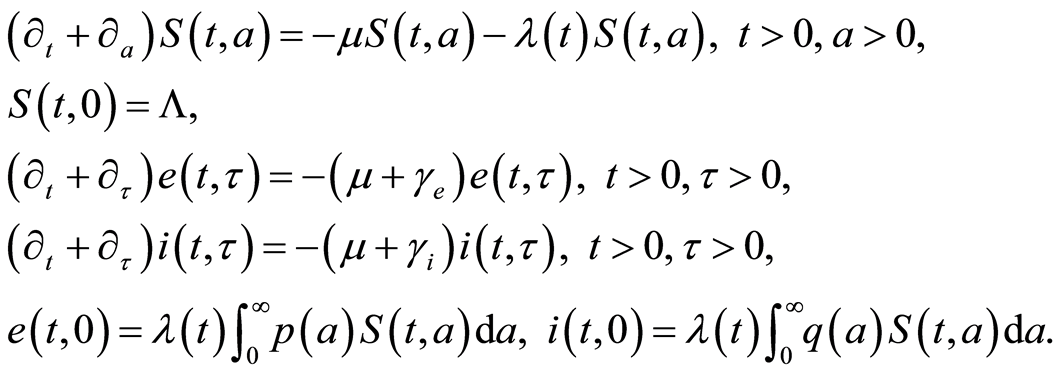 (1.15)
(1.15)
supplemented together with the boundary conditions:
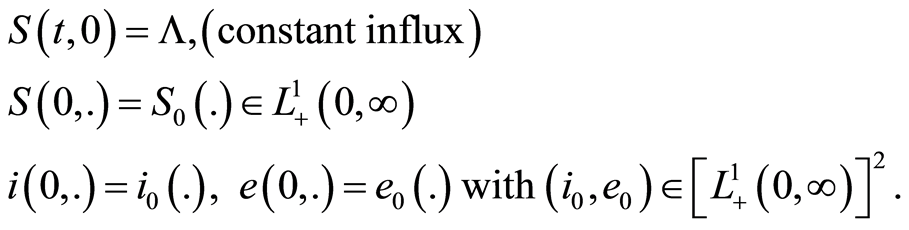 (1.16)
(1.16)
it remains to model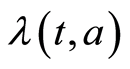 , the force of infection, and those general form can be written in the form
, the force of infection, and those general form can be written in the form
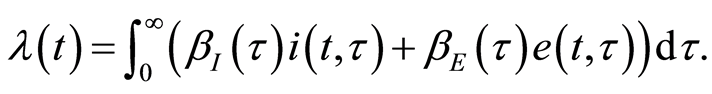 (1.17)
(1.17)
where 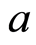 is the chronological age and
is the chronological age and 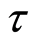 is the time since the infective(s) are contaminated. Another similar problem (with
is the time since the infective(s) are contaminated. Another similar problem (with ) is:
) is:
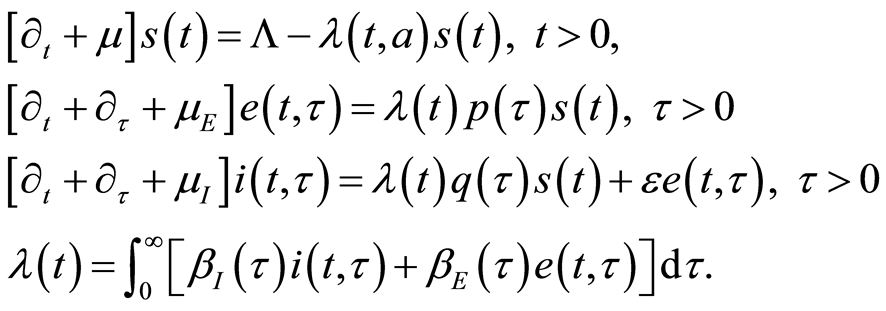 (1.18)
(1.18)
supplemented together with the boundary conditions:
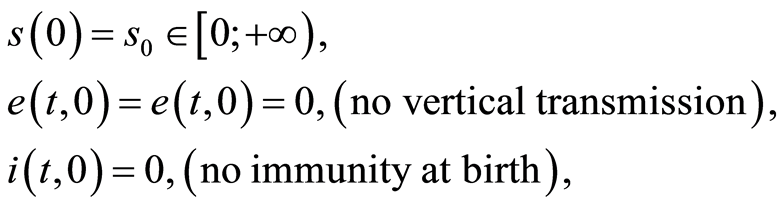 (1.19)
(1.19)
We strongly believe that Assumptions 2 and 3 could be relaxed if we use usual tools of functional analysis by splitting functions  and
and  in the form
in the form 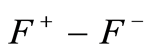 as a difference of two well-chosen positive functions
as a difference of two well-chosen positive functions 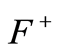 and
and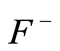 . Then one can use the constant-sign cases on
. Then one can use the constant-sign cases on 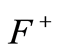 and
and .
.
Acknowledgements
Authors are grateful to Reviewers, Pr Bekolle, Dr. A. Ducrot, Dr. Damakoa Irepran, Dr. Kamgang J. C. and GDM-MIAP group for helpful remarks or comments on the manuscript.
References
- Houpa, D.D.E., Miamdjo Tagne, E. and Kouakep, T.Y. (2014) A Model for Hepatitis B Disease with Age-Dependent Susceptibility. JMCS, 4, accepted. http://scik.org/index.php/jmcs/article/view/1431
- Zuckerman, A.J. (1976) The A, B, C Viruses. Nature, 259, 363-364.
- Fall, A.A., Gauthier, S. and Abderrahman, I. (2010) Modélisation de la Transmission Verticale de l’Hépatite B. CARI 2010 Report.
- WHO (2013) Centre des Médias: Hépatite B. http://www.who.int/mediacentre/factsheets/fs204/en/index.html
- Pasquini, P. and Cvjetanović, B. (1988) Mathematical Models of Hepatitis B Infection. Annali dell’Istituto Superiore di Sanità, 24, 245-250.
- Bonzi, B., Fall, A.A., Iggidr, A. and Sallet, G. (2011) Stability of Differential Susceptibility and Infectivity Epidemic Models. Journal of Mathematical Biology, 62, 39-64. http://dx.doi.org/10.1007/s00285-010-0327-y
- Inaba, H. (1990) Threshold and Stability Results for an Age-Structured Epidemic Model. Journal of Mathematical Biology, 28, 411-434. http://dx.doi.org/10.1007/BF00178326
- Nokes, D.J., Hall, A.J., Edmunds, W.J., Medley, G.F. and Whittle, H.C. (1993) The Influence of Age on the Development of the Hepatitis B carrier State. Proceedings of the Royal Society B: Biological Sciences, 253, 197-201. http://dx.doi.org/10.1098/rspb.1993.0102
- Zou, L., Ruan, S. and Zhang, W. (2010) An Age-Structured Model for Transmission Dynamics of Hepatitis B. SIAM, 70, 3121-3139.
- Kouakep, T.Y., Ducrot, A. and Houpa, D.D.E. (2013) A Model for Hepatitis B with Chronological and Infection Ages. Applied Mathematical Sciences, 7, 5977-5993.
- Melnik, A.V. and Korobeinikov, A. (2013) Lyapunov Functions and Global Stability for SIR and SEIR Models with Age-Dependent Susceptibility. Mathematical Biosciences and Engineering, 10, 369-378. http://dx.doi.org/10.3934/mbe.2013.10.369
- WHO (1996) Hepatitis B and Breastfeeding. http://www.who.int/maternal_child_adolescent/documents/pdfs/hepatitis_b_and_breastfeeding.pdf
- Magal, P., McCluskey, C.C. and Webb, G.F. (2010) Liapunov Functional and Global Asymptotic Stability for an Infection-Age Model. Applicable Analysis, 89, 1109-1140. http://dx.doi.org/10.1080/00036810903208122
- Magal, P. (2001) Compact Attractors for Time-Periodic Age Structured Population Models. Electronic Journal of Differential Equations, 2001, 1-35.
- Magal, P. and Ruan, S. (2009) On Semilinear Cauchy Problems with Non-Dense Domain. Advances in Differential Equations, 14, 1041-1084.
- Thieme, H.R. (1997) Quasi-Compact Semigroups via Bounded Pertubation. In: Arino, O., Axelrod, D. and Kimmel, M., Eds., Advances in Mathematical Population Dynamics-Molecules, Cells and Man, World Scientific Publishing, River Edge, 691-711.
- Djidjou, D.R. and Ducrot, A. (2013) An Age-Structured Within-Host Model for Multistrain Malaria Infections. SIAM Journal on Applied Mathematics, 73, 572-593. http://dx.doi.org/10.1137/120890351
- Sell, G.R. and You, Y. (2002) Dynamics of Evolutionary Equations. Springer, New York. http://dx.doi.org/10.1007/978-1-4757-5037-9
- Hale, J.K. (1986) Asymptotic Behavior and Dynamics in Infinite Dimensions, in Nonlinear Differential Equations. Hale, J.K. and Martinez-Amores, P., Eds., Pitman, Marshfield.
- Hale, J.K. (1988) Asymptotic Behavior of Dissipative Systems. Mathematical Surveys and Monographs 25, American Mathematical Society, Providence.
- Hale, J.K. and Waltman, P. (1989) Persistence in Infinite-Dimensional Systems. SIAM Journal on Mathematical Analysis, 20, 388-395. http://dx.doi.org/10.1137/0520025
- LaSalle, J.P. (1976) The Stability of Dynamical Systems. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970432
- Sall Diallo, A., Sarr, M., Fall, Y., Diagne, C. and Kane, M.O. (2004) Hepatitis B Infection in Infantile Population of Senegal. Dakar Medical, 49, 136-142.
- Magal, P. (2009) Perturbation of a Globally Stable Steady State and Uniform Persistence. Journal of Dynamics and Differential Equations, 21, 1-20. http://dx.doi.org/10.1007/s10884-008-9127-0
NOTES

*Corresponding author.


