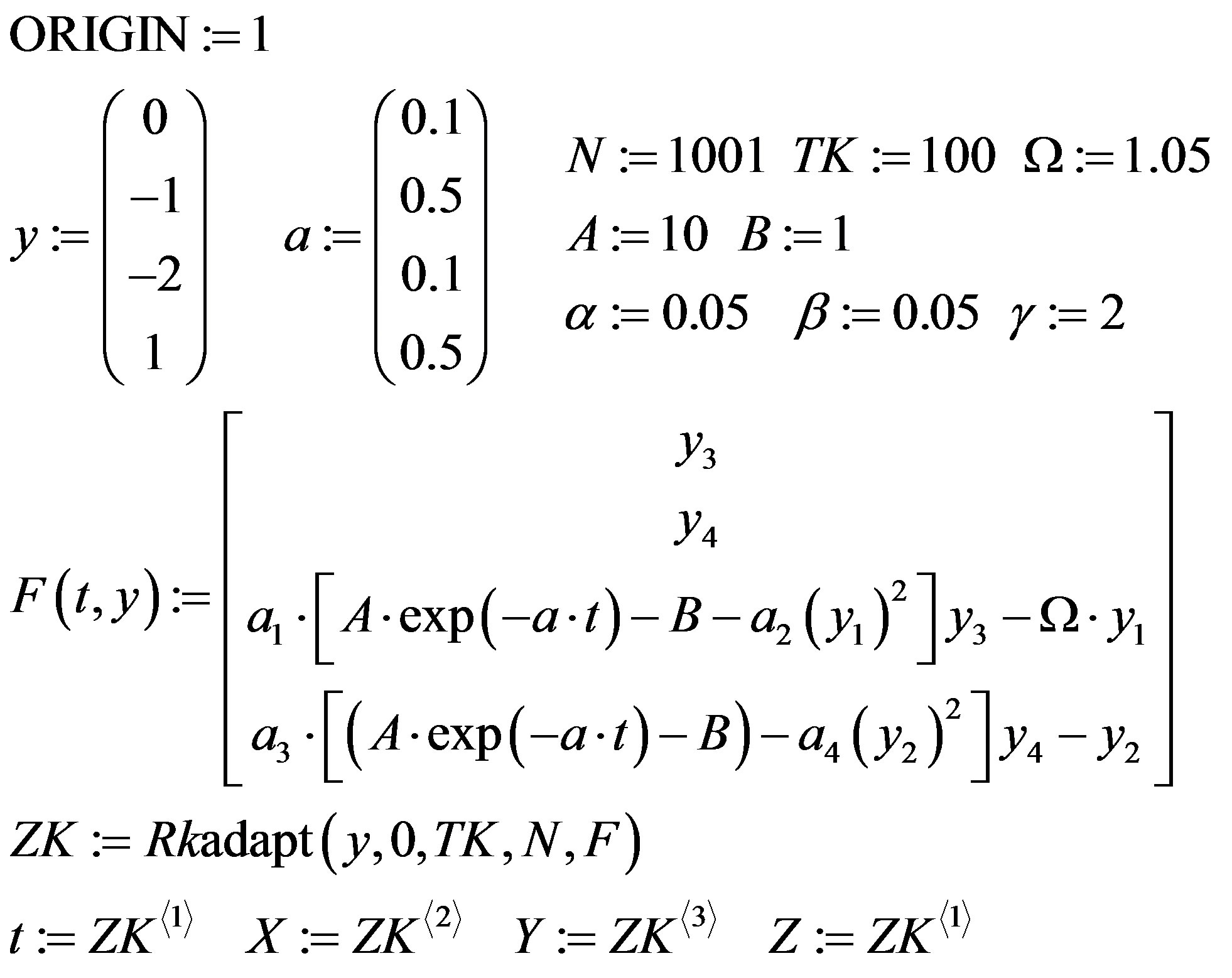Natural Science
Vol.4 No.7(2012), Article ID:20791,8 pages DOI:10.4236/ns.2012.47068
Tropical cyclone, as powerful natural self-oscillatory systems, and wind-energetic a way of struggle against it wang#t1:sp——The analysis of a cyclone from a position of the theory of vibrationswang#t1:ep
![]()
Moscow State Institute of Radio Electronics and Automatics (MIREA), Moscow, Russia; Kaganovwil@gmail.com
Received 22 September 2011; revised 24 October 2011; accepted 10 November 2011
Keywords: tropical cyclone; model; self-oscillations; wind electrogenerator; the fan; negative feedback
ABSTRACT
It is considered three phases of development of a tropical cyclone: the origin, the steady-state regime and the termination, coinciding with three phases of self-oscillatory process: oscillation buid-up, dynamic balance and failure of selfoscillations. The rough size of energy of a cyclone, as column of air rotating with high speed, at initial and final stages of development and comparison of the received sizes with nuclear and hydrogen bombs is calculated. The model of the electronic oscillator with negative active conductivity by the numerical solution of the equation of the Van-der-Pol is analyzed. Formal coincidence of transient in this model with increase of capacity of vortical air formation, that allows to make mnemonic model of a cyclone in the form of volume self-oscillatory system is shown. The numerical solution of the made equations allows to construct schedules of dynamic process for each of particles of the investigated environment. The general recipe on restraint of development of a cyclone by compulsory entering into it of attenuation is given. Realization of this recipe by means of group of platforms with powerful wind-electrogenerator and the fans and uses of a principle of negative feedback is shown. The results of laboratory experiment confirming idea, taken as a principle struggle against an arising air whirlwind, by transformation of a laminar stream in chaotic, turbulent are resulted. For fuller check offered a wind-energetic method of struggle against a cyclone carrying out of more scale experiment is necessary.
1. THEORY
1.1. Essence of a Problem
The cyclones periodically arising in a tropical zone of the Earth, possess enormous energy, comparable with energy of a nuclear bomb at an origin stage, and hydrogen—after full formation. Cyclone action leads to numerous human victims and huge destructions. So, for example, only the cyclone of “Katrina” operating in North Atlantic pool in 2005, has caused the USA an economic damage at the rate about 90 billion dollars. All attempts to bridle or at least to reduce destructive force of a cyclone haven’t crowned yet success. We will make attempt to offer for the decision of the given global problem one of branches of renewed electric power industry—wind. We will ask a question: whether it is impossible to stop by means of group of powerful wind electrogenerators development of a tropical cyclone at the initial stage of its origin? We will consider at first that represents a cyclone as powerful natural power formation.
1.2. Three Phases of Development of a Tropical Cylone
The phase 1 is connected with origin of the cyclone representing atmospheric formation with lowered pressure of air in the center and with air streams, twirled in a spiral with speed of a wind more than 17 km/s (figure 1) [1,2]. There is such cyclonic whirlwind over tropical water area of ocean in temperature 26˚C - 27˚C at latitude between 50˚ and 20˚. The heated-up air sated with a moisture, rising from an ocean surface on the big height, it is cooled, owing to what water steams are condensed, allocating heat feeding with energy arising cyclone.


Figure 1. Photos of a tropical cyclone.
Approximate dependence of temperature of air T on height over a surface of ocean with temperature 27˚C can be described by means of the characteristic of falling type from the negative derivative considering fall of temperature on 0.50 on each 100 m of height:
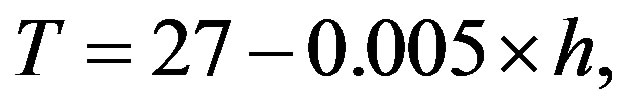 (1)
(1)
where h height in m.
The schedule of function (1) is constructed on figure 2. In the bottom part of a cyclone there can be air moving to the axis center. But the great bulk of air which has arisen cyclonic formations, under the influence of terrestrial Coriolis force connected with rotation of the Earth, starts to rotate round a quasivertical axis counter-clockwise in northern hemisphere and on hour—in southern.
The phase 2 includes the gradual development of a cyclone connected first of all with increase to 150 km and more of radius rotating with high speed to 40 - 50 km/s of a column of air in height from 2 to 20 km, surrounded in the weight concerning cold and motionless air. Achievement finally a cyclone of the maximum energy and an establishment of a condition of dynamic balance between thermal energy of evaporation feeding a cyclone, and cooling of ocean owing to hashing of its waters then the further increase in the sizes of cyclonic formation stops.
The phase 3 is connected with cyclone destruction when total energy of all losses (cooling at the expense of ocean, the friction about a terrestrial surface, overcoming of obstacles) starts to surpass thermal energy, feeding vortical air formation.
Having presented a cyclone in the form of a rotating column of air (figure 3), we will estimate its energy. Weight of the cyclone:
 (2)
(2)
where H—cyclone height, m; R—radius of the cyclone, m; r(h)—the density of air decreasing with height h at a normal state from r(0) = 1225 kg/m3.
Considering an ascending stream of air, we will accept r = 0.8 kg/m3 = const at any value of height. Then kinetic energy of a rotating column of air:
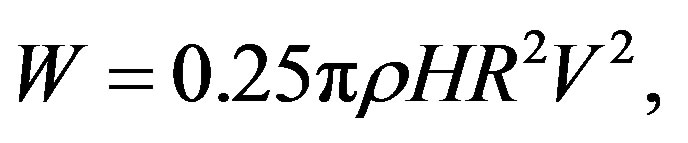 (3)
(3)
where V (km/s)—speed of a wind on cyclone periphery, R (m)—radius a rotating column of air.
Having accepted for an arising cyclone V = 13 m/s, H = 10 km and R = 10 km, we will receive according to (3) for energy: W = 1014 J. For the generated cyclone we will accept: V = 27 m/s, H = 10 km and R = 150 km. In this
Figure 2. Dependence of temperature of air on height.
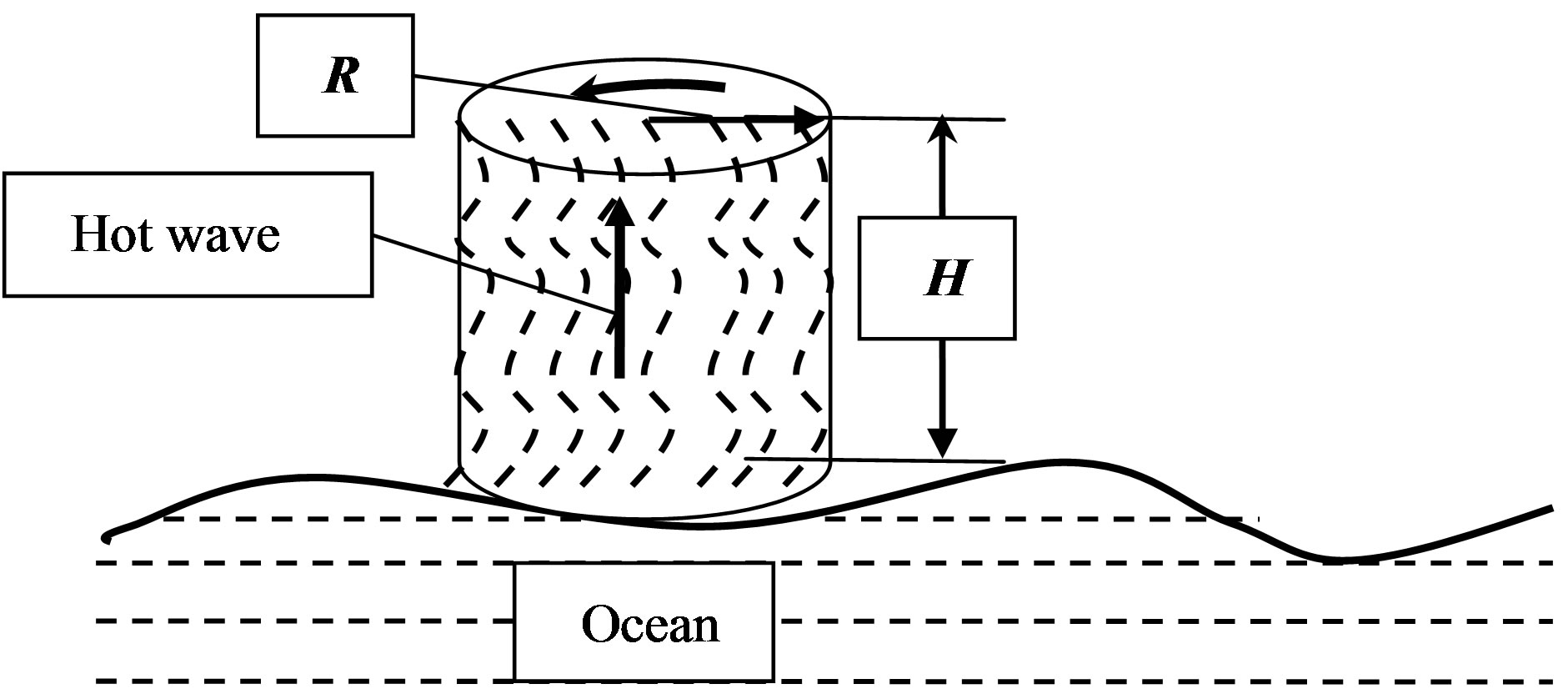
Figure 3. The schematical image of a cyclone in the form of a rotating column of air.
case we will receive: W = 1017 J. For comparison we will specify that the energy allocated at explosion of a nuclear bomb in a trinitrotoluene equivalent 20 Kt, makes 1014 J, and hydrogen in 20 Mt –1017 J. From the resulted figures it is visible that at a stage of origin of a tropical cyclone its energy is comparable with energy of a nuclear bomb, and on final—hydrogen.
From positions of physics the cyclone is the original thermal car in which warmly, selected from ocean, it will be transformed to kinetic energy of a rotating air whirlwind. Such transformation is possible thanks to reduction of temperature of air with height, i.e. to negative value of a derivative 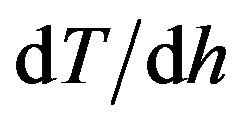 < 0 (figure 1), and to rotation of the Earth.
< 0 (figure 1), and to rotation of the Earth.
From a position of the theory of vibrations the cyclone —a rotating column of air round a vertical axis—can be treated as volumetric self-oscillatory process with three phases of the development, aspiring to a limiting cycle— to an equilibrium state between the energy feeding a cyclone (evaporation thermal energy), and total energy of all losses (cooling at the expense of ocean, a friction with a surface, overcoming of obstacles etc.).
For comparison we will consider at first more simple case of self-oscillatory process also connected with presence at object of the falling characteristic from a negative derivative.
1.3. The Short Analysis of the Electronic Oscillator with Negative Active Conductivity
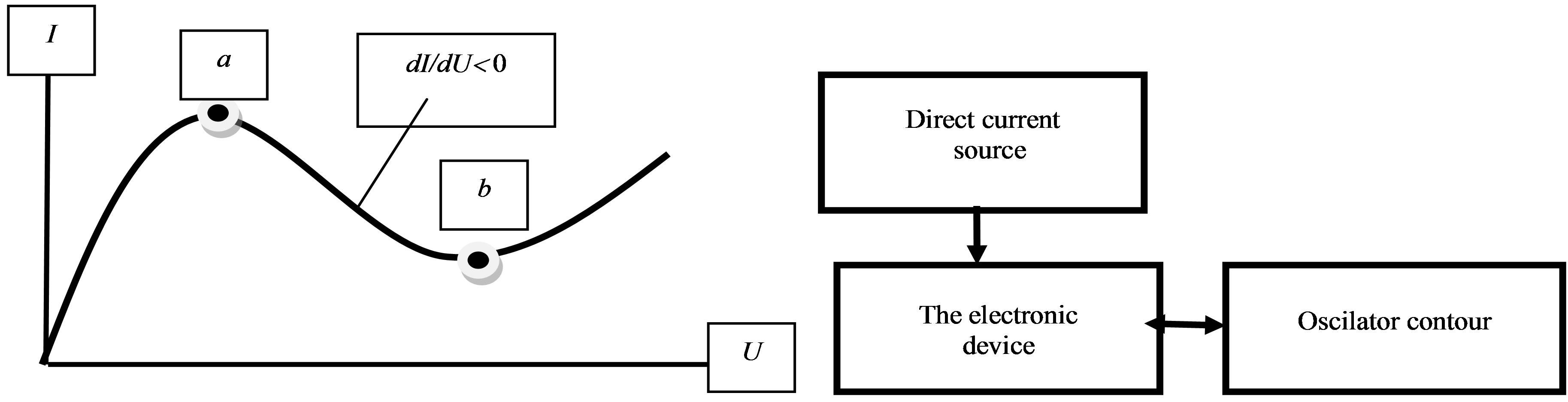
It is known two basic types of electronic oscillators: with positive feedback and with negative active conductivity [3].
The block diagram of the second type of the oscillatory contour consisting of the power supply of a direct current, oscillatory system and the device with negative active conductivity it agree characteristic volt-ampernoj (a site а-б), shown on figure 4(a) it is resulted on figure 4(b). Its work, as well as the first type of the oscillator, can be described by means of the equation of the Van-der-field [3]:
 (4)
(4)
where x—нормированная amplitude of fluctuations.
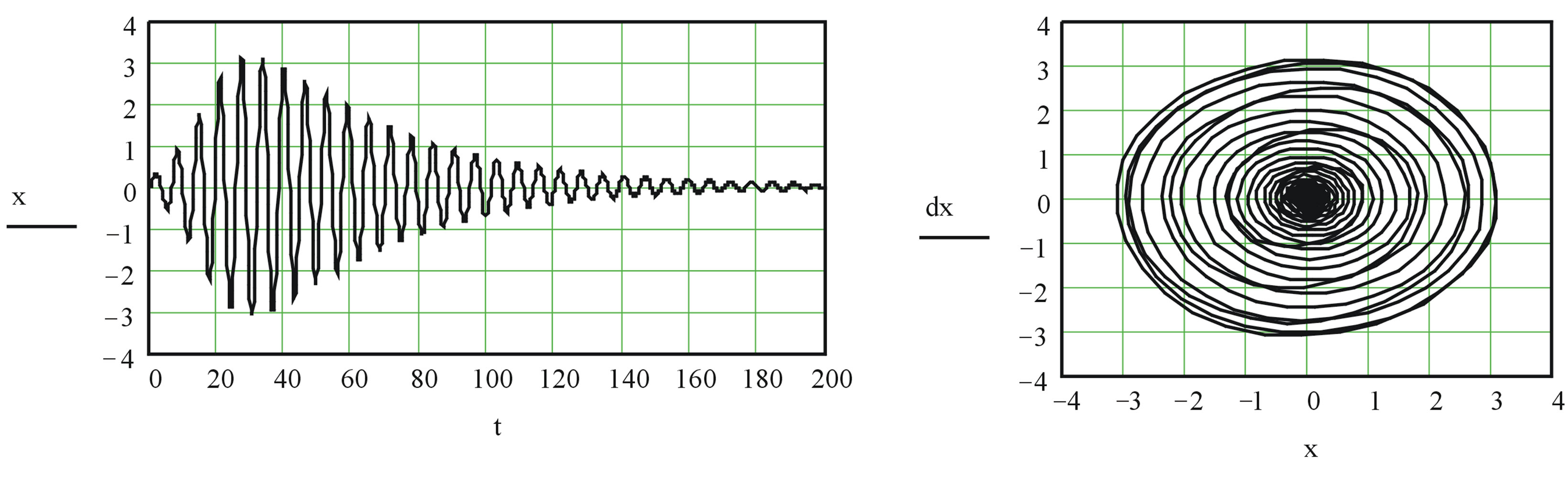
The numerical decision of the eq.4 under the program in the environment of Mathcad (The appendix 1) is possible at almost any values of constant factors а1 and а2. The example of the decision of the given equation at а1 = 0.1 and а2 = 0.5, a = 0, A = 10 B = 0 in the form of the transient schedule x(t) and a phase portrait dx/dt = Ф(x) with a limiting steady cycle is shown on figure 5. Process includes sites of gradual increase of fluctuations and the established mode with constant amplitude. For failure of self-oscillations in system it is necessary to bring in it attenuation. Let this attenuation is brought by means of the external influence described by function F(t) = Aexp(–at) – B. Then we will receive the following modified equation of the Van-der-field describing work of the oscillator:
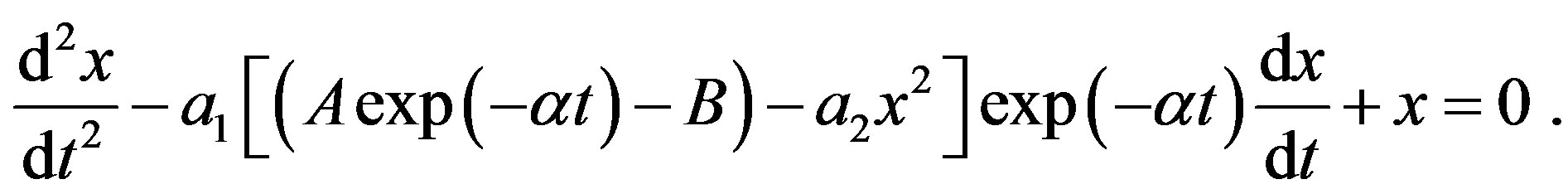 (5)
(5)
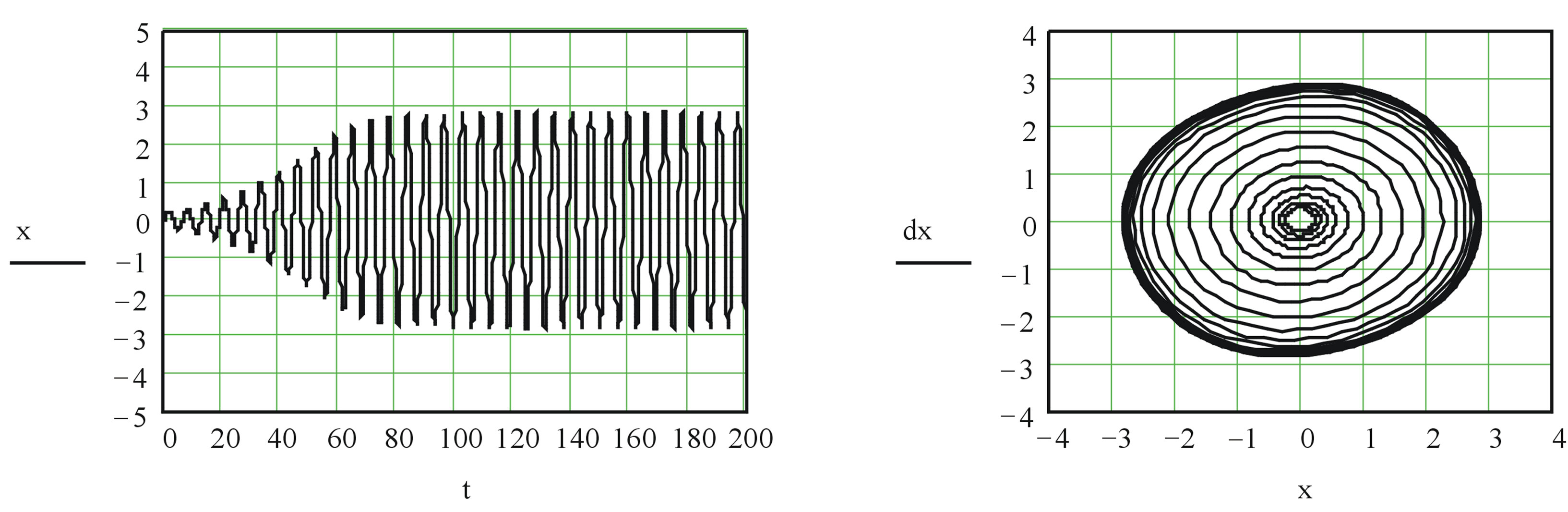
The decision of the eq.6 under the program resulted in Application 1, at а1 = 0.05, а2 = 0.5, a = 0.05, A = 10, B = 1 in the form of the schedules similar to first case, it is shown on figure 6. Thanks to entering into the oscillator of additional losses of fluctuation after achievement of some maximum fade. This process of increase and the further attenuation of self-oscillations is visually traced and on a phase portrait: at first fluctuations aspire to a limiting cycle, and then they start to be braided, aspiring to the center. Thus, in this case process of self-oscillations instead of two has all three described above a phase: increase of fluctuations, dynamic balance and failure of self-oscillations.
1.4. Mnemonic Model of a Tropical Cyclone
Making a start from the eq.5, we will make mathematical model of the tropical cyclone considered as self-oscillatory system of volume type in rectangular
 (a) (b)
(a) (b)
Figure 4. The oscillator with negative active conductivity: (a) volt-ampernaja the characteristic; (b) the block diagram.
 (a) (b)
(a) (b)
Figure 5. Transient (a) and a phase portrait of the oscillator (b).
 (a) (b)
(a) (b)
Figure 6. Transient (a) and a phase portrait (b) the oscillator with compulsory attenuation.
system of coordinates at spiral character of movement of air:
 (6)
(6)
According to the assumptions accepted in aerohydrodynamics of the eq.6 reflect dynamic process for each of particles of the investigated environment. We will solve system of the eq.6 numerical way under the program by means of a method of Runge-Kutta of 4th order in mathematical Mathcad environment (The application 2). The schedules received as a result of calculation under the program in the absence of external braking influence on system (factors α = 0, β = 0, A = 1, B = 0) and value of factors а1 = 0.2, а2 = 0.02, а3 = 0.2, а4 = 0.02, g = 2, Ω = 1.01 are resulted figure 7. On schedules it is accurately looked through spiral character of development of the process, a tropical cyclone reminding under the form.
The analysis of the eq.7 shows what to stop development of self-oscillatory process of volume type it is possible, as well as at the analysis of this process on a plane, by gradual entering into system of additional losses. By analogy to the eqs.5 and 6 mathematical models of a cyclone in this case will become:
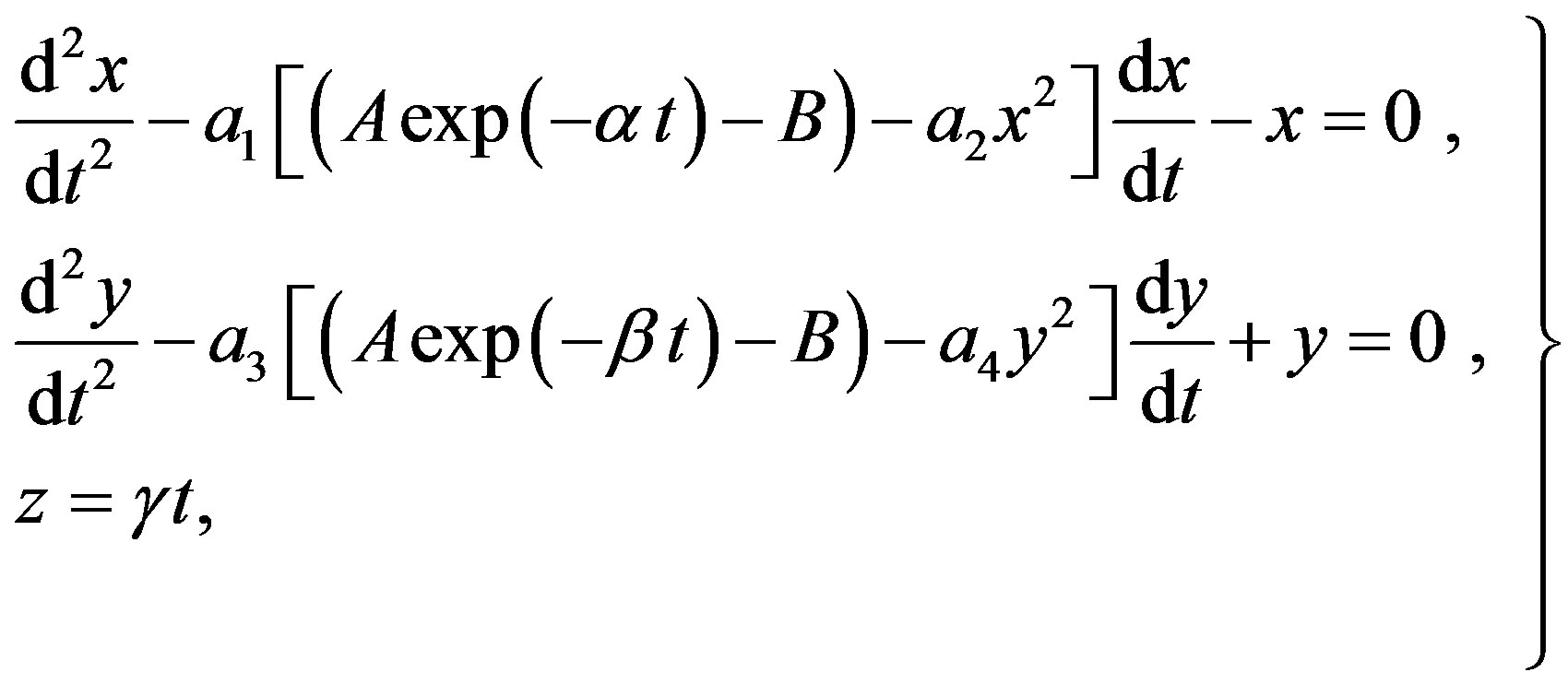 (7)
(7)
where factors α > 0 and β > 0.
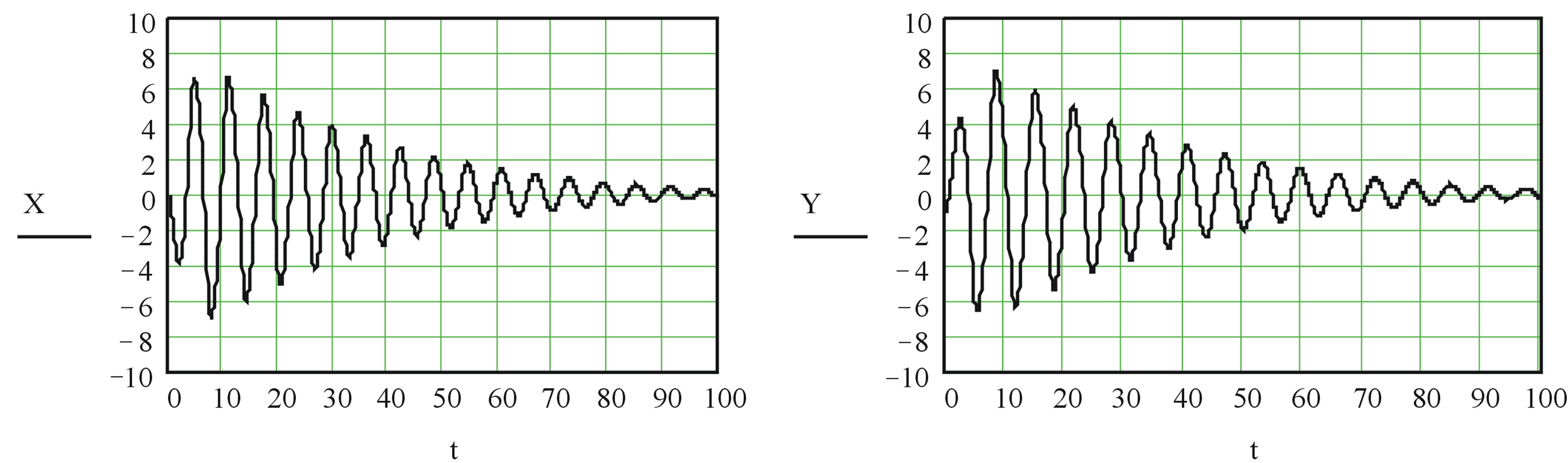
The example of the decision of the eq.7 at values of factors а1 = 0.1, а2 = 0.5, а3 = 0.1, а4 = 0.5, α = 0.05, β = 0.05, g = 2, Ω = 1.05, A = 10, B = 1 is resulted on figure 8. In this case, as well as in an example shown on figure 6, process of self-oscillations instead of two has all three described above a phase: increase of fluctuations, dynamic balance and failure of self-oscillations.
1.5. Vetroenergetichesky Way of Entering of Attenuation in Self-Oscillatory Process
The eq.7 gives the general recipe on restriction of development of self-oscillatory process in system by entering into it of compulsory losses, but, naturally, don’t answer a question as practically it can be carried out.
 (a)
(a)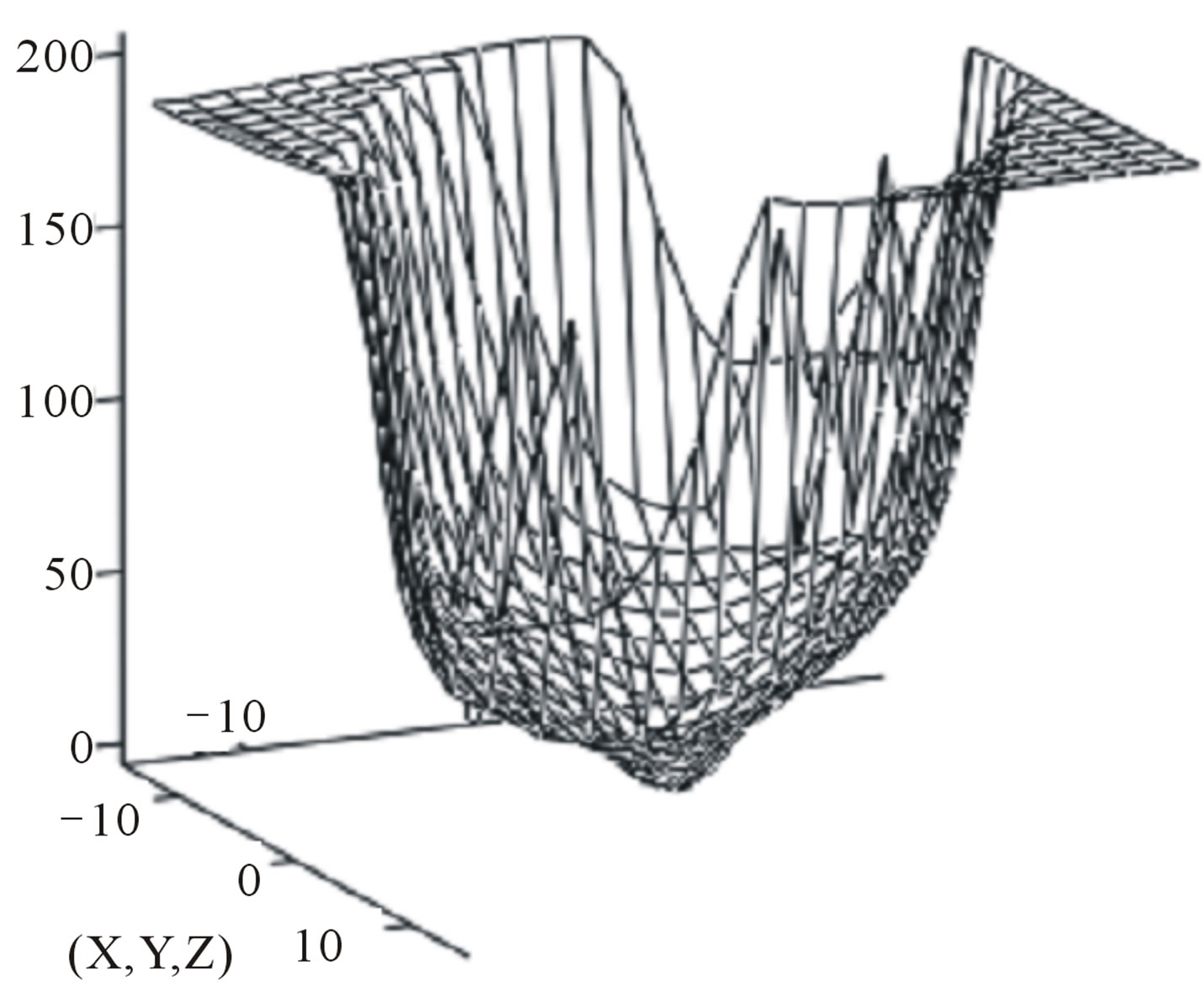 (b)
(b)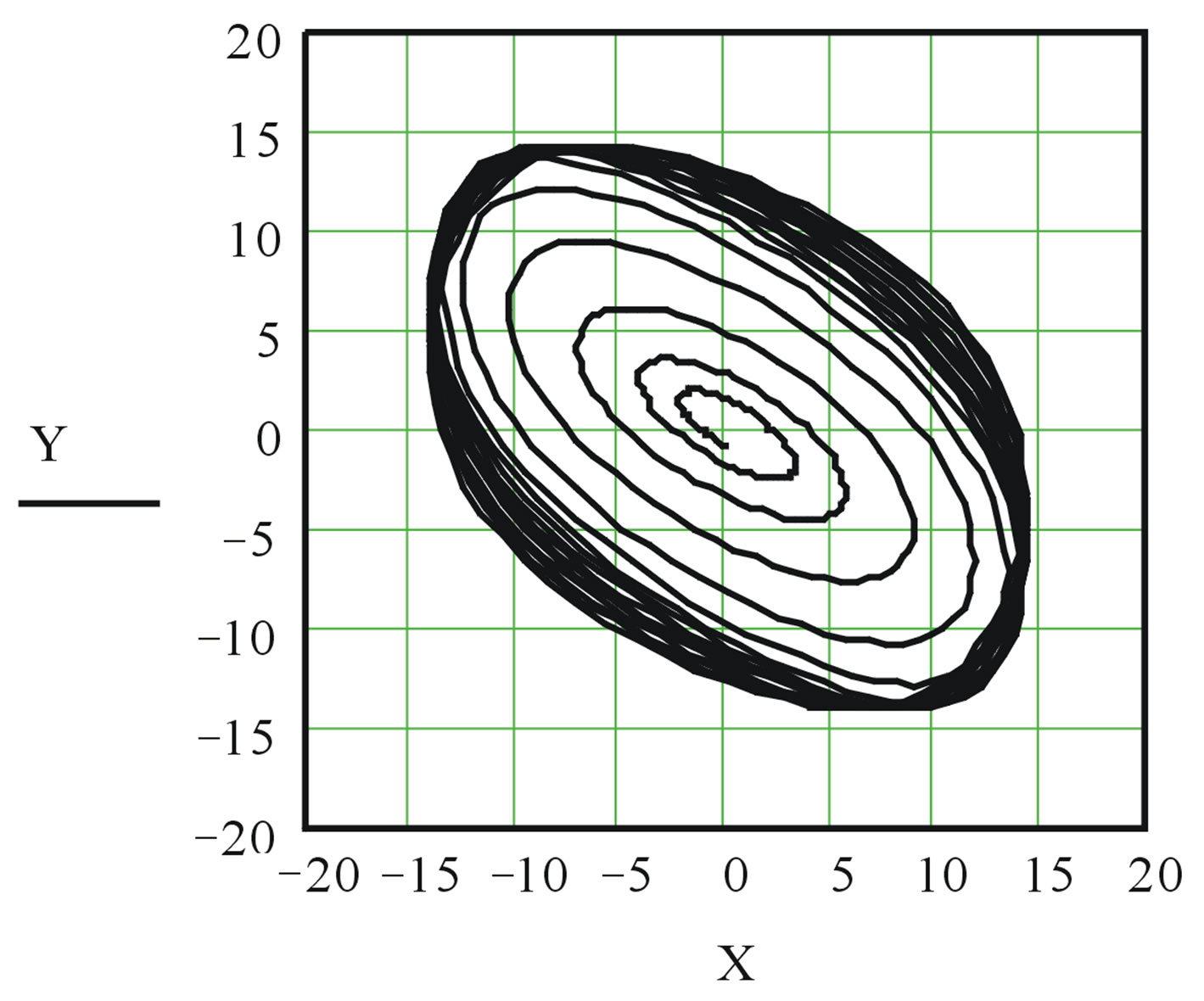 (c)
(c)
Figure 7. Transient (a); A phase portrait (b); Two-dimensional (c) and three-dimensional (d) the image of model of a cyclone.
 (a)
(a)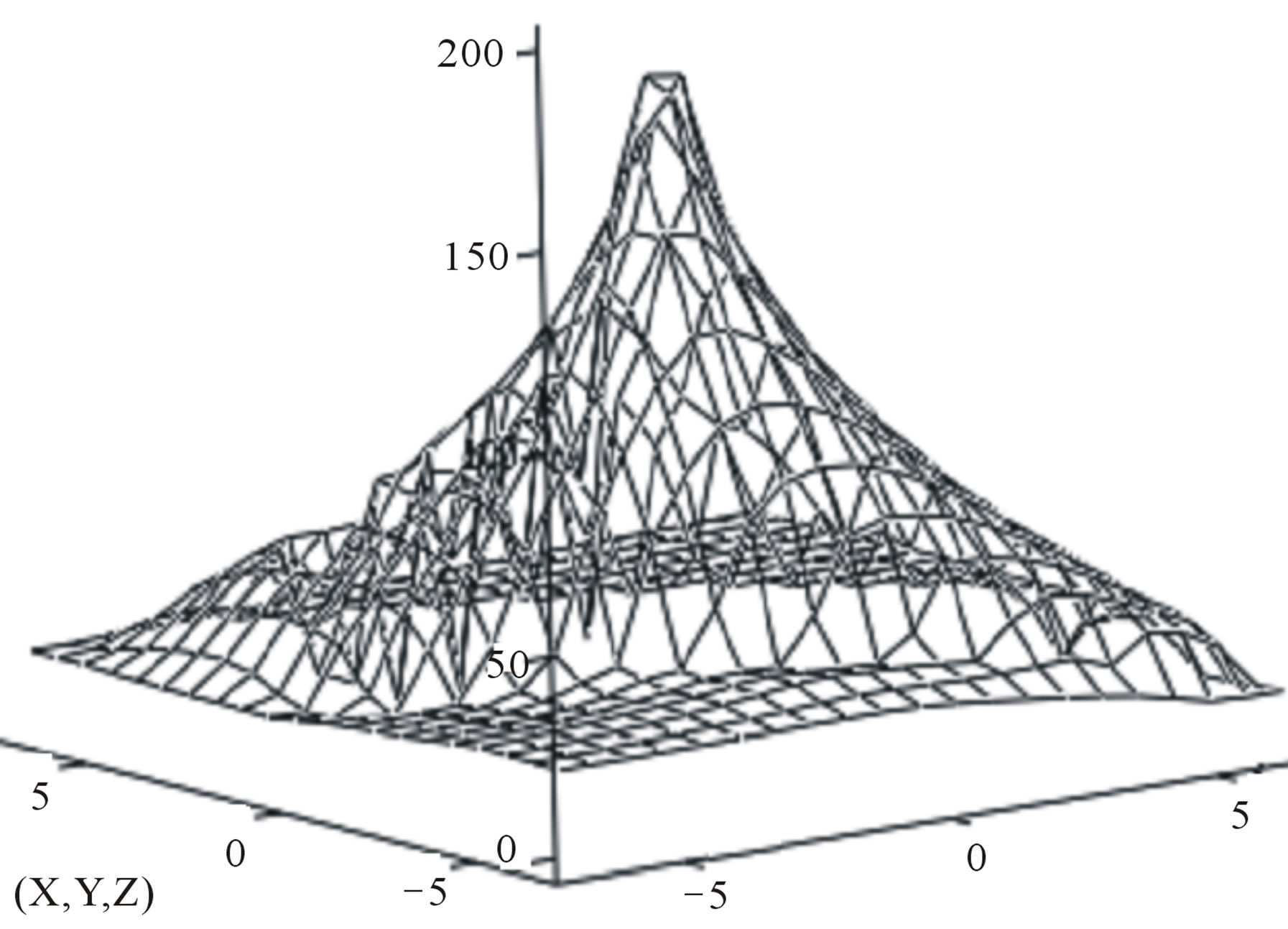 (b)
(b)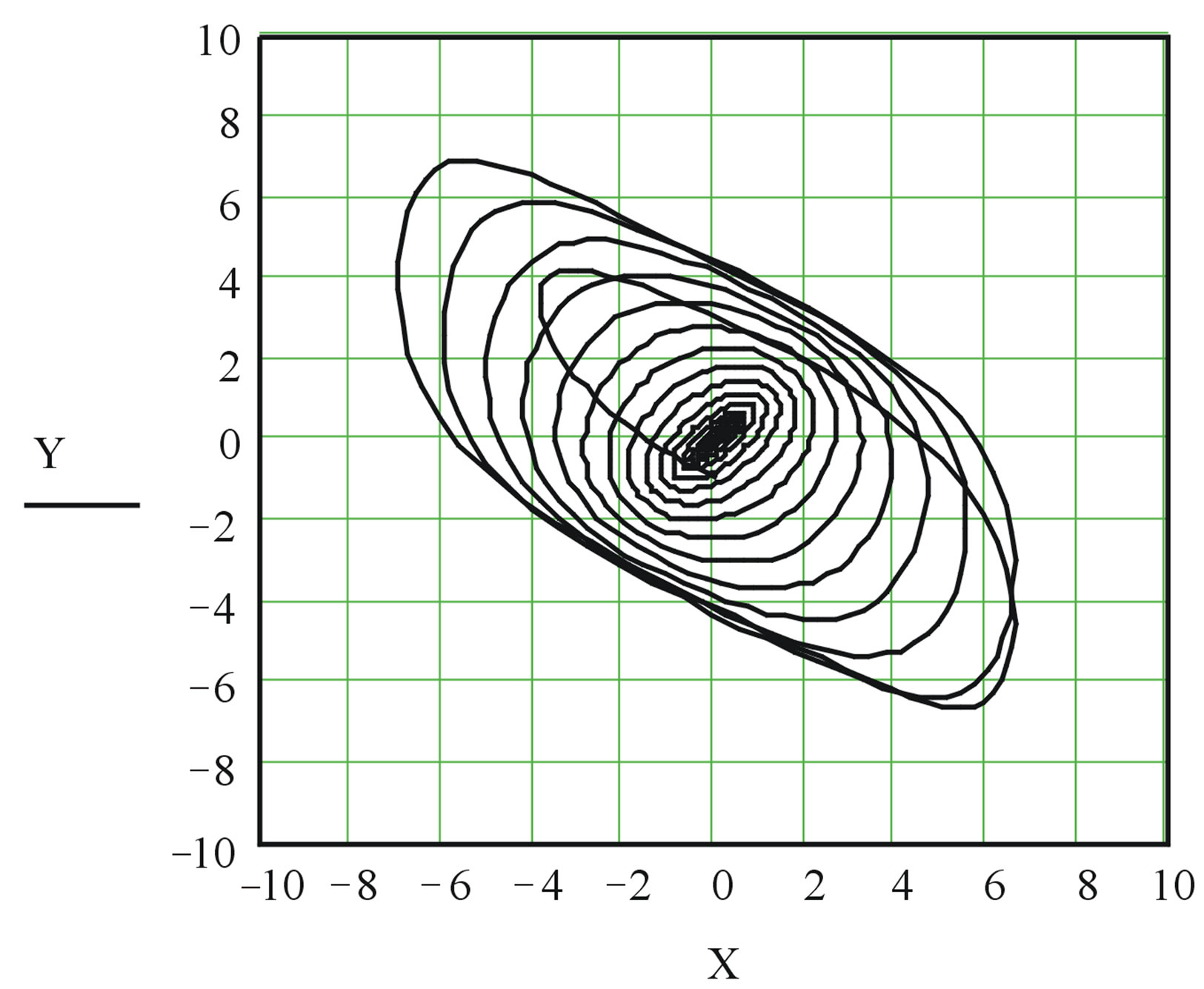 (c)
(c)
Figure 8. Transient (a, b); Two-dimensional (c) and three-dimensional (d) the image of model of a cyclone of type with compulsory attenuation.
Let’s consider thereupon platform work on which one end it is established powerful wind generator, and on another—the fan. At the analysis of work of the wind electrogenerator it is necessary to consider three kinds of transformation of energy and accordingly three kinds of capacity: kinetic energy in unit of time an air stream with a speed V; mechanical energy of a rotating propeller or the turbine and electric energy of the wind electrogenerator. Thus capacity PG @ V3. Considering a great speed of a cyclonic wind, capacity а wind electrogenerator it is possible to accept equal PG = 1 Gw. Such capacity has, for example, with the wind electrogenerator the turbine of the vertical type, developed by firm MWTT from Arigony. The received electric energy is used for an electric motor food on which axis the propeller or the turbine is established. At the efficiency equal of 50%, the work made by such fan:
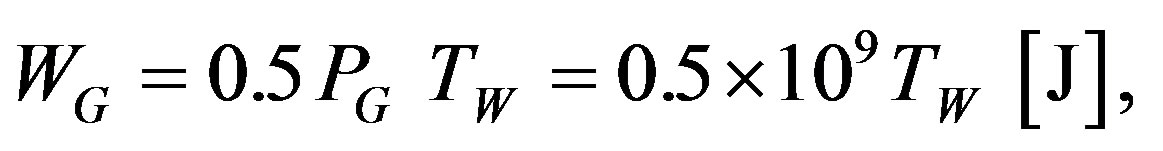 (8)
(8)
where TW—a fan operating time in s.
Similar group of the wind generators-fans established on a platform, it is necessary to place on cyclone periphery (figure 9). Propellers of fans should rotate clockwise, i.e. in a direction opposite to rotation of a vortical air stream in northern hemisphere that should promote braking of development of a cyclone. Thus, in considered model the part of kinetic energy of a cyclone at first will be transformed to electric energy of group of wind electrogenerators which then turns to the energy injected by means of fans in the form of local directed air streams in the basic, “parent” stream in an opposite direction from it and consequently braking development of last. Such power system with negative feedback on energy can be presented in the form of the block diagram resulted on figure 10. First of all two parameters estimate work of the given system: the relation of the “organized” energy WG thrown in the basic air stream by fans, to kinetic
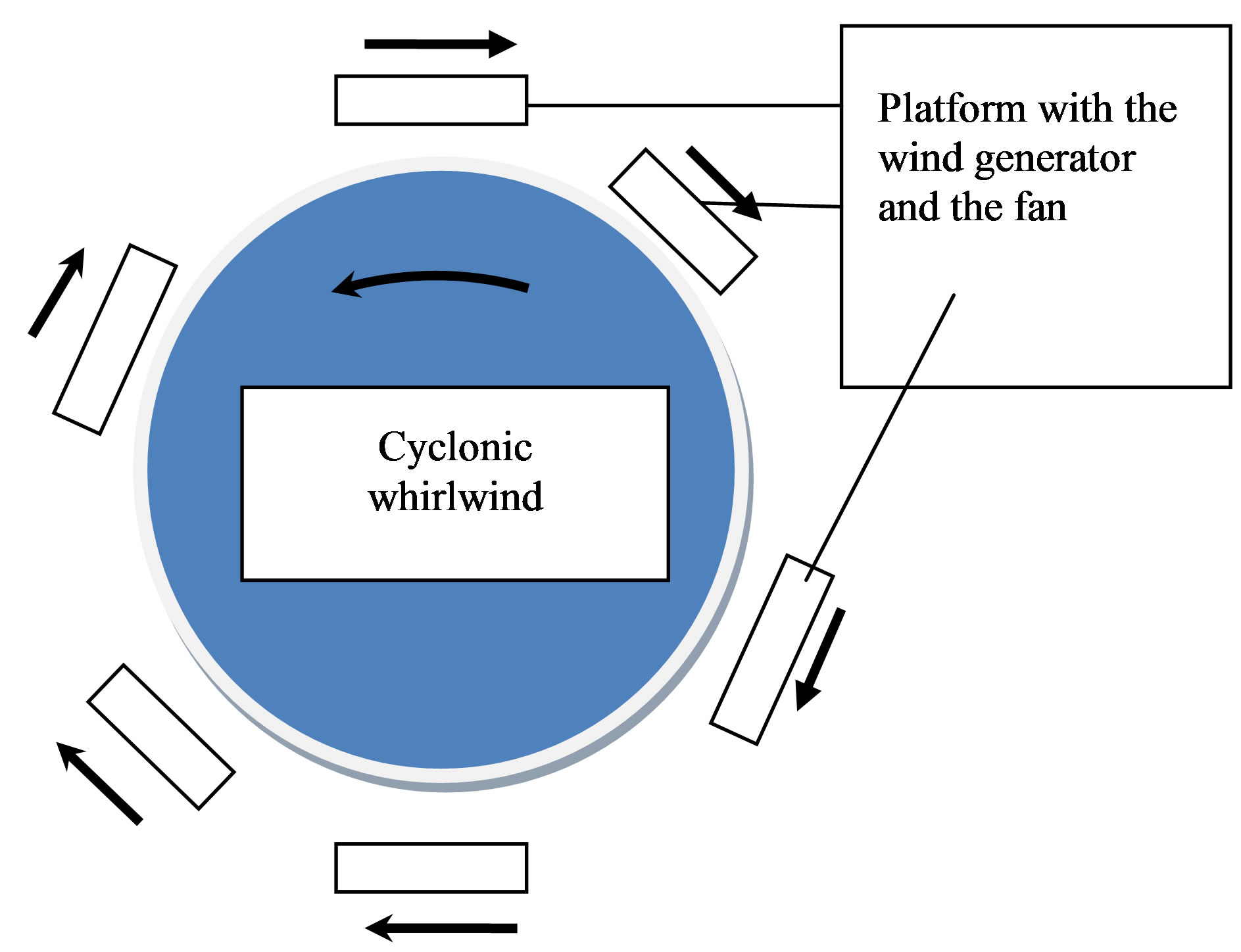
Figure 9. The platforms which had on periphery of a cyclone.

Figure 10. The block diagram of a power system with negative feedback.
energy of “parent” stream WC, т.е a cyclone. We name the given relation in power factor of feedback k =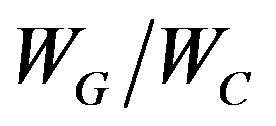 .
.
The second parameter characterizes the inertial properties of the system connected with time of a raising of heated-up air sated moisture from a surface of ocean till the moment of condensation of water steams and allocation by them of heat, feeding with energy a cyclone. At vertical speed of a raising of air V = 1 m/s and height on which there is a condensation of steams, in 5 - 10 km, we will receive for given time ТC = 5000 - 10,000s. During ТC fans should inject such quantity of the “organized” energy which its development should start to brake into a cyclone. Parameters k and ТC define values of factors α > 0 and β > 0 in the eq.8.
The physical mechanism of possible prevention of development of a tropical cyclone at the initial stage when its development can be stopped by means of group of wind generators-fans is that in general. The last can be placed by the special high-speed ships operated by radio and directed to a zone of origin of cyclonic formation after its detection by means of meteorological companions.
2. LABORATORY EXPERIMENT
For check of working capacity of the idea taken as a principle offered way of struggle against the arising cyclone, the following experiment has been made. At the bottom of a cylindrical vessel in diameter of 25 sm and height 40 sm the fan creating a vortical air stream counter-clockwise (cyclone imitation) in 0.05 has been placed m3/s. Over this fan four small fans rotating clockwise, with total capacity of wind streams nearby 0.005 m3/s (figure 11) have been placed. At the bottom of a vessel the water which is warmed up from below to temperature of boiling and production of steam is poured. At inclusion only the big fan in a vessel the cyclic stream of laminar type of warmed up air was formed. At simultaneous inclusion of all five fans the laminar stream was transformed to the turbulent. For the best super-vision
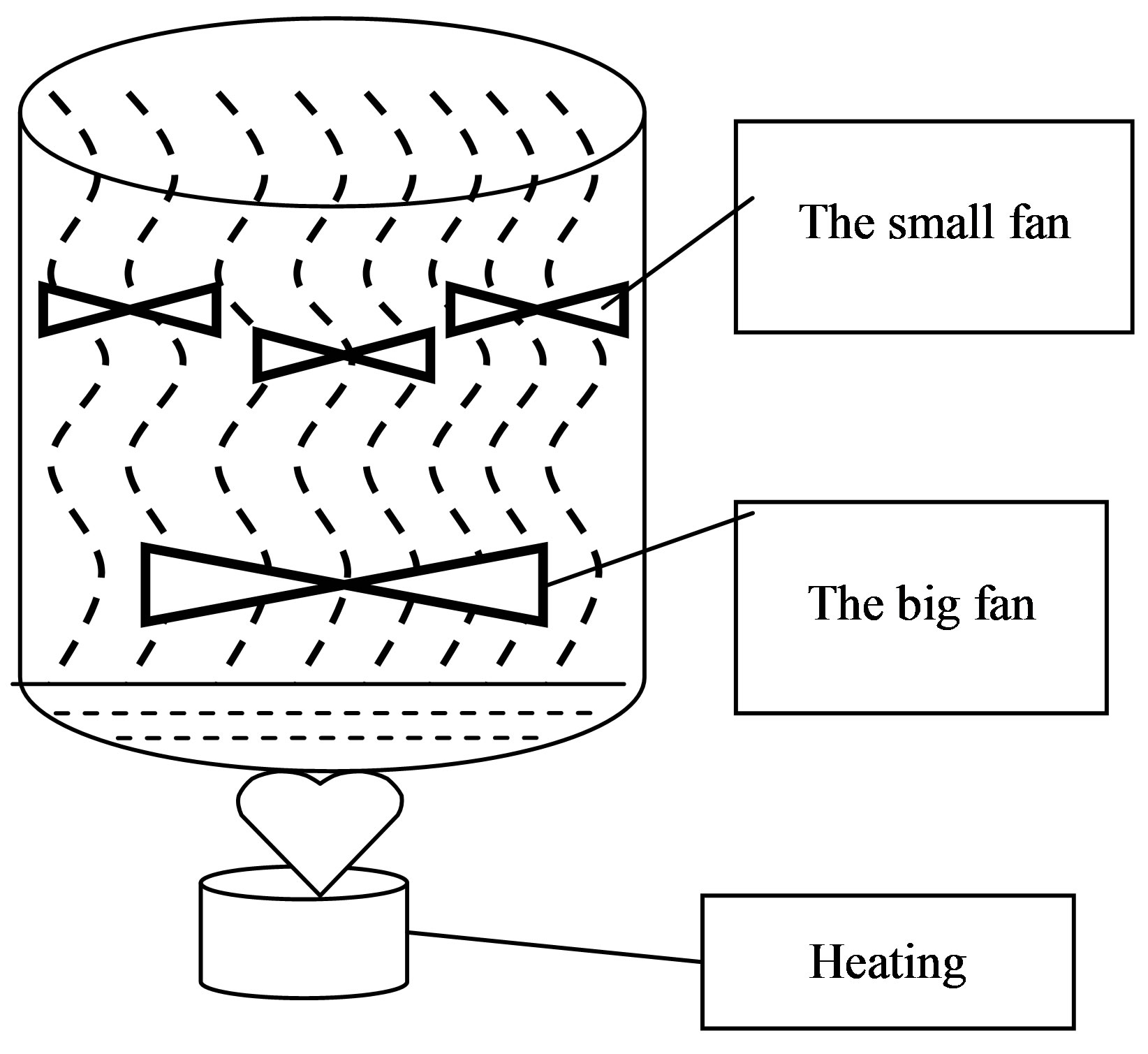
Figure 11. The laboratory installation modeling destruction of a cyclone.
over process of transformation of a laminar stream of air in turbulent in water the metal iodine giving to steams pink coloring has been dissolved.
Thus, the made laboratory experiment has confirmed idea of possible braking of powerful vortical cyclic process by means of other specially organized streams twirled in the opposite side. According to experiment value of factor k = 0.1.
Let’s in passing notice that usually try to get rid from turbulent, whirl of gas and a liquid, creating additional losses and to keep the laminar, ordered process of movement. The opposite recipe here is offered: a laminar stream to transform in chaotic, turbulent which will interfere with cyclone development.
3. QUANTITATIVE ESTIMATION OF PARAMETERS OF WORKING SYSTEM
From resulted above the data follows that for the worker wind-energetic systems of destruction of a cyclone at the initial stage of its origin it is possible to accept factor k = 0.1, and for calculation of energy of fans time TW = 2000с < TC. As a result for energy of one fan at its capacity in 0.5 Gw it agree (8) we will receive: WG ≈ 1012 J. Hence, at energy of a cyclone at initial stage WC = 1014 J and factor k = 0.1 for its destruction 10 generators-fans is required.
4. THE CONCLUSIONS
From the spent analysis and laboratory experiment such conclusions follow:
• The energy destroying a cyclone, should be comparable to its kinetic energy, roughly 1:10, therefore to brake the cyclone it is necessary at the initial stage of its origin;
• Energy of braking as the source should use a cyclone by direct selection from it parts of energy with the help wind electrogenerator and transformations of their electric energy to air streams by means of powerful fans; at the heart of such transformation the principle of negative feedback consisting in this case in injection in a cyclone of additional energy in an opposite direction from the basic movement lies;
• It is necessary to transform the ordered, air streams rotating on a spiral in chaotic, turbulent which won’t allow to a cyclone to develop free;
• For full check of the offered idea on cyclone destruction at the initial stage of its development more fullscale experiment in pool in diameter more 50 m is required.
REFERENCES
- Pogosjan, H.P. (1976) Cyclone’s. Meteo Publisher.
- Kachurin, L.G. (1978) Physical of a basis of influence on atmospheric processes. Meteo Publisher.
- Kaganov, V.I. (2005) Radio engineering chains and signals. The computerized course. Forum Publisher.
APPENDIX 1
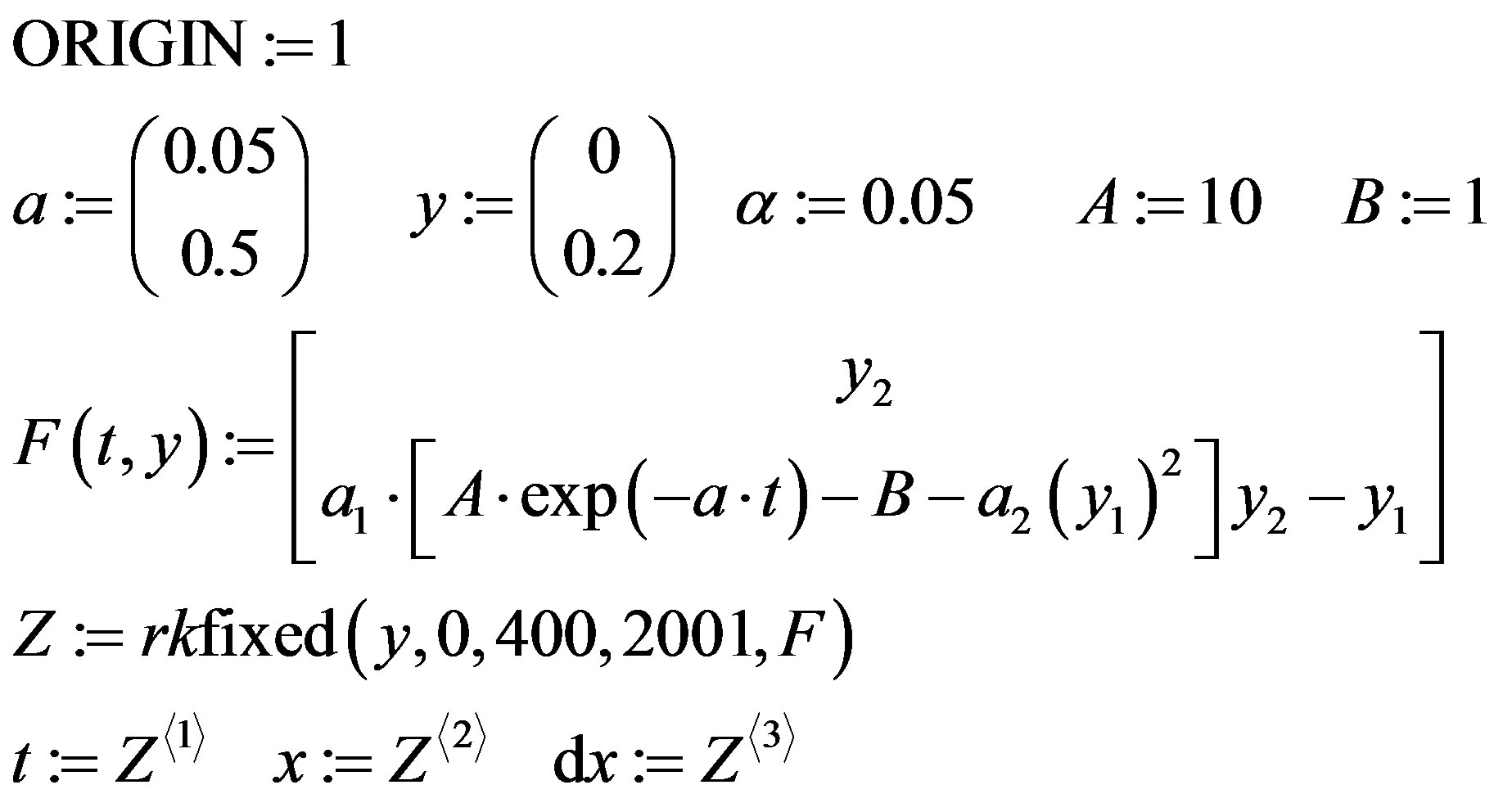
APPENDIX 2