Journal of Modern Physics
Vol. 2 No. 9 (2011) , Article ID: 7143 , 7 pages DOI:10.4236/jmp.2011.29122
Spin Polarization of the Uniform Three-Dimensional Electron Gas
Groupe de Physique des Semi-Conducteurs, Département de Physique, Université de Perpignan via Domitia, LAMPS, Perpignan, France
E-mail: huynh@univ-perp.fr
Received March 23, 2011; revised April 29, 2011; accepted May 23, 2011
Keywords: Electron Gas, Correlation Energy; Spin Stiffness, Total Energy, Spin Susceptibility, Paramagnetic-and-Ferromagnetic Phase Transitions, Wigner States
ABSTRACT
A simple-and-analytic form for total energy (or ground-state energy) in the uniform three-dimensional electron gas, expressed as a function of any Wigner-Seitz radius rs and relative spin polarization ζ is obtained with a very good accuracy of 0.036% from the Stoner model and our interpolation between high-and-low density limits with use of a two-point approach for the correlation energy and spin stiffness at rs = 1 and 70. This suggests a satisfactory desciption of some physical properties such as: paramagnetic-ferromagnetic phase transition and thermodynamic-and-optical phenomena.
1. Introduction
First of all, in the uniform three-dimensional electron gas (U3DEG) at zero temperature, it should be noted that the state of this system is entirely specified by the WignerSeitz radius rs being related to the total electron density n by: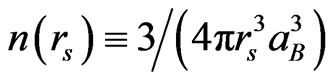 , where aB = 0.53 × 10–8 cm is the Bohr radius, and the relative spin polarization ζ defined by:
, where aB = 0.53 × 10–8 cm is the Bohr radius, and the relative spin polarization ζ defined by: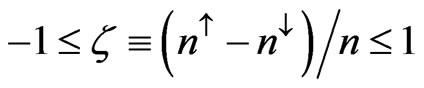 . Here,
. Here, 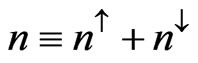 , and
, and 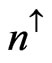 and
and 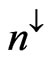 mean the up-and down-spin electron densities, respectively, noting that the two particular values of ζ (= 0 and ±1) denote the paramagnetic (P) and ferromagnetic, (F) states, respectively. Furthermore, all the energies given in the following are calculated in Rydbergs (Ry). Such an U3DEG is one of the basic models of many-body physics, and has been investigated for over 73 years [1-14]. In particular, for ζ = 0, some physical properties at any rs such as: Ferrell’s condition for the stability of the total energy [7], electronic pressure and compressibility [7], virial theorem [12], asymptotic forms for plasmon-dispersion. Coefficients obtained in low-and-high plasmon-energy limits [10], and spin susceptibility [8,9,11], were expressed in terms of the total energy and correlation energy, and their respective derivatives, being denoted in general forms for a presentation simplicity as:
mean the up-and down-spin electron densities, respectively, noting that the two particular values of ζ (= 0 and ±1) denote the paramagnetic (P) and ferromagnetic, (F) states, respectively. Furthermore, all the energies given in the following are calculated in Rydbergs (Ry). Such an U3DEG is one of the basic models of many-body physics, and has been investigated for over 73 years [1-14]. In particular, for ζ = 0, some physical properties at any rs such as: Ferrell’s condition for the stability of the total energy [7], electronic pressure and compressibility [7], virial theorem [12], asymptotic forms for plasmon-dispersion. Coefficients obtained in low-and-high plasmon-energy limits [10], and spin susceptibility [8,9,11], were expressed in terms of the total energy and correlation energy, and their respective derivatives, being denoted in general forms for a presentation simplicity as: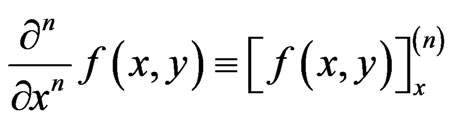 ,
, 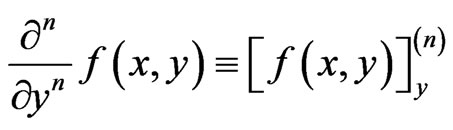 , for n = 1, 2, …
, for n = 1, 2, …
The aim of the present paper is to investigate a simpleand-analytic form for E(rs, ζ) in the U3DEG, obtained with a very good accuracy of 0.036% from the Stoner model, an interpolation between high-and-low density limits (HLDL), and a two-point approach for correlation energy Ec(rs, ζ) and spin stiffness αc(rs) at rs = 1 and 70, giving rise to a satisfactory description of some physical properties such as: PF-phase transition and thermodynamic-and-optical phenomena.
2. Accurate and Simple Analytic Form for E(rs, ζ) at Any rs and ζ
Accounting for a neutralizing positive background and denoting , the total energy per particle is given by:
, the total energy per particle is given by:
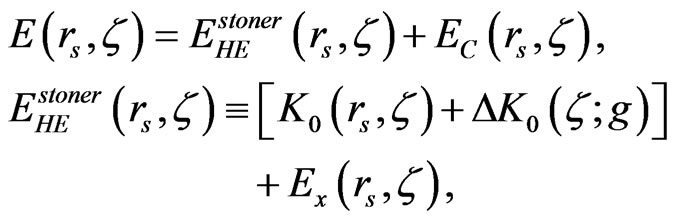 (1)
(1)
where  is the exchange energy,
is the exchange energy, 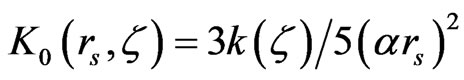 is the kinetic energy at Fermi surface,
is the kinetic energy at Fermi surface, 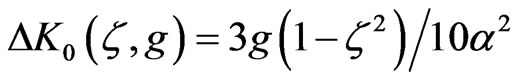 is the kinetic energy correction calculated within the mean-field Hartree-Fock approximation using the noninteracting wave function (i.e., a Stoner model [10]), and g is an empirical parameter chosen so that the relative errors of E(rs, ζ) for any rs and are minimized (its value is given in Table 1). Moreover, we use in this work a general spin-interpolation formula for Ec(rs, ζ) proposed by Vosko et al. [5]
is the kinetic energy correction calculated within the mean-field Hartree-Fock approximation using the noninteracting wave function (i.e., a Stoner model [10]), and g is an empirical parameter chosen so that the relative errors of E(rs, ζ) for any rs and are minimized (its value is given in Table 1). Moreover, we use in this work a general spin-interpolation formula for Ec(rs, ζ) proposed by Vosko et al. [5]
 (2)
(2)
In Equations (1) and (2), the three functions k(ζ), h(ζ) and f(ζ) are defined by:
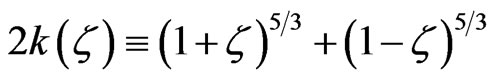 ,
, 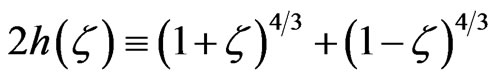 ,
, 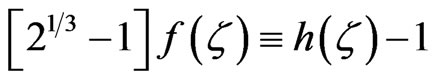 that gives:
that gives: 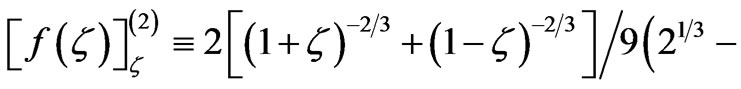
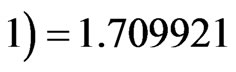 for ζ = 0.
for ζ = 0.
From Equations (1) and (2) one notes that: E(rs, ζ) = Ec(rs, –ζ) and Ec(rs, ζ) = Ec(rs, –ζ), reducing to the interval: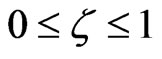 , and that if the three functions: Ec(rs, 0), Ec(rs, 1) and αc(rs), represented by X(rs; a), are known, then Ec (rs, ζ) and E(rs, ζ) are therefore determined. Here, the function X(rs; a) can be expressed in terms of its two exact asymptotic results given in HLDL, G(rs) and W(rs, a),
, and that if the three functions: Ec(rs, 0), Ec(rs, 1) and αc(rs), represented by X(rs; a), are known, then Ec (rs, ζ) and E(rs, ζ) are therefore determined. Here, the function X(rs; a) can be expressed in terms of its two exact asymptotic results given in HLDL, G(rs) and W(rs, a),
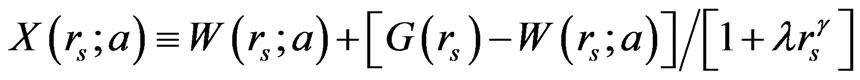 , (3)
, (3)
reducing in the HDL to: 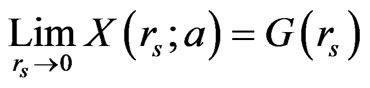 and in the LDL to:
and in the LDL to: . Thus, the present method used to obtain our result (3) for X(rs; a) is the interpolation between HLDL, being similar to those also used in [8,9,11]. It should be noted that this is the unique method used to obtain the analytic expression for X(rs; a) at any rs.
. Thus, the present method used to obtain our result (3) for X(rs; a) is the interpolation between HLDL, being similar to those also used in [8,9,11]. It should be noted that this is the unique method used to obtain the analytic expression for X(rs; a) at any rs.
In the HDL, in which the random-phase approxima
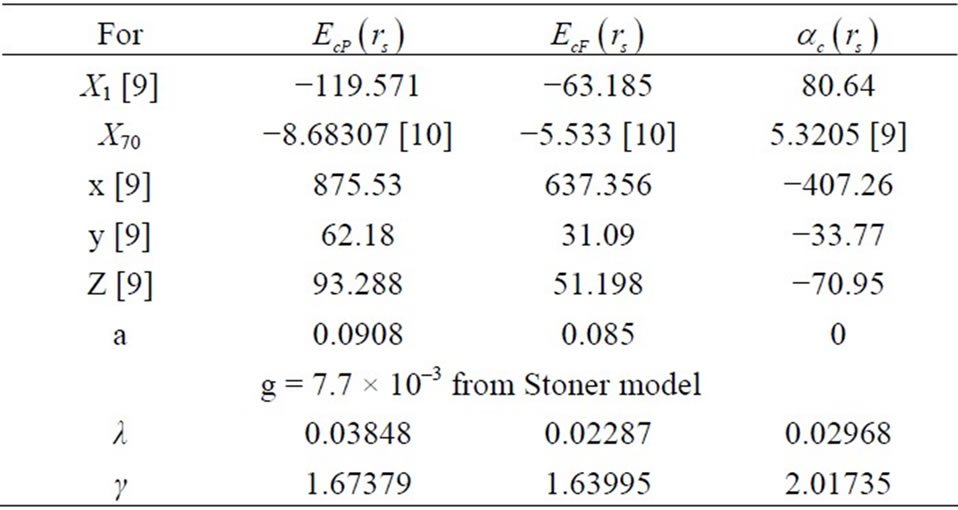
Table 1. Parameters of the best fit to Equations (4) and (7). Energies in mRy.
tion (RPA) may be used, the function G(rs) can be written under a condensed Gell-Mann-and-Bruecker’s as [2,9]:
G(rs) = yln(rs) – z,(4)
where the values of y and z [13] are given in Table 1.
In the LDL (or beyond RPA), the function W(rs) can be written under a condensed Wigner’s form [1,9] as:
W(rs) = –x/(a + rs),(5)
where the values of the empirical parameter a are chosen so that the relative errors of E(rs, ζ) for any rs and ζ are minimized. The values of a and x [9] are reported in Table 1.
Going back to Equation (3), in order to determine the constants λ and γ, we now use a two-point approach by denoting: 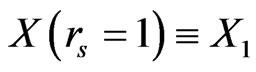 [9] and
[9] and 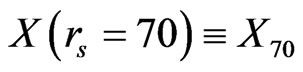 [9,10], being reported in Table 1. Thus, those constants λ and γ are determined by:
[9,10], being reported in Table 1. Thus, those constants λ and γ are determined by:
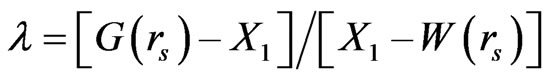 for rs = 1,(6)
for rs = 1,(6)
and
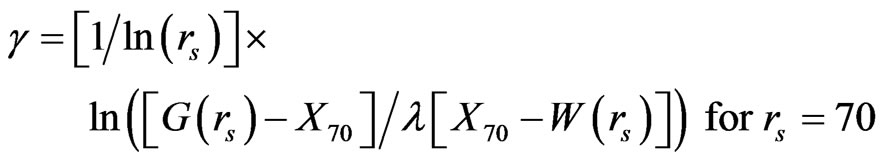 (7)
(7)
In summary, from Equations (3)-(7) and Table 1, the correlation energy Ec(rs, ζ) given in Equation (2) and total energy E(rs, ζ) in Equation (1) are thus determined. Then, in order to calculate the relative errors (RE) of E(rs, ζ) from the present result (1) and those from other approximate results evaluated from [4,8,9,11], neglecting the Stoner model, we will use the accurate results obtained from their diffusion Monte Carlo (DMC) method [4] by using backflow wave functions and twist averaged boundary conditions to obtain the accurate values of E(rs, ζ) at low densities  and for
and for  with standard errors in units of 10–8 Ry. This formula of RE is defined by: 1-(Approximate results/ZLC’s results). So, it is found that our present results of E(rs, ζ) are accurate to within 0.036% while other approximate ones [4, 8,9,11] only give: 0.24%, 0.29%, 0.42% and 0.471%, respectively. In Table 2, for a comparison, we only report our results of RE and those obtained from [4,11].
with standard errors in units of 10–8 Ry. This formula of RE is defined by: 1-(Approximate results/ZLC’s results). So, it is found that our present results of E(rs, ζ) are accurate to within 0.036% while other approximate ones [4, 8,9,11] only give: 0.24%, 0.29%, 0.42% and 0.471%, respectively. In Table 2, for a comparison, we only report our results of RE and those obtained from [4,11].
Furthermore, if neglecting the Stoner model [i.e., g = 0], then the maximal RE in absolute value of the present results is now found to be equal to 0.0625% (>0.036%), suggesting that such a Stoner model used is needed to obtain a better accuracy.
Now, it is interesting to extend our numerical results of E(rs, ζ) for 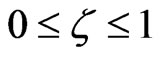 at higher density range:
at higher density range: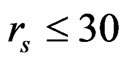
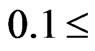 , being reported in Table 3, in which for a comparison we also include some CA’s results [4].
, being reported in Table 3, in which for a comparison we also include some CA’s results [4].
Some physical properties derived from our accurateand-simple forms for E(rs, ζ) and Ec(rs, ζ) given in Equa-
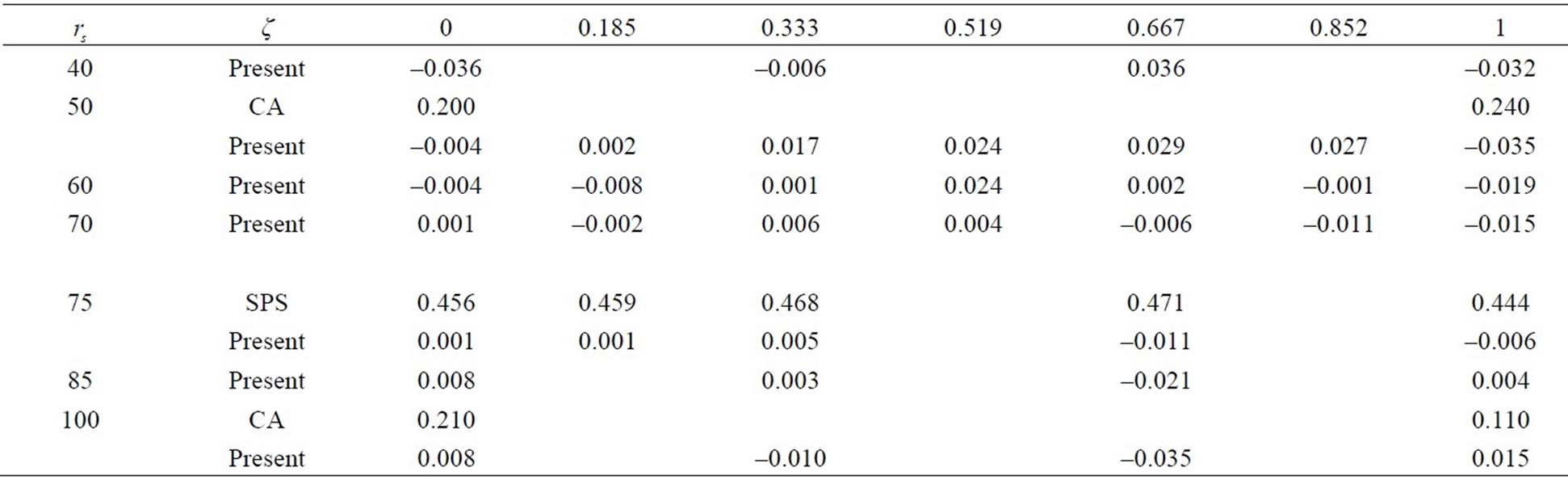
Table 2. REs (%) of the present results of E(rs, ζ) (Present) are compared with those of CA [4] and SPS [11].
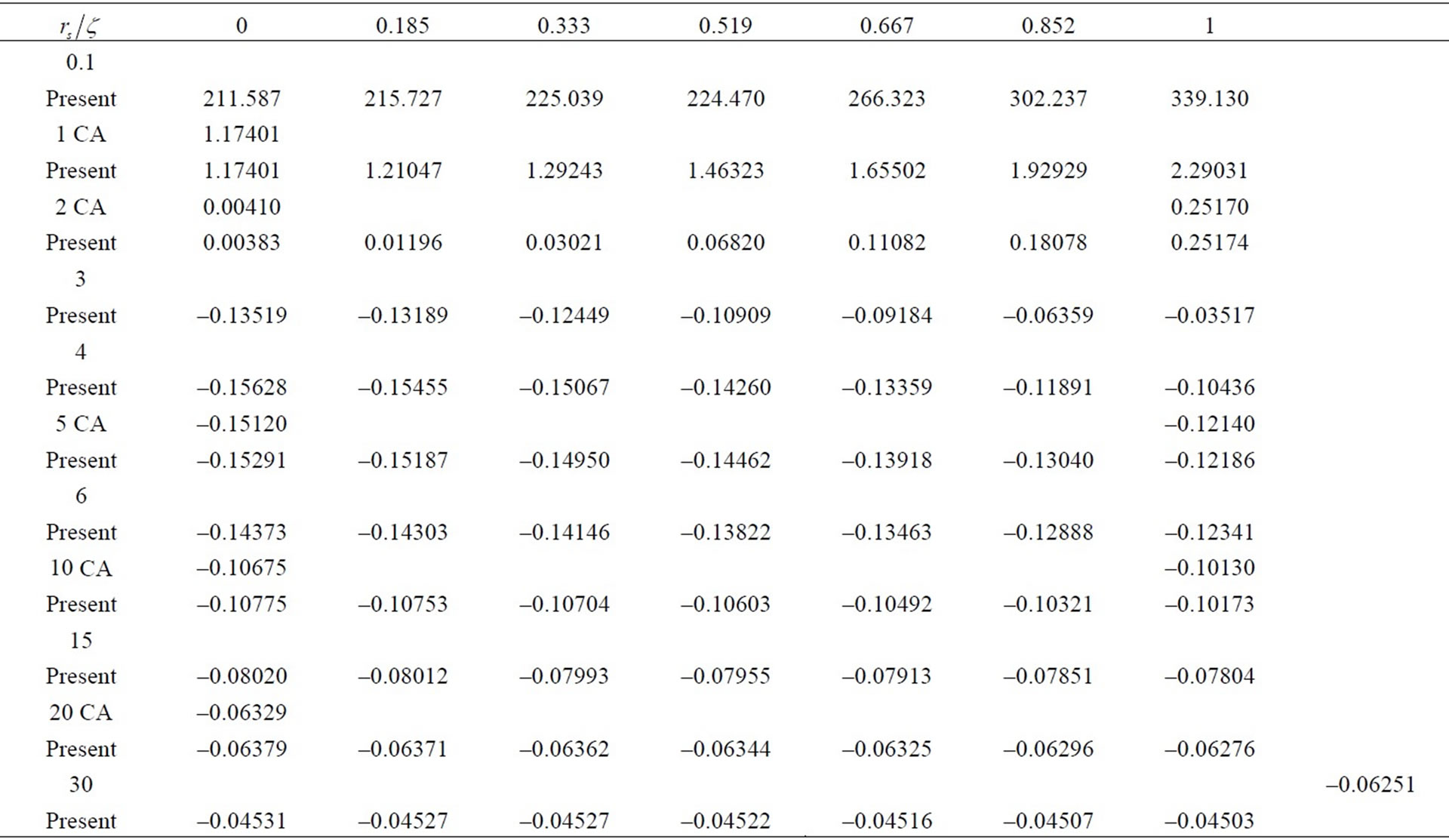
Table 3. Present results of total energy for 0 ≤ ζ ≤ 1 and in 0.1 ≤ rs ≤ 30 compared with CA [4].
tions (1,2) are investigated as follows.
3. Phase Transition
3.1. First-Order Phase Transition from the Total Energy
From the three states such as: the P-state represented by EP(rs), the F-state by EF(rs), and the Fermi Wigner crystal (W) state by [13]:
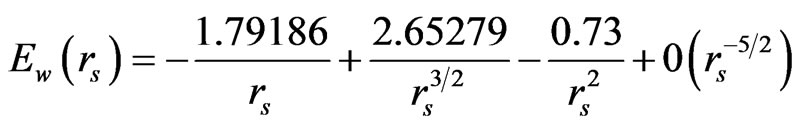
being obtained at low electron densities and beyond RPA, we can evaluate the total-energy differences: 
 and
and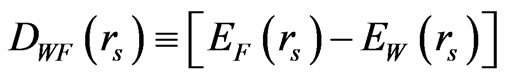 .
.
1) The DFP(rs) is negative for rs < 78.147 (the P-phase) and positive for rs > 78.147, giving rise to a first-order PE-phase transition which occurs at a critical value: rsC = 78.147, in accordance with CA’s data [4]: rsC = 75 ± 5 and with ZLC’s data [10]: 75 < rsC < 85. One notes that this critical value: rsC = 78.147 corresponds to a critical density: nC = 3.37 × 1018 cm3 being found to be equivalent to the metal-insulator transition in the n-type excited intrinsic Si occurring at 2.71 × 1018 cm3 [13] and in the P-Si at 3.52 × 1018 cm3 [14].
2) The DWF(rs) is negative for rs < 115.49 (the F-phase) and positive for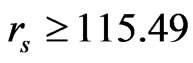 , giving rise to the WFphase transition which occurs at a critical value: rsC = 115.49, in good agreement with CA’s data [4]: rsC = 100 ± 20.
, giving rise to the WFphase transition which occurs at a critical value: rsC = 115.49, in good agreement with CA’s data [4]: rsC = 100 ± 20.
We futher evaluate the total-energy difference times as: 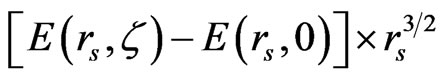 (Ry) and plot versus spin polarization ζ for different values of rs in the following Figure 1.
(Ry) and plot versus spin polarization ζ for different values of rs in the following Figure 1.
Some concluding remarks are given below.
1) At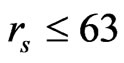 , the system is P, with the unpolarized phase stable.
, the system is P, with the unpolarized phase stable.
2) As the electron density decreases, at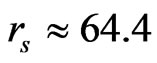 , the system becomes unstable with respect to spin fluctuations while ZLC [10] obtained the corresponding instable point at
, the system becomes unstable with respect to spin fluctuations while ZLC [10] obtained the corresponding instable point at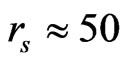 .
.
3) The partially polarized states become stable at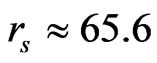 .
.
4) As the electron density continues to decrease, the fully polarized state has a lower energy with respect to unpolarized state at 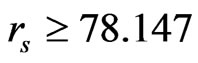 while a corresponding ZLC’s estimation [10] is
while a corresponding ZLC’s estimation [10] is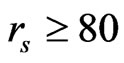 . We also find that the partially polarized state has an even lower energy.
. We also find that the partially polarized state has an even lower energy.
3.2. Second-Order Phase Transition from the Spin Susceptibility
First of all, if denoting the unit vector, Bohr magneton, magnetic field and spin susceptibility, respectively, by: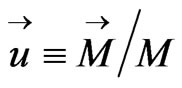 ,
,  , B(G) and χ (erg/cm3·G2) the magnetization vector is given by:
, B(G) and χ (erg/cm3·G2) the magnetization vector is given by: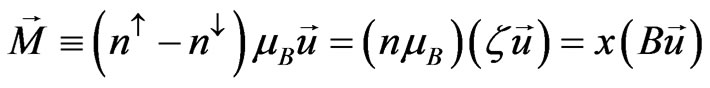 , leading to: B
, leading to: B

Figure 1.  vs ζ for different rs.
vs ζ for different rs.
= ζnµB/χ. Then, the interaction-energy density U required to build up this magnetization is given by
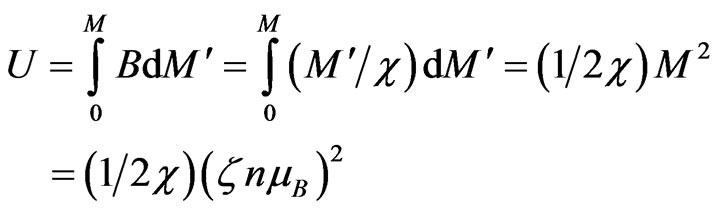 . (8)
. (8)
Now, from Equation (1), by a variable change: x = cζ, c being a length unit, x thus varies from –c to c and the U3DEG induces from the Hook’s law an elastic (or conservative) force for :
: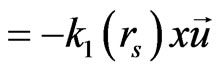
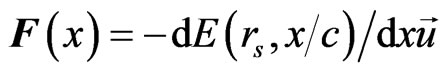 , where the spring constant (or force constant) is defined by:
, where the spring constant (or force constant) is defined by: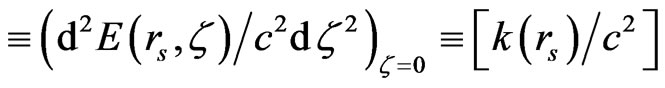
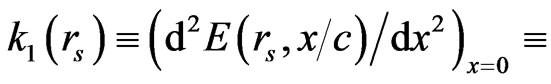 , that gives:
, that gives:
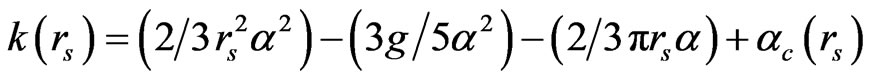 being a simple-and-analytic form and used to compute following physical quantities.
being a simple-and-analytic form and used to compute following physical quantities.
Then, in such an elastic-force model, the work required to build up the magnetization is

being used to define the interaction-energy density by: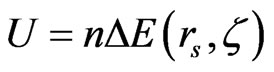 , identical to the result (8), that leads to a simple form for the spin susceptibility χ(erg/cm3·G2) as:
, identical to the result (8), that leads to a simple form for the spin susceptibility χ(erg/cm3·G2) as:
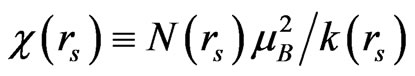 (9)
(9)
We now evaluate our present result (9) and plot versus rs in the following Figure 2, in which we also report other results from [8,9], indicating that our present result of χ shows a singularity at a critical value: 65.6, defining thus the second-order PF-phase transition, which can be compared with ZLC’s result [10]: 50.
4. Some Thermodynamic-Optical Phenomena
1) We first investigate the Ferrell’s condition for the stability of the total energy E(rs, ζ) defined by [7]:
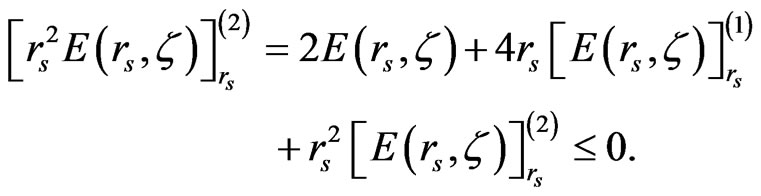 (10)
(10)
Our numerical calculation indicates that it is valid up to a superior value of rs found to be given by: rsS =1200, 1400, 2200, 2300, 2600, 2700, 16000 and +∞ for ζ = 0, 0.5, 0.78, 0.79, 0.83, 0.84, 0.99 and 1, respectively, suggesting that rsS increases with increasing ζ.
2) The electronic pressure is defined [7] and related to the generalized virial theorem given in Equation (A4) of
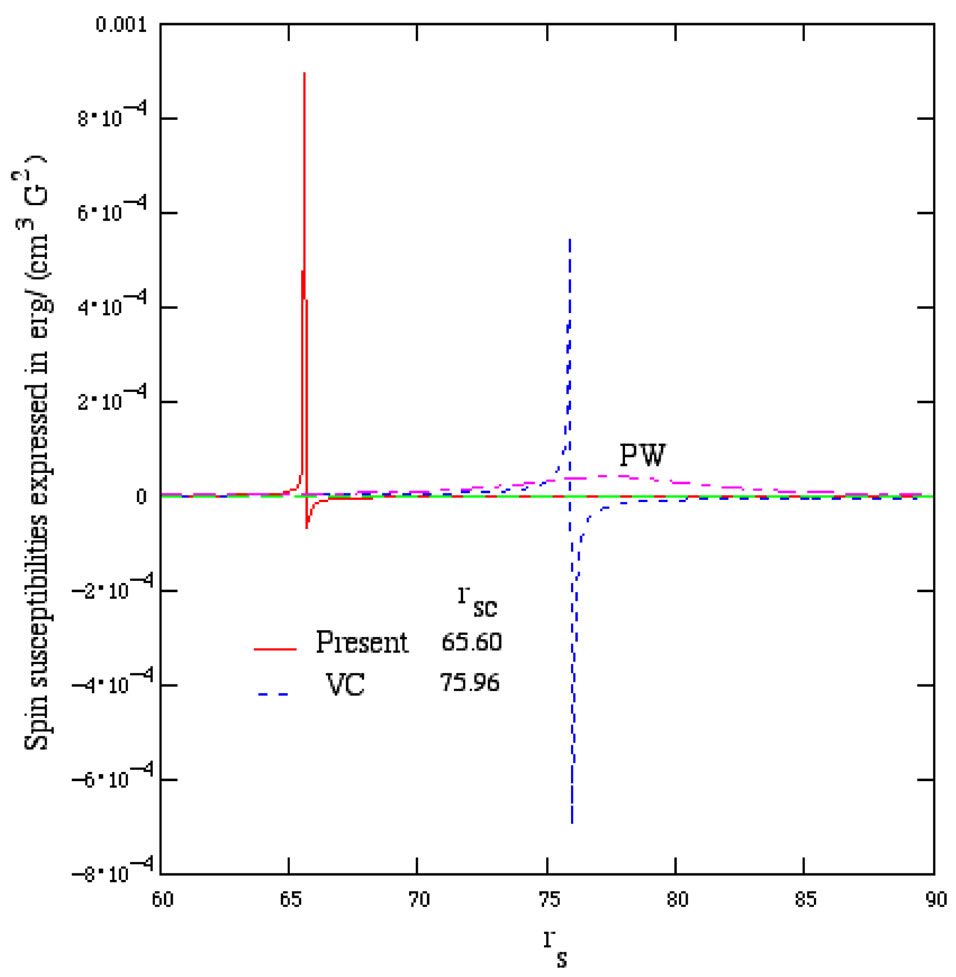
Figure 2. Spin susceptibilities vs rs.
the Appendix A by:
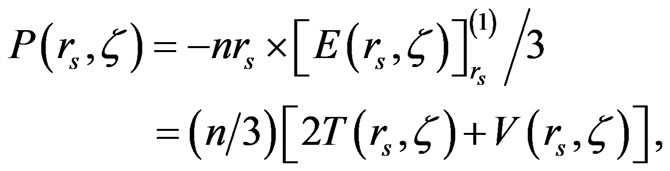 (11)
(11)
which becomes negative for rs ≥ 4.1908 at ζ = 0 (in good accordance with the Ichimaru’s result [7], rs > 4.2), for rs ≥ 4.569 at ζ = 0.5, and for rs ≥ 5.653 at ζ =1. This means that the equilibrium densities of the total energy E(rs, ζ) occur at 4.1908, 4.569 and 5.653 for ζ = 0, 0.5 and 1, respectively, suggesting that those values increase with increasing ζ.
3) The compressibility of the non-interacting U3DEG is defined by: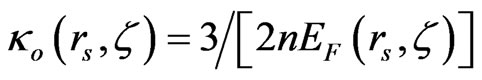 , where EF(rs, ζ) is the Fermi energy, and via the compressibility sum rule, the inverse reduced compressibility can thus be evaluated by:
, where EF(rs, ζ) is the Fermi energy, and via the compressibility sum rule, the inverse reduced compressibility can thus be evaluated by:
 , (12)
, (12)
where γo(rs, ζ) is determined in Equation (B3) of the the Appendix B.
Our numerical calculation indicates that it becomes negative for rs ≥ 5.2597 at ζ = 0 (in good accordance with the Ichimaru’s result [7]: rs > 5.3), for rs ≥ 5.08 at ζ = 0.5, and for rs ≥ 4.55 at ζ =1, noting also that this negative compressibility does not imply an instability of the system when a rigid background of compensating charge is assumed.
4) Finally, in order to compare the two functions γ∞ and γo determined in Equations (B2) and (B3) of the Appendix B, we can study the asymptotic forms for plasmon dispersion coefficient β as follows.
For sufficiently low plasmon energies (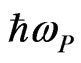 ) and if one disregards the relaxation effect in the short-time domain, β is thus reduced to [7]:
) and if one disregards the relaxation effect in the short-time domain, β is thus reduced to [7]:
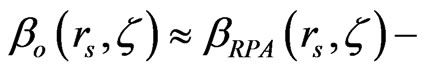 , where
, where 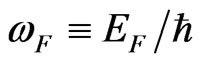 and in the RPA: βRPA = 3ωF/5ωp, and for a sufficiently high plasmon energies, one obtains [7]:
and in the RPA: βRPA = 3ωF/5ωp, and for a sufficiently high plasmon energies, one obtains [7]: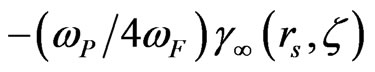
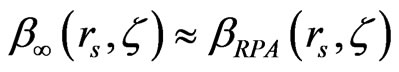 . Therefore, one gets:
. Therefore, one gets:
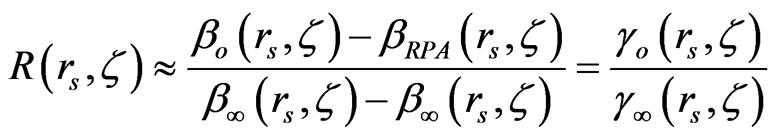 . (13)
. (13)
giving for any rs and ζ: 1.3 ≤ R(rs, ζ) ≤1.7, meaning that (rs, ζ) >1 or βo(rs, ζ) > β∞(rs, ζ) .
5. Concluding Remarks
In summary, we have developed simple analytic forms for E(rs, ζ) and Ec(rs, ζ), by basing on the Stoner model and interpolation between correct HLDL with the use of a two-point approach for correlation energy and spin stiffness at rs =1 and 70, giving rise to:
1) A best precision of the order of 0.036% for our present form for total energy, being found to be more accurate compared with other works [4,8,9,11], as given in Table 2, and 2) A satisfactory description of some physical properties such as: PF-phase transition and thermodynamic and optical phenomena, as given in above Sections 3 and 4.
6. Acknowledgements
The author wishes to thank the referee of the original manuscript for her (his) helpful remarks and suggestions, which have greatly improved the presentation of this paper, and also Dr. Chesneau Xavier for his interest in this work.
REFERENCES
- E. P. Wigner, “On the Interaction of Electrons in Metal,” Physical Review, Vol. 46, No. 11, 1934, pp. 1002-1011. doi:10.1103/PhysRev.46.1002
- M. Gell-Mann and K. A. Bruecker, “Correlation Energy of an Electron Gas at High Density,” Physical Review, Vol. 106, No. 2, 1957, pp. 364-368. doi:10.1103/PhysRev.106.364
- R. A. Coldwell-Horsfall and A. A. Maradudin, “ZeroPoint Energy of an Electron Lattice,” Journal of Mathematical Physics, Vol. 1, No.5, 1960, pp. 395-405. doi:10.1063/1.1703670
- D. M. Ceperley and B. J. Alder, “Ground State of the Electron Gas by a Stochastic Method,” Physical Review Letters, Vol. 45, No. 7, 1980, pp. 566-569. doi:10.1103/PhysRevLett.45.566
- S. H. Vosko, L. Wilk and M. Nusair, “Accurate SpinDependent Electron Liquid Correlation Energies for Local Spin Density Calculations: a Critical Analysis,” Canadian Journal of Physics, Vol. 58, 1980, pp. 1200- 1211.
- J. P. Perdew and A. Zunger, “Self-Interaction Correction to Density-Functional Approximations for Many-Electron Systems,” Physical Review B, Vol. 23, No. 10, 1981, pp. 5048-5079. doi:10.1103/PhysRevB.23.5048
- S. Ichimaru, “Strongly Coupled Plasmas: High-Density Classical Plasmas and Degenerate Electron Liquids,” Review of Modern Physics, Vol. 54, No. 4, 1982, pp. 1017- 1059.
- J. P. Perdew and Y. Wang, “Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy,” Physical Review B, Vol. 45, No. 23, 1992, pp. 13244-13249. doi:10.1103/PhysRevB.45.13244
- H. Van Cong, “About a Simple Expression for the Homogeneous Electron Gas Correlation Enery, Accurate at Any Electron Density and Relative Spin Polarization, and Its Applications,” Physica Status Solidi B, Vol. 205, 1998, pp. 543-552. doi:10.1002/(SICI)1521-3951(199802)205:2<543::AID-PSSB543>3.0.CO;2-U
- F. H. Zong, C. Lin and D. M. Ceperley, “Spin Polarization of the Low-Density Three-Dimensional Electron Gas,” Physical Review E, Vol. 66, No. 3, 2002, Article ID: 036703. doi:10.1103/PhysRevE.66.036703
- J. Sun, J. P. Perdew and M. Seidl, “Correlation Energy of the Uniform Electron Gas from an Interpolation between Highand Low-Density Limits,” Physical Review B, Vol. 81, No. 8, 2010, Article ID: 085123. doi:10.1103/PhysRevB.81.085123
- N. H. March, “Kinetic and Potential Energies of an Electron Gas,” Physical Review, Vol. 110, No. 3, 1958, pp. 604-605. doi:10.1103/PhysRev.110.604
- H. Van Cong, “Bandgap Changes in Excited Intrinsic (Heavily Doped) Si and Ge,” Physica B, Vol. 405, No. 4, 2010, pp. 1139-1149. doi:10.1016/j.physb.2009.11.016
- H. Stupp, M. Hornung, M. Lakner, O. Madel and H. V. Löhneysen, “Possible Solution of the Conductibility Exponent Puzzle for the Metal-Insulator Transition in Heavily Doped Uncompensated Semiconductors,” Physical Review Letters, Vol. 71, No. 16, 1993, pp. 2634-2637. doi:10.1103/PhysRevLett.71.2634
Appendix A. Generalized Virial Theorem
If denoting the average kinetic and potential energies by T(rs, ζ) and V(rs, ζ), respectively, the conjunction taken here is then given in the form:
T(rs, ζ) + V(rs, ζ) = E(rs, ζ ). (A1)
From [8], from which we replace the correlation energy by the total energy, the chemical potential for electrons of spin σ is defined by:
 (A2)
(A2)
where sgn σ is +1 for s = ↑ and –1 for s = ↓ .Taking into account Equation (A2), we define the average kinetic energy, expressed in terms of chemical potentials: 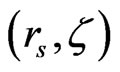
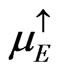 and
and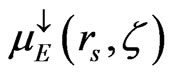 , by [8]:
, by [8]:

which reduces to:
 (A3)
(A3)
Then, replacing the conjunction (A1) in Equation (A3), the virial theorem generalized to the case of 0 ≤ ζ ≤ 1 is proved:
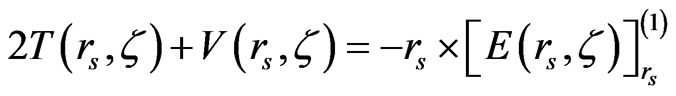 , (A4)
, (A4)
reducing to that given in [12] for ζ = 0. Our numerical calculation indicates that this result (A4) becomes negative for rs ≥ 4.1908 at ζ = 0, for rs ≥ 4.569 at ζ = 0.5, and for rs ≥ 5.653 at ζ =1, meaning that the equilibrium densities of the total energy E(rs, ζ) occur at rsEq = 4.1908, 4.569 and 5.653 for ζ = 0, 0.5 and 1, respectively, suggesting that those values of rsEq increase with increasing ζ.
Appendix B. Useful Expressions γo(∞)(rs, ζ)
The analytic forms for γo(rs, ζ) and γ∞(rs, ζ) as ζ = 0 developed in [7] are now generalized to the case of any ζ. The function γo(rs, ζ) may be related to γ∞(rs, ζ) by [7]:
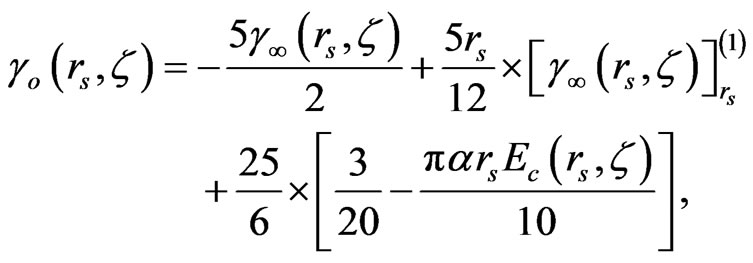 (B1)
(B1)
where the function γ∞(rs, ζ) used to calculate the total energy can be defined by [7]:
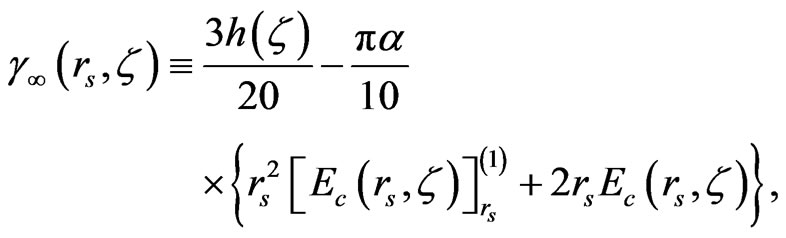 (B2)
(B2)
being replaced in Equation (B1) one finally gets:
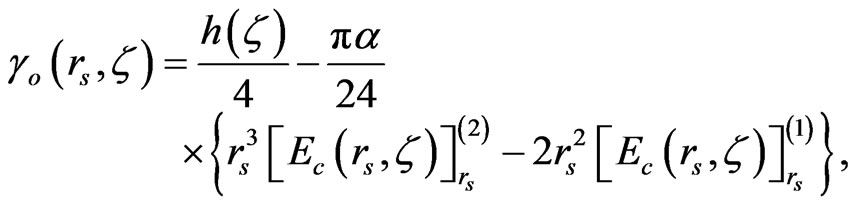 (B2)
(B2)
noting that Equations (B1,B2) for ζ = 0 are well identical to Ichimaru’s results [7].

