Applied Mathematics
Vol.07 No.09(2016), Article ID:66816,14 pages
10.4236/am.2016.79084
Generalization of Uniqueness of Meromorphic Functions Sharing Fixed Point
Harina P. Waghamore, Sangeetha Anand
Department of Mathematics, Jnanabarathi Campus, Bangalore University, Bangalore, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 January 2016; accepted 24 May 2016; published 27 May 2016
ABSTRACT
In this paper, we study the uniqueness problems of entire and meromorphic functions concerning differential polynomials sharing fixed point and obtain some results which generalize the results due to Subhas S. Bhoosnurmath and Veena L. Pujari [1] .
Keywords:
Entire Functions, Uniqueness, Meromorphic Functions, Fixed Point, Differential Polynomials

1. Introduction and Main Results
Let 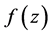 be a non constant meromorphic function in the whole complex plane
be a non constant meromorphic function in the whole complex plane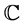 . We will use the following standard notations of value distribution theory:
. We will use the following standard notations of value distribution theory: 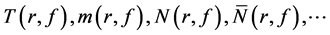 (see [2] [3] ). We de-
(see [2] [3] ). We de-
note by 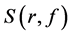 any function satisfying
any function satisfying  as
as 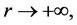 possibly outside of a set with
possibly outside of a set with
finite linear measure.
Let a be a finite complex number and k a positive integer. We denote by  the counting function for zeros of
the counting function for zeros of  in
in 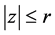 with multiplicity
with multiplicity 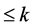 and by
and by  the corresponding one for which multiplicity is not counted. Let
the corresponding one for which multiplicity is not counted. Let  be the counting function for zeros of
be the counting function for zeros of 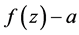 in
in  with multiplicity
with multiplicity 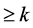 and
and 
counted. Set
Let 

a-points of both 



is not counted. Similarly, we have notation
We say that f and g share a CM (counting multiplicity) if 



In 2004, Lin and Yi [4] obtained the following results.
Theorem A. Let f and g be two transcendental meromorphic functions, 



where h is a non constant meromorphic function.
Theorem B. Let f and g be two transcendental meromorphic functions, 



In 2013, Subhas S. Bhoosnurmath and Veena L. Pujari [1] extended the above theorems A and B with respect to differential polynomials sharing fixed points. They proved the following results.
Theorem C. Let f and g be two non constant meromorphic functions, 



where h is a non constant meromorphic function.
Theorem D. Let f and g be two non constant meromorphic functions, 



Theorem E. Let f and g be two non constant entire functions, 



In this paper, we generalize theorems C, D, E and obtain the following results.
Theorem 1. Let f and g be two non constant meromorphic functions, 



For
For
Theorem 2. Let f and g be two non constant entire functions, 



2. Some Lemmas
Lemma 2.1 (see [5] ). Let 




where 
Lemma 2.2 (see [2] ). Let 




Lemma 2.3 (see [2] ). Let f be a non constant meromorphic function and let k be a non-negative integer, then
Lemma 2.4 (see [6] ). Suppose that 



Lemma 2.5 (see [7] ). Let 


let 





Lemma 2.6 (see [8] ). Let


The following lemmas play a cardinal role in proving our results.
Lemma 2.7 Let f and g be two non constant meromorphic functions. If 


Proof. Applying Nevanlinna’s second fundamental theorem (see [3] ) to

By first fundamental theorem (see [3] ) and (1), we have

We know that,

Therefore, using Lemma 2.3, (2) becomes
Using 

since
This completes the proof of Lemma 2.7.
Lemma 2.8 Let f and g be two non constant entire functions. If 



Proof. Since f and g are entire functions, we have
3. Proof of Theorems
Proof of Theorem 1. By assumption, 


Then, H is a meromorphic function satisfying
By (3), we get
Therefore,

From (6), we easily see that the zeros and poles of H are multiple and satisy

Let

Then, 

We have,

Therefore,
and thus

Now, we discuss the following three cases.
Case 1. Suppose that neither 




Using (8), we note that
since, 

But

Using (14) and (15) in (13), we get
Since f and g share ¥ IM, we have
Using this with (8), we get

If 




Similarly,

Let

By Lemma 2.6, we have
Since
By the first fundamental theorem, we have

we have

where 
From (16)-(21), we get
Using Lemma 2.3, we get

Let
Then



Note that
Simplifying, we get

or

Combining (23) and (24), we get

By 




If 


On integrating, we get

Since

Substituting this in
that is,
From (9), we obtain

Applying Lemma 2.2, to the above equation, we get

Note that,
Using (29), we get

By, Lemmas 2.3, 2.4 and (30), we have
We obtain

Case 2. Suppose that 


Applying Lemma 2.2 to the above equation, we have

By Lemmas 2.3, 2.4 and (32), we have
Using Lemma 2.7, we get

Since
Therefore, 

On integrating, we get

We claim that


We have,
similarly,
Using Lemma 2.4, we have

Thus,

similarly,
Therefore, (36) becomes,
which contradicts

Let 


If h is not a constant, then with simple calculations we get contradiction (refer [9] ). Therefore h is a constant. We have from (40) that


Case 3. Suppose that 

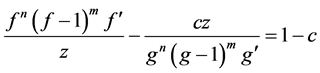
Applying Lemma 2.2 to above equation, we have

Using Lemmas 2.4, 2.3 and (42), we have
Using Lemma 2.7, we get

Since
Therefore
Hence,

Let 


Hence,

Let 





Let 






In the same manner as above, we have similar results for zeros of


By Nevanlinna’s second fundamental theorem, we have from (45), (46) and (49) that,

Similarly,

From (50) and (51), we get
since
This completes the proof of Theorem 1.
Proof of Theorem 2. By the assumption of the theorems, we know that either both f and g are two transcendental entire functions or both f and g are polynomials. If f and g are transcendental entire functions, using 



where k is a non-zero constant. Suppose that

Apply Lemma 2.2 to above equation, we have
Since f is a polynomial, it does not have any poles. Thus, we have
Therefore,

Using Lemmas 2.4, 2.3 and (54), we have
Using Lemma 2.8, we get

since


On Integrating, we get

We claim that


Proceeding as in Theorem 1,
we get
Cite this paper
Harina P. Waghamore,Sangeetha Anand, (2016) Generalization of Uniqueness of Meromorphic Functions Sharing Fixed Point. Applied Mathematics,07,939-952. doi: 10.4236/am.2016.79084
References
- 1. Bhoosnurmath, S.S. and Pujari, V.L. (2013) Uniqueness of Meromorphic Functions Sharing Fixed Point. International Journal of Analysis, 2013, Artical ID: 538027, 12 p.
- 2. Yang, C.-C. and Yi, H.-X. (2003) Uniqueness Theory of Meromorphic Functions, Mathematics and Its Applications. Kluwer Academic Publishers, Dordrecht.
- 3. Yang, L. (1993) Value Distribution Theory. Translated and Revised from the 1982 Chinese Original, Springer, Berlin.
- 4. Lin, W.C. and Yi, H.X. (2004) Uniqueness Theorems for Meromorphic Functions Concerning Fixed-Points. Complex Variables, Theory and Application, 49, 793-806.
- 5. Xu, J.-F., Lü, F. and Yi, H.-X. (2010) Fixed-Points and Uniqueness of Meromorphic Functions. Computers & Mathematics with Applications, 59, 9-17.
- 6. Yang, C.C. (1972) On Deficiencies of Differential Polynomials, II. Mathematische Zeitschrift, 125, 107-112.
http://dx.doi.org/10.1007/BF01110921 - 7. Yi, H.X. (1990) Meromorphic Functions That Share Two or Three Values. Kodai Mathematical Journal, 13, 363-372.
- 8. Frank, G. and Reinders, M. (1998) A Unique Range Set for Meromorphic Functions with 11 Elements. Complex Variables, Theory and Application, 37, 185-193.
- 9. Waghamore, H.P. and Shilpa, N. (2014) Generalization of Uniqueness Theorems for Entire and Meromorphic Functions. Applied Mathematics, 5, 1267-1274.
http://dx.doi.org/10.4236/am.2014.58118




































































