Applied Mathematics
Vol.5 No.6(2014), Article ID:44595,6 pages DOI:10.4236/am.2014.56092
New Applications to Solitary Wave Ansatz
Muhammad Younis1, Safdar Ali2
1Centre for Undergraduate Studies, University of the Punjab, Lahore, Pakistan
2Department of Mathematics, Minhaj University, Lahore, Pakistan
Email: younis.pu@gmail.com, safdarali.mu@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 14 December 2013; revised 14 January 2014; accepted 24 January 2014
ABSTRACT
In this article, the solitary wave and shock wave solitons for nonlinear Ostrovsky equation and Potential Kadomstev-Petviashvili equations have been obtained. The solitary wave ansatz is used to carry out the solutions.
Keywords:Solitary Wave Solitons, Shock Wave Solitons, The Ostrovsky Equation, The Potential Kadomstev-Petviashvili Equation, Solitary Wave Ansatz

1. Introduction
Nonlinear wave phenomena appear in various scientific and engineering fields such as electrochemistry, electromagnetics, fluid dynamics, acoustics, cosmology, astrophysics and plasma physics. See references [1] -[4] .
In recent time, the numerous approaches have been developed to obtain the solutions of nonlinear equations. For example the  -expansion method [5] [6] , the first integral method [7] , the adomian decomposition method [8] , the generalized differential transform method [9] , Jacobi elliptic method [10] , the automated tanhfunction method [11] and the modified simple equation method [12] etc.
-expansion method [5] [6] , the first integral method [7] , the adomian decomposition method [8] , the generalized differential transform method [9] , Jacobi elliptic method [10] , the automated tanhfunction method [11] and the modified simple equation method [12] etc.
Nonlinear wave is one of the fundamental objects of nature and a growing interest has been given to the propagation of nonlinear waves in the dynamical system. The solitary wave ansatz method [13] [14] is rather heuristic and processes significant features that make it practical for the determination of single soliton solutions for a wide class of nonlinear evolution equations. The solitary wave and shock wave solitons have been obtained, using solitary wave ansatz method, for nonlinear Ostrovsky equation and Potential Kadomstev-Petviashvili (PKP) equation, and we clearly see the consistency, which has recently been applied successfully.
The Ostrovsky equation is, a model of ocean currents motion, read as
 (1.1)
(1.1)
where  and
and ![]() are constants. Parameter
are constants. Parameter 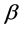 determines the type of dispersion, namely,
determines the type of dispersion, namely,  (negativedispersion) for surface and internal waves in the ocean and surface waves in a shallow channel with an uneven bottom;
(negativedispersion) for surface and internal waves in the ocean and surface waves in a shallow channel with an uneven bottom; 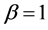 (positive dispersion) for capillary waves on the surface of liquid or for oblique magneto-acoustic waves. Parameter
(positive dispersion) for capillary waves on the surface of liquid or for oblique magneto-acoustic waves. Parameter 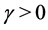 measures the effect of rotation.
measures the effect of rotation.
The Potential Kadomstev-Petviashvili (PKP) equation has been considered in the following manner
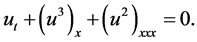 (1.2)
(1.2)
2. Solitary Waves Solitons
In this section, the solitary wave solution or non-topological solution to the Ostrovsky Equation (1.1) and Potential Kadomstev-Petviashvili Equation (1.2) have been found using the following solitary wave ansatz. For this, we have
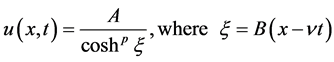 (2.3)
(2.3)
where  is the amplitude of the solitons,
is the amplitude of the solitons, 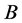 is the inverse width of the solitons and
is the inverse width of the solitons and  is the velocity of the solitary wave.
is the velocity of the solitary wave.
2.1. OS-BBM Equation
From the Equation (2.3), it can be followed
 (2.4)
(2.4)
 (2.5)
(2.5)
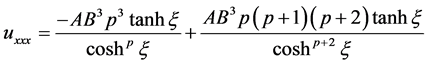 (2.6)
(2.6)
 (2.7)
(2.7)
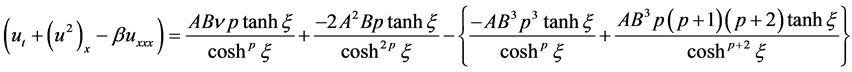
 (2.8)
(2.8)
After substituting Equations (2.4)-(2.8) into (1.1), the following equation is obtained
 (2.9)
(2.9)
It may be noted that  is being calculated when exponents
is being calculated when exponents 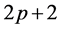 and
and  are equated equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. Thus, we can write
are equated equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. Thus, we can write

Solving the above system of equations and also set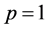 , then it can be written
, then it can be written
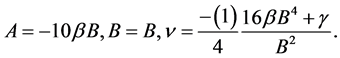
Hence, the solitary wave solution of the OS-BBM equation is given by
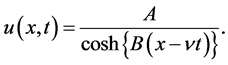 (2.10)
(2.10)
2.2. Potential Kadomstev-Petviashvili (PKP) Equation
It can, thus, be written from Equation (2.3) as follows
 (2.11)
(2.11)
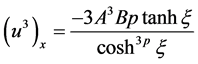 (2.12)
(2.12)
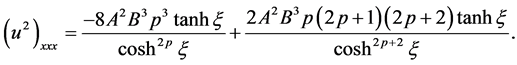 (2.13)
(2.13)
After substituting Equations (2.11)-(2.13) into Equation (1.2), the following equation is obtained
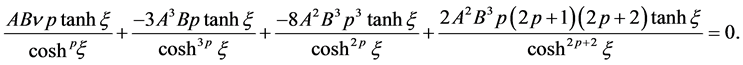 (2.14)
(2.14)
It may be noted that  is being calculated when exponents
is being calculated when exponents  and
and 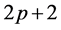 are equated equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. Thus, we can write
are equated equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. Thus, we can write

Solving the above system of equations and also set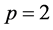 , then it can be written
, then it can be written

Hence, the solitary wave solution of the Potential Kadomstev-Petviashvili (PKP) equation is given by
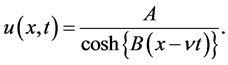 (2.15)
(2.15)
3. Shock Waves Solitons
In this section, the shock wave solution or topological solution to the Ostrovsky Equation (1.1) and Potential Kadomstev-Petviashvili Equation (1.2) have been found using the following solitary wave ansatz. For this, we can write
 (3.16)
(3.16)
where  and
and  are free parameters and are the amplitude and inverse width of the soliton, while
are free parameters and are the amplitude and inverse width of the soliton, while  is the velocity of the soliton. The value of the exponent
is the velocity of the soliton. The value of the exponent ![]() is determined later.
is determined later.
3.1. OS-BBM Equation
Following Equation (3.16), it can be written
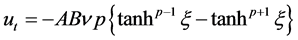 (3.17)
(3.17)
 (3.18)
(3.18)
 (3.19)
(3.19)
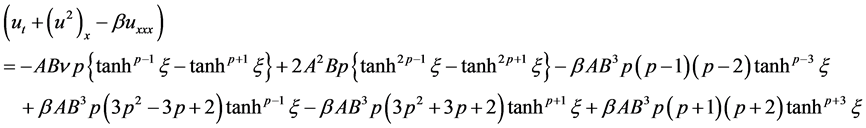
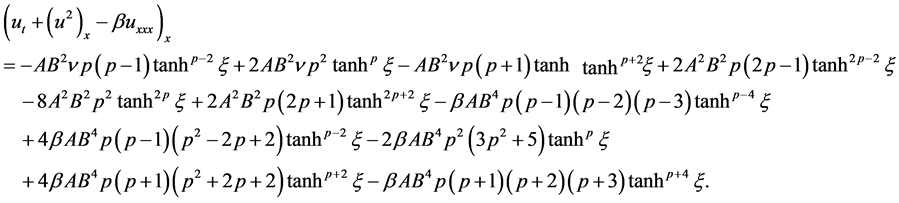 (3.20)
(3.20)
After substituting Equations (3.17)-(3.20) into (1.1), the following equation is obtained
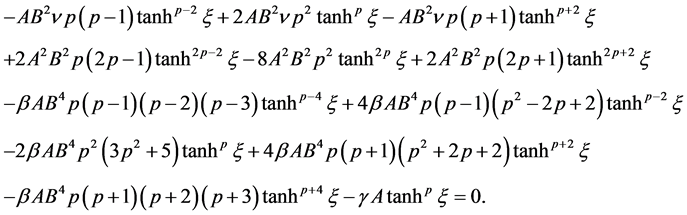
It may be noted that 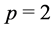 is being calculated when exponents
is being calculated when exponents  and
and 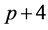 are to be set equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. It can, thus, be written as
are to be set equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. It can, thus, be written as
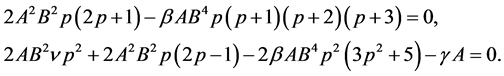
Solving the above system of equations and also set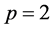 , then it can be written
, then it can be written

Hence, the solitary wave solution of the OS-BBM equation is given by
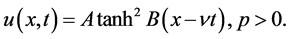 (3.21)
(3.21)
3.2. Potential Kadomstev-Petviashvili (PKP) Equation
From Equation (3.16), it can be followed
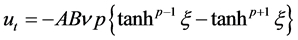 (3.22)
(3.22)
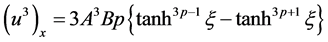 (3.23)
(3.23)
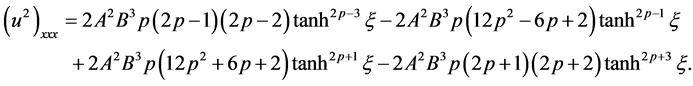 (3.24)
(3.24)
After substituting Equations (3.22)-(3.24) into (1.2), the following equation is obtained
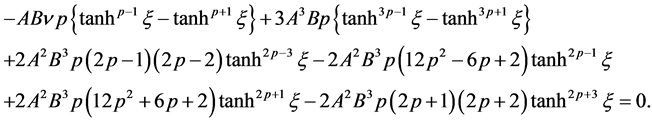
It may be noted that  is being calculated when exponents
is being calculated when exponents 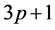 and
and 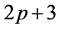 are to be set equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. It can, thus, be written as
are to be set equal to each other. Furthermore, set the coefficients of the linearly independent terms to zero. It can, thus, be written as

Solving the above system of equations and also set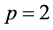 , then it can be written
, then it can be written

Hence, the solitary wave solution of the Potential Kadomstev-Petviashvili (PKP) equation is given by
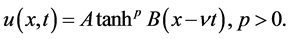 (3.25)
(3.25)
4. Conclusion
The growing interest of nonlinear waves has been given to the propagation in the dynamical system. The solitary wave ansatz method is rather heuristic and processes significant features that make it practical for the determination of single soliton solutions for a wide class of nonlinear evolution equations. The solitary wave and shock wave solitons have been constructed, using the solitary wave ansatz method, for Ostrovsky equation and Potential Kadomstev-Petviashvili equation and we clearly see the consistency, which has recently been applied successfully.
References
- Johnson, R.S. (1970) A Non-Linear Equation Incorporating Damping and Dispersion. Journal of Fluid Mechanics, 42, 49-60. http://dx.doi.org/10.1017/S0022112070001064
- Glöckle, W.G. and Nonnenmacher, T.F. (1995) A Fractional Calculus Approach to Self Similar Protein Dynamics. Biophysical Journal, 68, 46-53. http://dx.doi.org/10.1016/S0006-3495(95)80157-8
- Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- He, J.H. (1999) Some Applications of Nonlinear Fractional Differential Equations and Their Applications. Bulletin of Science and Technology, 15, 86-90.
- Younis, M., Zafar, A., Ul-Haq, K. and Rahman, M. (2013) Travelling Wave Solutions of Fractional Order Coupled Burgers? Equations by
 -Expansion Method. American Journal of Computational and Applied Mathematics, 3, 81-85.
-Expansion Method. American Journal of Computational and Applied Mathematics, 3, 81-85. - Younis, M. and Zafar, A. (2014) Exact Solution to Nonlinear Differential Equations of Fractional Order via (G'/G)-Expansion Method. Applied Mathematics, 5, 1-6. http://dx.doi.org/10.4236/am.2014.51001
- Younis, M. (2013) The First Integral Method for Time-Space Fractional Differential Equations. Journal of Advanced Physics, 2, 220-223. http://dx.doi.org/10.1166/jap.2013.1074
- Wang, Q. (2006) Numerical Solutions for Fractional KDV-Burgers Equation by Adomian Decomposition Method. Applied Mathematics and Computation, 182, 1048-1055. http://dx.doi.org/10.1016/j.amc.2006.05.004
- Liu, J. and Hou, G. (2011) Numerical Solutions of the Spaceand Time-Fractional Coupled Burgers Equations by Generalized Differential Transform Method. Applied Mathematics and Computation, 217, 7001-7008. http://dx.doi.org/10.1016/j.amc.2011.01.111
- Liu, S.K., Fu, Z.T., Liu, S.D. and Zhao, Q. (2001) Jacobi Elliptic Function Expansion Method and Periodic Wave Solutions of Nonlinear Wave Equations. Physics Letters A, 289, 69-74. http://dx.doi.org/10.1016/S0375-9601(01)00580-1
- Parkes, E.J. and Duffy, B.R. (1996) An Automated Tanh-Function Method for Finding Solitary Wave Solutions to Non-Linear Evolution Equations. Computer Physics Communications, 98, 288-300. http://dx.doi.org/10.1016/0010-4655(96)00104-X
- Younis, M. and Zafar, A. (2013) The Modified Simple Equation Method for Solving Nonlinear Phi-Four Equation. International Journal of Innovation and Applied Studies, 2, 661-664.
- Triki, H. and Wazwaz, A.-M. (2011) Dark Solitons for a Combined Potential KdV and Schwarzian KdV Equations with t-Dependent Coefficients and Forcing Term. Applied Mathematics and Computation, 217, 8846-8851. http://dx.doi.org/10.1016/j.amc.2011.03.050
- Bekir, A., Aksoy, E. and Guner, O. (2012) Bright and Dark Soliton Solitons for Variable Cefficient Diffusion Reaction and Modified KdV Equations. Physica Scripta, 85, 35009-35014. http://dx.doi.org/10.1088/0031-8949/85/03/035009

